Sustained acoustic emissions following tensile crack propagation in a crystalline rock

Abstract

We show that simple breakage of a crystalline rock (gabbro) in tension begets further breakage of rock in the area around the first crack that is self-sustaining and spontaneous and that is detected via sustained acoustic emissions (AE). The result is a sequence of AE events that is statistically similar to aftershocks from earthquakes, that scales with the size of the main crack, and that we were able to observe for days following the initial breakage in laboratory-scale experiments. A new model for aftershock generation that is based on residual strain relaxation is shown to be consistent with the observed hyperbolic decay of the event rate with time and with the manner in which the decay law scales with the size of the main rupture.

1 Introduction

Rock breakage has long been associated with microcracking and, in turn, microcracking has long been associated with generation of dynamic events that serve as sources for radiating acoustic waves (Hardy 1972; Kranz 1983). At the laboratory scale this process is known as acoustic emission (AE). Because of its association with microcracking, AE monitoring has played a critical role in fundamental studies of the microcracking processes that precede macroscopic rock failure (Lockner 1993; Zietlow and Labuz 1998). Furthermore, although far less recognized or understood, AE has been observed to continue after the specimen is unloaded. These “AE aftershocks” were firstly observed following uniaxial compression experiments (Scholz 1968). Other authors have observed aftershocks sequences following rock failure in compression in the laboratory and, expanding on the work of Scholz (1968), have observed statistical similarities to earthquake tremors (Davidsen et al. 2007; Goebel et al. 2012; Baró et al. 2013). AE aftershocks have also been observed in recent experiments following the generation of hydraulically-driven cracks (Chitrala et al. 2011; Bunger et al. 2014).

While the mechanisms leading to microcracking/AE production as loading increases prior to failure or as a hydraulically-driven crack propagates are relatively well understood, at least in principle, the mechanism leading to AE generation after the specimen has already failed macroscopically and after loading is removed remains unclear. In the case of sustained AE following unloading after failure in uniaxial compression, Scholz (1968) proposes a model based on the presumed existence of a region of locally fluctuating stresses in the region(s) of the specimen that sustained inelastic deformation during the loading period. In contrast, Chitrala et al. (2011) explain sustained AE after relieving the fluid pressure that drove their laboratory-scale hydraulic fractures as being associated with crushing and/or shearing of asperities on the crack faces as the macroscopic crack closed.

Scholz’s uniaxial compression experiments (Scholz 1968) led to complicated patterns of failure and as a result it is unclear whether the continued AE was due to breakage of intact rock near the fracture tips or if it was actually generated from the vicinity of fully-fractured crack surfaces. On the other hand, Chitrala et al. (2011) provide no analysis in support of their proposed asperity-based model, and since then, the experiments of Bunger et al. (2014) are not consistent with the asperity-based model because they show that AE aftershocks are only generated after the macrocrack is first created and not after its surfaces are separated a second time and it is allowed to close again.

Considering all of these arguments, the mechanical origins of AE aftershocks remain unclear. Hence, we have performed two series of experiments. The first series consists of hydraulic fractures driven by glycerine through laboratory rock specimens. In the second series we created tensile fractures in the same rock material by breaking notched beams in a 3-point bending configuration. In both experimental series, AE was monitored throughout the loading, unloading, and for several hours to several days after the specimens were unloaded and left to rest on a laboratory bench in a temperature controlled laboratory. This paper presents the data from these experiments along with a new model for aftershock generation based on relaxation of residual strain in the vicinity of the main rupture surface. The new model is shown to explain not only the hyperbolic decay of the event rate with time, i.e. Omori’s law (Omori 1894), but also it explains why some of the Omori’s law parameters are observed to scale with the size of the main rupture surface.

2 Experimental procedures

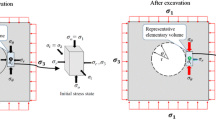
The hydraulic fracturing experiments were conducted by injecting fluid (glycerine) at 0.2 ml/min into an isolated section of a central vertical borehole (16 mm diameter) in $200\times 200\times 120$ mm, specimens prepared from a South Australian gabbro marketed as Adelaide Black Granite (Fig. 1a). No external loading was applied to the specimen and fracture growth was driven by fluid pressure in the wellbore and within the growing hydraulic fracture.

Fig. 1

Sketches of experimental configurations. a Hydraulic fracturing experiments [after Bunger et al. (2014)]. b Notched beam in three point bending experiments. The reaction frame holding the hydraulic piston in b is omitted for clarity and in both cases a nominal crack is included for reference

On the other hand, the notched beam experiments consisted of 3-point bending tests on beams with cross-section of 43 mm high and 24 mm deep. The supports were spaced at a width of 180 mm and centrally located 5 mm deep notches were present on the lower surface of each sample.

For the hydraulic fracturing experiments, acoustic emissions were monitored using an array of 32, 100–900 kHz, 20.3 mm diameter sensors distributed on the six surfaces of the specimens. Events were located based on the first compressional wave arrival at each transducer using the classical Geiger algorithm (Geiger 1910) with collapsing grid search minimization. Location error is calculated from the differences between the measured travel time and the theoretical travel time from the event source to each transducer. The data set presented here is restricted to events located with a RMS error of $<$2 mm. Event magnitudes were estimated based on the mean of the waveform amplitudes measured at each transducer weighted by the distance between the transducer and the event location (Applied Seismology Consultants 2010).

For the notched beam experiments, AE was monitored using an array of 20 transducers of the same kind used for the hydraulic fracturing experiments. Note that the 20.3 mm diameter transducers are relatively large compared with the beam specimens, resulting in not only high sensitivity to low energy events but also location uncertainty that was generally greater than for the hydraulic fracturing experiments. The data set presented here is restricted to events that were located with a RMS error of $<$6 mm.

3 Experimental observations

Figure 2 presents the cumulative events versus time for representative experiments of each type (additional experiments are included in “Appendix 1”. Figure 2 also includes the fluid injection pressure for the hydraulic fracturing experiment and the applied load for the notched beam experiment. As in previous hydraulic fracturing experiments (Chitrala et al. 2011), we observe AE prior to peak pressure, during hydraulic fracture propagation, and after fracture propagation ceases with an increase in aftershock frequency coming after the injection ceases and the fluid pressure is released.

Fig. 2

Evolution of injection pressure (hydraulic fracturing experiment) or loading force (notched beam experiments) along with cumulative AE events, where each event is indicated by an open circle on the pressure curve and the vertical dashed line corresponds to shut-in (isolation from the injection system) for the hydraulic fracturing experiment and the point where the two halves of the beam were separated and placed on a benchtop for the notched beam experiment. a Hydraulic fracturing experiment 1, where the point marked with an asterisk (*) corresponds to tightening of a fitting. b Notched beam experiment 1

The increase in event rate just after the fluid pressure is relieved in the hydraulic fracturing experiments is consistent with the experiments of Chitrala et al. (2011). In order to test the hypothesis that the aftershocks are generated exclusively through crack closure on asperities, in some tests fluid injection was recommenced so as to re-open the hydraulic fracture and to subsequently allow it to close again [as further described in Bunger et al. (2014)]. In doing so, we observed no impact on the aftershock event rate, and thus our results are not consistent with the hypothesis that the aftershocks are due to closure on asperities which should have been suppressed and then rejuvenated by this reopening and closure cycle. Alongside this observed inconsistency between our measurements and the closure on asperities hypothesis, the notched beam experiments demonstrate that aftershocks occur even in the complete absence of interaction between the opposing crack surfaces. In order to avoid any possible interaction, the two halves of the beam were separated and set apart from one another on the laboratory bench top. From this evidence, we contend that the post-unloading events shown in Fig. 2 are not caused by closure on asperities or any other surface-to-surface interaction mechanism.

Recalling that we are presenting only events that are located with an RMS error of ${<}2$ mm for the hydraulic fracturing experiments and ${<}6$ mm for the beam experiments, the experimental data clearly shows that the events are concentrated in the vicinity of the macrocrack surfaces. As expected, there is some scatter around the macrocrack surfaces, which is consistent with previous studies in which this scatter is interpreted to be indicative of the extent of the process zone (e.g. Zietlow and Labuz 1998). There are, however, a few widely scattered events that satisfy the RMS error cutoff, appear to be real-events in terms of waveform, and which nonetheless do not locate in the vicinity of the macrocrack. Hence we present these data although a clear explanation of them is not possible.

Figure 3 presents locations of events for hydraulic fracture experiment 1. Events are distinguished here as pre-peak, indicating they occurred prior to the injection pressure reaching its maximum value, post-peak, indicating they occurred between peak pressure and shut-in, and post shut-in. We observe firstly that the event cloud grows to cover much of the domain eventually occupied by the hydraulic fracture within the minute or so leading up to peak pressure. During the post peak period, the events are distributed all around the nominal fracture surface, indicating that many of these events were not produced from near the fracture’s leading edge. Finally, a three-dimensional inspection confirms the observation in these two view points that the events are more localized around a common plane after shut-in than they were during the propagation that occurred prior to peak pressure. These events are confirmed to cluster around the hydraulic fracture surface by comparison with the surface location ascertained by cutting the block in half after the experiment was complete (Fig. 4).

Fig. 3

Locations of events for hydraulic fracture experiment 1, looking from the top of the specimen (left) and from the South (right). The color scale is in seconds from the time of peak pressure and the small, unfilled circles indicate event locations from the previously displayed time period

Fig. 4

Locations of events for hydraulic fracture experiment 1 in a 20 mm thick North-South section through the center of the block. Locations are superimposed on a photograph corresponding to the mid-plane of the of the 20 mm thick section after the block was cut in half

Similarly, Fig. 5 gives locations of events for beam experiment 1. Events are distinguished here as (from top): Initial loading, the period from about 12–1.5 min prior to failure during which nearly half of the events came from the supports and are associated with the specimen seating under the loading, while the remaining events concentrate along the East-West center line of the specimen where the macroscopic fracture growth eventually occurs; Pre-peak, during which events concentrate along the East-West center line and become particularly localized in the 20 mm or so immediately above the notch just before specimen failure; Post failure, which are the aftershock events that are not included in the reported aftershock data set owing to the fact that the specimen was being manually handled during this time period; Unloaded, during which the specimen halves were sitting separately on the laboratory bench and which comprise the reported aftershock data set. Note that the aftershocks locations in this beam test are concentrated around the crack surface, although apparently less so than prior to specimen failure. This observation, however, should be taken with some caution because the locations are also less accurate during the “unloaded” period owing to the fact that they are only making use of the half of the transducer array that is attached to their respective half of the specimen, whereas prior to failure all transducers in the array could be used for event location purposes.

Fig. 5

Locations of events for beam experiment 1, looking from the top of the specimen (left) and from the South (right). The color scale is in seconds from the time of peak load and the small, unfilled circles indicate event locations from the previously displayed time period

4 Magnitude and event frequency statistics

Past investigations have shown statistical similarities between AE in the laboratory and seismicity associated with earthquakes (Davidsen et al. 2007; Goebel et al. 2012; Baró et al. 2013). These investigations have focused on failure of rocks in compression. Here we show statistical similarity between our experiments for failure of rocks in tension and earthquake statistics.

Firstly, the distributions of magnitudes for earthquake aftershock sequences tend to follow the Gutenberg–Richter law (Gutenberg and Richter 1954; Shcherbakov et al. 2004)

$$\begin{aligned} \log _{10}N(\ge M) =a_{gr}-b M , \end{aligned}$$

(1)

where $N(\ge M)$ denotes the number of events with magnitude greater $M$ and where $a_{gr}$ and $b$ are constants. Often for earthquakes $b\simeq 1$. So also, for our experiments (Fig. 6) the aftershock magnitudes are distributed according to the Gutenberg–Richter law with $b\simeq 1$ for the beam tests and $b=1.6$ and $b=1.9$ for the hydraulic fracturing tests over the time ranges $0<t<1000$ s and $t>1000$ s, respectively.

Fig. 6

Distribution of magnitudes of aftershock events, where the dashed line shows the best fit of the Gutenberg–Richter law (Eq. 1). a, b Hydraulic fracturing experiment 1, showing the distributions for a $0<t<1000$s and b $t>1000$ s wherein it can be seen that as time increases the larger magnitude events cease. c Notched beam experiment 2, where Eq. (1) is fit to the data over the range $-3.5<M<-2$

Secondly, the event frequency for earthquake aftershocks tends to follow an empirical decay law that is given by $\mathrm {d}N/\mathrm {d}t=k/(t+t_0)^a$, where $N$ is the cumulative number of events at time $t$ from the main rupturing event, $t_0$ is a time shift, $k$ is the decay coefficient, and $a\simeq 1$ (Utsu 1961). Integrating with respect to time for the case $a=1$ [Omori’s law, Omori (1894)] gives

$$\begin{aligned} N=k\ln (t+t_0)+c, \end{aligned}$$

(2)

where $c$ is the constant of integration. Figure 7 shows the post unloading cumulative event data along with model predictions using parameters chosen to give a least-squares best-fit between the model and data, noting that here we take $t$ as the time since unloading. The match between Eq. (2) and the data shows that the aftershocks for both types of experiments follow an Omori’s law frequency decay (see additional data in “Appendix 1”). However, there is one modification. For the hydraulic fracturing experiments, we consistently obtain a change in slope at about 1000 s after shut-in and pressure relief. This break in slope is not observed in the aftershocks in the notched beam tests and so its physical origin should be particular to the conditions attained in the hydraulic fracturing experiments. One possibility is that it is associated with the time at which the crack closes, but the origin of this second regime remains the subject of ongoing investigations.

Fig. 7

Cumulative post unloading events (dots) versus the shifted time since unloading along with best-fit prediction (solid lines) based on Eq. (2). a Hydraulic fracturing experiment 1, where the data has been fit with two lines, for $0<t<1000$ s and $t>1000$ s. b Notched beam experiment 1, wherein it is also apparent that the events tend to be temporally clustered

The statistical similarity between the aftershock sequences produced by the two types of experiments also extends to the scaling of the event frequency with the nominal crack area, defined practically as the area of the region circumscribed by the leading edge of the crack. The nominal crack area is obtained here from direct measurements on the specimens after they are cut into 15 mm serial sections once experimentation is completed. Inspection of the best fit values from three hydraulic fracturing experiments and two beam tests (Table 1) indicates that the time shift $t_0$ does not correlate with the area. Nor do the values of the coefficients $k$ and $c$ correlate with the area in the second stage of the hydraulic fracturing aftershocks, $t>1000$ s. However, for the first stage of the hydraulic fracturing aftershocks, $0<t<1000$ s, and for the beam tests, we find that $k$ and $c$ scale with the nominal crack area with a strong correlation, as shown in Fig. 8, thus showing that the event frequency $\mathrm {d}N/\mathrm {d}t$ and its integral scale with the size of the main crack.

Table 1 Parameters giving a best match between Eq. (2, main article) and the data from three hydraulic fracturing experiments (HF) and twe beam tests (B).

5 Residual strain aftershock model

Scholz (1968) suggested that the aftershocks are generated by the time-dependent propagation of microcracks according to a static fatigue failure that is driven by the residual stresses left after propagation of a main crack. While the experiments neither prove nor disprove this theoretical background, here we retain Scholz’s premise that local tensile stresses lead to time-dependent failure of microcracks according to a static fatigue law while proposing that it is useful to consider the residual strain left after unloading to be the fundamental quantity. We are then able to consider the residual stress (i.e. the first principal stress component) $\sigma _r\sim E(N) \varepsilon _r$, where $\varepsilon _r$ is the local residual strain, $N$ is the cumulative number of events, and $E$ is Young’s modulus.

By taking $E$ to be a function of the cumulative number of aftershocks, $N$, we have introduced a relaxation law that can be formalized to rigorously account for the degradation of the elastic modulus in a material with a growing number of microcracks. Based on Salganik’s model (Salganik 1973)

$$\begin{aligned} E\approx E_m\exp \left( -\alpha \frac{N\langle r^3\rangle }{V}\right) , \qquad \alpha =1.64 \pm 9\,\% , \end{aligned}$$

(3)

where $E_m$ is the Young’s modulus of the material between the cracks, $N$ is the number of microcracks, $V$ is the volume of rock affected by aftershock generation, and $\langle r^3\rangle$ is the average cube of the cracks’ radii.

Fig. 8

Best fit values of $k$ and $c$ (Eq. 2) versus the nominal crack area for each experiment, where $r^2$ is the coefficient of determination

This relaxation law replaces Scholz’s ad hoc assumption that each region fails only once and that when it does the stress changes so as to fall outside the range that will ever produce another event. By doing so, we introduce a theory that not only matches the Omori’s law event frequency decay observed in the current experimental data (as Scholz’s theory does as well), but also that naturally expresses the Omori’s law parameters (Eq. 2) in terms of quantities that are rooted in theory, that are in principle independently obtainable, and that will be shown to be consistent with the observed scaling of $k$ and $c$, but not $t_0$, with the size of the main fracture (Fig. 8).

Our proposed model thus consists of:

• 1. The residual strain field, given as a distribution of $\varepsilon _r$, that we assume is left behind after propagation of the main crack.

• 2. A linear relationship between the residual strain field and local first principal stress $\sigma _r$ according to Hooke’s law, $\sigma _r\sim E \varepsilon _r$.

• 3. A relaxation law $E(N)$ (Eq. 3) whereby the elastic modulus decreases with increasing number of microcracks.

• 4. A static fatigue law relating the expected value of the time to local failure (microcracking), which is assumed to be the generative mechanism for acoustic emissions, to the local stress $\sigma _r$ and that, by inversion, expresses the probability that a volume of rock subjected to a certain stress will fail in a given time. These are discussed in detail in “Appendix 2”.

Then, provided that the number of microcracks already generated is much smaller than the number of locations for potential microcrack extension, which we will denote $N_0$, the rate of aftershock generation is given simply by $N_0 p_{\sigma }$, with the probability rate $p_{\sigma }$ taken from an appropriate static fatigue law. With experimental data supporting either a negative exponential or power law (“Appendix 2”), let us choose the power law description of static fatigue, which gives the probability rate

$$\begin{aligned} p_{\sigma }=\frac{1}{\tau _0}\left( \frac{\sigma }{\sigma _m}\right) ^n , \end{aligned}$$

(4)

where $\tau _0$ is the characteristic time of elementary failure, $\sigma _m$ is the stress of microcrack initiation, and exponent $n$ is an experimentally-determined parameter. Combining with Hooke’s law ($\sigma _r\sim E(N) \varepsilon _r$) and the relaxation law (Eq. 3) leads to

$$\begin{aligned} \left\{ {\begin{array}{l} {\frac{{dN}}{{dt}} = \frac{N_0}{\tau _0} \left( \frac{E_m \varepsilon _r}{\sigma _m}\right) ^n \exp \left( \alpha n \frac{N\langle r^3\rangle }{V}\right) } \\ {N|_{t=0} =0 } \\ \end{array}} \right. \end{aligned}$$

(5)

where the initial condition assumes that time is counted from the moment the aftershocks started. The solution is given by Eq. (2), wherein we have

$$\begin{aligned} k= & {} \frac{V}{n\alpha \langle r^3\rangle }, \nonumber \\ c= & {} -k \ln t_0, \nonumber \\ t_0= & {} \frac{\tau _0 V}{\alpha \langle r^3\rangle n N_0}\left( \frac{\sigma _m}{E_m\varepsilon _r}\right) ^{n}. \end{aligned}$$

(6)

Taking, then, $N_0=\rho _c V$ where $\rho _c$ is the density of potential sites for microcracking per unit volume, and further letting $V=A\delta$ where $A$ is the nominal area of the main fracture and $\delta$ is the thickness of the zone affected by residual strain, the analysis predicts that $t_0$ will be independent of the nominal area of the main fracture ($A$), while on the other hand

$$\begin{aligned} k\propto A, \quad c\propto A, \quad \frac{dc/dA}{dk/dA}=-\ln t_0. \end{aligned}$$

(7)

The observed linear scaling of $k$ and $c$ with $A$ for $0<t<1000$s (Fig. 8) is therefore consistent with the theory. Furthermore, for this same time frame, the range of $t_0$ gives $\ln t_0$ in the approximate range of 4–5 (Table 1). Hence, the ratio of the slope of $c$ versus $A$ to the slope of $k$ versus $A$, which is $-4.7$ according to Fig. 8, is in the theoretically-predicted range and there is some promising evidence that the residual strain theory proposed here is able to also shed some light on the origin of the time shift $t_0$ that was originally proposed by Omori (1894) but has not been clearly connected to mechanical processes.

6 Conclusions

Tensile breakage of rock is observed to produce aftershocks that are spatially clustered around the crack surface and that cannot be attributed to crack closure. These aftershocks sequences are statistically similar between hydraulic fractures and notched beam tests; in both cases the cumulative events after unloading follow Omori’s law with the coefficients, but not the time shift, scaling with the nominal crack area. In this regard the experiments are extremely consistent from one test to the next, that is to say, the repeatability for the crystalline rock and experimental configurations used in this study was very good.

The observations from these experiments are consistent with an aftershock mechanism based on static fatigue driven by a stochastic distribution of residual strain remaining after unloading. Adding theoretical considerations to the interpretation of the experimental results, we propose ongoing rock mechanics research that aims at quantifying the impacts of environment, loading conditions before and after rupture, and of rupture surface size and detailed geometry on these aftershock sequences. This proposed direction of research will provide unique insight into stochastic time dependent rock fracture mechanisms underlying seismic and engineering hazards associated with the long-term stability of rocks under stress.

Appendices

Appendix 1: Additional experimental data

The main article presents a selection of the experimental data. In its support, we here provide a compendium of data from the experiments.

Figure 9 gives the evolution of injection pressure (hydraulic fracturing experiment) or loading force (notched beam experiments) along with cumulative AE events for the experiments not included in the main article. Consistent with the data in the main article, we observe AE prior to peak pressure, during hydraulic fracture propagation, and after fracture propagation ceases with an increase in aftershock frequency coming after the injection ceases and the fluid pressure is released.

Fig. 9

Evolution of injection pressure (hydraulic fracturing experiment) or loading force (notched beam experiments) along with cumulative AE events for the experiments not included in the main body of the paper. For clarity, only the first 6000 s after peak pressure/load is shown. Open circles superimposed on the pressure record correspond to AE events and the vertical dashed line corresponds to shut-in (isolation from the injection system) for the hydraulic fracturing experiments and the point where the two halves of the beam were separated and placed on a benchtop for the notched beam experiments. a Hydraulic fracturing experiment 2, where the point indicated by the asterisk (*) corresponds to the first event, subsequent tightening of the fitting resulting in a slight pressure decrease, and continued pressurization with a reduction of the injection rate from 1 to 0.2 ml/min. b Hydraulic fracturing experiment 3, which was performed in the same block and 20 mm above experiment 2. c Notched beam experiment 2

Figure 10 presents cumulative post unloading events versus the shifted time since unloading along with best-fit prediction based on frequency decay following the Omori law for the experiments not included in the main body of the paper. The observations are consistent with Fig. 7 in the main article, namely: (1) aftershocks for both types of experiments follow an Omori’s law frequency decay, (2) for the hydraulic fracturing experiments, we consistently obtain a change in slope at about 1000 s after shut-in and pressure relief.

Fig. 10

Cumulative post unloading events versus the shifted time since unloading along with best-fit prediction based on frequency decay following the Omori law for the experiments not included in the main body of the paper. For the hydraulic fracturing experiments the data have been fit with two lines, for $0<t<1000$ s and $t>1000$ s. a Hydraulic fracturing experiment 2. b Hydraulic fracturing experiment 3, which was performed in the same block and 20 mm above experiment 2. c Notched beam experiment 2, wherein it is apparent that the events tend to be temporally clustered

Appendix 2: Static fatigue laws

It is usually assumed (Scholz 1968) that the aftershocks are caused by local fractures (microcracks) of a particular type generated with time under subcritical stress—the stress below the failure stress. This phenomenon called static fatigue or delayed failure and is usually described by two types of laws: the exponential law and the power law.

The exponential law was developed by Zhurkov in 1965 [see reprint in Zhurkov (1984)] in the frame of his theory of kinetic fracture. It is assumed that the delayed failure is caused by thermal-fluctuation mechanism and the average life time of a sample loaded to stress is determined by the Arrhenius-type law

$$\begin{aligned} \tau =\tau _0\exp \left[ \frac{U_0-\gamma \sigma }{\hat{k}T}\right] \end{aligned}$$

(8)

where $\tau _0$, $U_0$ and $\gamma$ are material parameters: the characteristic time of elementary failure, the activation energy and the parameter characterizing the mechanical properties of the material, respectively (Kuksenko et al. 1996), $\hat{k}$ is Boltzman’s constant, and $T$ is the absolute temperature.

We now determine the probability of failure under the given stress. We note that the average time before failure referred to in Eq. (8) is the lifetime averaged over a number of independently loaded samples. In this case the average lifetime is $\tau =1/p_{\sigma }$, where $p_{\sigma }$ is the probability of sample failure under stress $\sigma$ during time $\tau _0$ (the probability rate). From here,

$$\begin{aligned} p_{\sigma }=\frac{1}{\tau _0}\exp \left[ -\frac{U_0-\gamma \sigma }{\hat{k}T}\right] \end{aligned}$$

(9)

Scholz (1968) used a similar form of static fatigue law in his analysis.

On the other hand, the power law has been found empirically for different types of loading and different brittle materials and rocks. It is usually refereed to in relation with the effect of environment such as moisture [see review by Gy (2003)]. It can be expressed as

$$\begin{aligned} \tau =\tau _0\left( \frac{\sigma }{\sigma _m}\right) ^{-n} \end{aligned}$$

(10)

Here $\tau _0$ is the characteristic time of elementary failure, $\sigma _m$ is the stress of microcrack initiation, and exponent $n$ is an experimentally-determined parameter. Similar to Eq. (9), the probability of sample failure under stress $\sigma$ during time $\tau _0$ (probability rate) using the power law of static fatigue is

$$\begin{aligned} p_{\sigma }=\frac{1}{\tau _0}\left( \frac{\sigma }{\sigma _m}\right) ^n \end{aligned}$$

(11)

The static fatigue behavior of the South Australian gabbro was tested using un-notched beams that were loaded in 3-point bending (Fig. 11a) up to a fixed load that was held until the specimen ruptured. The loading was ramped up over a period of 12 s. Figure 11b, c shows the empirical relationship between $\langle t \rangle$ and $\sigma$, where the stress $\sigma$ is given for this experimental configuration by $\sigma =3 P L/(2u d^2)$, where $P$ is the applied load, $L$ is the span between the two lower supports, and $d$ and $u$ are the specimen thicknesses measured in the direction parallel to and normal to loading, respectively. From these results it is clear that under tensile loading (produced in this case by bending), the relationship between the time to failure and the applied stress can be equally well-described as negative exponential (Fig. 11b) or power-law (Fig. 11b).

We conclude that in spite of the difference in mathematical form between the two probability rate laws embodied by Eqs. (9) and (11), existing experimental data is insufficient to judge which more accurately describes the behavior of rocks (Botvina (e.g. 1999) and Fig. 11). Following the route of Scholz (1968) one can obtain Omori’s law using the exponential static fatigue law (Eq. 9), while on the other hand, the analysis in the main paper shows that the power law relationship leads to Omori’s law when one makes a different assumption to Scholz (1968) regarding the relaxation behavior of the rock during microcrack generation.

Fig. 11

The static fatigue behavior of the South Australian gabbro, showing a the experimental setup, b empirical negative exponential relationship between $\langle t \rangle$ and $\sigma$, and c empirical power-law relationship between $\langle t \rangle$ and $\sigma$