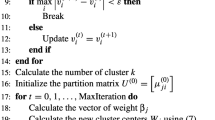1 Introduction

In the literature on data analysis, a great deal of attention is paid to statistical methods for interval-valued data, in different research areas. See, e.g., Denoeux and Masson (2000), Coppi and D’Urso (2002), D’Urso and Giordani (2004, 2006), Guru et al. (2004), Carvalho and Lechevallier (2009), Leite et al. (2012), Duarte Silva and Brito (2015).

In particular, in a classical cluster analysis framework different interesting methods have been suggested. Gowda and Diday (1991) proposed a clustering method for symbolic data. Guru et al. (2004) proposed a similarity measure for compare interval-valued data and a modified agglomerative method for clustering symbolic data. Carvalho et al. (2006) proposed a partitional dynamic clustering method for interval data based on adaptive Hausdorff distances. Carvalho and Lechevallier (2009) suggested clustering methods for interval data based on single adaptive distances. Recently an interesting line of research has focused on clustering of interval-valued data based on fuzzy approaches (Carvalho and Tenório 2010) and, in particular, on robust fuzzy clustering methods capable to neutralize the disruptive effects of outlier interval-valued data (D’Urso and Giordani 2006; D’Urso et al. 2015b. For an overview on different robust approaches to fuzzy clustering, refer to D’Urso and De Giovanni (2014).

In this regards, following a noise approach, D’Urso and Giordani (2006) proposed a robust Fuzzy C-means clustering for interval-valued data in which the outliers are assigned to the so-called noise cluster. Recently, D’Urso et al. (2015b) suggested a robust Fuzzy C-medoids clustering based on the trimmed approach, i.e. the clustering procedure is applied to the data after discarding a fixed fraction of outlying data. The “optimum” percentage of data discarded in the clustering process and, thus, not considered in the optimization problem, is determined combining a validity criterion with the trimming algorithm. Starting from the whole data set and having fixed a minimum retention percentage of the objects (\(\ge \)50 %), the number of clusters and a trimming step, the stopping rule corresponds to the greatest improvement of the validity criterion (Kim et al. 1996; D’Urso et al. 2015b).

In this paper, following the so-called metric approach, we propose a robust fuzzy version of the Partitioning Around Medoids (PAM) for interval-valued data. In particular, our clustering method inherits the advantages of the PAM clustering approach and of the fuzzy theory (D’Urso et al. 2015b) and it is capable to neutralize the negative effects of possible outliers in the dataset by considering a suitable robust metric, i.e. an exponential transformation of the Euclidean distance between interval-valued data.

The paper is organized as follows. In Sect. 2, we describe the robust fuzzy clustering for interval-valued data belonging to the metric approach. In Sect. 3, we present the result of a simulation study while in Sect. 4 we apply our method to two real world cases. In Sect. 5 some final remarks conclude the paper.

2 A robust fuzzy partitioning around medoids method for interval-valued data

There are different real cases in which the empirical information is imprecise, i.e., it is represented by intervals. In particular, we can distinguish the following situations:

  • Interval-valued data may occur due to a lack of knowledge, that is when the true value of a variable is unknown and only an interval of values including the true value is available. Thus, the available information is imprecise and therefore cannot be correctly expressed by means of a single value.

  • Interval-valued data may arise as the result of aggregating huge databases, which are impossible, or at least very difficult, to analyse in the original form.

  • The data are intrinsically interval-valued, i.e, the phenomena are naturally explained by using intervals. Examples are the monthly temperature in meteorological stations or the daily rate of exchange between euro and dollar or euro and sterling. For example, in case of daily temperatures or daily air pollution levels registered in different places or the mineral concentrations of food items, it could be more interesting to consider the minimum and maximum values registered than the average ones, because they offer more detailed information about the examined phenomenon taking into account the variability of the features involved. Data in which each observation is an interval of values –indicated by a minimum and a maximum– are called interval-valued data. Notice that the intervals not necessarily pertain to the observed maxima and minima, but, for instance, they could pertain to interquartile intervals, or to the middle 90 % the scores (Giordani and Kiers 2004).

An interval-valued datum can be formalized as \(x_{ij}=[\underline{x}_{ij},\overline{x}_{ij}],\,i=1,\ldots ,I;\, j=1,\ldots ,J\), where \(x_{ij}\) represents the j-th interval-valued variable observed on the i-th object; \(\underline{x}_{ij}\) and \(\overline{x}_{ij}\) denote, respectively, the lower and upper bounds of the interval. Each object is represented geometrically by a hyperrectangle in \(\mathfrak {R}^j\) having \(2^J\) vertices. The \(2^J\) vertices correspond to all the possible (lower bound, upper bound) combinations. In particular, in \(\mathfrak {R}\;(J=1)\) the generic object is represented by a segment; in \(\mathfrak {R}^2\;(J=2)\), it is represented by a rectangle with \(2^2=4\) vertices, and so on (Cazes et al. 1997).

Alternatively, an interval valued datum can be represented in terms of its midpoint (center), \(m_{ij}=\frac{\overline{x}_{ij}+\underline{x}_{ij}}{2},\,i=1,\ldots ,I;\, j=1,\ldots ,J\), and of its radius (spread), \(r_{ij}=\frac{\overline{x}_{ij}-\underline{x}_{ij}}{2},\,i=1,\ldots ,I;\, j=1,\ldots ,J\). In this way, the lower and upper bounds of the interval-valued datum can be obtained as \(m_{ij}-r_{ij}\) and \(m_{ij}+r_{ij}\), respectively.

Thus, by considering the previous reformulation of the interval-valued data, we have: \(x_{ij}=(m_{ij},r_{ij});\;i=1,\ldots ,I;\;j=1,\ldots ,J\). Note that the center-radius representation is simple and convenient because the range is a common measure of variability of a random variable and it is often employed for estimation purposes in various empirical applications.

Interval-valued data can be corrupted by noise and outliers. In particular, we can distinguish three possible types of outlier interval-valued data, i.e. outlier interval-valued data with outlier midpoint (center) (see, e.g., Fig. 1, case 1), with outlier radius (spread) (see, e.g., Fig. 1, case 2), with outlier midpoint and outlier radius (see, e.g., Fig. 1, case 3).

Fig. 1
figure 1

Examples of different types of outlier interval-valued data in \(\mathfrak {R}^2\)

Full size image

In order to deal with the above types of outlier, we propose a fuzzy clustering method based on a robust metric.

Let \(\{\mathbf {x}_1=(\mathbf {m}_1, \mathbf {r}_1), \ldots , \mathbf {x}_i=(\mathbf {m}_i, \mathbf {r}_i),\ldots , \mathbf {x}_I=(\mathbf {m}_I,\mathbf {r}_I)\}\) be a set of I vector objects (data matrix) and \(\{\widetilde{\mathbf {x}}_1 = (\widetilde{\mathbf {m}}_1, \widetilde{\mathbf {r}}_1), \ldots , \widetilde{\mathbf {x}}_c=(\widetilde{\mathbf {m}}_c, \widetilde{\mathbf {r}}_c), \ldots ,\widetilde{\mathbf {x}}_C =(\widetilde{\mathbf {m}}_C,\widetilde{\mathbf {r}}_C)\}\) a subset of the previous set with cardinality C, where \(\widetilde{\mathbf {m}}_c\) and \(\widetilde{\mathbf {r}}_c\) denote, respectively, the midpoint and radius vectors of the c-th medoid. The Fuzzy C-medoids clustering model for interval-valued data with exponential distance (ExpFCMd-ID) can be formalized as follows:

$$\begin{aligned} \begin{aligned}&\min :\, \sum \limits _{i=1}^{I}\sum \limits _{c=1}^{C}u_{ic}^m {}_{exp}D^2(\mathbf {x}_{i},\widetilde{\mathbf {x}}_{c})\\&\qquad =\sum \limits _{i=1}^{I}\sum \limits _{c=1}^{C}u_{ic}^m \left[ 1-\exp \left\{ -\beta \left( \sum \limits _{j=1}^{2^J} \Vert (\mathbf {m}_{i}+\mathbf {r}_{i}*\mathbf {h}_{\nu })- (\widetilde{\mathbf {m}}_{c}+\widetilde{\mathbf {r}}_{c}*\mathbf {h}_{\nu })\Vert ^2 \right) \right\} \right] \\&\qquad =\sum \limits _{i=1}^{I}\sum \limits _{c=1}^{C}u_{ic}^m \left[ 1-\exp \left\{ -\beta \left( 2^J\Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c}\Vert ^2+ 2^J\Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{c}\Vert ^2 \right) \right\} \right] \\&\qquad \approx \sum \limits _{i=1}^{I}\sum \limits _{c=1}^{C}u_{ic}^m \left[ 1-\exp \left\{ -\beta \left( \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c}\Vert ^2+\Vert \mathbf {r}_{i}- \widetilde{\mathbf {r}}_{c}\Vert ^2\right) \right\} \right] \\&\text {s.t: }\,\sum _{c=1}^{C}u_{ic}=1,\quad u_{ic}\ge 0 \end{aligned} \end{aligned}$$
(1)

where \({}_{exp}D^2(\mathbf {x}_{i},\widetilde{\mathbf {x}}_{c})\) is the squared exponential distance between \(\mathbf {x}_i=(\mathbf {m}_i, \mathbf {r}_i)\) and \(\widetilde{\mathbf {x}}_c=(\widetilde{\mathbf {m}}_c, \widetilde{\mathbf {r}}_c)\) (Wu and Yang 2002; D’Urso and Giordani 2004); the symbol \(*\) is the Hadamard product, that is the element-wise product of two matrices (vectors) of the same order; the vectors \(\mathbf {h}_{\nu },\,\nu =1,\ldots ,2^J\) help us to define every vertex of the hyper-rectangle associated to each object separately, since their elements are equal to \(\pm 1\) in order to refer exactly to every vertex; \(u_{ic}\) represents the fuzzy membership of the i-th object to the c-th cluster; \(m>1\) is a weighting exponent that controls the fuzziness of the partition; \(\beta \) is a suitable parameter (positive constant) determined according to the variability of the data.

As for the squared exponential distance \({}_{exp}D^2(\mathbf {x}_{i},\widetilde{\mathbf {x}}_{c})\), we use the exponential version (Wu and Yang 2002) of the distance measure for interval-valued data proposed by D’Urso and Giordani (2004) and successively adopted by D’Urso and Giordani (2006) and D’Urso et al. (2015b). Notice that the exponential distance was adapted to the case of imprecise data by D’Urso and De Giovanni (2014). The exponential distance is a weighted distance that assigns different weights to each data point, according to whether a data point is noisy or not and thus it is more robust to the presence of outliers. In fact, the exponential distance assigns small weights to outliers and larger weights to those points that are more compact in the data set.

The membership degrees in (1) can be obtained heuristically in many different ways. For instance, following Krishnapuram et al. (2001), we consider the Lagrangian function:

$$\begin{aligned} \begin{aligned} L_m(u_{ic},\lambda )&= \sum _{i=1}^{I}\sum _{c=1}^{C}u_{ic}^m {}_{exp}D^2(\mathbf {x}_{i},\widetilde{\mathbf {x}}_{c})- \lambda \left( \sum _{c=1}^{C}u_{ic}-1\right) \\&=\sum _{i=1}^{I}\sum _{c=1}^{C}u_{ic}^m \left[ 1-\exp \left\{ -\beta \left( \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c}\Vert ^2+\Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{c}\Vert ^2\right) \right\} \right] - \lambda \left( \sum _{c=1}^{C}u_{ic}-1\right) \end{aligned} \end{aligned}$$
(2)

and, by taking the partial derivatives and setting them to 0 we obtain:

$$\begin{aligned}&\displaystyle \frac{\partial L_m(\mathbf {u}_i,\lambda )}{\partial u_{ic}}=0 \, \Leftrightarrow \, mu_{ic}^{m-1} \left[ 1-\exp \left\{ -\beta \left( \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c}\Vert ^2+\Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{c}\Vert ^2\right) \right\} \right] -\lambda =0&\nonumber \\\end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle \frac{\partial L_m(\mathbf {u}_i,\lambda )}{\partial \lambda }=0\, \Leftrightarrow \, \sum _{c=1}^{C}u_{ic}-u=0.&\end{aligned}$$
(4)

From (3) we obtain:

$$\begin{aligned} u_{ic}=\left( \frac{\lambda }{m \left[ 1-\exp \left\{ -\beta \left( \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c}\Vert ^2+\Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{c}\Vert ^2\right) \right\} \right] }\right) ^{\frac{1}{m-1}} \end{aligned}$$
(5)

and, by substituting (5) in (4), with some algebra:

$$\begin{aligned} \left( \frac{\lambda }{m}\right) ^{\frac{1}{m-1}}=\frac{1}{\sum _{c=1}^{C}\left( \frac{1}{\left[ 1-\exp \left\{ -\beta \left( \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c}\Vert ^2+\Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{c}\Vert ^2\right) \right\} \right] }\right) ^{\frac{1}{m-1}}}. \end{aligned}$$
(6)

Finally, substituting (6) in (5) we obtain the iterative solutions:

$$\begin{aligned} u_{ic}= \frac{1}{\sum \limits _{c'=1}^{C} \left[ \frac{ 1-\exp \left\{ -\beta \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c}\Vert ^2+\Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{c}\Vert ^2 \right\} }{ 1-\exp \left\{ -\beta \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{c'}\Vert ^2+\Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{c'}\Vert ^2 \right\} }\right] ^{\frac{1}{m-1}}}. \end{aligned}$$
(7)

Notice that when the objective function (1) is minimized, the subset \(\widetilde{\mathbf {X}}\) corresponding to the solution provides a fuzzy partition via (7). However, the objective function (1) cannot be minimized by means of the alternating optimization algorithm, because the necessary conditions cannot be derived by differentiating it with respect to the medoids. Nonetheless, following Fu’s heuristic algorithm for a crisp version of the objective function in (1), a fuzzy clustering algorithm to obtain a local optimal solution can be retrieved (Krishnapuram et al. 2001). The steps of our clustering procedure are shown in Algorithm 1.

figure a

The role of the parameter \(\beta \) is crucial both for the distance and for the detection of the membership degrees of each unit to each cluster. Figure 2 shows the effect of increasing values of \(\beta \) on the exponential distance (the 45\(^\circ \) dotted line represents the Euclidean distance).

First, it should be noted that the exponential distance is bounded by 1. Second, as the value of \(\beta \) increases, the distance tends more rapidly to its maximum value. Hence, if \(\beta \) is too high, in the classification process each unit is a singleton, since it has no neighbours.

Fig. 2
figure 2

Effect of \(\beta \) on the exponential distance \({}_{exp}D(\mathbf {x}_{i},\mathbf {x}_{j})\)

Full size image

Figure 3 shows different membership curves for different values of \(\beta \) obtained with the ExpFCMd-ID model in the case of two clusters with midpoint of the medoids equal to 0.5 and 0.6, respectively. The curve with circle points represents the membership degrees obtained with the Fuzzy C-medoids clustering model for interval-valued data (FCMd-ID, D’Urso et al. 2015b). If \(\beta \) is very small the ExpFCMd-ID membership curve is very close to the FCMd-ID membership curve, but tends to 0.5 more rapidly as the distance with respect to the medoids increases. As \(\beta \) increases, even for rather small value of \(\beta \), like \(\beta =1\), the ExpFCMd-ID membership curve is very different from to the FCMd-ID membership curve, and it assigns membership close or equal to 0.5 to data that are only slightly far from the midpoint medoids.

Fig. 3
figure 3

Effect of the parameter \(\beta \) on the membership degrees (7)

Full size image

Based on the behaviour of the distance and of the membership degrees for varying values of \(\beta \), and following Wu and Yang (2002), we set \(\beta \) as the inverse of a measure of the variability of the data:

$$\begin{aligned} \beta = \left[ \frac{\sum _{i=1}^{I}D(\mathbf {x}_i,\widetilde{\mathbf {x}}_q)^2}{I} \right] ^{- 1}= \left[ \frac{\sum _{i=1}^{I}\left( \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{q}\Vert ^2+ \Vert \mathbf {r}_{i}-\widetilde{\mathbf {r}}_{q}\Vert ^2\right) }{I} \right] ^{- 1} \end{aligned}$$
(8)

where

$$\begin{aligned} \widetilde{\mathbf {x}}_q=(\widetilde{\mathbf {m}}_q,\widetilde{\mathbf {r}}_q): q={\mathop {\hbox {argmin}}\limits _{1\le i\le I}} \sum _{i'=1}^{I}\left( \Vert \mathbf {m}_{i}-\widetilde{\mathbf {m}}_{i'}\Vert ^2+\Vert \mathbf {r}_{i}- \widetilde{\mathbf {r}}_{i'}\Vert ^2\right) \end{aligned}$$

i.e., \(\widetilde{\mathbf {x}}_q=(\widetilde{\mathbf {m}}_q,\widetilde{\mathbf {r}}_q)\) is the unit closest to all other units.

By looking at Fig. 3, if \(\beta \) is large (low variability) the model based on the exponential distance assigns membership degrees values approximately equal to 0.5 to all the units that are not close to the medoids. The case of low variability of data is consistent with the presence of well-separated clusters, and each unit that is not close to the medoids is likely to be an outlier. On the contrary, if \(\beta \) is small (large variability) the model based on the exponential distance has a behaviour similar to the non-robust FCMdC-ID model, when data are not far away from the medoids, but tends to assign membership degrees approximately equal to 0.5 for units that are distant from the medoids. This case is compatible with the situation in which there are overlapping clusters, but also with the case in which there are well-separated clusters in a very noisy environment, i.e. with a large fraction of data that are outliers with respect to the well-separated clusters.

More in general, when there are C clusters ExpFCMd-ID assigns membership degrees approximately equal to \(1/C (c=1,\ldots ,C)\).

See Wu and Yang (2002) for further insights on the robustness of the exponential distance.

3 A simulation study

To investigate the performance of ExpFCMd-ID, a simulation study has been carried out. The proposed model has also been compared with other fuzzy clustering models for interval-valued data, the Fuzzy C-medoids (FCMd-ID, D’Urso et al. 2015b), and two robust models, the Trimmed Fuzzy C-medoids (TrFCMd-ID, D’Urso et al. 2015b), and the Noise Cluster-based Fuzzy C-medoids (NcFCMd-ID), which is the PAM-based version of the Noise Cluster-based Fuzzy C-means model for interval-valued data (NcFCM-ID) proposed by D’Urso and Giordani (2006). Notice that we consider the NcFCMd-ID model to draw a comparison between PAM-based model, since this approach is inherently slightly more robust than the k-means based approach (García-Escudero and Gordaliza 2005).

Three data generation scenarios have been considered. In each scenario the simulated dataset is constructed in such a way that two well-separated clusters (\(C=2\)) are generated.

In the centers scenario, the radii of the interval-valued data are all randomly generated from U[0, 1] whereas the centers of the data belonging to the first cluster (I / 2 observations) are drawn from a U[0, 1] and those belonging to the second cluster (I / 2 observations) from a U[1.5, 2.5]. Thus, in the centers scenario, the observation objects are distinguished with respect to the values of the centers.

In the spreads scenario, the centers of the interval-valued data are randomly generated from a U[0, 1], whereas the radii of the interval-valued data belonging to the first cluster (I / 2 observations) are drawn from a U[0, 1] and those belonging to the second cluster (I / 2 observations) from a U[1.5, 2.5]. Therefore, in the spreads scenario, the observation objects are distinguished with respect to the radii.

Finally, in the centers and spreads scenario, the centers and the radii of the interval-valued data belonging to the first cluster (I / 2 observations) are all randomly generated from U[0, 1], whereas the centers and the radii belonging to the second cluster (I / 2 observations) are drawn from a U[1.5, 2.5].

Each simulated dataset is composed by eighty objects (\(I=80\)) and two interval-valued variables (\(J=2\)).

For the purpose of evaluating the robustness of the proposed model in presence of outliers, three different percentages of outliers (10, 20 and 30 %) have been added to the 80 objects, thus yielding to three datasets for each scenario. In the centers scenario, the centers of the outliers are generated from a Gaussian distribution N(4.5, 2) and the values of the radii from a U[0, 1]; in the spreads scenario, the radii of the outliers are generated from a Gaussian distribution N(4.5, 2) and the values of the centers from a U[0, 1]; in the centers and spreads scenario, both the centers and the radii of the outliers are generated from a Gaussian distribution N(4.5, 2).

For each scenario the data generating process has been replicated 100 times.

Table 1 Data and outlier generation processes for the three scenarios
Full size table

The data generation processes are summarized in Table 1. The expected values of the random generated variables for the three scenarios are depicted in Fig. 4. For the sake of completeness, on the x- and y-axis are reported the expected values of the midpoints, while the minimum and maximum of the expected values of the two interval-valued variables are reported near the vertices of the rectangles representing the variables in \(\mathfrak {R}^2\).

Fig. 4
figure 4

Expected values of the interval-valued random variables

Full size image

The main goal of this simulation study is to evaluate the proposed model with respect to two aspects:

  1. 1.

    the capability to identify the two equal sized and well-separated clusters generated according to the schemes illustrated in Table 1 when a given percentage of outliers is added to the dataset;

  2. 2.

    the ability to identify cluster prototypes which are not too distant from the “ideal” centers, given by the expected values of the underlying generative random variables, irrespective of the number of outliers added to the dataset.

In particular, to evaluate the robustness of a clustering model with respect to misclassification in the presence of outliers, the Fuzzy Rand Index (FRI, henceforth) (Anderson et al. 2010) has been used. FRI allows to compare the “theoretical” hard partitions in two clusters generated with the generation processes illustrated in Table 1 with the fuzzy partitions obtained. FRI ranges between 0 and 1. The closer FRI is to 1, the better is the classification performance of the model.

To assess the robustness with respect to prototype detection in the presence of outliers, we considered the index of robustness detection, rd, illustrated in D’Urso et al. (2015b) that compares the medoids obtained in the presence of outliers with the ideal centers. The index in case of \(\alpha \cdot I\) outliers (\(0<\alpha <1\)) is defined as follows:

$$\begin{aligned} \begin{aligned}&rd((\tilde{x}_{1,ideal},\tilde{x}_{2,ideal}),(\tilde{x}_{1,\alpha \cdot I},\tilde{x}_{2,\alpha \cdot I}))\\&=\frac{d(\tilde{x}_{1,ideal},\tilde{x}_{1,\alpha \cdot I})+d(\tilde{x}_{2,ideal},\tilde{x}_{1,\alpha \cdot I})+d(\tilde{x}_{1,ideal},\tilde{x}_{2,\alpha \cdot I})+d(\tilde{x}_{2,ideal},\tilde{x}_{2,\alpha \cdot I})}{2 \cdot d(\tilde{x}_{1,ideal},\tilde{x}_{2,ideal})} \end{aligned} \end{aligned}$$
(9)

where \(\tilde{x}_{c,\alpha \cdot I}\) denotes the medoid of cluster c in the case of \(\alpha \cdot I\) outliers, \(\tilde{x}_{c,ideal}\) the ideal center of cluster c and d the distance for interval-valued data. Notice that \(rd((\tilde{x}_{1,ideal},\tilde{x}_{2,ideal}),(\tilde{x}_{1,\alpha \cdot I},\tilde{x}_{2,\alpha \cdot I}) )\ge 1\), where equality holds only if the two elements of (\(\tilde{x}_{1,ideal},\tilde{x}_{2,ideal})\) are equal to the two elements of (\(\tilde{x}_{1,\alpha \cdot I},\tilde{x}_{2,\alpha \cdot I})\). The more rd departs from 1, the worse is the capability of the model to detect the ideal centers of the clusters.

For each scenario, both indices are averaged over the 100 simulation runs.

We have also set two values of the fuzziness parameter m, 1.5 and 2 respectively, to detect how the clustering performance is affected by this parameter.

Results for both the mean values of FRI and rd, averaged over the 100 replications of the simulation, are presented in Table 2 with respect to different percentages of outlier and fuzziness parameters.

Table 2 Performances of the models
Full size table

As it can be seen from Table 2, the average values of FRI recorded for ExpFCMd-ID are always very high and close to 1. Another remarkable finding is that the clustering performance of ExpFCMd-ID is slightly affected by the percentage of outliers. This is in line with the discussion at the end of Sect. 2 (see Fig. 3). Notice that as the fraction of outliers increases, the variability of the data increases and so the value of \(\beta \) decreases. In our case, the value of \(\beta \) ranges in (0.1, 0.2), decreasing as the percentage of outliers increases. In such situation, ExpFCMd-ID is capable of detect the two well-separated clusters, while data that are not compact in the two clusters are considered as outliers.

This result hold true even if we increase the percentage of outliers for values higher than 30 %.

Fig. 5
figure 5

Classification performance of the ExpFCMd-ID model

Full size image

In Fig. 5 are reported the average FRI values obtained with ExpFCMd-ID when the simulated datasets are contaminated with a percentage of outliers up to 90 %. It should be noted that ExpFCMd-ID is capable to identify the presence of the two well-separated clusters, even in very noisy environment, and that the classification performance degrades very slowly as the percentage of outliers increases. Indeed, even with 90 % of outliers added to the simulated datasets, the average value of FRI is higher than 0.7, which is a remarkable results given the noisiness of the dataset.

A similar pattern can be seen for the capability of detecting prototypes. The values of rd obtained with ExpFCMd-ID are always close to 1, irrespective of the scenario, of the percentage of outliers and of the values of the fuzziness parameter. In addition, the value of rd increases very slowly as the percentage of outliers increases.

From a comparative viewpoint, ExpFCMd-ID outperforms the non-robust FCMd-ID model, but also the two robust models taken into consideration in this simulation study, TrFCMd-ID and NcFCMd-ID. Indeed, as for the classification performance, the FRI values obtained with ExpFCMd-ID are always higher and closer to 1 than those obtained with the remaining models. By the same token, the rd values recorded with the proposed model are always lower and closer to 1 than those observed with FCMd-ID, TrFCMd-ID and NcFCMd-ID.

4 Applications

4.1 Air pollution data

In this section we illustrate an air quality study based on daily emissions of nitrogen monoxide (NO). NO concentration has been detected in fourteen monitoring stations located in Rome and its surroundings. The list of the stations is reported in the first column of Table 3. Data were collected in 2012, from January 1 December 31.

Data are drawn from the database BRACEFootnote 1, which is maintained by ISPRA (Istituto per la Protezione e la Ricerca Ambientale), the Italy’s Institute for Environmental Protection and Research.

Daily maximum and minimum values were collected during the period considered. Then these values were averaged over each quarter yielding to four interval-valued variables.

Note that the same data source has been employed in D’Urso et al. (2015a), but the data were differently treated. In D’Urso et al. (2015a) the log-differences of the daily emissions of NO were considered, while in this paper we analysed the average minimum and maximum values of the air pollutant in each quarter. Indeed, the focus in D’Urso et al. (2015a) was on daily rates of change of the pollutant concentration, while in this paper we are interested in the (average) daily excursions of NO concentration.

For comparison’s sake we make use both of FCMd-ID and of the proposed robust model ExpFCMd-ID. By adopting the Fuzzy Silhouette criterion, which is an extension to the fuzzy framework of the well-known Silhouette criterion (Campello and Hruschka 2006), two clusters are detected with both models.

Table 3 Membership degrees
Full size table

In Table 3 are reported the membership degrees of each station to each cluster both for FCMd-ID (second and third columns respectively) and for ExpFCMd-ID (last two columns). As it can be seen, results are similar. Indeed, the values of \(\beta \) is very close to 0 (see Sect. 2). In Fig. 6 are reported the evolution over time observed for the maximum and minimum values of NO concentration (solid lines), which indicates the average daily excursion in each quarter, and the midpoint values (dashed line). With both methods the first cluster, whose medoid is Ciampino (Fig. 6a), is more characterized by non-urban stations or station situated in a park (Malagrotta, Tenuta del Cavaliere and Villa Ada). The daily excursion is rather low in each quarter. Again, the composition of the second cluster is similar with both models, since it comprises stations located in residential areas, like Arenula, Cinecittà, Cipro and L.go Magna Grecia, and the daily excursion is more pronounced especially at the beginning and at the end of the period observed. One difference is that with FCMd-ID the medoid of the second cluster is L.go Magna Grecia (Fig. 6b), while with ExpFCMd-ID it is Cipro (Fig. 6c). The more striking difference, is that C.so Francia is allocated in the second cluster with a high membership degree with FCMd-ID, while with ExpFCMd-ID its membership degrees are approximately equally split across the two clusters (Table 3). This indicates that this station is considered an outlier when one adopts ExpFCMd-ID (see the related discussion at the end of Sect. 2). Indeed, evolution over time of NO excursion recorded in C.So Francia is at odds with the medoids, as it can be seen in Fig. 6d, since both the midpoint values and the daily excursion are higher than for the other station.

Also notice that D’Urso et al. (2015a) found that C.so Francia is an outlier, thus corroborating our findings obtained with ExpFCMd-ID. This is likely due to its characteristics, since it is a very large road, situated in a residential area, but used mainly to access to/depart from Rome centre. In conclusion, our findings, also corroborated by previous analysis, shows that FCMd-ID does not individuate a possible outlier (C.so Francia), whereas ExpFCMd-ID does.

Fig. 6
figure 6

Medoids and outliers. a Ciampino (1st medoid, FCMd-ID and ExpFCMd-ID), b L.go Magna Grecia (2nd medoid, FCMd-ID), c Cipro (2nd medoid, ExpFCMd-ID), d C.so Francia (outlier, ExpFCMd-ID)

Full size image

4.2 Bicycle riders data

We analysed data gathered on a sample of Toronto inhabitants. The survey focused particularly on the commuting behaviour, but several socio-demographic characteristics were collected. Data are freely available on the Toronto Open Data websiteFootnote 2. The survey provides four interval valued variables, i.e. age, commuting time, commuting distance and household income. Other socio-demographic categorical variables are gender, health status, education degree and working status. In the clustering process we considered only the interval-valued data, while the categorical variable were employed for an ex-post evaluation of the clusters obtained.

We have considered only individuals who live in Central Toronto and use for their commute principally bicycle or e-bike (electric-assisted bicycle).

After dropping individuals with missing or anomalous values for the categorical socio-demographic variables, we ended up with a sample of 458 individuals. The main characteristics of the sample are reported in the first column of Table 4.

Table 4 Interval-valued variables and socio-demographic characteristics of the respondents (percentages)
Full size table
Fig. 7
figure 7

Radar plots for interval-valued variables (mean values)

Full size image

As it can be seen, 13.76 % of the sample use e-bike for commuting reasons.

As for the interval-valued variables, most of the respondents are aged between 18 and 34 years, commute for relatively short distance and time, and they are almost equally distributed across income classes, apart the first class, in which falls only 7 % of the sample.

Concerning the categorical socio-demographic variables, the sample is composed mainly by individuals with an excellent health status (which is likely related to the transport used), with an university degree and employee.

The mean values of the four interval-valued variable are displayed in the first panel of Fig. 7 (“Sample”, the black points, connected with solid lines, refer to the midpoint of each variable, while the red points, connected with dashed lines, refer to the radii). This figure is reported as a benchmark for the corresponding figures for the clusters.

Fig. 8
figure 8

Ternary plots for FCMD-ID and ExpFCMd-ID

Full size image

Both FCMd-ID and ExpFCMd-ID were applied to the dataset containing the four interval-valued variables. The value of \(\beta \) obtained by applying ExpFCMd-ID is equal to 0.2, thus indicating a large variability in the data and, possibly, a noisy environment. By adopting the Fuzzy Silhouette criterion, three clusters are identified when applying the ExpFCMd-ID to data. In Fig. 8 are reported the membership degrees obtained with both FCMd-ID (Fig. 8a) and ExpFCMd-ID (Fig. 8b). When FCMd-ID is used the three clusters partition is almost identical to the two clusters partition, as it can be seen from the fact that the points representing the membership degrees are aligned on a straight line (see Fig. 8a). The only difference between the partitions with two and three clusters is that in the latter one unit is “forced” to be the medoid of the added cluster. For this reason, we no longer discuss the results of FCMd-ID.

Figure 8b shows the membership degrees for the three clusters solution obtained with ExpFCMd-ID. The red triangle shaped dots represent the outliers, i.e. the individuals for which the membership degrees are approximately equally split across clusters. The presence of these outlier is likely to prevent the non-robust FCMd-ID clustering model to detect a sensible result with three clusters.

As previously said, Fig. 7 displays the radar plots computed on the interval-valued variables, for the whole sample and for the three clusters. The values reported for the three clusters are the weighted mean of the midpoints and of the radii of each variables, with weights given by the membership degrees.

With respect to the whole sample, the first cluster is composed mainly by younger individuals, with lower income and who travel for shorter distances. Clusters 2 and 3 are more similar, with the exception of the average household income.

These results are also confirmed by the values reported in the last three columns of Table 4. These values are the weighted percentage of individuals in each cluster for each category of the socio-demographic variables observed on the sample. The weighted percentage are computed by summing the membership degrees of the individuals with a given attribute, divided by the sum of membership degrees for the considered cluster.

Table 4 allows also for a further insights about the socio-demographic characteristics of individuals in each cluster. As it can be seen, individuals in the first cluster are characterised by an excellent health status, most of them have an university degree and are employees. Conversely, in the third cluster there is a higher (weighted) percentage of individuals with high school diploma (or similar undergraduate degree) and there are more self employed workers. The second cluster presents intermediate values between the first and the third for most of the categories of the socio-demographic variables.

5 Final remarks

In several real life and research situations data are collected in the form of intervals. To analyze interval-valued data, usually researchers summarize the original data into single values, such as the centers or the medians of the intervals, but by doing so some important information in the original data may be lost. Indeed, in the last years several efforts have been made to extend methods or develop new approaches to analyse these type of data taking into account their interval structure.

In this paper we have addressed the problem of clustering interval-valued data corrupted by noise and outliers considering the Fuzzy C-medoids model. To deal with the presence of outliers we have implemented a robust metric based on the exponential distance that assigns small weights to outliers and larger weights to those points that are more compact in the data set.

We have presented the results of simulation studies pertaining to three possible types of outlier interval-valued data: outlier midpoint (center)–inlier radius (spread); inlier midpoint–outlier radius; outlier midpoint–outlier radius.

The proposed model has been evaluated by comparison with other fuzzy clustering models for interval-valued data considering two aspects: the capability of identifying the natural clusters (even when the simulated datasets are contaminated with an increasing number of outliers) and the ability to identify cluster prototypes which are not too distant from the “ideal” centers, given by the expected values of the generative random variables, irrespective of the number of outliers. Results show that the proposed approach is more able to distinguish the natural clusters as well as to detect prototypes.

Eventually, we have analysed two real interval-valued data sets concerning the emissions of nitrogen monoxide detected in fourteen monitoring stations located in Rome and its surroundings and the commuting behaviour of bicycle riders that live in the centre of Toronto and use for their commute principally bicycle or e-bike (electric-assisted bicycle).

In both cases the proposed approach has shown to be useful in identifying the “natural” clusters even in presence of outliers.

The use of the robust metric in the framework of regression trees based method for change point detection in interval-valued time series affected by outliers is the subject of ongoing research.

Also the adoption of the exponential distance for self-organizing maps is worth exploring in future research.

Finally, the utilization of the exponential transformation of other types of distance measures (Xu 2012) in a fuzzy partitioning around medoids procedure or in other typologies of fuzzy clustering, e.g. entropy-based fuzzy clustering (Dey et al. 2011) and bi-objective fuzzy clustering (Hung 2007), will be considered for the interval-valued data case.