Abstract
We revisit the general theory of finite-strain deformations in fluid-saturated porous media via the thermodynamics of nonequilibrium processes. Our aim is the thermodynamically consistent derivation of governing equations that satisfy the principle of material frame indifference, starting with the minimal number of assumptions. In the first part, we treat the relative fluid velocity as a constitutive variable, and hence fully determined by the macroscopic thermodynamic state of the continuum. However, this hypothesis is not rich enough to account for the tortuosity effect in poroacoustics, second-gradient effects, or Brinkman’s correction to Darcy’s law, thus motivating its relaxation in the second part, where we consider the relative fluid velocity as an independent kinematic variable. This approach yields an additional balance equation reflecting, in an average sense, the micromechanics of the fluid flow, which is derived from the principle of virtual power. Finally, we show that the resulting general model is consistent with Biot’s linear theory of acousto-poro-elasticity.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The continuum modeling of fluid flow through deformable porous media started in the 1920’s with the work of Karl von Terzaghi [67], motivated by problems in soil mechanics. Terzaghi’s work was based on elasticity theory combined with a phenomenological law relating the fluid flow rate to the pressure, introduced in 1856 by Henry Darcy [26]. In the 1940’s and 1950’s, the biphasic models of porous media were introduced, consisting of balance laws for each of the solid and fluid phases related by macroscopic interaction laws based on micromechanical considerations. These models started with the work of Biot [9–12] on poroelasticity and formed the basis for many subsequent studies in this area under quasistatic and dynamic conditions. In the late 1960’s and early 1970’s the theories of rational thermodynamics [20, 68] were first applied to the macroscopic modeling of fluid mixtures, e.g., see [27, 42, 45, 59]. It is only in the 1980’s that extensive research was done to apply the continuum thermodynamics principles to model the macroscopic behavior of deformable, saturated porous continua (e.g., see [14, 21, 30, 47–49]) using the aforementioned fluid mixtures theories, where the porous continuum is seen as a mixture of a solid and a fluid. Using the tools of nonequilibrium thermodynamics, considerable research followed to extend the linearized Biot’s theory to finite strains [13] and later to introduce additional physical mechanisms, such as plasticity, creep, chemical aging, phase changes, second-gradient effects, etc. A detailed accounting of these works is beyond the scope of this article, the reader is referred to [22, 23, 29] and the references therein. In parallel to continuum models, the rise of homogenization theories resulted in an additional body of research aiming to establish the links between physical mechanisms at the microscale and the macroscopic behavior of fluid-saturated deformable porous media, e.g., see [1–3, 5–7, 16, 24, 25, 29] and the book by Bear [8].
Most of the models derived at the continuum scale were shown to be consistent with Biot’s theory upon linearization. However, when derived in the linear regime, these models can show inconsistencies with the principles of rational thermodynamics principles upon their extension to nonlinear regimes, as explained for instance by [71, 73, 75], who points out that most biphasic models are not always consistent with the principle of material frame indifference. Moreover, most of poroelasticity models are, at some point of their derivation, based on the phenomenological split of the stress tensor into two macroscopic stress tensors: one for the solid and another for the fluid, two (or more) corresponding linear-momentum balances are introduced, energies and interaction terms are defined for each phase, and the resulting set of constitutive restrictions can be in contradiction with thermodynamic principles as discussed in Sect. 4.3.
Our goal is to propose a general continuum theory for finite-strain poroelasticity that circumvents the use of mixture theories and, using the least number of assumptions, to provide a thermodynamically consistent derivation of the governing equations that satisfy the principle of material frame indifference. We show that the introduction of interaction terms and splits between fluid and solid physics as performed in mixture theories, are not necessary to derive a continuum poromechanics model. In this work, we adopt a unique linear momentum balance, an approach that is used in the recent continuum multiphysics literature such as in electromagnetic couplings [52], electronic couplings in semi-conductors [41], atomic diffusion in solids [34], hydrogels [18, 19], ionic polymers [76]. We describe a porous medium as a solid skeleton that contains a connected network of holes (usually called pores) that are filled with a fluid flowing through this network. We consider that the pores are always saturated by a single fluid. We are interested in the macroscopic response of the continuous porous medium and not in the details of the processes that take place at the microscale, the goal being to macroscopically couple the mechanics of the deformable solid skeleton with the motion of the fluid flowing trough.
The remainder of this paper is organized as follows. The notations employed and definitions of the fundamental fields are presented in Sect. 2 and in Sect. 3, respectively. In Sect. 4, we treat the relative velocity of the fluid as a constitutive variable. We derive, using the direct approach of continuum mechanics, the unique thermodynamically admissible field equations and compare them with the existing literature. However, this hypothesis is not rich enough to capture the tortuosity effect in elasto-poro-acoustics, second-gradient effects, or Brinkman’s correction. In Sect. 5, we treat the relative velocity of the fluid as a kinematic descriptor of the continuum. This additional kinematic descriptor requires a supplementary balance equation derived from the principle of virtual power and reflecting, in an average sense, the micromechanics of the fluid flow. The resulting model is shown to be consistent with Biot’s linear theory of acousto-poro-elasticity. The presentation is concluded by a discussion in Sect. 6. Some additional details are given in the appendices: key definitions and results on material frame indifference in Appendix A, details of the derivation of the energy flux vector \(\mathbf {h}\) in Appendix B, and the justification for the final expressions of the generalized Fourier and Darcy laws in Appendix C.
2 Notations
Dyadic notation convention is followed here; since several variations exist in the literature, a brief overview of the version used in this paper is presented below.Footnote 1
-
Scalars are denoted by script Latin or Greek letters (e.g., \(a\), \(b\), \(c\), \(m\), \(\alpha \), \(\beta \), \(\gamma \), \(\psi \), \(M\), \(\Psi \), etc).
-
Vectors are denoted by bold small case Latin or Greek letters, e.g., \(\mathbf{a}\), \(\mathbf{b}\), \(\mathbf{c}\), \(\boldsymbol{\alpha }\), \(\boldsymbol{\beta }\), \(\boldsymbol{\gamma }\), etc. Their components are denoted using the script version of the same symbols \(\mathrm{a}_{{i}}\), \(\alpha _{{i}}\), etc.
-
Second-order tensors are denoted by BOLD UPPER CASE Latin or Greek letters, e.g., \(\mathbf{A}\), \(\boldsymbol{\Sigma }\). Their components are denoted using the script versions of the corresponding symbol \(\mathrm{A}_{{ij}}\), \(\Sigma _{{ij}}\).
-
Third-order tensors are denoted by the bold uppercase \(\boldsymbol{\mathfrak{FONT}}\), e.g., \(\boldsymbol{\mathfrak{U}}\) and their components by \(\mathfrak{U}_{{ijk}}\).
-
Fourth-order tensors are denoted by the bold uppercase
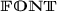 , e.g.,
, e.g., 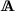 and their components by
and their components by 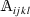 .
. -
Sets of variables are denoted by script uppercase calligraphic \(\mathcal{FONT}\), e.g., ℒ, \(\mathcal{S}\), \(\mathcal{V}\).
There are two notable exceptions to the aforementioned convention. To stay consistent with usual notations in solid mechanics, we denote the spatial position of a point in the current configuration by the vector \(\mathbf{x}\) and reference coordinate vector of the corresponding material point by \(\mathbf{X}\). Moreover, the Cauchy stress (second order tensor) is denoted by the bold small case letter \(\boldsymbol{\upsigma }\).
Spatial differentiation is indicated by two nabla operators: the small nabla operator \({\scriptstyle \boldsymbol{\nabla }}\) for the current configuration and the corresponding large nabla operator \(\boldsymbol{\nabla } \) for the reference configuration
Dyadic notation uses a dot \(\boldsymbol{\cdot } \) for the single contraction operation. Examples of contraction operations between tensors of various ranks, spatial gradients and derivatives of a tensor field quantity with respect to another tensor field quantity using the proposed notation are given below in Cartesian coordinates

where the use of Einstein’s convention of summation over repeated indices is adopted. The standard dyadic notation for the tensor product between vectors is also used as well as the transposition operation for second-order and third-order tensors
Finally we introduce the wedge product (∧) of two vectors \(\mathbf{a}\) and \(\mathbf{b}\) as the rank two antisymmetric tensor
3 Kinematics and transport identities
We define the saturated porous material as a continuum and to each material point we assign an apparent density of skeleton \(m_{{s}}\left ( {\mathbf{x},t} \right ) \) and an apparent density of fluid \(m_{{f}}\left ( { \mathbf{x},t} \right ) \) defined as the masses of skeleton and fluid per unit current volume of the continuum as opposed to true density, the mass per unit volume of each material. We denote by \(\Omega \) and \(\omega \) the reference and current configurations, respectively. A material point of the skeleton is defined by its position \(\mathbf{X}\) in the reference configuration and is mapped at time \(t\) to the spatial point \(\mathbf{x}= \boldsymbol{\chi } \left ( {\mathbf{X} ,t } \right ) \). As fluid flows through the solid, we adopt the following Eulerian description of mass transfer in the continuum:
-
(i)
The apparent mass density \(m_{{s}}\) is associated with the velocity , where the superposed dot represents the material time derivative (at \(\mathbf{X}\) fixed).
-
(ii)
The apparent mass density \(m_{{f}}\) flows with the absolute macroscopic velocity \(\mathbf{v}_{{f}} \left ( { \mathbf{x} , t } \right ) \).
In deriving the governing equations, we write the balance laws in Sect. 4 in the current configuration on an arbitrary material control volume \(v \subset \omega \) which follows the motion of the solid skeleton material points (Fig. 1). We allow the volume \(v\) to be crossed by a material discontinuity surface \(s\). We further assume there is no sliding or debonding of the continuum at the discontinuity surface, i.e., \(s\) deforms with the continuum following the mapping \(\boldsymbol{\chi } \left ( {\mathbf{X}, t } \right ) \) and the skeleton displacement and velocity are continuous across \(s\) so that
where \(\left [\!\![. \right ]\!\!]\) denotes the jump of a field value across the interface \(s\).
An important role in the theory is played by the relative fluid velocity \(\mathbf{v}_{{r}}\) defined by:
Following the introduction of the primitive variables \(m_{{s}}\) and \(m_{{f}}\), we define the total mass density of the continuum \(m_{{t}}\), its average velocity \(\mathbf{v}\), and the mass ratios \(c_{{s}}\) and \(c_{{f}}\) as
It follows that
It is also useful to introduce the definition of the material time derivative, denoted by a superposed dot for scalars and vectors defined in an Eulerian description \((\mathbf{x}, t)\) (derivation at \(\mathbf{X}\) fixed)
In this work we repeatedly make use of the localization procedure of continuum mechanicsFootnote 2 that allows us to convert the integral form of a balance law on an arbitrary control volume \(v\) into a differential equation and a boundary/interface condition, due to the arbitrariness of the control volume selected. To this end we need two ingredients: first the Reynolds transport theorem applied to a material control volume in the current configuration \(v\) moving with the skeleton at speed \(\mathbf{v}_{{s}}\); for any tensorial field \(\mathbf{f}({\mathbf{x}},t)\) we have
and second the divergence theorem that applies to an arbitrary control volume \(v\) with boundary \(\partial v\) containing a material discontinuity surface \(s\) moving with the skeleton at speed \(\mathbf{v}_{{s}}\), where \(\mathbf{n}\) the outward unit normal vector; the divergence theorem states
4 The relative fluid velocity \(\mathbf{v}_{{r}}\) as a constitutive field
In this section, we place ourselves in the constitutive macroscopic regime for the fluid relative velocity. The goal is to use the principles of thermodynamics to derive the macroscopic field equations pertaining to the modeling of porous media.
In the macroscopic modeling of porous media, it is common to consider the fluid and the solid as two superimposed continua, and apply to each the conservation laws of mass, momentum, and energy, as well as the Clausius-Duhem inequality. This is the mixture-theory approach [13, 14, 21], also named biphasic-theory approach, in reference to the original work of [9, 13]. The mixture-theory for porous materials has proved its efficiency in the modeling of physical experiments (see, e.g., [22] for an extensive list of models and applications). However, from the point of view of thermodynamics of nonequilibrium processes, we identified some inconsistencies in this approach, such as the non-objectivity of Darcy’s law (see (4.69) and (4.70)), the ad-hoc choices for the definitions of kinetic energy (see (4.58)) and the assumed splitting of the stress tensor into skeleton and fluid parts (see (4.59)). These points are discussed in detail in Sect. 4.3.
In the mixture and biphasic theories, the continuum is split such that each constituent (fluid and solid) is treated as a single continuum at the macroscopic scale with its own momentum and energy balances, and entropy imbalance. By construction of these theories, the relative velocity \(\mathbf{v}_{{r}}\) is defined as a kinematic variable. This requires the introduction of terms that account for interactions between distinct phases and the definition of stress, energy density, entropy density, for every constituent. For example, the mechanical power expenditures and kinetic energies are usually defined at the macroscopic scale by analogy with the expressions of such terms at the microscale. The introduction of such phenomenology can lead to inconsistencies, as mentioned above. Various phenomenological hypotheses are introduced depending on the physical problem under consideration (rocks, clay, bones, living tissue, sand, etc) leading to different models in the literature.
In contrast, the goal of this work is to provide a general framework with the minimum number of assumptions and let thermodynamics provide all the unknown constitutive equations for the energy and heat fluxes as well as the total stress measure. We show that the aforementioned phenomenological split into solid and fluid fields is not necessary to derive a consistent macroscopic model when the fluid relative velocity is treated as a constitutive field. We use the principles of thermodynamics [20, 62, 63, 68] to derive the admissible forms of the field equations, without any phenomenological assumptions or split. The derivation of the model is based on the following modeling choices:
-
(C-1)
For Sect. 4, we treat the fluid relative velocity \(\mathbf{v}_{{r}}\) as a constitutively prescribed variable. We shall show that this choice is not rich enough to capture some physical phenomena such as Brinkman’s correction of Darcy’s law, the tortuosity correction in acoustics, etc. The results of changing this assumption to consider the fluid relative velocity \(\mathbf{v}_{{r}}\) as a kinematic descriptor, will be presented in Sect. 5.
-
(C-2)
There is no mass exchange between the solid and the fluid.
-
(C-3)
Following Noll [63], we make a type-I constitutive assumption for the expression of the linear momentum density. A type-I assumption aims to model the interactions of the continuum with the universe (e.g., we postulate the standard inertial form of the linear momentum). The type-II assumptions characterize the interactions between different parts of the system. Both these assumptions are required to be objective.
-
(C-4)
We work in an inertial reference frame.
-
(C-5)
The generalized traction introduced in the linear momentum balance only depends on the outward unit normal vector of a surface \(\mathbf{n}\) so that the Cauchy tetrahedron theorem applies and there exists a generalized second-order tensor \(\boldsymbol{\upsigma }\) such that \(\mathbf{t}=\mathbf{n} \boldsymbol{\cdot } \boldsymbol{\upsigma }\).
-
(C-6)
There are no internal sources of momentum or energy.
-
(C-7)
We do not distinguish between a solid and a fluid temperatures (thermal equilibrium at the miscroscale).
-
(C-8)
The thermodynamic state does not depend on high-order gradients (equal or greater than 2), in order to simplify the algebra. There are no difficulties in generalizing the present framework to account for higher-order gradients. The reader can refer to Sect. 5 for an example of this extension.
4.1 Balance Laws
4.1.1 Mass conservation
When writing the mass balances, we assume (C-2) that there is no loss or creation of mass and no mass exchange between the skeleton and the fluid. Hence any change of mass in the control volume \(v\) enters through the boundary \(\partial v\).
Solid skeleton The integral form of mass conservation for the solid skeleton is
Applying the Reynolds transport theorem (3.6) yields the local form
and the corresponding jump condition on surface \(s\) is automatically satisfied in view of assumption (3.1).
Fluid content The control volume moves with the skeleton velocity \(\mathbf{v}_{{s}}\) and the fluid flows with an absolute velocity \(\mathbf{v}_{{f}}\), hence by definition of \(m_{{f}}\) and \(\mathbf{v}_{{f}}\), the fluid mass balance is
resulting in the following local form
and the associated interface condition on the surface \(s\)
4.1.2 Linear momentum balance
In continuum mechanics, the linear momentum is associated to mass in motion and defined as the product of a mass with its velocity. As obvious as it may seem, this is actually an assumption, more specifically a constitutive assumption of type-I [63], modeling the interactions of the continuum with the universe. In other fields of physics, the linear momentum can take different forms; e.g., in the continuum modeling of solid mechanics coupled to electromagnetism, a generalized linear momentum density is introduced [52].
In the present continuum model, in accordance with (C-3), we use the approach of [63] and postulate an explicit form of the linear momentum of a control volume \(v\), where the two masses are moving at two different velocities (see definitions of \(m_{{t}}\) and \(\mathbf{v}\) in (3.3))
Even if we do not use any homogenization argument in this work, note that the expression (4.6) of the linear momentum could be seen as the homogenized form of the linear momenta of the solid and fluid materials at the microstructure [25].
We assume \(\mathbf{b}\) to be the external body force per unit mass acting on the continuum with no consideration of body forces on each constituent, since according to (C-6), there is no internal source of momentum. We introduce a generalized traction vector \(\mathbf{t}\left ( {\mathbf{x},t} \right ) \) modeling the linear momentum variation occurring through the boundary of the control volume \(\partial v\). In accordance with (C-5), we further assume that the Cauchy tetrahedron postulate holds, relating the generalized traction \(\mathbf{t}\) to a generalized Cauchy stress tensor \(\boldsymbol{\upsigma }\left ( {\mathbf{x},t} \right ) \). Ignoring external forces on the discontinuity surface \(s\), the integral form of the linear momentum balance has the simplest possible form
In writing (4.7) we deviate from Biot’s classical biphasic-theory of poromechanics [13, 22] where one usually adds a linear momentum flux brought across the boundary \(\partial v\) by the fluid mass in motion of the form \(-\int _{v} m_{{f}}\mathbf{v}_{{f}}(\mathbf{v}_{{r}} \boldsymbol{\cdot } \mathbf{n}) \ \mathrm{d}a\). The contribution of these missing surface flux terms is accounted for by the generalized stress tensor \(\boldsymbol{\upsigma }\) whose expression will be determined via thermodynamics principles. Applying the Reynolds transport theorem in (3.6) and the divergence theorem in (3.7) and substituting the mass balances (4.2) and (4.4) into the integral form of linear momentum balance (4.7) we obtain in view of the arbitrariness of the volume \(v\) and surface \(\partial v\) the local form
and the associated interface condition on the surface \(s\)
4.1.3 Angular momentum balance
The balance of angular momentum follows the simple form of the linear momentum equation (4.7). Recalling the definition of the wedge product ∧ of two vectors in Sect. 2, the balance of angular momentum of a control volume \(v\) (taken with respect to the origin \(O\) of the inertial frame) is stated as
The local form is obtained by substituting (4.2) and (4.4) and (4.8), resulting in the following relationFootnote 3
Using \(\mathbf{v}_{{s}}\wedge \mathbf{v}_{{s}}=\boldsymbol{0}\), from (4.11) we obtain
where the symmetry condition applies to the combination \(\boldsymbol{\upsigma }+m_{{f}}\mathbf{v}_{{r}}\otimes \mathbf{v}_{{s}}\), a direct result of our choice of the simple form of the linear momentum balance in (4.7).
4.1.4 Energy balance
It is usual in mechanics to split the total energy of the control volume \(v\) into the sum of its internal energy and its kinetic energy.Footnote 4 In this work, we do not postulate any such split in order to avoid any phenomenological bias in the thermodynamic derivations of the constitutive restrictions. It is also common in the literature to see a split of the internal energy of the continuum into the solid internal energy and the fluid internal energy, an approach that misses the coupling energy between the two phases. Different approaches of this split can be found.
In [70, 72], the internal energies of the fluid and the solid are introduced separately. The coupling is achieved by the introduction of a porosity balance, and in [71] it is shown that higher-order gradients of this porosity are necessary to retrieve the coupling terms described in Biot’s theory. In [17, 22], the authors split the internal energy into an internal energy for the solid and the fluid and sum them into a total energy for the derivation of thermodynamic restrictions. When giving an explicit expression to the free energy, they split it again into the sum of a skeleton energy, a fluid and a coupling energy. Several versions of this approach exist that account for the interaction energy in the framework of mixtures, see, e.g., the interface energy introduced in Equation (18) of [65].
To avoid the difficulties associated with the phenomenological split, we consider an energy density \(\epsilon \), resulting in a total energy \(\int _{v} \epsilon \ \mathrm{d}v\) of the control volume. The time variation of this total energy is decomposed into a volume integral term on \(v\) and a boundary integral term on \(\partial v\). The volume integral consists of two terms: the contribution by the external body force \(\mathbf{b}\) which expends mechanical power on the continuum, in accordance with the definition in the linear momentum balance (4.7). Since \(\mathbf{b}\) is assumed uniform and identical for all continua (e.g., gravity), we write its power expenditure on the control volume as \(\int _{v} m_{{t}}\mathbf{v} \boldsymbol{\cdot } \mathbf{b}\ \mathrm{d}v\), and the contribution by the external energy source density \(q\) (often called the radiative flux) as \(\int _{v} q \ \mathrm{d}v\).
By (C-6), we assume there is no internal source of energy in the continuum. Therefore, the energy variations of the control volume \(v\) caused by the interactions with the surrounding material only occur through the boundary \(\partial v\). We deviate again from the usual biphasic mixture theories and we do not postulate any stress decomposition or any power expenditure associated to the fluid or to the solid. Instead, we use the formalism of an unspecified energy flux (e.g., see the work of [45, 59] on fluid mixture thermodynamics). By (C-5), we postulate that this surface contribution is associated to a directional flux vector \(\mathbf{h}\) and takes the form \(- \int _{\partial v } \mathbf{h} \boldsymbol{\cdot } \mathbf{n}\ \mathrm{d}a\). Consequently, the integral form of the energy balance isFootnote 5
One can appreciate the generality of the formulation (4.13) where the energy density is not split into internal and kinetic energy or into solid and fluid energy. In the boundary term, all the physics is hidden in the generic flux \(\mathbf{h}\). We do not write explicit energy fluxes or mechanical power expenditures associated to mechanical traction .Footnote 6 The local form of the energy balance is
with the associated interface condition on the surface \(s\)
Using (4.8) to substitute the external body force \(\mathbf{b}\) in (4.14), one obtains a more explicit form of the local form of the energy balance
This completes the writing of the mass, linear and angular momenta and energy balances in their most general form, without any introduction of phenomenological terms. The next step is to explore the second principle of thermodynamics.
4.1.5 Entropy imbalance
Let \(\eta \) be the entropy density of the continuum, where once again we do not differentiate between the solid and the fluid entropies. Recalling the modeling choice (C-7), according to which we do not differentiate between the temperature of the skeleton and one of the fluid, and denoting by \(\theta \) the absolute temperature of the continuum, the second law of thermodynamics is stated by the inequality
where no entropy is associated to the discontinuity surface. In (4.17), we follow again the formalism of [45] and [59] since we do not give any physical interpretation to flux vector \(\mathbf{q}\), which is not defined as a heat flux (and hence takes no part in the energy balance (4.13)). The term \(\mathbf{q}/\theta \) is the flux of entropy at the boundary of the control volume \(\partial v\). However, we follow the discussion of equation (3.2) in [59] according to which the entropy source density is defined as \(q/\theta \) with the energy source density \(q\) introduced in the energy balance (4.13).
In local form, the entropy inequality is
and the associated interface condition on the surface \(s\) is
Combining the local forms (4.16) and (4.18) to eliminate the external energy source \(q\) we obtain
Instead of working with the energy density \(\epsilon \), it is more convenient to introduce the free energy \(\psi \) by
which allows us to rewrite (4.20) as follows
4.2 Constitutive restrictions
4.2.1 Framework of the Coleman-Noll procedure
To complete the set of governing equations derived from the general principles, we need to specify the expressions of \(\eta \), \(\mathbf{q}\), \(\mathbf{v}_{{r}}\), \(\psi \), \(\boldsymbol{\upsigma }\) and \(\mathbf{h}\). At this point, we do not yet require constitutive restrictions for these fields since this would imply their material frame indifference.Footnote 7
The free energy \(\psi \) is used here as the most convenient alternative to the total energy density \(\epsilon \). The unknowns \(\boldsymbol{\upsigma }\), \(\mathbf{h}\) and \(\mathbf{q}\) were also introduced to represent any general surface contribution to the linear momentum balance, the energy balance and the entropy imbalance, respectively. Therefore, these terms can (and actually will) depend on inertial terms and other non-objective terms. This is why, at this stage of the derivation they are not required to be material frame indifferent.
GuidedFootnote 8 by [20], the inequality (4.20) must be used to derive thermodynamic restrictions on these quantities. To do so, we must define a set of thermodynamic variables. The primitive kinematic descriptors of the system are the deformation mapping \(\boldsymbol{\chi }\), the mass densities \(m_{{s}}\) and \(m_{{f}}\), and the temperature \(\theta \). Therefore, we expect the thermodynamic state to be fully described by their values as well as their successive gradients and time derivatives. Consequently, we postulate here the following set of thermodynamic variables:
where \(\mathbf{F}=\left ( { \boldsymbol{\nabla } \boldsymbol{\chi }} \right ) ^{\top}\) is the deformation gradient of the continuum, \(\mathcal{S}\) is the set of scalar thermodynamic variables and \(\mathcal{G}\) the set of the first spatial gradients of \(\mathcal{S}\). We henceforth make a distinction between the set \(\mathcal{L}_{{O}}\) and the skeleton velocity field \(\mathbf{v}_{{s}}\). It can be shown (see Appendix A) that an objective quantity cannot depend on \(\mathbf{v}_{{s}}\) and hence only the set \(\mathcal{L}_{{O}}\) can be used to describe objective fields.
We make the assumption that the thermodynamic state of the system can be fully described by the set of independent fields (4.23). The additional assumption of homogeneity of the material allows us to drop the dependence on \(\chi \). Recall that according to assumption (C-1), the relative fluid velocity \(\mathbf{v}_{{r}}\) is treated as a constitutive variable and we postpone for Sect. 5 the study of \(\mathbf{v}_{{r}}\) as an independent kinematic descriptor.
The inequality (4.22) must hold for any admissible thermodynamic process described by the set ℒ defined in (4.23). Applying the principle of equipresence [68], the thermodynamic state is then defined by
As explained at the beginning of this subsection, some of the quantities in (4.24) can still be linked to inertial effects, hence the accounting for the dependence on \(\mathbf{v}_{{s}}\). In the forthcoming algebra, when a term of (4.24) is required to be objective, it will depend on the objective restriction of ℒ, denoted in (4.23) by \(\mathcal{L}_{{O}}\).
The presence of time derivatives and spatial gradients in the entropy inequality (4.20) – or equivalently in (4.22) – requires the consideration of time derivatives and higher-order spatial gradients of ℒ. With this observation in mind, the Coleman-Noll procedure can be decomposed in two steps:
-
1.
Identify the time derivatives and spatial gradients of (4.23) that can take arbitrary values for any given thermodynamic set ℒ. The requirement that (4.22) holds for any arbitrary value of these quantities will give necessary restrictions, leading to equalities on the fields of (4.24).
-
2.
The remaining terms of (4.22) represent the dissipation of the system. This will give sufficient conditions, leading to inequalities that the fields that appear in (4.24) must satisfy.
4.2.2 Necessary restrictions in volume
Consider the set of time derivatives and higher order spatial gradients of ℒ. Because of the mass balances (4.2) and (4.4), the time rates of mass densities and their second gradients are related. Moreover, \({\scriptstyle \boldsymbol{\nabla }}\mathbf{v}_{{s}}\) and are also related. Following the same procedure as [45], it is straightforward to show that and can also be assigned arbitrarily. Also note that second gradients are arbitrary symmetric second order tensors. Thus we define the set \(\mathcal{L}^{\star}\) of arbitrarily assignable fields
Applying the chain rule of time derivation to in (4.22) and after substitution of the mass balances (4.2) and (4.4), the local form of the entropy imbalance is found to be

For simplicity, we introduce the following notations for the solid \(\mu _{{s}}\) and fluid \(\mu _{{f}}\) chemical potentials
The chemical potentials are introduced as a renaming of variables. This is a different status than in theories in which that are introduced as primitive variables in the energy balance and the relation (4.27) are found to be constitutive restrictions (see, e.g., [19, 34, 37, 46, 50, 56]).
In order to extract all the necessary constitutive restrictions from (4.26) we will first consider the arbitrary variations of the time-rates of (4.25) and then the variations of the second order spatial gradients.
Results using arbitrary time rates
Given any admissible thermodynamic state ℒ, the time-rate quantities of \(\mathcal{L}^{\star}\) in (4.25) can be assigned arbitrarily and only appear linearly in (4.26), yielding the following necessary restrictions
implying that the free energy \(\psi \) is independent of \({\scriptstyle \boldsymbol{\nabla }}m_{{s}}\), \({\scriptstyle \boldsymbol{\nabla }}m_{{f}}\), \({\scriptstyle \boldsymbol{\nabla }}\theta \), \({\scriptstyle \boldsymbol{\nabla }}\mathbf{F}\) and \(\mathbf{v}_{{s}}\). We further assume here that the material is isotropic and hence \(\psi \) and all the other fields are a function of , the left Cauchy-Green tensor, instead of \(\mathbf{F}\). Moreover, requiring the HelmholtzFootnote 9free energy \(\psi \) to be objective, it must depend on the invariants \(\mathcal{I}(\mathbf{B})\) (see Appendix A)
Note that (4.29) implies from (4.27) the same dependence for the chemical potentials
and (4.26) can now be simplified toFootnote 10
To simplify the ensuing calculations, we introduce the symmetrized stress \(\boldsymbol{\upsigma }^{\star}\) and the elastic stress \(\boldsymbol{\upsigma }^{e}\)
We also introduce an inertially modified energy flux vector \(\tilde{\mathbf{k}}\), related to the energy flux vector \(\mathbf{h}\) by
To proceed we need to study the term \(\boldsymbol{\upsigma }^{*}-\boldsymbol{\upsigma }^{e}\) multiplying \({\scriptstyle \boldsymbol{\nabla }}\mathbf{v}_{{s}}\) in (4.31). By definition, the relative fluid velocity \(\mathbf{v}_{{r}}\) is objective (see Appendix A). Hence, \(\mathbf{v}_{{r}}\) is independent of \(\mathbf{v}_{{s}}\). The dependence on \({\scriptstyle \boldsymbol{\nabla }}\mathbf{v}_{{s}}\) in the inequality (4.31) can only come from the divergence of \(\tilde{\mathbf{k}} (\mathcal{L} )\).
According to the angular momentum balance (4.12), \(\boldsymbol{\upsigma }^{\star}\) is symmetric and by construction, \(\boldsymbol{\upsigma }^{e}\) is symmetric as well. Hence we can rewrite (4.31) using the definitions in (4.32) and (4.33) as
At this point we require that \(\boldsymbol{\upsigma }^{\star}\) and \(\tilde{\mathbf{k}}\) to be objective fields and hence to not depend on \(\mathbf{v}_{{s}}\). As shown in [40], this choice does not imply any loss of generality in the derivation of the constitutive restrictions. The term \({\scriptstyle \boldsymbol{\nabla }}\mathbf{v}_{{s}}\) therefore appears linearly in (4.31) and, making it vary arbitrarily, we obtain
Moreover, all the remaining terms of (4.31) are now constitutive and hence required to be objective, giving
Results using arbitrary second order gradients
In order to advance further in the exploitation of (4.36), we need to recall the material frame indifference principle and the hypothesis of isotropyFootnote 11 made in (4.29). In Appendix B, we show that the constitutive vector \(\mathbf{k} (\mathcal{L}_{{O}} )\) defined in (4.36) vanishes identically
thus providing the expression for the objective, constitutive energy flux vector \(\mathbf{h}(\mathcal{L}_{{O}})\) from (4.33) and (4.36)2
with the stress tensor \(\boldsymbol{\upsigma }^{e}\) given by (4.32). To prove that \(\mathbf{k} = \boldsymbol{0}\), we assumed that the material is isotropic, in which case the only possible choice for the energy flux is given by (4.38). In case of anisotropy, we cannot prove that (4.38) is the only valid choice, although it remains thermodynamically admissible since the entropy production inequality is still satisfied. Therefore, the expression of the unknown energy flux (4.38) can also be used for anisotropic material.
This completes the first step of the Coleman-Noll procedure providing the necessary conditions, constitutive equalities for the entropy \(\eta \), free energy \(\psi \), stress \(\boldsymbol{\upsigma }\) and flux vectors \(\mathbf{h}\) and \(\mathbf{q}\) in\(~\mathbf{x} \in v\). The remaining terms in the entropy imbalance (4.36) represent the dissipation \(D\) of the system
4.2.3 Necessary restrictions on surface
As seen in Sect. 4.1, there are four interface conditions on the surface \(s\)
associated respectively with the mass balance (4.4), linear momentum balance (4.8), energy balance (4.14) and entropy imbalance (4.18), where the last inequality is modified from its original version by additionally assuming a continuous temperature field across the surface \(s\) (\(\left [\!\![\theta \right ]\!\!]=0\)). Using (4.38) into the last two equations of (4.40), one obtains with the help of the first two equations in (4.40) and the relations in (3.1), (4.32), (4.33) and (4.35) the following surface inequality
Assuming no dissipation at the discontinuity surface (called ideal surface), the inequality (4.41) yields an equality at the surface \(s\) since \(\mathbf{v}_{{r}}\) and \(\mu _{f}\) are thermodynamically independent (see [51, 53, 55, 66])
Notice that the above interface continuity applies to a dynamic-like chemical potential of the fluid. In case of an incompressible fluid, the chemical potential is usually equivalent to pressure divided by its mass density. Hence (4.42) looks like a continuity of a Bernoulli-like quantity. Additionally, if one neglects the kinetic terms in (4.42) for the case of an incompressible fluid, then the condition is equivalent to the continuity of the fluid pressure, the usual Dirichlet condition used in poromechanics.
4.2.4 Sufficient restrictions
We proceed with the second step of the Coleman-Noll procedure, described in Sect. 4.2.1, starting from the dissipation inequality (4.39) and seeking restrictions on the admissible expressions for \(\mathbf{q}\) and \(\mathbf{v}_{{r}}\). Requiring \(\mathbf{q}\) and \(\mathbf{v}_{{r}}\) to be objective vector fields (cf. Appendix A), for any \(\mathbf{Q} \in O(3)\)Footnote 12
Taking the particular case of \(\mathbf{Q} = - \mathbf{I}\) (see the discussion around equation (3.16) of [20]), we obtain
Defining as homogeneous the state where the gradients of state variables vanish, i.e., \(\mathcal{L}_{{O}}^{h} \subset \mathcal{L}_{{O}}\) (see definition in (4.23)), where , (4.44) leads to the following conditions
From (4.45) and following the formalism of [45], we can write the following Taylor expansions for \(\mathbf{q}\) and \(\mathbf{v}_{{r}}\) near an homogeneous state

where the following tensors are introducedFootnote 13

and where denotes – by abuse of notation – the norm of the difference between the values of thermodynamic variables in the sets \(\mathcal{L}_{{O}}\) and \(\mathcal{L}_{{O}}^{h}\). Here \(\mathbf{K}_{{\theta }}\), \(\mathbf{K}_{{s}}\), \(\mathbf{K}_{{f}}\), \(\mathbf{D}_{{\theta }}\), \(\mathbf{D}_{{s}}\), \(\mathbf{D}_{{f}}\) are objective rank two tensors and  ,
,  are objective rank three tensors.
are objective rank three tensors.
As shown in Appendix C, the above expressions for \(\mathbf{q}\) and \(\mathbf{v}_{{r}}\) can be re-written as
where the pressure gradient-like term
was introduced – by abuse of notation since no pressure is defined here – to allow comparison with poromechanics literature.Footnote 14 The second-order tensors \(\mathbf{K}_{{\theta }}\), \(\mathbf{K}_{{p}}\), \(\mathbf{D}_{{\theta }}\), \(\mathbf{D}_{{p}}\) are objective functions of \((m_{{s}},m_{{f}},\theta ,\mathbf{B})\). The direct application of representation theorems (see Appendix A or [68]) implies that they must have the following form:
where \(k_{{0}}\), \(k_{{1}}\), \(k_{{2}}\), \(d_{{0}}\), \(d_{{1}}\) and \(d_{{2}}\) are scalar functions of \((m_{{s}},m_{{f}},\theta ,\mathcal{I}(\mathbf{B}))\), where \(\mathcal{I}(\mathbf{B})\) is the set of the scalar invariants of \(\mathbf{B}\). Finally, from (4.48), the positivity of the dissipation (4.39) also implies that the matrix
We have thus obtained, as sufficient conditions, the coupled thermo-mechanical version for Fourier’s law for \(\mathbf{q}\) and Darcy’s law for \(\mathbf{v}_{{r}}\), thus concluding the second part of the Coleman-Noll procedure.
4.3 Discussion
The stage is now set to interpret the results obtained thus far and compare them with existing theories in finite-strain poromechanics. In expressing the integral laws for linear and angular momenta, energy, and entropy, we used their simplest possible form. The unknown quantities introduced are i) a generalized traction \(\mathbf{t}\) and the associated Cauchy stress \(\boldsymbol{\upsigma }\) for the interaction with the surrounding material, ii) the total energy density \(\epsilon \), the total energy flux \(\mathbf{h}\), and the entropy flux \(\mathbf{q}\) vectors. We determined their expressions via the principles of thermodynamics without any phenomenological bias.
In this section we substitute the obtained expressions into the initial balances in order to identify and discuss the physics and put the resulting equations in perspective with existing literature. To avoid confusion, the equations cited from other works in the literature are preceded by ⋆⋆⋆.
Before proceeding with the interpretation of these expressions, it may be useful to record some alternative expressions of the above results in the reference configuration of the skeleton. Define the solid and fluid mass densities per unit reference volume of skeleton \(M_{s}\) and \(M_{f}\) and the corresponding free energy \(\Psi \)
where \(\mathrm{J}= \det \mathbf{F}\) is the determinant of the deformation gradient. Using (4.52) into (4.27) and (4.35), one obtains the following relations for the chemical potentials \(\mu _{s}\), \(\mu _{f}\) and \(\boldsymbol{\upsigma }^{e}\)
The skeleton mass conservation (4.2) can then be written as , so that, the dependence on \(M_{{s}}\) is equivalent to a dependence on a reference mass density \(M_{{s}}^{0}\). Therefore, if we further assume that the continuum is uniform, then solid mass density dependence can be dropped, i.e., \(\Psi = \Psi (M_{{f}}, \theta , \mathcal{I}(\mathbf{C}))\).
4.3.1 Linear momentum balance
Substituting the expression of the generalized stress tensor (4.32) and (4.53) into (4.7), we obtain the following integral form of the linear momentum balance
where \(\boldsymbol{\upsigma }^{e}\) is given by (4.53)3.
Recall that  is the expression of the linear momentum that we postulated to describe the inertia of the whole continuum, a type-I constitutive assumption. This choice is consistent with mixture theories as well as with the homogenization studies (see, e.g., [25]). We also defined a unique body force which is applied to all constituents, hence the expression
is the expression of the linear momentum that we postulated to describe the inertia of the whole continuum, a type-I constitutive assumption. This choice is consistent with mixture theories as well as with the homogenization studies (see, e.g., [25]). We also defined a unique body force which is applied to all constituents, hence the expression  .
.
The main assumption of this approach is that \(\mathbf{v}_{{r}}\) is defined constitutively, as assumed in (C-1). We have just mathematically proved that, under these modeling choices, the only thermodynamically admissible choice of the generalized traction yields expression  and
and  . The expression of the stress tensor in
. The expression of the stress tensor in  and given in (4.53), is standard in continuum poromechanics. However, the flux of linear momentum across the boundary
and given in (4.53), is standard in continuum poromechanics. However, the flux of linear momentum across the boundary  is different from the one adopted in the poromechanics literature, see, e.g., [13, 22], where the linear momentum brought by \(\mathbf{v}_{{r}}\) at the boundary is due solely to the fluid motion \(m_{{f}}\mathbf{v}_{{f}}\). This difference is even more evident if we write the pointwise form of the linear momentum balance (4.8) as
is different from the one adopted in the poromechanics literature, see, e.g., [13, 22], where the linear momentum brought by \(\mathbf{v}_{{r}}\) at the boundary is due solely to the fluid motion \(m_{{f}}\mathbf{v}_{{f}}\). This difference is even more evident if we write the pointwise form of the linear momentum balance (4.8) as
where the expression for the fluid acceleration has been introduced, while in the biphasic continuum models of poromechanics (see, e.g., [21, 22]) the momentum equation typically reads
Moreover, we compare  to the work of [25] where the authors compared the biphasic macroscopic approach to an homogenization result. Interestingly, the homogenization process brings a correction term that is included in the definition of the macroscopic partial stress tensors, a correction that takes the form (see Eq. (25) of [25]) \({ < \rho _{{(\alpha )}}\mathbf{v}_{{(\alpha )}}^{\prime}\otimes \mathbf{v}_{{(\alpha )}}^{\prime}>} \) where \(\rho _{{(\alpha )}}\) is the mass density of phase \(\alpha \) at the microscale, \(\mathbf{v}_{{(\alpha )}}^{\prime}\) is the difference between the microscale velocity of phase \(\alpha \) and its average velocity at the macroscale and <.> denotes the averaging operator over the representative volume element of the homogenization process. It is interesting to note the similarity between this averaging correction and
to the work of [25] where the authors compared the biphasic macroscopic approach to an homogenization result. Interestingly, the homogenization process brings a correction term that is included in the definition of the macroscopic partial stress tensors, a correction that takes the form (see Eq. (25) of [25]) \({ < \rho _{{(\alpha )}}\mathbf{v}_{{(\alpha )}}^{\prime}\otimes \mathbf{v}_{{(\alpha )}}^{\prime}>} \) where \(\rho _{{(\alpha )}}\) is the mass density of phase \(\alpha \) at the microscale, \(\mathbf{v}_{{(\alpha )}}^{\prime}\) is the difference between the microscale velocity of phase \(\alpha \) and its average velocity at the macroscale and <.> denotes the averaging operator over the representative volume element of the homogenization process. It is interesting to note the similarity between this averaging correction and  .
.
To summarize, the first expression of the linear momentum balance (4.55) is similar to the fluid mixture theories, while the second expression (4.56) is the usually adopted model in biphasic poromechanics. The direct application of thermodynamic principles performed in Sect. 4, where \(\mathbf{v}_{{r}}\) is a constitutive field and the linear momentum density is given by (4.6), results in (4.55). Finding the governing equations for the non-diffusive regime, i.e., releasing of assumption (C-1) and letting \(\mathbf{v}_{{r}}\) be a kinematic variable, requires a different method using the virtual power approach, as presented in Sect. 5.
4.3.2 Energy balance
Recall that in the energy balance introduced in (4.13), we use a total energy per unit volume \(\epsilon \) without partitioning it into an internal and kinetic part. To compare and contrast our result with those found in the existing literature, by recalling (4.21), we obtain with the help of (4.38) the following integral form of the energy balance

The kinetic terms  and
and  are consistent with our discussion in Sect. 4.3.1 but different from the biphasic approach where one would have expected a kinetic energy of the form
are consistent with our discussion in Sect. 4.3.1 but different from the biphasic approach where one would have expected a kinetic energy of the form
and a corresponding flux across the boundary
These differences are explained by the same argument as in Sect. 4.3.1, namely, the current theory is consistent with the fluid mixture approach.
It is equally interesting to look at the mechanical power expenditure at the boundary  and
and  . In biphasic theories for poromechanics, the mechanical power expenditure is a priori divided into two contributions [22]
. In biphasic theories for poromechanics, the mechanical power expenditure is a priori divided into two contributions [22]
such that \(\boldsymbol{\upsigma }_{{s}}\) is introduced as the Cauchy stress tensor applying to the solid material and \(\boldsymbol{\upsigma }_{{f}}\) on the fluid and the assumption that \(\boldsymbol{\upsigma }_{{f}} = - \phi p_{{f}}\mathbf{I}\), where \(\phi \) is the porosity and \(p_{{f}}\) is the hydrostatic pressure in the fluid. In Sect. 4, we do not postulate any partitioning of the total stress tensor \(\boldsymbol{\upsigma }\) into a solid and fluid part. In order to compare the above expression against our terms  and
and  , further manipulation of the these terms is needed as discussed next.
, further manipulation of the these terms is needed as discussed next.
4.3.3 Relating the chemical potential of the fluid to its pressure
We introduce the Lagrangian porosity \(\Phi \),Footnote 15 and relate it to the fluid density \(\rho _{{f}}\) by the saturation condition
Considering \(\Psi (M_{{f}}, \theta , \mathcal{I}(\mathbf{C})) = \widehat{\Psi} (\Phi , \rho _{{f}}, \theta , \mathcal{I} ( \mathbf{C}) )\) and taking its partial derivatives with respect to \(\rho _{{f}}\) and \(\Phi \)
We can postulate an additive decomposition of the free-energy, as is usual in large strain poromechanicsFootnote 16
where \(\Psi _{{mech}}\) is the strain energy of the dry porous medium (empty pores), \(\psi _{{f}}\) is the free-energy of the pure fluid and \(\Psi _{{int}}\) is defined as the interaction energy resulting from the fluid filling of the pores. Equations (4.61) and (4.53) now become
Pushing the comparison to the poromechanics literature further, we adopt the standard expression for the fluid energy (see [40])
where \(\mu _{{f}}^{0} (\theta )\) is the reference energy at temperature \(\theta\) and atmospheric pressure, \(\rho _{{f}}^{0}\) is the reference density of the fluid at atmospheric pressure and \(\chi _{{\theta }}\) is the isothermal compressibility coefficient.
Given specific choices of \(\Psi _{{int}}\), it can be shown that the following approximation holds for small deformations (see [17, 40])
where \(b_{{Biot}}\) is a constant coefficient, called Biot’s coefficient in linearized poroelasticity. It represents the contribution of the microscopic compressibility of the solid on the macroscopic stress. From (4.63) to (4.65)
In equation (4.66)3 we recognize the well-known Terzaghi’s effective stress, used in soil mechanics (consolidation theory), corrected by the Biot’s coefficient to account for the microscopic compressibility (in the limit of an incompressible solid material, \(b_{{Biot}}\rightarrow 1\)). Moreover, the saturation condition (4.60) gives equation (4.63)2 that generalizes Euler’s identity for the Gibbs’ free energy in thermodynamics of fluids.
Note also that (4.66)2 represents an equilibrium of pressure: the pressure of the fluid filling the pores is equal to \(\partial \Psi _{{int}}/ \partial \Phi \) that can be interpreted as the pressure in the solid at the microscopic scale. We have thus shown that our formalism allows us to retrieve the expected phenomenology and that the thermodynamic identity (4.63)2 is mathematically derived, instead of postulated as a general principle.
Finally, using (4.66), the contributions of  and
and  in the energy balance (4.57) are now
in the energy balance (4.57) are now

in agreement with the biphasic theory (4.59): in the first term, the stress working against \(\mathbf{v}_{{s}}\) is the solid stress component and in the second the stress working against \(\mathbf{v}_{{f}}\) is the fluid stress component while the third term retrieves the phenomenological flux of fluid energy associated to the relative motion \(\mathbf{v}_{{r}}\).
4.3.4 Darcy’s law
We now turn our attention to Darcy’s law, which models the fluid flow through the porous medium, derived in Sect. 4.2.4. For the sake of simplicity we neglect the thermal couplings and consider an isothermal process. Substituting (4.66) into the linear momentum balance (4.55) and (4.48)2 one obtains
where \(\nu \) is the kinematic viscosity of fluid, and \({\mathbf{D}}\) the permeability tensor of the porous material. One can see from the first part of (4.68) that \(\mathbf{v}_{{r}}\), as a combination of objective terms, is objective.
In the poromechanics literature [25] one finds the following form of Darcy’s law
or denoting by the tortuosity vector (\(a > 1\)), with a correction [22],
It is not possible to retrieve either (4.69) or (4.70) from (4.68) in a thermodynamically consistent continuum approach under the assumption of a constitutive field \(\mathbf{v}_{{r}}\).
The tortuosity correction is defined by [10] in the linear regime of acoustics in porous media to account for added mass effects at the microscale. In fluid-structure interaction theory, the concept of added mass is used to model the change of the apparent inertia of a solid oscillating in a fluid. At the macroscale, the tortuosity term appears as a coupling inertial mass between the solid and the fluid. In [22], the tortuosity is introduced as a correction to the kinetic energy with a multiscale argument: due to the fluid viscosity and the tortuous geometry of pores, the homogenized kinetic energy must be greater that the kinetic energy defined from macroscopic velocities in (4.58).
To better understand why we cannot retrieve (4.69) or (4.70) within the hypothesis (C-1) of Sect. 4, we note that Darcy’s law in the form (4.69) is derived from a dissipation of the form (see, e.g., [22])
A sufficient condition for (4.71) to hold is
with \(\mathbf{D}\) positive definite. There are several reasons why this conclusion is inconsistent with thermodynamics:
-
The purpose of the Coleman-Noll procedure is to find constitutive restrictions. By definition, the constitutive laws are specific to the material under consideration and describe the interactions between the particles of the body [63]. Therefore, no external load \(\mathbf{b}\) should appear in the dissipation when we apply the Coleman-Noll procedure.
-
In order to apply the Coleman-Noll procedure, we must ensure that the dissipation is positive for any admissible process. This gives restrictions on the admissible form of \(\mathbf{v}_{{r}}\) by means of Taylor expansions, as detailed in Sect. 4.2.4. It is not consistent to go straight to the conclusion that the first term of (4.71) is minus the second one, especially since the term \(\boldsymbol{\upgamma }_{{f}}\) involves \(\mathbf{v}_{{s}}\) and \(\mathbf{v}_{{r}}\).
-
Since the main assumption of this model is to consider \(\mathbf{v}_{{r}}\) as a constitutive variable, it must be objective (see Appendix A). The formulation with the inertial terms \({\boldsymbol{\upgamma }_{{f}} - \mathbf{b}}\) in (4.69) or the one with the inertial term \({\boldsymbol{\upgamma }_{{f}} - \mathbf{b} +\mathbf{a}}\) in (4.70) do not guarantee the objectivity of \(\mathbf{v}_{{r}}\).
-
Regarding the tortuosity coefficient in (4.70), it corresponds to a correction in the macroscopic kinetic energy due to an effect of added mass and inhomogeneity of fluid velocity at the microscale [22]. However, under the assumptions of this approach, we showed that adding such a term in the kinetic energy would not change the energy balance (4.13) as we do not specify the form of the kinetic energy. In fact, we have established that the only admissible form of the kinetic energy was
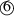 in (4.57).
in (4.57).
By assuming \(\mathbf{v}_{{r}}\) to be a kinematic descriptor in the next Sect. 5, we prove that it its possible to obtain expressions similar to (4.70) that accounts for tortuosity.
5 The relative fluid velocity \(\mathbf{v}_{{r}}\) as a kinematic descriptor
In Sect. 4, we have considered the fluid relative velocity \(\mathbf{v}_{{r}}\) as a constitutive variable. In spite of its advantages – objectivity of the governing equations, simplest possible form of conservation laws, consistently derived expressions for the total stress and energy flux – the model is not rich enough to capture such phenomena as Brinkman’s correction of Darcy’s law [15], the tortuosity correction in acoustics [10, 11], etc.
To capture these phenomena, we relax the fundamental assumption of Sect. 4 and consider the fluid relative velocity \(\mathbf{v}_{{r}}\) as an independent kinematic descriptor. Associated with this additional kinematic descriptor is an additional balance law, which is derived using the principle of virtual power. This has been widely used in solid mechanics [31, 38, 39] and in poromechanics [28, 57, 64]. Note that the use of a supplementary equation to model physical phenomena at the microscale is similar to the concept of microforces in phase transformation theories [32, 33, 43] and chemical diffusion in solids [4]. Following the statement of the corresponding balance laws, we use the thermodynamics of nonequilibrium processes to obtain the constitutive restrictions.
5.1 Kinematics
To write the power expenditures needed for the variational derivation of the balance laws, we follow the method proposed by [44] as stated in [4]: “the power expended by each ‘rate-like’ kinematic descriptor is expressible in terms of an associated force system consistent with its own balance”. We use a Lagrangian formalism: principles are written in the reference configuration of the skeleton.
Recall the definition of the skeleton mapping introduced in Sect. 2: \(\mathbf{x} = \boldsymbol{\chi } ( \mathbf{X}, t)\) where \(\mathbf{X}\) is the position of a skeleton material point in the reference configuration of the skeleton. The mapping \(\boldsymbol{\chi }\) is considered as the kinematic descriptor of the skeleton deformation. We also need a kinematic descriptor for the fluid motion. We use the formalism of Wilmański [69, 72] and define the fluid inverse mapping \(\boldsymbol{\chi }_{{f}}^{-1}\)
where \(\mathbf{X}_{{f}}(\mathbf{x},t)\) is defined as the position in the skeleton reference configuration of the fluid particle that coincides at time \(t\) with the skeleton at \(\mathbf{x}\). As introduced in [69], the motion of a fluid particle \(\mathbf{v}_{{f}} \ \mathrm{d}t\) during a time interval \(\ \mathrm{d}t\) is due to the motion of the skeleton \(\mathbf{v}_{{s}} \ \mathrm{d}t\) plus the change of the reference position of the fluid , thus giving the following expression for , defined as the reference relative velocity \(\mathbf{V}_{{r}}\)
Appealing to (4.52)1, the localization of the skeleton mass balance (4.1) yields the counterpart of (4.2)
Therefore, if we assume the continuum to be uniform in the reference configuration, there is no need to account for \(M_{{s}}\) as a kinematic descriptor.
Also from (4.52)2, the mass balance (4.3) yields
where \(\boldsymbol{\nabla } \) is the referential gradient (not be confused with its current counterpart \({\scriptstyle \boldsymbol{\nabla }}\)) defined in Sect. 2. From (5.4) it follows that the time rates cannot be assigned independently of its spatial gradient \(\boldsymbol{\nabla } M_{{f}}\).
5.2 Quasistatic regime
5.2.1 Power expenditures
Let \(P_{{\mathcal{V}}}^{i} \) be the internal power expenditure in any Lagrangian control volume \(\mathcal{V}\), and \(P_{{\mathcal{V}}}^{e}\) the external power expenditure and choose the following set of kinematic descriptors
The choice of (5.5) is made from the kinematic fields \(\left \lbrace \boldsymbol{\chi } , \mathbf{X}_{{f}}, M_{{f}} \right \rbrace \) presented in Sect. 5.1 and their spatial gradients. The first-order gradients are considered for all fields while the second-order gradient is only considered for the skeleton deformation in order to retrieve the second-order gradient poromechanics features [64]. One could have considered higher-order gradients, but our choice is made to limit the complexity of the derivation; there are no conceptual difficulties to extending the model to higher gradients.
Following the approach of [4, 44], the time rates of (5.5) must expend power against associated conjugate forces. Hence one can define the following general expression for the internal power expenditure \(P_{{\mathcal{V}}}^{i}\) in a material control volume in the reference configuration

where \(\pi \) is the scalar power conjugate of , and \(\boldsymbol{\beta }\) (resp. \(\mathbf{t}\), and \(-\boldsymbol{\xi }\)) is the vector field conjugate of (resp. and ). Also, \(-\mathbf{S}^{\top}\) (resp. \(-\boldsymbol{\Sigma }^{\top}\)) is the second-order tensor conjugate of (resp. ). Finally \(- \boldsymbol{\mathfrak{C}}^{\top}\) is the third-order tensor conjugate of . The adopted minus signs and transpositions are introduced for convenience as they allow to retrieve familiar expressions of continuum mechanics.
Similarly to (5.6), the external power expenditure \(P_{{\mathcal{V}}}^{e}\) for a control volume \(\mathcal{V}\) is defined

Some confusion may arise about the current notations compared to similar ones in Sect. 4. Given the high number of fields that are manipulated here in Sect. 5, we chose to associate a single letter subscript to the external power conjugate of each kinematic descriptor: we denote with the subscript \((~)_{{A}}\) (resp. \((~)_{{V}}\)) the conjugate field quantity associated to the external power expenditure on the surface (resp. in the volume). No subscript is used for the fields involved in the internal power expenditure.
We consider that, for any arbitrary time, all the kinematic fields of \(\mathcal{K}\) in (5.5) are known and fixed and define independently from them, the set of virtual velocitiesFootnote 17
such that (5.4) is verified. In analogy to (5.6) we define the internal virtual power \(P_{{\mathcal{V}}}^{i}(\mathcal{K}^{\ast})\)

and in analogy to (5.7) we define the external virtual power \(P_{{\mathcal{V}}}^{e}(\mathcal{K}^{\ast})\) by

5.2.2 Material frame indifference principle
The principle of material frame indifference states that, for any change of current frame, any Lagrangian control volume \(\mathcal{V}\) (unchanged by any change of current frame) and any virtual velocities set \(\mathcal{K}^{\ast}\)
where the prime \((\ )^{\prime}\) denotes the image in the new frame.
A change of current frame can be described by a proper orthogonal tensor \(\mathbf{Q}(t)\) and a translation vector \(\mathbf{a}(t)\) such that the skeleton mapping is transformed as
By definition of the scalar \(M_{{f}}\), it is unchanged by the change of current frame. Also, since \(\boldsymbol{\nabla } \) is the gradient in the reference frame, it is invariant by change of current frame. Following [4], we assume that the virtual velocity field of skeleton is transformed as the actual one, i.e.,
Finally, by (5.2), the Lagrangian relative velocity is also invariant by any change of current frame. A direct substitution in (5.11), accounting for (5.4), gives for any Lagrangian volume \(\mathcal{V}\)

The pointwise form of (5.14) must hold for any virtual velocity field , which yields the condition
Assigning arbitrary values to the vector and the virtual velocity gives the following condition
which can be seen as the invariance by translation of the internal power expenditure. Varying and arbitrarily and setting , yields the following transformation
Varying and arbitrarily yields
Finally, note that the second-order tensor is a skew tensor. Making it vary arbitrarily with \(\mathbf{Q} = \mathbf{I}\) gives the symmetry conditionFootnote 18
which corresponds to the local form of the angular momentum balance.
In the relations (5.15) and (5.18)2, one can see that because of the mass conservation (5.4), the scalar \(\pi \) does not contribute by itself and can enter in the definition of \(\boldsymbol{\beta }\) and \(\boldsymbol{\Sigma }\). Henceforth, we will then omit the contribution of \(\pi \) and work with the following renaming of the fields \(\boldsymbol{\beta }\) and \(\boldsymbol{\Sigma }\)
and the same renaming is valid for \(\boldsymbol{\beta }_{{A}}\), \(\boldsymbol{\beta }_{{V}}\), \(\boldsymbol{\Sigma }_{{A}}\) and \(\boldsymbol{\Sigma }_{{V}}\). This renaming is not applicable to the work conjugate of \(\boldsymbol{\nabla } M_{f}\). By taking the gradient of (5.4), one can see that can be expressed as a function of and can take any arbitrary values, independently of the other rates, thus explaining (5.18)1.
5.2.3 Principle of virtual power
The principle of virtual power states that following equality must hold for any virtual velocities (5.8) and any volume \(\mathcal{V}\)
Introducing the fields
where \(\mathbf{N}\) is the outward unit normal vector to the boundary \({\partial \mathcal{V}}\), and performing successive integrations by parts in (5.21) yields the following form of the principle of virtual power, for any control volume \(\mathcal{V}\) and for any virtual velocities

The balance law (5.23) must hold for any and , giving the following local equationsFootnote 19
The integrals on the boundary \(\partial \mathcal{V}\) in (5.23) must hold for any rates and any volume \(\mathcal{V}\), yielding
Equation (5.24)1 is the extension of the usual linear momentum balance to the framework of second-gradients poromechanics [64], and we can then interpret \(\tilde{\mathbf{t}}_{{V}}\) as the usual mechanical body force. Accordingly, the condition at the interface (5.25)2 gives a boundary condition for the generalized stress tensor \(\mathbf{S}^{\top}- \boldsymbol{\nabla } \boldsymbol{\cdot } \boldsymbol{\mathfrak{C}}^{\top}\). Also note that the second-gradient framework gives a supplementary interface condition (5.25)3 on \(\boldsymbol{\mathfrak{C}}\).Footnote 20
The principle of virtual power also enables us to derive a supplementary balance equation (5.24)2. Note that this supplementary equation is derived within a fully macroscopic framework, without postulating any linear momentum balance on the fluid at the microscale. This supplementary balance law is accompanied by two interface conditions (5.25)5 and (5.25)6.
Having derived the balance laws of the system, we can now use the Coleman-Noll procedure to obtain constitutive restrictions as done in Sect. 4.
5.2.4 Energy balance and entropy imbalance
We start by writing the integral form of the energy balance in its most general form
where the subscript \(R\) indicates Lagrangian quantities, associated with the reference configuration, as opposed to the Eulerian quantities used in Sect. 4. In analogy to (4.13), we consider an open system and the unknown flux at the boundary is denoted by \(\mathbf{h}_{{R}}\).
Similarly to (4.17), we write the integral form of the entropy inequality as
where, \(\mathbf{q}_{{R}}/\theta \) is the entropy flux at the boundary. In the present quasistatic setting, we introduce the Lagrangian free energy \(\Psi \) and the flux difference vector \(\mathbf{k}_{{R}}\)
Combining (5.26) and (5.27) and appealing to (5.28), the local form of the dissipation equation yields

5.2.5 Thermodynamic restrictions
To derive the set of thermodynamic restrictions, we define the following set of thermodynamic variablesFootnote 21
We only consider the second gradient of the skeleton deformation mapping and not the second gradient of the fluid mapping. This choice is motivated by the previous choice of kinematic variables of the principle of virtual power (see (5.5)). Also note that we dropped the trivial dependence on \(M_{{s}}\) which is constant by assuming a uniform distribution of the reference skeleton mass density.
Applying the chain rule, (5.29) can be written as

Due to the fluid mass conservation (5.4), cannot be assigned arbitrary values independently from and . Taking the gradient of (5.4) yields
such that cannot be assigned arbitrary values either. However, considering the second gradient of (5.4), the rate can be assigned arbitrarily values, independently of the fields of (5.30). Therefore it is not needed to substitute the mass balance in the corresponding term in (5.31).
Substituting with (5.4) into (5.31) and setting gives

Before extracting thermodynamic restrictions from (5.33), attention must be paid to the term involving \(\mathbf{k}_{{R}}\). The divergence term in (5.33) can be written as

where \(f\) is only a function of the thermodynamic variables (5.30). Substituting (5.34) into (5.33) and making \(\boldsymbol{\nabla } ^{3}\boldsymbol{\chi }\), \(\boldsymbol{\nabla } ^{3}M_{{f}}\), \(\boldsymbol{\nabla } ^{2}\theta \), \(\boldsymbol{\nabla } ^{2}\mathbf{X}_{{f}}\) vary arbitrarily gives the following necessary restrictions:
As opposed to the results of Sect. 4, the restrictions (5.35) do not imply a necessary value for the unknown flux. It is possible to extract information on the admissible forms that \(\mathbf{k}_{{R}}\) could take and the reader can refer to the extended work of [27, 31, 59] for procedures to derive such admissible forms. The choice of the explicit expression of \(\mathbf{k}_{{R}}\) can be based on the phenomenological behavior observed experimentally.
The standard choice \(\mathbf{k}_{{R}}=\boldsymbol{0}\) is compatible with these restrictions. Note that this choice is not a necessary consequence of the thermodynamic restrictions as in Sect. 4, since this theory is general enough to allow other forms of the unknown energy flux \(\mathbf{k}_{{R}}\).
Consequently, from (5.33) and varying , , , , , , , , , arbitrarily, one obtains the following necessary conditions
The dissipation inequality (5.33), using the above results of (5.36), simplifies to
From (5.37) and (5.36) one has
where the dissipative tensors \(\mathbf{S}^{d} \), \(\boldsymbol{\Sigma }^{d}\) and \(\boldsymbol{\beta }^{d}\) can depend on the rates , and .
Consequently, the dissipation equation (5.37) can be restated as
At this point, the same procedure as in Sect. 4.2.4 can be applied to write Taylor expansions of \(\mathbf{S}^{d} \), \(\boldsymbol{\Sigma }^{d}\), \(\boldsymbol{\beta }^{d}\) and \(\mathbf{q}_{{R}}\). For the sake of simplicity, we neglect the cross couplings and consider only linear terms

where \(\mathbf{D}_{{R}}\) and \(\mathbf{K}_{{R}}\) are second-order and  and
and  are fourth-order positive semi-definite tensors, thus completing the derivation of the thermodynamic restrictions.
are fourth-order positive semi-definite tensors, thus completing the derivation of the thermodynamic restrictions.
We retrieve the usual expression for the viscoelasticity of the solid skeleton through the fourth-order tensor  associated to the dissipative part of the stress tensor \(\mathbf{S}^{d}\). Also, recalling from (5.2) that is the reference relative velocity, the fourth-order tensor
associated to the dissipative part of the stress tensor \(\mathbf{S}^{d}\). Also, recalling from (5.2) that is the reference relative velocity, the fourth-order tensor  can be interpreted as the macroscopic viscosity tensor associated to the motion of the fluid.
can be interpreted as the macroscopic viscosity tensor associated to the motion of the fluid.
5.2.6 Summary and discussion
By substituting the above obtained results of (5.36), (5.38) and (5.40) into the balance laws (5.24), derived from the principle of virtual power, we obtain the final form of the two governing equations. The first, associated to and corresponding to (5.24)1 is the quasistatic linear momentum balance

The second governing equation, associated to and corresponding to (5.24)2 states the supplementary linear momentum balance associated to the fluid flow

As expected, the quasistatic linear momentum balance (5.41) reduces in the absence of inertial effects to its counterpart (4.55) or (4.56) obtained in Sect. 4. The formalism adopted in Sect. 5 allows for additional physics, as seen from viscoelasticity and second-gradient effects (see also [64]). The advantage of the virtual power approach is evident in the supplementary linear momentum balance law (5.42), which provides a generalized form of Darcy’s law with Brinkman correction [15], and a Cahn-Hilliard type contribution modeling effects of the gradients of mass densities (see also [4]).
Also note the status change of Darcy’s law, which was a constitutive law in Sect. 4 and now appears as a balance equation. If in addition we consider a uniform material, the dependence of \(\Psi \) on the fluid displacement \(\mathbf{X}_{{f}}\) can be dropped so that \({\partial \Psi}/{\partial \mathbf{X}_{{f}}} = \boldsymbol{0}\), thus further simplifying (5.42).
5.3 Dynamical regime
By considering the fluid motion as a kinematic descriptor in Sect. 5.2, we succeeded in extending the model of Sect. 4 to account for viscoelasticity, second-gradient mechanics in the linear momentum balance, and high-order corrections of Darcy’s law such that Brinkman’s term, and a Cahn-Hilliard type contribution. However, this model is still not rich enough to account for tortuosity, considered next.
5.3.1 The power of acceleration
To include inertial effects, we need to augment the quasistatic principle of virtual power (5.21) by introducing the virtual power of acceleration \(P_{{\mathcal{V}}}^{a} (\mathcal{K}^{\ast})\) such that
We have to provide an explicit expression for \(P_{{\mathcal{V}}}^{a} (\mathcal{K}^{\ast})\) and thus we define the macroscopic Eulerian acceleration of the skeleton \(\boldsymbol{\gamma }_{{s}}\), of the fluid \(\boldsymbol{\gamma }_{{f}}\) and of the average continuum \(\boldsymbol{\gamma }_{{v}}\) by
where \(\mathbf{v}_{{f}}(\mathbf{x},t)\) is the fluid velocity, defined in Sect. 4 and linked to \(\boldsymbol{\chi }\) and \(\mathbf{X}_{{f}}\) by (5.2), and \(\mathbf{v}\) is the average velocity of the continuum defined in (3.4)2.
To define the power of acceleration we consider two alternatives. The first follows the approach of biphasic theories [28, 33, 38, 39], by summing the inertia of each continuum

where, in the current configuration, the power of acceleration is macroscopically expended by the skeleton velocity (resp. fluid velocity) against the skeleton acceleration (resp. fluid acceleration).
The second alternative, of an averaged continuum, has a unique acceleration \(\boldsymbol{\gamma }_{{v}}\) and takes the form

In the next subsections, we explore the different outcomes of these two choices.
5.3.2 Reconciliation with the biphasic theory
In this section, we use the definition of the virtual power of acceleration given in (5.45). By applying again the procedure followed in Sect. 5.2.4 and Sect. 5.2.5 one obtains the following, counterpart to (5.28), definitions of the free-energy \(\Psi \) and the vector \(\mathbf{k}_{{R}}\)
For the reasons given in Sect. 5.2.5, we take \(\mathbf{k}_{{R}} = \boldsymbol{0} \), leading to the linear momentum balance

and, using the reference relative velocity \(\mathbf{V}_{{r}}\) in (5.2), to the supplementary balance law for the fluid

In the linear momentum balance (5.48), we retrieve the form of inertia that usually appears in the biphasic approach of poromechanics (see (4.69)). More importantly, in the extended Darcy’s law (5.49), we retrieve the inertial correction \(M_{{f}}\mathbf{F}^{\top}\boldsymbol{\cdot } \boldsymbol{\gamma }_{{f}}\) that is present in the work of [21, 22, 25] and was discussed in Sect. 4.3.4. However, it is important to note the difference between these works and the current result, since in their approach, the Darcy’s law was derived constitutively and we have shown in Sect. 4 that this approach cannot give the current expression (5.49).
The fundamental difference in our approach is the fact that in (5.49), the external body force \(\tilde{\boldsymbol{\beta }}_{{V}}\) is thermodynamically distinctFootnote 22 from the external body force of the linear momentum balance \(\tilde{\mathbf{t}}_{{V}}\), thus resolving the problem of objectivity associated to Darcy’s law in the biphasic theory, as discussed in Sect. 4.3.4. Indeed, the external load \(\tilde{\boldsymbol{\beta }}_{{V}}\) can transform so that (5.49) stays objective while in (4.69), the body force \(\mathbf{b}\) cannot transform to ensure the objectivity of both the linear momentum balance (4.56) and Darcy’s law (4.69).
5.3.3 Reconciliation with the mixture approach
Consider the second choice of virtual power of acceleration (5.46). By applying again the procedure followed in Sect. 5.2.4 and Sect. 5.2.5 one obtains the following, counterpart to (5.28), definitions of the free-energy \(\Psi \) and the vector \(\mathbf{k}_{{R}}\)
Once again, taking \(\mathbf{k}_{{R}} = \boldsymbol{0} \), and using (5.2) leads to the following linear momentum balance

and the supplementary balance law for the fluid

This result is hardly surprising, since the direct approach of Sect. 4 is based on a constitutive assumption of type-I, defining the linear momentum balance as \(m_{{s}}\mathbf{v}_{{s}}+m_{{f}}\mathbf{v}_{{f}}\), which means that we adopted the framework of the average medium theory (see discussion pertaining to equation (4.6)).
5.3.4 Tortuosity correction
The definitions (5.45) and (5.46) for the virtual power of acceleration enabled us to retrieve respectively the biphasic and the mixture theories from a unified macroscopic framework that is consistent with thermodynamics and the principle of material frame indifference. However, these models still cannot account for the dynamic tortuosity correction that has been described in [10, 12] as an added mass effect at the microscale.
From a macroscopic point of view (e.g., in [22]), the tortuosity correction is also associated to the difference between the average of the fluid kinetic energy at the microscale, and the macroscopic kinetic energy computed from the macroscopic velocity \(\mathbf{v}_{{f}}\). Indeed, the nonuniformity of the fluid velocity at the microscopic scale (due to viscosity and/or the tortuous geometry of the pores), implies that the average of the local kinetic energy should be greater that the macroscopically computed kinetic energy. Note that this interpretation of the tortuosity correction from a kinetic energy point of view could be also reinterpreted from the added mass effect of [10, 12]. Indeed, in fluid-structure interactions, it is a common result to find that the inertial mass involved in the added mass effect is computed from the kinetic energy of the fluid that is put in motion by the solid oscillations.
In order to retrieve the tortuosity correction, we add a term in the definition of the virtual power of acceleration, in the spirit of a modified inertia due to the relative motion of the fluid with respect to the solid. The simplest correction would be to modify (5.45) as follows
where \(c_{{a}}\) is a constant scalar coefficient. In this case, the free energy \(\Psi \) takes the form
while the unknown vector \(\mathbf{k}_{{R}}\) remains the same as in (5.47). The linear momentum balance is identical to the biphasic linear momentum balance (5.51) but Darcy’s law changes to

We have developed a methodology to derive a poromechanical model in finite strain, consistent the principle of material frame indifference. Our approach is different from the work of [74], since this author introduces an objective relative acceleration as a thermodynamic variable, in order to proceed to the Coleman-Noll procedure.
5.4 Comparison to Biot’s linear acousto-poro-elasticity theory
It is of interest to compare the linearized version of the general governing equation of porous media (5.48) and (5.55) to the linearized Biot’s theory of acousto-poro-elasticity [10, 11, 75]. The latter can be described by the following coupled systemFootnote 23
where \(m_{{s}}^{0}\), \(m_{{f}}^{0}\) are respectively the initial apparent mass density of the skeleton and the fluid, \(a\) (named tortuosity coefficient, see, e.g., [10, 74]) and \(\pi \) are constant scalars. In addition, \(\boldsymbol{\upsigma }_{{s}}\) and \(p_{{f}}\) respectively represent the stress of the solid and the pressure of the fluid; assuming the initial state is not preconstrained, these quantities can be written as follows
with \(A\), \(N\), \(Q\), \(R\) material constants. In the above equations is the skeleton displacement of a solid particle initially at \(\mathbf{X}\) and \(\mathbf{U}\) is the fluid displacement of a fluid particle initially at \(\mathbf{X}_{{f}}\), related by
which for small strains (Lagrangian and Eulerian descriptions coincide, \({\mathbf{F }} = {\mathbf{I }}\)) (5.58) agrees with (5.2).
Note that in Biot’s linear acoustics theory for poroelastic saturated materials, neither the porosity nor the fluid density are independent fields. The coupled system of equations is written as functions of the two displacements, the one of the skeleton \(\mathbf{u}\) and the one of the fluid particle \(\mathbf{U}\) (see [75]). Equation (5.56)1 represents the total linear momentum balance, while equation (5.56)2 is the linear momentum balance of the fluid that can be also interpreted as Darcy’s law, depending on the macroscopic approach adopted.
Upon linearization of (5.48) and (5.55) about the initial state of the system, neglecting body forces and high-order gradient terms and introducing the standard notation for the small strain gives to the first order
where at small strains and for an isotropic material, we have defined the Darcy tensor in (5.55) as . A direct comparison of the left-hand side of (5.59)2 to its counterpart in (5.56) gives \(c_{{a}}=m_{{f}}^{0}\left ( {a-1} \right ) \).
In (5.59)2, one can see a dependence of \(\psi \) on \({\scriptstyle \boldsymbol{\nabla }}\mathbf{X}_{{f}}\), which represents the macroscopic deformation gradient of the fluid particle. Recalling the isotropy of the porous medium, we further assume that in the linear kinematics regime, the Helmholtz free-energy \(\psi \) only depends on the volumetric change \({\scriptstyle \boldsymbol{\nabla }} \boldsymbol{\cdot } \mathbf{X}_{{f}}\) and hence for small strains and for isotropic material, we define the small strain, isotropic, Helmholtz free energy as the sum of \(\psi _{{f}}\), associated to the fluid filling the pores and its interaction with the skeleton, plus the elastic energy of the skeleton \(\psi _{{s}}\)
where \(\lambda \) and \(G\) are respectively the Lamé constants of the linearly elastic skeleton. By comparing the right-hand sides of (5.56) and (5.59), one can rewrite the quantities \(\boldsymbol{\upsigma }_{{s}}\) and \(p_{{f}}\) in (5.57)
To compare (5.61) with (5.57), we must relate the apparent fluid mass density change \(m_{{f}}- m_{{f}}^{0}\) to the volumetric change \({\scriptstyle \boldsymbol{\nabla }} \boldsymbol{\cdot } \mathbf{X}_{{f}}\). This result is obtained by linearizing the fluid mass balance (5.4) and assuming \(\left \vert (m_{{f}}- m_{{f}}^{0})/m_{{f}}^{0} \right \vert \ll 1\) and \(\left \vert {\scriptstyle \boldsymbol{\nabla }}\left ( {{m_{{f}}}/{m_{{ f}}^{0}}} \right ) \right \vert \ll 1\) yielding the following linear equation for small strains
We are now in a position to establish that for the linearized, small-strain case, the system (5.56), (5.57) can be retrieved from (5.48) and (5.55). A substitution of (5.60) into (5.61), gives upon linearization about \(m_{{f}}^{0}\), \({\scriptstyle \boldsymbol{\nabla }} \boldsymbol{\cdot } \boldsymbol{U} = 0\), \(\boldsymbol{\epsilon } = \boldsymbol{0}\) and in view of (5.62) the following expressions for the constants in (5.57)
By assuming the decomposition (5.60) of the free energy in the small strain regime, we have thus recovered upon linearization of the general model presented in Sect. 5, the linearized Biot’s theory of acousto-poro-elasticity [10, 11, 75].
6 Conclusion
Poromechanics is a vital research field in mechanics with a long history, starting with the pioneering works of Terzaghi and Biot and continues vigorously to date with applications ranging from soil mechanics to gels and tissue engineering. As presented in Sect. 1, the goal of this paper is to derive a thermodynamically consistent continuum theory of large-strain poroelasticity satisfying the principle of material frame indifference, without recourse to mixture theory and by making the minimal number of assumptions. In doing so, we are able to clarify the modeling assumptions underlying different models found in the literature.
Specifically, we treat the porous medium as a single continuum, whose fluid content changes with the motion of the fluid relative to the skeleton. In Sect. 4, we consider the relative velocity of the fluid \(\mathbf{v}_{{r}}\) as a constitutive field. In this case and for an isotropic skeleton we show, using the direct approach of continuum mechanics and the Coleman-Noll procedure, that there is a unique thermodynamically consistent set of field equations and constitutive relations, which we subsequently compare to existing models. These equations are similar to those of fluid-mixture theories in which a quadratic fluid relative velocity appears in the linear-momentum balance [42, 45, 59], but they differ from those of biphasic models [21, 22]. Interestingly, the resulting quadratic velocity correction is similar to a term that arises during the homogenization of the biphasic model but cannot be explicitly calculated [25]. Nonetheless, the quadratic corrective term is negligible compared with the orders of magnitude generally considered in boundary-value problems of poromechanics.
The governing equations derived under the assumption that \(\mathbf{v}_{{r}}\) is a constitutive field are not rich enough to account for such features as tortuosity and Brinkman’s correction. In Sect. 5, we relax this assumption by treating the relative fluid velocity as an independent kinematic variable. Using the principle of virtual power we derive a set of equations appropriate for large strains and consistent with thermodynamics and material frame indifference. Depending on the definition of the power of acceleration, we can retrieve in a thermodynamically consistent way to obtain the corresponding governing equations with and without the quadratic velocity term.
Importantly, the use of the principle of virtual power circumvents the need to postulate a-priori the linear-momentum balance for the fluid, as is done on a phenomenological basis in mixture theory. Moreover, since we do not postulate separate momentum balances for the solid and fluid phases, we do not need to introduce terms to account for the interactions between these phases, as is done in mixture theory, a task that would have required further phenomenological assumptions. We can thus obtain from such a balance Darcy’s law in its most general form, see (5.42), which contains Brinkman’s correction, a term of the Cahn-Hilliard type and an additional contribution due to the dilation of the fluid, as given by \(\partial \Psi /\partial \boldsymbol{\nabla }\mathbf{X}_{{f}}\).
We also note the importance of having an external body loading \(\tilde{\boldsymbol{\beta }}_{{V}}\) in Darcy’s law that is thermodynamically independent from the external load of the linear momentum balance \(\tilde{\mathbf{t}}_{{V}}\). This enables us to ensure the objectivity of Darcy’s law. Depending on the explicit choice for the power of acceleration, we show that we can retrieve the dynamic formalism of Sect. 4 (similar to fluid mixture, where inertia is that of the averaged continuum), and the formalism of the biphasic theories. Finally, we show that our method also allows for formulations with tortuosity corrections that are consistent with the laws of thermodynamics at finite strains as well as with the linear acousto-poro-elasticity theories of Biot (see Sect. 5.4).
In conclusion, the two different but complementary approaches proposed in Sect. 4 and Sect. 5 clarify the bases of various nonlinear theories of poromechanics, while keeping the number of modeling assumptions to a minimum and ensuring the compliance of the governing equations with the principle of material frame indifference. We finally add that the proposed methodology should be helpful in obtaining homogenization models that aim to relate micromechanical mechanisms to macroscopic behavior and in guiding the selection of the energy densities and the dissipative tensors by providing a consistent framework for the thermodynamic restrictions of the resulting governing equations.
Notes
It is tacitly assumed that all boundary value problems here are set in the three-dimensional Euclidean space
 . A Cartesian basis is used for all field quantities, although the proposed dyadic notation allows for a straightforward conversion to curvilinear coordinates.
. A Cartesian basis is used for all field quantities, although the proposed dyadic notation allows for a straightforward conversion to curvilinear coordinates.For a detailed explanation of the localization procedure see any standard textbook in continuum mechanics, e.g., [58].
No further restriction is obtained from the jump relations.
It is common, e.g., [22], to write the kinetic energy density of the continuum as the sum of the macroscopic energy of the skeleton and the fluid \(m_{{s}}\mathbf{v}_{{s}}^{2}/2+m_{{f}}\mathbf{v}_{{f}}^{2}/2\). In order to account for the inhomogeneity of the fluid velocity at the microscopic scale (due to the viscosity of the fluid and to the geometrical tortuosity of the pores channels), a tortuosity correction \(a\mathbf{v}_{{r}}^{2}\) can also be introduced [21, 22]. However, as discussed in the sequel, this assumption leads to objectivity inconsistencies in the Darcy’s law (Sect. 4.3.4).
In this part, we assume that no energy is carried by the discontinuity surface, i.e., no surface tension phenomena.
For comparison with existing theories, the reader can for instance refer to [17, 22], where the total stress is decomposed into a solid and a fluid component, such that the power expenditure is \(\int _{\partial v} [ (\boldsymbol{\upsigma }_{{s}} \boldsymbol{\cdot } \mathbf{n}) \boldsymbol{\cdot } \mathbf{v}_{{ s}}+(\boldsymbol{\upsigma }_{{f}} \boldsymbol{\cdot } \mathbf{n}) \boldsymbol{\cdot } \mathbf{v}_{{f}}] \ \mathrm{d}a\) with a flux of fluid internal and kinetic energy \({- \int _{\partial v } [(\epsilon _{{f}} + (1/2){m_{{f}}} \mathbf{v}_{{f}}^{2}) (\mathbf{v}_{{r}} \boldsymbol{\cdot } \mathbf{n})]\ \mathrm{d}a}\), which requires the use of supplementary fields \(\boldsymbol{\upsigma }_{{s}}\), \(\boldsymbol{\upsigma }_{{f}}\), \(\epsilon _{{f}}\). To close the problem, the addition of supplementary fields requires supplementary equations and constitutive restrictions, and most of the times supplementary phenomenological assumptions.
This principle states that the intrinsic response of the continuum must be independent of the frame of reference used to describe the system in the current configuration. See Appendix A for a detailed explanation of the principle.
This is the approach chosen in our work. However other procedures do exist to deal with constitutive restrictions. For instance the modeling work of [70, 72] is based on a thermodynamic approach using Lagrange multipliers. The interested reader is referred to the work of [54] for details on this alternative.
We can now use this terminology since \(\psi \) is independent of velocities
For the isotropic material, note the identity \(\mathbf{B} \boldsymbol{\cdot } (\partial \psi /\partial \mathbf{B}) = (\partial \psi /\partial \mathbf{B}) \boldsymbol{\cdot } \mathbf{B} =\mathbf{F} \boldsymbol{\cdot } ( \partial \psi /\partial \mathbf{C}) \boldsymbol{\cdot } \mathbf{F}^{\top}\) where is the right Cauchy-Green tensor.
Although a restrictive hypothesis, it allows us to find a unique energy flux \(\mathbf{h}\) using the principle of material frame indifference and thermodynamics.
Where \(O(3)\) is the set of all orthogonal rank two tensors \(\mathbf{Q}\), i.e., \(\mathbf{Q} \boldsymbol{\cdot } \mathbf{Q}^{\top}= 1\), where \(\det \mathbf{Q}=\pm 1\).
The minus signs introduced in order to end with positive definite thermal conductivity and dissipation tensors, according to standard literature conventions.
In the dissipation equation (4.39) the term \(c_{{f}}{\scriptstyle \boldsymbol{\nabla }} \boldsymbol{\cdot } \boldsymbol{\upsigma }^{e} + m_{{f}}{\scriptstyle \boldsymbol{\nabla }}\mu _{{f}}\) appears as the conjugate of \(\mathbf{v}_{{r}}\).
Volume of pores per unit reference volume of skeleton; related to the Eulerian porosity \(\phi \) by \(\Phi = \mathrm{J}\phi \).
We use the upper asterisk \((\ )^{\ast}\) to distinguish the virtual velocities from the corresponding actual fields.
Recall that \(\boldsymbol{\mathfrak{C}}\,\raisebox {6pt}{\rotatebox {90}{$\mathbin {{\normalbaselines \text{\textbf {.}}\text{\textbf {.}}\text{\textbf {.}}}}$}}\,( \boldsymbol{\nabla } ^{2} \boldsymbol{\chi })^{\top}= \mathfrak{C}_{{ijk}} \boldsymbol{\nabla } _{{jk}}^{2} \chi _{{i}}\) and \(\boldsymbol{\mathfrak{C}}^{\top} \!\boldsymbol {:}\!\boldsymbol{\nabla } ^{2} \boldsymbol{\chi } = \mathfrak{C}_{{ijk}} \boldsymbol{\nabla } _{{ jk}}^{2} \chi _{{l}} \mathbf{e}_{{i}}\mathbf{e}_{{l}}\).
From (5.23) one can see that the introduction of \(\mathbf{S}_{{V}}\), \(\boldsymbol{\Sigma }_{{V}}\), \(\boldsymbol{\xi }_{{V}}\) and \(\boldsymbol{\mathfrak{C}}_{{V}}\) was not necessary and that we could have worked from the beginning with the body external loadings \(\tilde{\mathbf{t}}_{{V}}\) and \(\tilde{\boldsymbol{\beta }}_{{V}}\) (the first one acting in the linear momentum balance (5.24)1 and the second one acting in the supplementary balance equation (5.24)2).
In the literature, \(\boldsymbol{\mathfrak{C}}\) is sometimes called the hyper-stress tensor [64].
One could have considered higher-order spatial gradients of \(M_{{f}}\), however, there is no difficulty in showing that the constitutive restrictions do not imply any dependency on them. We did not consider the time derivatives of the variables \(M_{{f}}\), \(\boldsymbol{\nabla } M_{{f}}\) and \(\boldsymbol{\nabla } ^{2}M_{{f}}\) either, since the fluid mass balance (5.4) connects their variations to variables in (5.30).
When solving boundary value problems, we can still choose to take them both equal to gravity.
Recall that by definition, a constitutive variable is required to be objective.
In the general theory of material frame indifference [60, 61], the change of frame occurs through a proper orthogonal transformation. This enables the theory to account for polarized materials with chiral symmetries. In the current model, following the same argument as [20] in their remark about equation (3.13), we extend the principle to non-proper orthogonal tensors. Indeed in the present case, we assume there is no microstructural polarization of the material, hence the possibility to take \(\mathbf{Q}=-\mathbf{I}\).
Note that their determinant is −1, these tensors represents planar symmetries.
References
Allaire, G.: Homogenization of the stokes flow in a connected porous medium. Asymptot. Anal. 2(3), 203–222 (1989). https://doi.org/10.3233/ASY-1989-2302
Allaire, G., Raphael, A.L.: Homogenization of a convection–diffusion model with reaction in a porous medium. C. R. Math. 344(8), 523–528 (2007). https://doi.org/10.1016/j.crma.2007.03.008
Allaire, G., Mikelić, A., Piatnitski, A.: Homogenization of the linearized ionic transport equations in rigid periodic porous media. J. Math. Phys. 51(12), 123103 (2010). https://doi.org/10.1063/1.3521555
Anand, L.: A cahn–hilliard-type theory for species diffusion coupled with large elastic–plastic deformations. J. Mech. Phys. Solids 60(12), 1983–2002 (2012). https://doi.org/10.1016/j.jmps.2012.08.001
Auriault, J.L., Sanchez-Palencia, E.: Etude du comportement macroscopique d’un milieu poreux sature deformable. J. Méc. 16(4), 575–603 (1977)
Auriault, J.L., Borne, L., Chambon, R.: Dynamics of porous saturated media, checking of the generalized law of darcy. J. Acoust. Soc. Am. 77(5), 1641–1650 (1985). https://doi.org/10.1121/1.391962
Auriault, J.L., Geindreau, C., Boutin, C.: Filtration law in porous media with poor separation of scales. Transp. Porous Media 60(1), 89–108 (2005). https://doi.org/10.1007/s11242-004-3649-7
Bear, J.: Dynamics of Fluids in Porous Media. Elsevier BV, Amsterdam (1972)
Biot, M.A.: General theory of three-dimensional consolidation. J. Appl. Phys. 12(2), 155–164 (1941). https://doi.org/10.1063/1.1712886
Biot, M.A.: Theory of propagation of elastic waves in a fluid-saturated porous solid. i. low-frequency range. J. Acoust. Soc. Am. 28(2), 168–178 (1956). https://doi.org/10.1121/1.1908239
Biot, M.A.: Theory of propagation of elastic waves in a fluid-saturated porous solid. II. higher frequency range. J. Acoust. Soc. Am. 28(2), 179–191 (1956). https://doi.org/10.1121/1.1908241
Biot, M.A.: Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 33(4), 1482–1498 (1962). https://doi.org/10.1063/1.1728759
Biot, M.A.: Theory of finite deformations of porous solids. Indiana Univ. Math. J. 21(7), 597–620 (1972). https://www.jstor.org/stable/24890361
Bowen, R.M.: Compressible porous media models by use of the theory of mixtures. Int. J. Eng. Sci. 20(6), 697–735 (1982). https://doi.org/10.1016/0020-7225(82)90082-9
Brinkman, H.C.: A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Flow Turbul. Combust. 1(1), 27 (1949). https://doi.org/10.1007/bf02120313
de Buhan, P., Chateau, X., Dormieux, L.: The constitutive equations of finite strain poroelasticity in the light of a micro-macro approach. Eur. J. Mech. A, Solids 17(6), 909–921 (1998). https://doi.org/10.1016/s0997-7538(98)90501-0
Chapelle, D., Moireau, P.: General coupling of porous flows and hyperelastic formulations—from thermodynamics principles to energy balance and compatible time schemes. Eur. J. Mech. B, Fluids 46, 82–96 (2014). https://doi.org/10.1016/j.euromechflu.2014.02.009
Chester, S.A., Anand, L.: A coupled theory of fluid permeation and large deformations for elastomeric materials. J. Mech. Phys. Solids 58(11), 1879–1906 (2010). https://doi.org/10.1016/j.jmps.2010.07.020.
Chester, S.A., Anand, L.: A thermo-mechanically coupled theory for fluid permeation in elastomeric materials: application to thermally responsive gels. J. Mech. Phys. Solids 59(10), 1978–2006 (2011). https://doi.org/10.1016/j.jmps.2011.07.005.
Coleman, B.D., Noll, W.: The thermodynamics of elastic materials with heat conduction and viscosity. Arch. Ration. Mech. Anal. 13(1), 167–178 (1963). https://doi.org/10.1007/bf01262690
Coussy, O.: A general theory of thermoporoelastoplasticity for saturated porous materials. Transp. Porous Media 4(3), 281–293 (1989). https://doi.org/10.1007/bf00138040
Coussy, O.: Poromechanics. John Wiley and Sons, Ltd, New York (2004)
Coussy, O.: Mechanics and Physics of Porous Solids. John Wiley & Sons, Ltd, New York (2010). https://doi.org/10.1002/9780470710388
Coussy, O., Ulm, F.J.: Creep and plasticity due to chemo-mechanical couplings. Arch. Appl. Mech. 66(8), 523–535 (1996). https://doi.org/10.1007/bf00808142
Coussy, O., Dormieux, L., Detournay, E.: From mixture theory to biot’s approach for porous media. Int. J. Solids Struct. 35(34–35), 4619–4635 (1998). https://doi.org/10.1016/s0020-7683(98)00087-0
Darcy, H.: Les fontaines publiques de la ville de dijon. Victor Dalmont, Paris (1856)
Doria, M.L.: Some general results for non-reacting binary mixtures of fluids. Arch. Ration. Mech. Anal. 32(5), 343–368 (1969). https://doi.org/10.1007/bf00275645
Dormieux, L., Coussy, O., de Buhan, P.: Modélisation mécanique d’un milieu polyphasique par la méthode des puissances virtuelles. C. R. Acad. Sci. Paris, Ser. II 313, 863–868 (1991).
Dormieux, L., Kondo, D., Ulm, F.J.: Microporomechanics. John Wiley & Sons, Ltd, New York (2006). https://doi.org/10.1002/0470032006
Drumheller, D.S.: The theoretical treatment of a porous solid using a mixture theory. Int. J. Solids Struct. 14(6), 441–456 (1978). https://doi.org/10.1016/0020-7683(78)90009-4
Dunn, J.E., Serrin, J.: On the thermomechanics of interstitial working. Arch. Ration. Mech. Anal. 88(2), 95–133 (1985). https://doi.org/10.1007/bf00250907
Fried, E., Gurtin, M.E.: Continuum theory of thermally induced phase transitions based on an order parameter. Phys. D: Nonlinear Phenom. 68(3–4), 326–343 (1993). https://doi.org/10.1016/0167-2789(93)90128-n
Fried, E., Gurtin, M.E.: Dynamic solid-solid transitions with phase characterized by an order parameter. Phys. D: Nonlinear Phenom. 72(4), 287–308 (1994). https://doi.org/10.1016/0167-2789(94)90234-8
Fried, E., Gurtin, M.E.: Coherent solid-state phase transitions with atomic diffusion: a thermomechanical treatment. J. Stat. Phys. 95(5), 1361–1427 (1999). https://doi.org/10.1023/A:1004535408168.
Gajo, A.: A general approach to isothermal hyperelastic modelling of saturated porous media at finite strains with compressible solid constituents. Proc. R. Soc. A, Math. Phys. Eng. Sci. 466(2122), 3061–3087 (2010). https://doi.org/10.1098/rspa.2010.0018
Gajo, A.: Finite strain hyperelastoplastic modelling of saturated porous media with compressible constituents. Int. J. Solids Struct. 48(11–12), 1738–1753 (2011). https://doi.org/10.1016/j.ijsolstr.2011.02.021
Gajo, A., Loret, B.: The mechanics of active clays circulated by salts, acids and bases. J. Mech. Phys. Solids 55(8), 1762–1801 (2007). https://doi.org/10.1016/j.jmps.2007.01.005
Germain, P.: La methode des puissances virtuelles en mecanique des milieux continus, i: Theorie du second gradient. J. Méc. 12, 235–274 (1973). https://doi.org/10.2140/memocs.2020.8.153
Germain, P.: The method of virtual power in continuum mechanics. part 2: Microstructure. SIAM J. Appl. Math. 25(3), 556–575 (1973). https://doi.org/10.1137/0125053
Gil, L.: A general continuum theory of finite strain chemoporomechanics with application to subcutaneous injections. PhD thesis, Ecole Polytechnique (2020)
Guin, L., Jabbour, M., Triantafyllidis, N.: The p-n junction under nonuniform strains: general theory and application to photovoltaics. J. Mech. Phys. Solids 110, 54–79 (2018). https://doi.org/10.1016/j.jmps.2017.09.004
Gurtin, M.E.: On the thermodynamics of chemically reacting fluid mixtures. Arch. Ration. Mech. Anal. 43(3), 198–212 (1971). https://doi.org/10.1007/bf00251452
Gurtin, M.E.: Generalized ginzburg-landau and cahn-hilliard equations based on a microforce balance. Phys. D: Nonlinear Phenom. 92(3–4), 178–192 (1996). https://doi.org/10.1016/0167-2789(95)00173-5
Gurtin, M.E.: A gradient theory of single-crystal viscoplasticity that accounts for geometrically necessary dislocations. J. Mech. Phys. Solids 50(1), 5–32 (2002). https://doi.org/10.1016/s0022-5096(01)00104-1
Gurtin, M.E., Vargas, A.S.: On the classical theory of reacting fluid mixtures. Arch. Ration. Mech. Anal. 43(3), 179–197 (1971). https://doi.org/10.1007/bf00251451.
Gurtin, M.E., Fried, E., Anand, L.: The Mechanics and Thermodynamics of Continua. Cambridge University Press, Cambridge (2010)
Hassanizadeh, S.M.: Derivation of basic equations of mass transport in porous * media, part 1. macroscopic balance laws. Adv. Water Resour. 9, 196–206 (1986)
Hassanizadeh, S.M.: Derivation of basic equations of mass transport in porous media, part 2. generalized darcy’s and fick’s law. Adv. Water Resour. 9, 207–222 (1986)
Hassanizadeh, S.M., Gray, W.M.: General conservation equations for multi-phase systems: 3. constitutive theory for porous media flow. Adv. Water Resour. 3, 25–40 (1980)
Hong, W., Zhao, X., Zhou, J., Suo, Z.: A theory of coupled diffusion and large deformation in polymeric gels. J. Mech. Phys. Solids 56(5), 1779–1793 (2008). https://doi.org/10.1016/j.jmps.2007.11.010
Hou, J.S., Holmes, M.H., Lai, W.M., Mow, V.C.: Boundary conditions at the cartilage-synovial fluid interface for joint lubrication and theoretical verifications. J. Biomech. Eng. 111(1), 78 (1989). https://doi.org/10.1115/1.3168343
Kovetz, A.: Electromagnetic Theory. Oxford University Press, London (2000)
Lai, W.M., Hou, J.S., Mow, V.C.: A triphasic theory for the swelling and deformation behaviors of articular cartilage. J. Biomech. Eng. 113(3), 245 (1991). https://doi.org/10.1115/1.2894880
Liu, I.S.: Method of lagrange multipliers for exploitation of the entropy principle. Arch. Ration. Mech. Anal. 46(2), 131–148 (1972). https://doi.org/10.1007/bf00250688
Liu, I.S.: A solid–fluid mixture theory of porous media. Int. J. Eng. Sci. 84, 133–146 (2014). https://doi.org/10.1016/j.ijengsci.2014.07.002
Loret, B., Simões, F.M.: Articular cartilage with intra- and extrafibrillar waters: a chemo-mechanical model. Mech. Mater. 36(5–6), 515–541 (2004). https://doi.org/10.1016/s0167-6636(03)00074-7
Madeo, A., dell’Isola, F., Ianiro, N., Sciarra, G.: A variational deduction of second gradient poroelasticity II: an application to the consolidation problem. J. Mech. Mater. Struct. 3(4), 607–625 (2008). https://doi.org/10.2140/jomms.2008.3.607
Malvern, L.: Introduction to the Mechanics of a Continuous Medium. Prentice Hall, New York (1969)
Müller, I.: A thermodynamic theory of mixtures of fluids. Arch. Ration. Mech. Anal. 28(1), 1–39 (1968). https://doi.org/10.1007/bf00281561.
Murdoch, A.: Objectivity in classical continuum physics: a rationale for discarding the ‘principle of invariance under superposed rigid body motions’ in favour of purely objective considerations. Contin. Mech. Thermodyn. 15(3), 309–320 (2003). https://doi.org/10.1007/s00161-003-0121-9
Murdoch, A.I.: On criticism of the nature of objectivity in classical continuum physics. Contin. Mech. Thermodyn. 17(2), 135–148 (2005). https://doi.org/10.1007/s00161-004-0192-2
Noll, W.: The foundations of classical mechanics in the light of recent advances in continuum mechanics. In: The Foundations of Mechanics and Thermodynamics, pp. 31–47. Springer, Berlin Heidelberg (1974). https://doi.org/10.1007/978-3-642-65817-4_2
Noll, W.: La mécanique classique, basée sur un axiome d’objectivité. In: The Foundations of Mechanics and Thermodynamics, pp. 135–144. Springer, Berlin Heidelberg (1974). https://doi.org/10.1007/978-3-642-65817-4_8
Sciarra, G., dell’Isola, F., Coussy, O.: Second gradient poromechanics. Int. J. Solids Struct. 44(20), 6607–6629 (2007). https://doi.org/10.1016/j.ijsolstr.2007.03.003
Seguin, B., Walkington, N.J.: Multi-component multiphase flow through a poroelastic medium. J. Elast. 135(1–2), 485–507 (2019). https://doi.org/10.1007/s10659-018-09721-9
Sun, D.N., Gu, W.Y., Guo, X.E., Lai, W.M., Mow, V.C.: A mixed finite element formulation of triphasic mechano-electrochemical theory for charged, hydrated biological soft tissues. Int. J. Numer. Methods Eng. 45(10), 1375–1402 (1999). https://doi.org/10.1002/(sici)1097-0207(19990810)45:10%3C1375::aid-nme635%3E3.0.co%3B2-7
Terzaghi, K.: Theoretical Soil Mechanics. John Wiley & Sons, Inc., New York (1943). https://doi.org/10.1002/9780470172766
Truesdell, C., Noll, W.: The Non-linear Field Theories of Mechanics. Springer, Berlin Heidelberg (1992). https://doi.org/10.1007/978-3-662-13183-1
Wilmański, K.: Lagrangean model of two-phase porous material. J. Non-Equilib. Thermodyn. 20(1), 50–77 (1995). https://doi.org/10.1515/jnet.1995.20.1.50
Wilmański, K.: A thermodynamic model of compressible porous materials with the balance equation of porosity. Transp. Porous Media 32(1), 21–47 (1998). https://doi.org/10.1023/a:1006563932061
Wilmański, K.: Thermodynamical admissibility of biot’s model of poroelastic saturated materials. Arch. Mech. 54(5–6), 709–736 (2002)
Wilmański, K.: On thermodynamics of nonlinear poroelastic materials. J. Elast. 71(1–3), 247–261 (2003). https://doi.org/10.1023/b:elas.0000005591.06930.f7
Wilmański, K.: Some questions on material objectivity arising in models of porous materials. In: Rational Continua, Classical and New, pp. 183–195. Springer, Milan (2003). https://doi.org/10.1007/978-88-470-2231-7_14
Wilmański, K.: Tortuosity and objective relative accelerations in the theory of porous materials. Proc. R. Soc. A, Math. Phys. Eng. Sci. 461(2057), 1533–1561 (2005). https://doi.org/10.1098/rspa.2004.1423
Wilmański, K.: A few remarks on biot’s model and linear acoustics of poroelastic saturated materials. Soil Dyn. Earthq. Eng. 26(6–7), 509–536 (2006). https://doi.org/10.1016/j.soildyn.2006.01.006
Xiao, Y., Bhattacharya, K.: Modeling electromechanical properties of ionic polymers. In: Bar-Cohen, Y. (ed.) Smart Structures and Materials 2001: Electroactive Polymer Actuators and Devices. SPIE, Bellingham (2001). https://doi.org/10.1117/12.432658
Acknowledgements
This work has been conducted as part of the PhD thesis of the lead author (see [40]) – under a CIFRE agreement between BD Medical Pharmaceutical Systems and the Laboratoire de Mécanique des Solides at the Ecole Polytechnique – who gratefully acknowledges the help of his colleagues at both Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Material frame indifference
Definitions
The principle of material frame indifference (also called objectivity) states that the constitutive laws of a continuous medium must be invariant under any change of the reference frame used for their description (see (5.12) in Sect. 5.2.2 for definition of corresponding coordinate transformations). Denoting the variables in the new frame of reference with the upper prime symbol \((\ )^{\prime}\) and any proper orthogonal tensor corresponding to the change of frame by \(\mathbf{Q}\), objective variables must satisfy

where \(a\) is a scalar, \(\mathbf{v}\) is a vector, \(\mathbf{A}\) is a second-order tensor, \(\boldsymbol{\mathfrak{W}}\) is a third-order tensor and  is a fourth-order tensor.
is a fourth-order tensor.
Application to the Helmholtz free energy
The isotropic scalar Helmholtz free energy \(\psi (\mathcal{S}, \mathbf{B} )\) is required to be objective (recall that \(\mathcal{S}\) are the scalar independent thermodynamic variables defined in (4.23) and \(\mathbf{B}\) is the left Cauchy-Green tensor), therefore for any proper orthogonal tensor \(\mathbf{Q}\)
since the scalar thermodynamic variables \(\mathcal {S}\) are objective (\(\mathcal {S}^{\prime}=\mathcal {S} \)) and the invariants of \(\mathbf{B}\) are independent of rigid body rotations.
Application to the relative fluid velocity
The relative velocity \(\mathbf{v}_{{r}}= \mathbf{v}_{{f}}- \mathbf{v}_{{s}}\) is taken to be a constitutive variable in Sect. 4, and hence must be objective.Footnote 24 This could seem counter-intuitive, since velocities are not objective due to the time dependence of the proper orthogonal tensor \(\mathbf{Q}\); fortunately the relative fluid velocity is objective. Indeed, consider two spatial points \(\mathbf{x}_{{f}}\) and \(\mathbf{x}_{{s}}\) moving respectively at \(\mathbf{v}_{{f}}\) and \(\mathbf{v}_{{s}}\), we have from (5.12) the following change of frame relation for the relative velocity:
In poromechanics theories, since \(\mathbf{v}_{{f}}\) and \(\mathbf{v}_{{s}}\) are defined at the same Eulerian point \(\mathbf{x}=\mathbf{x}_{{f}}=\mathbf{x}_{{s}}\), the relative velocity \(\mathbf{v}_{{r}}\) is objectiveFootnote 25 since (A.3) reduces to a form that satisfies the objectivity requirement for a vector in (A.1)2
Application to second-order tensors
Condition (A.1)3 must hold for all the second-order tensors of (4.50). A direct application of the representation theorem (see, e.g., [68]) yields the general form of the second-order permeability tensors \(\mathbf{D}_{{\cdots }}\)
with similar expressions for the second-order conductivity tensors \(\mathbf{K}_{{\cdots }}\).
Objectivity and dependence on \(\mathbf{v}_{{s}}\)
For any field quantity (scalar, vector, tensor) \(f (\mathcal{S}, \mathcal{G}, \mathbf{B}, \mathbf{v}_{{s}})\) to be objective (recall the definitions for the thermodynamic variables \(\mathcal{S, G}\) in (4.23)) it must satisfy, according to (5.12), for any vector \(\mathbf{c}\) (and for the special case \(\mathbf{Q}= \mathbf{I}\))

thus establishing that any objective field quantity \(f\) should be independent of \(\mathbf{v}_{{s}}\).
Appendix B: Derivation details for the energy flux vector \(\mathbf{{h}}\)
In this appendix, we present the proof yielding the expression (4.38) for the energy flux \(\mathbf{h}\). First we recall that from the principle of material frame indifference and the hypothesis of isotropy, the term \(\mathbf{k}\) in (4.36) has the following dependence
Applying the chain rule of differentiation to the divergence term \({\scriptstyle \boldsymbol{\nabla }} \boldsymbol{\cdot } \mathbf{k}\) in (4.36) yields
where \(f (\mathcal{L}_{{O}})\) is a scalar function of the thermodynamic variables \(\mathcal{L}_{{O}}\) only.
We introduce for simplicity the notation \(\mathbf{g}^{\alpha}\ (\alpha = 1, 2, 3)\), for the gradients of \(m_{{s}}\), \(m_{{f}}\), \(\theta \) and \(\mathfrak {W}\) for the gradient of \(\mathbf{B}\)
Given any admissible state \(\mathcal{L}_{{O}}\), the second gradients in (B.2) can be assigned arbitrarily, yielding the following restrictions

Taking partial derivatives of \(\mathbf{k}\) from (B.4) with respect to \(\mathbf{g}^{\alpha}\) and \(\mathfrak{W}\), we show the vanishing of its following mixed derivatives
Considering the Taylor expansion of \(\mathbf{k}\) around an homogeneous state (recall definition given prior to (4.45)), the expansion terms of order higher than 3 are identically null by (B.5), giving the exact expression

Applying the principle of material frame indifference to (B.6) gives for the particular case of \(\mathbf{Q} = - \mathbf{I}\),Footnote 26 the following expression for \(\mathbf{k}\)

By (B.7) the objectivity of \(\mathbf{k}\) implies the objectivity of the second rank tensors \(\partial \mathbf{k} / \partial \mathbf{g}^{\alpha}\) and the fourth rank tensor 

From (B.8)1, \(\partial \mathbf{k} / \partial \mathbf{g}^{\alpha}(\mathcal{L}^{h}_{{ O}})\) is an objective second-order tensor which is a function of symmetric variables. Using the mathematical theory of representation of objective tensors (see proof below)
Since \(\partial \mathbf{k} / \partial \mathbf{g}^{\alpha}(\mathcal{L}^{h}_{{ O}})\) is symmetric but also skew by (B.4)1, it follows that \(\partial \mathbf{k} / \partial \mathbf{g}^{\alpha}(\mathcal{L}^{h}_{{ O}})= \mathbf {0}\).
Similarly, equation (B.8)2 yields that  is an objective fourth-order tensor and also a function of symmetric variables. It follows from the antisymmetry conditions (B.4)2 that (see proof below)
is an objective fourth-order tensor and also a function of symmetric variables. It follows from the antisymmetry conditions (B.4)2 that (see proof below)

The two remaining terms of the Taylor expansion (B.7) are null, thus completing the proof of (4.37) stating \(\mathbf{k}(\mathcal{L}_{{O}}) = \boldsymbol{0}\).
Proof of (B.9)
This proof is inspired by the work of [68]. Consider an objective second order function \(\mathbf{A}(\mathbf{B})\). The principle of material frame indifference gives for any orthogonal tensor \(\mathbf{Q}\)
Moreover, the second-order tensor \(\mathbf{B}\) is real and symmetric, therefore it is diagonalizable in a real orthonormal basis with the associated eigen couples \((\beta _{{1}} , \mathbf{b}_{{1}})\), \((\beta _{{2}} , \mathbf{b}_{{2}} )\), \((\beta _{{3}} , \mathbf{b}_{{3}})\) such that
Consider the three orthogonal tensors \(\mathbf{Q}_{{1}}\), \(\mathbf{Q}_{{2}}\) and \(\mathbf{Q}_{{3}}\) such thatFootnote 27
Using \(\mathbf{Q}_{{i}}\) in (B.11) and multiplying both sides by \(\mathbf{b}_{{i}}\) gives with the help of (B.13)
establishing that the orthonormal eigenbasis of \(\mathbf{B}\) is also the eigenbasis for \(\mathbf{A}\), thus establishing its symmetry (B.9).
Proof of (B.10)
We show that if a fourth-order tensor function  with the antisymmetry conditions (B.4)2 is objective, then it must be null. Consider any objective second order tensor \(\mathbf{A}\) and define the second rank tensor
with the antisymmetry conditions (B.4)2 is objective, then it must be null. Consider any objective second order tensor \(\mathbf{A}\) and define the second rank tensor  by
by

The objectivity of  and \(\mathbf{A}\) imply the objectivity of the second order tensor
and \(\mathbf{A}\) imply the objectivity of the second order tensor  and, following the same procedure as in the previous proof, one can show that it is symmetric. Moreover, according to (B.4)2,
and, following the same procedure as in the previous proof, one can show that it is symmetric. Moreover, according to (B.4)2,  is also skew, and thus
is also skew, and thus

From the arbitrariness of \(\mathbf{A}\) we conclude that the tensor  is identically null, thus completing the proof of (B.10).
is identically null, thus completing the proof of (B.10).
Appendix C: Fourier and Darcy laws
In this appendix, we justify the final expression of the generalized Fourier and Darcy laws given in (4.48). Using the chain rule to take the gradient of \(\mu _{{f}}\), \(\mu _{{s}}\), \(\boldsymbol{\upsigma }^{e}\) from (4.30) and (4.35), one obtains

Following the work of [42, 45], consider that close to an homogeneous state \(\mathcal{L}_{{O}}^{h}\), the system (C.1) is invertible so that

For an easier comparison with poromechanics literature, recall from (4.48) the definition of the pressure gradient-like (since no pressure is defined) . Substituting (C.2) into (4.46) gives
Substituting the above expressions in (C.3) into the dissipation inequality (4.39) we obtain the inequality
Finally, requiring the inequality (C.4) to hold for any arbitrarily values of \({\scriptstyle \boldsymbol{\nabla }}\theta \), \({\scriptstyle \boldsymbol{\nabla }}\mu _{{s}}\), \({\scriptstyle \boldsymbol{\nabla }}\mu _{{f}}\) and \({\scriptstyle \boldsymbol{\nabla }}{p}\) we obtain the vanishing of the following coupling terms
thus yielding the expressions of \(\mathbf{q}\) and \(\mathbf{v}_{{r}}\) obtained in (4.48).
Rights and permissions
About this article
Cite this article
Gil, L., Jabbour, M. & Triantafyllidis, N. The Role of the Relative Fluid Velocity in an Objective Continuum Theory of Finite Strain Poroelasticity. J Elast 150, 151–196 (2022). https://doi.org/10.1007/s10659-022-09903-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-022-09903-6
Keywords
- Finite-strain poromechanics
- Nonequilibrium thermodynamics
- Material frame indifference
- Principle of virtual power
- Tortuosity



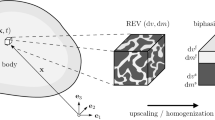

 , e.g.,
, e.g., 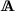 and their components by
and their components by 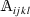 .
.
 in (
in (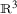 . A Cartesian basis is used for all field quantities, although the proposed dyadic notation allows for a straightforward conversion to curvilinear coordinates.
. A Cartesian basis is used for all field quantities, although the proposed dyadic notation allows for a straightforward conversion to curvilinear coordinates.