1 Introduction

The purpose of this paper is to highlight episodes marked by improvisation and uncertainty as a central feature of teachers’ classroom activity involving technology, and to analyze them as a way to better understand the complexity of teachers’ task with regard to technology integration. This complexity has been underestimated. Evidence for this statement is the small number of teachers really using computer applications with their students in the classroom, contrasting with the potentialities of digital technology highlighted by research and innovation and the emphasis put by authorities on this new dimension of education. Studies done at a general level generally do not help to tackle the complexity because they do not detail the purpose for which technology is used. Based on data from PISA, Eurydice (2004) stated that, in 2004, “in some countries (in particular France), the majority of pupils claim that they never—or almost never—use a computer” (p. 51). In France, authorities promote digital technology in education not as a topic by itself but as a contribution to existing subject teaching, especially mathematics. Eurydice’s observation then strongly suggests a quantitative gap between institutional expectations and classroom reality. There is also evidence of a qualitative gap: as compared to France, mathematics teachers in England tend to use technology on a more regular basis and, observing a panel of these teachers, Ruthven and Hennessy (2002) reported that they find technology most useful to enable general ‘pedagogical’ aspirations rather than for its ‘didactical’ contribution to mathematics learning.

From reports about diverse classroom uses of technology by teachers, a persistent observation is that unexpected phenomena and discrepancies between what was expected and what really happened frequently occur. Pre-service teachers observed by Abboud-Blanchard and Lagrange (2006) prepared for instance detailed worksheets and expected that, following these worksheets, students would work by themselves, executing instructions for the use of software and developing a mathematical reflection from the outcomes given by the computer. They thought that they could devote their activity to helping students with this mathematical reflection. In contrast to these expectations, teachers acted, rather, as technical assistants helping students simply to follow the worksheet.

Robert and Rogalski (2005, p. 271) say that there is some “internal economy”, or “logic” in the teacher’s activity, that explains his/her actions, and the nature of his/her decisions. Most teachers are not pleased when things in the classroom do not happen as they were expected to happen and are tempted to give up using technology. Those committed to integrating technology become cautious, presume hidden constraints and obstacles, and tend to privilege reassuring non-innovative approaches to the computer (Hennessy, Ruthven & Brindley 2005). Thus episodes of teachers’ activities marked by improvisation and uncertainty play a role in both quantitative and qualitative gaps and analyzing them could bring new knowledge about the ‘internal economy’ in the teacher’s activity that could support integration.

To develop the analysis, our choice is to gather data in settings where a curricular pressure fosters classroom use of a technological tool. In these settings, we are more likely to find teachers implementing technology in the classroom without being necessarily technology enthusiasts. We also wish to consider tools widely recognized as potentially contributing to mathematics teaching and learning because, more easily than innovative applications, they can be a matter for an analysis of the average teacher’s position towards technology. We also need an analytic framework. We are interested in theoretical frameworks that address the complexity of teachers’ activity. Robert and Rogalski (2002) noted: “teaching practices are to be seen as multidimensional, complex and consistent systems” (p. 506). Referring to teachers using technology, Monaghan (2004) also recognized that: “the whole undertaking involves a fusion of many factors” and he proposed “to find an holistic way to examine teachers’ practice” (p. 327).

2 Settings

2.1 The spreadsheet

Consistent with our choice to favor widely recognized tools, we considered a specific technology—the spreadsheet—for which, very early, innovators have proposed uses in mathematics teaching and learning. Mathematics education research studies acknowledged the spreadsheet’s potentialities for exploration of mathematical situations and students’ access to symbolism. As a recent example, Ainley, Bill, and Wilson (2005) showed that spreadsheet-based tasks could provide purposeful contexts for the use of algebra.

Haspekian (2005) discussed these potentialities. To support her discussion she experimented in two classes of very different profiles, both with regard to mathematics and to previous spreadsheet exposure. The task was made of simple questions like entering a formula to compute the mean of three numbers and fill it down. Haspekian was astonished by the results. First, no big differences existed between the classes. In both it took much time and effort by the students. The second astonishment was that teachers were confronted with unexpected difficulties when explaining, missing appropriate words to distinguish between the different operations and feedbacks in a cell. They got confused that explanations they gave were often inadequate, although they had no difficulties in operating the spreadsheet by themselves. The outcome of this brief presentation is that the spreadsheet suits our aims because of this evidence of potentialities as well as of unexpected phenomena.

2.2 A curriculum for upper secondary non-scientific students

A second decision was to observe teachers who use the spreadsheet independently of their personal choice or conviction and on a regular basis in well-adapted material settings. We found this conjunction of factors in the new French curriculum for upper secondary non-scientific classes existing since the year 2000 (BOEN 2000). It is intended for students more attracted by literature and arts than science, and who generally experience difficulties in mathematics. It aims to strengthen basic mathematical knowledge by favoring modelling, interpreting, and criticizing varied information. It recommends involving “mathematics use visible in society” (p. 1) that is to say graphs, tables, percentages… It “systematically proposes to put all the items into operation on a spreadsheet” (p. 1). It does not recommend the study of the spreadsheet for itself, but as a means for exploring and solving problems.

In the course defined by this new curriculum, the study of linear and exponential sequences derives from the focus on ‘visible mathematics’. Students are supposed to study ‘types of progression’ from examples of situations without the mathematical apparatus of sequences, but with the help of the spreadsheet. The spreadsheet is a means to get tables and graphs to represent and explore, and its symbolism is a way towards mathematical formalism, which is consistent with the spreadsheet’s potentialities identified by research. As a difference with other courses where most teachers ignore curricular recommendation about technology, spreadsheet use cannot be avoided because of the national evaluation—the baccalaureate—whose texts are written so that candidates could not succeed without spreadsheet knowledge.

3 Framework

Our framework should help to address the complexity of teachers’ activity involving classroom use of technology and to interpret episodes marked by improvisation and uncertainty. Many frameworks have been developed to analyze human activity following Leont’ev’s activity theory. Among these frameworks, Saxe’s (1991) cultural perspective adapted by Monaghan (2004) drew our attention. Like activity theory, it considers that an individual’s knowledge and practices are shaped and organized by experience as well as structured by logical systems. It also helps to understand how “artefacts and forms of social organization (…) are intrinsically related to the nature of (individual)’s intellectual construction” (Saxe 1991, p. 4). A central feature, particularly well-adapted for our purpose, is the notion of ‘emergent goals’: “Goals are emergent phenomena, shifting and taking new forms as individuals use their knowledge and skills alone and in interaction with others to organize their immediate contexts” (Saxe 1991, p. 16, 17). Considering emergent goals is particularly relevant for analysis when individuals do not have a fully reliable plan to accomplish their task but also have to deal with uncertainties of shifting circumstances. Because emergent goals challenge individuals’ expertise, they play a role in cognitive development especially by favoring new functions for already existing cultural forms.

Saxe (1991, p. 17) grouped the many factors implicated in the emergence of goals into four parameters. Monaghan (2004) provided a systematic analysis of the factors influencing teachers’ activity in technology-based lesson and of their interaction, based on this ‘four parameters model’. Here we retain the main factors pointed out by Monaghan in each of the parameters and their impact upon teachers’ activity.

Activity structure

Monaghan considers here the way teachers organize their classes and prepare students’ tasks and the decisions they take relatively to their role and activity as well as those of the students: he observed that the tasks and cycles of these lessons varied considerably across teachers and, in most cases, varied over time, technology tasks being ‘unsafe’ as compared to usual tasks.

Conventions–artefacts

While recognizing that mathematics teaching involves many cultural artefacts including systems of convention and notations, Monaghan privileges software and written resources in the study of teacher activity in technology-based lessons, considering that the way a software transforms mathematics is an important concern for a teacher and also that the shift towards technology use brings teachers to widely re-evaluate the content of their written material as well as the way they use it.

Social interactions

Monaghan observed a variety of ways in which technology affected social interactions in observed classrooms. Although technology lessons were notable for their diversity, most changes appeared in relationship to specific constraints and did not denote a clear developmental path towards adopting new roles.

Prior understandings

For Monaghan, mathematics teachers’ prior understandings of learning and teaching incorporate a range of beliefs and professional knowledge. Beliefs are globally independent of whether or not the lesson uses technology and were not reconsidered. In contrast, teachers’ knowledge of their teaching, generally tacit in ordinary lessons, had to be rethought deeply in order to incorporate technology use.

The cultural perspective will be the overarching activity theory framework, but we also assume that analyzing teachers’ classroom activity cannot be done without a perspective on mathematical learning and its specificities and these specificities are better tackled with the help of didactical constructs. Two of these constructs seem to us particularly useful because in models of mathematics teaching/learning they help to clarify issues critical for the teacher. The first is the concept of milieu that Brousseau (1997) introduced to model the interplay with a material or intellectual reality in students’ activity when they build new procedures and new knowledge. The concept of milieu is closely linked to adidactic situations that is to say situations where didactic intentions are disregarded: students perceive the need for building new procedures and new knowledge not as a constraint of the educational process, but rather as means to “play better” against the milieu. With regard to the teacher, Laborde and Perrin-Glorian (2005, p. 5) explain that the design of the milieu is critical for giving the students full responsibility with regard to knowledge. In the case of technology use, rich feedback is generally expected from the computer, but it is not easy to identify precisely the nature of the feedback and its effect on students’ activity.

The second construct is the notion of instrumented technique. Observing that many discourses about the use of technology strongly opposed the technical and the conceptual dimensions of the mathematical activity, Lagrange (2000) initiated a reflection on the relationship between these two dimensions. He has been influenced by Chevallard’s (1999)Footnote 1 model of praxeology (praxis and logos) linking types of tasks, techniques to perform these tasks, and theorizations developed to study properties of the techniques like efficiency, consistency, and field of validity. In this model, techniques play a unique role as a bridge between tasks and theorizations. In order to specify the relationship of techniques, respectively with tasks and with theorizations, Artigue (2002) introduced the idea of pragmatic and epistemic values of techniques:

Techniques are most often perceived and evaluated in terms of pragmatic value, that is to say, by focusing on their productive potential. But they have also an epistemic value, as they contribute to the understanding of the objects they involve, and thus techniques are a source of questions about mathematical knowledge. (p. 248)

Our hypothesis is that the question of the instrumented techniques brought about by technology and of their coordination with existing paper/pencil techniques is very difficult for teachers. The pragmatic value of instrumented techniques generally makes obsolete existing techniques, which existed because of their epistemic value. More or less consciously, teachers realize that this obsolescence breaks reliable ways to students’ conceptualization. Teachers are generally aware of the epistemic value of existing paper–pencil techniques—for instance they value by hand calculation as a contribution to understanding number structure—and they develop special classroom strategies in order for students to reflect upon the techniques. In contrast it is not easy to recognize the epistemic value of instrumented techniques and to develop associated strategies, which is the reason why we say that this epistemic value is potential.

4 Empirical study

As stated in the introduction, the purpose of the paper is to produce data and an analytic framework paying regard to the complexity of technology integration, especially focusing on episodes marked by improvisation and uncertainty. Then the goal of the empirical part of this paper is to provide evidence of the central role of the episodes and to examine the framework’s functionality to analyze these. We base this part on Ozdemir Erdogan’s (2006) doctoral thesis, in which she observed two teachers teaching the above-described course. They were chosen because both were experienced and conscientious teachers who nevertheless had very different perceptions of the epistemology of the course. Thus difficulties observed in the classroom would not be the consequence of insufficient professional skills and the differences should help to assess the functionality of the method for dissimilar teachers’ positions relatively to technology integration. Ozdemir Erdogan observed these teachers all along the above-described course by way of interviews and recordings of the lessons.

After presenting the two teachers, we examine Saxe’s parameters and how they account for the teachers’ activity and then we focus more precisely on their classroom activity, looking at episodes marked by improvisation and uncertainty. It appeared in the observations that these episodes happened repeatedly and sometimes concurrently in a single lesson: teachers were faced with a ‘flow’ of unexpected circumstances and questions challenging their professional knowledge rather than with isolated difficulties. To provide a realistic account of this flow for the analysis, we choose here to report on a single lesson for each teacher and to organize our analysis along this flow. This choice also makes it easier to consider the episodes in their didactic context: tasks given to the students and the knowledge at stake.

4.1 The teachers

We call one teacher Mrs. PSCEP and the other Mrs. PEX Footnote 2. Mrs. PSCEP taught for 35 years at upper secondary level and her first acquaintance with the spreadsheet was 15 years ago in a professional development course. When the curriculum changed, she had to adapt her teaching although she considered this curriculum less interesting and lacking mathematical rigor. She did not use technology in other classes and she explained this by saying that it would have required big efforts while she was not sure of the contribution to learning.

Mrs. PEX taught for 30 years at different levels. She tried to integrate technology in her teaching since the 1980s and participated in research projects. She volunteered to teach this course after the curriculum change. She tried to use technology as much as possible in other classes.

4.2 Parameters

We use here the factors identified by Monaghan as particularly influencing teachers’ activity to characterize the respective positions of Mrs. PSCEP and Mrs. PEX towards the use of technology in this curriculum.

Activity structures

We report first the global structure for the whole period devoted to sequences and then the structure for individual sessions.

Mrs. PSCEP devoted 3 weeks to sequences and Mrs. PEX about 6 weeks. Mrs. PSCEP’s structure was simple: the notion of sequence was presented to the students the first week, then arithmetical sequences the second, and geometrical sequences the third. This structure is not consistent with the curriculum, since the study of situations and the notion of progression should be privileged. Mrs. PEX presented situations corresponding to the two types of progression in the first week. Two weeks were then devoted to studying criteria and techniques for recognizing each type and 3 weeks to the study of situations, using the types of progression as tools for modelling.

The course was 2 hours per week, one with the whole class and one in half classes. Teachers had to decide how to use them. Mrs. PSCEP taught the whole class in an ordinary classroom and the half class in a computer room. In both classes, whole class sessions were devoted to the presentation of the mathematical content and half class sessions to “applications” with the spreadsheet. Mrs. PSCEP’s students worked individually following a worksheet. Mrs. PEX adopted another organization. She had the whole class hour in a computer room: students worked in teams with a computer at their disposal. She devoted the half class hour to a report on the teamwork and to a synthesis. Teams reporting their work could use a computer hooked to a video projector and to a network.

Conventions–artefacts

We consider here the spreadsheet whose use is compulsory in this course and the written material that teachers prepared for the students. In the whole class hour Mrs. PSCEP’s students had to work with paper and pencil. In the half class it was clear that they had to work on the spreadsheet: Mrs. PSCEP’s worksheets were really specific about this use, referring to cells and formulas. In Mrs. PEX’s lessons, the students had the spreadsheet and paper/pencil always at their disposal and the worksheets gave no instruction to use either or both artefacts.

Social interactions

Mrs. PSCEP’s interactions with students were similar in the computer and in the regular room. These interactions were very frequent and generally between herself and a single student. In contrast, in Mrs. PEX’s classroom these schemes were not the same in the whole and half classes. In the whole class, students interacted in teams and Mrs. PEX spoke infrequently and generally to encourage students to work as a team. In the half class, during the report of teamwork Mrs. PEX spoke much more, questioning the team and prompting the rest of the class for their reaction.

Prior understandings

In Mrs. PSCEP’s view, technology was introduced in this course in order that students learn about spreadsheets. For her, beside the use of technology, the mathematical content was not different from the previous curriculum. She thought that technology does not bring a very concrete contribution, but has a positive effect on the behavior of her students whom she considered weak and not interested in mathematics. Changing students’ image of mathematics was Mrs. PEX’s goal when using technology in this class. She was happy with the new curriculum because the use of technology that she tried to promote often without much success among colleagues and parents was now compulsory. She explained that a majority of her students failed in mathematics, and thus her priority was to make a different entry into mathematics. She considered the activities about progressions indicated by the curriculum to be very important for students’ learning.

4.3 Teachers’ classroom activity

We analyze now observations in the two teachers’ classrooms. As announced above, we analyze a single lesson for each teacher. Consistent with our goal of observing teachers in ordinary settings, we were not involved in the teachers’ decisions regarding tasks presented to the students. The teachers were also not in the same school and had no common preparation work. They nevertheless chose similar situations as a basis for students’ tasks during the first week: the “birthday” situation (Fig. 1), and “comparing progressions” situations (Fig. 2), one about insects populations (Mrs. PSCEP) and the other about bank accounts (Mrs. PEX). This is a reason why we choose this lesson. We present and discuss these situations before reporting on each of the teachers’ activity.

Fig. 1
figure 1

The “birthday” situation

Full size image
Fig. 2
figure 2

Spreadsheet solutions for the “birthday” situation

Full size image

4.3.1 The “birthday” situation

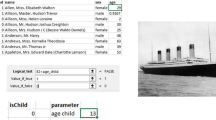
The yearly deposit is a linear progression. Computing the deposit for a given year by hand or mentally is not difficult. Using a spreadsheet, one has to make a column for the years (column A in Fig. 2), then enter 100 in an adjacent cell like B1, enter below a formula like =100 + 2*A2 and fill down this formula (Fig. 2a). If one wants to make the initial deposit a parameter, a formula with an absolute reference like =$B$1 + 2*A2 can be entered and filled down instead (Fig. 2b).

Let us compare the by hand and the spreadsheet techniques. At first sight, spreadsheet software is designed to help a user to efficiently reach a solution and then the value of spreadsheet techniques should be mostly pragmatic. Here paradoxically, this value does not exist. As compared to the easy mental calculation of values, making columns of numbers and formulas is a tedious process for students who do not know how to use this tool efficiently. The formula and the technique of filling down, in accordance with the curriculum’s epistemology of the connection between spreadsheet and mathematics, has an epistemic value as a way to express a relationship. Using an absolute, rather than a relative reference for the initial value is potentially epistemic: absolute references correspond to the mathematical idea of parameter, whereas relative references correspond to variables and thus using both kinds of references is linked to the idea of literals having different algebraic status.

4.3.2 Comparing progressions

The “insects” and “bank account” situations (Fig. 3) are basis for tasks of implementing and comparing linear and exponential progressions on the spreadsheet. To implement exponential progressions, students can break down the calculation by entering a column for the increase. It should help them because they often have difficulties in interpreting an augmentation of x% as a multiplication by 1 + x/100. Calculating large series of values should help students to recognize the different characteristics of the two progressions and to prepare a comparison.

Fig. 3
figure 3

Comparing progressions

Full size image

5 Mrs. PSCEP’s classroom activity

In accordance with Mrs. PSCEP’s activity format, this session took place in a computer room and followed a whole class lesson without computers during which Mrs. PSCEP had introduced the notion of sequence: the mathematical notation, the modes of generation, and the properties. The objective of the half class session was to “apply” this knowledge by using a spreadsheet. Before this lesson, the students had already used the spreadsheet to work on other topics.

The tasks presented to the students (Fig. 4) came directly from a textbook (Misset 2001, p. 128). Question a in exercise 1 (“birthday” situation), gave priority to the mathematical notion of sequence and notation and privileged by hand calculation in the understanding of the situation. In question b, a table and three formulas were provided and students only had to complete the electronic sheet. The first formula, although congruent to the definition, does not work, because of the way filling down functions: B2 has to be understood as the deposit the preceding year and not the initial deposit. The second formula is recursive, that is to say that it refers each year to the deposit of the preceding year. Then this formula does work, although it is not congruent to the definition. The third formula corrects the first by way of an absolute reference to the initial deposit. Question c asked for a formula giving, each year, the sum of the deposit from Sabine’s birth. In exercise 2 (the “insects” situation), the mathematical generation of the sequences was given. Students had to “justify” the formulas and to apply them in the spreadsheet, then to observe the behavior of the sequences.

Fig. 4
figure 4

Mrs. PSCEP’s text for students

Full size image

Exercise 1 (32 min)

Overlooking the worksheet’s first question, a majority of students directly launched the spreadsheet and started to fill in the sheet. Most students began to enter the amounts of the deposits in column B that they easily calculated mentally. The following extract shows how Mrs. PSCEP was surprised by this behavior.

Student: (showing her sheet) Am I right?

Mrs. P SCEP : (reading the values) Yes…(she realizes that the correct values were entered and not calculated)…And how do you proceed?

Student: I calculate

Mrs. P SCEP : No, you must not calculate, the spreadsheet must calculate!

Student: But it is quicker than with the computer

Mrs. P SCEP : But go until 200 years like that?

Student: But this poor girl will never be 200 years old!

Other students, like in the following extract, entered a formula in each cell (= B2 + 2*A3 in cell B3, =B3 + 2*A3 in cell B4, etc.) The extract also shows how Mrs. PSCEP spent the next quarter of an hour prompting the students more or less individually to enter and fill down formulas.

Mrs. P SCEP : What happens to you…? No, no, do not make like that.

Student 2: Me?

Mrs. P SCEP : One should not type each time the calculation.

Student 2: But why not?

Mrs. P SCEP : It is necessary that… I want to be able… Take your formula and fill down.

When the students began to work on question b, Mrs. PSCEP was again surprised: the students did not try the third formula, arguing that the second formula worked. Again all her activity during the next quarter of an hour was to prompt students individually to try the third formula. She did not really succeed in convincing them of the interest of this task, and also failed to make them understand the different functioning of the formulas. In the following extract, we see a student reluctant to try the third formula because if it had not worked, she would have had to redo the column.

Mrs. P SCEP : Did you choose between the three formulas?

Student: Yes this one (She shows the second formula on her screen).

Mrs. P SCEP : Did you try the third one?

Student: No, I did not.

Mrs. P SCEP : Then please try.

Student: But, after that I will have to do it again!

Mrs. PSCEP became aware that her activity format of individual interaction with the students was not adapted for this question and she devoted the first part of the next half class session to the difference between relative and absolute reference.

Question c was very difficult for the students. They generally entered a formula adding the two preceding years’ values that works only for the first line. Some of them realized that they were wrong and called the teacher. Mrs. PSCEP tried to help them while also dealing with the preceding difficulties. She had a lot of trouble to understand what the students wanted to do and gave inadequate indications: for instance she recommended entering a formula via the automatic summation button and this formula was not adequate to be filled down.

Exercise 2 (12 min)

Because of the above difficulties, only a minority of students tackled this task. Most of them skipped the mathematical justification of the two definitions. They translated the definitions into spreadsheet formulas. They probably read the values requested to observe the behavior of the sequences, but did not write down their observations. Mrs. PSCEP did not insist on a written report, and so the students could overlook the mathematical justifications.

5.1 Mrs. PEX’s classroom activity

The task (Fig. 5) was given in the preceding whole class session. In this session, students had to work in teams on two tasks, one about the “birthday” situation (exercise 1) and the other one about the “bank account” situation (exercise 2). The half class session was made up of reports of two teams each of them about one exercise and followed by a synthesis by Mrs. PEX.

Fig. 5
figure 5

Mrs. PEX’s text for students

Full size image

Exercise 1 (22 min)

Consistent with Mrs. PEX’s conception of written material, the text gave no indication concerning the tool to be used. Thus students could do question 1 (yearly deposit) mentally. Because the addition of 19 integers is not easy by hand, it is likely that Mrs. PEX added the second question (money that Sabine has on her 18th birthday) in order to promote spreadsheet use. As we said above, Mrs. PEX privileged teamwork in the whole class sessions and left it up to the students whether to use the spreadsheet or not. In the interview before the half class session, she said to the observer that she expected that the discussion directed by her would bring students to the understanding of the underlying notion of linear progression. For her it was important to present the use of absolute references as a way to generalize the situation, highlighting the initial value.

Consistent with her idea that the students should be able to choose the more adequate tool for a task, Mrs. PEX asked a team of students to present their work to the class and told them that they were free to choose an environment (spreadsheet or blackboard). The team started to present its work to the class without the spreadsheet, giving its interpretation and calculating the first three deposits. Actually the team had only a limited understanding of the situation and had a lot of difficulty to explain how they proceeded. Mrs. PEX asked them to redo and write the calculations on the chalkboard.

$$100 + 2 \times 2 = 104,\quad 100 + 2 \times 3 = 106,\quad 100 + 2 \times 4 = 108.$$

At this moment, she realized that continuing like that, students could approach a formula for the deposit at the year n without using the spreadsheet. Then a goal emerged: to make the students use the spreadsheet. This goal was important for her because, in her understanding of the course, students’ use of the spreadsheet was a means for them to access the notions. It was unexpected because her idea was that the students would prefer to use the tool rather than calculate by hand. She achieved this goal, by way of a dialog with the class, insisting on the “modern” aspect of technology in contradiction with her position on the role of artefacts.

Mrs. P EX : What there now? You are waiting for what? You do all calculations by hand? There is a more modern means to do that? There is a more modern means to do that, you make by hand?

Students: Technology tool

Mrs. P EX : That is?

Students: The spreadsheet

Mrs. P EX : The spreadsheet, then go ahead.

The student who was presenting launched the spreadsheet but he used it as a way to display the results previously calculated mentally, entering each value individually. He took care to use a monetary layout for the deposit and to arrange titles in the worksheet.

Mrs. PEX was not happy with that and insisted on using formulas and the fill down functionality first for entering a list of years and then the corresponding list of deposits. After the student obtained a table like in Fig. 2, she again was not content and she asked what would happen if the grandmother changed the initial deposit.

Mrs. P EX : […] Suppose this grandmother has another grandson, she uses the same rule, but she gives 150 € at the beginning.

Student: OK

Mrs. P EX : Please go on.

Student: Do I change everything?

Mrs. P EX : Only one!! You must make one change.

There was then a misunderstanding. Mrs. PEX was thinking of the possibility to use an absolute reference to the first deposit in the formula of Fig. 2, in order that a change in this first deposit would change the others, while the student thought that “one change” meant that it would be enough to change the value in the formula. Two problems appeared, first the initial deposit did not change and the formula was not changed below. Mrs. PEX asked for the help of other students who correctly proposed to change the initial deposit and to use an absolute reference to this cell in the formula.

In the next question, Mrs. PEX’s students in contrast to Mrs. PSCEP’s, had only to calculate this sum at Sabine’s 18th birthday and they could easily use the automatic summation. After this report, Mrs. PEX made a summary, declaring that the progression of the deposits in Sabine’s account is “linear” and that the next exercise would bring another type of progression: “exponential”.

Exercise 2 (26 min)

Mrs. PEX selected a team who used the spreadsheet and who generally performed well. The students of this team tried to download the sheet they prepared in the preceding session, but the network failed and they had to re-enter their formulas. For progression A, they used a recursive definition with absolute reference to the constant increase. For progression B, they calculated first the yearly interest with an absolute reference to the constant rate of change, and then they added recursively this interest to the capital of the previous year. After the report, Mrs. PEX stressed that this two-step calculation did not show the exponential nature of the progression.

Mrs. P EX : Progression A is linear. What about progression B?

Students: Exponential!

Mrs. P EX : How do you know? Do you know that each value is multiplied by a constant coefficient?

Students:…

Mrs. P EX : I am talking to you (the team reporting). Can you use the spreadsheet to answer my question? That is to say how do we pass from the capital one year to another year?

The student activating the spreadsheet understood that she had to make it compute the quotient between two successive values. She entered and filled down the relevant formula, obtaining a constant series of values 1.02. Then Mrs. PEX explained the rate of change in sequence B.

Mrs. P EX : Now, can we link 1.02 to the data? Could we find it directly?

Students:…

Mrs. P EX : Go on!

Students: Zero, two, it is 2 percent!

Mrs. P EX : Look at the formula you wrote, what does it mean? What did you write?

Students: C3 plus E2, absolute value… over 100.

Mrs. P EX writes on the blackboard

C4 = C3 + $E$2×C3/100

Mrs. P EX : OK, we will do some mathematics. Here, this is the spreadsheet language. Now let us talk mathematics. V is the account position. How will we call the preceding position?

Students: X

Mrs. P EX : X, as you want, then V equals X plus… What can I write? I cannot write E2, absolute reference, it is the spreadsheet language!

Students: It is two.

Mrs. P EX : Two… times…

Students: X

Mrs. P EX : X divided…

Students: by 100.

Mrs. P EX writes on the blackboard \(V = X + \frac{{2 \times X}}{{100}}\)

Mrs. P EX : divided by 100… Good, I do mathematics now. I can factorize X. Why?There I can write X times 1 plus 2 percent, that is to say X times…

Students: 1.02

Mrs. P EX completes by \(V = X + \frac{{2 \times X}}{{100}} = X\left( {1 + \frac{2}{{100}}} \right) = X\left( {1,02} \right)\)

Mrs. P EX : OK you can write this down. Does everybody understand why? It is one point zero… Are you surprised? No, we already saw that… Remember, you can use any letter to factorize. In an exam you are not allowed to use the spreadsheet language, except when it is explicitly requested.

Mrs. PEX’s discourse draws a sharp borderline between mathematics and the spreadsheet notation. “In an exam you are not allowed…” is evidence that institutional pressure of the baccalaureate plays a role: her students might be evaluated by teachers refusing a proof based on spreadsheet notation, considered as lacking rigor. After the class, Mrs. PEX explained that she generally based proofs on names of columns. She did not do that because she had not, at this time, introduced her students to this functionality. She had then to choose between doing algebra on spreadsheet formulas and using usual algebraic notation. Her choice was conservative and marked by the institutional pressure.

6 Interpretation

6.1 Parameters and classroom activity

The difference of structure between the two teachers’ activity is apparent. For both, the global course structure is deeply linked with prior understanding. For Mrs. PSCEP, linear and exponential sequences were a minor subject that can be taught in 3 weeks. Tasks were broken into subtasks. Mrs. PSCEP did not realize that some were quite difficult or that the students did not have the necessary knowledge. Mrs. PEX devoted twice as much time to a subject that she thought important in a non-scientific curriculum: her goal was not to expose notions but to develop students’ proficiencies for understanding situations and modelling; students thus had to tackle a variety of situations by themselves.

The weekly structure and the classroom interaction also reflected the prior understandings. Mrs. PSCEP’s scheme was simple and consistent with her view of the learning of mathematical notions: one whole class session for introducing notions and notations followed by a half class session for application. She privileged individual check of answers. Mrs. PEX chose an “explore then discuss and synthesize” scheme adapted to building proficiencies and encouraged peer interaction.

The spreadsheet’s affordances and constraints had a big influence upon activity structures and classroom interaction. Mrs. PSCEP saw the spreadsheet as a tool for application, more significant for students’ “general culture” and motivation than for mathematical learning. Then the spreadsheet reinforced Mrs. PSCEP’s presentation/application scheme: mathematics was presented by exposition when no spreadsheet was used, and applied with the spreadsheet. For Mrs. PEX, in conformity with the curriculum, the spreadsheet was the right tool to introduce exploration and modelling into the students’ classroom activity.

Regarding social interaction, the two teachers considered more or less consciously the spreadsheet as a means to progress towards their aspirations. Mrs. PEX saw the computer environment as means to implement classroom discussion based on teamwork. Mrs. PSCEP privileged individual interaction. The organization of her computer class with one computer for each student made her feel that she would be able to control students’ work individually. We observed that Mrs. PSCEP’s individual checks were often inadequate when students used the spreadsheet, because Mrs. PSCEP could not really control how a task was performed: for instance, Mrs. PSCEP was observed to be satisfied to see proper values in a column, assuming that they were obtained by way of a formula, while the student just entered mentally calculated values.

6.1.1 Teachers’ emergent goals

From this report we identify what we called episodes of improvisation and uncertainty, and interpret them in terms of emergent goals.

Compelling students to use the spreadsheet.

This goal emerged at the beginning of Mrs. PEX’s session. She first announced to the students that they were free to use paper/pencil or computer, but she had to change her discourse when she became aware that the task would be done without spreadsheet use. We analyze this as an effect of conflicting parameters. Mrs. PEX’s views of the role of artefacts and of social interactions were consistent: students as individuals should be free to choose what they think is the appropriate tool and her relation to students should maintain this freedom. But this view conflicted with her prior understanding of the role of technology in the relationship between students and mathematics. Her main goal was to bring students towards understanding the notion of progression by way of spreadsheet formulas. To achieve this main goal, it was necessary that students use the spreadsheet. This was not obvious because the task could be easily done mentally. Mrs. PEX achieved this implicit goal, by insisting on the “modern” aspect of technology in contradiction with her position on the role of artefacts.

Making students use the spreadsheet as a calculation tool.

The two teachers were surprised when students entered values calculated mentally or individual formulas instead of entering and filling down a single formula. Both teachers insisted on a supposed pragmatic value of the second technique especially its efficiency in the case of “big values”. Students resisted, sometimes on the funny side: “this poor girl will never be 200 years old” (First extracts in section 5, Mrs. PSCEP’s classroom activity).

Making students use absolute references.

This goal appeared differently in the two classes. In Mrs. PSCEP’s task, three formulas were proposed. Students did not see why they should try the third formula. Mrs. PSCEP had to prompt them for that. In her scheme of individual interaction with a student, she could not really explain the notion and she went back the next week to the two formulas insisting on a supposed pragmatic interest of using absolute references. In Mrs. PEX’s task, using a numerical constant inside the formula was relevant. In terms of the theory of situations, the “milieu” did not make absolute reference a necessity. Mrs. PEX promptly changed this milieu by introducing another grandchild. This helped her to justify the use of absolute reference by pragmatic reasons. This type of behavior has been observed as a constant of ordinary teaching by Hersant and Perrin-Glorian (2005):

adidactic situations are rare, but one can observe situations that have some adidactic potential. This means that there is a milieu, which provides some feedback to the actions of the students, but the feedback alone may be insufficient for the students to produce new knowledge on their own. In this case, the teacher may have to intervene to modify the milieu, for example, so that the student becomes aware of an error. (p. 117)

It means that in ordinary teaching, teachers do not organize an adequate milieu for learning, but sometimes elements of this milieu are present and teachers more or less consciously adapt them in view of their goals. Here this adaptation is done in some haste confirming that emergent goals are, by nature, hastily dealt with and also showing Mrs. PEX’s qualities for improvising.

Making clear the exponential nature of a progression with proportional increase.

Mrs. PEX’s discourse after the report on exercise 2 seems to us relatively unprepared and contradictory with her understanding of the curriculum’s epistemology. It was important for her that students become aware that one passes from a value of the progression to the next by multiplying by a constant coefficient and understand why. Again, the “milieu” did not help, because precisely with a spreadsheet, students could easily “break” the calculation, computing first the increase and then adding it to the current value. She then reminded students of their “old” knowledge (“we already saw that…”) In Mrs. PEX’s epistemology of the spreadsheet, the notation specific of this tool could be a means for students to understand algebraic treatments despite their inability with the standard algebraic notation. One can then expect that she would permit a factorization in a spreadsheet formula. However, in the course of action, she had doubts about the validity of such a transformation especially with regard to the position of colleagues that might negatively evaluate her students. She improvised a discourse contradicting her epistemology: mathematics would begin when one gives up with the spreadsheet notation. It is a characteristic of emergent phenomena that they generate contradictions between conceptions and practice, compelling individuals to take prompt decisions.

6.1.2 Interpretation

The analysis of the milieu proposed for the third emergent goal (Making students use absolute references) can be extended to the others. The absence of an adequate milieu for inducing students to use the spreadsheet as a calculation tool compelled Mrs. PEX to a technophile discourse contradicting her balanced view of the role of technology. There was also no milieu that could make students express the series V of exercise 2 as an exponential progression. The teachers were different with regard to this analysis. Mrs. PSCEP’s exposition/application activity format made the absence of the milieu not so critical: closed tasks and authority were means to coerce students towards the desired behavior. In contrast Mrs. PEX changed the milieu for the third goal, revealing that she was more or less conscious of the importance of an adequate milieu for students’ understanding. The way she wrote the second question of exercise 1 also shows that, compared to Mrs. PSCEP, she took better care of how students could do this task.

Thinking of the value of instrumented techniques at stake in the episodes can be a basis for a second analysis. The underlying goals could be described as making students give up their spontaneous technique to try another. Certainly the teachers attached importance to techniques for their epistemic values, but speaking to the students, they rather insisted on a supposed pragmatic value. Students were not convinced. It seems that teachers prefer to give superficial reasons rather than discuss in depth the interest of a technique. An exception was Mrs. PEX’s treatment of the calculation of series V: she did not criticize the students’ calculation on the basis of a poor pragmatic value but rather insisted on the interest of another calculation to make clear the exponential nature of the series.

The above episodes appear as endeavors in response to unexpected difficulties rather than prepared action; thus the notion of “emergent goal” is adapted to give account of teachers’ motivations underpinning their activity. While the two preceding analyses based on didactical constructs highlight weaknesses in these experienced teachers’ activity, the cultural approach should help to understand the reasons for these weaknesses. Saxe (1991) introduced emergent goals to give account of observations of the Oksapmin in New Guinea. These people have a traditional way of counting, using parts of the body as representation of numbers. Some of them trade in the modern way, and while the main goal for them is to realize a good trade, unexpected goals appear, like the necessity of adding a biceps to a forearm!

This brings us to consider cultural systems involved in classroom use of technology. Students saw the spreadsheet as a means to neatly display data. It is consistent with the social representations of technological tools. People are generally not aware of the real power of the computer, which is the possibility of doing controlled automatic calculation on a data set, even when they use spreadsheet features based on this capability. Mrs. PSCEP’s and Mrs. PEX’s saw the spreadsheet as a mathematical tool. They were surprised because they did not realize that other representations could exist. For them, it was very important that students share this representation. They saw the technique of entering and filling down a formula as evidence of a ‘correct’ representation of the spreadsheet. In contrast, students considered that this technique, difficult to understand for them, had no real practical advantage.

In Mrs. PSCEP’s episode about absolute reference, students’ representation of the tool made them content with one working formula. Generally, in social practices with tools, people are satisfied when they know one way to reach a goal, and they need strong reasons to try another. In contrast, Mrs. PSCEP viewed the question relatively to her teaching goal.

The episode of Mrs. PEX explaining the exponential nature of a series also brings evidence of a competition between systems of values introduced with the spreadsheet: while factoring a spreadsheet formula would be compatible with Mrs. PEX’s epistemology of the spreadsheet, she was concerned that colleagues would penalize her students in an exam for doing that.

7 Conclusion and discussion

Mrs. PSCEP and Mrs. PEX encountered repeatedly what we called in the introduction episodes marked by improvisation and uncertainty, although they taught for 3 years a well-established curriculum. Thanks to Saxe’s cultural approach and to other constructs we identified key elements to understand these episodes. Goals emerging were relative to spreadsheet techniques to be used by the students. Teachers did not think of these goals as the real cognitive aims. This partly explains that the tasks they prepared did not establish a milieu that could help to reach these goals.

The way both teachers justified spreadsheet techniques to students, insisting on a supposed pragmatic value, seems to us confusing. In Mrs. PEX’s case, the technophile language she used might well obliterate in the students’ eyes her otherwise balanced ideas about technology and mathematics. As mathematics teachers, Mrs. PSCEP and Mrs. PEX knew more or less consciously the potential epistemic value of those techniques, but seemed to have difficulty opening a dialog with the students about the values associated with techniques. The notion of emergent goals helped us to understand how the episodes were an outcome of divergent cultural representations of the spreadsheet. We saw that mathematics teachers have an understanding of the spreadsheet as an automatic calculation tool and a support for teaching/learning that prevented them from anticipating students’ resistances resulting from common social representations of the spreadsheet.

This synthesis stressed similarities between these two very different teachers. Further analysis brings evidence that the two teachers’ activities do not have the same potential for evolving. Mrs. PSCEP was in an impasse. Her tendency to act on an exposition/application activity format and a teacher/student individual interaction scheme had been reinforced by the spreadsheet and consequently application was replaced by narrow spreadsheet tasks. With regard to individual parameters, Mrs. PEX’s dispositions towards technology integration were, in our opinion, excellent, but globally they conflicted and Mrs. PEX had to make real efforts to get herself out of such conflicts. Thus good dispositions are not a guarantee of easy integration. We identified key features that could condition an evolution: awareness of the multiple cultural representations of the spreadsheet and of the necessity of bringing students to use representations consistent with the spreadsheet as a mathematical tool, necessity of establishing an adequate milieu for that and a more conscious approach to spreadsheet techniques with regard to their epistemic and pragmatic values.

These findings certainly depend on the context of the curriculum, software and teachers that we studied here. Another limitation is that important issues like teachers’ linguistic difficulties when explaining the spreadsheet functioning reported by Haspekian (2005) are not addressed by our study. Despite these limitations, analyzing the flow of emerging goals in a lesson has proved in this study to be efficient for detecting crucial features conditioning the professional evolution of very different teachers. The framework was also helpful: while didactical constructs like milieu and techniques highlighted weak points in these teachers’ activity, the cultural approach helped to understand the reasons for these weaknesses.

This has implications for research because we assume that our framework and findings are able to shed light onto the complexity of integration in other contexts: issues like multiple conflicting representations of a tool, the necessity of an adequate milieu and awareness of the role of tool techniques are not limited to our context. This also has implications in teacher professional development. Emerging goals will play a role in the progress of teachers’ knowledge related to technology, but our study suggests that it cannot be the consequence of teachers’ activity alone and thus conceiving appropriate strategies of teacher development is essential. While strategies based on the transmission of “good practices” taking little care of the complexity of the integration fail to engage teachers, reflecting upon actual more or less unsatisfactory classroom activities might help them to identify possible evolutions (Emprin 2007). As a tool for teachers to clarify their beliefs, knowledge, and decisions, as well as to learn to deal with shifting goals in the classroom, the framework we used here could facilitate a strategic shift towards reflectivity in teacher professional development about technology.