Measuring the Impact of Water Supply Interruptions on Household Welfare

Abstract

Water scarcity frequently leads to a need for rationing. The choice of an adequate rationing method should be based on the impact on consumer welfare that is produced by each rationing plan. Some rationing schemes, such as the frequently used supply interruption method, can be regarded as changes in the characteristics of the good (in this case, time availability) that do not modify the pre-set consumer budget. Under the standard theoretical restrictions on consumer behavior compensating or equivalent variations/surpluses cannot be used to identify the impacts of these methods on household welfare. In this paper, we propose a set of sufficient conditions with respect to the utility function that allows for the evaluation of the compensating or equivalent variations/surpluses associated with changes in goods’ quality, even if those goods are considered to be essential for consumers. We use these conditions to compare the welfare losses associated with the water supply cuts implemented in Seville (Spain) to those that would result if water was instead rationed using price changes.

1 Introduction

The importance of water stems from the fact that it satisfies a broad range of needs in its roles as both a necessary good upon which public health and life depend and as a basic input for most agricultural and industrial production processes. Demographic pressures and economic development will therefore lead to a continual growth in the demand for water that will require greater volumes of water to be allocated to meet various needs.¹ On the other hand, climate change is altering rainfall patterns around the world (IPCC 2013; Bates et al. 2008) causing decreasing levels of average rainfall, rising temperatures and lower water availability in some geographical zones.² Such increases in demand and local decreases in supply suggest that water supply stress will increase over time in some zones, leading to more frequent water shortages and calling for stronger rationing.

Although governing authorities frequently resort to supply cuts,³ a variety of other rationing methods can be implemented (Winpenny 1994; Olmstead and Stavins 2009; Garcia-Valiñas et al. 2015). Therefore, a comparative analysis of the impact of different policies for limiting water consumption is useful for guiding water management during periods of stress. Many studies have focused on this topic (e.g. Moncur 1987; Renwick and Archibald 1998; Garcia-Valiñas 2006; Roibas et al. 2007; Grafton and Ward 2008; Mansur and Olmstead 2012).

Several previous studies have analyzed the impact of supply interruptions on household welfare using the concept of consumer surplus (Garcia-Valiñas 2006; Roibas et al. 2007; Grafton and Ward 2008; Mansur and Olmstead 2012). Alternatively, analysis sometimes uses contingent valuation or choice experiment techniques (Hensher et al. 2005; Genius et al. 2008; Vasquez et al. 2009; McDonald et al. 2010) in order to estimate the willingness to pay and/or to be compensated for reductions on water consumption and/or its quality. However, none of these studies have evaluated welfare losses in terms of standard consumer theory, which considers compensating or equivalent variations/surpluses.⁴ In this respect, Roibas et al. (2007) prove that the use of those measures to evaluate changes in good’s characteristics is not feasible under standard theoretical restrictions.

In this paper, we propose a set of restrictions regarding the utility function that allow for exact measures of consumer welfare which can subsequently be used for evaluating the impact of supply cuts. We apply these restrictions to a specific utility functional form, the Stone-Geary utility function, and use this function to analyze the impact of the supply cuts that occurred over the course of the drought that affected the city of Seville (Spain) during the first half of the 1990s. This analytical tool allows for making decisions as to which is the preferred rationing method in terms of welfare, improving the results compared with other classical approaches based on consumer surplus.

The remainder of this paper is organized as follows. Section 2 reveals the restrictions that must be satisfied by the utility function to evaluate the impact of supply cuts on welfare through the use of compensating or equivalent surpluses. Section 3 discusses the empirical specifications of this study. Section 4 describes the effects of the drought in Seville in the early 1990s and the main response initiatives that were implemented by the water supplier; this section also presents the data set for the investigation. The estimates and welfare results are provided in Section 5. Finally, Section 6 concludes the manuscript.

2 Measuring the Welfare Losses that are Associated with Supply Cuts

Consumer behavior data can be used to analyze consumer evaluations of certain characteristics of goods through the use of hedonic prices (Rosen 1974). However, the use of hedonic prices requires prices to depend on the characteristics of goods; this condition is not satisfied in various situations, such as scenarios that involve interruptions in water or electricity supplies. Supply interruptions can be regarded as reductions in one specific characteristic of a good, its availability. These interruptions impose the condition that the good in question can only be acquired during periods when the supply is uninterrupted.⁵

For utility functions that satisfy standard theoretical properties (differentiability, monotonicity and quasi-concavity), it is impossible to derive compensating or equivalent surpluses that accurately reflect changes in the characteristics of goods. Mäler (1971) shows that weak complementarity is a sufficient condition to identify welfare losses.⁶ Weak complementarity could be defined as: $\frac{{\delta U\left( {o,x_{2} , \ldots , x_{n} ,c} \right)}}{\delta c} = 0$, where U(·) is the utility function and c is a characteristic of good x₁. Thus, weak complementarity requires that the utility function is defined when x₁ is null implying therefore, the non-essentiality of x_1. A good “is non-essential if combinations of other goods can be found that will compensate the individual for its complete absence” (Bockstael and McConnell 1993 p. 1248). That is, x₁ is non-essential if for every $x_{1}^{0}$ there exists a vector $\left( {x_{2}^{1} , \ldots , x_{n}^{1} } \right)$ such that:

$$ U\left( {x_{1}^{0} , x_{2}^{0} , \ldots , x_{n}^{0} ,c} \right) = U\left( {0, x_{2}^{1} , \ldots , x_{n}^{1} ,c} \right) $$

(1)

Therefore, these restrictions are useful to evaluate the impact of, for example, environmental changes in the demand for outdoor recreation (Phaneuf et al. 2000; von Haefen and Phaneuf 2003; von Haefen 2008). However, given that water is necessary for survival, non-essentiality could be considered too strong an assumption for that good.

In this study we use a primal analysis to demonstrate that under standard theoretical restrictions, the impossibility of identifying compensating and equivalent surpluses is related to the fact that the marginal utilities of the goods are not observable.⁷ Then, we identify sufficient restrictions for the utility function that allows for exact measures of welfare to be identified without assuming non-essentiality.

For simplicity, we assume that the consumer purchases two goods: water (x₁) and other goods (x₂). We also assume that consumer behavior depends on a variable (c) that corresponds to supply cuts duration and affects consumer utility. In this context, the consumer’s utility maximization can be expressed as follows:

$$ \begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{{x_{1} ,x_{2} }} U\left( {x_{1} ,x_{2} ,c} \right) } \\ {s.t: p_{1} x_{1} + p_{2} x_{2} = R} \\ \end{array} $$

(2)

here p₁ and p₂ are prices and R is income. Substituting the Marshallian demands into the first order conditions for utility maximization we find:

$$ - p_{1} x_{1} \left( {p_{1} ,p_{2} ,R,c} \right) - p_{2} x_{2} \left( {p_{1} ,p_{2} ,R,c} \right) + R \equiv 0 $$

(3a)

$$ - \lambda p_{1} + U_{1} \left[ {x_{1} \left( {p_{1} ,p_{2} ,R,c} \right),x_{2} \left( {p_{1} ,p_{2} ,R,c} \right),c} \right] \equiv 0 $$

(3b)

$$ - \lambda p_{2} + U_{2} \left[ {x_{1} \left( {p_{1} ,p_{2} ,R,c} \right),x_{2} \left( {p_{1} ,p_{2} ,R,c} \right),c} \right] \equiv 0 $$

(3c)

where U_i (·) is the derivative of the utility function with respect to x_i. Differentiating (3) with respect to c we obtain:

$$ \left( {\begin{array}{*{20}c} 0 & { - p_{1} } & { - p_{2} } \\ { - p_{1} } & {U_{11} } & {U_{12} } \\ { - p_{2} } & {U_{12} } & {U_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\delta \lambda /\delta c} \\ {\delta x_{1} /\delta c} \\ {\delta x_{2} /\delta c} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ { - U_{1c} } \\ { - U_{2c} } \\ \end{array} } \right) $$

(4)

Solving for the derivatives of the Marshallian demands:

$$ \left( {\begin{array}{*{20}c} {\delta x_{1} /\delta c} \\ {\delta x_{2} /\delta c} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {p_{2}^{2} /H} & { - p_{1} p_{2} /H} \\ { - p_{1} p_{2} /H} & {p_{1}^{2} /H} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {U_{1c} } \\ {U_{2c} } \\ \end{array} } \right) $$

(5)

where H is the determinant of the first matrix in (4). Therefore, as the budget set remains unchanged, the first equation in (4) implies a linear relationship between the Marshallian demand derivatives $\left( {\delta x_{1} /\delta c = - \left( {p_{2} /p_{1} } \right)\left( {\delta x_{2} /\delta c} \right)} \right)$ and thus, the matrix multiplying the derivatives of marginal utilities with respect to c in (5) is not of full rank, preventing the identification of those derivatives from the Marshallian ones. Consequently, it becomes impossible to integrate U_1c and U_2c to recover the marginal utilities and prevents the evaluation of the effect of changes in c on the utility function.

A graphical analysis can help to illustrate the nature of the analyzed identification problem. From equations in (4) we obtain:

$$ \left( {\frac{1}{{p_{1} }}U_{1c} - \frac{1}{{p_{2} }}U_{2c} } \right) = \frac{1}{{p_{2} }}\left( {U_{12} \frac{{\delta x_{1} }}{\delta c} + U_{22} \frac{{\delta x_{2} }}{\delta c}} \right) - \frac{1}{{p_{1} }}\left( {U_{11} \frac{{\delta x_{1} }}{\delta c} + U_{12} \frac{{\delta x_{2} }}{\delta c}} \right) $$

(6)

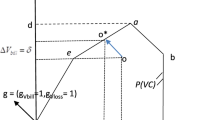
Figure 1 illustrates Eq. (6), showing the consumer reactions that are induced by changes in c. The initial equilibrium x⁰ is associated with c⁰. The change from c⁰ to c¹ changes the indifference map, generating a final equilibrium x¹. The solid indifference curve U(x¹, c⁰) illustrates the marginal rate of substitution (MRS) in x¹ in the initial indifference map associated with c⁰.

Fig. 1

Changes in consumption due to changes in c

The right-hand side of Eq. (6) includes the derivatives of the marginal utilities with respect to x₁ and x₂ and is therefore related to changes in the MRS that are exclusively caused by the change in consumption from x⁰ to x¹ if c is maintained at its initial value (c⁰). In Fig. 1, this change is represented by the difference between the MRS in x⁰ and the MRS in x¹, evaluated over the solid indifference curve U(x¹, c⁰). The left-hand side of Eq. (6) includes the derivatives of the marginal utilities with respect to c and therefore reflects the change in consumer MRS in x¹ related to the transition from the solid indifference curve (U(x¹, c⁰)) associated with c⁰ to the dashed curve (U(x¹, c¹)) associated with c¹.

It is clear that if there are sufficient observations for each value of c, it is possible to estimate the Marshallian demand functions that correspond to each of these values and thereby recover the shape of both indifference maps. However, as utility is not observable, under standard consumer preference restrictions, it is impossible using the Marshallian demands to assess the effects of changes in c on consumer utility for two reasons that emerge in the graphical analysis. First, any influence of c on the utility function that leaves the MRS unaffected implies that the consumer does not react to changes in c. Therefore, it would be impossible to identify variations in utility from the (absent) consumer reaction. Second, it is possible to observe the changes in the MRS that are generated by changes in c (the left-hand side of Eq. (6)). However, as is clear from Eq. (5), the change in each individual marginal utility cannot be identified from the Marshallian demands. Thus, it becomes impossible to integrate the marginal utilities to determine the changes in consumer utility.

It is possible, however, to identify a set of sufficient conditions for the utility function that allows for the effect of c on consumer utility to be evaluated without requiring non-essentiality. Compensated and equivalent surpluses associated to changes in c can be identified if the utility function verifies:

P1

The utility function does not include any autonomous component that depends only on c.

P2

The marginal utility of one of the goods is independent of c.

P1 implies that the utility function cannot be expressed as $U^{*} \left( {x_{1} ,x_{2} ,c} \right) + U^{C} \left( c \right)$. P1 becomes a necessary condition because any autonomous component $U^{C} \left( c \right)$ would not affect marginal utilities and would therefore generate no influence on consumer behavior. As mentioned above, effects on utility that do not generate consumer reactions cannot be evaluated by observing consumer behavior.

P2 Assuming that the marginal utility of x₂ is independent of c$\left( {U_{2c} = 0} \right)$, the utility function can be expressed in the following form:

$$ U\left( {x_{1} ,x_{2} ,c} \right) = U^{0} \left( {x_{1} ,c} \right) + U^{1} \left( {x_{1} ,x_{2} } \right) $$

(7)

Under P2, equations in (5) imply:

$$ U_{1c}^{0} = \left( {2\frac{{p_{1} }}{{p_{2} }}U_{12} - U_{11} - \frac{{p_{1}^{2} }}{{p_{2}^{2} }}U_{22} } \right)\frac{{\delta x_{1} }}{\delta c} $$

(8)

which allow U_1c to be identified from the Marshallian demand of x₁. Therefore, simple integration of $U_{1c}^{0}$ allows the effect of c on the marginal utility of x₁ to be recovered:

$$ \int U_{1c}^{0} \left( {x_{1} ,c} \right)dc = U_{1}^{0} \left( {x_{1} ,c} \right) $$

(9)

Therefore, once $U_{1}^{0} \left( {x_{1} ,c} \right)$ is identified and P1 is taken into account, the simple integration of $U_{1}^{0} \left( {x_{1} ,c} \right)$ allows the effect of c on consumer utility to be recuperated:

$$ \int U_{1}^{0} \left( {x_{1} ,c} \right)dx_{1} = U^{0} \left( {x_{1} ,c} \right) $$

(10)

It is worth noting that given a utility function verifying P1 and P2, only affine transformations of that function generate utility functions fulfilling P1 and P2 (see “Appendix A”).

This analysis could easily be extended to the general n-dimensional case. In this situation, P1 would remain unchanged, and P2 would again imply the existence of at least one good with a marginal utility that is independent of c. Therefore, these restrictions have an appealing interpretation. P1 implies that consumers extract welfare by consuming goods and suggests that the characteristics of these goods are only relevant through the act of consumption. P2 requires that the utility extracted from at least one of the available goods to be independent of the evaluated characteristic. In our empirical application, we evaluate the effect of interruptions in the water supply on consumer welfare. It therefore appears reasonable to assume that the utility that is obtained from various activities, such as attending the theater or taking a tourist trip, will be independent of the duration of water supply cuts.

3 The Empirical Model

To calculate the compensating surplus associated with supply cuts in the empirical application of this study, we specify a demand function that is based on a Stone-Geary utility function. If a consumer purchases two goods, this function takes the form:

$$ U = b_{1} \ln \left( {x_{1} - a_{1} } \right) + \left( {1 - b_{1} } \right)\ln \left( {x_{2} - a_{2} } \right) $$

(11)

where b₁ and a_i are parameters of the utility function. Based on this functional form, the maximization of utility can be understood as a process in which the household purchases a subsistence level of each good i that does not depend on price and then allocates fixed proportions of the leftover income (which is known as supernumerary income) to each good or service in accordance with the parameter (b₁) (see Deaton and Muellbauer 1980; or Chung 1994; for more details). This utility function has frequently been used to analyze residential water demand, particularly during the past decade (see Al-Qunaibet and Johnston 1985; Gaudin et al. 2001; Martínez-Espiñeira and Nauges 2004; Madhoo 2009; Meran and von Hirschhausen 2009; Nauges et al. 2009; Schleich 2009; Monteiro 2010; Garcia-Valiñas et al. 2010; Dharmaratna and Harris 2012; Renzetti et al. 2015; Clarke et al. 2017). One reason that this function is frequently used may be because previous studies found very low own-price elasticities, possibly indicating that a portion of water consumption could be unresponsive to price changes; this phenomenon corresponds to the subsistence or non-discretionary consumption concept that is implicitly assumed by the Stone-Geary utility function. In addition, this utility function enjoys the advantages of being theoretically consistent. Unless the subsistence or minimum consumption threshold is zero, elasticity is non-constant. Finally, when using the Stone-Geary functional form, the Hicksian demands and the expenditure function can be analytically derived. The use of more flexible functional forms would require the compensating surplus to be identified by numerical calculation. Table 8 in the “Appendix B” illustrates certain aspects of the studies that have applied this functional form for the modeling of residential water demand,⁸,⁹

Including supply cuts (c) in the Stone-Geary function in a manner that satisfies properties P1, and P2 yields:

$$ U = b_{1} \ln \left( {x_{1} - a_{1} } \right) + \left( {1 - b_{1} } \right)\ln \left( {x_{2} - a_{2} } \right) + b_{2} \ln \left( {x_{1} - a_{1} } \right)c $$

(12)

It is assumed that the consumer maximizes this utility function subject to the following budget constraint:

$$ R = px_{1} + x_{2} $$

(13)

In the previous equation p denotes the price of x₁ and x₂ corresponds to expenses for other goods in the empirical application of this study, so its price is equal to one. The Marshallian demand functions are:

$$ x_{1} = a_{1} + \frac{{\left( {R - pa_{1} - a_{2} } \right)}}{p}\frac{{\left( {b_{1} + b_{2} c} \right)}}{{\left( {1 + b_{2} c} \right)}} $$

(14a)

$$ x_{2} = a_{2} + \left( {R - pa_{1} - a_{2} } \right)\frac{{\left( {1 + b_{1} } \right)}}{{\left( {1 + b_{2} c} \right)}} $$

(14b)

The following Hicksian demand functions correspond to the proposed functional form:

$$ x_{1}^{h} = \left[ {\frac{{b_{1} + b_{2} c}}{{\left( {1 - b_{1} } \right)p}}} \right]^{{\left( {\frac{{1 - b_{1} }}{{1 + b_{2} c}}} \right)}} \exp \left( {\frac{U}{{1 + b_{2} c}}} \right) + a_{1} $$

(15a)

$$ x_{2}^{h} = \left[ {\frac{{\left( {1 - b_{1} } \right)p}}{{b_{1} + b_{2} c}}} \right]^{{\left( {\frac{{b_{1} + b_{2} c}}{{1 + b_{2} c}}} \right)}} \exp \left( {\frac{U}{{1 + b_{2} c}}} \right) + a_{2} $$

(15b)

Once these Hicksian demand functions are specified, it is possible to obtain the expenditure function, which can be used to calculate the compensating surplus associated with changes in c:

$$ e\left( {p,U,c} \right) = \left[ {\left( {\frac{{1 - b_{1} }}{{b_{1} + b_{2} c}}} \right)^{{\left( {\frac{{b_{1} - 1}}{{1 + b_{2} c}}} \right)}} + \left( {\frac{{1 - b_{1} }}{{b_{1} + b_{2} c}}} \right)^{{\left( {\frac{{b_{1} + b_{2} c}}{{1 + b_{2} c}}} \right)}} } \right]p^{{\left( {\frac{{b_{1} + b_{2} c}}{{1 + b_{2} c}}} \right)}} \exp \left( {\frac{U}{{1 + b_{2} c}}} \right) + a_{1} p + a_{2} $$

(16)

The empirical application that is developed in this study is based on the estimation of the Marshallian demand for x₁ in Eq. (14a). In particular, the equation to be estimated is:

$$ x_{1it} = a_{1} + \frac{{R_{i} - p_{it} a_{1} - a_{2} }}{{p_{it} }}\left( {\frac{{b_{1} + b_{2} c_{t} }}{{1 + b_{2} c_{t} }}} \right) + e_{it} $$

(17)

where:

$$ a_{1} = g_{1} + b_{NPER} NPER_{i} + b_{TEMP} TEMP_{t} + b_{RAIN} RAIN_{t} + b_{QUAL} QUAL_{t} + \mathop \sum \limits_{T = 1992}^{2000} b_{T} D_{T} $$

(18)

and x_1it is the water consumption of consumer i in period t; p_it is the price that this consumer pays for water in period t; R_i is the consumer’s income; TEMP_t is the average temperature during each period; RAIN_t corresponds to the total rainfall; NPER_i is the number of persons in the consumer’s household; QUAL_t is a dummy variable that indicates the existence of drops in pressure and/or chemical parameters that determine the quality of the product; D_T is a set of year dummies; c_t is the duration of supply interruptions, measured in hours per quarter; a₂, g₁and b’s denotes parameters to be estimated; and e_it is the error term.

4 Water Provision in Seville

4.1 Cyclical Shortages

Seville is a city with more than 700000 inhabitants (INE 2011) that in the past has been severely affected by water scarcity problems. This city is located in Andalusia, a region in southern Spain that exhibits the greatest levels of water stress of any area in the European Union (European Environment Agency 2009). In recent decades, water supply and sanitation in the city and certain surrounding municipalities have been the responsibility of the Seville Municipal Water Company (EMASESA); during this time, several water emergencies have arisen that necessitated water restriction initiatives. The first two emergencies occurred from 1974 to 1976 and from 1981 to 1983. The third emergency, which is the focus of the empirical analysis in this paper, was experienced during the first half of the 1990s.¹⁰ Table 1 presents the status of water reserves in reservoirs near Seville during these droughts, illustrating the seriousness of these water shortages.

Table 1 Water reserves in Seville during drought periods

In the drought which occurred from 1992 to 1996, water shortages first appeared at the end of 1991, and the situation worsened during the following year. The first water consumption restrictions to address these shortages, which were formally introduced through the publication of municipal edicts,¹¹ were implemented at the beginning of 1992. These edicts specified the conditions under which water would be supplied and the responses that were expected from consumers. The implemented restrictions included interruptions in water supply and reductions in water pressure. These restrictions were particularly intense during 1993 and 1995; during this period, water supply interruptions sometimes lasted for up to 12 h per day.¹² In addition to restrictions on the hours of water availability, the water quality was also affected during this drought. Despite the efforts of the supplier to guarantee this quality, the unusual weather conditions and the consequent decision to diversify the sources of water supply led to a considerable deterioration of water quality. The health authorities were forced to provisionally relax water standards; in order to justify this laxity, these authorities offered the argument that the drought constituted a period of “exceptional conditions”.

4.2 Data

Equation (17) has been estimated using a balanced panel that consists of quarterly observations for 208 Sevillian households with individual water meters.¹³ The sample period ranges from the fourth quarter of 1991 to the third quarter of 2000. The data was obtained from several sources. The Seville municipal water supply firm (EMASESA) provided information about water consumption per household (x₁), the price of water and the presence of quality restrictions for the supplied water (QUAL). A two-part tariff with three blocks is adopted in Seville. The fixed fee depends on the meter caliber. The fixed fee and the blocks of water prices are presented in Tables 9 and 10 in “Appendix C”. The price considered in the empirical analysis is the household’s marginal price.¹⁴ The quality variable is a dummy that was set equal to 1 if there were changes in water pressure and/or the chemical parameters that determine the quality of the product. The durations of the supply cuts (c_t) were calculated from the municipal edicts that were announced to Sevillian citizens.

A proxy for household income (R) is obtained from an estimation based on the location of the sampled homes within the Seville municipality. The Seville Revenue Office has provided information on the fiscal category of the street where the household is located,¹⁵ and a level of disposable income (La Caixa 2000) has been assigned to each category. This estimation was originally designed to assess household income in 1998; for the purposes of this study, the estimated incomes (expressed in €) have been indexed to 2002 price levels.

Data regarding temperature and rainfall (TEMP, RAIN) were provided by the Spanish National Meteorological Institute and reflects important climatic differences among the four quarters of the year (Table 2 shows the quarter average of temperature and rainfall). We use the arithmetic mean of the maximum daily temperatures and total rainfall that were registered during each quarter.

Table 2 Meteorological conditions per quarter

Finally, the number of users per household (NPER) was obtained by dividing the total number of people in each building, as provided by the Spanish census, by the number of households in each building. We could only obtain the exact number of individuals per household in the case of large families (families with 4 or more members) because of the application of water tariff discounts that were dependent on household size. Difficulties in obtaining information prevented us from determining how the number of people in each household varies over time. Hence, this variable only exhibits variation across the different households and is assumed to remain constant over time. The information for this variable was provided by the Seville City Council and EMASESA. The main descriptive statistics related to the variables and the consumed quantities are presented in Table 3.

Table 3 Variable descriptive statistics

5 Results

From the household perspective, most of the variables in the demand equation could be considered as exogenous or predetermined variables (income, number of persons, quality dummy, supply cuts duration, temperature and rainfall). However, marginal price is expected to be endogenous when block tariffs apply (Olmstead et al. 2007; Olmstead 2009). Thus, the estimation was performed through a non-linear two stage least squares estimator with instrumental variables,¹⁶ using the TSP econometric software package.¹⁷ All the exogenous and predetermined variables along with the inverse of block prices and their interaction with income and supply cuts were used as instrumental variables. Table 4 provides the parameter estimates.

Table 4 The parameter estimates of the demand function

In general, the parameter estimates are statistically significant. The price elasticity of the demand for water is calculated for a representative household. This household is characterized by the average monthly income (= 1583 €) and by a number of members equal to four (which is the whole number closest to the sample mean). The representative household is assumed to demand water at the largest yearly marginal price (as it is expected to demand more than 60 cubic meters of water) and the yearly average of temperature and rainfall. It is assumed also the absence of restrictions on water quality and availability. For this household, the elasticity of demand ranges from − 0.29 to − 0.43, depending on temperature, rainfall and the parameter interacting with the corresponding year dummy. This result is consistent with previous studies on water demand (Arbués et al. 2003; Worthington and Hoffman 2008). Moreover, these elasticities are similar to that found by other studies using the same dataset but quite different demand specifications. In particular, Garcia-Valiñas (2006) found elasticity to be equal to − 0.53 while Roibas et al. (2007) found a − 0.33 value for demand elasticity. The estimation of parameter b₁ reveals that income has a positive and significant influence on water demand. The estimated value of b₂ is negative and significant, indicating that supply interruptions reduce water marginal utility and then, water consumption. Only three parameters associated with year dummy variables becomes significant and negative evidencing a rather stable demand over the sample period. The remaining parameters also have the expected sign. The effects of temperature, rainfall and the number of individuals per household are positive and significant, and cutbacks in quality produce very significant reductions in water consumption.

We next use the above parameter estimates to compute welfare losses associated to supply cuts and the welfare losses that would take place if the same reduction in consumption were achieved by increasing the price of water as is shown in Eqs. (19a) and (19b):

$$ WL^{c} \left( {c = \overline{c} } \right) = CS\left( {c = \overline{c} } \right) + \left[ {p\left( {x_{1} \left( {c = 0} \right) - x_{1} \left( {c = \overline{c} } \right)} \right)} \right] $$

(19a)

$$ WL^{p} \left( {p = p^{R} } \right) = CV\left( {p = p^{R} } \right) + \left[ {px_{1} \left( {c = 0} \right) - p^{R} x_{1} \left( {c = \overline{c} } \right)} \right] $$

(19b)

where $WL^{c} \left( {c = \overline{c} } \right)$ is the welfare loss when the average water supply disruption is applied $\left( {\overline{c} } \right)$; $CS\left( {c = \overline{c} } \right)$ is the compensating surplus associated to that average supply cut; $x_{1} \left( {c = 0} \right)$ is water consumption when no supply cut takes place and $x_{1} \left( {c = \overline{c} } \right)$ is water consumption when the average supply interruption applies; $CV\left( {p = p^{R} } \right)$ is the compensating variation associated to the price rationing scheme; $p^{R}$ is the price that would generate the same reduction in water consumption than the average supply cut (virtual price); finally, $WL^{p} \left( {p = p^{R} } \right)$ is the welfare loss when price rationing is put in practice. Thus, welfare losses include both: the consumer welfare losses and the changes in the water utility’s revenues generated by each rationing regime.¹⁸ The welfare losses are calculated for the representative household demanding water in 1993, which is the year with the largest supply interruption duration (359 h per quarter). Table 5 shows the values defining the representative household in the welfare loss evaluation.

Table 5 Simulation values

Figure 2 shows the distribution of the differences of welfare losses between the two regimes across the 208 households. A strong heterogeneity is observed and the histogram is far from adopting a normal shape.

Fig. 2

Histogram of the difference between welfare losses (€) of supply cut and price rationing (WLc $\left( {c = \overline{c} } \right) -$ WLp$\left( {p = p^{R} } \right)$)

Note: WLc $\left( {c = \overline{c} } \right):$ welfare loss under supply cut; WLp$\left( {p = p^{R} } \right)$: welfare loss under price rationing

As the elasticity of the demand for water has a clear impact on the effectiveness of the price rationing procedure and this elasticity depends on household income, several income levels have been considered. Table 6 shows the results of the welfare evaluation for the eight income categories. Several aspects deserve some attention from this analysis. First, differences in consumer welfare losses between the two rationing regimes are small and, given their standard deviations, the Wald test shows that these differences are not significant. Nevertheless, it seems that the greater the water consumption, the larger the demand elasticity and the greater the advantage of the price rationing scheme over the supply interruptions, in terms of the consumer welfare losses. Moreover, Table 6 shows the percentage of household’s water bill over income,¹⁹ before rationing (B) and after rationing by means of supply interruption (Bc) or price (Bp). On average, the weight of water expenditures over household’s income is lower than 3%, so no significant water poverty issues are detected under any scenario.²⁰ Although the relationship is non-linear, water expenditure weight increases with income, and it is always lower in the case of supply cut rationing.

Table 6 Welfare losses depending on income level

Moreover, when the variation of the water utility’s revenues is taken into account the advantage of price rationing always becomes significant (see the last file in Table 6). Note that rises in price imply higher revenues for the water company when the demand is inelastic. This fact underlines the advantage of price rationing from the social welfare perspective as per our case. If the price elasticity was large enough price rationing would generate revenue reductions and then, the preferred rationing scheme could be the supply cuts for the lower income households. When comparing the highest and lowest income categories (Cat. 1/Cat. 8), we observe that the difference between welfare losses of prices and supply cuts for the richest is three times the difference for the poorest.

Finally, we perform a simulation analysis in which we calculate the welfare losses associated to each rationing procedure (supply cuts and price rationing) for a range of water consumption reductions from 2.5 to 15% of their initial values. Moreover, to simplify the simulation, only three different levels of income are considered: the highest income in the first quartile (q1 = 1363 €) of the income distribution, the mean value (= 1583 €) and the highest income in the third quartile (q3 = 1712 €). Table 7 and Fig. 3 summarize the results of this simulation exercise.

Figure 3 represents graphically the compensating variations/surpluses under different income levels and consumption reduction aims. On the one hand, for lower income levels and higher consumption reduction objectives, price rationing generates higher consumer welfare losses than supply cuts. So, low-income households would prefer supply cut rationing when targeted reduction in consumption is higher. On the other hand, and in terms of compensating variation/surpluses, high-income households would prefer price rationing.

Fig. 3

Compensating variations/surpluses (€) depending on targeted reduction of water consumption (%)

Note: CV $\left( {p = p^{R} } \right)$: compensating variations under price rationing; CS $\left( {c = \overline{c} } \right)$: compensating surpluses under supply cut

However, results are slightly different when changes in a household’s water expenditure are taken into account. From Table 7 further interesting conclusions can be highlighted. First, price rationing is always the preferred system as the difference between welfare losses is always significant in favor of the rationing procedure. Nevertheless, when the targeted reduction in consumption is small, the gap between welfare losses generated by the two alternative rationing methods becomes narrower. Since values are very close in this scenario, operating and maintenance costs of both rationing methods would probably emerge as a key issue when making a decision about the more efficient option.²¹ However, when the targeted reduction in consumption increases, the advantage of the price rationing procedure grows. In this respect, a 15% reduction in consumption generates welfare losses that are lower for the price rationing in a range from 27 € to 34 € per household²² each quarter. Hence, the aggregate social welfare loss that would be avoided by adopting a price rationing procedure is really important and should be taken into account.

Table 7 Differences of welfare losses (€) depending on targeted reduction of water consumption (WLc $\left( {\varvec\bf{c} = \overline{c} } \right) -$WLp$\left( {p = p^{R} } \right)$)^a

Note that these estimates are far from those obtained under a baseline linear demand model. Thus, using a linear demand function and the consumer surplus as a welfare measure, and considering the simulation values in Table 5, the average welfare losses generated by supply cuts are huge compared with those generated by price rationing. As a consequence, policy implications and conclusions would be extremely different. The results of this model are presented in “Appendix D”.

6 Conclusions

Water scarcity is a cyclical problem that is expected to occur regularly around the world. Policies to limit water consumption are frequently implemented in response to this problem. The evaluation of the impact of these policies on welfare is recommendable in order to design an efficient rationing scheme. However, certain methods that are used to reduce water consumption, such as the commonly implemented measure of supply cuts, cannot be easily evaluated because they do not affect the pre-set consumer budget.

In this study, we propose a set of sufficient conditions that allow for the identification of the welfare impact of supply cuts without encompassing the non-essentiality of the good. Under these conditions, consumption data can be used to evaluate consumer welfare losses. Assuming that these conditions are applicable, we evaluate the impact of the water supply interruptions that occurred in Seville in the 1990 s and compare the results with the welfare losses that would have resulted if the consumption reductions had been achieved by increasing the price of water.

Our results reveal that a rationing method based on price increases would have had a lower impact on consumer welfare than the supply cuts that were actually implemented in Seville during the examined period. We develop a simulation analysis that suggests that the targeted reduction in consumption could have impact on welfare calculations. Looking exclusively at compensating variation/surplus results, we detect that low-income households would prefer supply cut interruption when the targeted consumption reduction is relatively high. Moreover, high-income households would choose price rationing for any of the targets considered.

However, once that we consider the changes in the water utility’s revenues generated by each rationing regime, even for moderate reductions in consumption the advantage of the price rationing procedure becomes significant. So, in the case of Seville, the price instrument seems to be preferred to supply interruptions in terms of welfare. In particular, the welfare difference favors the price rationing scheme in 18.44 € for the average household. This fact implies that the aggregate benefits of switching to this method amounts to approximately 3651000 € per quarter. On top of that, this figure would grow for large targeted reductions in water consumption.

Note that conclusions and policy implications could be completely different if a non-adequate theoretical/empirical framework is applied (see baseline model in “Appendix D”). Definitively, we have provided an analytic tool to calculate welfare variations in an accurate way, in order to make the right decisions when managing water services.

Appendices

Appendix A

Given a monotonic twice differentiable transformation f, the function $f\left( U \right)$ only verifies P2$\left( {\frac{{\delta^{2} f\left( U \right)}}{{\delta x_{2} \delta c}} = 0} \right)$ if f is an affine transformation. The marginal utility of x₂ becomes:

$$ \frac{\delta f\left( U \right)}{{\delta x_{2} }} = \frac{\delta f\left( U \right)}{\delta U}\left( {\frac{\delta U}{{\delta U^{0} }}\frac{{\delta U^{0} }}{{\delta x_{2} }} + \frac{\delta U}{{\delta U^{1} }}\frac{{\delta U^{1} }}{{\delta x_{2} }}} \right) $$

(A1)

which, taking into account that $\frac{{\delta U^{0} }}{{\delta x_{2} }} = 0$ and $\frac{\delta U}{{\delta U^{1} }} = 1$ becomes:

$$ \frac{\delta f\left( U \right)}{{\delta x_{2} }} = \frac{\delta f\left( U \right)}{\delta U}\frac{{\delta U^{1} }}{{\delta x_{2} }} $$

(A2)

and, therefore:

$$ \frac{{\delta^{2} f\left( U \right)}}{{\delta x_{2} \delta c}} = \frac{{\delta^{2} f\left( U \right)}}{{\delta U^{2} }}\frac{\delta U}{\delta c}\frac{{\delta U^{1} }}{{\delta x_{2} }} + \frac{\delta f\left( U \right)}{\delta U}\frac{{\delta^{2} U^{1} }}{{\delta x_{2} \delta c}} $$

(A3)

Taking into account that $\frac{{\delta^{2} U^{1} }}{{\delta x_{2} \delta c}} = 0$, P2 is verified only if $\frac{{\delta^{2} f\left( U \right)}}{{\delta U^{2} }} = 0$ which implies that f is an affine transformation.

Appendix B

Table 8 Residential water demand functions based on a Stone-Geary utility function

Appendix C

Table 9 Fixed fee (€)

Table 10 Block dimension and price

Appendix D

The baseline linear demand model estimated is the following:

$$ \begin{aligned} x_{1} & = b_{1} + b_{NPER} NPER_{i} + b_{TEMP} TEMP_{t} + b_{RAIN} RAIN_{t} + b_{QUAL} QUAL_{t} + \mathop \sum \limits_{T = 1992}^{2000} b_{T} D_{T} \\ & \quad + b_{R} R + b_{c} c + b_{p} p \\ \end{aligned} $$

(D1)

Tables 11 and 12 show the main results of the estimation/simulation based on the previous linear demand function and the consumer surplus as a welfare method.

Table 11 Baseline linear demand model estimation^a

Table 12 Consumer surplus (€) under alternative rationing schemes: baseline model