Environmental Quality, Public Debt and Economic Development

Abstract

This article analyzes the consequences on capital accumulation and environmental quality of environmental policies financed by public debt. A public sector of pollution abatement is financed by a tax or by public debt. We show that if the initial capital stock is high enough, the economy monotonically converges to a long-run steady state. On the contrary, when the initial capital stock is low, the economy is relegated to an environmental poverty trap. We also explore the implications of public policies on the trap and on the long-run stable steady state. In particular, we find that government should decrease debt and increase pollution abatement to promote capital accumulation and environmental quality at the stable long-run steady state. Finally, a welfare analysis shows that there exists a level of public debt that allows a long run steady state to be optimal.

1 Introduction

Environmental protection programs are often constrained by long-term fiscal objectives which impose to control public deficits and public debt evolution. These long-term constraints have important short-term implications for developed countries, but weigh even more heavily on developing countries. Indeed, the latter countries have often high level of public debt to GDP ratio which in turn may hamper their fiscal policies. The search for financing mechanisms that do not increase debt burden has renewed interest in debt-for-nature swaps.¹ Therefore, debtor countries reduce their debt burden, and free up budgetary resources for environmental spending. In 1991, the Paris Club² introduced a clause that allowed members to convert all official public debt through debt swaps with social or environmental objectives (Jha and Schatan 2001; Ruiz 2007). This led to a marked increase in debt-for-nature initiatives. Canada, Finland, France, Sweden, Switzerland and the United States were the first countries to make use of the Paris Club clause in the environmental sphere (see Moye 2003). Finally, debt swaps were part of the negotiating text for the Copenhagen summit.³

The aim of the paper is to analyze the interactions between public debt and environmental policy. Basically, debt for nature swap is a very specific case where a pre-existing public debt is finally devoted to environmental protection. But, more generally, Government may also decide to increase the public debt in order to finance its environmental protection program. On the contrary, a pre-existing high level of debt could be an obstacle for the launching of new environmental protection programs. More generally, we study the long-term macroeconomic impacts of environmental policies under a debt stabilization constraint, when public actions to protect the environment are at least partially financed by public funds. Could public debt be a solution⁴ or an obstacle for the financing of environmental policies? In other words, what could be the implications on the welfare of the funding of environmental policies by issuing public debt?

We consider a two-period overlapping generations model à la Diamond (1965) with an environmental externality. Indeed, longevity is increasing in current environmental quality, while production harms future environmental quality. We assume that public environmental maintenance expenditure could be financed by issuing public debt. Moreover, a debt stabilizing constraint imposes a constant level of debt per capita. Methodologically, we draw on Chakraborty (2004) who has first considered endogenous mortality⁵ in the standard overlapping generations model with production. He examines interactions between pervasive ill-health and economic growth. As he points out, the probability that a average 15-year old would die before reaching age 60, was three times as high in sub-Saharan Africa as in the richer OECD economies. He goes on to suggest that when life expectancy is low, agents would place little emphasis on the future, and hence, would invest little in productive long-term assets, thereby getting stuck in a low level of real activity. Based on this model, we then add elements pertaining to the interactions between public debt and publicly-funded activities that are designed to abate pollution, improving hence the environmental quality.

Our model shows that the initial conditions on the capital stock determine the long-run value of the environmental quality. Namely, if the initial capital stock is high enough, the economy monotonically converges to a long-run steady state. On the contrary, when the initial capital stock is low, the economy is relegated to an environmental poverty trap. In opposition to many papers (John and Pecchenino 1994; John et al. 1995; Mariani et al. 2010), we find that the economy may be characterized by a conflict between environmental quality and capital accumulation. We hence show that increasing debt to finance environmental protection programs reduces the capital stock at the long-run stable steady state, and improves environmental quality. Finally, we find that when the government decreases debt and increases environmental protection spending (like the debt-for-nature swaps solution), it may improve capital accumulation and environmental quality at the long-run steady state. Moreover, we finally find that a policy based on debt emission may be welfare improving. Indeed, we show that there is a level of debt for which a long run steady state is optimal.

Previous papers have analyzed the consequences of environmental policies on environmental quality, growth and welfare (Howarth and Norgaard 1992; John and Pecchenino 1994; John et al. 1995; Jouvet et al. 2000). Nevertheless, in all these studies, government cannot fundpollution abatement programs by issuing public debt. In consequence, they only consider tax financing schemes. However, debt financing has already been introduced in dynamic models with environmental concerns (Bovenberg and Heijdra 1998; Heijdra et al. 2006), but these contributions focus on a different issue than ours. Instead of using debt to finance a share of pollution abatement, debt policy makes possible to redistribute welfare gains from future to existing generations. In our model, the role of the public debt is twofold: as usual, it redistributes welfare among young and old generations, but first of all, it finances the public pollution abatement sector.⁶ Hence, the redistribution properties of the public debt are limited by the environmental actions of the government.

Finally, in our paper, we also take into account the impact of environmental quality on health and life expectancy.⁷ This assumption is justified by the results of an increasing number of empirical studies measuring the health effects of pollution (OECD 2008). These relationships are nowadays well-documented and are probably the most striking features of the negative impact of pollution on individuals. Recently, Kampa and Castanas (2008) and Neuberg et al. (2007) confirm that exposures to air pollutants are linked to reduced life expectancy.⁸ The relation between longevity and the environment is studied by Pautrel (2008), Jouvet et al. (2010), Mariani et al. (2010) and Varvarigos (2010). In these articles, the economy faces a trade-off between financing education and health programs or environmental protection programs. But, once again, they do not consider the possibility for governments to fight environmental degradation by issuing public debt.

In the next section, we present the model. The intertemporal equilibrium is defined in Sect. 3. The fourth section looks at the steady-states, while Sect. 5 is devoted to dynamic analysis. Finally, Sect. 6 presents the comparative statics and Sect. 7 is devoted to welfare analysis. The last section concludes. Technical details are relegated to the “Appendix”.

2 The Model

We consider an overlapping generations model with discrete time, $t=0,1,\ldots ,+\infty$, and three types of agents: consumers, firms and a government.

2.1 Consumers

Consumers live for two periods. The size of the generation born at period $t$ is $N_{t}$. Each person will have $n\geqslant 1$ children during his youth. Hence, the generation born at the next period will have a size $N_{t+1}=nN_{t}$. When old, each one has a longevity $\beta (e_{t})\in ( \underline{\beta },1)$, with $1>\underline{\beta }>0, 0<\beta ^{\prime }(e_{t})<{\widetilde{\beta }}$ and ${\widetilde{\beta }}>0$ not too large. Moreover, we assume $|\beta ^{\prime \prime }(e)/\beta ^{\prime }(e)|<\overline{\beta }$, with $\overline{\beta }>0$.⁹ In the following, $E_{t}$ denotes aggregate environmental quality¹⁰ at period $t$ and, following John et al. (1995), we consider that $e_{t}\equiv E_{t}/N_{t}$ corresponds to a measure of per capita environmental quality in period $t$. We assume that the longevity of an old living at period $t+1$ positively depends on this index of environmental quality faced by the household during his youth.¹¹

Preferences of an household born at period $t$ are represented by a log-linear utility function $\left( W_{t}\right)$ defined over consumption when young $c_{t}$ and old $d_{t+1}$, which depends on the longevity $\beta (e_{t})$:

$$\begin{aligned} W_{t}\equiv ln(c_{t})+\beta (e_{t}) ln(d_{t+1} ) \end{aligned}$$

(1)

At the first period of life, an household born at period $t$ supplies inelastically one unit of labor, remunerated at the competitive real wage $w_{t}$, and pays taxes $\tau _{t}\geqslant 0$. He shares his net income between saving $\sigma _{t}$, through available assets, and consumption $c_{t}$. At the second period of life, saving, remunerated at the real gross return ${\bar{r}}_{t+1}$,¹² is used to consume the final good. $d_{t+1}$ represents consumption of an household with longevity $\beta (e_{t})$ during his second period of life. To abstract from the risk associated with uncertain lifetimes, we follow Yaari (1965), Blanchard (1985) and Chakraborty (2004) in assuming a perfect annuity market whereby all savings are intermediated through mutual funds. At the end of her youth, each individual deposits her savings with a mutual fund. The mutual fund invests these savings in capital (the sole asset) and guarantees a gross return of ${\bar{r}}_{t+1}$ to the surviving old. If a fund earns a gross return $r_{t+1}$ on its investment, then perfect competition ensures that in equilibrium, ${\bar{r}}_{t+1}=r_{t+1}/\beta (e_{t})$. In other words, a consumer maximizes his utility function (1) under the two following budget constraints:

$$\begin{aligned} \sigma _{t}+c_{t}&= w_{t}-\tau _{t} \end{aligned}$$

(2)

$$\begin{aligned} d_{t+1}&= {\bar{r}}_{t+1}\sigma _{t}=\frac{r_{t+1}}{\beta (e_{t})}\sigma _{t} \end{aligned}$$

(3)

Since the longevity is taken as given by the household, we deduce the following saving function:

$$\begin{aligned} \sigma _{t}=\frac{\beta (e_{t})}{1+\beta (e_{t})}(w_{t}-\tau _{t}) \end{aligned}$$

(4)

We note that saving is an increasing function of longevity. When lifespan increases, agents discount more the future and it also raises the return on savings. On the other hand, poverty traps may result if the incentive to save for the next period of life is particularly sensitive to environmental quality, or if the environmental quality is very low. Therefore, high mortality distorts savings incentives and leads to poverty.

2.2 Firms

Since each young consumer supplies inelastically one unit of labor, labor used in production at period $t$ is $N_t$. Then, the production is given by $y_{t}= f(k_{t})N_t$, where $k_{t}=K_t /N_t$ denotes the capital-labor ratio. Assuming a Cobb–Douglas technology, we further have $f(k_t)=k_t^s$, with $s\in (0,1)$ the capital share in total income. From profit maximization, we get:

$$\begin{aligned} r_{t}&= sk_{t}^{s-1} \equiv r(k_{t}) \end{aligned}$$

(5)

$$\begin{aligned} w_{t}&= (1-s)k_{t}^{s} \equiv w(k_{t}) \end{aligned}$$

(6)

2.3 Environmental Quality

In this economy, we consider that production degrades environmental quality, while public spending, i.e. public environmental abatement, $G_{t}\ge 0$ improves it.¹³ Assuming linear relationships, environmental quality follows the motion:

$$\begin{aligned} E_{t+1}=(1-m)E_{t}+\gamma G_{t}-\alpha f(k_{t})N_{t} \end{aligned}$$

(7)

where $\alpha >0$ represents the rate of pollution coming from firms’ activities, $\gamma >0$ the efficiency of public abatement, and $m\in (0,1)$ determines the speed of return of the environment to $0$ (which could be interpreted as the natural level of the environmental index).¹⁴

2.4 Public Sector

The aim of the government is to improve environmental quality, using public spending $G_{t}$ to provide pollution abatement and environmental protection programs. To finance these expenditure, as seen above, the government levies taxes $\tau _{t}\ge 0$, or can use debt $B_{t}$. This means that a share of present pollution abatement is financed by future generations, assuming hence that generations who will benefit from the public environmental protection should pay for it. This assumption corresponds to a beneficiary-payer principle, enhancing the willingness to implement the environmental policy. Indeed, one of the results of the literature is to show that environmental taxation implies such a welfare loss for present generations that its implementation cannot be wished: one of the generations that would decide it would also bear the heaviest burden. In our model, the living generations should more easily accept public pollution abatement if a share of these activities are financed through public debt, instead of taxes on revenues or consumptions.

The intertemporal budget constraint of the government can be written:

$$\begin{aligned} B_{t}=r_{t}B_{t-1}+G_{t}-N_{t}\tau _{t} \end{aligned}$$

(8)

with $B_{-1}\ge 0$ given.

3 Intertemporal Equilibrium

We define the following variables per worker, $b_{t-1}\equiv B_{t-1}/N_{t}$ and $g_{t}\equiv G_{t}/N_{t}$. Equilibrium on the asset market is ensured by:

$$\begin{aligned} n(k_{t+1}+b_{t})=\sigma _{t} \end{aligned}$$

(9)

where the individual saving $\sigma _{t}$ is given by (4). Moreover, the budget constraint of the government (8) can be rewritten:

$$\begin{aligned} nb_{t}=r(k_{t})b_{t-1}+g_{t}-\tau _{t} \end{aligned}$$

(10)

and the law of motion of environmental quality becomes:

$$\begin{aligned} ne_{t+1}=(1-m)e_{t}+{\gamma }\! g_{t}-\alpha f(k_{t}) \end{aligned}$$

(11)

In order to avoid explosive public expenditure and debt, we assume that debt per worker $b_{t}=b$ and public expenditure per worker $g_{t}=g$ are constant. This also means that debt $B_{t}$ and government spending $G_{t}$ grow both at the rate $n-1$. In this case, Eq. (10) determines the level of the tax faced by each young consumer:

$$\begin{aligned} \tau _{t}=(r(k_{t})-n)b+g \end{aligned}$$

(12)

Therefore, an intertemporal equilibrium can be defined as follows:

Definition 1

Given $e_0\in \mathbb{R }$ and $k_{0}\in \mathbb{R }_{++}$, an intertemporal equilibrium is a sequence $(e_t, k_{t})\in \mathbb{R }\times \mathbb{R }_{++}, t=0,1,\ldots ,+\infty$, such that the following equations are satisfied:

$$\begin{aligned} e_{t+1}&= \frac{1}{n}[(1-m)e_t+{\gamma }\! g-\alpha k_{t}^s ] \equiv H(e_t,k_t)\end{aligned}$$

(13)

$$\begin{aligned} k_{t+1}&= \frac{\beta (e_t )}{n(1+\beta (e_t ))} [(1-s)k_{t}^{s}-(sk_t^{s-1}-n)b-g ] -b \equiv G(e_t,k_t) \end{aligned}$$

(14)

We notice that the dynamics are driven by a two-dimensional dynamic system, with two predetermined variables.

4 Steady States

A steady state $(e, k)\in \mathbb{R }\times \mathbb{R }_{++}$ satisfies:

$$\begin{aligned} e&= \frac{{\gamma }\! g-\alpha k^s }{n-1+m} \equiv \theta (k) \end{aligned}$$

(15)

$$\begin{aligned} \Psi (e) \equiv \frac{1+\beta (e)}{\beta (e )}&= \frac{ (1-s)k^{s}-(sk^{s-1}-n)b-g}{ n(k+b)} \equiv \Phi (k) \end{aligned}$$

(16)

Equivalently, a steady state is a solution $k\in \mathbb{R }_{++}$ solving $\Omega (k) \equiv \Psi (\theta (k))=\Phi (k)$. Hence, to study the existence, the uniqueness and the multiplicity of stationary equilibria, we start by analyzing the functions $\theta (k), \Psi (e)$ and $\Phi (k)$.

We note that, on one hand, $\theta (k)$ is strictly decreasing ($\theta ^{\prime }(k)<0$) and convex ($\theta ^{\prime \prime }(k)>0$), with $\theta (0)=\frac{\gamma g}{n-1+m}$ and $\theta (+\infty )=-\infty$. On the other hand, using the assumptions on $\beta (e), \Psi (e)$ is decreasing, with $\Psi (-\infty )=1+1/\underline{\beta }$ and $\Psi (+\infty )=2$. We deduce that $\Omega (k)$ is strictly increasing, from $\Omega (0)=\Psi \left( \frac{ \gamma g}{n-1+m}\right) \in \left( 2,1+1/\underline{\beta }\right)$ to $\Omega (+\infty )=\Psi (-\infty )=1+1/\underline{\beta }$. We further remark that $\Omega ^{\prime }(k)$ is sufficiently low for strictly positive values of $k$ if ${\widetilde{\beta }}$ is weak enough. Indeed, $\Omega ^{\prime }(k)= \frac{\beta ^{\prime }(e)}{\beta (e)^{2}}\frac{\alpha sk^{s-1}}{n-1+m}$ and $\beta ^{\prime }(e)<\widetilde{\beta }$.

Consider now the function $\Phi (k)$. Whatever the values of $b\geqslant 0$ and $g\geqslant 0$ are, we get $\Phi (+\infty )=0$. Moreover, we have:

$$\begin{aligned} \Phi ^{\prime }(k)=\frac{g-nb-h(k)}{n(k+b)^{2}} \end{aligned}$$

(17)

where

$$\begin{aligned} h(k)\equiv (1-s)^{2}k^{s}-bs(3-2s)k^{s-1}-s(1-s)b^{2}k^{s-2} \end{aligned}$$

(18)

is strictly increasing ($h^{\prime }(k)>0$), from $h(0)=-\infty$ to $h(+\infty )=+\infty$ when $b>0$, and from $h(0)=0$ to $h(+\infty )=+\infty$ when $b=0$. Therefore, if $b=g=0, \Phi ^{\prime }(k)<0$ for all $k>0$ and $\Phi (0)=+\infty$. In contrast, if either $b>0$ or $g>0$, there exists a unique $k^{*}$ such that $\Phi ^{\prime }(k)>0$ ($\Phi ^{\prime }(k)<0$) for $k<k^{*}$ ($k>k^{*}$). This means that $\Phi (k)$ is inverted U-shaped. Moreover, $\Phi (0)=-\infty$.

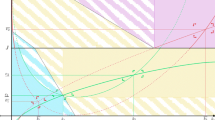
We deduce that if $b=g=0$, there is a unique steady state with positive capital (see Fig. 1).

Fig. 1

One steady state when $b=g=0$

Consider now the more interesting case where either $g>0$ or $b>0$. Since $\Omega (k)$ is increasing and $\Phi (k)$ is inverted U-shaped, there may generically exist either two steady states, or no stationary equilibrium. As we will see know, this depends on the level of $b$ and $g$. We will show that if either $b$ or $g$ becomes too large, stationary solutions do no more exist.

To simplify the analysis, we assume that ${\widetilde{\beta }}$ is low enough, ensuring that the function $\Omega (k)$ has a slope quite flat. In this case, there is two steady states $k_{1}$ and $k_{2}$ if $\Omega (k^{*})<\Phi (k^{*})$, such that $k_{1}<k^{*}<k_{2}$ (see Fig. 2).

Fig. 2

Two steady states when $b>0$ and $g>0$

Assuming that $b=0$, we have $\Phi (k)=\frac{(1-s)k^{s}-g}{nk}$. We deduce that $k^{*}=[g/(1-s)^{2}]^{1/s}$ and $\Phi (k^{*})=ns(1-s)^{2s-1}g^{-(1-s)/s}$. Therefore, when $b$ and $g$ tend to $0$, $\Phi (k^{*})>1+1/\underline{\beta }>\Omega (k^{*})$.

Note that:

$$\begin{aligned} \frac{d \Phi (k^{*})}{d g}&= \frac{\partial \Phi (k^{*})}{\partial k^{*}} \frac{\partial k^{*}}{\partial g}+\frac{\partial \Phi (k^{*})}{\partial g}= \frac{\partial \Phi (k^{*})}{\partial g}<0 \end{aligned}$$

(19)

$$\begin{aligned} \frac{d \Phi (k^{*})}{d b}&= \frac{\partial \Phi (k^{*})}{\partial k^{*}} \frac{\partial k^{*}}{\partial b}+\frac{\partial \Phi (k^{*})}{\partial b}= \frac{\partial \Phi (k^{*})}{\partial b}<0 \end{aligned}$$

(20)

Moreover, $lim_{g\rightarrow +\infty }\Phi (k)<0$ and $lim_{b\rightarrow +\infty }\Phi (k)=1-sk^{s-1}/n<1$. Since $\Omega (k)>2$, there exist levels of debt $\overline{b}>0$ and public spending $\overline{g}>0$ such that there are two steady states for $g<\overline{g}$ and $b<\overline{b}$, while there is no stationary solution for either $g>\overline{g}$ or $b>\overline{b}$.

The following proposition summarizes these results:

Proposition 1

Assume that $\widetilde{\beta }$ is sufficiently low. When $b=g=0$, there is a unique steady state with positive capital. In contrast, when $b>0$ and $g>0$, there are levels of debt $\overline{b}>0$ and public spending $\overline{g}>0$ such that there exist two steady states, namely $k_2>k_1>0$, for $g<\overline{g}$ and $b<\overline{b}$, while there is no stationary solution for either $g>\overline{g}$ or $b>\overline{b}$.

As a direct implication, when there exist two steady states, the one characterized by the highest level of capital is also defined by the lowest environmental quality. Indeed, using (15), we have $e_1 = \theta (k_1)> \theta (k_2)=e_2$.

5 Dynamics

As it is summarized in Proposition 1, two steady states with positive production may coexist. Using a phase diagram, we now qualitatively analyze the dynamics in this most interesting case, where $0<b<\overline{b}$ and $0<g<\overline{g}$. This allows us to have a picture about convergence. Does it exist a poverty trap for a set of initial conditions $(k_{0},e_{0})$? What are the conditions to converge to the steady state with the largest capital-labor ratio? What is the role of the policy parameters $b$ and $g$?

Using (13), we immediately see that $e_{t+1}\geqslant e_{t}$ if and only if $e_{t}\leqslant \theta (k_{t})$, where $\theta (k)$ is given by (15). Hence, the locus such that $e_{t}$ is stationary describes a negatively slopped curve in the space $(k_{t},e_{t})$. Below this curve, $e_{t}$ is increasing, whereas above it, $e_{t}$ is decreasing (see also Fig. 3).

Fig. 3

Phase diagram

Using (14), we deduce that $k_{t+1}\geqslant k_t$ is equivalent to $\Psi (e_t)\leqslant \Phi (k_t)$, where $\Psi (e)$ and $\Phi (k)$ are given by (16). Since $\Psi (e_t)$ is decreasing, $\Psi (e_t)\leqslant \Phi (k_t)$ is equivalent to $e_t\geqslant \Psi ^{-1}\circ \Phi (k_t) \equiv \Gamma (k_t)$.

Since there exists a unique $k^{*}$ such that $\Phi ^{\prime }(k)>0$ ($\Phi ^{\prime }(k)<0$) for $k<k^{*}$ ($k>k^{*}$) and $\Psi (e)$ is decreasing, we deduce that the locus $e_{t}=\Gamma (k_{t})$ is U-shaped in the space $(k_{t},e_{t})$. Moreover, above this curve, $k_{t}$ is increasing, while below it, $k_{t}$ is decreasing (see Fig. 3).

Using all these results, the dynamics are determined as in Fig. 3. Obviously the two points, where the curves $\theta (k_{t})$ and $\Gamma (k_{t})$ cross, correspond to the two steady states $(k_{1},e_{1})$ and $(k_{2},e_{2})$.

This analysis allows to have a global picture of the dynamics. Recalling that both $k_{t}$ and $e_{t}$ are predetermined variables, this suggests that the steady state $(k_{2},e_{2})$ is stable, while the other one $(k_{1},e_{1})$ is an unstable saddle. The study of local dynamics confirms these stability properties:

Proposition 2

The steady state $(k_{1},e_{1})$ is a saddle. Moreover, for ${\widetilde{\beta }}$ sufficiently low, $(k_{2},e_{2})$ is locally stable.

Proof

See “Appendix B”. $\square$

This means that starting with initial conditions, such that the capital-labor ratio is not too low, the economy converges to the steady state with the higher capital stock. In contrast, the existence of the saddle with $k_{1}>0$ implies that there is a poverty trap. Indeed, if the initial capital stock is too small, capital decreases and the economy can never reach the steady state $(k_{2},e_{2})$. In opposition to many papers (e.g. John and Pecchenino 1994; John et al. 1995; Mariani et al. 2010), we show that a conflict between environmental quality and capital accumulation may exist. This is because we do not consider private engagement in pollution abatement, pollution is hence a pure externality for households. This conflict seems quite realistic as it squares with the increasing part of the Environmental Kuznets Curves, which corresponds to many developing countries or to some global pollutants, like CO${_2}$ emissions.

To understand the occurrence of the poverty trap, assume first that there is no debt ($b=0$), i.e. public expenditure is financed by taxation ($\tau _{t}=g>0$). In this case, if the capital stock is too low, the wage is quite small, implying that the disposable income is not large enough to sustain capital accumulation. However, this may be mitigated by a larger longevity, which improves savings. Therefore, a higher initial environmental quality makes the emergence of the trap harder.

A closely related intuition explains why debt promotes the existence of the trap. The main effect comes from the fact that in the presence of a positive debt, a share of savings is devoted to buy unproductive assets ($b$). Therefore, if the initial capital stock is again too low, the disposable income of young households is not large enough to sustain the growth of the capital stock.

Recent empirical works confirm the existence of such an environmental poverty trap. For instance, Tol (2011) estimates finite-mixture classification-cum-regression models to show that the international cross-section of per capita income, fertility, and mortality supports that there are two equilibria (one poverty trap and one with exponential growth). Thol concludes that there may thus be a climate-related poverty trap where Green House Gas emissions and climate change increase disease burdens that reinforce poverty.

6 Comparative Statics

We analyze comparative statics to clearly see the effects of government intervention, through $b$ and $g$, on the levels of capital and environment per worker at the two steady states. Why is it relevant to study comparative statics at the two steady states? On one hand, $(k_{2},e_{2})$ is stable and an economy converges to this equilibrium in the long run as long as its initial conditions are not too low. On the other hand, $(k_{1},e_{1})$ marks, in a sense, the boundary of the trap.

The two-dimension system that defines the steady state solutions writes [see Eqs. (13) and (14)]:

$$\begin{aligned} \left( n-1+m\right) e&= {\gamma \!}g-\alpha k^{s}\end{aligned}$$

(21)

$$\begin{aligned} n(k+b)\frac{1}{\beta (e)}&= (1-s)k^{s}-sk^{s-1}b-g-nk \end{aligned}$$

(22)

Total differentiation of Eqs. (21) and (22) yields:

$$\begin{aligned} A\left[ \begin{array}{c} dk \\ de\end{array} \right] =\left[ \begin{array}{c@{\quad }c} 0&\gamma \\ -\beta (e)sk^{s-1}-n&-\beta (e) \end{array} \right] \left[ \begin{array}{c} db \\ dg\end{array} \right] \end{aligned}$$

(23)

with

$$\begin{aligned} A=\left[ \begin{array}{c@{\quad }c} \xi&\chi \\ \kappa&\zeta \end{array} \right] =\left[ \begin{array}{c@{\quad }c} \alpha sk^{s-1}&n-1+m \\ n\left( 1+\beta \left( e\right) \right) -s\beta (e)(1-s)k^{s-2}\left[ k+b \right]&-\frac{\beta ^{\prime }(e)}{\beta (e)}n(k+b)\end{array} \right] \end{aligned}$$

Lemma 1

The determinant of A is positive (negative) when it is evaluated at the steady state with low capital $(k_{1},e_{1})$ (high capital $(k_{2},e_{2})$).

Proof

See “Appendix C”. $\square$

System (23) writes:

$$\begin{aligned} \left[ \begin{array}{c} dk \\ de\end{array} \right] =\frac{1}{\det A}\left[ \begin{array}{c@{\quad }c} \chi \left[ \beta (e)sk^{s-1}+n\right]&\zeta \gamma +\chi \beta (e) \\ -\xi \left[ \beta (e)sk^{s-1}+n\right]&-\kappa \gamma -\beta (e)\xi \end{array} \right] \left[ \begin{array}{c} db \\ dg\end{array} \right] \end{aligned}$$

We further assume $\widetilde{\beta }$ sufficiently low. This ensures that $\zeta \gamma +\chi \beta (e)>0$. We also note that $\kappa$ can be rewritten:

$$\begin{aligned} \kappa = -n (k+b) \beta (e)\Phi ^{\prime }(k) \end{aligned}$$

Since $\Phi ^{\prime }(k_1)>0>\Phi ^{\prime }(k_2), \kappa \gamma +\beta (e)\xi$ is strictly positive at the steady state $k_2$, whereas it has an indeterminate sign at $k_1$.

We deduce the total consequences of variations of public debt or of public abatement, as summarized in the following proposition and in Table 1.

Table 1 Final effect on equilibrium (k, e)

Proposition 3

Assume ${\widetilde{\beta }}$ sufficiently low. The effects of an increase in debt per capita $b$ and an increase in public abatement per capita $g$ on the capital stock and on the environmental quality at the steady state with low capital $(k_{1},e_{1})$ and high capital $(k_{2},e_{2})$ follow the sign given in Table 1.

In other words, a higher debt and a higher public abatement reduces capital but improves environmental quality at the stable steady state. Opposite effects are observed for the unstable saddle steady state, except for the effect of $g$ on environmental quality which is indeterminate. This means that, in most of the configurations, the range of initial conditions $(k_{0},e_{0})$, such that the economy is relegated to a trap, becomes larger.

The mechanisms underlying these results are quite intuitive. Let us focus on the steady state $(k_{2},e_{2})$ as it is the stable one. Any increase of the public debt $(db>0)$ will induce a crowding-out effect on capital accumulation, private saving will support the financing of the public debt instead of the private investment. Doing so, the capital stock decreases and production of goods decreases too. This turns to a fall in pollutant emissions which enhances environmental quality. On the other hand, any increase of public engagement $(dg>0)$, ceteris paribus, will require a higher tax rate, that will also slow down the economic activity.

Still focusing on the stable steady state $(k_{2},e_{2})$, we study whether the government intervention, summarized by the two instruments $b$ and $g$, can improve both capital accumulation and environmental quality. In order to conciliate higher environmental quality with capital accumulation evolution, we show that government should decrease debt and increase environmental protection programs (as in the debt-for-nature swaps solution).¹⁵

Using the differentiation of the steady state with respect to $b$ and $g$, at the equilibrium $(k_2,e_2)$ where $det A<0, dk>0$ and $de>0$ are equivalent to:

$$\begin{aligned} db<G_1 dg \text{ and} db>G_2 dg \end{aligned}$$

with

$$\begin{aligned} G_1&= - \frac{\zeta \gamma +\chi \beta (e) }{\chi \left[ \beta (e)sk^{s-1}+n\right] } \\ G_2&= - \frac{\kappa \gamma +\beta (e)\xi }{ \xi \left[ \beta (e)sk^{s-1}+n\right] } \end{aligned}$$

We may easily see that because $detA<0$, we have $G_{2}<G_{1}<0$. This allows us to deduce the following proposition:

Proposition 4

Assume $\widetilde{\beta }$ sufficiently low. At the stable steady state $(k_{2},e_{2})$, both capital and environmental quality increase ($dk>0$, $de>0$) if and only if government spending increases ($dg>0$) and debt reduces ($db<0$), according to:

$$\begin{aligned} G_{2}dg<db<G_{1}dg \end{aligned}$$

The main intuition of this result is the following. A higher public spending improves environmental quality through public abatement. It also reduces capital accumulation because of a higher level of taxation. To ensure a higher level of capital, a lower debt is required to reduce its crowding out effect and promote capital accumulation.

7 Welfare Analysis

In this section, we investigate whether a policy summarized by the parameters $g$ and $b$ allows to reach the optimal allocation. In line with the previous section where we focus on comparative statics at the steady states, we focus on stationary allocations. Our aim is to prove that one of the steady states previously studied may be optimal for an appropriate choice of the policy parameters.¹⁶

We think that this is especially relevant for the stable steady state $(k_{2},e_{2})$ to which the economy may converge. Actually, we will show in the following that a specific level of public debt can decentralize the optimal allocation.

The social planner faces the two resource constraints:

$$\begin{aligned} e&= \frac{ \gamma g-\alpha k^s}{n-1+m} \end{aligned}$$

(24)

$$\begin{aligned} c+\frac{\beta (e)}{n}d&= k^s-nk-g \end{aligned}$$

(25)

Using these two equations, we substitute $c$ and $e$ into the utility function $lnc+\beta (e)lnd$. Maximizing with respect to $d$ and $k$, we obtain the following optimal trade-off:

$$\begin{aligned} \Gamma (k)=\Sigma (k) \end{aligned}$$

(26)

where

$$\begin{aligned} \Gamma (k)&\equiv sk^{s-1}-n\end{aligned}$$

(27)

$$\begin{aligned} \Sigma (k)&\equiv \frac{\beta ^{\prime }(e)}{1+\beta (e)}\frac{\alpha sk^{s-1}}{n-1+m}(k^{s}-nk-g)\left[ ln\left( \frac{n}{1+\beta (e)}(k^{s}-nk-g)\right) -1\right] \nonumber \\ \end{aligned}$$

(28)

and $e$ is given by (24). Note that, as shown in “Appendix D”, the second order conditions are satisfied for $|\beta ^{\prime \prime }(e)/\beta ^{\prime }(e)|<\overline{\beta }$, with $\overline{\beta }>0$ a constant sufficiently low. If there is no impact of environmental quality on the agent’s preferences ($\beta ^{\prime }\left( e\right) =0$), then $\Sigma (k)=0$ which implies that optimal capital stock is characterized by the standard golden rule of capital. As far as $\beta ^{\prime }\left( e\right) >0,$ Eqs. (26) and (27) fix the optimal capital stock at a modified green golden level, which takes into account the impact of pollutant emissions on longevity and welfare.

Let $\sigma (k)\equiv k^s-nk$. This is a concave function, increasing for $k\leqslant {\widetilde{k}}$ and decreasing for $k\geqslant {\widetilde{k}}$, with ${\widetilde{k}}=(s/n)^{1/(1-s)}$. An optimal allocation requires $\sigma (k)>g$. For $g<\sigma ({\widetilde{k}})=(s/n)^{s/(1-s)}(1-s)$, there exist two solutions $\underline{k}$ and $\overline{k} (>\underline{k})$ solving $\sigma (k)=g$. Therefore, any stationary optimal allocation should belong to $(\underline{k}, \overline{k})$.

Since $\Sigma (\underline{k})=\Sigma (\overline{k})=0$ and $\Gamma (\underline{k})>0>\Gamma (\overline{k})$, there exists a solution ${\hat{k}}$ solving (26). The second order conditions being satisfied for all solutions, it is unique.

Proposition 5

Assume that $g<(s/n)^{s/(1-s)}(1-s)$ and $|\beta ^{\prime \prime }(e)/\beta ^{\prime }(e)|<\overline{\beta }$, with $\overline{\beta }>0$ a constant sufficiently low. There is a unique stationary optimal allocation ${\hat{k}}\in (\underline{k},\overline{k})$ solving (26), where $\underline{k}$ and $\overline{k}$ are the solutions of $k^{s}-nk=g$.

The question we address now is whether a decentralized steady state may be optimal, for an appropriate choice of the policy parameters $b$ and $g$.

Rewriting (16), a steady state of the decentralized economy is a solution $k$ which satisfies:

$$\begin{aligned} b \left[ sk^{s-1}+\frac{n}{\beta (\theta (k))} \right] =(1-s)k^s -g- nk\frac{1+\beta (\theta (k))}{\beta (\theta (k))} \end{aligned}$$

(29)

A steady state is optimal if $k={\hat{k}}$. Given public spending $g$, there is a unique level of debt $b={\hat{b}}$ ensuring the optimality of the steady state, with:

$$\begin{aligned} {\hat{b}}=\frac{(1-s){\hat{k}}^{s}-g-n{\hat{k}}\frac{1+\beta (\theta ({\hat{k}}))}{\beta (\theta ({\hat{k}}))}}{s{\hat{k}}^{s-1}+\frac{n}{\beta (\theta ({\hat{k}}))}} \end{aligned}$$

(30)

Proposition 6

Assume that $g<(s/n)^{s/(1-s)}(1-s)$ and $|\beta ^{\prime \prime }(e)/\beta ^{\prime }(e)|<\bar{\beta }$, with $\bar{\beta }>0$ a constant sufficiently low. A steady state is optimal if, for a given level of $g, b={\hat{b}}$, where ${\hat{b}}$ is given by (30).

Note that the level of debt ${\hat{b}}$ allowing optimality is positive if $n {{\hat{k}}}<\frac{\beta (\theta ({{\hat{k}}}))}{1+\beta (\theta ({{\hat{k}}}))}[(1-s) {\hat{k}}^{s}-g]$.

Proposition 6 shows that a well-defined level of public debt internalizes the two inefficiencies that characterizes the economy: the dynamic inefficiency induced by the non-altruistic behavior of the households and the environmental externality due to pollutant emissions from production. These two inefficiencies are deeply linked and both have consequences on capital accumulation. Agents’ egoism affects directly individual saving rate while pollution affects indirectly this saving rate via changes in longevity. It is the crowding-out impact of the public debt that plays an important role on the capital stock equilibrium and drives the economy towards optimality, whatever the level of $g$. The latter point is not surprising since we assume no private pollution abatement, in opposition to many papers (John and Pecchenino 1994; John et al. 1995; Mariani et al. 2010; Fodha and Seegmuller 2012).

8 Conclusion

Among several countries, non explosive public debt is a major constraint. Nevertheless, the growing concerns about the environmental degradation (biodiversity losses, climate change...) lead many governments to fight against pollution and hence, to increase environmental spending. In many countries, the pollution mitigation induces the adoption of environmental taxes bearing on households, alongside with the increase of the individual environmental engagements.

In this paper, public abatement is not only financed by taxation, but also by debt emission. We show that, under a stabilizing debt constraint, the environmental public policy may lead the economy to an environmental poverty trap. Indeed, with a higher level of public debt, the stabilization of the latter reduces households’ share of income devoted to productive saving. This result is reinforced by a larger public spending. This allows us to recommend that policy-makers should carefully evaluate the level of public debt before increasing their environmental engagement.

For developing countries that are converging towards a higher capital stock equilibrium, both a decrease of public debt and an increase of public spending may be a win-win solution (debt-for-nature swaps). In addition, there is a level of public debt allowing to implement optimality of a steady state. These results suggest that an appropriate environmental policy partly financed by debt may be relevant.

Appendices

Appendix A: An Example of Longevity Function

Assume $\beta (e)=\frac{\alpha +x}{a+x}$ with $x=e-\underline{e}$ and $0<\alpha <a$. In our paper, we take the limit case where $\underline{e}$ tends to $-\infty$. This simplification allows to have that $\beta (e)$ is defined for all $e\in \mathbb{R }$. This function needs to satisfy: $\underline{\beta }<\beta (e)<1$, $0<\beta ^{\prime }(e)<\widetilde{\beta }$ and $|\beta ^{\prime \prime }(e)/\beta ^{\prime }(e)|<\overline{\beta }$. We hence have:

$$\begin{aligned} \beta ^{\prime }(e)&= \frac{a-\alpha }{(a+x)^{2}}>0 \\ \beta ^{\prime \prime }(e)&= \frac{-2(a-\alpha )}{(a+x)^{3}}<0 \end{aligned}$$

which implies that:

$$\begin{aligned} \left|\frac{\beta ^{\prime \prime }(e)}{\beta ^{\prime }(e)}\right|=-\frac{\beta ^{\prime \prime }(e)}{\beta ^{\prime }(e)}=\frac{2}{a+x} \end{aligned}$$

We assume $\left( i\right) a=\frac{2}{\overline{\beta }}; \left( ii\right) \alpha =\frac{2}{\overline{\beta }}\left( 1-\frac{2\widetilde{ \beta }}{\overline{\beta }}\right)$ and $\left( iii\right) \underline{\beta }$ sufficiently low, such that $\underline{\beta }<1-\frac{2\widetilde{ \beta }}{\overline{\beta }}.$ Of course, this requires $\overline{\beta }>2\widetilde{\beta }$. We deduce that:

$$\begin{aligned}&\underline{\beta }<\frac{\alpha }{a}<\beta (e)<1 \\&0<\beta ^{\prime }(e)<\frac{a-\alpha }{a^{2}}=\widetilde{\beta } \\&\left|\frac{\beta ^{\prime \prime }(e)}{\beta ^{\prime }(e)}\right|<\frac{2}{a}=\overline{\beta } \end{aligned}$$

Appendix B: Proof of Proposition 2

We differentiate the dynamic system (13)–(14) in the neighborhood of a steady state:

$$\begin{aligned} de_{t+1}&= \frac{1-m}{n}de_t -\frac{\alpha sk^{s-1}}{n} dk_t \\ dk_{t+1}&= (k+b)\frac{\beta ^{\prime }(e)}{\beta (e)(1+\beta (e))}de_t +\frac{\beta (e)}{n(1+\beta (e))} (1-s)sk^{s-2}(k+b) dk_t \end{aligned}$$

The trace $T$ and the determinant $D$ of the associated characteristic polynomial $P(\lambda )\equiv \lambda ^2 -T\lambda +D=0$ are given by:

$$\begin{aligned} T&= \frac{1-m}{n}+\frac{\beta (e)}{n(1+\beta (e))}(1-s)sk^{s-2}(k+b) \end{aligned}$$

(31)

$$\begin{aligned} D&= \frac{1-m}{n}\frac{\beta (e)}{n(1+\beta (e))} (1-s)sk^{s-2}(k+b) +\frac{\alpha sk^{s-1}}{n}(k+b)\frac{\beta ^{\prime }(e)}{\beta (e)(1+\beta (e))} \end{aligned}$$

(32)

Since $T>0$ and $D>0$, we have $P(-1)=1+T+D>0$. We now determine $P(1)=1-T+D$. After some computations, we get:

$$\begin{aligned} P(1)=\frac{n+m-1}{n}\frac{\beta (e)}{1+\beta (e)}(k+b)\left( \Omega ^{\prime }(k)- \Phi ^{\prime }(k)\right) \end{aligned}$$

(33)

with $\Omega ^{\prime }(k)=\frac{\alpha sk^{s-1}}{n-1+m}\frac{\beta ^{\prime }(e)}{\beta (e)^2}$ and $\Phi ^{\prime }(k)=\frac{g-nb-h(k)}{n(k+b)^2}$. Therefore, at the steady state $k_1$, we have $P(1)<0$, because $\Omega ^{\prime }(k)< \Phi ^{\prime }(k)$. This shows that this is a saddle. At the steady state $k_2$, we have $\Omega ^{\prime }(k)>\Phi ^{\prime }(k)$, implying that $P(1)>0$. This steady state is stable or unstable, depending on the value of $D$ with respect to $1$.

Choose ${\widetilde{\beta }}$ sufficiently small. Since $\beta ^{\prime }(e)<\widetilde{\beta }, D<1$ requires:

$$\begin{aligned} \frac{1-m}{n}\frac{\beta (e)}{n(1+\beta (e))} (1-s)sk^{s-2}(k+b)<1 \end{aligned}$$

(34)

We can show that this is equivalent to $\Phi ^{\prime }(k)<0$, which shows that the steady state $k_2$ is stable. $\square$

Appendix C: Proof of Lemma 1

Using the definition of the matrix $A$, we can compute:

$$\begin{aligned} det A&= \xi \zeta -\chi \kappa \\&= \beta (e) (n-1+m)\left[ (1-s)sk^{s-2}(k+b)-n\frac{1+\beta (e)}{\beta (e)} \right. \\&\left. -n(k+b)\frac{\beta ^{\prime }(e)}{\beta (e)^2}\frac{\alpha sk^{s-1}}{n-1+m} \right] \end{aligned}$$

One may easily see that this expression is equivalent to:

$$\begin{aligned} det A = \beta (e) (n-1+m)n(k+b)(\Phi ^{\prime }(k)-\Omega ^{\prime }(k)) \end{aligned}$$

Recall that $\Phi ^{\prime }(k_1)>\Omega ^{\prime }(k_1)$, while $\Phi ^{\prime }(k_2)<\Omega ^{\prime }(k_2)$. We deduce that $detA>0$ when the matrix $A$ is evaluated at the steady state $\left( k_{1},e_{1}\right)$, while $detA<0$ when the matrix $A$ is evaluated at the steady state $\left( k_{2},e_{2}\right)$. $\square$

Appendix D: Second Order Conditions for the Optimal Solution

The social planner solves $Max_{k,d} H(d, k)$, with:

$$\begin{aligned} H(d, k)\equiv \ln \left[ k^s -nk -g-\beta \left( \frac{\gamma g-\alpha k^s}{n-1+m} \right) \frac{d}{n} \right] + \beta \left( \frac{\gamma g-\alpha k^s}{n-1+m} \right) \ln d \end{aligned}$$

The first order conditions are give by¹⁷:

$$\begin{aligned} H_d&= -\frac{\beta (e)\frac{1}{n}}{k^s-nk-g-\beta (e)\frac{d}{n}}+\beta (e)\frac{1}{d}=0 \end{aligned}$$

(35)

$$\begin{aligned} H_k&= \frac{sk^{s-1}-n+\frac{\alpha sk^{s-1}}{n-1+m}\beta ^{\prime }(e)\frac{d}{n}}{k^s-nk-g-\beta (e)\frac{d}{n}}-\beta ^{\prime }(e)\frac{\alpha sk^{s-1} }{n-1+m} \ln d =0 \end{aligned}$$

(36)

The Hessian matrix is given by:

$$\begin{aligned} \left[ \begin{array}{cc} H_{dd}&H_{dk} \\ H_{kd}&H_{kk} \end{array} \right] \end{aligned}$$

with:

$$\begin{aligned} H_{dd}&= -\beta (e)(1+\beta (e))\frac{1}{d^2}<0 \\ H_{dk}&= \beta (e) \frac{n}{d^2} \left( sk^{s-1}-n+\frac{\alpha sk^{s-1}}{n-1+m}\beta ^{\prime }(e)\frac{d}{n} \right) = H_{kd} \\ H_{kk}&= -\left[ \frac{n}{d}\left( sk^{s-1}-n+\frac{\alpha sk^{s-1}}{n-1+m} \beta ^{\prime }(e)\frac{d}{n} \right) \right] ^2 \\&-\frac{n}{dk} \left[ (1-s)n +\frac{\beta ^{\prime \prime }(e)}{\beta ^{\prime }(e)} \frac{\alpha sk^{s-1}}{n-1+m}(n-sk^{s-1})\right] \end{aligned}$$

We deduce that

$$\begin{aligned} H_{dd}H_{kk}-H_{dk}^2&= \beta (e)(1+\beta (e))\frac{n}{d^3 k}\left[ (1-s)n +\frac{\alpha sk^{s}}{n-1+m}\frac{\beta ^{\prime \prime }(e)}{\beta ^{\prime }(e)}(n-sk^{s-1}) \right] \\&+\beta (e)\frac{n^2}{d^4}\left[ sk^{s-1}-n+\frac{\alpha sk^{s-1}}{n-1+m} +\beta ^{\prime }(e)\frac{d}{n} \right] ^2 \end{aligned}$$

The second order conditions require $H_{dd}<0$, $H_{kk}<0$ and $H_{dd}H_{kk}-H_{dk}^2>0$. They are satisfied for $|\beta ^{\prime \prime }(e)/\beta ^{\prime }(e)|<\overline{\beta }$, with $\overline{\beta }>0$ a constant sufficiently low. $\square$