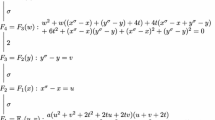The geometry of $(t\mod q)$-arcs

Abstract

In this paper, we give a geometric construction of the three strong non-lifted $(3\mod 5)$-arcs in ${{\,\textrm{PG}\,}}(3,5)$ of respective sizes 128, 143, and 168, and construct an infinite family of non-lifted, strong $(t\mod q)$-arcs in ${{\,\textrm{PG}\,}}(r,q)$ with $t=(q+1)/2$ for all $r\ge 3$ and all odd prime powers q.

1 Introduction

An $[n, k, d]_q$-code is a q-ary linear code with length n, dimension k, and minimum Hamming distance d. Given the field size q, a main problem in coding theory is to optimize the three remaining parameters. The minimal length of a linear code over $\mathbb {F}_q$ for fixed dimension k and minimum distance d is bounded below by $\sum _{i = 0}^{k-1} \lceil \frac{d}{q^i} \rceil$. Codes attaining this bound are called Griesmer codes, see [3].

It is well known that classes of isomorphic $[n, k, d]_q$-codes are in one-to-one correspondence with classes of projectively equivalent multisets of points, called $(n, n-d)$-arcs in ${{\,\textrm{PG}\,}}(k-1, q)$, see for instance [2]. An arc is called a Griesmer arc if the corresponding code is a Griesmer code.

The strong $(t\mod q)$-arcs were introduced and investigated in [5, 7, 9, 10] in connection with the extendability problem for Griesmer arcs. This problem is related in turn to the problem of the existence and extendability of arcs associated with Griesmer codes. In [5] the classification of the strong $(3\mod 5)$-arcs was used to rule out the existence of the hypothetical Griesmer $[104,4,82]_5$-code, one of the four undecided cases for codes of dimension 4 over $\mathbb {F}_5$. It turns out that apart from the many strong $(3\mod 5)$-arcs obtained from the canonical lifting construction, there exist three non-lifted strong $(3\mod 5)$-arcs of respective sizes 128, 143, and 168. This is a counterexample to the conjectured impossibility of strong $(3\mod 5)$-arcs in geometries over $\mathbb {F}_5$ in dimensions larger than 2 from Landjev and Rousseva [8] and Rousseva [13]. The three arcs are found by a computer search, but display regularities which suggest a nice geometric structure.

In this paper, we give a geometric, computer-free construction of the three non-lifted strong $(3\mod 5)$-arcs in ${{\,\textrm{PG}\,}}(3,5)$. Two of them are related to the non-degenerate quadrics of ${{\,\textrm{PG}\,}}(3,5)$. Their construction can be generalized further to larger fields and larger dimensions.

2 Preliminaries

Let $\mathcal {P}$ denote the set of points and $\mathcal {H}$ be the set of hyperplanes of ${{\,\textrm{PG}\,}}(r, q)$. We have $|\mathcal {P}| = |\mathcal {H}| = (q^{r+1}-1)/(q-1)$. Every mapping $\mathcal {K}:\mathcal {P}\rightarrow \mathbb {N}$ from $\mathcal {P}$ to the non-negative integers is called a multiset (of points) in ${{\,\textrm{PG}\,}}(r, q)$. We extend such a mapping additively to subsets $\mathcal {Q}$ of $\mathcal {P}$, i.e., $\mathcal {K}(\mathcal {Q}) = \sum _{P \in \mathcal {Q}} \mathcal {K}(P)$. If S is an s-dimensional subspace, using the algebraic dimension, we speak of an s-space, i.e., 1-spaces are points, 2-spaces are lines, and r-spaces in ${{\,\textrm{PG}\,}}(r, q)$ are hyperplanes. We also write $\mathcal {K}(S)$ associating an s-space S with the set of its points. The integer $\mathcal {K}(P)$ is also called the multiplicity of a point $P \in \mathcal {P}$ and $n:= \mathcal {K}(\mathcal {P})$ the cardinality of $\mathcal {K}$. For each integer i, an i-point is a point P with multiplicity $\mathcal {K}(P) = i$; similarly, an i-line is a line $\ell$ with multiplicity $\mathcal {K}(\ell ) = i$, and an i-hyperplane H is a hyperplane with multiplicity $\mathcal {K}(H) = i$. The support of $\mathcal {K}$ is given by $supp(\mathcal {K}) = \{P \in \mathcal {P}:\mathcal {K}(P) > 0\}$. By $a_i$ we denote the number of hyperplanes $H \in \mathcal {H}$ with $\mathcal {K}(H) = i$ and call the sequence $(a_i)_{i \in \mathbb {N}}$ the spectrum of $\mathcal {K}$, whereas we denote by $\lambda _i$ the number of i-points of $\mathcal {K}$.

A multiset $\mathcal {K}$ with cardinality n and satisfying $\mathcal {K}(H) \le s$ for all hyperplanes $H \in \mathcal {H}$ is called an $(n, \ge s)$-arc or an (n, s)-arc if additionally there exists a hyperplane H with $\mathcal {K}(H) = s$. Similarly, a multiset $\mathcal {K}$ with cardinality n and $\mathcal {K}(H) \ge s$ for all $H \in \mathcal {H}$ is called an $(n, \ge s)$-blocking set with respect to hyperplanes.

An (n, s)-arc $\mathcal {K}$ in ${{\,\textrm{PG}\,}}(r, q)$ is called t-extendable if there exists an $(n+t, s)$-arc $\mathcal {K}'$ in ${{\,\textrm{PG}\,}}(r, q)$ with $\mathcal {K}'(P) \ge \mathcal {K}(P)$, for all $P \in \mathcal {P}$. The arc $\mathcal {K}$ is said extendable, if it is t-extendable for some $t \ge 1$.

An arc $\mathcal {K}$ in ${{\,\textrm{PG}\,}}(r, q)$ is called a $(t \mod q)$-arc, if $\mathcal {K}(\ell ) \equiv t \pmod {q}$, for every line $\ell$. By double-counting it is immediate to see that also $\mathcal {K}(S) \equiv t \pmod {q}$ is satisfied for every subspace S of larger dimension. Since increasing the point multiplicities of arbitrary points by multiples of q preserves the property of being a $(t \mod q)$-arc, we can assume that the point multiplicities are integers contained in the interval $[0,q-1]$. If the maximum point multiplicity of $\mathcal {K}$ is at most t, i.e., $\mathcal {K}(P) \le t$ for all $P \in \mathcal {P}$, then $\mathcal {K}$ is said to be a strong $(t \mod q)$-arc.

The interest in $(t\mod q)$-arcs arises in the context of Griesmer codes. Indeed, it is quite common in coding theory that hypothetical Griesmer codes are associated with certain arcs, that are called t-quasidivisible. Moreover, the extendability of these t-quasidivisible arcs is related to the structure of particular strong $(t\mod q)$-arcs associated with them, see [7, 10] for more details. Here, we focus on $(t\mod q)$-arcs. There exist several straightforward constructions of $(t\mod q)$-arcs [7, 9, 10]. The first is the so-called sum-of-arcs construction.

Theorem 1

Let $\mathcal {K}$ and $\mathcal {K}'$ be a $(t_1 \mod q)$- and a $(t_2 \mod q)$-arc in ${{\,\textrm{PG}\,}}(r,q)$, respectively. Then $\mathcal {K}+\mathcal {K}' :P \in \mathcal {P}\mapsto \mathcal {K}(P) + \mathcal {K}'(P) \in \mathbb {N}$ is a $(t \mod q)$-arc with $t \equiv t_1 + t_2 \pmod q$. Similarly, $\alpha \mathcal {K} :P \in \mathcal {P}\mapsto \alpha \mathcal {K}(P) \in \mathbb {N}$, where $\alpha \in \{ 0,\dots ,\dots , p-1\}$ and p is the characteristic of $\mathbb {F}_q$, is a $(t \mod q)$-arc with $t\equiv \alpha t_1\pmod q$.

For the special case of $t=0$, and $q=p$ we have that the sum of two $(0\mod p)$-arcs and the scalar multiple of a $(0\mod p)$-arc are again $(0\mod p)$-arcs. Hence the set of all $(0\mod p)$-arcs is a vector space over $\mathbb {F}_p$, cf. [9]. The second construction is the so-called lifting construction, see [9, p. 230].

Theorem 2

Let $\mathcal {K}_0$ be a (strong) $(t\mod q)$-arc in a projective s-space $\varSigma$ of ${{\,\textrm{PG}\,}}(r, q)$, where $1 \le s < r$. For a fixed projective $(r-s-1)$-space $\varGamma$ of ${{\,\textrm{PG}\,}}(r, q)$, disjoint from $\varSigma$, let $\mathcal {K}$ be the arc in ${{\,\textrm{PG}\,}}(r, q)$ defined as follows:

• For each point P of $\varGamma$, set $\mathcal {K}(P)=t$;

• For each point $Q \in {{\,\textrm{PG}\,}}(r, q) \setminus \varGamma$, set $\mathcal {K}(Q)=\mathcal {K}_0(R)$, where $R=\langle \varGamma , Q \rangle \cap \varSigma$.

Then $\mathcal {K}$ is a (strong) $(t\mod q)$-arc in ${{\,\textrm{PG}\,}}(r,q)$ of cardinality $q^{r-s} \cdot |\mathcal {K}_0| + t \frac{q^{r-s}-1}{q-1}$.

Arcs obtained by the lifting construction are called lifted arcs. If $\varSigma$ is a point, then we speak of a lifting point. The iterative application of the lifting constructions gives the more general version stated above. In the other direction, in [9, Lemma 1] it has been shown that the set of all lifting points forms a subspace. We shall find it helpful to use the following result in the sequel.

Corollary 1

Let $\mathcal {K}$ be a $(t \mod q)$-arc in ${{\,\textrm{PG}\,}}(r, q)$. If for every point P there is a line $\ell$ through P such that the multiplicities of the q points of $\ell$ distinct from P are not the same, then such an arc is not lifted.

Let $\mathcal {K}$ be a $(t \mod q)$-arc in ${{\,\textrm{PG}\,}}(r,q)$, then $\mathcal {K}^{\perp } :H \in \mathcal {H} \mapsto (\mathcal {K}(H)-t)/q \in \mathbb {N}$ is called the dual arc of $\mathcal {K}$. In the case when $r = 2$, then $\mathcal {K}^\perp$ is an $((m-t)q+m,m-t)$-blocking set in the dual plane, where $\mathcal {K}$ has cardinality $mq + t$. Therefore, the classification of strong $(t\mod q)$ arcs in ${{\,\textrm{PG}\,}}(2,q)$ is equivalent to that of certain plane blocking sets [8].

Theorem 3

A strong $(t\mod q)$-arc $\mathcal {K}$ in ${{\,\textrm{PG}\,}}(2,q)$ of cardinality $mq+t$ exists if and only if there exists an $((m-t)q+m,\ge m-t)$-blocking set $\mathcal {B}$ with line multiplicities contained in the set $\{m-t,m-t+1,\dots ,m\}$.

The condition that the multiplicity of each point is at most t turns out to be very strong. For $t=0$, we have that the only strong $(0\mod q)$-arc is the trivial zero-arc. For $t=1$ the strong $(1\mod q)$-arcs are the hyperplanes. For $t=2$ all strong $(2\mod q)$ arcs in ${{\,\textrm{PG}\,}}(r,q)$, for $r\ge 3, q\ge 5$, turn out to be lifted [9]. In ${{\,\textrm{PG}\,}}(2,q)$, all $(2\mod q)$-arcs are also known (cf. [5, Lemma 3.7]). Apart from one sporadic example, all such arcs are again lifted. It was conjectured in [8] that all strong $(3\mod 5)$-arcs in ${{\,\textrm{PG}\,}}(r,5)$, $r\ge 3$, are lifted. The computer classification reported in [5] shows that this conjecture is wrong: there exist $(3\mod 5)$-arcs of respective sizes 128, 143, and 168 that are not lifted. In the next sections we give a geometric (computer-free) description of these arcs and define an infinite class of strong $(t\mod q)$-arcs in ${{\,\textrm{PG}\,}}(r,q)$, $r\ge 3$, that are not lifted.

3 The arc of size 128

In order to explain the $(3\mod 5)$-arcs of size 128 in ${{\,\textrm{PG}\,}}(3,5)$, we need the geometric description of all strong $(3\mod 5)$-arcs in ${{\,\textrm{PG}\,}}(2,5)$ of sizes 18, 23, 28, and 33. They are all obtained from Theorem 3 and can be found in [5, 9].¹

In their description we make use of notation for some of the points of ${{\,\textrm{PG}\,}}(2,5)$.

Let the points $X_1,X_2,X_3,X_4$ form a quadrangle and set:

$$\begin{aligned} \begin{array}{lll} Y_1=\langle X_1,X_2\rangle \cap \langle X_3,X_4\rangle , &{} Y_2=\langle X_1,X_3\rangle \cap \langle X_2,X_4\rangle , \\ Y_3=\langle X_1,X_4\rangle \cap \langle X_2,X_3\rangle , &{} Z_1=\langle Y_1,Y_2\rangle \cap \langle X_1,X_4\rangle , \\ Z_2=\langle Y_1,Y_2\rangle \cap \langle X_2,X_3\rangle , &{} Z_3=\langle Y_1,Y_3\rangle \cap \langle X_1,X_3\rangle , \\ Z_4=\langle Y_1,Y_3\rangle \cap \langle X_2,X_4\rangle ,&{} Z_5=\langle Y_2,Y_3\rangle \cap \langle X_1,X_2\rangle , \\ Z_6=\langle Y_2,Y_3\rangle \cap \langle X_3,X_4\rangle . &{} \end{array} \end{aligned}$$

Furthermore, let $U_1,U_2$ be the remaining two points on the line $\langle Y_1,Y_2\rangle$, i.e. the points on this line are $Y_1,Y_2,Z_1,Z_2,U_1,U_2$. Similarly, denote by $U_3,U_4$ be the remaining two points on the line $\langle Y_1,Y_3\rangle$, and by $U_5,U_6$ be the remaining two points on the line $\langle Y_2,Y_3\rangle$. The points so defined are presented on the figure below.

Theorem 4

Let $\mathcal {K}$ be a strong $(3\mod 5)$-arc in ${{\,\textrm{PG}\,}}(2,5)$.

• (a) If $|\mathcal {K}|=18$ then $\mathcal {K}$ is the sum of three lines.

• (b) If $|\mathcal {K}|=23$ then it has $\lambda _3=3,\lambda _2=4,\lambda _1=6$. The points $X_i$ are 2-points, the points $Y_j$ are 3-points and the points $Z_k$ are 1-points.

• (c) If $|\mathcal {K}|=28$ then it has $\lambda _3=6,\lambda _1=10$. The 3-points form an oval, and the 1-points are the internal points to this oval.

• (d) If $|\mathcal {K}|=33$ there exist ten non-isomorphic arcs. These are:

(d-i):

The duals of the complements of the seven (10, 3)-arcs in ${{\,\textrm{PG}\,}}(2,5)$ (cf. [6]); the possible $\lambda _i$’s are:

$$\begin{aligned} \lambda _3=3+j,\lambda _2=9-3j,\lambda _1=6+3j,j=0,1,2,3; \end{aligned}$$

(d-ii):

The dual of the multiset which is complement of the (11, 3)-arc with four external lines plus one point which is not on a 6-line ($\lambda _3=6,\lambda _2=5,\lambda _1=5$);

(d-iii):

The dual of a blocking set in which one double point forms an oval with five of the 0-points; the tangent to the oval in the 2-point is a 3-line ($\lambda _3=6,\lambda _2=5,\lambda _1=5$);

(d-iv):

The modulo 5 sum of three non-concurrent lines: two of them are lines of 3-points and one is a line of 2-points ($\lambda _3=8,\lambda _2=4,\lambda _1=1$).

Let us note that the strong $(3\mod 5)$-arcs have 13-lines in cases (d-ii), (d-iii), and (d-iv). The seven arcs in (d-i) are obtained as duals of projective (21, 3)-blocking sets. These are complements of (10, 3)-arcs. The types of all 8- and 3-lines are obtained from the types of the 0- and 1-points of the corresponding (10, 3)-arc and are given in Table 4 in [6]. Of special interest to us are the $(3\mod 5)$-arcs obtained from (10, 3)-arcs of types (B5) and (B7) (cf. [6], Table 3). In the arcs of the first type have the points $X_i$ are of multiplicity 3, the points $U_j$—of multiplicity 2, and the points $Y_k$ and $Z_l$—of multiplicity 1. In the arcs of the second type, the 3-points form an oval, and the 1 points are the external points to this oval.

Lemma 1

Let $\mathcal {K}$ be a strong $(3\mod 5)$-arc in ${{\,\textrm{PG}\,}}(3,5)$ of cardinality 128. Then all lines with a 0-point are of multiplicity 3 or 8. Furthermore, all 8-lines with a 0-point are of type (3, 3, 1, 1, 0, 0, 0) or (3, 2, 2, 1, 0, 0).

Proof

Assume there exists a 13-line. Then all planes through this line have multiplicity at least 33 (Theorem 4) and hence $|\mathcal {K}|\ge 6\cdot 33-5\cdot 13=133$, a contradiction.

Similarly, if an 8-line L has a 0-point and is not of the type (3, 3, 1, 1, 0, 0) or (3, 2, 2, 1, 0, 0) then it is incident with planes of multiplicity at least 33 (cf. Theorem 4). Now we can use once again the same counting argument.$\square$

For the types of the lines with a 0-point we adopt the following notation.

The table below presents the types of the lines through a 0-point in a strong $(3\mod 5)$-arc $\mathcal {K}$ in ${{\,\textrm{PG}\,}}(2,5)$ of multiplicity 18, 23, 28, and 33. For the arcs of cardinality 33, we list just the two types that are admissible in a 128-arc in ${{\,\textrm{PG}\,}}(3,5)$. By Lemma 1 these turn out to be the arcs in (d-i) obtained from (10, 3) arcs of type (B5) and (B7) (cf. [6]).

Consider a $(3\mod 5)$-arc $\mathcal {K}$ in ${{\,\textrm{PG}\,}}(3,5)$ that is of multiplicity 128. Let $\varphi$ be a projection from an arbitrary 0-point P to a plane $\pi$ not incident with P:

$$\begin{aligned} \varphi \left\{ \begin{array}{ccc} \mathcal {P}\setminus \{P\} &{}\mapsto &{} \pi \\ Q &{}\mapsto &{} \pi \cap \langle P,Q\rangle . \end{array}\right. \end{aligned}$$

Here $\mathcal {P}$ is again the set of points of ${{\,\textrm{PG}\,}}(3,5)$. Note that $\varphi$ maps the lines through P into points from $\pi$, and the planes through P into lines in $\pi$. We define the induced arc $\mathcal {K}^{\varphi }:\pi \rightarrow \mathbb {N}_0$ by

$$\begin{aligned} \mathcal {K}^{\varphi }(Q)\,= \,\sum _{\varphi (X)=Q} \mathcal {K}(X). \end{aligned}$$

It is clear that P is incident with 3- and 8-lines, only (Theorem 4). A point in the projection plane is said to be of type ($\alpha$), ($\beta$), or ($\gamma _i$) if it is the image of a line of the same type.

We define a special arc $\mathcal {F}$ of cardinality 128 in ${{\,\textrm{PG}\,}}(2,5)$ with seven 8-points and twenty four 3-points:

$$\begin{aligned} \mathcal {F}(T)=\left\{ \begin{array}{cl} 8 &{} \text { if } T=X_i \text { or } Y_j,\;\;\; i=1,2,3,\; j=1,2,3,4\\ 3 &{} \text { otherwise.} \end{array}\right. \end{aligned}$$

Proposition 1

Let $\mathcal {K}$ be a strong $(3\mod 5)$-arc in ${{\,\textrm{PG}\,}}(3,5)$ of cardinality 128. Let $\varphi$ be the projection of $\mathcal {K}$ from a 0-point P onto a plane disjoint from that point. Then for every choice of P the arc $\mathcal {K}^{\varphi }$ is isomorphic to the arc $\mathcal {F}$ described above. Moreover, the points $X_i$ are of type $(\beta )$, the points $Y_j$ are of type $(\alpha )$, the points $Z_k$ are of type $(\gamma _3)$, the points $U_l$ are of type $(\gamma _1)$, and all the remaining points are of type $(\gamma _2)$.

The induced arc $\mathcal {K}^{\varphi }$ is presented on the picture below.

Proof

By Lemma 1 the arc $\mathcal {K}^{\varphi }$ has seven 8-points and twenty-four 3-points. Moreover, the 8-points are of type $(\alpha )$ or $(\beta )$. First we are going to prove that at most three of the seven 8-points are collinear.

(1) Assume that six of the 8-points are collinear. Clearly, every 8-point is on a 28-line (a line with two 8-points) and hence all 8-points are of type ($\alpha$). Obviously, every 3-point is also incident with a 28-line. Hence all 3-points are of type ($\gamma _1$) or ($\gamma _3$). But now a line with one 8-point cannot have points of type ($\gamma _2$), which is a contradiction with the structure of the $(3\mod 5)$-arc of size 23.

(2) Assume that five of the 8-points are collinear and let L be the line that is incident with them. Here there are two possibilities: the line through the two 8-points off L meets L in a 3-point or in an 8-point. In both cases all 8-points are of type $(\alpha )$. Now there exists a line with exactly one 8-point which has at least four 3-points that are not of type ($\gamma _2$). This is a contradiction with the structure of the $(3\mod 5)$-arc of size 23.

(3) A similar argument rules out the possibility of four collinear 8-points. In all cases these the seven 8-points have to be of type $(\alpha )$. Now every 23-line has to be incident with four points of type $(\gamma _2)$, which is easily checked to be impossible.

(4) We are going to consider in detail the case when at most three 8-points in the projection plane are collinear.

(4a) Assume there exists an oval of 8-points, $A_1,\ldots ,A_6$, say, and let B be the seventh 8-point. Every 8-point is on a line with two 8-points, and so all 8-points have to be of type ($\alpha$). Let $\langle B,A_1,A_2\rangle$ be a secant to the oval through Y. The lines $\langle A_1,A_j\rangle$, $j=3,4,5,6$, are images of planes without 2-points. Now an external line to the oval through B is a 23-line and has at most one point of type ($\gamma _2$), a contradiction.

(4b) In a similar way, we can rule out the case where there exist five 8-points no three of which are collinear. We have to consider the different possibilities for the line defined by the remaining two 8-points: secant, tangent, or external line to the oval formed by the former five points and one additional point which has to be a 3-point.

(4c) We have shown so far that there are at most three collinear 8-points. It is clear that there exist at least two lines that contain three 8-points. We consider the case where these lines meet in a 3-point. Denote the 8-points on these two lines by $A_i, B_i$, $i=1,2,3$, and the seventh 8-point—by C. We assume that $A_1,A_2,A_3$ are collinear and that so are $B_1,B_2,B_3$. Each of the lines $\langle A_i,C\rangle$, $i=1,2,3$, also contains three 8-points; otherwise there exist five 8-points no three of which are collinear—a case already considered. Without loss of generality, let the triples $A_i,B_i, C$, $i=1,2,3$, be collinear. Now it is clear that all the points $A_i, B_i$ are of type ($\alpha$). The point C is also forced to be of type $(\alpha )$ since a 33-line has either one or all three 8-points of type $(\alpha )$. Again, we can use the fact that a 23-line has to be incident with four points of type $(\gamma _2)$, which is clearly impossible for two the 23-lines through C.

(5) Up to this point w have proved that the seven 8-points of $\mathcal {K}^{\varphi }$ should satisfy the following conditions: (i) each line contains at most three 8-points, (ii) lines incident with three 8-points meet in an 8-point, (iii) every 5-tuple of 8-points contains a collinear triple. The only possible configuration of 8-points is the vertices of a quadrangle plus the three diagonal points, i.e. the configuration isomorphic to the points $X_i$, $Y_j$, $i=1,2,3,4$, $j=1,2,3$, defined in the beginning of the section.

Furthermore, the diagonal points (those corresponding to the $Y_j$’s) have to be of type ($\alpha$) while the vertices of the quadrangle (the $X_i$’s) are forced to be of type ($\beta$). This is due to the fact that through each of the vertices of the quadrangle there is a line with a single 8-point which meets the three lines defined by the diagonal points of type $(\alpha )$ in three different 3-points that are not of type ($\gamma _2$). Thus we get the picture below.

The fact that a 23-line through a point of type $(\alpha )$ contains four points of type $(\gamma _2)$ and one point of type $(\gamma _1)$ identifies the six points of type $(\gamma _1)$.

Furthermore, a line with two points of type $(\alpha )$ must contain also two points of type $(\gamma _1)$ and two points of type $(\gamma _3)$. This identifies the six 3-points of type $(\gamma _1)$. The remaining 3-points are all of type $(\gamma _2)$. This implies the suggested structure. $\square$

Lemma  1 implies that given a non-lifted, strong $(3\mod 5)$-arc $\mathcal {K}$ of cardinality 128, every 0-point is incident with

• Three 8-lines of type (3, 3, 1, 1, 0, 0),

• Four 8-lines of type (3, 2, 2, 1, 0, 0),

• Six 3-lines of type (3, 0, 0, 0, 0, 0),

• Twelve 3-lines of type (2, 1, 0, 0, 0, 0),

• Six 3-lines of type (1, 1, 1, 0, 0, 0)

Now this implies that

• $\#$(3-points) $=3\cdot 2+4\cdot 1+6\cdot 1 = 16$,

• $\#$(2-points) $=4\cdot 2+12\cdot 1 = 20$,

• $\#$(1-points) $=3\cdot 2+4\cdot 1+12\cdot 1+6\cdot 3 = 40$,

• $\#$(0-points) $=1+3\cdot 1+4\cdot 1+6\cdot 4+12\cdot 3+2\cdot 6 = 80$.

Furthermore, each 0-point is incident with six 33-planes, three 28-planes eighteen 23-planes and four 18-planes. Moreover the number of 0-points in a 33-plane is 12, in a 28-plane—15, in a 23-plane—18, and in an 18-plane—16. This makes it possible to compute the spectrum of $\mathcal {K}$. We have

$$\begin{aligned} a_{33}= & {} \frac{80\cdot 6}{12}=40 \\ a_{28}= & {} \frac{80\cdot 3}{15}=16, \\ a_{23}= & {} \frac{80\cdot 18}{18}=80, \\ a_{18}= & {} \frac{80\cdot 4}{16}=20. \end{aligned}$$

From the structure of the plane $(3\mod 5)$-arcs with 18-, 23-, 28- and 33-arcs, one can conclude that no three 2-points are collinear. In other words they form a 20-cap C. Moreover, this cap has spectrum: $a_6(C)=40, a_4(C)=80, a_3(C)=20, a_0(C)=16$. It is not extendable to the elliptic quadric; in such case it would have (at least 20) tangent planes. Thus, this cap is complete and isomorphic to one of the two caps $K_1$ and $K_2$ by Abatangelo et al. [1]. It is not $K_2$ since it has a different spectrum (cf. [1]). Hence the 20-cap on the 2-points in ${{\,\textrm{PG}\,}}(3,5)$ is isomorphic to $K_1$.

Assume that $\mathcal {K}$ is a 128-arc with twenty 2-points that form the Abatangelo–Korchmáros–Larato cap $K_1$. We are going to demonstrate that $\mathcal {K}$ is uniquely determined by the 2-points. Consider a 3-plane of the cap and fix a 2-line L in it. The planes through L are denoted by $\pi _i$, $i=0,\ldots ,5$. It is clear that four of the planes $\pi _i$ are of multiplicity 6 (with respect to the cap), and two of them, $\pi _0$ and $\pi _1$ say, are of multiplicity 3. This implies that with respect to $\mathcal {K}$ $\pi _0$ and $\pi _1$ are 18-planes, and $\pi _i$, $i=2,\ldots ,5$, are 33-planes.

Denote by A and B the 2-points on L. Let also $C_0$ and $C_1$ be the other 2-points in $\pi _0$ and $\pi _1$, respectively. The lines $\langle A,B\rangle$, $\langle A,C_0\rangle$, $\langle B,C_0\rangle$, $\langle A,C_1\rangle$, $\langle B,C_1\rangle$ are all of type (2, 2, 1, 1, 1, 1). Now the planes $\langle A,C_0,C_1\rangle$ and $\langle B,C_0,C_1\rangle$ have to be 18-planes (the sum of three non-concurrent lines). This is the only possibility for a plane containing two lines of type (2, 2, 1, 1, 1, 1) meeting in a 2-point. Therefore the line $\langle C_0,C_1\rangle$ is also a line of type (2, 2, 1, 1, 1, 1). Set $C_i=\pi _i\cap \langle C_0,C_1\rangle$, $i=2,\ldots ,5$.

Note that the lines $\langle A,C_i\rangle$, $\langle B,C_i\rangle$, $i=2,\ldots ,5$, are of type (2, 1, 0, 0, 0). Note also that $C_i$ is a diagonal point of the quadrangle in $\pi _i$ formed by the 3-points. The other two diagonal points (denoted by D and E) are 1-points on L. Each of the lines $\langle C_i,D\rangle$ and $\langle C_i,E\rangle$ is of type (2, 2, 1, 1, 1, 1). Denote by $F'_i,F''_i$ (resp. $G'_i,G''_i$) the remaining two 1-points on $\langle C_i,D\rangle$ (resp. $\langle C_i,E\rangle$). Now the 3-points in $\pi _i$ are the intersections of the lines $\langle D,F'_i\rangle$, $\langle D,F''_i\rangle$ with the lines $\langle E,G'_i\rangle$, $\langle E,G''_i\rangle$ and all points in the planes $\pi _i$, $i=2,3,4,5$, are determined uniquely.

An alternative construction using few orbits The 128-cap is easily constructed if we assume that it is fixed by the collineation group G of the cap $K_1$. It is a semidirect product of an elementary abelian group of order 16 and a group isomorphic to $S_5$ [1]. Hence $|G|=1920$. The action of G on ${{\,\textrm{PG}\,}}(3,5)$ splits the point set of ${{\,\textrm{PG}\,}}(3,5)$ into four orbits on points, denoted by $O_1^P,\ldots ,O_4^P$, and the set of lines into six orbits, denoted by $O_1^L,\ldots ,O_6^L$. The respective sizes of these orbits are

$$\begin{aligned}{} & {} |O_1^P|=40, |O_2^P|=80, |O_3^P|=20, |O_4^P|=16; \\{} & {} |O_1^L|=160, |O_2^L|=240, |O_3^L|=30, |O_4^L|=160, |O_5^L|=120, |O_6^L|=96. \end{aligned}$$

The corresponding point-by-line orbit matrix $A=(a_{ij})_{4\times 6}$, where $a_{ij}$ is the number of the points from the i-th point orbit incident with any line from the j-th line orbit is the following

$$\begin{aligned} A=\left( \begin{array}{cccccc} 3 &{} 1 &{} 4 &{} 1 &{} 2 &{} 0 \\ 3 &{} 4 &{} 0 &{} 2 &{} 2 &{} 5 \\ 0 &{} 1 &{} 2 &{} 2 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 2 &{} 1 \end{array} \right) . \end{aligned}$$

Set $w=(w_1,w_2,w_3,w_4)$. Here $w_i$ is the multiplicity of the points from the i-th point orbit. We look for solutions of the equation $wA\equiv 3\varvec{j}\pmod {5}$, where $\varvec{j}$ is the all-one vector, subject to the conditions $w_i\le 3$ for all $i=1,2,3,4$. The set of all solutions is given by

$$\begin{aligned} \{w=(w_1,w_2,w_3,w_4)\mid w_i\{0,\ldots 4\}, \\ w_2\equiv 1-w_1\pmod {5}, w_3\equiv 4-2w_1\pmod {5}, w_4=3\}. \end{aligned}$$

There exist two solutions that satisfy $w_i\le 3$: $w=(3,3,3,3)$ and $w=(1,0,2,3)$. The first one yields the trivial $(3\mod 5)$-arc formed by three copies of the whole space. The second one gives the desired arc of size 128.

It should be noted that the weight vectors (0, 3, 2, 4), (1, 2, 0, 4), (2, 1, 3, 4), and (3, 0, 1, 4) yield strong $(4\mod 5)$-arcs of cardinalities 344, 264, 284, and 204, respectively, that are not lifted.

4 Strong $\left( \frac{q+1}{2} \mod q\right)$-arcs from quadrics and the arcs of size 143 and 168

For an arbitrary odd prime power q and an integer $r\ge 2$, let ${\mathcal {Q}}$ be a quadric of ${{\,\textrm{PG}\,}}(r, q)$ and let F be the quadratic form defining ${\mathcal {Q}}$. This means that a point $P(x_0,\ldots ,x_{r})$ of ${{\,\textrm{PG}\,}}(r, q^2)$ belongs to ${\mathcal {Q}}$ whenever $F(x_0,\ldots , x_{r})=0$. The points of ${{\,\textrm{PG}\,}}(r, q)$ outside ${\mathcal {Q}}$ are partitioned into two point classes, say $\mathcal {P}_1$ and $\mathcal {P}_2$. Indeed, if $P(x_0, \ldots , x_{r})$ is a point of ${{\,\textrm{PG}\,}}(r, q) {\setminus } {\mathcal {Q}}$, then P belongs to $\mathcal {P}_1$ or $\mathcal {P}_2$, according as $F(x_0,\ldots , x_{r})$ is a non-square or a square in $\mathbb {F}_q$. Now we define the arcs $\mathcal {K}_1$ and $\mathcal {K}_2$ in the following way:

• $\mathcal {K}_1$: for a point P of ${{\,\textrm{PG}\,}}(r, q)$ set

  $$\begin{aligned} \mathcal {K}_1(P)=\left\{ \begin{array}{cl} \frac{q+1}{2} &{} \text { if } P\in \mathcal {Q}, \\ 1 &{} \text { if } P \in \mathcal {P}_1, \\ 0 &{} \text { if } P \in \mathcal {P}_2. \end{array}\right. \end{aligned}$$

  (1)

• $\mathcal {K}_2$: for a point P of ${{\,\textrm{PG}\,}}(r, q)$ set

  $$\begin{aligned} \mathcal {K}_2(P)=\left\{ \begin{array}{cl} \frac{q+1}{2} &{} \text { if } P\in \mathcal {Q}, \\ 0 &{} \text { if } P \in \mathcal {P}_1, \\ 1 &{} \text { if } P \in \mathcal {P}_2. \end{array} \right. \end{aligned}$$

  (2)

The following result is well-known.

Proposition 2

[11, Theorem 5.18] Let $f(x)=ax^2+bx+c$, where $a,b,c,\in \mathbb {F}_q$, $a\ne 0$, q odd. If $\mathbb {F}_q=\{\alpha _0,\alpha _1,\ldots ,\alpha _{q-1}\}$. Denote by S the list of the following elements from $\mathbb {F}_q$:

$$\begin{aligned} a, f(\alpha _0),f(\alpha _1),\ldots ,f(\alpha _{q-1}). \end{aligned}$$

Then

• (a) If f(x) has two distinct roots in $\mathbb {F}_q$ the list S contains two zeros, $(q-1)/2$ squares and $(q-1)/2$ non-squares;

• (b) If f(x) has one double root in $\mathbb {F}_q$ then S contains a zero and q squares, or a zero and q non-squares;

• (c) If f(x) is irreducible over $\mathbb {F}_q$ then S contains $(q+1)/2$ squares and $(q+1)/2$ non-squares.

Theorem 5

Let the $\mathcal {K}_1$ and $\mathcal {K}_2$ be the arcs defined in (1) and (2), respectively. Then $\mathcal {K}_i$ is a $\left( \frac{q+1}{2} \mod q\right)$ arc of ${{\,\textrm{PG}\,}}(r, q)$, $i = 1, 2$. Moreover, if $\mathcal {Q}$ is non-degenerate, then both arcs are not lifted.

Proof

Let $\ell$ be a line of ${{\,\textrm{PG}\,}}(r, q)$, then $\mathcal {Q} \cap \ell$ is a quadric of $\ell$. Then, from Proposition 2, it follows that

$$\begin{aligned} \mathcal {K}_i(\ell ) = {\left\{ \begin{array}{ll} 2 \cdot \frac{q+1}{2} + \frac{q-1}{2} &{} \text{ if } |\ell \cap \mathcal {Q}| = 2, \\ \frac{q+1}{2} + q &{} \text{ if } |\ell \cap \mathcal {Q}| = 1 \text{ and } |\ell \cap \mathcal {P}_i| = q, \\ \frac{q+1}{2} &{} \text{ if } |\ell \cap \mathcal {Q}| = 1 \text{ and } |\ell \cap \mathcal {P}_i| = 0, \\ \frac{q+1}{2} &{} \text{ if } |\ell \cap \mathcal {Q}| = 0. \end{array}\right. } \end{aligned}$$

Therefore $\mathcal {K}_i$ is a $\left( \frac{q+1}{2} \mod q\right)$ arc of ${{\,\textrm{PG}\,}}(r, q)$, $i = 1, 2$. If $\mathcal {Q}$ is non-degenerate, then through every point of ${{\,\textrm{PG}\,}}(r, q)$ there exists a line r that is secant to $\mathcal {Q}$. By construction, the line r has two $\frac{q+1}{2}$-points, $\frac{q-1}{2}$ 1-points and $\frac{q-1}{2}$ 0-points. Hence by Corollary 1, $\mathcal {K}_i$ is not lifted. $\square$

Corollary 2

If r is odd, then

$$\begin{aligned} |\mathcal {K}_i| = {\left\{ \begin{array}{ll} \frac{q+1}{2} \cdot \frac{( q^{\frac{r+1}{2}} + 1)(q^{\frac{r-1}{2}} - 1)}{q-1} + \frac{q^r + q^{\frac{r-1}{2}}}{2} &{} \text{ if } \mathcal {Q} \text{ is } \text{ elliptic },\\ \frac{q+1}{2} \cdot \frac{( q^{\frac{r-1}{2}} + 1)(q^{\frac{r+1}{2}} - 1)}{q-1} + \frac{q^r - q^{\frac{r-1}{2}}}{2} &{} \text{ if } \mathcal {Q} \text{ is } \text{ hyperbolic }. \end{array}\right. } \\ \end{aligned}$$

If r is even, then

$$\begin{aligned} |\mathcal {K}_1| = \frac{q+1}{2} \cdot \frac{(q^r - 1)}{q-1} + \frac{q^r - q^{\frac{r}{2}}}{2}, \\ |\mathcal {K}_2| = \frac{q+1}{2} \cdot \frac{(q^r - 1)}{q-1} + \frac{q^r + q^{\frac{r}{2}}}{2}. \end{aligned}$$

Remark 1

In the case when the quadric $\mathcal {Q}$ is degenerate, then it is not difficult to see that the arc $\mathcal {K}_i$, $i = 1, 2$, is lifted. Let $\mathcal {Q}$ be a non-degenerate quadric of ${{\,\textrm{PG}\,}}(r, q)$, then $\mathcal {K}_1$ and $\mathcal {K}_2$ are projectively equivalent if r is odd, but they are not in the case when r is even. On the other hand, if r is odd, there are two distinct classes of non-degenerate quadrics, namely the hyperbolic quadric and the elliptic quadric. Therefore in all cases Theorem 5 gives rise to two distinct examples of non lifted $\left( \frac{q+1}{2} \mod q\right)$ arcs of ${{\,\textrm{PG}\,}}(r, q)$. For more details on quadrics we refer the interested reader to [4].

Remark 2

In the case when $r = 2$ and $\mathcal {Q}$ is non-degenerate, then from Theorem 5 two $(3 \mod 5)$-arcs in ${{\,\textrm{PG}\,}}(2, 5)$ arise, namely $\mathcal {K}_1$ and $\mathcal {K}_2$. The arc $\mathcal {K}_1$ has cardinality 28, spectrum $(a_3, a_8) = (16, 15)$ and number of i-points $(\lambda _1, \lambda _3) = (10, 6)$. Hence $\mathcal {K}_1$ coincides with Example (c) in Theorem 4. The arc $\mathcal {K}_2$ has cardinality 33, spectrum $(a_3, a_8) = (10, 21)$ and number of i-points $(\lambda _1, \lambda _3) = (15, 6)$. In this case $\mathcal {K}_2^\perp$ is a (21, 3)-blocking set in the dual plane and $\mathcal {K}_2$ falls in one of the Examples (d)(i) in Theorem 4. If $\mathcal {Q}$ is degenerate, then $(3 \mod 5)$-arcs in ${{\,\textrm{PG}\,}}(2, 5)$ of cardinalities 18 or 43 arise, cf. [5, Table 1].

4.1 The arcs of size 143 and 168

In [5], the following two strong non-lifted $(3\mod 5)$-arcs in ${{\,\textrm{PG}\,}}(3,5)$ were constructed by a computer search.

(1):

An arc of cardinality 143, with spectrum $(a_{18}, a_{28}, a_{33})= (26, 65, 65)$, number of i-points $(\lambda _0, \lambda _1, \lambda _3) = (65, 65, 26)$ and automorphism group of order 62400.

(2):

An arc of cardinality 168, with spectrum $(a_{28}, a_{33}, a_{43})= (60, 60, 36)$, number of i-points $(\lambda _0, \lambda _1, \lambda _3) = (60, 60, 36)$ and automorphism group of order 57600.

These arcs can be recovered from Theorem 5. Indeed, if $\mathcal {Q}$ is an elliptic quadric of ${{\,\textrm{PG}\,}}(3,5)$, then $\mathcal {K}_1$ is a non lifted $(3 \mod 5)$ arc of ${{\,\textrm{PG}\,}}(3, 5)$ of size 143, whereas if $\mathcal {Q}$ is a hyperbolic quadric of ${{\,\textrm{PG}\,}}(3, 5)$, then $\mathcal {K}_1$ is a non lifted $(3 \mod 5)$ arc of ${{\,\textrm{PG}\,}}(3, 5)$ of size 168.

5 Further examples $(t \mod q)$-arcs

A set of type (m, n) in ${{\,\textrm{PG}\,}}(r, q)$ is a set $\mathcal {S}$ of points such that every line of ${{\,\textrm{PG}\,}}(r, q)$ contains either m or n points of $\mathcal {S}$, $m < n$, and both values occur. Assume $m > 0$. Then the only sets of type (m, n) that are known, exist in ${{\,\textrm{PG}\,}}(2, q)$, q square, and are such that $n = m + \sqrt{q}$. In particular, sets of type $(1,1+ \sqrt{q})$ either contain $q+ \sqrt{q} + 1$ points and are Baer subplanes or $q\sqrt{q} + 1$ points and are known as unitals. For more details on sets of type (m, n) in ${{\,\textrm{PG}\,}}(2, q)$ see [12] and references therein. If $\mathcal {S}$ is an (m, n) set in ${{\,\textrm{PG}\,}}(r, q)$, $r > 2$, then necessarily q is an odd square, $m = (\sqrt{q} - 1)^2/2$, $n = m + \sqrt{q}$ and $|\mathcal {S}| = \frac{1 + \frac{q^r-1}{q-1}(q - \sqrt{q}) \pm \sqrt{q}^r}{2}$, see [14]. However no such a set is known to exist if $r > 2$.

Theorem 6

Let $\mathcal {S}$ be a set of type $(m, m + \sqrt{q})$ in ${{\,\textrm{PG}\,}}(r, q)$, q square. Let $\mathcal {K}$ be the arc of ${{\,\textrm{PG}\,}}(r, q)$ such that $\mathcal {K}(P) = \sqrt{q}$, if $P \in \mathcal {S}$ and $\mathcal {K}(P) = 0$, if $P \notin \mathcal {S}$. Then $\mathcal {K}$ is an $(m\sqrt{q} \mod q)$-arc of ${{\,\textrm{PG}\,}}(r, q)$.

Proof

Let $\ell$ be a line of ${{\,\textrm{PG}\,}}(r, q)$. If $|\ell \cap \mathcal {S}| = m$, then $\mathcal {K}(\ell ) = m \sqrt{q}$, whereas if $|\ell \cap \mathcal {S}| = m + \sqrt{q}$, then $\mathcal {K}(\ell ) = m \sqrt{q} + q$. $\square$

In ${{\,\textrm{PG}\,}}(r, q)$, q square, let $\mathcal {H}$ be a Hermitian variety of ${{\,\textrm{PG}\,}}(r, q)$, i.e., the variety defined by a Hermitian form of ${{\,\textrm{PG}\,}}(r, q)$. It is well-known that a line of ${{\,\textrm{PG}\,}}(r, q)$ has 1, $\sqrt{q}+1$ or $q+1$ points in common with $\mathcal {H}$. Let $\mathcal {K'}$ be the arc of ${{\,\textrm{PG}\,}}(r, q)$ such that $\mathcal {K'}(P) = \sqrt{q}$, if $P \in \mathcal {H}$ and $\mathcal {K'}(P) = 0$, if $P \notin \mathcal {H}$.

Theorem 7

${\mathcal {K}}'$ is a $(\sqrt{q} \mod q)$-arc of ${{\,\textrm{PG}\,}}(r, q)$. Moreover, if $\mathcal {H}$ is non-degenerate, then ${\mathcal {K}}'$ is not lifted.

Proof

Let $\ell$ be a line of ${{\,\textrm{PG}\,}}(r, q)$. Then

$$\begin{aligned} \mathcal {K'}(\ell ) = {\left\{ \begin{array}{ll} \sqrt{q} &{} \text{ if } |\ell \cap \mathcal {H}| = 1, \\ \sqrt{q} + q &{} \text{ if } |\ell \cap \mathcal {H}| = \sqrt{q} + 1, \\ \sqrt{q}(1 + q) &{} \text{ if } |\ell \cap \mathcal {H}| = q + 1. \end{array}\right. } \end{aligned}$$

If $\mathcal {H}$ is non-degenerate, then through every point of ${{\,\textrm{PG}\,}}(r, q)$ there exists a line r such that $|\mathcal {H} \cap r| = \sqrt{q}+1$. By construction, the line r has $\sqrt{q}+1$ $\sqrt{q}$-points and $q-\sqrt{q}$ 0-points. Hence $\mathcal {K'}$ is not lifted. $\square$