A review on distance based time series classification

Abstract

Time series classification is an increasing research topic due to the vast amount of time series data that is being created over a wide variety of fields. The particularity of the data makes it a challenging task and different approaches have been taken, including the distance based approach. 1-NN has been a widely used method within distance based time series classification due to its simplicity but still good performance. However, its supremacy may be attributed to being able to use specific distances for time series within the classification process and not to the classifier itself. With the aim of exploiting these distances within more complex classifiers, new approaches have arisen in the past few years that are competitive or which outperform the 1-NN based approaches. In some cases, these new methods use the distance measure to transform the series into feature vectors, bridging the gap between time series and traditional classifiers. In other cases, the distances are employed to obtain a time series kernel and enable the use of kernel methods for time series classification. One of the main challenges is that a kernel function must be positive semi-definite, a matter that is also addressed within this review. The presented review includes a taxonomy of all those methods that aim to classify time series using a distance based approach, as well as a discussion of the strengths and weaknesses of each method.

1 Introduction

Time series data are being generated everyday in a wide range of application domains, such as bioinformatics, financial fields, engineering, etc (Keogh and Kasetty 2002). They represent a particular type of data due to their temporal nature; a time series is an ordered sequence of observations of finite length which are usually taken through time, but may also be ordered with respect to another aspect, such as space. With the growing amount of recorded data, the interest in researching this particular data type has also increased, giving rise to a vast amount of new methods for representing, indexing, clustering, and classifying time series, among other tasks (Esling and Agon 2012). This work focuses on time series classification (TSC), and in contrast to traditional classification problems, where the order of the attributes of the input objects is irrelevant, the challenge of TSC consists of dealing with temporally correlated attributes, i.e., with input instances $x_i$ which are defined by complete ordered sequences, thus, complete time series (Bagnall et al. 2017; Fu 2011).

Time series classification methods can be divided into three main categories (Xing et al. 2010): feature based, model based, and distance based methods. In feature based classification methods, the time series are transformed into feature vectors and then classified by a conventional classifier such as a neural network or a decision tree. Some methods for feature extraction include spectral methods such as discrete Fourier transform (DFT) (Faloutsos et al. 1994) or discrete wavelet transform (DWT), (Popivanov and Miller 2002) where features of frequency domain are considered, or singular value decomposition (SVD) (Korn et al. 1997), wsingular value decomposition (SVD) (Korn et al. 1997), where eigenvalue analysis is carried out in order to reduce the set of features while retaining the relevant information. On the other hand, model based classification assumes that all time series in a class are generated by the same underlying model, and thus a new series is assigned with the class of the model that best fits. Some model based approaches are formed using auto-regressive models (Bagnall and Janacek 2014; Corduas and Piccolo 2008) or hidden Markov models (Smyth 1997), among others. Finally, distance based methods are those in which a (dis)similarity measure between series is defined, and then these distances are introduced in some manner within distance-based classification methods such as the k-nearest neighbour classifier (k-NN) or Support Vector Machines (SVMs). This work focuses on this last category: distance based classification of time series.

Until now, almost all research in distance based classification has been oriented to defining different types of distance measures and then exploiting them within k-NN classifiers. Due to the temporal (ordered) nature of the series, the high dimensionality, the noise, and the possible different lengths of the series in the database, the definition of a suitable distance measure is a key issue in distance based time series classification. One of the ways to categorize time series distance measures is shown in Fig. 1; Lock-step measures refer to those distances that compare the ith point of one series to the ith point of another (e.g., Euclidean distance), while elastic measures aim to create a non-linear mapping in order to align the series and allow comparison of one-to-many points [e.g., Dynamic Time Warping (Berndt and Clifford 1994)]. These two types of measures consider the important aspect to define the distance is the shape of the series, but there are also structure based or edit based measures, among others (Esling and Agon 2012). In this sense, different distance measures are able to capture different types of dissimilarities, and, even if in theory there is a best distance for each case (Li et al. 2004), in practice it is hard to find it. Nevertheless, the experimentation in Esling and Agon (2012), Xing et al. (2010), Wang et al. (2013), Chen et al. (2013), Ding et al. (2008), Lines and Bagnall (2015) and Xi et al. (2006) has shown that, on average, the DTW distance seems to be particularly difficult to beat.

Fig. 1

Mapping of Euclidean distance (lock-step measure) versus mapping of DTW distance (elastic measure) (Wang et al. 2013)

One of the simplest ways to exploit a distance measure within a classification process is by employing k-NN classifiers. One could expect that a more complex classifier would outperform the performance of the 1-NN and, as such, the bad performance of these complex classifiers may be attributed to the inability of the classifiers to deal with the temporal nature of the series using the default settings. On the other hand, it is known that the underlying distance is crucial to the performance of the 1-NN classifier (Tan et al. 2005) and, hence, the high accuracy of 1-NN classifiers may arise from the efficiency of the time series distance measures—which take into consideration the temporal nature—for classification. In this way, methods that exploit the potential of these distances within more complex classifiers have emerged in the past few years (Kate 2015; Jalalian and Chalup 2013; Marteau and Gibet 2014), achieving performances that are competitive or outperform the classic 1-NN.

These new approaches aim to take advantage of the existing time series distances to exploit them within more complex classifiers. We have differentiated between two new ways of using distance measures in the literature: the first employs the distance to obtain a new feature representation of the series (Kate 2015; Iwana et al. 2017; Hills et al. 2014), i.e., a representation of the series as an order-free vector, while the second uses the distance to obtain a kernel (Gudmundsson et al. 2008; Cuturi and Vert 2007; Marteau and Gibet 2014), i.e., a similarity between the series that will then be used within a kernel method. Both approaches have achieved competitive classification results and, thus, different variants have arisen (Jeong and Jayaraman 2015; Zhang et al. 2010; Lods et al. 2017). The purpose of this review is to present a taxonomy of all those methods which are based on time series distances for classification. At the same time, the strengths and shortcomings of each approach are discussed in order to give a general overview of the current research directions in distance based time series classification.

The rest of the paper is organized as follows: in Sect. 2 the taxonomy of the reviewed methods is presented, as well as a brief description of the methods in each category. In Sect. 4 a discussion on the approaches in the taxonomy is presented, where we draw our conclusions and specify some future directions.

2 A taxonomy of distance based time series classification

As mentioned previously, the taxonomy we propose intends to include and categorize all the distance based approaches for time series classification. A visual representation of the taxonomy can be seen in Fig. 2. From the most general point of view, the methods can be divided into three main categories: in the first one, the distances are used directly in conjunction with k-NN classifiers; in the second one, the distances are used to obtain a new representation of the series by transforming them into features vectors, while in the third one, the distances are used to obtain kernels for time series.

Fig. 2

A visual representation of the proposed taxonomy of distance based time series classification methods

2.1 k-Nearest Neighbour

This approach employs the existing time series distances within k-NN classifiers. In particular, the 1-NN classifier has mostly been used in time series classification due to its simplicity and competitive performance (Ding et al. 2008; Lines et al. 2012). Given a distance measure and a time series, the 1-NN classifier predicts the class of this series as the class of the object closest to it from the training set. Despite the simplicity of this rule, a strength of the 1-NN is that as the size of the training set increases, the 1-NN classifier guarantees an error lower than two times the Bayes error (Cover and Hart 1967). Nevertheless, it is worth mentioning that it is very sensitive to noise in the training set, which is a common characteristic of time series datasets. This approach has been widely applied in time series classification, as it achieves, in conjunction with the DTW distance, the best accuracies achieved on many benchmark datasets. As such, quite a few studies and reviews include the 1-NN in the time series literature (Bagnall et al. 2017; Wang et al. 2013; Lines and Bagnall 2015; Kaya and Gündüz-Öüdücü 2015), and hence, it is not going to be further detailed in this review.

2.2 Distance features

In this group, we include the methods that employ a time series distance measure to obtain a new representation of the series in the form of feature vectors. In this manner, the series are transformed into feature vectors (order-free vectors in ${\mathbb {R}}^{N}$), overcoming many specific requirements that are encountered in time series classification, such as dealing with ordered sequences or handling instances of different lengths. The main advantage of this approach is that it bridges the gap between time series classification and conventional classification, enabling the use of general classification algorithms designed for vectors, while taking advantage of the potential time series distances. In this manner, calculating the distance features can be seen as a preprocessing step, thus, the transformation can be used in combination with any classifier. Note that even if these methods also obtain some features from the series, they are not considered within feature based time series classification, but within distance based time series classification. The reason is that the methods in feature based time series classification obtain features that contain information about the series themselves, while distance features contain information relative to their relation with the other series. Three main approaches are distinguished within this category: those that directly employ the vector made up of the distances to other series as a feature vector, those that define the features using the distances to some local patterns, and those that use the distances after embedding the series into some vector space.

2.2.1 Global distance features

The main idea behind the methods in this category is to convert the time series into feature vectors by employing the vector of distances to other series as the new representation. Firstly, the distance matrix is built by calculating the distances between each pair of samples, as shown in Fig. 3. Then, each row of the distance matrix is used as a feature vector describing a time series, i.e., as input for the classifier. It is worth mentioning that this is a general approach (not specific for time series) but becomes specific when a time series distance measure is used. Learning with the distance features is also known as learning in the so-called dissimilarity space (Pȩkalska and Duin 2005). For more details on learning with global distance features in a general context, see Pȩkalska and Duin (2005), Chen et al. (2009), Pȩkalska et al. (2001) and Graepel et al. (1999).

Fig. 3

A visual representation of the global distance features method

Even if learning with distance features is a general solution, it is particularly advantageous for time series; the distance to each series is understood as an independent dimension and the series can be seen as vectors in a Euclidean space. This new representation enables the use of conventional classifiers that are designed for feature vectors, while it takes advantage of the existing time series distances. However, learning from the distance matrix has some important drawbacks; first, the distance matrix must be calculated, which may be costly depending on the complexity of the distance measure. Then, once the distance matrix has been calculated, learning a classifier may also incur large computational cost, due to the possible large size of the training set. Note that in the prediction stage, the consistent treatment of a new time series is straightforward—just the distances from the new series to the series in the training set have to be computed—but it can also become computationally expensive depending on the distance measure. Henceforth, given a distance measure d, we will refer to the methods employing the corresponding distance features as $\hbox {DF}_{d}$ .

After this brief introduction of the distance based features, a summary of the methods employing them is now presented. Gudmundsson et al. (2008) made the first attempt at investigating the feasibility of using a time series distance measure within a more complex classifier than the k-NN. In particular, they aimed at taking advantage of the potential of Support Vector Machines (SVMs) on the one hand, and of Dynamic Time Warping (DTW) on the other. First, they converted the DTW distance measure into two DTW-based similarity measures, shown in Eq. (1). Then, they employed the distance features obtained from these similarity measures, $\hbox {DF}_{GDTW}$ and $\hbox {DF}_{NDTW}$, in combination with SVMs for classification.

$$\begin{aligned} GDTW(TS_{i}, TS_{j})= & {} \exp \left( - \frac{DTW( TS_{i}, TS_{j} )^2}{ \sigma ^2} \right) , \nonumber \\ NDTW(TS_{i}, TS_{j})= & {} -DTW( TS_{i}, TS_{j}) \end{aligned}$$

(1)

where $\sigma > 0$ is a free parameter and $TS_{i},TS_{j}$ are two time series. They concluded the new representation in conjunction with SVMs is competitive with the benchmark 1-NN with DTW.

In Jalalian and Chalup (2013), the authors introduced a Two-step DTW-SVM classifier where the $\hbox {DF}_{DTW}$ are used in order to solve a multi-class classification problem. In the prediction stage, the new time series is represented by the distance to all the series in the training set and a voting scheme is employed to classify the series using all the trained SVMs in a one-vs-all schema. They concluded that even if $\hbox {DF}_{DTW}$ achieves acceptable accuracy values, the prediction of new time series is too slow for real world applications when the training set is relatively big.

Additionally, based on the potential of using distances as features for time series classification, Kate (2015) carried out a comprehensive experimentation in which different distance measures are used as features within SVMs. In particular, they tested not only $\hbox {DF}_{DTW}$ but also a constrained version $\hbox {DF}_{DTW-R}$ [a window-size constrained version of DTW which is computationally faster (Sakoe and Chiba 1978)], features obtained from the Euclidean distance $\hbox {DF}_{ED}$ and also concatenations of these distance features with other feature based representations. In their experimentation, they showed that even the $\hbox {DF}_{ED}$, when used as features with SVMs, outperforms the accuracy of 1-NN classifier based on the same Euclidean distance. An extension of Kate (2015) was presented in Giusti et al. (2016), who argued that not all relevant features can be described in the time domain (frequency domain can be more discriminative, for example) and added new representations to the set of features. Specifically, they generalized the concept of distance features to other domains and employed four different representations of the series with six different distance measures, giving rise to 24 distance features. For each representation of the series $R_{i}$, $i=1,\dots , 4$, they computed six different distance features $\hbox {DF}_{d_{1}}^{R_{i}}, \dots , \text {DF}_{d_{6}}^{R_{i}}$. In their experimentation on 85 datasets from UCR,¹ they showed that using representation diversity improves the classification accuracy. Finally, in their work about early classification of time series, Mori et al. (2017) benefit from Euclidean distance features $\hbox {DF}_{ED}$ in order to classify the series with SVMs and Gaussian Processes (Rasmussen and Williams 2006).

Recently, Wu et al. (2018b) proposed another distance feature approach for time series classification in which is based on Random Features (Rahimi and Recht 2008) approximation. Following the methodology of the D2KE kernel (Wu et al. 2018a) discussed in Sect. 2.3, the authors exploit the idea of randomly sampled time series and employ the distances from the original series to the random series as features: $\hbox {DF}_{RF}$. The random series are defined by D segments—where the length D is a user-defined parameter-, each segment associated with a random number. The idea is that these random series can be interpreted as the possible shapes of the time series. In the experiments carried out on 16 UCR datasets, they compare their representation—in combination with SVMs—against 6 state-of-the-art distance based classification methods. In particular, they propose two variants of their method: the first employs a large number of random series, while the second employs a small number. The experimentation shows that the first approach outperforms the accuracies of the baseline methods but incurs in large computational times, while the second obtains comparable accuracies in less time (reducing the time complexity from quadratic to linear).

With the aim of addressing the limitation of the high computational cost of the DTW distance, Janyalikit et al. (2016) proposed the use of a fast lower bound for the DTW algorithm, called LB_Keogh (Keogh and Ratanamahatana 2005). Employing $\hbox {DF}_{LB\_Keogh}$ with SVMs, Janyalikit et al. showed in their experimentation on 47 UCR datasets that their method speeds the classification task up by a large margin, while maintaining the accuracies comparing with the state-of-art $\hbox {DF}_{DTW-R}$ proposed in Kate (2015).

As previously mentioned, another weakness of using distances as features is the high dimensionality of the distance matrix, since for n instances a $n \times n$ matrix is used as the input to the classifier. In view of this, Jain and Spiegel (2015) proposed a dimensionality reduction approach using Principal Component Analysis (PCA) in order to keep only those dimensions that retain the most information. In their experimentation they compare the use of $\hbox {DF}_{DTW}$ with the reduced version of the same matrix, $\hbox {DF}_{DTW+PCA}$ in combination with SVMs. They showed PCA can have a consistent positive effect on the performance of the classifier but this effect seems to be dependent of the choice of the kernel function applied in the SVM. Note that for prediction purposes, they transform the new time series using the PCA projection learned from the training examples and, hence, the prediction process will also be significantly faster.

Another dimensionality reduction approach used in these cases is prototype selection, employed by Iwana et al. (2017). The idea is to select a set of k reference time series, called prototypes, and compute only the distances from the series to the k prototypes. The authors pointed out that the distance features let each feature be treated independently and, consequently, prototype selection can be seen as a feature selection process. As shown in Jain and Spiegel (2015), this dimensionality reduction technique not only speeds up the training phase but also the prediction of new time series. The proposed method uses the AdaBoost (Freund and Schapire 1997) algorithm, which is able to select discriminative prototypes and combine a set of weak learners. They experimented with $\hbox {DF}_{DTW+PROTO}$ and analyzed different prototype selection methods.

To conclude this section, a summary of the reviewed methods of Global distance features for TSC can be found in Table 1.

Table 1 Summary of global distance feature approaches

2.2.2 Local distance features

In this section, instead of using distances between entire series, distance to some local patterns of the series are used as features. Instead of assuming that the discriminatory characteristics of the series are global, the methods in this section consider that they are local. As such, the methods in this category employ the so-called shapelets (Ye and Keogh 2009), subsequences of the series that are identified as being representative of the different classes. An example of three shapelets belonging to different time series can be seen in Fig. 4. An important advantage of working with shapelets is their interpretability, since an expert may understand the meaning of the obtained shapelets. By definition, shapelets are subsequences and as such, the methods employing shapelets are not a priori applicable to other types of data. However, it is worth mentioning that the original shapelet discovery technique, proposed by Ye and Keogh (2009), is carried out by enumerating all possible candidates (all possible subsequences of the series) and using a measure based on information theory that takes $O(n^2m^4)$, where n is the number of time series and m is the length of the longest series. Thereby, most of the work related to shapelets has focused on speeding up the shapelet discovery process (He et al. 2012; Mueen et al. 2011; Rakthanmanon and Keogh 2013; Ye and Keogh 2011) or on proposing new shapelet learning methods (Grabocka et al. 2014). However, we will not focus on that but rather on how shapelets can be used within distance based classification.

Fig. 4

Visual representation of two shapelets ($\hbox {Shap}_{1}$ and $\hbox {Shap}_{2}$) and six time series from the Coffee dataset (UCR). These shapelets are identified as being representative of class membership: $\hbox {Shap}_{1}$ belongs to class 1, as can be seen in the three time series ($\hbox {T}_{1}$, $\hbox {T}_{2}$ and $\hbox {T}_{3}$) which belong to class 1, while $\hbox {Shap}_{2}$ belongs to class 2, as can be seen in the three time series ($\hbox {T}_{4}$, $\hbox {T}_{5}$ and $\hbox {T}_{6}$) which belong to class 2

Building on the achievements of shapelets in classification, Lines et al. (2012) introduced the concept of Shapelet Transform (ST). First, the k most discriminative (over the classes) shapelets are found using one of the methods referenced above. Then, the distances from each series to the shapelets are computed and the shapelet distance matrix shown in Fig. 5 is constructed. Finally, the vectors of distances are used as input to the classifier. In Lines et al. (2012), the distance between a shapelet of length l and a time series is defined as the minimum Euclidean distance between the shapelet and all the subsequences of the series of length l. Shapelet transformation can be used in combination with any classifier and, in their proposal, the authors experimented with seven classifiers (C4.5, 1-NN, Naïve Bayes, Bayesian Network, Random Forest, Rotation Forest and SVMs) and 26 datasets, showing the benefits of the proposed transformation.

Fig. 5

Example of the local distance features methods using ST

Hills et al. (2014) provided an extension of Lines et al. (2012) that includes a comprehensive evaluation which analyzes the performance of the seven aforementioned classifiers using the complete series and the ST as input. As such, the authors concluded that the ST gives rise to improvements in classification accuracy in several datasets. In the same line, Bostrom and Bagnall (2014) proposed another shapelet learning strategy (called binary ST) and evaluated their ST in conjunction with an ensemble classifier on 85 UCR datasets, showing that it clearly outperforms conventional approaches of time series classification.

Recently, Li and Lin (2018) proposed another approach that exploits time series distances in a novel way: their method maps the series into a specific dissimilarity space in which the different classes are effectively separated. This specific dissimilarity space is defined based on what they call Separating References (SRs), which, in practice, are subsequences. These SRs are found, by means of an evolutionary process, such that the distances between the SRs and series belonging to different classes differs with a large margin. The corresponding decision boundaries that split the classes in the dissimilarity space are also found during the same process. As such, this approach does not specifically employ distances as features but, since it is very related to the methods in this category, it has been included. They experiment with 40 UCR datasets showing that their Evolving Separating References (ESR) approach is competitive with the benchmark TSC methods, being particularly suitable for datasets in which the size of learning set is small.”

Lastly, Wang et al. (2016) introduced another representative subsequence based approach that is similar to shapelet based methods but from a novel perspective. Their method first transforms the real-valued series into discrete-valued series using Symbolic Aggregate approXimation (SAX) (Lin et al. 2007) and employs a grammar induction (GI) procedure (Senin et al. 2014) to generate a pool of representative pattern candidates. Then, it selects the most representative patterns from these candidates and transforms them back into subsequences. Finally, the series are represented by a vector containing the distances from the series to these subsequences, and the classification is carried out using SVMs.A significant difference between this method, called Representative Pattern Mining (RPM), and shapelet based methods is that, while a shapelet may be representative of more than one class—exclusiveness is not required—, in RPM the representative subsequences can only belong to one class. In addition, the pattern discovery in RPM is much more efficient than the existing shapelet discovery procedures.

To sum up, a summary of the reviewed methods that employ Local distance features can be found in Table 2.

Table 2 Summary of local distance feature approaches

2.2.3 Embedded features

The methods presented until now within the Distance features category employ the distances directly to create feature vectors representing the series, however, this is not the only way to use the distances. In the last approach within this section, the methods using Embedded features do not employ the distances directly as the new representation. Instead, they make use of them to obtain a new representation. In particular, the distances are used to isometrically embed the series into some Euclidean space while preserving the distances.

The distance embedding approach is not a specific method for time series. In many areas of research, such as empirical sciences, psychology, or biochemistry, it is common to have (dis)similarities between the input objects and not the objects per se. As such, one may learn directly in the dissimilarity space mentioned in Sect. 2.2.1, or one may try to find some vectors whose distances approximate the given (dis)similarities. If the given dissimilarities come from the Euclidean distance, it is possible to easily find some vectors that approximate the given distances. This is known in literature as metric multidimensional scaling (Borg and Groenen 1997). On the contrary, if the distances are not Euclidean (or even not metric), the embedding approach is not straightforward and many works have addressed this issue in research (Pȩkalska et al. 2001; Graepel et al. 1999; Wilson et al. 2014; Jacobs et al. 2000).

In the case of time series, this approach is particularly advantageous since a vector representation of the series is obtained such that the Euclidean distances between these vectors approximate the given time series distances. The main motivation is that many classifiers are implicitly built on Euclidean spaces (Jacobs et al. 2000) and this approach aims to bridge the gap between the Euclidean space and elastic distance measures. However, as it will be seen, the consistent treatment of new test instances is not straightforward and it is an issue to be considered.

As examples in TSC, Hayashi et al. (2005) and Mizuhara et al. (2006) proposed, for the first time, a time series embedding approach in which a vector representation of the series is found such that the Euclidean distances between these vectors approximate the DTW distances between the series, as represented in Fig. 6. They applied three embedding methods: multidimensional scaling, pseudo-Euclidean space embedding, and Euclidean space embedding by the Laplacian eigenmap technique (Belkin and Niyogi 2002). They experimented with linear classifiers and a unique dataset [Australian Sign Language (ASL) (Lichman 2013)], in which their Laplacian eigenmap-based embedded method achieved a better performance than the 1-NN classifier with DTW.

Fig. 6

Example of the stages of embedded distance features methods using the approach proposed by Hayashi et al. (2005)

Another approach presented by Lei et al. (2017) first defines a DTW based similarity measure, called DTWS, following the relation between distances and inner products (Adams 2004) (see Eq. 2). Then they search for some vectors such that the inner product between these vectors approximates the given DTWS:

$$\begin{aligned} DTWS(TS_{i},TS_{j}) = \frac{DTW(TS_{i},0)^{2} + DTW(TS_{j},0)^2 - DTW(TS_{i}, TS_{j})^2}{2} \end{aligned}$$

(2)

where 0 denotes the time series of length one of value 0. Their method learns the optimal vector representation preserving the DTWS by a gradient descent method, but a major drawback is that it learns the transformed time series, but not the transformation itself. The authors propose an interesting solution to deal with the high computational cost of DTW, which consists of assuming that the obtained DTWS similarity matrix is a low-rank matrix. As such, by applying the theory of matrix completion, sampling only $O(n \log n)$ pairs of time series is enough to perfectly approximate a $n \times n$ low-rank matrix (Sun and Luo 2016). However, it is not possible to transform new unlabeled time series, which makes the method rather inapplicable in most contexts.

Finally, Lods et al. (2017) presented a particular case of embedding that is based on the shapelet transform (ST) presented in the previous section. Their proposal learns a vector representation of the series (the ST), such that the Euclidean distance between the representations approximates the DTW between the series. In other words, the Euclidean distances between the row vectors representing each series in Fig. 5 approximate the DTW distances between the corresponding time series. The main drawback of this approach is the time complexity in the training stage: first all the DTW distances are computed and then, the optimal shapelets are found by a stochastic gradient descent method. However, once the shapelets are found, the transformation of new unlabeled instances is straightforward, since it is done by computing the Euclidean distance between these series and shapelets. Note that the authors do not use their approach for classifying time series but for clustering, but since it is closely related to the methods in this review and their transformation can be directly applied to classification, it has been included in the taxonomy.

As previously mentioned, an important aspect to be considered in the methods using embedded features is the consistent treatment of unlabeled test samples, which depends on the embedding technique used. In the work by Mizuhara et al. (2006), for instance, it is not clearly specified how unlabeled instances are treated. The method by Lei et al. (2017), on the other hand, learns the transformed data and not the transformation, hence it is not applicable to real problems. Lastly, in the approach by Lods et al. (2017), new instances are transformed by computing the distance from these new series to the learnt shapelets.

To end this section, a summary of the reviewed methods employing Embedded distance features for TSC can be found in Table 3.

Table 3 Summary of embedded distance feature approaches

2.3 Distance kernels

The methods within this category do not employ the existing time series distances to obtain a new representation of the series. Instead, they use them to obtain a kernel for time series. Before going in-depth into the different approaches, a brief introduction to kernels and kernel methods is presented.

2.3.1 An introduction to kernels

The kernel function is the core of kernel methods, a family of pattern recognition algorithms, whose best known instance is the Support Vector Machine (SVM) (Cortes and Vapnik 1995). Many machine learning algorithms require the data to be in feature vector form, while kernel methods require only a similarity function (known as kernel) expressing the similarity over pairs of input objects (Shawe-Taylor and Cristianini 2004). The main advantage of this approach is that one can handle any kind of data including vectors, matrices, or structured objects, such as sequences or graphs, by defining a suitable kernel which is able to capture the similarity between any two pairs of inputs. The idea behind a kernel is that if two inputs are similar, their output on the kernel will be similar, too.

More specifically, a kernel $\kappa$ is a similarity function

$$\begin{aligned} \kappa :&\; {\mathcal {X}} \times {\mathcal {X}} \rightarrow {\mathbb {R}} \\&(x,x') \rightarrow \kappa (x,x') \end{aligned}$$

that for all $x,x' \in {\mathcal {X}}$ satisfies

$$\begin{aligned} \kappa (x, x') = \langle \Phi (x) , \Phi (x') \rangle \end{aligned}$$

(3)

where $\Phi$ is the mapping from ${\mathcal {X}}$ into some high dimensional feature space and $\langle , \rangle$ is an inner product. As Eq. (3) shows, a kernel $\kappa$ is defined by means of a inner product $\langle \,,\rangle$ in some high dimensional feature space. This feature space is called a Hilbert space and the power of kernel methods lies in the implicit use of these spaces (Vapnik 1998).

In practice, the evaluation of the kernel function is one of the steps within the phases of a kernel method. Figure 7 shows the usage of the kernel function within a kernel method and the stages involved in the process. First, the kernel function is applied to the input objects in order to obtain a kernel matrix (also called Gram matrix), which is a similarity matrix with entries $K_{ij}=\kappa (x_{i},x_{j})$ for each input pair $x_{i}$, $x_{j}$. Then, this kernel matrix is used by the kernel method algorithm in order to produce a pattern function that is used to process unseen instances.

Fig. 7

The stages involved in the application of kernel methods (Shawe-Taylor and Cristianini 2004)

An important aspect to consider is that the class of similarity functions that satisfies (3), and hence are kernels, coincides with the class of similarity functions that are symmetric and positive semi-definite (Shawe-Taylor and Cristianini 2004).

Definition 1

(Positive semi-definite kernel) A symmetric function $\kappa :{{\mathcal {X}}}\times {{\mathcal {X}}}\rightarrow {\mathbb {R}}$ satisfying

$$\begin{aligned} \sum _{i=1}^{n}\sum _{j=1}^{n}c_{i}c_{j}\kappa (x_{i},x_{j})\ge 0 \end{aligned}$$

(4)

for any $n\in {\mathbb {N}}, x_{1},\dots ,x_{n}\in {\mathcal {X}}, c_{1},\dots ,c_{n}\in {\mathbb {R}}$ is called a positive semi-definite kernel (PSD) (Schölkopf 2001).

As such, any PSD similarity function satisfies (3) and (since it is a kernel) defines an inner product in some Hilbert space. Moreover, since any kernel guarantees the existence of the mapping implicitly, an explicit representation for $\Phi$ is not necessary. This is also known as the kernel trick (see Shawe-Taylor and Cristianini 2004 for more details).

Remark 1

We will also refer to a PSD kernel as a definite kernel.

Remark 2

We will informally denominate indefinite kernels to non-PSD kernels which are employed in practice as kernels, even if they do not strictly meet the definition.

Providing the analytical proof of the positive semi-definiteness of a kernel is rather cumbersome. In fact, a kernel does not need to have a closed-form analytic expression. In addition, as Fig. 7 shows, the way of using a kernel function in practice is via the kernel matrix and, hence, the definiteness of a kernel function is usually evaluated experimentally for a specific set of inputs by analysing the positive semi-definiteness of the kernel matrix.

Definition 2

(Positive semi-definite matrix) A square symmetric matrix ${\mathbf {K}} \in {\mathbb {R}}^{n \times n}$ satisfying

$$\begin{aligned} {\mathbf {v}}^T {\mathbf {K}} {\mathbf {v}} \ge 0 \end{aligned}$$

(5)

for any vector ${\mathbf {v}} \in {\mathbb {R}}^{n}$ is called a positive semi-definite matrix (Schölkopf 2001).

The following well-known result is obtained from Shawe-Taylor and Cristianini (2004):

Proposition 1

The inequality in Eq. (5) holds $\Leftrightarrow$ all eigenvalues of ${\mathbf {K}}$ are non-negative.

Therefore, if all the eigenvalues of a kernel matrix are non-negative, this kernel function is considered PSD for the particular instance set in which it has been evaluated. In this manner, the definiteness of a kernel function is usually studied by the eigenvalue analysis of the corresponding kernel matrix. However, a severe drawback of this approach is that the analysis is only performed for a particular set of instances, and it cannot be generalized.

After introducing the basic concepts related to kernels, some examples of different types of kernels are now presented. As previously mentioned, one of the main strengths of kernels is that they can be defined for any type of data, including structured objects, for instance:

• Kernels for vectors Given two vectors ${\mathbf {x}}, \mathbf {x'}$, the popular Gaussian Radial Basis Function (RBF) kernel (Shawe-Taylor and Cristianini 2004) is defined by

  $$\begin{aligned} \kappa ({\mathbf {x}}, \mathbf {x'}) = \exp \left( - \frac{|| {\mathbf {x}}- \mathbf {x'} ||^2}{2 \sigma ^2} \right) \end{aligned}$$

  (6)

  where $\sigma > 0$ is a free parameter.

• Kernels for strings Given two strings, the p-spectrum kernel (Leslie et al. 2002) is defined as the number of sub-strings of length p that they have in common.

• Kernels for time series Give two time series, a kernel for time series returns a similarity between the series. There are plenty of ways of defining a similarity. For instance, two time series may be considered similar if they are generated by the same underlying statistical model (Rüping 2001). In this review, we will focus on those kernels that employ a time series distance measure to evaluate the similarity between the series.

Therefore, in this category denominated Distance kernels, instead of using a distance to obtain a new representation of the series, the distances are used to obtain a kernel for time series. As such, the methods in this category aim to take advantage of the potential of time series distances and the power of kernel methods. Two main approaches are distinguished within this category: those that construct and employ an indefinite kernel, and those that construct kernels for time series that are, by definition, PSD.

2.3.2 Indefinite distance kernels

The main goal of the methods in this category is to convert a time series distance measure into a kernel. Most distance measures do not trivially lead to PSD kernels, so many works focus on learning with indefinite kernels. The main drawback of learning with indefinite kernels is that the mathematical foundations of the kernel methods are not guaranteed (Ong et al. 2004). The existence of the feature space to which the data is mapped (Eq. 3) is not guaranteed and, due to the missing geometrical interpretation, many good properties of learning in that space (such as orthogonality and projection) are no longer available (Ong et al. 2004). In addition, some kernel methods do not allow indefinite kernels (due to the implementation or the definition of the method) and some modifications must be carried out, but for others the definiteness is not a requirement. For example, in the case of SVMs, the optimization problem that has to be solved is no longer convex, so reaching the global optimum is not guaranteed (Chen et al. 2009). However, note that good classification results can still be obtained (Bahlmann et al. 2002; Decoste and Schölkopf 2002; Shimodaira et al. 2002), and as such, some works focus on studying the theoretical background about SVMs feature space interpretation with indefinite kernels (Haasdonk 2005). Another approach, for instance, employs heuristics on the formulation of SVMs to find a local solution (Chen et al. 2006) but, to the best of our knowledge, it has not been applied to time series classification. Converting a distance into a kernel is not a specific challenge of time series and there is a considerable amount of work done in this direction in other contexts (Chen et al. 2009; Haasdonk and Bahlmann 2004).

Fig. 8

Different approaches taken with indefinite distance kernels

For time series classification, most of the work focuses on employing the distance kernels proposed by Haasdonk and Bahlmann (2004). They propose to replace the Euclidean distance in traditional kernel functions, such as the Gaussian kernel in Eq. (6), by the problem specific distance measure. They called these kernels distance substitution kernels. In particular, we will call the following kernel Gaussian Distance Substitution (GDS) (Haasdonk and Bahlmann 2004):

$$\begin{aligned} GDS_{d}(x, x') = \exp \left( - \frac{d( x, x' )^2}{ \sigma ^2} \right) \end{aligned}$$

(7)

where $x, x'$ are two inputs, d is a distance measure and $\sigma > 0$ is a free parameter. This kernel can be seen as a generalization of the Gaussian RBF kernel presented in the previous section, in which the Euclidean distance is replaced with the distance calculated by d. For the GDS kernel, the authors in Haasdonk and Bahlmann (2004) state that $\hbox {GDS}_{d}$ is PSD if and only if d is isometric to an L-2 norm, which is generally not the case. As such, the methods which use this type of kernel for time series generally employ indefinite kernels.

Within the methods employing indefinite kernels, there are different approaches, and for time series classification we have distinguished three main directions (shown in Fig. 8). Some of them just learn with the indefinite kernels (Kaya and Gündüz-Öüdücü 2015; Bahlmann et al. 2002; Shimodaira et al. 2002; Pree et al. 2014; Jeong et al. 2011) using kernel methods that allow this kind of kernels and without taking into consideration that they are indefinite; others argue that the indefiniteness adversely affects the performance and present some alternatives or solutions (Jalalian and Chalup 2013; Gudmundsson et al. 2008; Chen et al. 2015b); finally, others focus on a better understanding of these distance kernels in order to investigate the reason for the indefiniteness (Zhang et al. 2010; Lei and Sun 2007).

Employing indefinite kernels

Bahlmann et al. (2002) made the first attempt to introduce a time series specific distance measure within a kernel. They introduced the GDTW measure presented in Eq. (1) as a kernel for character recognition with SVMs. This kernel coincides with the GDS kernel in Eq. (7), in which the distance d is replaced by the DTW distance, i.e., $\hbox {GDS}_ {DTW}$. They remarked that this kernel is not PSD since simple counter-examples can be found in which the kernel matrix has negative eigenvalues. However, they obtained good classification results and argued that for the UNIPEN² dataset, most of the eigenvalues of the kernel matrix were measured to be non-negative, concluding that somehow, in the given dataset, the proposed kernel matrix is almost PSD. Following the same direction, Jeong et al. (2011) proposed a variant of $\hbox {GDS}_ {DTW}$ which employs the Weighted DTW (WDTW) measure in order to prevent distortions by outliers, while Kaya and Gündüz-Öüdücü (2015) also employed the GDS kernel with SVMs, but instead of using the distance calculated by the DTW, they explored other distances derived from different alignment methods of the series, such as Signal Alignment via Genetic Algorithm (SAGA) (Kaya and Gündüz-Öüdücü 2013). Pree et al. (2014) proposed a quantitative comparison of different time series similarity measures used either to construct kernels for SVMs or directly for 1-NN classification, concluding that some of the measures benefit from being applied in an SVM, while others do not. Note that in this last work, how they construct the kernel for each distance measure is not exactly detailed.

There is another method that employs a distance based indefinite kernel but takes a completely different approach to construct the kernel: the idea of this kernel is to, rather than use an existing distance measure, incorporate the concept of alignment between series into the kernel function itself. Many elastic measures for time series deal with the notion of alignment of series. The DTW distance, for instance, finds an optimal alignment between two time series such that the Euclidean distance between the aligned series is minimized. Following the same idea, in DTAK, Shimodaira et al. (2002) align two series so that their similarity is maximized. In other words, their method finds an alignment between the series that maximizes a given similarity (defined by the user), and this maximal similarity is used directly as a kernel. They give some good properties of the proposed kernel but they remark that it is not PSD, since negative eigenvalues can be found in the kernel matrices of DTAK (Cuturi 2011).

On the other hand, Gudmundsson et al. (2008) employed the DTW based similarity measures they proposed (shown in Eq. 1) directly as kernels. Their method achieved low classification accuracies and the authors claimed that another way of introducing a distance into a SVM is by using the distance features introduced in Sect. 2.2.1. They compared the performance of DTW based distance features and DTW based distance kernels, concluding that distance features outperform the distance kernels due to the indefiniteness of these second ones.

Dealing with the indefiniteness

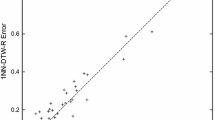
There is a group of methods that attribute the poor performance of their kernel methods to the indefiniteness, and propose some alternatives or solutions to overcome these limitations. Jalalian and Chalup (2013), for instance, proposed the use of a special SVM called Potential Support Vector Machine (P-SVM) (Hochreiter and Obermayer 2006) to overcome the shortcomings of learning with indefinite kernels. They employed the $\hbox {GDS}_ {DTW}$ kernel within this SVM classifier which is able to handle kernel matrices that are neither positive definite nor square. They carried out an extensive experimentation including a comparison of their method with the 1-NN classifier and with the methods presented by Gudmundsson et al. (2008). They conclude that their DTW based P-SVM method significantly outperforms both distance features and indefinite distance kernels, as well as the benchmark methods in 20 UCR datasets.

Regularization

Another approach that tries to overcome the use of indefinite kernels consists of regularizing the indefinite kernel matrices to obtain PSD matrices. As previously mentioned, a matrix is PSD if and only if all its eigenvalues are non-negative, and a kernel matrix therefore can be regularized by clipping all the negative eigenvalues to zero, for instance. This technique has been usually applied for non-temporal data (Chen et al. 2009; Wu et al. 2005a, b) but it is rather unexplored in the domain of indefinite time series kernels. Chen et al. (2015b) proposed a Kernel Sparse Representation based Classifier (SRC) (Zhang et al. 2012) with some indefinite time series kernels and applied spectrum regularization to the kernel matrices. In particular, they employed the $\hbox {GDS}_{DTW}$, $\hbox {GDS}_{ERP}$ [Edit distance with Real Penalty (ERP) (Chen and Ng 2004)] and $\hbox {GDS}_{TWED}$ [Time Warp Edit Distance (TWED) (Marteau 2009)] kernels and their method checks whether the kernel matrix obtained for a specific dataset is PSD. If it is not, the corresponding kernel matrix is regularized using the spectrum clip approach.

Regarding this approach, it is also worth mentioning that in the work by Gudmundsson et al. (2008), the authors point out that they tried to apply some regularization to the kernel matrix subtracting the smallest eigenvalue from the diagonal but they found out that the method achieved a considerably low performance. Additionally, the authors added that matrix regularization can lead to matrices with large diagonal entries, which may result in overfitting (Weston et al. 2003).

Finally, the consistent treatment of training and new unlabeled instances is not straightforward and is also a matter to bear in mind (Chen et al. 2009). When new unlabeled instances arrive, the kernel between them and the training set has to be computed. If the kernel matrix corresponding to the training set has been regularized, the kernel matrix corresponding to the unlabeled set should also be modified in a consistent way, which is not a trivial operation. Therefore, the benefit of matrix regularization in the context of time series is an open question.

Analyzing the indefiniteness

The last group of methods do not focus on solving the problems of learning with indefinite kernels but, instead, focus on a better understanding of these distance kernels and their indefiniteness. Lei and Sun (2007) theoretically analyze the $\hbox {GDS}_ {DTW}$ kernel, proving that it is not a PSD kernel. This is because DTW is not a metric [it violates the triangle inequality (Casacuberta et al. 1987)] and non-metricity prevents definiteness (Haasdonk and Bahlmann 2004). That is, if d is not metric, $\hbox {GDS}_ {d}$ is not PSD. However, the contrary is not true and, hence, the metric property of a distance measure is not a sufficient condition to guarantee a PSD kernel. In any case, Zhang et al. (2010), hypothesized kernels based on metrics give rise to better performances than kernels based on distance measures which are not metrics. As such, they define what they called the Gaussian Elastic Metric Kernel (GEMK), a family of GDS kernels in which the distance d is replaced by an elastic measure which is also a metric. They employed $\hbox {GDS}_{ERP}$ and $\hbox {GDS}_{TWED}$ and stated that, even if the definiteness of these kernels is not guaranteed, they did not observe any violations of their definiteness in their experimentation on 20 UCR datasets. In fact, these kernels are shown to perform better than the $\hbox {GDS}_ {DTW}$ and the Gaussian kernel in those experiments. The authors attribute this to the fact that the proposed measures are both elastic and obey metricity. In order to provide some information about the most common distance measures applied in this context, Table 4 shows a summary of properties of the main distance measures employed in this review. In particular, we specify if a given distance measure d is a metric or not, if it is an elastic measure or not, and if the corresponding $\hbox {GDS}_ {d}$ is proven to be PSD or not.

Table 4 Summary of distance properties used in GDS

To sum up, there are some results that suggest a relationship between the metricity of the distance and the performance of the corresponding distance kernel. However, it is hard to investigate the contribution of metricity in the accuracy since several factors take part in the classification task. The definiteness of a distance kernel seems to be related to the metricity of given distance-metric distances seem to lead to kernels that are closer to definiteness than those based on non-metric distances-, and the definiteness of a kernel may directly affect on the accuracy. In short, the relationship between metricity, definiteness and performance is not clear and is, thus, an interesting future direction of research.

To conclude, a summary of the reviewed methods of Indefinite distance kernels can be found in Table 5.

Table 5 Summary of indefinite kernel approaches

2.3.3 Definite distance kernels

We have included in this section those methods that construct distance kernels for time series which are, by definition, PSD. First of all, we want to remark that there are other kernels for time series in the literature that are PSD but have not been included in this review. We have only incorporated those kernels based on time series distances and, in particular, those which construct the kernel functions directly on the raw series. Conversely, the Fourier kernel (Rüping 2001) computes the inner product of the Fourier expansion of two time series, and hence, does not compute the kernel on the raw series but on the Fourier expansion of them. Another example is the kernel by Gaidon et al. (2011) for action recognition, in which the kernel is constructed on the auto-correlation of the series. There are also smoothing kernels that smooth the series with different techniques and then define the kernel for those smoothed representations (Troncoso et al. 2015; Kumara et al. 2008; Sivaramakrishnan and Bhattacharyya 2004; Lu et al. 2008). On the contrary, we will focus on those that define a kernel directly on the raw series. Regarding those included, all of them aim to introduce the concept of time elasticity directly within the kernel function by means of a distance, and we can distinguish two main approaches: in the first, the concept of the alignment between series is exploited, while in the second, the direct construction of PSD kernels departing from a given distance measure is addressed.

Xue et al. (2017) proposed the Altered Gaussian DTW (AGDTW) kernel, in which, first, the alignment that minimizes the Euclidean distance between the series is found, as in DTW. For each pair of time series ${TS_{i}}$ and ${TS_{j}}$, once this alignment is found, the series are modified to this alignment resulting in ${TS_{i}}'$ and ${TS_{j}}'$. Then, if S is the maximum length of both series, the AGDTW kernel is defined as follows:

$$\begin{aligned} \kappa _{AGDTW}(TS_{i}, TS_{j}) = \sum _{s=1}^{S} \exp \left( - \frac{|| {TS_{i}}_s'- {TS_{j}}_s' ||^2}{\sigma ^2} \right) \end{aligned}$$

Since AGDTW is, indeed, a sum of Gaussian kernels, they provide the proof of the definiteness of the proposed kernel.

There is another family of methods that also exploits the concept of alignment but, instead of considering just the optimal one, considers the sum of the scores obtained by all the possible alignments between the two series. Cuturi and Vert (2007) claimed that two series can be considered similar not only if they have one single good alignment, but rather if they have several good alignments. They proposed the Global Alignment (GA) kernel that takes into consideration all the alignments between the series and provide the proof of its positive definiteness under certain mild conditions. It is worth mentioning that they obtain kernel matrices that are exceedingly diagonally dominant, that is, that the values of the diagonal in the matrix are many orders of magnitude larger than those out of the diagonal. Thus, they use the logarithm of the kernel matrix because of possible numerical problems. That transformation makes the kernel indefinite (even if it is not indefinite per se), so they apply some kernel regularization to turn all its eigenvalues positive. However, since the kernel they obtain is PSD and it is because of the logarithm transformation that it becomes indefinite, it has been included within this section. In Cuturi (2011), the author elaborates on the GA kernels, give some theoretical insights, and introduce an extension called Triangular Global Alignment (TGA) kernel, which is faster to compute and also PSD.

There is another kernel that takes a similar approach. In their work about periodic time series in astronomy, Wachman et al. (2009) investigate the similarity between just shifted time series. In this way, they define a kernel that takes into consideration the contribution of all possible alignments obtained by employing just time shifting:

$$\begin{aligned} K_{shift}(TS_{i},TS_{j}) = \sum _{s=1}^{n} e^{\gamma \langle TS{_{i}}, TS{_{j}}_{+ s}\rangle } \end{aligned}$$

where $\gamma \ge 0$ is a user-defined constant. In this way, the kernel is defined by means of a sum of inner products between $TS_{i}$ and all the possible shifted versions of $TS_{j}$ with a shift of s positions. The authors provided the proof of the PSD of the proposed kernel.

On the other hand, there are methods that, instead of focusing on alignments, address the construction of PSD kernels departing from a given distance measure. These methods can be seen as refined versions of the GDS kernel in which the obtained kernel is PSD. Marteau and Gibet (2010) elaborate on the indefiniteness of GDS kernels derived from elastic measures, even when such measures are metrics. As previously mentioned, metricity is not a sufficient condition to obtain PSD kernels. They postulated that elastic measures do not lead to PSD kernels due to the presence of min or max operators in their definitions, and define a kernel where they replaced the min or max operators by a sum ($\sum$). In Marteau et al. (2012), these same authors define what they called an elastic inner product, eip. Their goal was to embed the time series into an inner product space that somehow generalizes the notion of the Euclidean space, but retains the concept of elasticity. They provide proof of the existence of such a space and showed that this eip is, indeed, a PSD kernel. Since any inner product induces a distance (Greub 1975), they obtained a new elastic metric distance $\delta _{eip}$ that avoids the use of min or max operators. They evaluated the obtained distance within a SVM by means of the $\hbox {GDS}_{\delta _{eip}}$ kernel, in order to compare the performance of $\delta _{eip}$ with the Euclidean and DTW measures. Their experimentation showed that elastic inner products can bring a significant improvement in accuracy compared to the Euclidean distance, but the $\hbox {GDS}_{DTW}$ kernel outperforms the proposed $\hbox {GDS}_{\delta _{eip}}$ in the majority of the datasets.

They extended their work in Marteau and Gibet (2014) and introduced the Recursive Edit Distance Kernels (REDK), a method to construct PSD kernels departing from classical edit or time-warp distances. The main procedure to obtain PSD kernels is, as in the previous method, to replace the min or max operators by a sum. They provided the proof of the definiteness of these kernels when some simple conditions are satisfied, which are weaker than those proposed in Cuturi and Vert (2007) and are satisfied by any classical elastic distance defined by a recursive equation. Note that, while in Marteau et al. (2012) the authors define an elastic distance and construct PSD kernels with it, in Marteau and Gibet (2014) the authors present a method to construct a PSD kernel departing from any existing elastic distance measure. As such, the REDK can be seen as a refined version of the GDS kernel which leads to PSD kernels. In this manner, they proposed the $\hbox {REDK}_{DTW}$, $\hbox {REDK}_{ERP}$ and $\hbox {REDK}_{TWED}$ methods and compare their performance with the corresponding distance substitutions kernels $\hbox {GDS}_{DTW}$, $\hbox {GDS}_{ERP}$ and $\hbox {GDS}_{TWED}$. An interesting result they reported is that REDK methods seem to improve the performance of non-metric measures in particular. That is, while the accuracies of $\hbox {REDK}_{ERP}$ and $\hbox {REDK}_{TWED}$ are slightly better than the accuracies of $\hbox {GDS}_{ERP}$ and $\hbox {GDS}_{TWED}$, in the case of DTW the improvement is really significant. In fact, they presented some measures to quantify the deviation from definiteness of a matrix and showed that while $\hbox {GDS}_{ERP}$ and $\hbox {GDS}_{TWED}$ are almost definite, $\hbox {GDS}_{DTW}$ is rather far from being definite. This makes us wonder if metricity implies proximity to definiteness, and in addition, if accuracy is directly correlated to the definiteness of the kernel.

Furthermore, they explored the possible impact of the indefiniteness of the kernels on the accuracy by defining several measures to quantify the deviation from definiteness based on eigenvalue analysis. If ${\mathbf {D}}_{\delta }$ is a distance matrix, $\hbox {GDS}_{{\mathbf {D}}_{\delta }}$ is PSD if and only if ${\mathbf {D}}_{\delta }$ is negative definite (Cortes et al. 2004), and ${\mathbf {D}}_{\delta }$ is negative definite if it has a single positive eigenvalue. In this manner, the authors studied the deviation from definiteness of some distance matrices, and stated that when the distance matrix ${\mathbf {D}}_{\delta }$ was far from being negative definite, the $\hbox {REDK}_{\delta }$ outperforms the $\hbox {GDS}_{\delta }$ kernel in general, while when the matrix is close to negative definiteness, $\hbox {REDK}_{\delta }$ and $\hbox {GDS}_{\delta }$ perform similarly.

Recently, Wu et al. (2018a) introduced another distance substitution kernel, called D2KE, that addresses the construction of a family of PSD kernels departing from any distance measure. It is not specific for time series but in their experimentation they include a kernel for time series departing from the DTW distance measure. Their kernel employs a probability distribution over random structured objects (time series in this case) and defines a kernel that takes into account the distance from two series to the randomly sampled objects. In this manner, the authors point out that the D2KE kernel can be interpreted as a soft version of the GDS kernel, which is PSD. Their experimentation on four time series datasets showed that their $\hbox {D2KE}_{DTW}$ kernel outperforms other distance based approaches such as 1-NN or $\hbox {GDS}_{DTW}$ both in accuracy and computational time.

To conclude this section, a summary of the reviewed methods on Definite distance kernels can be found in Table 6.

Table 6 Summary of definite distance kernels

3 Computational cost

An important aspect that has not been addressed in depth when presenting the taxonomy is the computational cost of the methods included. The time complexity of the classification methods, in general, is dominated by the learning phase and depends on the size of the dataset from which the model is learnt; in distance based classification, in addition to the size of the dataset—understood as the number of instances—, the complexity of both the learning and prediction phases also depends on the computational cost of the employed distance measure. At the same time, the cost of the distance measure also highly depends on the lengths of the series we are working with. In this way, many time series distances, especially the most commonly employed measures (DTW, ERP, TWED...), are characterized by a quadratic complexity on the length of the series, which results in methods which are very time consuming for cases in which the length of the series is large. In this context, many of the methods that employ common time series distance measures usually turn out to be too time consuming for real world applications. Even if this is so, and even if some of the reviewed works experimentally evaluate the running times of their methods or aim at speeding up their learning processes, most of them do not even address this issue. Thereby, in this section, a brief overview of the complexity of distance based TSC methods is provided in order to review the computational specificities of the methods in each category of the taxonomy.

First of all, it is important to highlight that one of the most significant differences between distance based and non-distance based classification methods (from the point of view of the computational cost) is the time complexity of the prediction phase. In non-distance based methods, normally, the learning phase depends on the size of the training dataset but, once the model is learnt, the prediction of unlabeled instances does not depend on this dataset and is usually independent from the size of the dataset. In distance based classification, on the contrary, both the learning and the prediction stages computationally depend on the size of the dataset and on the chosen distance measure, so they must both be taken into account. Thereby, from now, we are going distinguish between the computational cost of the learning and the prediction phases of the reviewed methods. Note that we are going to provide a general computational time analysis of the methods but there are exceptions which do not exactly fit into the computational characterization that we provide for each category.

In the case of the methods based on the 1-NN classifier, there is no learning phase and the computational cost of prediction is determined by the size of the dataset and the complexity of the distance measure (which, in turn, depends on the lengths of the series). For instance, the distances DTW, ERP or TWED have a complexity of $O(n^2)$, where n is the length of the longest time series, while the cost of the Euclidean distance is O(n). As such, the computational cost of predicting an unlabeled time series using the DTW distance, for instance, is $O(n^2m)$ (where m is the size of the training dataset), since the m distances between the unlabeled series and the series in the dataset have to computed. The approach adopted by most researchers to accelerate this process is to speed up the computation of the employed distance measure, for example by using the fast lower bound for the DTW (Keogh and Ratanamahatana 2005), which reduces the complexity of the distance to O(n) (Esling and Agon 2012).

Regarding the methods that exploit distances as features, it is important to note that the computation of the distances and the learning/prediction of the classifier are two independent steps with their corresponding computational costs. In the learning stage, first, the pairwise distances between all the series in the dataset are computed—as a preprocessing step—to obtain the distance features, which are then used as input for learning the classifier. We focus only on the complexity of the first step, which is specific for distance based methods: the computational cost of this step depends on the complexity of the distance measure, as well as on the size of the training dataset. For instance, computing the DTW distance matrix of the m series in a dataset has a complexity of $O(n^2m^2)$. For prediction, the distances from the new unlabeled series to all the series in the training dataset have to be computed also as a preprocessing step. Then, the obtained distance features are introduced into the classifier to predict the unknown label. As in the previous case, the distance computation depends on the complexity of the distance measure and the size of the dataset. As such, an important drawback is that, for cases with large datasets or high time consuming distances, the prediction can become unrealistically time consuming. In view of this, several approaches have been taken to mitigate the effect of these two factors: Janyalikit et al. (2016) employed the fast lower bound to speed up the computation of the distances (from quadratic to linear), while Iwana et al. (2017) and Jain and Spiegel (2015) address the issue of reducing the dimension of the distance matrix that is used as input to learn the model. The former proposed using time series prototypes and used the distances to them instead of calculating the entire distance matrix, while the latter applied PCA in order to reduce its dimensionality.

In the shapelet based approaches, there are some preprocessing steps in order to obtain the features before the application of the classifier. In the learning phase, first, a shapelet discovery stage is carried out in which the best shapelets are learnt and, then, the pairwise distances between the series in the dataset and the obtained shapelets are computed. The initially proposed shapelet discovery technique takes $O(n^4m^2)$, which turns out to be very time consuming for real world applications. As such, over the years, many methods have been proposed to speed up this search (He et al. 2012; Mueen et al. 2011; Rakthanmanon and Keogh 2013; Ye and Keogh 2011). Once the shapelets have been discovered, the computational cost of calculating the pairwise distances between series and shapelets depends on the complexity of the distance, the number of series and the number of shapelets. The distance between a series and a shapelet is computed using the Euclidean distance most of the times -which has a complexity of O(n)-, so, once the shapelets are learnt, the distance computation has a complexity of O(nms), where s is the number of shapelets. This number is determined in the shapelet discovery process, which usually involves techniques such as candidate pruning or shapelet clustering in order to reduce the amount of shapelets (Hills et al. 2014; Ye and Keogh 2009). In the prediction phase, the shapelet based methods require a preprocessing step that involves a distance computation between the new unlabeled series and the learnt shapelets, which has O(ns) complexity in the case of the commonly employed Euclidean distance.

For the embedding based methods, the pairwise distances between the series in the dataset have to be computed before they are embedded into another space. In the learning, this process has $O(n^2m^2)$ complexity (with the DTW distance, for example), while the complexity of the embedding process depends on the specific technique employed. Hayashi et al. (2005) and Mizuhara et al. (2006), for instance, applied multidimensional scaling, pseudo-Euclidean space embedding, and Euclidean space embedding by the Laplacian eigenmap technique, but they do not specify the computational cost of these methods so it is hard to draw conclusions. Lei et al. (2017) and Lods et al. (2017), employed gradient descent based techniques, and, while the formers do not specify the complexity of the method, the latter points out that the complexity of the learning phase is quite high. Then, the obtained features are introduced into a classifier. In prediction, the pairwise distances between the unlabeled series and the training dataset have to be computed, which has a complexity of $O(n^2m)$ for cases using DTW (Hayashi et al. 2005; Mizuhara et al. 2006).

In the methods that employ distance kernels, there is no preprocessing step and the series are directly used as input to the given kernel method. However, the distance kernels are derived from time series distances, so the computational cost of the kernel methods is mainly dominated by the computation of the kernel matrix (analogous to the distance matrix). In particular, this computation depends on the complexity of the distance measure from which the kernel is derived as in (Bahlmann et al. 2002; Jeong et al. 2011; Chen et al. 2015b) methods. As such, the distance substitution kernels derived from DTW, ERP, EDR or TWED are computationally more expensive ($O(n^2 m^2)$) than the Gaussian RBF kernel ($O(nm^2)$), for instance. In the prediction phase, the kernel matrix—computed in the learning phase—is extended with the pairwise values between the unlabeled series and the series in the dataset, which has the same complexity as the previous 1-NN or global distance features methods.

Apart from the distance substitution kernels, the review includes other distance kernels that are specific for time series and whose computational cost has to be analysed more in depth. The kernel proposed by Cuturi and Vert (2007) considers all the alignments instead of only the optimal one and, thus, has a complexity of $O(n^2m^2)$ in the learning learning phase and $O(n^2m)$ in prediction phase. In view of this, the same authors proposed another version of the kernel (Cuturi 2011), which, by means of adding additional constraints on the allowed alignments, is faster than the original kernel but equally accurate. In the definite kernel derived from an elastic inner product proposed by Marteau et al. (2012), the computational cost is evaluated experimentally and the authors show that the proposed elastic kernel has a complexity of O(n). As such, the learning phase takes $O(nm^2)$, while the prediction phase O(nm). In other words, they obtained an elastic kernel for time series that is characterized by a linear complexity instead of the quadratic complexity derived from the traditional elastic distances, which is a significant improvement.

From a general point of view, it is hard to draw accurate comparative results between the methods presented due to their variants and the lack of experimental computational time results available in the published works. Wu et al. (2018b) carried out the most comprehensive evaluation of the computational cost of several distance based TSC methods until now. They first compare their $\hbox {DF}_{RF}$ distance features method with two embedding methods: the method proposed by Mizuhara et al. (2006), and the one by Lods et al. (2017), concluding that their method outperforms the other two, both in accuracy and in computational time. In addition, two variants of their method are also evaluated on 16 UCR datasets against other baseline distance based TSC approaches (1-NN with DTW, the GA kernel (Cuturi and Vert 2007) and $\hbox {DF}_{DTW}$ (Kate 2015)); the first variant of their method outperforms the other approaches in accuracy but involves a high computational cost, while the second variant achieves competitive accuracies, significantly reducing the required computational time.

To summarize, distance based TSC methods have usually quadratic complexity both in the length of the series and in the size of the dataset, due to the common use of elastic measures. In this context, if the series are long enough or the size of dataset is large, the methods can become too time consuming for real world applications. As such, it is an important aspect to be considered. Some of the methods take this into account and evaluate the running time of their method but, in general, in our opinion, it has not been addressed enough. There are some attempts to speed up the distance based methods (Janyalikit et al. 2016; Iwana et al. 2017; Jain and Spiegel 2015; Cuturi 2011; Marteau et al. 2012) but it is still a direction in which there is considerable room for improvement. In addition, we think that a comprehensive comparison of the running times of the methods would be a great contribution as future work.

4 Discussion and future work

In this paper, we have presented a review on distance based time series classification and have included a taxonomy that categorizes all the discussed methods depending on how each approach uses the given distance. We have seen that from the most general point of view, there are three main approaches: those that directly employ the distance together with the 1-NN classifier, those that use the distance to obtain a new feature representation of the series, and those which construct kernels for time series departing from distance measure. The first approach has been widely reviewed, so we refer the reader to Wang et al. (2013), Ding et al. (2008) and Serrà and Arcos (2014) for more details about the discussion.

Regarding the methods that employ a distance to obtain a new feature representation of the series, these approaches have been considerably studied for time series as it bridges the gap between traditional classifiers (that expect a vector as input) and time series data, taking advantage of the existing time series distances. In addition, some methods within this category have outperformed existing time series benchmark classification methods (Kate 2015). Note that distance features can be seen as a preprocessing step, where a new representation of the series is found which is independent of the classifier. Depending on the specific problem, these representations vary and can be more discriminative and appropriate than the original raw series (Hills et al. 2014). As such, an interesting point that has yet to be addressed is to compare the different transformations of the series in terms of how discriminative they are for classification.

Nevertheless, learning with the distance features can often become cumbersome depending on the size of the training set and a dimensionality reduction technique must be applied in many cases in order to lower the otherwise intractable computational cost. Some of the methods (Iwana et al. 2017; Jain and Spiegel 2015) reduce the dimensionality of the distance matrix once it is computed. Another direction focuses on time series prototype selection (Iwana et al. 2017), that is, selecting some representative time series in order to compute only the distances to them instead of to the whole training set. It is worth mentioning that there has been some work done in this context in other dissimilarity based learning problems (Pȩkalska et al. 2006) but it is almost unexplored in TSC. Due to the interpretability of the time series and, in particular, of their prototypes, we believe that this is a promising future direction of research.

Another feature based method consists of embedding. The embedded distance features have only been employed in combination with linear classifiers (Mizuhara et al. 2006) or the tree based XGBoost classifier (Lods et al. 2017), which, in our opinion, do not take direct advantage of the transformation. The main idea of the embedded features is that if the Euclidean distances of the obtained features are computed, the original time series distances are approximated. In this way, we believe classifiers that compute Euclidean distances within the classification task (such as the SVM with the RBF kernel, for instance) will profit better from this representation. In addition, in the particular case of kernel methods, the use of embedded features can be seen as a kind of regularization; the RBF kernel obtained from the embedded features would be a definite kernel that approximates the GDS indefinite kernel.

As already pointed out, the third way of using a distance measure is trying to construct kernels departing from these existing distances. However, these distances do not generally lead to PSD kernels. Both distance features and distance kernel approaches are not specific for time series, and some work has been done to compare the benefits of each approach in a general context. Chen et al. (2009) mathematically studied the influence of distances features and distances kernels within SVMs in a general framework. In time series classification, Gudmundsson et al. (2008) and Jalalian and Chalup (2013) address the problem of experimentally evaluating whether it is preferable to use distance features or distance kernels. Both works assert that the indefiniteness of the distance kernels negatively affects the performance, although their proposals are restricted to the DTW distance. It would be interesting to comprehensively compare these two approaches taking into account different distances, kernels and classifiers in order to draw more general conclusions.

The problem of the definiteness of a kernel has been widely addressed within the methods in this review. Note that the definiteness of a kernel guarantees the mathematical foundations of the kernel method and, therefore, it seems natural to think that definiteness and performance are correlated, which is the assumption of almost all the methods. Some authors confirm that the performance is still good and do not care about the indefiniteness of the kernels, while, in general, the research focuses mainly on trying to somehow deal with the indefiniteness of the kernels. Isolating the contribution of the definiteness of a kernel to the performance is rather challenging due to the many other factors (optimization algorithm or the choice of the kernel function) that also affect it. However, since the relation between definiteness and accuracy is a general matter—not specific for time series, and in fact, not specific for distance kernels—, a promising future direction would be to evaluate whether there exists or not a direct correlation between them.

Within the methods that try to deal with the indefiniteness there are two main directions. The first uses kernel based classifiers that can handle indefinite kernels. This approach is almost unexplored in time series classification, since only the P-SVM by Jalalian and Chalup (2013) has been applied, achieving very competitive results. Indeed, there are some studies on learning with indefinite kernels from a general point of view (Ong et al. 2004), and considering that indefinite kernels appear often within TSC, this approach may be interesting future work.

The second approach, called kernel regularization, aims to adapt the indefinite kernel to be PSD. As in the previous direction, this is also an almost unexplored approach for time series. Only eigenvalue analysis has been applied with ambiguous results. Chen et al. (2015a) used eigenvalue regularization techniques but they do not evaluate the regularization itself, while Gudmundsson et al. (2008) argued that the method after kernel regularization achieves lower performance than the method with the indefinite kernel. One of the main shortcomings of this specific regularization is that it is data dependent, and, in addition, the consistent treatment of new test samples is not straightforward. As previously mentioned, it is not clear whether regularization is helpful or whether the new kernel becomes so different from the initial one that the information loss is too big; this is an open question which has not been studied in detail.

As previously mentioned, another direction focuses on a better understanding of the indefiniteness of these kernels. Concerning the GDS kernels, which are distance kernels valid for any type of data, the first attempt in the time series domain was to define kernels departing from distances that are metrics. Although it has been proven that the metric property does not guarantee the definiteness of the induced GDS kernel, Zhang et al. (2010) argued that the performance of metric distance kernels is significantly better than those defined with non-metric distances, suggesting that kernels with metric distances are closer to definiteness. In addition, Marteau and Gibet (2014) conjecture that the reason of the indefiniteness is the presence of min or max operators in the recursive definition of time series distance measures. An interesting observation is that these discussions arise from time series distances but are, regardless, general issues concerning the characteristics of a distance measure and the derived GDS kernel. Even if the mentioned works address the relation between metricity and definiteness, this connection is not yet clear. It is also an interesting future research direction due to the generalizability of the problem and the possible applications.

Cuturi and Vert (2007), by contrast, focused on the specific challenge of constructing ad-hoc kernels for time series. As such, they found a direct way of constructing PSD kernels that take into account the time elasticity by defining a kernel that does not consider just the optimal alignment between two series but, instead, considers all the possible alignments. Moreover, given an elastic distance measure defined by a recursive equation, Marteau (2009) address the construction of distance based PSD kernels. Their kernel can be seen as a particular case of GDS kernel for elastic measures that become PSD by replacing the min or max operators in the recursive definition of the distance by a sum. By using this trick, they obtain kernels for time series that take into account time elasticity and are also PSD. Their comprehensive experimentation shows that SVM based approaches which use these kernels clearly outperform the 1-NN benchmark approaches, even for the DTW distance. Furthermore, they reported that the REDK kernel brings significant improvement in comparison with the GDS kernel, especially when the kernel matrices of the GDS kernels are far from definiteness, which in their particular case corresponds to the non-metric measures. However, they experimented with just two metric and one non-metric measures which is not enough to draw strong conclusions.

It is also worth mentioning that many methods introduced in the taxonomy are not specific for time series, but become specific when a time series distance is employed. In particular, only the methods that are based on shapelets and the methods that construct kernels for time series considering the concept of alignment between series are specific for time series. The rest of the methods are general methods of distance based classification for any type of data. An interesting observation is that questions or problems arising for time series can be extrapolated to a general framework. In the same manner, some of the presented approaches are specific for some classifiers (1-NN, kernel methods), while others can be used in combination with any classifier. Also note that many of the methods, such as those which employ global distance features, embedded features or indefinite distance kernels, are directly applicable in the case of multivariate or streaming time series, provided a suitable distance for this kind of series is defined. The extension of these methods for multivariate or streaming time series could be a possible future direction. It would be interesting also to extend other methods, such as the shapelet based methods or the ad-hoc definite kernels, to these kind of time series, since, in these cases, the adaptation of the methods by itself would be a great contribution.

To conclude, note that in contrast to the number and variety of existing kernels for other types of data, there are rather few benchmark kernels for time series in current literature (Shawe-Taylor and Cristianini 2004). Therefore, we would like to highlight the value of these kernels for time series, especially those that are able to deal with the temporal nature of the series and are PSD.