Chaotic coexistence of librational and rotational dynamics in the averaged planar three-body problem

Abstract

Through an appropriate change of reference frame and rescalings of the variables and the parameters introduced, the Hamiltonian of the three-body problem is written as a perturbed Kepler problem. In this system, new Delaunay variables are defined and a suitable configuration of the phase space and the mass parameters is chosen. In such a system, wide regions of librational and rotational motions where orbits are regular and stable are found. Close to the separatrix of these regions, the existence of chaotic motions presenting a double rotational and librational dynamics is proved, numerically, through Poincaré sections and the use of FLI.

1 Introduction

In this paper, a numerical study of the three-body problem has been done in order to prove existence of chaotic motions for some configurations. Many authors have covered this issue, see as references, for example, Celletti (2010), Delshams et al. (2019), Froeschle et al. (2000), Féjoz and Guardia (2016), Fejoz et al. (2014), Guardia et al. (2016), Guardia et al. (2019), Laskar and Robutel (1995). We specify that we deal with the Hamiltonian of the full three-body problem, where “full” is used as opposed to the so-called restricted problem; thus, the three bodies have no negligible masses and the motion of each one is ruled by mutual Newtonian gravitational attraction. The idea, already used in previous articles such as Chen and Pinzari (2021), Daquin et al. (2023), Di Ruzza et al. (2020), Di Ruzza and Pinzari (2022) and coming from papers (Pinzari 2019, 2020a, b), is to consider, in principle, no Newtonian interaction between the three bodies as dominant. We use new coordinates (see Pinzari 2019) associated with the three bodies and through suitable rescalings of variables and time we write the new Hamiltonian describing the model as the sum of a Keplerian part ruling the motion of two of three bodies plus a part depending on all the three bodies. This remaining part is not necessarily small with respect to the Keplerian part, but indeed, we choose a region of the phase space such that the remaining part of the Hamiltonian becomes a perturbation. Thus, we deal with a “perturbed Keplerian problem”. In the current paper, the assumptions that will be made to get the perturbed problem concern the order of magnitude of the energies describing the Hamiltonian. The aim is to find suitable initial conditions where chaotic motions appear. In the configuration that we propose, we are able to prove, numerically, a large region of the reduced phase space where stable and regular motions are present and a small zone where particular kinds of motions with a double dynamic nature exist, i.e. orbits where librational and rotational motions alternate, oscillating with chaotic frequencies. This is shown through the use of appropriate Poincaré sections and through the use of the Fast Lyapunov Indicator (FLI), namely a finite time dynamical chaos indicators which monitor the growth over time of the tangent vector under the action of the tangent flow (for a detailed presentation see, for example, papers (Lega et al. 2016; Guzzo and Lega 2014)). The FLI has been used to study many chaotic dynamics as well as the stable and unstable manifolds of normally hyperbolic invariant manifolds of the three-body problem (see, for example, Lega et al. 2010; Guzzo and Lega 2012). In our configuration, we do not prove the existence of one or more hyperbolic fixed point, but using the FLI we are able to prove, numerically, the existence of chaotic structures in the phase space. The paper is structured as follows: In Sect. 2, we introduce the model and the general setting. In Sect. 3, we present a specific configuration and we analyze the phase space of isoenergetic orbits of such configuration. In Sect. 4, we introduce the FLI and the phase space is again analyzed in order to find regions where chaotic motions take place. Finally, in Sect. 5, conclusions and perspective are proposed.

2 Description of the model

We fix an orthogonal reference frame (i, j, k) in the Euclidean space, which we identify with ${\mathbb {R}}^3$. In such a space, we consider three bodies $P_1,P_2,P_3$ with masses $m_1, m_2, m_3$ interacting through the gravity only. The Hamiltonian $\mathcal {H}_\textrm{3b}$ describing the dynamics of the three bodies can be written as

$$\begin{aligned} \mathcal {H}_\textrm{3b}= \frac{{\Vert y_1\Vert }^2}{2 m_{1}} + \frac{{\Vert y_2\Vert }^2}{2 m_2}+\frac{{\Vert y_3\Vert }^2}{2 m_{3}}-\frac{ m_{1} m_2}{\Vert x_1-x_2\Vert }-\frac{ m_{1} m_3}{\Vert x_1-x_3\Vert }-\frac{m_2 m_3}{\Vert x_2-x_3\Vert } , \end{aligned}$$

(1)

where $x_1,x_2,x_3 \in \mathbb {R}^3$ are the position coordinates of the three bodies and $y_1,y_2,y_3 \in \mathbb {R}^3$ are their respective linear momenta; $\Vert \cdot \Vert$ denotes the Euclidean distance and, finally, the gravity constant has been conventionally fixed to one. In our study, the motion of the three bodies is confined in a plane, so it has been called planar problem, choosing positions and impulses $x_1,x_2,x_3, y_1,y_2,y_3 \in \mathbb {R}^2$. We reduce the translation symmetry relating the positions of two (out of three) masses to the position of the third one, as described in (§ 5 Giorgilli 2008). Contrarily to the usual practice, we choose $P_2$ as reference body with mass $m_2=\mu$ (usually, the unit mass is chosen) as depicted in Fig. 1. With such choice, the Hamiltonian governing the motions of the $P_1,P_3$ with masses $m_1 =1$ and $m_3 = \kappa$, respectively, is

$$\begin{aligned} H_\textrm{3b}(x,x',y,y')= \frac{\kappa +\mu }{\kappa \mu } \frac{\Vert y\Vert ^2}{2}-\frac{\kappa \mu }{\Vert x\Vert } + \frac{\mu +1}{\mu } \frac{\Vert y'\Vert ^2}{2} - \frac{\mu }{\Vert x'\Vert }-\frac{\kappa }{\Vert x-x'\Vert } + \frac{1}{\mu }y\cdot y' , \end{aligned}$$

where $x, x' \in \mathbb {R}^2$ are the position coordinates of $P_1$ and $P_3$, respectively, and $y, y' \in \mathbb {R}^2$ are their respective linear momenta; the body $P_2$ is at the origin of the reference system.

Fig. 1

A schematic model of the three-body problem we deal with

We perform a rescaling of coordinates as follows:

$$\begin{aligned} (x,x') \rightarrow \frac{\kappa +\mu }{\mu ^2\kappa ^2}(x,x') ,\qquad (y,y') \rightarrow \frac{\mu ^2\kappa ^2}{\kappa +\mu } (y,y'), \qquad t\rightarrow \frac{\mu ^3\kappa ^3}{\kappa +\mu }t \end{aligned}$$

(with t denoting the time). It does not alter the equations of motion provided that $H_\textrm{3b}$ is changed to

$$\begin{aligned} H_\textrm{3b}(x,x',y,y') = \frac{\Vert y\Vert ^2}{2}-\frac{1}{\Vert x\Vert } + \delta \biggl ( \frac{\Vert y'\Vert ^2}{2} -\frac{\alpha }{\Vert x-x'\Vert } -\frac{\beta }{\Vert x'\Vert } + \gamma \, y\cdot y' \biggr ) , \end{aligned}$$

(2)

with

$$\begin{aligned} \alpha := \frac{\kappa +\mu }{\kappa \mu (\mu +1)} , \qquad \beta := \frac{\kappa +\mu }{\kappa ^2(\mu +1)} , \qquad \gamma := \frac{1}{\mu +1} , \qquad \delta := \frac{\kappa (\mu +1)}{\kappa +\mu } , \end{aligned}$$

being the current mass parameters depending on $\mu$ and $\kappa$. The first two terms $\frac{{\Vert y \Vert }^2}{2}-\frac{1}{{\Vert x \Vert }}$ are called Keplerian part and, assuming it takes negative values, it generate motions for the body of coordinates (x, y) on an ellipse.

The Hamiltonian (2) has four degrees of freedom, and in the following step, we aim to reduce it to a three degrees of freedom system. The Hamiltonian $H_\textrm{3b}$ is invariant under the group of transformations SO(2), namely orthogonal rotations. Introducing a set of canonical coordinates in a suitable rotating system, we reduce this symmetry obtaining a three degrees of freedom system. To this aim, we introduce the total angular momentum, which is a constant of motion, as

$$\begin{aligned} \textrm{C} = x \times y \cdot k + x' \times y' \cdot k \end{aligned}$$

where $k = i \times j$ is the unit vector orthogonal to plane where motions take place, and then, we define a six-dimensional “rotation-reduced phase space”  introducing 6 new canonical coordinates

$$\begin{aligned} (\Lambda ,R,G,\ell , r,g). \end{aligned}$$

We denote by $\mathbb {E}$ the ellipse generated by the Keplerian part of Eq. (2) for a given initial datum (x, y). Finally, we define a couple of Delaunay variables $(\Lambda ,G,\ell ,g) \in \mathbb {R}^2 \times \mathbb {T}^2$ for the body $P_3$ with respect to $P_2$ as follows:

• $\Lambda = \sqrt{a} ,\quad \text {where } a \text { is the semi-major axis of }\mathbb {E} ,$

• $G = x \times y \cdot k$ is the angular momentum of the third body $P_3 \,$,

• $\ell \text { is } \text {the mean anomaly of } x \text { from the pericenter } P \text { of }\mathbb {E} ,$

• $g \text { is } \text {the angle detecting the pericenter of } \mathbb {E} \text { with respect the direction of } x',$

and a radial-polar couple coordinate $(R,r) \in \mathbb {R}^2$ for the body $P_1$ as:

• $R = y' \cdot \frac{x'}{\vert x' \vert } ,$

• $r = \vert x' \vert ,$

namely R is the radial velocity of $P_1$ and r is the Euclidean length of $x'$. We underline that the coordinates $(R, G,\Lambda ,r,g,\ell )$ refer to a frame moving with $P_1$ and they have been introduced to reduce the symmetry of rotations (we refer to Pinzari 2019 for an exhaustive definition of the variables). The Hamiltonian (2) written in the new coordinates appears as

$$\begin{aligned} H_C(\Lambda ,R,G,\ell (\xi ,\Lambda ,G),r,g) = -\frac{1}{2\Lambda ^2} + \delta \, \Big ( \frac{R^2}{2} + \frac{(C-G)^2}{2 \, r^2} - \alpha \, U_\textrm{pot} -\frac{\beta }{r}+ \gamma \, I \Big ) ,\nonumber \\ \end{aligned}$$

(3)

where the mean anomaly $\ell$ is related by the eccentric anomaly $\xi$ by means of the Kepler Equation

$$\begin{aligned} \ell = \xi - e \sin {\xi } , \end{aligned}$$

and e is the eccentricity of the ellipse $\mathbb {E}$ given by

$$\begin{aligned} e = \sqrt{1- \frac{G^2}{\Lambda ^2}} ; \end{aligned}$$

$U_\textrm{pot} = U_\textrm{pot}(\Lambda ,R,G,\xi ,r,g)$ is the Newtonian potential and $I = I(\Lambda ,R,G,\xi ,r,g)$ is the indirect term. We rewrite Hamiltonian (3) as

$$\begin{aligned} H_C(\Lambda ,R,G,\xi ,r,g) = -\frac{1}{2\Lambda ^2} + \delta \, \Big ( K_0 +K_1 +U + P \Big ) , \end{aligned}$$

(4)

where $-1/(2 \, \Lambda ^2)$ is the Keplerian term, and

$$\begin{aligned} K_0= & {} \frac{R^2}{2} + \frac{C^2}{2 \, r^2} - \frac{\beta }{r} \nonumber \\ K_1= & {} \frac{-2 \,C \, G + G^2}{2 \, r^2} \nonumber \\ U= & {} -\alpha \, U_\textrm{pot} \nonumber \\ P= & {} \gamma \, I \end{aligned}$$

(5)

are, respectively, the kinetic term, the disturbing term, the Newtonian potential term and the indirect term. We remark that after the symmetry reduction, the Hamiltonian depends parametrically on the total angular momentum C.

Hamiltonian (3) is a 3 degrees of freedom system and, as it has been done in Di Ruzza and Pinzari (2022), we split the term inside parentheses as the sum of its $\ell$-average (denoted by ${\overline{H}}_C$) and the zero-average part (denoted by ${\widetilde{H}}_C$):

$$\begin{aligned} H_C(\Lambda ,R,G,\ell ,r,g) = -\frac{1}{2\Lambda ^2} + \delta \, \Big ( {\overline{H}}_C(\Lambda ,R,G,r,g) + {\widetilde{H}}_C(\Lambda ,R,G,\ell ,r,g) \Big ) . \end{aligned}$$

(6)

We claim two main assumptions. The first is that the Keplerian term is much more bigger than the zero-averaged term:

$$\begin{aligned} \Bigg \Vert -\frac{1}{2\Lambda ^2}\Bigg \Vert \gg \delta \, \Vert {\widetilde{H}}_C \Vert , \end{aligned}$$

(7)

where $\Vert \cdot \Vert$ is some norm of functions. Under condition (7), perturbation theory (see for example Arnold 1963) allows to conjugate Hamiltonian (6) to

$$\begin{aligned} H_C(\Lambda ,R,G,\ell ,r,g) = -\frac{1}{2\Lambda ^2} + \delta \, {\overline{H}}_C(\Lambda ,R,G,r,g) + O_2(\Lambda ,R,G,\ell ,r,g) , \end{aligned}$$

(8)

where $O_2$ represents a remainder term depending on all the coordinates. Let us now consider the system (8) when the remainder is neglected: the Keplerian term in eq. (8) becomes an additive term which does not change the equation of motions, so we can consider $\Lambda$ as a constant parameter and, without loss of generality, we can fix it equal to 1.

Moreover, we can reabsorb the parameter $\delta$ through a change of time, and the system can be reduced to a new Hamiltonian ${\overline{H}}_C$, which is given by

$$\begin{aligned} {\overline{H}}_C(R,G,r,g) = \frac{R^2}{2} + \frac{(C-G)^2}{2 \, r^2} + {\overline{U}}(G,r,g) -\frac{\beta }{r} , \end{aligned}$$

(9)

where

$$\begin{aligned} {\overline{U}}(G,r,g) = - \frac{\alpha }{2\pi } \int _0^{2\pi } \frac{\textrm{d}\ell }{\Vert x - x' \Vert } . \end{aligned}$$

(10)

Hamiltonian ${\overline{H}}_C(R,G,r,g)$ is a 2 degrees of freedom system. With the notations defined in (5), Hamiltonian (9) can be rewritten as

$$\begin{aligned} {\overline{H}}_C(R,G,r,g) = K_0(R,r) + K_1(G,r) + {\overline{U}}(G,r,g). \end{aligned}$$

(11)

Now, we state the second assumption, namely we ask for

$$\begin{aligned} \Vert K_0\Vert \gg \Vert {\overline{U}} \Vert \gg \Vert K_1\Vert \quad \rightleftarrows \quad \Vert K_0\Vert \gg \Vert U \Vert \gg \Vert K_1\Vert . \end{aligned}$$

(12)

Remark 1

Note that term $P= \gamma \, y \cdot y'$ in Eq. (5) is a $\ell$-zero-average term, so it is part of the term ${\widetilde{H}}_C$ together with the $\ell$-zero-average part of the Newtonian potential $U_\textrm{pot}$.

We claim the following conjecture:

Conjecture 2.1

(Di Ruzza and Pinzari 2022, Conjecture 1.1) Under Assumptions (7) and (12), at a first approximation, the motion of $(\Lambda (t), R(t), G(t), \ell (t),r(t),g(t))$ ruled by Hamiltonian (4) is as follows:

• $\Lambda (t)\sim 1$ remains almost constant and $\ell (t)\sim t$ moves fast;

• the motion (R(t), r(t)) is ruled by $K_0$;

• the motion (G(t), g(t)) is ruled by the non-autonomous Hamiltonian ${\overline{U}}( r (t), \cdot , \cdot )$.

The main purpose of this article is to numerically study the dynamics of the systems governed by Hamiltonian (11) when Conditions (7) and (12) are satisfied.

3 Numerical studies in the averaged Hamiltonian system

Let us analyze a set of parameters where Assumptions (7) and (12) are fulfilled. We choose $\mu =2,\, \kappa = 0.1$ which implies $\alpha = 3.5 , \beta = 70 , \gamma = 0.333333 , \delta = 0.142857$. Then, we take $C= 10^2$. We look for some ad hoc initial conditions for Hamiltonian (4) as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \Lambda = 1 \\ R = 0 \\ G = G_0 \\ \xi = \xi _0\\ r = C^2/\beta \\ g = g_0 \end{array} \right. \end{aligned}$$

(13)

where the choice $(R,r)=(0,C^2/\beta )$ is such that the term $K_0$ reaches its minimum and the body $P_3$ moves in uniform circular motion of radius r; $G_0\in (-\Lambda , \Lambda ), \, \xi _0, g_0 \in [0, 2\pi ]$ could be chosen in suitable way.

3.1 Energy terms comparison

Fixing $G_0,\xi _0,g_0$, in the left panel of Fig. 2, we can see the orders of the Hamiltonian terms given in Eq.(5) propagated for a given period under the flow given by Eq. (4). Changing $G_0$, the four terms modify a little without changing the orders of magnitude. Changing $\xi _0$ and $g_0$ we just get horizontal translations (in time phasing) of the figure. It is easy to verify that Assumptions (7) and (12) are fulfilled recalling that $\Lambda = 1$ implies $\Vert -\frac{1}{2\Lambda ^2}\Vert = \frac{1}{2}$.

In an analogous way, we define parameters and initial conditions for the averaged Hamiltonian (9), choosing as parameters $\mu =2,\, \kappa = 0.1$, which implies $\alpha = 3.5 , \beta = 70$; $C= 10^2$; $\Lambda = 1$ and ad hoc initial conditions as:

$$\begin{aligned} \left\{ \begin{array}{l} R = 0 \\ G = G_0 \\ r = C^2/\beta \\ g = g_0 \end{array} \right. , \end{aligned}$$

(14)

for some $G_0 \in (-1,1)$ and $g_0\in [0, 2\pi ]$. In the right panel of Fig. 2, we can compare the orders of magnitude of the terms $K_0,K_1,U$ in such case. In this section, we analyze the motions taken place in this configuration, in the averaged system.

Fig. 2

Left: orders of magnitude of terms $K_0$ in dark-green, $K_1$ in blue, U in red, P in light-green, multiplied by $\delta$, referred to the Hamiltonian (4); right: orders of magnitude of terms $K_0,K_1,U$, respectively in dark-green, blue, red, referred to the Hamiltonian (9)

3.2 Analysis of the three-dimensional phase space

Let us start by describing the motion in the averaged system ruled by Eq. (9). In our computation, the Newtonian averaged potential ${\overline{U}}$ (Eq. (10)) is expanded in power series of the small parameter $a/r =1/r$ and the series is truncated at order 10, which, after a check of the error of truncation, is chosen as good compromise between precision and working time of the machine.

We fix the total energy, namely we fix the value of the Hamiltonian (9) taken in suitable initial conditions so to reduce the phase space from dimension 4 to 3. At the beginning, we consider initial conditions in Eq. (14) with $G_0 = 0.8$ and $g_0 = \pi /2$ and analyze the three-dimensional phase space (g, G, r). Such a space appears foliated by regular invariant two-dimensional manifolds where the motions take place. To better visualize the three-dimensional structure, we propose, in both Figs. 3 and 4, two different simulations: in the upper panels, we show the propagation of the trajectories with ${\overline{U}}$ truncated at order 2 and in the bottom panels the propagation of the trajectories with ${\overline{U}}$ truncated at order 10 (it has been done just for a better visualization). Let us describe the first case: as it can be seen in the upper left panel of Fig. 3, the trajectories belong to cylinders orthogonal to the (g, G)-plane; the variable g circulates in $[0,2\pi ]$ when the variable $G\in I_c$ and librates when $G\in I_l$ for suitable real intervals $I_c, I_l$ which will be analyzed in the following. In the upper right panel, a zoom on the variable G allows to see the cylinder which librating trajectories belong to. At the center of the librating island, an elliptic trajectory, represented as a magenta segment, lies in the three-dimensional space: this trajectory is associated with the elliptic fixed point of coordinates $(g,G)= (\pi ,0.9985968919390512)$ of the Poincaré map defined in the next section; the variables g, G of such trajectory remain constant, while the variable r oscillates along the real interval $I_r$ which will be specified in the following. In the upper left panel of Fig. 3, it is also highlighted in orange a particular trajectory named last trajectory. This trajectory is peculiar because it belongs to a unidimensional curve parallel to the (g, G)-plane, namely the variable r remains constant during the motion. We called it last trajectory because, when $g = \pi$, the variable G takes the minimum value $G_{\min }$ of the interval $I_c$ and for values smaller than $G_{\min }$ no motion takes place for the fixed value of the energy: we mean that, for the fixed value of the energy, initial conditions (g, G, r) are not admissible for $G<G_{\min }$.

In the upper left panel of Fig. 4, the projection on the (G, r)-plane of the trajectories is represented. In such figure, we can well see the last trajectory in orange and the elliptic trajectory in magenta and how the range of the variable r increases from the former to the latter. In the right panel of Fig. 4, the projection on the (r, R)-plane of the trajectories is represented. In this figure, we highlight again with an orange point the last trajectory whose variables $r = r_\textrm{last}$ and $R = 0$ remain constant and in magenta the elliptic trajectory where the variation of the variables r and R is maximum. In the bottom panels of Figs. 3 and 4 (where the same simulations with ${\overline{U}}$ truncated at order 10 are performed), we can see the manifolds just little deformed and displaced with respect to the previous case. The elliptic trajectory shown in magenta in the bottom right panel of Fig. 3 does not appear as a segment but as a closed curve with a very small variation in the variables g, G as well as the last trajectory shown in the bottom left panel of Fig. 3 has a very small but nonzero variation in the variable r. The same imperceptible but present differences can be seen in Fig. 4 between the upper and the bottom panels.

Let us show a physical interpretation of such results. The elliptic trajectory corresponds to the equilibrium configurations $g =\pi$, namely the pericenter P of the orbit of the body $P_3$ is on the line of the bodies $P_1$ and $P_2$, as depicted in Fig. 5. This stable equilibrium corresponds to a 1 : 1 resonance between the slow orbital revolution of the body $P_1$ and the precession of the pericenter P of the orbit of the body $P_3$. In such stable equilibrium configuration, the variable r, which is the distance between the bodies $P_1$ and $P_2$, oscillates along the interval $I_r$. Librations of g around the value $\pi$ correspond to librational motions about the 1 : 1 resonance just described. Circulations of g correspond to complete revolutions of the body $P_1$ with respect to the pericenter P of the orbit of the body $P_3$; in such case, varying the value of the angular momentum G from $G_{\min }$ to 1, the variation of the variable r varies from 0 (when $G = G_{\min }$ in the last trajectory) to the length of the interval $I_r$.

Fig. 3

Left: 3D visualizations of the isoenergetic trajectories in the three-dimensional space (g, G, r); right: zooms of the left figures. Upper: averaged Newtonian potential truncated up to the order 2; bottom: averaged Newtonian potential truncated up to the order 10

Fig. 4

Left: projections of the isoenergetic trajectories on the (G, r)-plane; right: projections of the isoenergetic trajectories on the (r, R)-plane. Upper: averaged Newtonian potential truncated up the order 2; bottom: averaged Newtonian potential truncated up the order 10

Fig. 5

Configuration such that the variable $g = \pi$, meaning that the pericenter P of the orbit of the body $P_3$ is on the line of the bodies $P_1$ and $P_2$, beyond $P_2$

3.3 The two-dimensional phase space and the Poincaré section

All the computation from now on have been done with the averaged Newtonian potential truncated at order 10.

Fixed the energy, we want to reduce the phase space from dimension 3 to dimension 2; we fix a bi-dimensional plane in the three-dimensional space (g, G, r) parallel to the (G, g)-plane such that the variable $r= r_\textrm{last}$, and we construct a Poincaré map as first return map on this fixed plane. Fixed $g = \pi$, we call $I_c = [G_\textrm{last}, G_c)$ the real interval such that the trajectories circulate and $I_l = (G_l,1)$ the real interval such that the trajectories librate, where $G_\textrm{last}< G_c< G_l <1$.

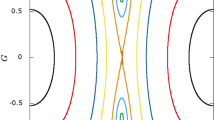
The Poincaré map shown in Fig. 6 has a very regular structure where we can recognize regular invariant tori circulating for $G \in I_c$ and closed curves librating for $G\in I_l$. In the left panel, we can see all the admissible range of the variable G, say $I_G$ and we see that, when $g = \pi$, for $G< G_\textrm{last}$ no orbit appears, as discussed in the previous section; in orange we see the section of the last trajectory and with the magenta point we can see the section of the elliptic trajectory; this point corresponds to the elliptic fixed point of the Poincaré map computed with a Newton algorithm. In the right panel, we see a zoom on the variable G where the region between circulating and librating trajectories is represented. Let us remark that, for a given value of G close to 1, the librations end at $g=0$ (that is also $g=2\pi$). As depicted in Fig. 7, this corresponds to a configuration where the pericenter P of the orbit of the body $P_3$ is on the line between the bodies $P_1$ and $P_2$ and it is an unstable configuration.

Fig. 6

Left: the Poincaré section of the trajectories with fixed energy, on a plane parallel to the (g, G)-plane and passing through the “last trajectory ”. Right: zoom of the left figure

Fig. 7

Configuration such that the variable $g = 0$, meaning that the pericenter P of the orbit of the body $P_3$ is between the bodies $P_1$ and $P_2$

We are particularly interested in the analysis of the region close to the separatrix which splits the phase space from the circulating to the librating zones. We wonder if there exists one or more orbits with initial conditions $(\pi , G, r)$, with $G \in (G_c,G_l)$ and for some $r \in I_r$ close to the separatrix and in the affirmative case we ask about the behavior of such orbits, namely if they are regular or if they show some kind of chaotic motion.

The Newton algorithm does not allow to find any hyperbolic fixed points as well as the analysis of the three-dimensional structure of the orbits does not provide elements to prove the existence of any suitable periodic orbit which could be associated with a hyperbolic fixed point. In the following section, we analyze the region close to the separatrix by means of an important tool of chaos indicator, namely the Fast Lyapunov Indicator.

4 Fast Lyapunov indicator analysis

Let us briefly recall some definitions and apply them to our problem. Let us consider the differential equation $\dot{x} = F(x)$ and let v(t) be the solution of the variational equation

$$\begin{aligned} \dot{v} = \Big [\frac{\partial F}{\partial x}(x(t)) \Big ]\cdot v. \end{aligned}$$

We define as Fast Lyapunov Indicator (FLI) of an initial condition $(x_0,v_0)$ at time T (see, for example Lega et al. 2016), the quantity

$$\begin{aligned} FLI(x_0,v_0;T) = \max _{0\le t\le T} \log \frac{\Vert v(t)\Vert }{\Vert v_0\Vert } , \end{aligned}$$

and we denote by N the logarithmic variation of the tangent vector as

$$\begin{aligned} N(x_0,v_0;t) = \log \frac{\Vert v(t)\Vert }{\Vert v_0\Vert } . \end{aligned}$$

(15)

In our case, $x = (R,G,r,g)$ and the differential equation is given by the Hamilton equations:

$$\begin{aligned} \left\{ \begin{aligned} \dot{R} = - \frac{\partial {\overline{H}}_C}{\partial r} \\ \dot{G} = - \frac{\partial {\overline{H}}_C}{\partial g} \\ \dot{r} = \frac{\partial {\overline{H}}_C}{\partial R} \\ \dot{g} = \frac{\partial {\overline{H}}_C}{\partial G} \end{aligned} \right. , \end{aligned}$$

(16)

where ${\overline{H}}_C$ is defined in (9).

Through the use of the chaos indicators, we intend to provide an accurate analysis of the transition zone between the circulating and the librating orbits, proving, numerically, the existence of weakly chaotic orbits in which circulating and librating phases coexist. Let us begin with this analysis. As in the previous section, we fix an energy value reducing the phase space from dimension 4 to 3; then, we fix a plane parallel to the (g, G)-plane, such that, $r = r_\textrm{last}$. We produce a two-dimensional grid of initial conditions (g, G) and we complete each two-dimensional initial condition $(g_0,G_0)$ to a four-dimensional initial condition $(R_0, G_0, r_0, g_0)$, where $r_0$ belongs to the plane and $R_0$ are such that all the initial conditions are isoenergetic; we propagate them under the Hamiltonian flow given by the map (16) computing the FLI of each orbit for a given time T. Then, we provide plots showing the FLI values with a color code according to their values and projected on the section (g, G) providing a stability chart. Stable orbits correspond to dark region, while chaotic orbits appear in yellow. Figure 8, upper panel, shows a grid of $1000 \times 1000$ equally spaced initial conditions (g, G) where $g \in [0, 2\pi )$; $G\in [G_\textrm{last},1)$ and $T = 10^4$ (the period, namely the time of first return on the Poincaré section of the elliptic three-dimensional phase space trajectory defined in Sect. 3.2, is about $t = 1000$, thus T is the time of about 10 periods). We can see that the admissible domain turns out to be very regular and stable; only in the highest part of the plot a thin curve appears with color coded less stable. The highest part is highlighted with a light-blue box. In the bottom panel, we enlarge this zone taking a grid of $1000 \times 1000$ initial conditions (g, G) where $g \in [0, 2\pi )$ and $G\in [0.994,1)$. In this case a sort of separatrix splitting the phase space into two regions is well visible. Comparing Fig. 6 with Fig. 8, it is evident that the separatrix splits the regions of circulating and librating orbits.

Fig. 8

Upper: FLI map on a grid of initial conditions on the (g, G)-plane over all the admissible domain. Bottom: a magnification of the upper figure

Let us continue by analyzing some particular orbits. As it is well-known, in stable orbits, FLIs have a logarithmic growth in time, while chaotic motions present FLIs with linear growth in time (see, for example, Froeschle et al. 2000). In Fig. 9, left panel, we consider orbits in all the admissible domain and represent them through their Poincaré section as computed before. We highlight some regular orbits, respectively, from bottom to top, in orange the last orbit, in red one rotational orbit, in blue a rotational orbit closer to the separatrix, in sky-blue a librational orbit close (but not very close) to the separatrix and, finally, with a magenta point the elliptic periodic orbit. In the same figure, in the right panel, we report the variation in time, for $T=10^4$ of the FLIs of the five orbits using the same color to represent the same orbit. What we can see is that all the selected orbits have a small growth from zero to a small relative value compared with the values of the legend in Fig. 8 and then that values remain constant for all the considered time T. The elliptic orbit (magenta) turns out to be the more stable orbit and the two orbits approaching to the separatrix have the FLI values little bit higher. Next, we do the same analysis to the orbits closer to the separatrix. In Fig. 10, in the left panel, we plot the Poincaré section of some orbits: in blue a rotational orbit and in light-green a librational one, both of them with very small FLI values (about 0.13) shown with the same color in the right panel. Another librational curve plotted in dark-green closer to the separatrix has a little bit higher FLI value (about 0.4). Finally, we plot three orbits (one in dark-red, one in pink and one in dark-blue) appearing overlapped and very close to the separatrix in the left panel of Fig. 10. Let us show in the right panel the evolution in time of the FLIs of these three orbits; the dark-red orbit corresponding to a rotational motion and the pink corresponding to a librational one have a greater growth with respect to the previous curves and both of them reach the same value (about 2) in a time equal to T. The dark-blue curve in the left panel is completely hidden by the previous two curves when G is close to 1, and in the right panel we can see the growth of its FLI in time is too much more greater than all the others. This orbit and the variation of its FLI in time has been studied extensively in Sect. 4.1.

Fig. 9

On the left, we highlight with different colors some orbits on the Poincaré section. On the right, we represent the evolution of the FLI versus time of initial conditions associated with the orbits represented in the left panel with the same colors, respectively

Fig. 10

As in Fig. 9, on the left, we highlight with different colors some orbits on a smaller region of the Poincaré section. On the right, we represent the evolution of the FLI versus time of initial conditions associated with the orbits represented in the left panel with the same colors, respectively

4.1 Analysis of orbits and respective FLI close to the separatrix

Let us concentrate the analysis on the three orbits plotted in dark-red, pink and dark-blue depicted in Fig. 10. We already told about the behavior of the dark-red and pink, being, respectively, rotational and librational orbits. The peculiarity of the dark-blue orbit is that it changes its dynamics from librational to rotational and vice versa. Let us show in Fig. 11, the three-dimensional projection on the space (g, G, r) of the three isoenergetic orbits we are talking about. In the upper left panel, we plot the dark-red rotational orbit: the variable g circulates from 0 to $2 \pi$; the variable G oscillates very close to 1, in particular its value is almost 1 when $g\in (0, \pi /2) \vee (3/2 \, \pi , 2\pi )$ and different from 1 when $g \in (\pi /2,3/2 \, \pi ,)$; the variable r oscillates in the admissible range $I_r$ (even if it is not well visible in this plot). In the upper right panel, the pink librational orbit is depicted: the variable g oscillates around $\pi$, in particular librates from $\pi /2$ to $3/2 \, \pi$; the variable G oscillates very close to 1, assuming the value almost 1 for a part of its period and less close values to 1 in the remaining part of the period; the variable r, as before, oscillates in the admissible range $I_r$. In the bottom left panel, we plot in dark-blue an orbit where rotational and librational motions coexist. In particular the variable g changes its oscillation in time passing from a rotational motion to a librational one, and vice versa. In the bottom right panel, the previous three orbits are plotted together to see the relation to each other. To better see how the three orbits behave in the three-dimensional space (g, G, r), we plot, in Fig. 12, a two-dimensional (upper) and a three-dimensional (bottom) projections on the (g, G)-plane and (g, G, r)-space, respectively: the blue orbit lies in a two-dimensional manifold constrained between the red and the pink ones. Orbits close to the blue one have strong sensitivity about initial conditions and this is an indication of the chaotic behavior of such kind of orbits. But, being a two degrees of freedom system, the chaos is bounded by the manifolds on which the rotational and librational orbits lie.

Fig. 11

Three-dimensional visualization of orbits close to the separatrix. Upper left: an orbit on rotational dynamics is depicted in dark-red; upper right: an orbit on a librational regime is depicted in pink; bottom left: an orbit changing from librational to rotational dynamics is depicted in dark-blue; bottom right: the previous three orbits are represented together

Fig. 12

Upper and bottom, respectively, a zoom of a two-dimensional (on the (g, G)-plane) and a three-dimensional (on the (g, G, r)-space) projection of the three orbits represented in Fig.  11

4.2 Analysis of the orbits changing their dynamics

Let us continue the analysis of the orbit with double behavior changing from rotational to librational dynamics and vice versa. We propagate this orbit (the dark-blue in previous figures) for a much more longer time, say $T =3 \cdot 10^6$. As we can see in the left panel of Fig. 13, the three-dimensional projection shows very well the double nature of this orbit. The variable g changes in time from circulating from 0 to $2 \pi$ to librating around $\pi$ and it is well represented in the left panel of Fig. 15, where g versus time is plotted. In the left panel of Fig. 13, we can see that, when the variable G is close to 1, the orbit is splitted into rotational and librational regimes; in particular, there exists a value of the variable r, say $r_m$, such that when G is close to 1, the orbit is in a rotational regime for each $r>r_m$ and in the librational regime for each $r<r_m$ with $r \in I_r$.

In the right panel of Fig. 13, we plot the variation of FLI of such orbit versus time. If the trend appeared to be with linear growth for a shorter time as shown in Fig. 10 (blue line in the right panel), for a longer time, the growth stops and the behavior of the FLI is completely constant. This seems to be in contrast with the chaotic behavior of this orbit, but, as told before, the orbit, although chaotic, cannot move in space because its manifold is constrained by the other manifolds. To analyze this phenomenon, we have done a study of the logarithmic variation of the tangent vector defined in Eq. (15).

Fig. 13

Orbit changing dynamics. On the left panel, we show a three-dimensional visualization of the orbit on the (g, G, r)-space. On the right panel, we show the evolution of the FLI versus time of such orbit

In Fig. 14, we plot the variation of N(t) of the considered orbit. In the upper left panel, where we plot the function N versus time, what is very evident is a “sort of”  periodic behavior over time of this function. The function N has peaks which highlight the chaotic behavior of the orbit in given moments, and the remaining time, has low values typical of regular orbits. We are interested in understanding when these peaks come out. Thus, we plot, in Fig. 14, upper right, bottom left and bottom right the variation of the function N versus the variable g, G, r, respectively. With respect to the variable g, the higher values are taken for $g =0, \pi , 2 \pi$; with respect to the variable G, we have just one peak, in fact all the higher values are concentrated in the same value of the variable G very close to 1; with respect to the r variable, we also have one peak and all the higher values are concentrated in a value of r, say $r= r_m$. Comparing these plots with the orbit plotted in Fig. 13, we can see how the higher values of the function N, are concentrated in the zone where the orbit changes its behavior from rotational to librational and vice versa. At the same time, the values of the function N are very low in the phases of rotational and librational motion. This shows the extremely regular behavior of the orbit when it is in the rotational and librational regimes and a chaotic behavior when the transitions from one regime to another occur.

Fig. 14

In this figure, the evolution of the logarithm of the variation of the tangent vector N defined by Eq. (15) is represented. Upper left: evolution of N versus time; upper right: evolution of N versus the variable g; bottom left: evolution of N versus the variable G; bottom right: evolution of N versus the variable r

In Fig. 15, we highlighted this aspect. In the left panel, the variation of the variable g versus time is plotted for a time $t= 3 \cdot 10^6$ and we see the change from the circulation from 0 to $2 \pi$ to the libration around $\pi$ (and vice versa) of such variable. In the right panel, we overlap two different quantities: in pink, we plot the variation of variable g versus time, and in dark-green, we plot the variation on the function N versus time, both for a longer time $t = 10^7$. The plot shows as the green peaks correspond to the transitions of the variable g from a regime to the other.

Fig. 15

Left: the variation of the variable g versus time is represented. Right: an overlap of the variation of the variable g in pink and of the quantity N in green versus time is represented

We want to show that this “sort of”  periodicity of transitions strictly depends on the initial conditions. We say a “sort of”  periodicity because the number of oscillations between one regime and the other is not constant. Let us recall the FLI map represented in the bottom panel of Fig. 8, and as it is shown in the left panel of Fig. 16, we fix a vertical segment in the (g, G)-plane depicted in sky-blue, such that $g = \pi$ and $G \in [0.99434,0.9944]$ and we compute the FLI for $10^6$ initial conditions on such segment. In the right panel of Fig. 16, we plot the FLI at time $T = 10^4$ versus the variable G, and we get a zone (although small) of initial conditions where the FLI grow more than the initial conditions in the rest of the domain. There are different peaks and, in that zone, the orbits present the double rotational and librational dynamics.

Fig. 16

Left: FLI map of a grid of initial conditions containing the separatrix. A small vertical segment intersecting the separatrix in $g =\pi$ is represented in sky-blue. Right: Value of FLI of initial conditions belonging to the sky-blue segment on the left panel

We compare two different orbits associated with different initial conditions; we show, for example, the two initial conditions corresponding to the first two peaks in the right panel of Fig. 16. We call the two orbits A and B with, respectively, the initial conditions:

$$\begin{aligned} \left\{ \begin{array}{l} R_A = -0.06593399672122671 \\ G_A = 0.9943612429022789 \\ r_A = 134.4581702919 \\ g_A = \pi \end{array} \right. \quad , \qquad \left\{ \begin{array}{l} R_B = -0.06593407847147810 \\ G_B = 0.9943632053971290 \\ r_B = 134.4581702919 \\ g_B = \pi \end{array} \right. . \end{aligned}$$

The distance in the four-dimensional space (R, G, r, g) of conditions A and B is about $1.9642 \cdot 10^{-6}$. We propagate the two initial conditions to get orbits A and B and, in Fig. 17, we plot the evolution of the variable g versus time of the two orbits for a short time. In the upper panels, in blue, the orbit A is represented and in the bottom panels, in red, the orbit B is depicted. In the left and right panels we plot two different time spans, from 0 to 15,000 and from 400,000 to 415,000, respectively. In the highlighted boxes, we show that the number of circulations from 0 to $2 \pi$ and the librations around $\pi$ changes from orbit to orbit; namely, the period between transitions is not constant for different initial conditions.

Fig. 17

The evolution of the variable g versus time is represented. Upper: orbit A and bottom orbit B

4.3 Changing orbits analyzed according to the variation of the variable r

The changing orbits analyzed in the previous section have initial conditions in the chaotic zone such that the value of the variable r is at about the middle of the admissible interval $I_r$, which corresponds to the value $r = r_\textrm{last}$. We want to analyze how the changing orbits behave when the value of the variable r changes. We have therefore produced new FLI maps in a vertical plane, i.e. in the (G, r)-plane for a given constant value of g. At the beginning, we plot a grid of $1000 \times 2000$ initial conditions (G, r) in the plane $g=\pi$ for $(G,r) \in I_G \times I_r$. We show the FLI map in Fig. 18. This plot is interesting for a global view of the admissible domain, where we could see a very regular structure unless a vertical line close to $G\simeq 0.994$ and the bottom and the upper borders.

Then, we have made a study of the filtered FLI (see Guzzo and Lega 2014), i.e. we considered again a grid on the (g, G)-plane and we have computed the FLI of each initial datum only when its orbit passed through determined regions of the phase space. In this way, we identified neighborhoods of the phase space where the FLI are higher than in the other areas. We identified, for example, the region $(g,G) \in (1.61,1.63)\times (0.99998,1)$ and in Fig. 19, we show the FLI map computed with a grid of $1500 \times 1000$ initial conditions $(g_0,G_0) \in (1.56,1.67)\times (0.99995,1)$.

At this point, we compute the FLI on a grid of $1000 \times 2000$ initial conditions $(G_0,r_0)$ in the domain $[0.9999,1) \times I_r$, with $g = 1.62$ and we plot in Fig. 20 the FLI map. We can see a vertical strip of initial conditions close to 1 where the FLI assume the higher values and a chaotic structure appears. We want to show the existence of changing chaotic orbits in all this vertical strip and how they change according to the initial value of the variable r.

Fig. 18

FLI map on a grid of initial conditions on the (G, r)-plane for $g=\pi$

Fig. 19

Magnification of the FLI map of Fig. 8, where a grid of initial conditions on the (g, G)-plane are considered

Fig. 20

FLI map on a grid of initial conditions in a domain on the (G, r)-plane for $g=1.62$

4.3.1 Inferior orbit

Let us choose an initial condition in the vertical chaotic strip of Fig. 20 such that the variable r has the minimum admissible value in $I_r$. Let us call the associated orbit “inferior orbit”. The initial condition is given as follows:

$$\begin{aligned} \left\{ \begin{array}{l} R_\textrm{inf} = -0.001636435302611866 \\ G_\textrm{inf} = 0.9999860000014306 \\ r_\textrm{inf} = 122.4300000071526 \\ g_\textrm{inf} = 1.62 \simeq 0.515662\, \pi \end{array} \right. . \end{aligned}$$

In the left panel of Fig. 21, we plot the three-dimensional projection of the orbit; as we can see the double dynamics is still present, although it appears different from the orbit represented in Fig. 13. In this case, during the phase of librational dynamics, the variation in r when the variable G is close to 1 appears very very small, while in the rotational regime the variation in r appears to span in all the range $I_r$. In the right panel of Fig. 21, we plot the variation in time of the FLI associated with this orbit and, as before, we see that, for a long time span, the growth stops and the graph of FLI versus time is constant. Thus, we analyze again the variation of the function N(t) defined in Eq. (15).

Fig. 21

Inferior orbit. On the left panel, we show a three-dimensional visualization of the orbit. On the right panel, we show the evolution of the FLI on a long time scale

In the upper left panel of Fig. 22, we plot the function N versus time. Also in this case, we see peaks with a sort of periodicity. The peaks correspond to the instants when the chaotic behavior of the orbit comes out, namely when it changes its dynamics from rotational to librational or vice versa. In the upper right, bottom left and bottom right, we plot the function N versus the variables g, G, r, respectively. In particular, we remark that the highest values of the function N are concentrated in only one peak in $G\simeq 1$ when the function is plotted versus G and in $r = r_\textrm{inf}$ when the function is plotted versus r. In the left panel of Fig. 23, we plot the evolution of the variable g of the inferior orbit versus time. The variable changes its regime from circulating from 0 to $2 \, \pi$ to librating around $\pi$. The phase of libration appears with a sort of periodicity for a very short time and it is highlighted in Fig. 24. It is completely in agreement with the three-dimensional visualization of the orbit represented in the left panel of Fig. 21. Moreover, in the right panel of Fig. 23, we overlap the variation in time of the variable g depicted in pink with the variation in time on the function N colored in dark-green. We can appreciate the superimposition of the changes of the variable g with the peaks of the function N. We want to better show this overlapping: in Fig. 24, we represent a zoom of the right panel of Fig. 23. We can see that each green peak of Fig. 23 corresponds, if enlarged, to two different peaks and they coincide with the transition from circulating to librating and vice versa of the variable g.

Fig. 22

In this figure, the evolution of the logarithm of the variation of the tangent vector N defined by Eq. (15) is represented. Upper left: evolution of N versus time; upper right: evolution of N versus the variable g; bottom left: evolution of N versus the variable G; bottom right: evolution of N versus the variable r

Fig. 23

Left: the variation of the variable g versus time is represented. Right: an overlap of the variation of the variable g (in pink) and of the quantity N (in green) versus time is represented

Fig. 24

Magnification of the right panel of Fig. 23

4.3.2 Superior orbit

The same analysis has been done for orbits with initial conditions in the chaotic zone such that $r = max\, I_r = r_\textrm{sup}$. We choose and show the orbit with initial condition:

$$\begin{aligned} \left\{ \begin{array}{l} R_\textrm{sup} = -0.001769070989625912 \\ G_\textrm{sup} = 0.9999869999885559 \\ r_\textrm{sup} = 146.3999998569489 \\ g_\textrm{sup} = 1.62 \simeq 0.515662\, \pi \end{array} \right. . \end{aligned}$$

Let us compare the left panels of Figs. 21 and 25. In the superior orbit, we can observe that, in the phase of rotational dynamics, the variation of variable r when the variable G is close to 1 is very very small, while in the librational regime the variation of r spans in the whole range $I_r$. The right panel of Fig. 25 shows the growth of FLI of the superior orbit. It does not look to be constant, but if we increase the propagation time it becomes constant. As for the previous orbits, we analyze the variation of the function N(t).

Fig. 25

Superior orbit. On the left panel, we show a three-dimensional visualization of the orbit. On the right panel, we show the evolution of the FLI on a long time scale

Figure 26 shows, again, peaks where the chaotic nature of this orbit comes out. In particular, from the bottom panels we see that high values of N(t) are concentrated, in this case, when G is close to 1 and $r= r_\textrm{sup}$ in agreement with the three-dimensional visualization of the orbit.

In the left panel of Fig. 27, we plot the variation of the variable g versus time and the double regime of circulating and librating motions is visible. Moreover, in the right panel of Fig. 27, we overlap, again, the variation in time of the variable g depicted in pink with the variation in time on the function N colored in dark-green. Also in this case, we can appreciate the superimposition of the transitions of dynamics of the variable g with the peaks of the function N. To better represent this overlapping, in Fig. 28, we show a magnification of the right panel of Fig. 27. We can see that each green peak of Fig. 27 corresponds, if enlarged, to two different peaks and they coincide with the transition of the variable g from librating to circulating and vice versa.

Fig. 26

In this figure, the evolution of the logarithm of the variation of the tangent vector N defined by Eq. (15) is represented. Upper left: evolution of N versus time; upper right: evolution of N versus the variable g; bottom left: evolution of N versus the variable G; bottom right: evolution of N versus the variable r

Fig. 27

Left: the variation of the variable g versus time is represented. Right: an overlap of the variation of the variable g (in pink) and of the quantity N (in green) versus time is represented

Fig. 28

Magnification of the right panel of Fig. 27

5 Conclusions and perspectives

We start from a standard formulation of the Hamiltonian of the full (meaning non-restricted) three-body problem (see Eq. (1)) and, introducing suitable transformations and new mass parameters, we rewrite the Hamiltonian, first, in the form of Eq. (4) for the non-averaged system, then, as Eq. (9) for the averaged case. In this context, we provide the existence of two wide regions of initial condition phase space where the motions are regular and stable and they can be librational or rotational. Close to the separatrix of these two regions, we find a zone of initial conditions where rotational and librational motions coexist for the same initial condition in a chaotic way.

These results could be related to the notion of “stickiness”, which are studied in several dynamical systems in different papers as, for example (Contopoulos et al. 1997; Dvorak et al. 1998). Sticky orbits can be found in the case of restricted three-body problem, for example in Tsiganis et al. (2000), where the authors studied the trojan asteroid Thersites which is in a stable $L_4$ librating position; they show, through many simulations, a high probability of the asteroid to “escape”  from its equilibrium, to unstable orbits or to jump from $L_4$ to $L_5$ and it is called, for this reason, a “jumping”  trojan. The same was proved in Sidorenko (2018) where the author shows also one more asteroid jumping from the libration about $L_4$ to libration about $L_5$ (thus, the author provides two examples, one for Jupiter and one for the Earth). Also in the restricted four-body problem (see for example Soulis et al. 2008), the authors prove the existence of a structure of ordered motion surrounded by sticky and chaotic orbits as well as orbits which rapidly escape to infinity. Two important issues differentiate the results of the current article with the notion of stickiness: first, the last cited articles deal with the restricted problem while the current paper concerns with the full problem; second, usually, stickiness time corresponds to the time to escape to infinity, while in the current paper the chaotic region is constrained by stable orbits so that the chaotic motion can not escape and can not diffuse. Nevertheless, it would be worth investigating the concept of stickiness in the full problem and looking for the existence of escaping to infinity orbits in the non-averaged case or in the spatial case.

However, the results obtained in this paper could be very interesting also in a wider context. The choice of our configuration is due in order to have the right weight for each term which composes the Hamiltonian and they depend on the parameters $\mu ,\kappa ,r,C$. Thus, one of the future goals is to determine, in a constructive way, the range of these 4 parameters where:

• the system is stable;

• the chaotic behavior appears;

• application to real celestial problems can be possible (for example, real asteroid systems, natural and artificial satellite motions, exoplanetary problems, hierarchical triple star/black hole systems, the Lidov–Kozai mechanism appearing in the spatial case);

• comparison between averaged and non-averaged Hamiltonian is possible.

The last one is already a work in progress, in fact, at the beginning of Sect. 3, we propose an initial configuration (Eq. (13)) such that both Assumptions (7) and (12) are fulfilled. Thus, we wonder if in the non-averaged system we have the onset of chaos and, being a three degrees of freedom problem we ask if and how the chaos could diffuse in the phase space.