Bandlimited implicit Runge–Kutta integration for Astrodynamics

Abstract

We describe a new method for numerical integration, dubbed bandlimited collocation implicit Runge–Kutta (BLC-IRK), and compare its efficiency in propagating orbits to existing techniques commonly used in Astrodynamics. The BLC-IRK scheme uses generalized Gaussian quadratures for bandlimited functions. This new method allows us to use significantly fewer force function evaluations than explicit Runge–Kutta schemes. In particular, we use a low-fidelity force model for most of the iterations, thus minimizing the number of high-fidelity force model evaluations. We also investigate the dense output capability of the new scheme, quantifying its accuracy for Earth orbits. We demonstrate that this numerical integration technique is faster than explicit methods of Dormand and Prince 5(4) and 8(7), Runge–Kutta–Fehlberg 7(8), and approaches the efficiency of the 8th-order Gauss–Jackson multistep method. We anticipate a significant acceleration of the scheme in a multiprocessor environment.

1 Introduction

We present a new numerical integration technique, developed by Beylkin and Sandberg at the University of Colorado (Beylkin and Sandberg 2014; Beylkin and Monzón 2002), and compare its performance in propagating orbits to existing techniques commonly used in Astrodynamics. The new scheme, dubbed the bandlimited collocation implicit Runge–Kutta (BLC-IRK) method, is an Implicit Runge–Kutta (IRK) collocation scheme which uses generalized Gaussian quadratures for bandlimited exponentials rather than the classical quadratures for orthogonal polynomials. We note that IRK methods have been constructed for a variety of polynomial based quadratures, such as Gauss–Legendre, Gauss–Lobatto, and Chebyshev (e.g., see discussions in Jones and Anderson 2012; Iserles 2009; Hairer et al. 2002). Among polynomial based IRK collocation schemes, only the scheme based on Gauss–Legendre quadratures achieves the highest order of approximation, is $A$-stable, and symplectic. The new BLC-IRK scheme is also $A$-stable and symplectic, achieves any user-selected accuracy and, in addition, allows one to use a large number of nodes within each time interval without the penalty of excessive node concentration near the endpoints of the interval. The properties of BLC-IRK scheme significantly affect the approach to using it in Astrodynamics.

Motivated by the need to improve the computational performance of existing schemes as the number of objects to be tracked orbiting Earth is expected to increase significantly in the near future, we compare the performance of the new scheme with the traditional methods used in Astrodynamics. The growing cloud of spent rocket bodies, defunct satellites, and other debris in Earth orbit is a serious threat to our use of space, particularly in densely populated low-Earth orbits and the orbits within the geosynchronous belt. In 2005, NORAD tracked about 10,000 objects and close approaches were already a common occurrence, taking place hundreds of times each week (Kelso and Alfano 2005). Currently, the public space catalog consists of between 15,000 objects¹ and 17,000 objects² in Earth orbit that are at least 10 centimeters in diameter. Although conjunction assessment for the entire space catalog is manageable at this time, it will become difficult in the near future. In part, the expected difficulty is due to the planned improvements in sensing and computation capabilities. These new capabilities are anticipated to increase the space catalog to hundreds of thousands, making the current method for performing orbit determination and conjunction assessment challenging. Since orbit determination and propagation take up a majority of the computation time, faster numerical integration techniques are considered necessary. Furthermore, fast integrators may be used for tracking and propagation of asteroids and can also aid Monte Carlo analyses used in research and mission design (Parcher and Whiffen 2011).

Recently, IRK methods have received a lot of attention for use in orbit and uncertainty propagation, mainly due to the fact that these methods can be parallelized and have improved stability properties when compared to the traditional methods (Barrio et al. 1999; Jones and Anderson 2012; Jones 2012; Bradley et al. 2012; Bai 2010; Bai and Junkins 2011a; Aristoff and Poore 2012; Aristoff et al. 2012, 2014; Herman et al. 2013). Specifically, Gauss–Legendre implicit Runge–Kutta (GL-IRK) is symplectic, $A$-stable, $B$-stable, and has been shown to outperform explicit Runge–Kutta (ERK) methods for both orbit propagation and uncertainty propagation (Jones 2012; Aristoff and Poore 2012; Aristoff et al. 2012, 2014). Similarly, BLC-IRK is both symplectic and $A$-stable (see Beylkin and Sandberg 2014 for details). Collocation methods have also been used for boundary value problems in trajectory design and optimization (Herman and Conway 1996, 1998; Betts and Erb 2003; Ozimek et al. 2009, 2010; Grebow et al. 2010, 2011; Bai and Junkins 2011b, 2012). Another method for parallelized evaluation of the force model, dubbed Modified Chebyshev–Picard Iteration (MCPI), uses the Gauss–Lobatto–Chebyshev nodes in an algorithm similar to collocation (Bai 2010; Bai and Junkins 2011a).

While a Runge–Kutta scheme with the Gauss–Legendre nodes provides an excellent discretization of a system of ordinary differential equations (ODEs), using a large number of nodes per time interval is not advisable. The reason is that the nodes of the Gauss–Legendre quadratures (as well as any other polynomial-based Gaussian quadratures) accumulate rapidly towards the end points of the interval. For such quadratures, the ratio of the distances between the nodes near the end of the interval and those in the middle, is asymptotically inversely proportionate to their number. This behavior effectively puts an upper limit on useful step size and the number of nodes, since computations become increasingly wasted near time interval boundaries as the number of nodes increases. On the other hand, the node accumulation of the generalized Gaussian quadratures for bandlimited functions is moderate and the ratio of distances is asymptotically a constant that depends only on the desired accuracy (further discussion may be found in Beylkin and Sandberg 2014). The consequence of this fact is that the solution may be sought on a large time interval using a large number of nodes. Since BLC-IRK is parallelizable at the node level, using more nodes can improve the speed of the implementation if multiple processors are used. Additionally, the use of generalized Gaussian nodes for bandlimited functions minimizes the total number of nodes required to achieve a given accuracy (Beylkin and Sandberg 2014; Beylkin and Monzón 2002). The implementation of BLC-IRK for this paper takes advantage of speed improvements during force model evaluation. We reduce the computational cost associated with iteration at each node by employing a low-fidelity force model for a majority of the required force evaluations. Forms of this technique used in Jones (2012) and Aristoff et al. (2014) have shown to vastly improve performance when applied to a GL-IRK scheme (see also Beylkin and Sandberg 2014).

Unlike the classical Gaussian quadratures for polynomials which integrate exactly a subspace of polynomials up to a fixed degree, the Gaussian type quadratures for exponentials in Beylkin and Monzón (2002) use a finite set of nodes to integrate an infinite set of functions, namely, $\left\{ e^{ibx}\right\} _{|b|\le c}$ on the interval $|x|\le 1$. While there is no way to accomplish this exactly, these quadratures are constructed so that all exponentials with $|b|\le c$ are integrated with accuracy of at least $\epsilon$, where $\epsilon$ is arbitrarily small but finite. We note that if the accuracy $\epsilon$ is chosen to be around $10^{-16}$, such quadratures are effectively exact within the double precision of machine arithmetic.

The class of functions well approximated by the bandlimited exponentials $\left\{ e^{ibx}\right\} _{|b|\le c}$ includes functions with the support of the Fourier transform restricted to the interval $[-c,c]$. A basis for such bandlimited functions was constructed in a series of seminal papers (Slepian and Pollak 1961; Landau and Pollak 1961, 1962; Slepian 1964, 1965, 1978, 1983) the goal of which was to optimize (simultaneously) the localization of functions in the space and Fourier domains. These papers showed that the time-limiting and band-limiting integral operator commutes with the differential operator whose eigenfunctions are the so-called Prolate Spheroidal Wave Functions (PSWFs) of classical mathematical physics, i.e., the integral and differential operators share the eigenfunctions. In spite of the importance of bandlimited functions, efficient quadratures for integrating and interpolating them were constructed only recently (Beylkin and Monzón 2002; Xiao et al. 2001). These quadratures are essential for using bandlimited functions in numerical analysis and, in particular, in the BLC-IRK method.

The intent of this paper is to provide a mathematical overview of the new BLC-IRK integration scheme and compare its efficiency in orbit propagation with other more commonly used techniques. We start by outlining the framework of implicit Runge–Kutta collocation based methods and describe the details of the new scheme. We then consider the advantages of the new framework, the required input parameters, and then compare them to other integration techniques. Three orbit types are used to compare results of four numerical integration techniques (frequently used in the Astrodynamics community): Runge–Kutta–Fehlberg 7(8), Dormand–Prince 8(7), Dormand–Prince 5(4), and an 8th-order Gauss–Jackson. A low-Earth orbit, Molniya orbit, and geostationary orbit are propagated for 3 revolutions using a $70\times 70$ gravity field and lunisolar perturbations. The dense output capability of BLC-IRK is then detailed and we conclude with a summary of the results and recommended future work.

2 Mathematical overview

This section details the mathematical techniques of the new BLC-IRK method as well as the basics of implicit Runge–Kutta and collocation methods to put the new scheme into context. We consider the initial value problem (IVP) for an ODE

$$\begin{aligned} \mathbf{y}' = {\varvec{f}}(t,\mathbf{y}), \; \; \mathbf{y}(0) = \mathbf{y}_0, \; \; t \ge 0. \end{aligned}$$

(1)

The solution $\mathbf{y}$ at some time $h$ can then be written as a Picard integral

$$\begin{aligned} \mathbf{y}(h) = \mathbf{y}_0 + \int \limits _0^h {\varvec{f}}(s , \mathbf{y}(s) ) \mathrm{d}s. \end{aligned}$$

(2)

Runge–Kutta methods are based on using quadratures for discretization of the integral in Eq. 2.

2.1 Runge–Kutta methods

While ERK are commonly used in Astrodynamics problems, the use of IRK methods is still infrequent. Runge–Kutta methods use $M$ stages (nodes) within a time interval to solve Eq. 2 above. The basic form of Runge–Kutta methods uses quadratures to integrate from time $t=0$ to time $t=h$ as

$$\begin{aligned} \mathbf{y}(h) = \mathbf{y}_0 + h \sum _{j=1}^M w_j {\varvec{f}}(h \tau _j, \mathbf{y}(h \tau _j)), \; \; \; \tau \in [0,1] \end{aligned}$$

(3)

with weights $\{w_j\}_{j=1}^M$ and nodes $\{\tau _j\}_{j=1}^M$. Using ${\varvec{\xi }}_i$ to denote values of the solution at the nodes $\mathbf{y}(h \tau _j)$, we have

$$\begin{aligned} {\varvec{\xi }}_i = \mathbf{y}_0 + h \sum _{j=1}^M S_{ij} {\varvec{f}}(h \tau _j, {\varvec{\xi }}_j), \end{aligned}$$

(4)

where $S$ is the integration matrix (Iserles 2009), and find $\mathbf{y}(h)$ as

$$\begin{aligned} \mathbf{y}(h) = \mathbf{y}_0 + h \sum _{j=1}^M w_j {\varvec{f}}(h \tau _j,{\varvec{\xi }}_j). \end{aligned}$$

(5)

The quadrature nodes $\{\tau _j\}_{j=1}^M$, weights $\{w_j\}_{j=1}^M$, and entries of the integration matrix $S_{ij}$ are typically displayed in a Butcher tableau,

$$\begin{aligned} \begin{array}{c | c} {\varvec{\tau }} &{} S \\ \hline &{} w^{T} \\ \end{array} \end{aligned}$$

(6)

which expands to

$$\begin{aligned} \begin{array}{c | c c c} \tau _1 &{} S_{1,1} &{} \cdots &{} S_{1,M} \\ \tau _2 &{} S_{2,1} &{} \cdots &{} S_{2,M} \\ \vdots &{} \vdots &{} &{} \vdots \\ \tau _M &{} S_{M,1} &{} \cdots &{} S_{M,M} \\ \hline &{} w_1 &{} \cdots &{} w_M \\ \end{array} \end{aligned}$$

(7)

We use $\tau$, $w$, and $S$, for representing nodes, weights, and the integration matrix and note that the variables $c$, $b$, and $A$ have also been used for this purpose in the literature.

In ERK methods, the integration matrix is lower triangular, $S_{ij} = 0$ for $j \ge i$, and, consequently, such methods are explicit. In IRK methods, the set of nonlinear equations in Eq. 4 has to be solved on each time interval. Several techniques are available, such as fixed-point or Newton iterations (Iserles 2009; Atkinson et al. 2009). The advantages, disadvantages, and implementation of each method are discussed in Jones and Anderson (2012), Hairer et al. (1993, 2002), and Hairer and Wanner (1996).

Historically, IRK methods have been used sparingly in Astrodynamics due to the additional computations required to iteratively solve for the values of the solution at the nodes $\mathbf{y}(h \tau _j)$ and the fact that ERK methods are simple to code, well-documented, and include several adaptive step methods. Advances in computational power and changes in computer architecture, however, have evened out the computational cost of explicit and implicit schemes. IRK methods lend themselves to multi-core computers and graphics processing units (GPUs) since, within a single iteration, the force model evaluation $\varvec{f}$ may be performed simultaneously at all nodes. We refer to Jones and Anderson (2012) for a summary of methods and references on this topic specific to Astrodynamics.

We note that in the traditional use of Runge–Kutta methods the time interval (or step size), $h$, is small, typically between 15 and 60 seconds for orbit propagation. In the new method, the time interval does not have to be small since the number of nodes, $M$, may be selected to be large.

2.2 Collocation IRK

Among IRK methods of particular interest are those based on collocation. Consider the polynomial, ${\varvec{u}}(t)$, matching the solution at the nodes,

$$\begin{aligned} \begin{array}{l} {\varvec{u}}(0) = \mathbf{y}_0 \\ {\varvec{\dot{u}}}(h \tau _j) = {\varvec{f}}(h \tau _j, u(h \tau _j)) \\ \end{array} \end{aligned}$$

(8)

where $\mathbf{y}(h\tau _j) = {\varvec{u}}(h\tau _j)$, $j=1,\dots ,M$. As demonstrated in e.g., Iserles (2009), this formulation leads to an IRK method. Introducing Lagrange interpolating polynomials $\{L_j(\tau )\}$ with nodes $\{\tau _j\}_{j=1}^M$, we approximate ${\varvec{f}}$ to a given accuracy $\epsilon$ on $[0,h]$,

$$\begin{aligned} \Vert {\varvec{f}}(h \tau , \mathbf{y}(h \tau )) - \sum _{j=1}^M {\varvec{f}}({h \tau }_j , \mathbf{y}({h \tau }_j )) L_j (\tau ) \Vert \le \epsilon , \; \; \; \tau \in [0,1]. \end{aligned}$$

(9)

Equation 2 is then rewritten using Eq. 9 as

$$\begin{aligned} \mathbf{y}({h \tau }_i ) = \mathbf{y}_0 + h \sum _{j=1}^M {\varvec{f}}({h \tau }_j , \mathbf{y}({h \tau }_j )) \int \limits _0^{{\tau }_i} L_j (s ) \text {d}s, \; \; \; i = 1, \ldots , M \end{aligned}$$

(10)

or

$$\begin{aligned} \mathbf{y}({h \tau }_i ) = \mathbf{y}_0 + h \sum _{j=1}^M S_{ij} {\varvec{f}}({h \tau }_j , \mathbf{y}({h \tau }_j )) \end{aligned}$$

(11)

where $S_{ij} = \int _0^{\tau _i} L_j(s)\text {d}s$ are the entries of the integration matrix. We use $M$ quadrature nodes such that

$$\begin{aligned} \mathbf{y}(h) = \mathbf{y}_0 + h \sum _{j=1}^M w_j {\varvec{f}}({h \tau }_j , \mathbf{y}({h \tau }_j )) \end{aligned}$$

(12)

yields the solution at time $t=h$ and, thus, Eqs. 11 and 12 form a collocation IRK scheme.

The most commonly used polynomial-based quadratures are Gauss–Legendre (Butcher 1964) and Gauss–Lobatto, although the use of Chebyshev quadratures (Barrio et al. 1999; Bai 2010; Bai and Junkins 2011a) has captured some attention in Astrodynamics recently. We note that only the Gauss–Legendre quadratures yield symplectic, $A$-stable IRK schemes with the maximum order $2M$, where $M$ is the number of stages (nodes).

2.3 New scheme: BLC-IRK

Polynomial-based quadrature has a long history of use due to tradition, ease of use, and node/order optimality (Jones and Anderson 2012; Iserles 2009). Polynomial-based quadratures are constructed so that

$$\begin{aligned} \int \limits _{-1}^1 f(x)W(x) \mathrm{d}x = \sum _{j=1}^M w_j f(\tau _j), \end{aligned}$$

(13)

for all polynomials $f$ less than some fixed degree. Here $W(x)\ge 0$ is the weight, $\tau _j$ are quadrature nodes, and $w_j$ are quadrature weights. Given a fixed number of nodes, $M$, the classical Gaussian quadratures maximize the degree of polynomials for which Eq. 13 is exact. We note that Gauss–Legendre quadratures correspond to the weight $W(x) = 1$ whereas Chebyshev quadratures correspond to the weight $W(x) = 1/\sqrt{1-x^2}$.

The new scheme described in this paper is a collocation IRK method that uses generalized Gaussian quadratures for bandlimited exponentials instead of polynomials (Beylkin and Sandberg 2014). Consult Beylkin and Monzón (2002) and Xiao et al. (2001) for the development of generalized Gaussian quadratures for exponentials. These quadratures are constructed so that

$$\begin{aligned} \bigg | \int \limits _{-1}^1 e^{2ictx} W(t) \text {d}t - \sum _{j=1}^M w_j e^{2ic {\tau }_j x} \bigg | < \epsilon ^2, \;\;\; x, {\tau }_j \in [ -1, 1] \end{aligned}$$

(14)

for the user-selected accuracy $\epsilon > 0$, bandlimit $2 c > 0$, and weights $w_j > 0$. The nodes $\tau _j$ and weights $w_j$ depend on the bandlimit and accuracy. In the BLC-IRK method the weight $W(t)=1$ and the nodes correspond to the zeros of discrete prolate spheroidal wave functions (DPSWFs) (Slepian 1978). As it is traditional, generalized Gaussian quadratures are constructed on the interval $[-1,1]$ although we use them on $[0,1]$ (with the appropriate linear transformation).

Beylkin and Monzón (2002) show that by finding quadrature nodes for exponentials with bandlimit $2c$ and accuracy $\epsilon ^2$, we can generate an interpolating basis for bandlimited functions with bandlimit $c$ and accuracy $\epsilon$. These interpolating basis functions are defined as

$$\begin{aligned} R_j (x) = \sum _{l=1}^M r_{jl} e^{ic {\tau }_l x} \end{aligned}$$

(15)

for $j = 1, \ldots , M$ with

$$\begin{aligned} r_{jl} = \sum _{k=1}^M w_j {\varvec{\Psi }}_k (\tau _j) \frac{1}{\eta _k} {\varvec{\Psi }}_k (\tau _l) w_l , \end{aligned}$$

(16)

where the matrix ${\varvec{\Psi }}_k (\tau _l)$ is obtained by solving an algebraic eigenvalue problem,

$$\begin{aligned} \sum _{l=1}^M w_l e^{i c {\tau }_l {\tau }_m} {\varvec{\Psi }}_k (\tau _l) = \eta _k {\varvec{\Psi }}_k (\tau _m), \ \ k,m=1,\dots ,M. \end{aligned}$$

(17)

Following Beylkin and Monzón (2002), accurate approximations to the first $M$ PSWFs are then defined as

$$\begin{aligned} {\varvec{\Psi }}_k (\tau ) = \frac{1}{\eta _k} \sum _{l=1}^M w_l {\varvec{\Psi }}_k (\tau _l) e^{i c {\tau }_l \tau }, \ \ k=1,\dots ,M. \end{aligned}$$

(18)

Given interpolating basis functions $R_j(s)$, the elements of the integration matrix for BLC-IRK are then computed as

$$\begin{aligned} S_{ij} = \int \limits _0^{\tau _i} R_j(s)\text {d}s . \end{aligned}$$

(19)

We note that in Beylkin and Sandberg (2014), the construction of interpolating functions and integration matrix is modified in order to assure that the resulting BLC-IRK method is symplectic.

The quadratures for exponentials offer certain advantages over polynomial-based quadratures. It is well known that the nodes of polynomial-based quadratures cluster significantly towards the ends of each interval as the number of nodes increases (a simple heuristic explanation is that polynomials can grow rapidly toward the end points of an interval causing high node concentration). Nodes of quadratures for exponentials, however, do not accumulate as rapidly at the endpoints.

Typically only a small number of nodes of polynomial-based quadratures are used in IRK methods to avoid oversampling at the interval boundaries (e.g., 2–4 nodes). Following Beylkin and Sandberg (2005), we define a ratio

$$\begin{aligned} r(M,\epsilon ) = \frac{\tau _2 - \tau _1}{\tau _{\lfloor M/2 \rfloor } - \tau _{\lfloor M/2 \rfloor - 1}}, \end{aligned}$$

(20)

to represent the extent of node accumulation near the interval endpoints. Since the distance between nodes decreases monotonically towards the end of the interval, Eq. 20 yields a quantitative comparison of node accumulation property. The ratio is the distance between two nodes closest to the interval edge divided by the distance between two nodes in the middle of the interval. Figure 1 displays the behavior of the ratio as a function of the number of nodes for polynomial-based quadratures and quadratures for exponentials.

Fig. 1

Comparison of node accumulation for exponential and polynomial-based quadratures. a Generalized Gaussian quadrature for bandlimited exponentials with different interpolation accuracies. Marker dots indicate values for quadratures used in this study. b Polynomial-based quadratures. Ratios approach zero as $1/M$

The ratio for polynomial-based quadrature nodes asymptotically approaches zero as the number of nodes increase. This ratio for nodes of quadratures for exponentials, however, approaches a finite limit. This asymptote is a function of the accuracy, $\epsilon$, to which the quadrature is constructed, as seen in Eq. 14. This property of generalized Gaussian quadratures for bandlimited functions allows us to use larger time intervals with a large number of nodes per interval when compared to polynomial-based methods.

We provide quadrature data needed to implement BLC-IRK numerical integration online. The accompanying data files are described in “Appendix”. Data files necessary to perform dense output, discussed in Sect. 4.2, are also given.

3 Implementation and analysis of BLC-IRK

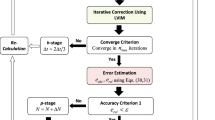
This section describes the input parameters necessary for the BLC-IRK method and demonstrates the effect these parameters have on the accuracy of orbit propagation around Earth. As mentioned previously, BLC-IRK is implemented using both a low- and high-fidelity force model to save computational effort during iteration. Figure 2 illustrates time intervals and nodes within these intervals to aid in our discussion.

Fig. 2

Example of nodes and intervals (for illustrative purposes only)

The current implementation of the BLC-IRK method requires 5 parameters to be specified by the user in order to execute the integration. Each parameter is described in the list below. We plan to develop an approach to determine appropriate values of each parameter automatically based on the orbit and force model.

• Accuracy ($\epsilon$): Interpolation accuracy for which the generalized Gaussian quadratures are constructed. In the current implementation this accuracy is fixed to $\epsilon \approx 10^{-13}$. It may be made available to the user in future implementations.

• Number of nodes per interval (bandlimit) ($M$): For a given accuracy $\epsilon$, the number of nodes per interval determines bandlimit and vice versa. More nodes per interval equates to a higher bandlimit.

• Number of Intervals ($N_I$): A time interval $N_I$ is similar to a step size $h$ in traditional integration schemes where $N_I = (t_f-t_0)/h$ and $t_f$ denotes the final time of the entire orbit propagation. Each interval contains the same number and placement of nodes (i.e., this is a fixed-step and fixed-order implementation). Choice of number of nodes, or bandlimit, will affect the number of intervals required to achieve a certain propagation accuracy, however, number of intervals $N_I$ is a user-defined input parameter. This is similar to choosing a step size in fixed-step integration schemes. As demonstrated later, there is a distinct, optimal $N_I$ for a given number of nodes per interval.

• Number of Low-Fidelity Force Model Iterations ($N_1$): The number of evaluations of the low-fidelity force model at each node before the high-fidelity force model is evaluated. Iteration is used to solve for each vector function, ${\varvec{\xi }}$, placing the solution at each node in a location that is close to its true location.

• Number of Iterations After Accessing High-Fidelity Model ($N_2$): The number of evaluations of the low-fidelity force model at each node after the high-fidelity force model has been evaluated once. Each iteration uses the same contribution from the high-fidelity model in combination with the updated low-fidelity information to refine the solution at each node.

Traditionally, evaluation of a high-fidelity force model dominates the computational load of any orbit propagation. The iteration process inside the current version of BLC-IRK has been modified from a traditional IRK method to make use of low-fidelity and high-fidelity force models to reduce the number of evaluations of the high-fidelity force model. IRK methods use iteration to solve the nonlinear equations for ${\varvec{\xi }}$, thus involving several calls to the force model, ${\varvec{f}}$, at each node. We first use a low-fidelity force model, ${\varvec{f}}_{\text {low}}$, containing point-mass and $3\times 3$ gravity field effects of the Earth, for the first few iterations to place the solution at each node close to the final value. The high-fidelity force model, ${\varvec{f}}_{\text {high}}$, is then evaluated once and the difference between the low- and high-fidelity model, ${\Delta }\!{\varvec{f}}$, is stored. The high-fidelity force model used in this study is comprised of a $70\times 70$ EGM96 gravity model (Lemoine et al. 1998) and third-body gravitational effects from the Sun and Moon. Drag and solar radiation pressure were omitted from this initial study to simplify the analysis. A second set of low-fidelity force model iterations is then used to finalize the iteration process. During this second set of iterations, ${\Delta }\!{\varvec{f}}$ is added to the low-fidelity evaluation. This improves the solution by using information from the high-fidelity force model without expending computation time evaluating it again. We rely on the assumption that the solution at each node is already close to its final value and that the high-fidelity perturbations do not vary much on this scale. Algorithm 1 describes the overall iteration process used in this study in greater detail.

The results in this paper were generated using a second call to the high-fidelity force model. The second evaluation ensures satisfactory orbit propagation accuracies in the current setup. However, the low-fidelity force model used here is not necessarily the optimal choice. The low-/high-fidelity force models and the iteration implementation can be adjusted for different situations. For example, a satellite in the Jovian system might want to include approximate third-body effects in the low-fidelity force model.

We also note that use of a single relative tolerance value for iteration instead of fixing the number of iterations $N_1$ and $N_2$ would improve the ease-of-use for the user and guarantee that excess computations were kept to a minimum. The use of a relative tolerance setting is common in many implementations of IRK schemes (e.g., for fixed-point iteration see Hairer et al. 2002 and Jones 2012) as well as adaptive step explicit Runge–Kutta schemes (see e.g., Prince and Dormand 1981). This paper specifies each iteration count in an effort to illustrate the low-/high-fidelity force model use. As demonstrated in the results, this method proves sufficient, but a more user-friendly interface may be desirable.

The force model evaluation may be accelerated using multi-core processors. While this is a property of all IRK methods, BLC-IRK will benefit the most from parallelization due to the large number of nodes per interval. Future work will include optimizing BLC-IRK for use with multiple cores and comparing evaluation times with other integration techniques (see e.g., Bai (2010) and Bai and Junkins (2011a) investigating the use of GPUs to parallelize a Chebyshev-based collocation method (MCPI) with tens to hundreds of nodes per interval).

3.1 Case study description

This investigation uses three types of orbits to evaluate BLC-IRK and compare its performance to commonly used integrators in the Astrodynamics community. A low-Earth orbit (LEO), geostationary orbit (GEO), and a Molniya orbit (MOL) were chosen to investigate different orbital regimes and eccentricities. Table 1 lists the Keplerian orbital elements at epoch ($0^{\text {h}}$ January 1st, 2011) for each of the three orbits and includes the perigee altitude, $h_p$.

Table 1 Initial osculating Keplerian orbital elements and perigee altitude of each orbit investigated in this study

A range of values for each BLC-IRK input parameter are used to examine the full range of accuracies. For each orbit type, BLC-IRK is implemented using 1–130 intervals over the duration of the propagation as well as 1–3 iterations for both $N_1$ and $N_2$. For all analyses that follow, results are displayed for propagations lasting 3 orbital revolutions of the orbit in question. The truth trajectory is generated by an 8th-order Gauss–Jackson (GJ 8) integration scheme using a 5-second time step. The Gauss–Jackson scheme is a multi-step predictor-corrector method that has been used by US Space Surveillance centers for orbit propagation for over 50 years and is especially efficient at propagating near-circular orbits (Jackson 1924; Fox 1984; Berry and Healy 2004; SPADOC Computation Center 1982). Note, however, that Gauss–Jackson is neither symplectic nor $A$-stable.

Evaluating the performance of a numerical integration scheme requires careful consideration of two things: (1) how to generate the truth trajectory, and (2) interpolation of the solution. Berry and Healy (2003) and Berry (2004) investigate several techniques for measuring integration error, specifically, what to use for the truth trajectory when propagating orbits with perturbations. They conclude that step size halving and higher-order integration both work well for generating truth trajectories when perturbations are present. As stated previously, we use truth trajectories generated by the GJ 8 scheme with a fixed step size of 5 seconds and compare integration accuracy only. The implementation of GJ 8 follows that of Berry and Healy (2004). The use of a small step size for truth requires us to assume that the use of a small step size yields a more accurate trajectory and that round-off error is not significantly affecting the solution. As the number of force model evaluations is increased, each integration method we are comparing approaches the reference trajectory with differences below $10^{-5}$ meters. This indicates that round-off error is not affecting our results for the accuracy range we are considering, i.e., $10^{-4}$ to $10^2$ meters. Other truth trajectories were also assessed, including GJ 8 with 2 and 10 second step sizes, and the 8th-order Dormand and Prince scheme, DOPRI 8(7), with similar steps. Each of these trajectories match the 5-second GJ 8 truth trajectory to the order of 10$^{-5}$ meters.

The interpolation strategy can have a notable impact on computing the error of an integration method. As depicted in Fig. 3, we interpolate the truth trajectory to times where we have a solution from the method we are comparing. A slightly different execution of interpolating at fixed 30-second intervals, however, has shown to introduce errors too large for this study on integration accuracy. This is especially true with high-order variable-step integration schemes because they take larger time steps than a lower 4th-order method. Since we are limiting ourselves to only interpolating the dense truth trajectory, error due to interpolation is essentially eliminated. Based on several tests, the observed maximum interpolation error is on the order of 10$^{-5}$ meters for the LEO and MOL orbits, and down to 10$^{-8}$ meters for GEO. These errors are below the accuracy range we are considering. The root-sum-square (RSS) position error at each time, $t_i$, is computed by

$$\begin{aligned} {\Delta } r_i = \begin{Vmatrix} \mathbf{X}_{\text {C}_i} - \mathbf{X}_{\text {T,interp}_i} \end{Vmatrix} \end{aligned}$$

(21)

where $\mathbf{X}$ denotes position solutions. The root mean square (RMS) position error for the entire trajectory is then computed using all ${\Delta } r_i$. All propagation comparison plots report this RMS error for the entire trajectory. The maximum and mean errors were also considered, however, these values are of the same order of magnitude as the RMS error. Given the log plots and similar behavior of each propagation scheme, the general error magnitude and performance relations between each scheme stay approximately the same. For this reason, we display the RMS values only.

Fig. 3

Illustration of interpolation strategy. $X$ denotes position solutions. Error comparisons are made at solution points of the method we are testing (e.g., BLC-IRK). The dense truth trajectory is interpolated to these points using a cubic spline to eliminate interpolation error

3.2 Intervals (step size)

First, we look at how the number of intervals affects propagation accuracy. Figure 4 shows the relationship between the number of intervals used per orbit and the RMS of position error for all three orbit types. When compared to a small number of intervals per orbit, adding intervals reduces the integration error significantly.

Fig. 4

RMS values of position errors for propagations of the LEO, GEO, and MOL orbits using a range of number of intervals per orbit. Each propagation has a duration of 3 orbit revolutions and uses 64 nodes per interval. Every combination of $\{1,2,3\}$ $N_1$ iterations and $\{1,2,3\}$ $N_2$ iterations were used

There reaches a point, however, where additional intervals do not reduce the integration error. Usually, this accuracy floor is caused by the finite precision of computing or the accumulation of roundoff error. In this case, it is due to the iteration algorithm being used for BLC-IRK, as described in Sect. 3. Standard implementations of IRK schemes used fixed-point, or Picard, iteration until convergence to some tolerance, e.g., 10$^{-13}$ (Hairer et al. 2002; Jones and Anderson 2012; Herman et al. 2013). However, a small amount of accuracy is sacrificed for faster evaluation time as fewer force model evaluations are performed, as is the case with the relatively few number of low-/high-fidelity force model evaluations used in this paper. This is acceptable when position accuracies below the micron or even centimeter level are not needed, or even possible, due to imperfect force model knowledge.

In operational use, an acceptable choice could be to aim for the “knee” in the curve, in terms of number of intervals, to ensure sufficiently accurate results while minimizing the number of force model calls. Determining the location of this knee automatically and reliably requires additional analysis due to its dependence on the orbit, force model, and number of nodes used.

3.3 Nodes

As mentioned previously, the number of nodes that are contained in each interval is tied to the bandlimit. Table 2 lists several node counts and their associated bandlimits. The displayed bandlimits are those that have been used to compute and store integration matrices, and are the only ones considered in this study.

Table 2 Number of nodes per interval and the corresponding bandlimits

Figure 5a illustrates the impact that number of nodes has on the relationship between number of function calls and integration accuracy. Note that when number of function calls is plotted for the BLC-IRK method, we are plotting the number of high-fidelity force model evaluations. This is justified by the fact that the high-fidelity force model requires several orders of magnitude more mathematical operations than the low-fidelity force model. This is mainly due to the high degree and order $70\times 70$ spherical harmonic gravity model computation.

Fig. 5

RMS values of position errors for the LEO orbit using a range of number of nodes per interval. Each propagation has a duration of 3 orbit revolutions and used every combination of $\{1,2,3\}$ $N_1$ iterations and $\{1,2,3\}$ $N_2$ iterations

The results reveal that the choice of node count does not affect how many high-fidelity force model evaluations are necessary to achieve a given accuracy. At first, the fact that the number of nodes does not affect the outcome of Fig. 5a seems odd. However, this feature is actually a byproduct of the node accumulation ratio of the generalized Gaussian quadratures illustrated in Fig. 1a. Since the ratio asymptotically approaches a constant greater than zero, additional force model evaluations are not wasted towards the interval endpoints as with polynomial-based quadratures. As nodes are added, the number of intervals required to achieve a given level of accuracy is reduced, thereby lowering the number of force model evaluations. This point is illustrated in Fig. 5b. Jones (2012) demonstrates this weakness of polynomial-based quadrature schemes by showing the diminishing return of adding nodes in a GL-IRK scheme. As nodes are added, there comes a point when the number of force model evaluations necessary to achieve the certain precision starts increasing. Therefore, BLC-IRK will benefit from parallelization even more than a polynomial-based scheme such as GL-IRK since additional nodes (and thus processors) may be added without the same diminishing return.

3.4 Symplectic property

As with GL-IRK methods (Sanz-Serna 1988), the BLC-IRK method is symplectic (Beylkin and Sandberg 2014). By imposing constraints on the integration matrix and weights of the generalized Gaussian quadratures, the BLC-IRK method becomes symplectic, making it an excellent tool for long-term orbit propagation. Specifically, in order to be symplectic a Runge–Kutta method must satisfy the conditions (Sanz-Serna 1988)

$$\begin{aligned} w_i S_{ij} + w_j S_{ji} - w_i w_j = 0, \; \; \; \; \; i,j = 1, \ldots , M. \end{aligned}$$

(22)

We demonstrate the symplectic property of the BLC-IRK method by using an energy-like integral analogous to the Jacobi integral of the Restricted Three-Body Problem. The Jacobi constant, $K$, is computed by

$$\begin{aligned} \frac{V^2}{2} - \frac{\mu }{R} - U'({{\varvec{R}}}) = K = \text {constant } \end{aligned}$$

(23)

where $\mu$ is the gravitational parameter of the central body, $R$ and $V$ are the orbital radius and inertial velocity of the satellite, respectively, and $U'(\mathbf{R})$ is the gravitational potential of the Earth (without the point-mass contribution) (Tapley et al. 2004; Bond and Allman 1996). Equation 23 is valid when the gravitational potential consists of zonal terms only. The inclusion of a time-varying gravity field, i.e., sectoral and tesseral terms, requires a slight modification to Eq. 23 (Bond and Allman 1996).

The Jacobi constant is an energy-like parameter that, in theory, remains constant over time when integrating a system involving a central gravity field. The purpose of a symplectic integrator is to enforce an approximate version of this property numerically since, otherwise, it is not maintained due to the finite precision of computation. The relative change in Jacobi constant compared to its initial value is plotted in Fig. 6 for a 10-year propagation of the LEO orbit using BLC-IRK and the explicit Runge–Kutta method DOPRI 8(7) (Prince and Dormand 1981). BLC-IRK maintains a bounded Jacobi constant over 10 years while the explicit Runge–Kutta method fails to maintain the Jacobi constant over long integration times. It is known that non-symplectic integrators (e.g., all ERK methods Sanz-Serna 1988) do not maintain a bounded energy, or Jacobi constant, due to the accumulation of roundoff error. The symplectic property of the BLC-IRK method is of great benefit to long-term propagations where the accumulation of roundoff error is a problem. In particular, long-term asteroid propagation and debris field evolution with timescales on the order of tens to hundreds of years benefit from using symplectic integrators. Breiter and Métris (1999), Mikkola (1999), and Mikkola et al. (2000) have also investigated symplectic schemes for use in space debris propagation and satellite tracking in Earth orbit.

Fig. 6

Change in Jacobi constant during a 10-year GEO propagation using point-mass and zonals $J_2-J_4$ only. BLC-IRK propagation performed using 4 intervals/orbit and 64 nodes/interval. DOPRI 8(7) propagation performed with a relative tolerance of $10^{-15}$ for step size control

4 Performance comparison

4.1 Orbit propagation

In this section, we compare the propagation efficiency of BLC-IRK to commonly used integration methods for the three orbits given in Table 1. Three of the four integration methods are explicit Runge–Kutta schemes with step size control and the fourth is the 8th-order Gauss–Jackson method.

• Runge–Kutta–Fehlberg 7(8) (RKF 7(8)13): a 13-stage explicit Runge–Kutta method of order 7 and an embedded method of order 8 used for step size control developed by Erwin Fehlberg (Fehlberg 1968). The software package Systems Tool Kit, by Analytical Graphics Inc., uses this as the default integrator (other options are available as well). The implementation of RKF 7(8) used in this study is not using local extrapolation (i.e., the 7th-order result is used as the solution).

• Dormand & Prince 8(7) (DOPRI 8(7)13 or RK 8(7)13): similar to the 13-stage RKF 7(8), but uses an 8th-order method for the solution and a 7th-order method for step size control (Prince and Dormand 1981).

• Dormand & Prince 5(4) (DOPRI 5(4)7 or RK 5(4)7): a 7-stage explicit Runge–Kutta method of order 5 and an embedded method of order 4 used for step size control (Dormand and Prince 1980). This integration scheme is available in MATLAB where it is known as ode45 (Shampine and Reichelt 1997). The integration matrix and weights of DOPRI 5(4) were designed with a beneficial feature called FSAL (first-same-as-last). This means that the final stage evaluation at time $t_n$ is equal to the first stage evaluation at the next time $t_{n+1}$, thus saving one evaluation of the force model per time step.

• Gauss–Jackson 8th-order (GJ 8): a multi-step predictor-corrector method of 8th-order which uses a fixed step size (Jackson 1924; Fox 1984; Berry and Healy 2004). This scheme has been used by US Space Surveillance Centers since the 1960’s due to its highly efficient propagation of near-circular orbits (SPADOC Computation Center 1982; Berry and Healy 2004).

In space surveillance and many other applications, we often have an option to sacrifice accuracy for reduced computation time. Thus, we desire an integration scheme which achieves a necessary level of accuracy while minimizing the number of force model evaluations and computation time required. We compare each integrator based on the number of force model evaluations (function calls) that are used to achieve various levels of position error. It is important to remember that this study evaluates integration error only and we are not considering the separate topic of force model errors. Note that the reported number of function calls for BLC-IRK is the number of high-fidelity force model evaluations only.

BLC-IRK is executed serially (without any parallelization) using 64 nodes per interval ($M$) and 2 function calls per node. Results for BLC-IRK are shown for propagations performed using $\{1,2,\ldots ,130\}$ intervals ($N_I$) and $\{1,2,3\}$ first set ($N_1$) and second set ($N_2$) iterations. Thus, the circular markers for BLC-IRK in the following figures are not connected by a line. Results for RKF 7(8), DOPRI 8(7), and DOPRI 5(4) are shown for propagations using relative tolerances ranging from $10^{-8}$ to $10^{-15}$. Relative tolerance is used to adaptively control step size for these three embedded ERK methods. The implementation of step size control closely follows that of Dormand and Prince (1980). Results for GJ 8 were generated using a wide range of fixed step sizes while a 5-second time step is used as truth for all comparisons. Note that GJ 8 was forced to use only 1 iteration (i.e., force model evaluation) per step. Details on the interpolation of the reference trajectory for integrator comparison can be found in Sect. 3.1.

Figure 7a contains results for the GEO propagation (see Table 1 for orbital elements) and demonstrates the well-known observation that more evaluations of the force model yields more accurate propagations with conventional schemes (until some accuracy floor is reached). BLC-IRK clearly outperforms all of the ERK methods in GEO, requiring many fewer function calls to achieve sub-centimeter accuracy. At the meter level, BLC-IRK closely matches the performance of GJ 8, but requires about twice as many function calls at the centimeter to millimeter range. The performance of BLC-IRK in GEO may be improved with a better selection of low-fidelity force model. The low-fidelity model used here is just an example. As mentioned in Sect. 3.2, the higher accuracy floor of BLC-IRK is due to the fact that we are not iterating to a small relative tolerance, but are instead performing only a few force model evaluations. While this floor is greater than the floor for the other methods, it is still well within force model errors.

Results of the LEO propagation, shown in Fig. 7b, demonstrate a significantly different distribution of integration schemes than Fig. 7a. Results for the ERK methods are now more clustered together and overlap slightly. This is due to the increased spatial variation in the disturbing gravity field at LEO. Each scheme is required to take small time steps to compensate for the increase in spatial variation of perturbations, resulting in similar propagation accuracies. Note that BLC-IRK closely matches the efficiency of GJ 8 and is more efficient than the explicit methods.

Fig. 7

Comparison of RMS position errors over a 3-orbit GEO (a) and LEO (b) propagation

Figure 8 demonstrates the differences in magnitude and temporal variation between the low- and high-fidelity force models for the LEO and GEO orbits. For both LEO and GEO, the difference in magnitude between the low- and high-fidelity models is several orders of magnitude smaller than that of the low-fidelity model itself. The fact that the low-fidelity model constitutes the bulk of the acceleration on a satellite is the reason for the benefit of using both low- and high-fidelity force models. Furthermore, the difference between the force models in LEO is greater than at GEO by about 1 order of magnitude. The smaller difference between the force models and the reduced spatial variation of acceleration in GEO allows the variable step methods to perform well. Since the Gauss–Jackson scheme uses a polynomial to generate an initial prediction of the solution at each time step, GJ 8 also performs well in the “smoothly” varying GEO regime.

Fig. 8

Comparison of low- and high-fidelity force models used in this study over 1 orbit period for GEO and LEO. The low-fidelity force model includes Earth point-mass and a $3\times 3$ gravity field. The high-fidelity force model includes Earth point-mass, a $70\times 70$ gravity field, and third-body gravitational forces from the Sun and Moon

As shown in Fig. 7b, BLC-IRK has the ability to match Gauss–Jackson in LEO, largely due to the fact that the low-/high-fidelity force model scheme has a greater advantage in that region. BLC-IRK uses approximately the same number of force model evaluations as GJ 8 at centimeter to millimeter accuracy and outperforms the ERK methods significantly. Since the majority of objects in the space catalog reside in the LEO regime, this approach is very compelling. Furthermore, BLC-IRK can be massively parallelized, using a separate processor for each node in an interval.

We now consider a highly eccentric test case ($e=0.74$), the Molniya orbit, shown in Fig. 9. With this orbit type the variable step size methods, particularly RKF 7(8) and DOPRI 8(7), show a vast improvement over the GJ 8 scheme. This makes intuitive sense since the variable step size integrators are able to take very large steps near apogee and then shrink back down towards perigee. Alternatively, the fixed-step GJ 8 is forced to use a small step size for the duration of the propagation in order to deal with the high dynamics at perigee. Since BLC-IRK is currently implemented as a fixed-step integrator, it performs similarly to GJ 8.

Fig. 9

Comparison of RMS position errors over a 3-orbit Molniya propagation

Table 3 provides a quantitative summary of the performance of each integration scheme. Additional entries are given for a 2-processor parallelized and an ideally parallelized implementation of BLC-IRK to demonstrate the ability of this IRK method when parallelization is taken advantage of. Since we are using 64 nodes per interval, ideally parallelized means the use of 64 processors and no communication overhead. This number of processors is easily taken care of if GPUs are utilized. Note that the term “ideal” is used because an actual parallel implementation would inherently contain added computation time due to communication/data transfer as well as memory management. This extra overhead could be quite large and is especially sensitive to implementation. Table 3 demonstrates that BLC-IRK outperforms Gauss–Jackson in all scenarios if only 2 processors are used. Using BLC-IRK with 2 processors even outperforms the explicit variable-step methods for the highly-elliptic Molniya orbit. A further improvement in efficiency can be gained by ideally parallelizing the implementation of BLC-IRK.

Table 3 Performance summary of integration methods over three orbit periods

This paper compares BLC-IRK with common ERK methods and the multistep GJ 8 scheme, but does not look at other IRK methods. A recent study by Herman et al. (2013), however, directly compares BLC-IRK with a fixed-step implementation of GL-IRK. Herman et al. (2013) demonstrates that BLC-IRK always performs as well or better than GL-IRK (i.e., requiring fewer function calls for the same accuracy). The study ensures a fair comparison by operating both schemes in fixed-step mode and uses fixed-point iteration instead of low- and high-fidelity force models. While BLC-IRK and GL-IRK perform quite similarly for GEO orbits, BLC-IRK outperforms GL-IRK in both LEO and highly-eccentric orbits, which is due to the improved node spacing of the BLC-IRK nodes. Similarly, the benefit of BLC-IRK over GL-IRK is enhanced as more nodes are used. Note that all cases in Herman et al. (2013) were restricted to the use of a large number of nodes (i.e., 32 and 200). Figure 1 of this paper implies that GL-IRK and BLC-IRK may not exhibit much of a difference for cases with fewer nodes.

Future work will include developing an efficient step size control algorithm for BLC-IRK. Unlike the embedded ERK methods that exist, no such IRK method has been developed with a second, embedded method, to be used for step size control. However, a few algorithms to control step size for IRK methods do exist. Jones (2012) discusses the implementation of a variable-step algorithm from Houwen and Sommeijer (1990) with a GL-IRK scheme. Jones (2012) demonstrates that the variable-step algorithm, dubbed VGL-$s$, improves upon the fixed-step GJ 8 for highly-eccentric orbits, but recommends that further work be done to improve the efficiency of the algorithm. Aristoff et al. (2014) develops a variable-step GL-IRK implementation, dubbed VGL-IRK, for orbit and uncertainty propagation and compares its performance against DOPRI 8(7), VGL-$s$, and MCPI. Aristoff et al. (2014) shows that their VGL-IRK scheme outperforms the other integration methods in LEO, GEO, and highly-eccentric orbits, making their variable-step version of GL-IRK very attractive. As BLC-IRK contains more efficient node spacing than GL-IRK, a variable-step implementation of BLC-IRK should outperform VGL-IRK, in theory. As mentioned, this is an important part of our future work. Other recently developed integration schemes (mainly symplectic) and comparison studies of note include Hubaux et al. (2012), Blanes and Iserles (2012), Blanes et al. (2013), Farrés et al. (2013), Rose and Dullin (2013), and Nguyen-Ba et al. (2013).

4.2 Dense output

All collocation-based IRK schemes have built-in interpolation to evaluate solutions at arbitrary points. This section outlines and examines the dense output capability of the BLC-IRK method. We first describe how to interpolate a solution computed at the quadrature nodes $\{\tau _m\}_{m=1}^M$ to an arbitrary time $\tau$. For clarity, we present the necessary equations for the case where the quadrature nodes $\tau _m$ lie on the interval $[-1,1]$, noting that if the time ${\tilde{\tau }}$ is given in the interval $[\alpha ,\beta ]$, we can easily rescale it to the interval $[-1,1]$ as $\tau = (2{\tilde{\tau }}-\alpha -\beta )/(\beta -\alpha )$. Data files necessary for executing the dense output algorithm are provided online and described in “Appendix”.

The input data for interpolation is given as the values $y(\tau _m)$ at the nodes $\tau _m \in [-1,1]$, $m=1,2,\ldots ,M$. The function $y(\tau )$ is then interpolated via

$$\begin{aligned} y(\tau ) = \sum _{k=1}^M b_k {\varvec{\Psi }}_k(\tau ), \end{aligned}$$

(24)

where the approximate PSWFs ${\varvec{\Psi }}_k(\tau )$ are defined in Eq. 18 and the coefficients $b_k$ satisfy the condition

$$\begin{aligned} y(\tau _m) = \sum _{k=1}^M b_k {\varvec{\Psi }}_k (\tau _m), \ \ m=1,2,\ldots ,M, \end{aligned}$$

(25)

so that

$$\begin{aligned} b_k = \sum _{m=1}^M B_{km} y(\tau _m), \end{aligned}$$

(26)

where the matrix $\{B_{km}\}_{k,m=1}^{M}$ is the inverse of $\{{\varvec{\Psi }}_k (\tau _m)\}_{m,k=1}^{M}$. From Eq. 18, we also have

$$\begin{aligned} y(\tau ) = \sum _{l=1}^M a_l e^{ic \tau _l \tau }, \end{aligned}$$

(27)

where

$$\begin{aligned} a_l = \sum _{k=1}^M A_{lk} b_k, \ \ \ A_{lk} = \frac{w_l}{\eta _k} {\varvec{\Psi }}_k (\tau _l). \end{aligned}$$

(28)

In the event that the matrix ${\varvec{\Psi }}_k(\tau _m)$ may be ill-conditioned for large $M$, we note that this matrix can be pre-computed with extended precision (e.g., using Mathematica), and then tabulated. Computing and storing matrix ${\varvec{\Psi }}_k (\tau _m)$ and its inverse in advance, we compute the coefficients $b_k$ and $a_k$ from the values $\{y(\tau _m)\}_{m=1}^M$ by applying these matrices. Matrix ${\varvec{\Psi }}_k (\tau _m)$ and its inverse may have to be computed and applied with extra precision to avoid losing accurate digits.

We use Eq. 27 to evaluate the function $y$ at arbitrary points in $[-1,1]$. The advantage of Eq. 27 is that we can use Unequally Spaced Fast Fourier Transform (USFFT) (Dutt and Rokhlin 1993; Beylkin 1995) to compute values of $y$ at $N$ points in $[-1,1]$ in $\mathcal {O} (N \log N) + \mathcal {O} (M)$ operations. However, if $M$ is relatively small (e.g., $M\le 64$), the direct evaluation via

$$\begin{aligned} y(\tau ) = \sum _{l=1}^M \mathcal {R}e(a_l) \cos (c \tau _l \tau ) - \mathcal {I}m(a_l) \sin (c \tau _l \tau ) , \end{aligned}$$

(29)

requires $\mathcal {O} (N M)$ operations and may turn out to be faster.

Figure 10 displays the interpolation accuracy achieved for a GEO propagation performed using BLC-IRK and the collocation algorithm. A 6-hour segment of the 3-orbit propagation is shown, revealing each of the 64 nodes used in this interval. Note that the y-axis has units of millimeters. The error grows over time because the actual BLC-IRK integrated trajectory is being interpolated and compared to the truth trajectory. Hence, the error already contained in the orbit propagation is still present. The BLC-IRK interpolation (blue line) yields a very smooth and continuous solution with errors similar to those of the nodes. This result highlights the benefit of collocation techniques.

Fig. 10

BLC-IRK collocation interpolation error for a GEO propagation. BLC-IRK propagation performed using 4 intervals/orbit and 64 nodes/interval. Interpolation is performed every 5 seconds. Note that the plotted error is due to both interpolation and integration

For comparison, Fig. 11 demonstrates the accuracy of Lagrange interpolation used on orbit propagations generated by BLC-IRK and DOPRI 8(7). Lagrange interpolation was chosen for comparison due to the easy implementation and long history of use of the polynomial-based scheme. During the same 6-hour time span shown in Fig. 10, the 5th-order Lagrange interpolation yields slightly larger errors than the collocation algorithm for BLC-IRK. However, the interpolation error in Fig. 11a has a maximum of only 0.1 mm. Note that this is only a 5th-order implementation of Lagrange and that a higher order Lagrange method (e.g., 7 or 9) yields errors similar to that of BLC-IRK collocation.

Fig. 11

Interpolation errors of BLC-IRK (a) and DOPRI 8(7) (b) trajectories using a $5{\mathrm{th}}$-order Lagrange scheme. Interpolations are performed every 5 seconds. A relative tolerance of $10^{-13}$ was used for step size control of the DOPRI 8(7) propagation

Figure 11b demonstrates the degraded accuracy achieved by interpolating a DOPRI 8(7) trajectory using a 5th-order Lagrange scheme as compared to BLC-IRK. Polynomial-based interpolation performs much better when using the higher density BLC-IRK nodes rather than the sparse DOPRI 8(7) steps.

It should also be noted that explicit Runge–Kutta schemes can have dense output capabilities as well. Several researchers have developed dense output schemes for the 5th- and 8th-order methods used in this study. Two dense output schemes have been developed for the DOPRI 5(4) method. Dormand and Prince (1986) develop a 4th-order “free” interpolant (meaning additional function evaluations are not required), which is also discussed in Hairer et al. (1993). Calvo et al. (1990) provides a 5th-order interpolant for the DOPRI 5(4) method, requiring 2 additional stage evaluations per step. Additionally, Bogacki and Shampine (1990) have developed a 5th-order “free” interpolant for the higher-order DOPRI 8(7) scheme. Tsitouras (2007) discusses several Runge–Kutta interpolants that have been developed and presents a new high-order interpolation method for the RK 9(8) developed by Tsitouras (2001). Other options include Runge–Kutta Triples which have dense output capability, including embedded ERK and Runge–Kutta–Nyström schemes (Montenbruck and Gill 2000).

While a few of the dense output options for ERK methods are “free”, they are of lower order than the integration scheme itself. Collocation methods allow for the state to be computed at anytime on the trajectory for “free”, utilizing a continuous solution that is coupled to the integration scheme. Even if another interpolation strategy (e.g., Lagrange) is desired, the increased density of solutions due to the collocation nodes provides a more accurate interpolated solution, as seen in Fig. 11.

5 Conclusions and future work

This paper describes a new numerical integration scheme, BLC-IRK, for orbit propagation and outlined its implementation towards propagating orbits with perturbing forces. As a symplectic and $A$-stable IRK method, BLC-IRK is of particular interest because it is parallelizable. In addition, the generalized Gaussian quadratures for bandlimited functions on which BLC-IRK is based, yield node spacing that is more efficient than traditional polynomial-based quadrature methods such as Gauss–Legendre, Gauss–Lobatto, and Chebyshev. This promotes the use of large time intervals and a large number of nodes per interval, reducing the computational load near the clustered endpoints as with polynomial-based quadratures. Additionally, the $A$-stable property of BLC-IRK makes its use appealing to solving stiff ODEs, including atmospheric entry.

We demonstrated superior performance of BLC-IRK over commonly used ERK methods for near circular orbits while closely matching GJ 8, even when operating in serial mode (no parallelization). Note that the GJ 8 results presented here were done with an implementation that uses one force model evaluation per step only. Ordinary versions of GJ 8 would likely contain iteration, resulting in several force model evaluations at each step. The presented BLC-IRK implementation of using both low- and high-fidelity force models is a major contributor to the efficiency. The specific execution can be tuned for each unique scenario, leaving room for improvement even on the implementation presented here. The low-fidelity model used here is just an example. Deep space and GEO scenarios may benefit from including a rough third-body contribution into the low-fidelity model. It should also be noted that this low-/high-fidelity implementation is applicable to any IRK method. While BLC-IRK is slightly less efficient than GJ 8, BLC-IRK is a brand new technique, leaving room for additional research and improvement. In contrast, the Gauss–Jackson scheme has been around for many years and has essentially maximized its potential. Gauss–Jackson is also neither symplectic nor $A$-stable. When applicable, parallelization would result in a significant improvement in efficiency over the GJ 8 scheme.

This paper outlined the dense output algorithm for BLC-IRK as well. We demonstrated that interpolating a BLC-IRK trajectory using its collocation algorithm yields a high accuracy, smooth, and continuous solution. We also showed that the accuracy of Lagrange interpolation of a BLC-IRK trajectory is superior to that of a Dormand and Prince 8(7) propagated orbit. This is an appealing aspect of collocation methods, where the higher node density provides a better base for interpolation. This is especially important to conjunction assessment where solutions are required at various points in time along a trajectory.

The current implementation of the BLC-IRK scheme requires several user-defined tuning parameters. While these parameters can affect the efficiency and accuracy of the resulting orbit propagation, this paper gives a rough idea of satisfactory choices for these parameters in several orbit regimes. Future work will aim to: (1) determine optimal low- and high-fidelity force models for Earth orbiting objects, (2) develop a step size control algorithm for BLC-IRK, and (3) investigate its use in boundary value problems. The first two items will allow a more autonomous and efficient implementation of BLC-IRK while the third allows for its use in trajectory optimization. It is also important to note that further systematic studies of the integration schemes compared in this paper and other recently developed integrators would aid in better defining the relative merits and capabilities of each scheme. We include data files online, containing all quadrature data, necessary for implementing BLC-IRK integration and interpolation. Details on the provided data can be found in the Appendix.

Appendix: BLC-IRK data files

ASCII-files with quadrature data for $M=24$ nodes (corresponding to bandwidth $c=2.5\pi$) and $M=70$ nodes (corresponding to bandwidth $c=20\pi$) are provided as an online resource. For each bandwidth, we provide six files:

• nodesM.txt: Contains the quadrature nodes $\{\tau _k\}_{k=1}^M$ for the interval $[-1,1]$.

• weightsM.txt: Contains the quadrature weights $\{w_k\}_{k=1}^M$ for the interval $[-1,1]$.

• integrationMatrixM.txt: Contains the elements of the integration matrix $S$ (stored row-wise) with respect to the interval $[-1,1]$.

• BmatrixM.txt: Contains the elements of the matrix $B$ (stored row-wise), Eq. (26), with respect to the interval $[-1,1]$.

• AmatrixRealPartM.txt: Contains the elements of the real part of the matrix $A$ (stored row-wise), Eqs. (28) and (29), with respect to the interval $[-1,1]$

• AmatrixImagPartM.txt: Contains the elements of the imaginary part of the matrix $A$ (stored row-wise), Eqs. (28) and (29), with respect to the interval $[-1,1]$.

These data files allow the reader to implement the BLC-IRK scheme for numerical integration and to perform the interpolation described in Sect. 4.2. The files are linked to the online version of the paper (Electronic Supplementary Material).