A strictly standardized thermal regime must be maintained in the energy-intensive equipment used in oil refining and chemical plants. A strictly standardized thermal regime must be maintained in the course of the operation of this equipment. Premature failure of individual parts of the equipment may occur under conditions of high temperatures. Overheating of the technological plants is related directly to a decrease in the productivity of the equipment and the quality of the output and may affect the safety with which operations are performed as well as the environment [1,2,3,4].

In view of the fact that the equipment used in oil refining and chemical enterprises is characterized by great geometric dimensions, it is difficult to use complicated active cooling systems which, in addition, leads to a reduction in the energy efficiency of the production cycles.

Thermosyphons, understood as systems designed to maintain the thermal regime of industrial equipment, have yet to enter into widespread use. In particular, only individual, special cases of the use of such systems in the oil-refining and chemical branches of industry are known [3, 4]. However, interest in these devices has grown significantly over the past seven years [5,6,7].

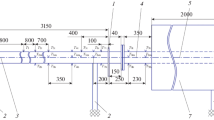
A thermosyphon is a closed vessel in the lower part of which is found a layer of liquid heat-transfer agent (Fig. 1). Once the lower cover of the thermosyphon has been heated, the heat-transfer agent begins to evaporate and, as it rises into the upper part of the thermosiphon, the steam is condensed. The condensate drains into the heating zone, again evaporates, and in this way the heating zone is cooled. There are only minor limitations imposed on the use of thermosyphons [8].

Fig. 1.
figure 1

Flow diagram of thermosyphon: 1) lower cover; 2) evaporation surface; 3) steam channel; 4) liquid film; 5) vertical wall; 6) condensation zone; 7) upper cover.

Full size image

Results of studies (basically experimental) of heat transfer processes in thermosyphons are known [5, 7]. Mathematical modeling of thermophysical and hydrodynamic processes in such devices are carried out within the framework of boundary-layer models [6] or the complete Navier–Stokes equations [9] for small steam channels. Even the regimes of emergency drying of the bottom cover of a thermosyphon within the framework of models of natural convection have been analyzed, but only for short steam channels [9,10,11]. In practical chemical and oil-refining machine construction, the principal high-temperature units and devices are large, hence the analysis of the laws governing the transfer of mass, impulse, and energy should be performed for relatively high thermosyphons (up to 2 m).

The objective of the present study is to carry out mathematical modeling of the influence of the longitudinal dimension of a closed two-phase thermosyphon of rectangular form on the efficiency of heat transfer with the use of the ANSYS FLUENT software package.

Statement of problem. Let us consider a thermosyphon of rectangular cross-section (cf. Fig. 1).

The equations of continuity, motion, and energy, solved for the region of steam and a liquid film, have the form

$$ \frac{\mathrm{\partial \uprho }}{\partial t}+\frac{\partial \left(\uprho u\right)}{\partial x}+\frac{\partial \left(\uprho \upupsilon \right)}{\partial y}=0; $$
(1)
$$ \frac{\partial {\uprho}_1{u}_1}{\partial t}+\frac{\partial \left({\uprho}_1{u}_1{u}_1\right)}{\partial x}+\frac{\partial \left({\uprho}_1{\upupsilon}_1{u}_1\right)}{\partial y}={\uprho}_1{g}_x-\frac{\partial {p}_1}{\partial x}+\frac{\partial }{\partial x}\left({\upmu}_1\frac{\partial {u}_1}{\partial x}\right)+\frac{\partial }{\partial y}\left({\upmu}_1\frac{\partial {u}_1}{\partial y}\right); $$
(2)
$$ \frac{\partial {\uprho}_1{\upupsilon}_1}{\partial t}+\frac{\partial \left({\uprho}_1{u}_1{\upupsilon}_1\right)}{\partial x}+\frac{\partial \left({\uprho}_1{\upupsilon}_1{\upupsilon}_1\right)}{\partial y}=\frac{\partial {p}_1}{\partial y}+\frac{\partial }{\partial x}\left({\upmu}_1\frac{\partial {\upupsilon}_1}{\partial x}\right)+\frac{\partial }{\partial y}\left({\upmu}_1\frac{\partial {\upupsilon}_1}{\partial y}\right); $$
(3)
$$ \frac{\partial {\uprho}_2{u}_2}{\partial t}+\frac{\partial \left({\uprho}_2{u}_2{u}_2\right)}{\partial x}+\frac{\partial \left({\uprho}_2{\upupsilon}_2{u}_2\right)}{\partial y}={\uprho}_2{g}_x-\frac{\partial {p}_2}{\partial x}+\frac{\partial }{\partial x}\left({\upmu}_2\frac{\partial {u}_2}{\partial x}\right)+\frac{\partial }{\partial y}\left({\upmu}_2\frac{\partial {u}_2}{\partial y}\right); $$
(4)
$$ \frac{\partial {\uprho}_2{\upupsilon}_2}{\partial t}+\frac{\partial \left({\uprho}_2{u}_2{\upupsilon}_2\right)}{\partial x}+\frac{\partial \left({\uprho}_2{\upupsilon}_2{\upupsilon}_2\right)}{\partial y}=\frac{\partial {p}_2}{\partial y}+\frac{\partial }{\partial x}\left({\upmu}_2\frac{\partial {\upupsilon}_2}{\partial x}\right)+\frac{\partial }{\partial y}\left({\upmu}_2\frac{\partial {\upupsilon}_2}{\partial y}\right); $$
(5)
$$ {\uprho}_1{C}_{p1}\left(\frac{\partial {T}_1}{\partial t}+{u}_1\frac{\partial {T}_1}{\partial x}+{\upupsilon}_1\frac{\partial {T}_1}{\partial y}\right)={\uplambda}_1\left(\frac{\partial^2{T}_1}{\partial {x}^2}+\frac{\partial^2{T}_1}{\partial {y}^2}\right); $$
(6)
$$ {\uprho}_2{C}_{p2}\left(\frac{\partial {T}_2}{\partial t}+{u}_2\frac{\partial {T}_2}{\partial x}+{\upupsilon}_2\frac{\partial {T}_2}{\partial y}\right)={\uplambda}_2\left(\frac{\partial^2{T}_2}{\partial {x}^2}+\frac{\partial^2{T}_2}{\partial {y}^2}\right), $$
(7)

where u and υ are the components of the velocity vector in projection onto the x- and y-axes, respectively; p, pressure; T, temperature; ρ, density; x, y, Cartesian coordinates; t, time; C p , heat capacity; g, gravitational acceleration; λ, heat conductivity; μ, dynamic viscosity; subscripts 1, 2 correspond to liquid and steam, respectively.

The initial conditions for the (1)–(7) system of equations are as follows:

$$ u\left(x,y\right)=0;\kern1em T\left(x,y\right)={T}_0;\kern1em p\left(x,y\right)={p}_0, $$

while the boundary conditions for system (1)–(7) are given by

$$ {\displaystyle \begin{array}{c}x=0,\kern1em 0<y<H,\kern1em \frac{\partial {T}_2}{\partial x}=0,\kern1em \frac{\partial {u}_2}{\partial x}=0,\kern1em \frac{\partial {\upupsilon}_2}{\partial x}=0;\\ {}x=L,\kern1em 0<y<H,\kern1em {\uplambda}_1\frac{\partial {T}_1}{\partial x}=0;\kern1em {u}_1={\upupsilon}_1=0;\\ {}x={x}_1,\kern1em {y}_1<y<{y}_1+{y}_2,\left\{\begin{array}{l}{T}_1={T}_2\\ {}{\uplambda}_1\frac{\partial {T}_1}{\partial x}={\uplambda}_2\frac{\partial {T}_2}{\partial x}\end{array},\left\{\begin{array}{l}{u}_1={u}_2=0\\ {}{\upupsilon}_2=0\end{array},\frac{\partial {\upupsilon}_1}{\partial x}=0;\right.\right.\\ {}y={y}_1,\kern1em 0<x<{x}_1,\left\{\begin{array}{l}{T}_1={T}_2\\ {}{\uplambda}_1\frac{\partial {T}_1}{\partial y}={\uplambda}_2\frac{\partial {T}_2}{\partial y}-{Q}_{\mathrm{e}}{w}_{\mathrm{e}}-{\upupsilon}_2{C}_p\uprho \left({T}_2-{T}_0\right);\kern1em {\upupsilon}_2=\frac{w_{\mathrm{e}}}{\uprho_2},\kern1em {\upupsilon}_1=\frac{w_{\mathrm{e}}}{\uprho_1};\end{array}\right.\\ {}y={y}_1+{y}_2,\kern1em 0<x<{x}_1,\left\{\begin{array}{l}{T}_2={T}_1\\ {}{\uplambda}_2\frac{\partial {T}_2}{\partial y}={\uplambda}_1\frac{\partial {T}_1}{\partial y}+{Q}_{\mathrm{c}}{w}_{\mathrm{c}}-{\upupsilon}_2{C}_p\uprho \left({T}_1-{T}_0\right);\kern1em {\upupsilon}_1=\frac{w_{\mathrm{c}}}{\uprho_1},\kern1em {\upupsilon}_2=0;\end{array}\right.\\ {}y=0,\kern1em 0<x<L,\kern1em {\uplambda}_1\frac{\partial {T}_1}{\partial y}={q}_{\mathrm{h}},\kern1em {u}_1={\upupsilon}_1=0;\\ {}y=H,\kern1em 0<x<L,\kern1em {\uplambda}_1\frac{\partial {T}_1}{\partial y}=\upalpha \left({T}_1-{T}_{\mathrm{am}}\right),\kern1em {u}_1={\upupsilon}_1=0,\end{array}} $$

where Q e and Q c are the heat of evaporation and heat of condensation, respectively, J/kg; w e and w c, mass rates of evaporation and condensation, kg/(m2·sec); and T am, ambient temperature.

The mass rates of evaporation and of condensation are calculated using the formula [9]

$$ {w}_{\mathrm{e}\left(\mathrm{c}\right)}=\upbeta \sqrt{\frac{M}{2\uppi {RT}_{\mathrm{s}}}}\left({p}_2-{p}_{\mathrm{s}}\right), $$

where p s and T s are the pressure and temperature of saturation; R, universal gas constant; M, molal mass; and β, accommodation coefficient.

Results and discussion. Numerical modeling of heat transfer was performed in a closed two-phase thermosyphon of rectangular form with transverse dimension L = 0.2 m for different lengths of the steam channel H (1, 1.5, and 2 m). The following densities of the heat flux q h on the lower cover of the thermosyphon in the section y = 0 were adopted: 2.8·104, 4.7·104, and 6.5·104 W/m2. The working fluid was water.

The results of numerical modeling of the temperature distribution (Fig. 2) show that with a height of the thermosyphon’s steam channel of 1 m and q h = 2.8·104 W/m2, the temperature drop between the lower and upper covers of the thermosyphon is at most 16 K. With a density of the heat flux on the lower cover of 4.7·104 W/m2 or 6.5·104 W/m2, the temperature drop in the study region is much less: 9 K and 6 K, respectively. This is due to the fact that with thermal loads of 4.7·104 or 6.5·104 W/m2 the temperature of the lower cover reaches the saturation temperature of the heat-transfer agent (370 K). The rate of evaporation is maximal; correspondingly, the pressure of the steam near the surface of the phase conversions and rate of leakage of the steam are also maximal.

Fig. 2.
figure 2

Temperature distributions with respect to y on the axis of symmetry of a thermosyphon of height: a) 1 m; b) 1.5 m; c) 2 m; q h, W/m2: 1) 2.8·104; 2) 4.7·104; 3) 6.5·104.

Full size image

At densities of the heat flux of 2.8·104, 4.7·104, or 6.5·104 W/m2 on the lower cover of a thermosyphon with longitudinal dimension 1.5 m (cf. Fig. 2 b), the temperature drop amounts to 20, 11, or 8 K, respectively. Even in the case of great thermal loads (4.7·104 or 6.5·104 W/m2), the temperature drop on the whole is slight, hence intensification of heating leads to more intensive displacement of steam through the channel of the thermosyphon and more rapid transfer of heat into the zone of condensation.

It is also important to note that an increase in the height of the steam channel with fixed values q h on the lower cover does not have any effect on the temperature of its surface.

Different characteristics are used to estimate the operating efficiency of thermosyphons [8], in particular, the effective thermal conductivity λeff of a thermosyphon.

The value of λeff characterizes the conditions of heat transfer through a thermosyphon in a heat conductivity regime corresponding in intensity to the regime realized under practical conditions. Figuratively speaking, the steam channel in such an approximation is replaced by a cylinder made of a material with very high (substantially greater than that of copper) thermal conductivity.

The effective thermal conductivity of a thermosyphon as a function of its height for different densities of the heat flux on the lower cover is represented in Fig. 3. Here, λeff increases as the thermal load increases, a result that confirms the conclusion that intensification of heating leads to a decrease in the temperature drop in the test region. An increase in the height of the steam channel from 1 to 2 m has a slight effect on the effective thermal conductivity of a thermosyphon under the operating conditions being considered here, which are sufficiently typical.

Fig. 3.
figure 3

Effective thermal conductivity as a function of height of thermosyphon: 1) q h = 2.8·104 W/m2; 2) q h = 4.7·104 W/m2; 3) q h = 6.5·104 W/m2.

Full size image

The distribution of the speed of the steam by height of the thermosyphon along the axis of symmetry of the channel (Fig. 1) is illustrated in Fig. 4. The variation in the speed of the steam in the steam channel as its height varies from 1 to 2 m is not significant. A decrease in speed occurs in a small upper part of the thermosyphon as a result of stagnation of the steam and its condensation on the surface of the upper cover. In the case of a density of the heat flux on the lower cover of 2.8·104 W/m2, the decrease in the speed of the steam is substantially greater than with q h = 4.7·104 W/m2 or q h = 6.5·104 W/m2, since with increasing thermal load the rate of evaporation and the pressure of the steam near the surface of evaporation both increase, and, correspondingly, the rate of outflow of the steam into the cold part of the steam channel similarly increases (the greater the value of q h, the higher is the pressure gradient in the steam channel).

Fig. 4.
figure 4

Variation in speed of steam with respect to y coordinate along axis of symmetry of 1-m high thermosyphon: 1) q h = 2.8·104 W/m2; 2) q h = 4.7·104 W/m2; 3) q h = 6.5·104 W/m2.

Full size image

Conclusion. The numerical investigations that have been carried out show that with constant thermal load, an increase in the vertical dimension of the thermosyphon studied here from 1 to 2 m leads to a slight increase in the temperature drop by height of the steam channel (from 2 to 4 K) with a variation in the density of the heat flux from 2.8·104 to 6.5·104 W/m2. It was established that with a maximal (in the range being considered) heat flux of 6.5·104 W/m2, the speed of the steam in the test region is also maximal, amounting to ~5 m/sec. The following conclusion may be drawn on the basis of the analysis and a generalization of the results of numerical modeling. In the case where the most significant factors (geometric dimensions and heat fluxes on the lower cover) are varied, closed two-phase thermosyphons may be effectively used to achieve effective heat transfer and realize the thermal regime of energy-intensive oil-refining and chemical equipment.

The present study was carried out within the framework of R&D work of State Assignment “Science” No.13.1339. 2014/K (Code of Federal Scientific and Technical Targeted Program is 2.1410.2014).