Existing models for predicting productivity with perforation well completion are based on empirical formulas of a finite element modeling method and on electrical simulation data. All known models are extremely simplified and cannot be used for an accurate productivity estimate. In this paper, we propose a new model for perforation of the near-wellbore zone, including empirical formulas for estimating productivity according to the type of reservoir behavior. The model is a simple and reliable method for optimizing and estimating formation productivity. We note the significant accuracy of a calculation using the proposed model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Perforation completion is one of the most widely used well completion methods in China. Methods for studying this type of well completion can be classified as experimental methods and theoretical methods. Experimental methods include real stationary simulation of perforation, electrical simulation, and field logging experiments. Theoretical methods include derivation of formulas and finite element simulation. Derivation of formulas is aimed at establishing the relationship between well production rate and the characteristics of the perforation, the reservoir, and the extent of damage to the reservoir. At the same time, finite element simulation presumes direct use of the basic formulas of filtration theory and variational principles to create the model, followed by application of the formulas from filtration theory to each individual element. Experimental methods require a large number of instruments and equipment, are not cheap, and take a considerable amount of time. The significant increase in calculating speed and memory size in modern computers have made the finite element method a convenient and economical way to predict the effect of completion parameters on well production rate [1].
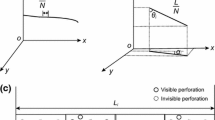
Basic parameters of the model. After perforation, the characteristics (length, diameter, and shape) of the perforation tunnels can be varied over a considerable range. Some tunnels can be blocked by fragments; the shape and thickness of the perforating skin can vary over broad ranges. Thus we need to establish the following assumptions and simplifications:
-
all channels are unblocked;
-
each tunnel is represented by a cylinder with a hemispherical top;
-
the diameter and length of all tunnels are the same;
-
the skin thicknesses are identical;
-
the perforations and the wellbore have infinite permeability (relative to the permeability of the reservoir rock).
Taking into account the assumptions given above, formations connected with the skins were not considered. Casing and cementing were neglected in the model because they do not allow for seepage. During development, the finite element model can be simplified by going from a three-dimensional problem to a two-dimensional problem, based on certain rules and local symmetry.
Comparison of the finite element model. The initial data in the model are [2, 3]: depth of damage, mm; perforating depth, mm; mean tunnel diameter, mm; skin thickness, mm; phasing angle; perforating density; length of perforation tunnels (only tunnels in one screw pitch are considered because of cyclic symmetry); geological range, established as equal to 40-160 wellbore radii; studied range (in this case, it is considered within the phasing angle range). During the simulation, by varying one of the parameters we can achieve the required stability of the tunnels and the maximum production rate.
Initial geophysical data for the model [4]: the initial horizontal and vertical permeability of the undamaged reservoir; the permeability of the damaged reservoir (the initial permeability is reduced due to filtrate and mud solids flowing into the strata); the skin permeability (the permeability is reduced due to compaction of the rock around the tunnel); the perforation permeability (the tunnels can be filled with gravel or remain unfilled, and so their permeability may be considered infinitely large relative to the permeability of the formation and the perforation permeability can be simulated based on vertical permeability ); geophysical data for the reservoir. All the initial data described are obtained experimentally.
Boundary conditions: formation pressure is propagated from the exterior boundary surface; the wellbore pressure is propagated to the entrance into the perforation tunnel. A pressure difference is created between the wellbore and the reservoir.
Basic formulas of the model for movement of liquid in the near-wellbore zone [5]. Let us assume that in the porous medium of the formation, single-phase Darcy flow occurs with no source or congruence. The horizontal permeability of the formation is k x = k y , the vertical permeability is k z , the hydrostatic pressure is p = p(x,y,z), the filtration rate (the Darcy velocity) is v x , v y , v z . The continuity equation is:
Darcy’s law:
Substituting (2) into (1), we obtain:
If the permeabilities are constant, then Eq. (3) can be simplified:
If the reservoir is isotropic, k x = k y = k and Eq. (4) becomes the Laplace equation.
The finite element equation. The studied space Ω has neither source nor congruence, and according to the law of conservation of mass, we can derive the equation:
According to the previously developed model based on the finite element method and a related method for the near-wellbore calculation, we can obtain data on the distribution of formation pressure upon perforation, the filtration rate distribution, the pressure gradient, and the production rate that can be used for optimization of the perforation.
Estimate of the production rate with perforation well completion. In the case of perforation completion of a single wellbore, based on data on the perforating depth and density and the phasing angle, we can use the finite element method to calculate the average flow rate at the tunnel exit. The flow rate in a single wellbore is:
where d is the diameter of the perforation tunnel; \( \overline{{{v_p}}} \). is the average flow rate in the perforation tunnel.
Assuming that the reservoir thickness is 1 m, the drawdown pressure is 1 MPa, and the perforating density is n/m, let us determine the daily flow per meter:
In the case of perforation completion of a single wellbore, for the same reservoir thickness and drawdown pressure as considered above, let us calculate the daily production of an open hole per meter:
where \( \overline{{{v_r}}} \) is the average velocity in a single tunnel; R 2 is the radius of the perforated well.
According to the definition of the productivity ratio PR, we obtain an expression for calculating it by combining formulas (5) and (6):
The model for perforation well completion proposed in this paper is applicable to oil and gas reservoirs. The flow characteristics of the liquid and the gas (under the flow conditions according to Darcy’s law) are the same, but the liquid and the gas have considerably different density and viscosity. The density and viscosity of the liquid vary with temperature, while these characteristics for the gas also depend significantly on pressure. In modeling the productivity of a gas well with perforation completion, the highest possible production rate in the standard state must be converted using the equation for the properties of the gas. The liquid production rate can be obtained directly for known density of the liquid and volume flow rate, which in turn is calculated according to the model we have proposed.
We constructed 5⋅7⋅7⋅6⋅10 = 14 700 models and a library of formulas for predicting the productivity as applied to oil and gas reservoirs. Each specific model allows us to calculate the productivity, and a total of 1470 computation modules are provided.
As an example of application of the model, let us consider well A in an oil field of the CNOOC company. The reservoir has low porosity and permeability. Initial data: mid-depth of the perforation interval, 2100 m; effective thickness of the formation, 20 m; average formation pressure, 25 MPa; formation temperature, 80°C; average reservoir permeability, 20 mD; oil density, 850 kg/m3; average reservoir porosity, 14%. Below we present the characteristics of the well perforating gun.
-
Angle, degrees .......................................................... 45
-
Depth of damaged zone, mm ................................... 150
-
Depth of compaction, mm ........................................ 12
-
Phasing angle, degrees .............................................. 90
-
Entrance diameter, mm ............................................. 10
-
Perforating density, m-1 ..............................................16
-
Perforating depth, mm ............................................ 600
Formula for predicting depth of damage L d :
where r w is the wellbore radius; B is the structure parameter; A is the regression coefficient; γ is the difference between the mud density and the formation pressure coefficient; H is the well depth; T is the mud soak time; r L is the fluid loss.
From mud monitoring data, we assume T = 7 days, L d = 15 cm. The above data were used to calculate the productivity of the well using the proposed model; the calculated value was compared with the actual productivity observed in the field:
-
Productivity ratio ..................................................... 0,866
-
Production, m3/day.
-
calculated ...................................................... 12,303
-
from field data ............................................... 13,205
-
Relative error, % ......................................................7
The proposed model has been applied to 100 wells in 20 fields of the CNOOC company. In most cases, the relative error of the productivity calculation is no greater than 10%, which lets us recommend the model for further application.
References
Zhiping Li, Yunlong Wu, and Yonggu Qing, Gas Reservoir Dynamic Analysis and Estimating Measure, Petroleum Industry Publishing Company, Beijing (2002).
Jisheng Yang, Techniques Base of Gas Producing Operation, Petroleum Industry Publishing Company, Beijing (1992).
Dacun Li and Thomas W. Engler, “Literature review on correlations of the non-Darcy coefficient,” in: SPE Permian Basin Oil and Gas Recovery Conference, Midland, Texas (2001), SPE70015.
Shilun Li, Natural Gas Engineering, Petroleum Industry Publishing Company, Beijing (2000).
Joseph Ansah, Mark A. Proett, and Mohamed Y. Soliman, “Advances in well completion design: A new 3D finite-element wellbore inflow model for optimizing performance of perforated completions,” in: International Symposium and Exhibition on Formation Damage Control, Lafayette, Louisiana, Society of Petroleum Engineers (2002), SPE73760.
Author information
Authors and Affiliations
Additional information
Translated from Khimiya i Tekhnologiya Topliv i Masel, No. 5, pp. 46 – 48, September – October, 2013.
Rights and permissions
About this article
Cite this article
Bi, S., Lian, Z. & Liu, G. New Finite Element Model for Perforation Well Completion. Chem Technol Fuels Oils 49, 439–443 (2013). https://doi.org/10.1007/s10553-013-0467-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10553-013-0467-z