1 Introduction

Over the last decades, several studies have investigated the influence of the ground-motion duration on the seismic response of soils and civil structures. While its effects on the behavior of the ground materials have been successfully identified, making that some methods consider this parameter within the formulae for the solution of multiple geotechnical engineering problems (Seed and Idriss 1971; Rauch and Martin 2000; Liu et al. 2001), its effects on structural response remain a subject of continuous discussion. The latter stems from the fact that the seismic performance of civil structures is demarked not only by the inherent characteristics of the seismic loadings—which depend on many seismological parameters characterizing the earthquake source, the wave propagation path between the source and the site of interest, and the soil and geological profile beneath the site—but also by many diverse parameters typifying the structural elements that define the capacity of each system. Moreover, for engineering purposes, it has been preferred to use the strong-motion duration, which represents the fraction considered intense of a ground motion at a site of interest, instead of the total ground-motion duration. Although the estimation of the strong-motion duration seems simple, a great number of methods can be found in the literature for its measurement, none of which has been accepted by the structural engineering community.

Table 1 summarizes the most relevant results of nine studies reported in the literature from 2006 to 2021 on the influence of the strong-motion duration in the seismic response of civil structures; another concise summary of studies carried out in past decades can be found in the research work of Hancock and Bommer (2006). Most of the researchers cited in Table 1 evaluated the seismic response of structures via incremental dynamic analyses (IDAs) (Vamvatsikos and Cornell 2002), for which worldwide ground-motion recordings were used. Therefore, Table 1 summarizes the structural systems analyzed, the number of accelerograms employed for the analyses, and the conclusions about the impact of the strong-motion duration on the damage measures or indices considered to evaluate the structural response. Note that the recordings used in the research works cited in Table 1 commonly contain accelerograms in two or three orthogonal components of the ground motion.

Table 1 Influence of the ground-motion duration on structural damage: relevant studies carried out between 2006 and 2021
Full size table

As per Table 1, one can tell that the effects of the strong-motion duration on structural response can be more evident for masonry or reinforced concrete buildings (whose stiffness and strength degrade under the action of seismic loadings) than for steel buildings. Regardless of the analyzed system, the significance attributed to the strong-motion duration in their seismic response relied mainly on the damage measure used to evaluate their performance. In this regard, most of the researchers reported that the strong-motion duration has a negligible effect on the estimates of maximum-response damage measures, whereas it has a significant effect on the estimates of energy-based damage measures. Various researchers cited in Table 1 focused on comparing the seismic response of structures subjected to accelerograms that were recorded during ground motions caused either by shallow crustal earthquakes or interplate earthquakes. Most of the researchers called the ground-motion recordings from shallow crustal earthquakes “short-duration ground motions” and those from interplate earthquakes “long-duration ground motions”. They concluded that long-duration ground motions tended to produce larger estimates of energy-based damage measures and, moreover, some of them report an increase in the estimates of certain deformation-based measures when large spectral accelerations were involved (e.g., Ruiz-García 2010; Barbosa et al. 2017).

It is important pointing that, although comparing the seismic response of a structure subjected to accelerograms of different durations is quite beneficial, the comparisons carried out in most of the studies cited in Table 1 lose sense due to the categorical way in which they were classified. For instance, based on the research work of Chandramohan et al. (2016a), Belejo et al. (2017) classified as long duration those ground-motion recordings having at least one accelerogram with strong-motion duration of 25 s as a minimum. In the mild opinion of the authors, doing this kind of classification appears subjective. As has been demonstrated in previous studies on seismology—e.g., in the research work of Anderson (2003)—, scattering, attenuation, and amplification (the first two principally related to the source-to-site distance and the latter to the local site conditions) greatly influence the seismic waves in such a way that even ground motions caused by earthquakes characterized by the same tectonic environment and recorded at the same site could be classified as short- or long-lasting.

It should also be mentioned that the local site conditions, as well as other seismological parameters, were disregarded in the majority of the studies cited in Table 1. For instance, except for the research works conducted by Ruíz-García (2010) and Chandramohan et al. (2016a), who considered accelerograms recorded at rock and firm soil sites, no attention was paid to ensure that the selected accelerograms were recorded in sites with similar local site conditions as those where the analyzed structures were located. It should be recognized that this omission was somehow avoided in some of the studies cited in Table 1 as the employed accelerograms were scaled in such a way that their response spectra matched a site-specific target spectrum. Aside, the foregoing undoubtedly leads to not-so-feasible results of the seismic response of the analyzed structures, as they are subjected to ground-motion scenarios that may not be representative of the geographical region where they are located (even if hypothetical locations are considered).

In light of this brief introduction, one can argue that the role of the strong-motion duration in the seismic response of structures cannot be ignored and that it must be considered in earnest as other ground-motion parameters commonly used in structural design methods. Currently, many international structural design standards, such as the ASCE (2016), Eurocode 8–1 (2004), and NTC-CDMX (2020), allow the application of either recorded or synthetic accelerograms on the base of a structure for its nonlinear analysis. However, although such standards establish minimum spectral amplitudes to be met by the accelerograms, they do not provide a concise specification for their duration, which is an indispensable parameter when the generation of synthetic accelerograms is required (Chandramohan et al. 2016a; López-Castañeda and Reinoso 2021, 2022). For instance, a simple mathematical expression for estimating the ground-motion duration caused by either interplate or intermediate-depth (intraslab) earthquakes is presented in the NTC-CDMX (2020) appendix. Nevertheless, structural practitioners cannot properly account for the randomness of the mentioned ground-motion parameter because no details of the variance defining the mathematical expression are provided. Moreover, as the given mathematical expression is conditional on specific scenario earthquakes (with moment magnitude, \({M}_{w}\), equal to 7.8 and hypocentral distance, \({R}_{hyp}\), equal to 265 km for interplate earthquakes, and with \({M}_{w}\) = 7.5 and \({R}_{hyp}\) = 110 km for intermediate-depth earthquakes) taken from the disaggregation of the uniform hazard spectrum (UHS) computations associated with a return period, \({T}_{r}\), of 250 years, the value of the ground-motion duration can be extremely misestimated when considering magnitudes and source-to-site distances different to those established in such standard. These arguments are sustained based on the results of several studies that have evaluated the behavior of the ground-motion duration in relation to other seismological parameters. For example, the ground-motion duration can increase significantly for a slight increase in the earthquake magnitude (Kempton and Stewart 2006; Bommer et al. 2009; Lee and Green 2014; López-Castañeda and Reinoso 2021, 2022). Thus, this paper aims to highlight the importance of correctly circumscribing the dimension and randomness of site-specific ground-motion duration when selecting accelerograms for structural response analyses.

The developments presented in this paper are briefly described as follows. First, an equivalent SDOF system whose properties were estimated from the dynamic characteristics and pushover curve of a steel frame designed by the plastic method (Goel and Chao 2008)is presented in Sect. 2. Then, the seismic response of the equivalent SDOF system, subjected to thirteen accelerograms recorded at four different soil-profile sites located in Mexico City, is analyzed in Sect. 3. The selected accelerograms are associated with four interplate earthquakes with \({M}_{w}\) varying from 7.3 to 7.5 that occurred in the Mexican subduction zone. Subsequently, in Sect. 4 several IDAs are conducted considering various sets of spectrally equivalent accelerograms. The accelerograms were simulated considering envelopes of accelerograms recorded at three different soil-profile sites in Mexico City. Moreover, the duration of the synthetic accelerograms was estimated based on a recently published ground-motion predictive equation (GMPE) developed by López-Castañeda and Reinoso (2022) that allows identifying the likelihood of future outcomes of the strong-motion duration as a function of three seismological parameters. Further, the effect of the strong-motion duration on the performance of the steel frame building (represented by the equivalent SDOF system) is evaluated via fragility curves in Sect. 5. The fragility functions were developed considering the structural displacement and an energy-based damage index as EDP. The discussion of the results is presented at the end together with the conclusion.

Before proceeding it should be said that, from a detailed inspection of the strong-motion data used in recent studies (such as those summarized in Table 1), there is a lack of research concerning the effects of long-lasting ground motions in the response of structures located in sites with soil conditions similar to those observed in Mexico City—the subsoil there can be characterized by alluvial sandy and silty layers with whole thickness greater than 110 m (Jaime-Paredes 1987)—. That is why the main objective of this paper is to advance the understanding of the influence of the ground-motion duration on the reliability of structures located in such a geographical region. Notice that the study of the seismic response of structures located in Mexico City is of vital importance because the biggest metropolis of the country is situated there and, as it is well known, it has been subjected to many catastrophic seismic hazards (Reinoso 2007). Broadly speaking, the vulnerability of structures in Mexico City owes to the fact that they are built on grounds whose motions present great amplification when subjected to tremors. Indeed, net amplifications of ~ 500 have been reached at some sites of Mexico City—which are the largest documented anywhere in the world—(Singh and Ordaz 1993; Chávez-García 1994). Consequently, as the ground-motion amplitude increases, the duration of the ground motion also increases. For instance, there is historical evidence of ground motions caused by interplate earthquakes with \({M}_{w}\) ≈ 7.5 occurred at \({R}_{hyp}\) ≈ 300 km from Mexico City that reached values of \({t}_{r}\) higher than 400 s (López-Castañeda and Reinoso 2022). Hence, structures located in Mexico City are exposed to constant stresses over prolonged periods of time, leading to strongly intensified demands.

The authors hope that what is presented below in this paper will serve as learning for the analysis of structures located in other geographical regions of the world that are severely affected by interplate earthquakes. Any improvement in the knowledge of structural reliability is always beneficial.

2 General description of the steel frame building and its equivalent SDOF system

The structural system analyzed in this work is based on an example presented in the book published by Goel and Chao (2008). The system consists of a four-story, one-bay steel frame building designed by the plastic method. The gravity loads, structural profiles, and the steel frame dimensions are presented in Fig. 1. A two-dimensional nonlinear finite element model (FEM) of the steel frame developed in the software ANSYS (ANSYS Inc. 2019) was used to establish the structural capacity of the system through a pushover analysis. The vibration modes and mass participation ratios that characterize the system were determined using a modal analysis. Table 2 summarizes the associated four vibration periods and mass ratios. As seen in Table 2, the first mode, with a corresponding period \({T}_{1}\) = 1.2 s, controls the response of the steel frame. As mentioned before, to establish the plastic capacity of the steel frame, an incremental static nonlinear analysis was performed considering a load pattern concordant to the first vibration mode. A yielding strength, \({F}_{y}\), of 379 kN and a ductility, \(\mu\), of ~ 3.3 were obtained from the pushover results. The collapse mechanism developed by the steel frame is depicted in Fig. 1.

Fig. 1
figure 1

Schematic of the moment-resisting steel frame model (left) and collapse mechanism developed by it when subjected to a pushover analysis considering a first mode lateral load pattern (right)

Full size image
Table 2 Modal properties of the four-story, one-bay steel frame
Full size table

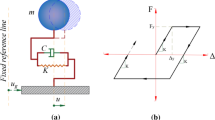
To performe a massive number of dynamic analyses at an affordable computational cost, an equivalent SDOF system of the steel frame was defined. The stiffness, \(k\), of the equivalent SDOF system was determined from the linear interval in the pushover curve, and its mass, \(m\), was computed so that the period matched that of the first mode of the analyzed steel frame. Structural damping of 5% of the critical value was considered for the equivalent SDOF system properties. The constitutive model of the simplified system considers an elastic–plastic behavior with hardening. The ultimate displacement, \({u}_{u}\), and the ultimate load, \({F}_{u}\), for the capacity curve of the equivalent SDOF system, were defined based on the pushover curve of the steel frame, these values served as a reference to determine the tangent modulus of the simplified system, i.e., the secondary stiffness, \(\alpha k\). Figure 2 depicts schemes for the equivalent SDOF system and its constitutive model as considered in this study. From Fig. 2b it can be observed that the area under the capacity curve of the equivalent SDOF system is slightly smaller than the pushover curve of the steel frame (~ 5% less). Nonetheless, negligible errors in the structural response are expected from this approximation since \(k\) and \({u}_{u}\) are the same for both systems. This criterion is concordant with the results presented by De Luca et al. (2013), who showed that maintaining these two parameters (initial stiffness and ultimate displacement) provided satisfactory results when employing equivalent bi-linear SDOF systems with hardening for IDAs.

Fig. 2
figure 2

a Schematics of the equivalent SDOF system and constitutive model considered for its development. b Nonlinear static pushover curve of the steel frame considering the first mode lateral load pattern and capacity curve of the equivalent SDOF system

Full size image

3 Ground-motion duration as recorded in Mexico City

Mexico City deals with ground motions caused by earthquakes associated with different tectonic environments, varying from infrequent shallow-crustal earthquakes originating in the active Trans-Mexican Volcanic Belt to very frequent interplate and intraslab earthquakes originating at the Mexican subduction zone—the former occurring at shallow depths (\(D\) ~ 20 km) along the contact area between the North American and Cocos plates and at source-to-site distances greater than 250 km from the city, and the latter occurring within the subducted Cocos Plate at intermediate-depths (\(D\) > 40 km) at source-to-site distances as close as ~ 140 km—(Kostoglodov and Pacheco 1999; Iglesias et al. 2002). Of the mentioned tectonic environments, both interplate and intraslab earthquakes represent the greatest seismic hazard to the city: as intraslab earthquakes show larger energy content at higher frequencies (\(f\) > 0.3 Hz) they commonly affect low-rise structures located in rock or stiff soil sites, whereas interplate earthquakes (which exhibit lower-frequency contents) commonly affect long-period structures located at soft soil sites. Although there is evidence that ground motions from intraslab earthquakes are more intense than those from interplate earthquakes, the local site conditions of sites located in Mexico City distress significantly ground motions caused by the last ones (Montalvo-Arrieta et al. 2003; Jaimes and Reinoso 2006; Heresi et al. 2020). This behavior is because that the seismic waves trapped in the soft soil of Mexico City are amplified at frequencies between 0.2 Hz to 0.7 Hz (Singh et al. 2015). For instance, ground motions at the lakebed zone of Mexico City could be up to 500 times greater than those observed in sites near the seismic sources (Singh and Ordaz 1993; Chávez-García 1994).

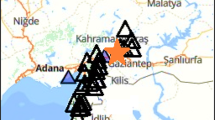
A map of Central Mexico showing the epicenters of four interplate earthquakes with values of \({M}_{w}\) varying from 7.0 to 7.5 occurred in the Mexican subduction zone is presented in Fig. 3. A map of Mexico City showing the location of four ground-motion recording stations, namely, CUP5, UC44, BO39, and AU11, is also presented in Fig. 3. According to the NTC-CDMX (2020), the dominant period \({T}_{s}\) of the sites where the stations are located is 0.5 s, 1.3 s, 2.5 s, and 4.0 s, respectively. Station CUP5 is located on the grounds of the central campus of UNAM, the National Autonomous University of Mexico. That area is characterized by deposits of granular soil and volcanic tuffs with sandy deposits interspersed. The other three stations are located in the lakebed area of Mexico City, which is characterized by highly compressible clay deposits separated by sandy layers containing silt, clay, and volcano ash. The thickness there can be greater than 50 m. The accelerograms recorded in stations CUP5, UC44, BO39, and AU11 during the selected earthquakes are presented on the left side of Figs. 4, 5, 6, and 7, respectively. As per these figures, there is a wide variation in the values of \({t}_{r}\) of accelerograms recorded in sites located within a ~ 8 km radius. While station CUP5 recorded accelerograms with values of \({t}_{r}\) greater than 80 s, stations UC44, BO39, and AU11 recorded accelerograms with values of \({t}_{r}\) greater than 100 s, 200 s, and 300 s, respectively.

Fig. 3
figure 3

Map of Central Mexico showing the epicenters of four interplate earthquakes with values of \({M}_{w}\) varying from 7.3 to 7.5. The subplot shows the territorial delimitation of Mexico City and the geographical location of four ground-motion recording stations, namely, CUP5, UC44, BO39, and AU11

Full size image
Fig. 4
figure 4

(Left) Accelerograms recorded in station CUP5 (\({T}_{s}\) = 0.5 s) during two interplate earthquakes. The area shaded in gray represents the time window in which the motion may be considered strong according to the definition of \({D}_{rS}\). (Right) Displacement histories of the equivalent SDOF system when subjected to the accelerograms. The gray line indicates the structural displacement measured considering only the significant portion of the accelerogram

Full size image
Fig. 5
figure 5

(Left) Accelerograms recorded in station UC44 (\({T}_{s}\) = 1.3 s) during four interplate earthquakes. The area shaded in red represents the time window in which the motion may be considered strong according to the definition of \({D}_{rS}\). (Right) Displacement histories of the equivalent SDOF system when subjected to the accelerograms. The red line indicates the structural displacement measured considering only the significant portion of the accelerogram

Full size image
Fig. 6
figure 6

(Left) Accelerograms recorded in station BO39 (\({T}_{s}\) = 2.5 s) during four interplate earthquakes. The area shaded in green represents the time window in which the motion may be considered strong according to the definition of \({D}_{rS}\). (Right) Displacement histories of the equivalent SDOF system when subjected to the accelerograms. The green line indicates the structural displacement measured considering only the significant portion of the accelerogram

Full size image
Fig. 7
figure 7

(Left) Accelerograms recorded in station AU11 (\({T}_{s}\) = 4.0 s) during three interplate earthquakes. The area shaded in blue represents the time window in which the motion may be considered strong according to the definition of \({D}_{rS}\). (Right) Displacement histories of the equivalent SDOF system when subjected to the accelerograms. The blue line indicates the structural displacement measured considering only the significant portion of the accelerogram

Full size image

In seismology, it is well known that, as the seismic waves propagate away from the source, they diminish their amplitude due to attenuation. However, when they reach the Valley of Mexico basin (where Mexico City is located), they amplify greatly due to the particular local site conditions that characterize such a geographic region. For instance, ground motions at the lakebed zone are amplified from 8 to 50 times with respect to the site where station CUP5 is located. The frequency at which the maximum amplification occurs varies from site to site and lies between 0.2 Hz and 0.7 Hz (Singh et al. 1988). Moreover, even ground motions at sites with soil conditions similar to those where station CUP5 is located present an amplification as large as 10 (in the frequency range of 0.2 Hz to 0.7 Hz) in comparison with ground motions at sites located outside Mexico City at similar source-to-site distances than station CUP5 (Ordaz and Singh 1992; Montalvo-Arrieta et al. 2003). As per Figs. 4 and 7 for the earthquake that occurred on March 20, 2012 at \({R}_{hyp}\) ≈ 340 km (Event 2) from the selected stations, the seismic waves came so attenuated that station CUP5 recorded a peak ground acceleration, \(PGA\), of ~ 12 cm/s2. But, as the seismic waves hit the lakebed area, the values of \(PGA\) increased up to ~ 51 cm/s2 at station AU11. The latter indicates that there is a positive correlation of \({T}_{s}\) with \(PGA\).

3.1 Strong-motion duration

Generally, the first and last amplitudes of ground motions are so small that they have little influence on the seismic response of structures. For this reason, a parameter termed strong-motion duration has been adopted to account for the portion of an accelerogram to be considered for earthquake engineering purposes (Salmon et al. 1992). Various definitions of the strong-motion duration can be found in the literature of which the most used is the relative significant duration, hereafter denoted as \({D}_{rS}\). Its definition is based on the accumulation of energy in an accelerogram and is defined by the integral of the square of either the ground acceleration, velocity, or displacement (Trifunac and Brady 1975; Dobry and Idriss 1978). If the integral of the ground acceleration is employed, \({D}_{rS}\) can be computed as the time elapsed between the instants in which the normalized Arias intensity, \({I}_{A}\), reaches two specified values, namely, \({NI}_{A1}=0.05\) and \({NI}_{A2}=0.95\). Note that \({I}_{A}\) is defined as (Arias 1970):

$${I}_{A}\left(\mathrm{t}\right)=\frac{\pi }{2g}{\int }{a}^{2}\left(t\right)dt$$
(1)

where \(a\left(t\right)\) is the ground acceleration at time \(t\) and \(g\) is the acceleration due to gravity. The normalized \({I}_{A}\) can be computed as:

$$H\left(t\right)=\frac{{I}_{A}\left(\mathrm{t}\right)}{\mathrm{max}\left({I}_{A}\left(t\right)\right)}$$
(2)

By definition, \(0\le H\left(t\right)\le 1\). The graphical representation of \(H(t)\) is known as a Husid plot (Husid 1969).

Although the measurement of \({D}_{rS}\) from accelerograms appears to be an easy task, care must be taken on how to measure \({t}_{r}\). That is, for an “ideal” accelerogram, \({t}_{r}\) truly represents the arrival of the first seismic wave and the departure of the last one. Nevertheless, accelerograms (as those shown in Figs. 4, 5, 6, and 7) are commonly recorded by devices having different trigger thresholds and different pre- and post-event memory availabilities. Therefore, there is a need to standardize the accelerograms to estimate the value of \({t}_{r}\) and, therefore, to objectively compare the strong-motion duration computed from different accelerograms. Following the criterion established by López-Castañeda and Reinoso (2021, 2022) to measure \({D}_{rS}\), \({t}_{r}\) is taken as the total time elapsed between the first and last excursions of an acceleration threshold equal to 2 cm/s2.

Being 2 cm/s2 such a low value of acceleration, the seismic response of a structural system (obtained by a dynamic analysis) is the same if it is subjected either to a “raw” accelerogram or to a portion of it that represents the strong-motion duration defined as \({D}_{rS}\) (but measured from the “raw” accelerogram bounded by the mentioned threshold). As an instance, the displacement histories of the equivalent SDOF system (defined in Sect. 2) when subjected to the “raw” accelerograms recorded in stations CUP5, UC44, BO39, and AU11, during the four interplate earthquakes presented in Fig. 3 are given in the right side of Figs. 4, 5, 6, and 7, respectively. Also, the displacement histories resulting from subjecting the equivalent SDOF system only to the portion of the accelerograms that constitutes their intense phase are shown in Fig. 3. As expected, the displacement histories resulting from using the entire signals are almost identical to the ones obtained using only the time window defined by \({D}_{rS}\). Hence, the maximum displacement, \({u}_{max}\), of the equivalent SDOF system was practically the same for both cases (the maximum difference being 0.69 cm).

4 Incremental dynamic analyses

In this study, IDAs were performed using synthetic accelerograms whose response spectra and duration are compatible with real earthquake scenarios affecting three hypothetical sites where the steel frame building (represented by the SDOF system defined in Sect. 2) is assumed to be located. The hypothetical sites are the same where stations UC44 (\({T}_{s}\) = 1.3 s), BO39 (\({T}_{s}\) = 2.5 s), and AU11 (\({T}_{s}\) = 4.0 s) are located. The mutually independent accelerograms were simulated by employing the well-known SIMQKE-I software (Gasparini and Vanmarcke 1976). The target response spectrum for the synthetic accelerograms generated for each site was taken as the UHS given in the NTC-CDMX (2020). For each site, various sets of accelerograms were generated having the same target spectrum but a different duration. In particular, one duration set consists of seven groups, each consisting of forty accelerograms and associated with one discrete value of \(PGA\), which varies from 0.1 g to 0.4 g in increments of 0.05 g. Figure 8 shows the target response spectrum considered for each site, along with the response spectra from an ensemble of the synthetic accelerograms.

Fig. 8
figure 8

(Left) Target response spectra for each site as given in the NTC-CDMX (2020) and response spectra of an aleatory set of synthetic accelerograms. (Right) Sample of four synthetic accelerograms generated for the site with \({T}_{s}\) = 1.3 s

Full size image

The duration of each group of synthetic accelerograms was defined based on the definition of \({D}_{rS}\). The portion of the accelerograms defined by \({D}_{rS}\) was used to analyze the seismic response of a given structure via nonlinear dynamic analysis because it would not be underestimated (as demonstrated in Sect. 3). Moreover, the computational cost for nonlinear analyses is reduced.

A GMPE proposed by López-Castañeda and Reinoso (2022) was used to estimate the expected value of \({D}_{rS}\) at each site. The GMPE was developed based on historical data of interplate earthquakes and using a linear mixed-effects model (Pinheiro and Bates 2000; Demidenko 2004) and has the following form

$$\mathrm{ln}\left({D}_{rS}\right)={\beta }_{0}+{\beta }_{1}\mathrm{ln}\left({T}_{s}\right)+\left({\beta }_{2}+{\beta }_{3} {M}_{w}\right)\mathrm{ln}\left(R\right)+\eta$$
(3)

where \(R\) is an explanatory variable representing the source-to-site distance and can be measured using either \({R}_{hyp}\) or \({R}_{rup}\); \(\mathrm{ln}\left({D}_{rS}\right)\), \(\mathrm{ln}\left({T}_{s}\right)\), and \(\mathrm{ln}\left(R\right)\) are the natural logarithms of \({D}_{rS}\), \({T}_{s}\), and \(R\), respectively; and \(\eta ={b}_{0}+e\) is the composite model error whose terms have prior distributions \({b}_{0}\sim \mathcal{N}\left(0,{\sigma }_{b}^{2}\right)\) and \(e\sim \mathcal{N}\left(0,{\sigma }_{w}^{2}\right)\). The estimates of the model coefficients \({\beta }_{i}\), i = 1, …, 3, and variances \({\sigma }_{b}^{2}\) and \({\sigma }_{w}^{2}\) are presented in Table 3. Specifically, Table 3 presents the parameter estimates for two GMPEs, namely, Model A and Model B. Model A considers \({R}_{rup}\) as the measure defining the explanatory variable \(R\), whereas Model B considers \({R}_{hyp}\) instead.

Table 3 Estimates of the model coefficients and variance components of the GMPE for \({D}_{rS}\) that was given in Eq. (3)
Full size table

It should be mentioned that, for the development of the GMPEs, López-Castañeda and Reinoso (2022) obtained the values of \({D}_{rS}\) from hundreds of accelerograms bounded by the acceleration threshold equal to 2 cm/s2. The accelerograms were recorded at sites located in the lakebed zone of Mexico City. Therefore, the GMPEs are regionally applicable.

Thus, the duration of the synthetic accelerograms is obtained from two earthquake-specific scenarios. The first scenario considered an earthquake with \({M}_{w}\) = 7.5 occurring at \({R}_{hyp}\) = 250 km. The second scenario considered an earthquake with same magnitude but occurring at \({R}_{hyp}\) = 500 km. For each site, Table 4 summarizes the variation of the mean of \({D}_{rS}\), denoted as \({\mu }_{{D}_{rS}}\), and the mean plus/minus one standard deviation of \({D}_{rS}\), denoted as \({\mu }_{{D}_{rS}}\pm {\sigma }_{{D}_{rS}}\), obtained using Model B. Note that, under the assumption that \({b}_{0}\) and \(e\) are normally distributed, it can be said that \(\mathrm{ln}\left({D}_{rS}\right)\) is also normally distributed with mean, denoted as \({\mu }_{\mathrm{ln}\left({D}_{rS}\right)}\), equal to the function \(f\left({T}_{s},{M}_{w},R,{\beta }_{i}\right)\), \(i\) = 1, …, 3, defining Eq. (3) and variance \({\sigma }_{T}^{2}={\sigma }_{w}^{2}+{\sigma }_{b}^{2}\). Then, \({D}_{rS}\) can be defined by a lognormal distribution with mean \({\mu }_{{D}_{rS}}\) and variance \({\sigma }_{{D}_{rS}}^{2}\), which can be computed as follows:

$${\mu }_{{D}_{rS}}=\mathrm{exp}\left({\mu }_{\mathrm{ln}\left({D}_{rS}\right)}+\frac{{\sigma }_{T}^{2}}{2}\right)$$
(4a)

and

Table 4 Mean and mean plus/minus one standard deviation of \({D}_{rS}\) computed using Model B
Full size table
$${\sigma }_{{D}_{rS}}^{2}=\left[\mathrm{exp}\left({\sigma }_{T}^{2}\right)-1\right]\mathrm{exp}\left(2{\mu }_{\mathrm{ln}\left({D}_{rS}\right)}+{\sigma }_{T}^{2}\right)$$
(4b)

From the results shown in Table 4, the expected value of \({D}_{rS}\) for the site with \({T}_{s}\) = 4.0 s is ~ 1.3 and ~ 1.8 times greater than the expected values of \({D}_{rS}\) for the sites with \({T}_{s}\) = 2.5 s and 1.3 s, respectively. The intense phase of the ground motion caused by an interplate earthquake with \({M}_{w}\) = 7.5 that occurred at \({R}_{hyp}\) = 250 km can vary from 65 to 102 s in the site with \({T}_{s}\) = 1.3 s, from 92 to 143 s in the site with \({T}_{s}\) = 2.5 s, and from 118 to 183 s in the site with \({T}_{s}\) = 4.0 s. The latter indicates that there is a positive correlation between \({T}_{s}\) and \({D}_{rS}\). On the other hand, regardless of the site, the estimates of \({\mu }_{{D}_{rS}}\) and \({\mu }_{{D}_{rS}}\pm {\sigma }_{{D}_{rS}}\) decrease by ~ 15% by increasing the value of \({R}_{hyp}\) to 500 km. The latter indicates that there is a negative correlation between \({R}_{hyp}\) and \({D}_{rS}\).

Thus, six sets of synthetic accelerograms were generated per site and value of \(PGA\). The synthetic accelerograms of each set have the same duration. For instance, Fig. 8 shows a sample of four synthetic accelerograms with a duration equal to 65 s, which corresponds to the estimate of \({\mu }_{{D}_{rS}}-{\sigma }_{{D}_{rS}}\) obtained for the site with \({T}_{s}\) = 1.3 s and considering \({R}_{hyp}\) = 250 km. It should be mentioned that, for the generation of the synthetic accelerograms, it was necessary to establish amplitude envelopes consistent with the intense phase of accelerograms recorded at each site caused by earthquake scenarios as those governing the design-level seismic loadings.

To evaluate the seismic response of the equivalent SDOF system when subjected to the synthetic accelerograms, two damage responses were evaluated, namely, the peak displacement of the system (i.e., \({u}_{max}\)) and the hysteretic energy, \({E}_{H}\), dissipated by it. Whereas the former was determined directly from each nonlinear dynamic analysis, the second was taken as the area enclosed by the hysteresis loop resulting from each analysis. These loops are presented as the isolated forces on the spring of the equivalent SDOF system and its displacement.

Figure 9 summarizes the structural responses corresponding to the case in which the equivalent SDOF system was subjected to the synthetic accelerograms with durations associated with an earthquake that occurred at \({R}_{hyp}\) = 250 km and from a site with \({T}_{s}\) = 1.3 s. Note that some intensities have been omitted in the figure for a clearer visualization of the results, which are presented as boxplots. It can be seen from Fig. 9 that the medians of both \({u}_{max}\) and \({E}_{H}\) increase as the strong-motion duration increases for values of \(PGA\) greater than 0.2 g. These tendencies are anticipated for cumulative response parameters such as hysteretic energy, whereas they might seem unusual for structural displacements. The incremental relation between the duration and structural displacement at these intensities is attributed to the fact that once the equivalent SDOF system starts to show inelastic behavior, the more it continues deforming, the more likely for the residual displacement to show greater values. On the other hand, the differences between the medians of both \({u}_{max}\) and \({E}_{H}\) are not noticeable for smaller values of \(PGA\) (e.g., of 0.1 g) because the equivalent SDOF system maintains a linear-elastic behavior. The same trends were observed for the case in which \({R}_{hyp}\) = 500 km.

Fig. 9
figure 9

IDA results from accelerograms with durations associated with an earthquake that occurred at \({R}_{hyp}\) = 250 km from a site with \({T}_{s}\) = 1.3 s

Full size image

In Fig. 10 are shown the IDA results for \({u}_{max}\) for all sites. These results consider the synthetic accelerograms whose duration was equal to the estimates of \({\mu }_{{D}_{rS}}-{\sigma }_{{D}_{rS}}\) computed for a distance \({R}_{hyp}\) = 500 km (colored blue, and hereafter called “short-duration ground motions”) and to the estimates of \({\mu }_{{D}_{rS}}+{\sigma }_{{D}_{rS}}\) computed for a distance \({R}_{hyp}\) = 250 km (colored red, and hereafter called “long-duration ground motions”). Analogously, Fig. 11 shows the IDA results for \({E}_{H}\) for all sites. From both figures two features are evident: (i) the median of responses seems to be greater for long-duration ground motions at greater values of \(PGA\) and (ii) the dispersion in the data is also proportional to the value of \(PGA\). From the dispersion of the data at large values of \(PGA\), it can be inferred that some observations show lesser values of hysteretic energy than others at lower values of \(PGA\). This is attributed to how the amplitudes are distributed along the accelerogram. That is, if the record displays the occurrence of large amplitudes of acceleration at an early time step, it is more likely for the equivalent SDOF system to reach its ultimate displacement at this step, leaving it with no opportunity of dissipating energy via damage, i.e., hysteresis. Figure 12 depicts three examples to illustrate this situation. Specifically, this figure shows the seismic response of the equivalent SDOF system when it is subjected to a sample of three synthetic accelerograms with a duration equal to 183 s, i.e., the estimate of \({\mu }_{{D}_{rS}}+{\sigma }_{{D}_{rS}}\) computed using Model B and taking \({T}_{s}\) = 4.0 s and \({R}_{hyp}\) = 250 km. Thus, a crucial factor in the proper simulation of accelerograms is how the amplitudes are distributed along the signal. As mentioned before, the distribution of amplitudes from accelerograms recorded at the selected stations was used as a reference for the generation of the synthetic accelerograms.

Fig. 10
figure 10

IDA results for \({u}_{\mathrm{max}}\). The blue boxplots correspond to the synthetic accelerograms whose duration was equal to the estimates of \({\mu }_{{D}_{rS}}-{\sigma }_{{D}_{rS}}\) computed for \({R}_{hyp}\) = 500 km. The red boxplots correspond to the synthetic accelerograms whose duration was equal to the estimates of \({\mu }_{{D}_{rS}}+{\sigma }_{{D}_{rS}}\) computed for a \({R}_{hyp}\) = 250 km

Full size image
Fig. 11
figure 11

IDA results for \({E}_{H}\). The blue boxplots correspond to the synthetic accelerograms whose duration was equal to the estimates of \({\mu }_{{D}_{rS}}-{\sigma }_{{D}_{rS}}\) computed for \({R}_{hyp}\) = 500 km. The red boxplots correspond to the synthetic accelerograms whose duration was equal to the estimates of \({\mu }_{{D}_{rS}}+{\sigma }_{{D}_{rS}}\) computed for \({R}_{hyp}\) = 250 km

Full size image
Fig. 12
figure 12

Influence of amplitude occurrence on hysteresis. The three accelerograms (upper figures) display the same values of \(PGA\) (0.4 \(g\)) and duration (183 s), which correspond to an earthquake that occurred at \({R}_{hyp}\) = 250 km from a site with \({T}_{s}\) = 4.0 s

Full size image

Recall that the equivalent SDOF system was modeled as bi-linear elastic–plastic (see Fig. 2b), but due to the \({F}_{k}\)-axis scale selected to represent the hysteresis in Fig. 12 this behavior is less notorious. A closer inspection of any of the hysteresis loops displayed in the figure can indicate the yielding force of ~ 400 kN and subsequent hardening, as defined in Sect. 2.

5 Influence of site-specific strong-motion duration on structural performance

Fragility functions are valuable tools for decision making in risk analysis and structural vulnerability evaluation because they provide a suitable prognosis of potential structural damage during an earthquake. Specifically, a fragility function describes the conditional probability of exceeding a specific damage state, say \(ds\), for different ground-motion levels \(im\) (Singhal and Kiremidjian 1996). Consider:

$${\overline{F} }_{damage|IM}\left(ds|im\right)=P\left(damage>ds|IM=im\right)$$
(5)

where \({\overline{F} }_{damage|IM}\) is the complementary cumulative distribution function (CDF) defined as:

$${\overline{F} }_{damage|IM}\left(ds|im\right)=1-P\left(damage\le ds|IM=im\right)$$
(6)

In this study, lognormal and extreme-value probability functions at each \(im\) were used to estimate the probabilities of exceedance of a specific \(ds\).

Thus, a fragility function can be expressed as a continuous function of a (real-valued) random variable \(IM\) as:

$${F}_{IM}\left(im\right)=\Phi \left(\frac{\mathrm{ln}\left(im\right)-\theta }{\lambda }\right)$$
(7)

where \(\Phi \left(\bullet \right)\) is the CDF of the standard normal distribution. The parameters \(\theta\) and \(\lambda >0\) are two real numbers. Developing of continuous fragility functions involved estimating the parameters \(\theta\) and \(\lambda\). Their estimators were determined from linear regression, knowing that \({\Phi }^{-1}\left[P\left(damage>ds|im\right)\right]=\frac{1}{\lambda }\mathrm{ln}\left(im\right)-\frac{\theta }{\lambda }\) resembles a model with the form \(y=ax+b\).

Afterward, fragility functions were developed considering two engineering approaches to characterize each \(ds\) of the steel frame building (represented by the equivalent SDOF system defined in Sect. 2). While the first approach uses \({u}_{max}\) as the EDP, the second approach uses an energy-capacity damage index. Moreover, for each approach, \(ds\) was defined according to various structural performance levels, namely, operational, life safety, and collapse (SEAOC 1999). Note that \(PGA\) was considered as \(IM\) and the values of \(im\) were taken equal to 0.1 g to 0.4 g in increments of 0.05 g for the estimation of Eq. (5). The results are presented next.

5.1 Fragility functions based on displacement

For the fragility functions based on displacement as EDP, the associated performance level to each \(ds\) was determined from the capacity curve of the equivalent SDOF system presented in Fig. 2, specifically:

  • For the operational performance level, \(ds\) was set equal to the yielding displacement of the equivalent SDOF system, i.e., \(ds\) = \({u}_{y}\)  = 17.7 cm.

  • For the life safety performance level, \(ds\) was set as \({u}_{y}+0.6{u}_{p}\), where \({u}_{p}={u}_{u}-{u}_{y}\). Here, \({u}_{u}\) = 58.6 cm is the ultimate displacement of the equivalent SDOF system. Therefore, \(ds\) was assumed equal to 42.2 cm.

  • For the last performance level, which is associated with the collapse of the structure, \(ds\) was considered equal to \({u}_{u}\).

The probability of exceeding each \(ds\) at each value of \(PGA\) was evaluated for the IDA results of \({u}_{max}\) obtained from the synthetic accelerograms whose duration was equal to \({\mu }_{{D}_{rS}}-{\sigma }_{{D}_{rS}}\) given that \({R}_{hyp}\) = 500 km, i.e., the short-duration ground motions, and to \({\mu }_{{D}_{rS}}+{\sigma }_{{D}_{rS}}\) given that \({R}_{hyp}\) = 250 km, i.e., the long-duration ground motions. For most cases, a lognormal distribution showed adequacy in representing the probability distribution of the structural displacements when analyzing each value of \(PGA\). The extreme value distribution showed a better representation of the data at large values of \(PGA\). The latter can be inferred, e.g., from Fig. 10, where the boxplots show notorious asymmetry in the sample distribution at \(PGA\) = 0.4 g for the site with \({T}_{s}\) = 4.0 s. Figure 13 shows the fragility curves developed for each site. The absolute differences in the probability of failure between the results from short- and long-duration ground motions for each \(ds\) are also presented in Fig. 13 beneath the graphic of its correspondent fragility functions. These differences in probability were computed as \(\Delta {F}_{PGA}=\left|{F}_{PGA}^{L}-{F}_{PGA}^{S}\right|\), where \({F}_{PGA}^{L}\) and \({F}_{PGA}^{S}\) are the estimates of continuous fragility for the long- and short-duration ground motions, respectively. The estimates of \(\theta\) and \(\lambda\) that describe the fragility functions are summarized in Table 5.

Fig. 13
figure 13

Fragility curves considering displacement as EDP (upper) and fragility difference (bottom) for the sites with \({T}_{s}\) equal to 1.3 s, 2.5 s, and 4.0 s. The dashed lines correspond to the operational performance level, the long-short dashed lines to the life safety performance level, and the solid lines to the collapse performance level

Full size image
Table 5 Estimates of the \(\theta\) and \(\lambda\) for the fragility functions developed in this study
Full size table

As seen in Fig. 13, for the operational performance level, which implies slight or minimum damage to the structure, negligible differences are seen in the fragility for sites with values of \({T}_{s}\) equal to 1.3 s or 2.5 s. In this case, values of \(\Delta {F}_{PGA}\) up to ~ 20% are observed for the site with \({T}_{s}\) = 4.0 s, which become notorious as \(PGA\) approaches 0.2 g. The latter can be attributed to the onset of yielding of the equivalent SDOF system at such values of \(PGA\). For the life safety performance level, higher probabilities of failure are seen in the fragility estimates computed from long-duration ground motions in comparison with those from short-duration ground motions. Particularly, the site with \({T}_{s}\) = 1.3 s displays a broad range of intensity for \(\Delta {F}_{PGA}\). This broadness might be attributable to the fact that such a site shows the greatest response-spectrum amplitudes in the range of periods near the fundamental period of the equivalent SDOF system, i.e., the structure is more excited when it starts to foray into an inelastic response. At the same time, the site with \({T}_{s}\) = 4.0 s shows a probability of damage 30% higher for long-duration ground motions. Negligible differences are seen for the site with \({T}_{s}\) = 2.5 s. Ultimately, greater differences in fragility estimates are seen for the performance level associated with the collapse of the structure. Values of \(\Delta {F}_{PGA}\) up to ~ 30% in the probability of collapse are seen for the site with \({T}_{s}\) = 4.0 s.

5.2 Fragility functions based on energy capacity

Based on energy functions (Chopra 1995) and the research work by Pujades et al. (2015), Díaz et al. (2017) proposed a damage index for steel buildings that can be obtained from the capacity curve of a structure. The expression for that damage index, denoted as \({DI}_{EC}\), is

$${DI}_{EC}={\eta }_{E}{E}_{S}{\left(u\right)}_{N}+\left(1-{\eta }_{E}\right){E}_{H}{\left(u\right)}_{N}$$
(8)

where \({E}_{S}{\left(u\right)}_{N}\) and \({E}_{H}{\left(u\right)}_{N}\) are, respectively, the strain energy and the hysteretic energy dissipated by the structure. They are a function of the displacement and are normalized with respect to their contribution to the energy capacity of the system. In Eq. (8), \({\eta }_{E}\) is a proportionality factor that defines how much the strain energy contributes to the damage to the structure. According to Díaz et al. (2017), values of \({\eta }_{E}\) ranging from 0.6 to 0.7 have been determined for steel structures.

For the development of the energy-based fragility curves, a value of \({\eta }_{E}\) equal to 0.68 was considered and the damage index \({DI}_{EC}\) associated with each performance level was determined by computing the normalized energy functions that intervene in Eq. (8) as follows:

$${E}_{S}{\left(u\right)}_{N}=\left\{\begin{array}{cc}0& 0\le u\le {u}_{y}\\ \frac{{E}_{S}\left(u\right)}{{E}_{S}\left({u}_{d}\right)}& {u}_{y}<u\le {u}_{u}\end{array}\right.$$
(9a)

and

$${E}_{H}{\left(u\right)}_{N}=\left\{\begin{array}{cc}0& 0\le u\le {u}_{y}\\ \frac{{E}_{H}\left(u\right)}{{E}_{H}\left({u}_{d}\right)}& {u}_{y}<u\le {u}_{u}\end{array}\right.$$
(9b)

where \({u}_{d}\) was taken as \({u}_{y}+0.6{u}_{p}\) for the life safety performance level and as \({u}_{u}\) for the collapse performance level.

Figure 14 shows a schematic for the determination of the energy functions based on the capacity curve of the SDOF system. Note that, by definition, the values of \(D{I}_{EC}\) are zero for displacements lesser than \({u}_{y}\). Thus, fragility functions associated with the operational performance level were omitted. Nevertheless, as can be inferred from the IDA results shown in Figs. 10 and 11, minimum differences between short- and long-duration ground motions were to be expected at this damage state. It is worth emphasizing that Díaz et al. (2017) normalized the energy functions by taking \({u}_{d}\) equal to \({u}_{u}\). Although this study considered such a value for analyzing the collapse performance level of the structure, \({u}_{d}\) =\({u}_{y}+0.6{u}_{p}\) was set to have a comparable index to evaluate the life safety performance level. For the probability estimates of these two performance levels, \(ds\) equals one.

Fig. 14
figure 14

Schematic for the determination of the energies \({E}_{S}\) and \({E}_{H}\) dissipated by the equivalent SDOF system

Full size image

Figure 15 shows the fragility curves developed for each site. The differences in the probability of failure between the results from short- and long-duration ground motions are also presented in the figure. The estimates of \(\theta\) and \(\lambda\) that describe the fragility functions are summarized in Table 5. Similar to the displacement-based fragility cases, an extreme value distribution showed adequacy in representing the probability distribution of \({DI}_{EC}\) at values of \(PGA\) of approximately 0.4 g, whereas a lognormal distribution showed better representation for the remaining values of \(PGA\). As displayed in Fig. 15, a higher probability of failure is evident for long-duration ground motions than for short-duration ground motions for all sites. Only negligible differences are seen at the site with \({T}_{s}\) = 2.5 s for the life safety performance level. This result might owe to the fact that the response spectrum of this site has its higher amplitudes far enough from \({T}_{1}\) (contrary to the sites with \({T}_{s}\) = 1.3 s and \({T}_{s}\) = 4.0 s, whose response spectra have peaks near \({T}_{1}\)). Notwithstanding, the higher differences in the probability of collapse are seen for the site with \({T}_{s}\) = 2.5 s.

Fig. 15
figure 15

Fragility functions considering hysteretic energy as EDP (upper) and fragility difference (bottom) for sites with \({T}_{s}\) equal to 1.3 s, 2.5 s, and 4.0 s. The long-short dashed lines represent the life safety performance level, whereas the solid lines the collapse performance level

Full size image

6 Discussion of the results and conclusions

Over the years, the strong-motion duration has been recognized as a parameter that influences earthquake damage potential on civil structures. However, it has not been considered with the formality that it deserves within the formulations dictated in any of the different technical standards for seismic design of structures. The foregoing can be attributed to the lack of consensus of the regulatory committees in matters as basic as how to define such a ground-motion parameter. Interesting proposals have been reported in the literature to include the strong-motion duration when selecting accelerograms for structural performance assessment. For instance, Chandramohan et al. (2016b) proposed a procedure to compute the source-specific target distribution of duration at a specific hazard level, based on a generalization of the conditional response spectrum methodology. Unfortunately, the scarcity of ground-motion data in several regions of the world somehow impedes the proper development of such spectra due to the deficit of GMPEs (not only for the strong-motion duration but for other ground-motion parameters as well). To overcome this need, the authors advocate the implementation or enhancement of accelerograph networks throughout the world, especially in highly seismic regions, to urgently develop GMPEs. At the same time, the scarcity of ground-motion data prompts researchers to use accelerograms recorded in different regions of the world as seismic loadings for nonlinear dynamic analysis. To passably resemble the maximum amplitudes and frequency content of said accelerograms with those expected in the site where the structures are located, various researchers scaled the selected accelerograms so that their response spectra matched a site-specific target spectrum. In all cases, the duration of the accelerograms remains intact. Therefore, no matter how much they resemble in amplitude and frequency content, such accelerograms are not fully representative of the site of interest.

Although it is important to gain knowledge of the performance of structures subjected to ground motions (using accelerograms), the action of arbitrarily and subjectively classifying them as short or long solely based on the tectonic environment of the causative earthquakes leads to results that may be disjointed. As shown in Sect. 3, ground-motion durations caused by an interplate earthquake with \({M}_{w}\) = 7.4 can increase more than 3.75 times from a site with \({T}_{s}\) = 0.5 s to a site with \({T}_{s}\) = 4.0 s within a ~ 8 km radius. This variation allows the authors to say that even ground-motion durations caused by the same tectonic environment could be qualitatively classified as short or long.

Thus, this study demonstrates the importance of proper characterization of ground-motion duration when selecting design accelerograms. Specifically, the global response of a four-story, one-bay steel frame (represented by an equivalent SDOF system) located at three hypothetical sites in Mexico City was evaluated via IDAs, for which spectrally equivalent accelerograms were simulated such that their duration became a varied parameter. Specifically, the simulated accelerograms contemplate only the portion that lasts the intense phase of the ground motion. The length of this portion was determined according to a recently published GMPE developed by López-Castañeda and Reinoso (2022) that allows estimating \({D}_{rS}\) as a function of the seismological parameters \({M}_{w}\), \({R}_{hyp}\), and \({T}_{s}\). For each one of the three hypothetical sites, the duration of the synthetic accelerograms was obtained from two specific earthquake scenarios. Whereas one scenario considers an earthquake of \({M}_{w}\) = 7.5 that occurred at \({R}_{hyp}\) = 250 km, the other considers that the same earthquake occurred at \({R}_{hyp}\) = 500 km. From the results given in Table 4, one can tell that \({D}_{rS}\) increases as \({T}_{s}\) increases. Overall, the differences in the estiamted values of duration are smaller for the scenario earthquake with \({R}_{hyp}\) = 500 km. Moreover, a difference of 46 s was obtained when comparing the estimates of \({\mu }_{{D}_{rS}}-{\sigma }_{{D}_{rS}}\) computed for \({R}_{hyp}\) = 500 km and the estimates of \({\mu }_{{D}_{rS}}+{\sigma }_{{D}_{rS}}\) computed for \({R}_{hyp}\) = 250 km, for the site with \({T}_{s}\) = 1.3 s. That is, \({D}_{rS}\) at that site can last from 56 to 102 s based on the considered earthquake scenarios. On the other hand, overall differences of 65 s and 83 s were computed for the sites with \({T}_{s}\) equal to 2.5 s and 4.0 s, respectively. Thus, as mentioned previously, even ground-motion durations caused by earthquakes with the same tectonic environment and by the same earthquake could be classified as short or long.

From the IDA results presented in Sect. 3 one can tell that the strong-motion duration has a significant effect on both displacement and energy demands of the structural system analyzed. As can be observed from Figs. 9, 10, and 11, higher differences in damage are seen when subjecting the system to accelerograms with longer durations in comparison with accelerograms having shorter durations. The magnitude of these differences depends highly on the response-spectrum characteristics of each site. While the influence of the strong-motion duration on energy-based demands may be fairly obvious, it is not so evident for displacement-based demands. However, as seen from Figs. 9 and 10, nontrivial differences in the values of \({u}_{max}\) are observed for all the sites when comparing short- and long-duration ground motions. These differences become more notorious at higher values of \(PGA\). This behavior is justified by the fact that, once the elastic limit of the analyzed structure is exceeded, the longer the system is displaced beyond this limit, the greater the expected deformations. Thus, longer accelerograms will more likely lead to higher values of inelastic displacement.

To delve more into the influence of the strong-motion duration on the seismic response of the analyzed structural system, the probability of reaching or exceeding damage states associated with various performance levels was also evaluated. In this regard, in addition to the classical approach for the development of fragility functions, which uses structural displacement as EDP, fragility functions were also developed based on the energy capacity of the analyzed structural system. As expected, for all sites, minimum differences between short- and long-duration ground motions were observed for a damage state related to the operational performance level of the structure. On the other hand, differences of ~ 30% were observed when considering displacement as EDP either for the life safety or collapse performance levels. Similar tendencies were observed when considering energy capacity as EDP but with differences up to 40%.

The results obtained in this study confirm that, as rightly mentioned by various researchers, e.g., Raghunandan and Liel (2013), for a complete seismic risk analysis, it is necessary to consider realistic earthquake scenarios that could affect the site where a structure of interest is located. In this regard, it should be mentioned that, although a certain degree of correlation is expected between the strong-motion duration and \(PGA\), in this study these ground-motion parameters had to be assumed mutually independent to explore their effect on the performance of the structural system analyzed (and also to be able to objectively compare the results with those reported in studies such as those summarized in Table 1). The next step leads to the generation of site-specific conditional spectra, and their consideration in the seismic design formulae given in structural standards. While this is happening, the use of site-specific design accelerograms is widely recommended. If these are simulated, it should be ensured that, besides their compatibility with the response spectra associated with the site of interest, their amplitude distribution and duration must also be compatible with envelopes of accelerograms recorded at the site, if possible.