REASSESS V2.0: software for single- and multi-site probabilistic seismic hazard analysis

Abstract

Probabilistic seismic hazard analysis (PSHA) is generally recognized as the rational method to quantify the seismic threat. Classical formulation of PSHA goes back to the second half of the twentieth century, but its implementation can still be demanding for engineers dealing with practical applications. Moreover, in the last years, a number of developments of PSHA have been introduced; e.g., vector-valued and advanced ground motion intensity measure (IM) hazard, the inclusion of the effect of aftershocks in single-site hazard assessment, and multi-site analysis requiring the characterization of random fields of cross-correlated IMs. Although software to carry out PSHA has been available since quite some time, generally, it does not feature a user-friendly interface and does not embed most of the recent methodologies relevant from the earthquake engineering perspective. These are the main motivations behind the development of the practice-oriented software presented herein, namely REgionAl, Single-SitE and Scenario-based Seismic hazard analysis (REASSESS V2.0). In the paper, the seismic hazard assessments REASSESS enables are discussed, along with the implemented algorithms and the models/databases embedded in this version of the software. Illustrative applications exploit the potential of the tool, which is available at http://wpage.unina.it/iuniervo/doc_en/REASSESS.htm.

1 Introduction

The classical (single-site) formulation of probabilistic seismic hazard analysis (PSHA) aims at evaluating the rate of earthquakes causing exceedance of any arbitrary ground-motion intensity measure (IM) threshold (im) at a site of interest (Cornell 1968). PSHA lies at the basis of seismic risk assessment according to the performance-based earthquake engineering paradigm (Cornell and Krawinkler 2000) and serves for the determination of seismic actions for structural design in several countries.

The probabilistic assessment of the seismic threat at a site is, in principle, not straightforward for structural engineers because it requires the employment of models and skills they do not typically have at hand. For this reason, during the last four decades, computer software to carry out PSHA have become available, starting from EQRISK (McGuire 1976). Other relevant codes are, for example, SEISRISK III (Bender and Perkins 1987), OpenSHA (Field et al. 2003) and CRISIS (Ordaz et al. 2013); see Danciu et al. (2010). Recently, the global earthquake model (GEM) foundation developed OpenQuake (Pagani et al. 2014) that has been adopted, among others, within the EMME (Giardini et al. 2018) and SHARE (Woessner et al. 2015) hazard assessment projects.

PSHA has been significantly extended since its introduction in the late sixties. For example, its classical version refers to a scalar IM, while advanced structural assessment procedures may require hazard in terms of vector-valued IMs (Baker and Cornell 2006b) or, equivalently, development of conditional hazard for secondary IMs (Iervolino et al. 2010). Typically, PSHA is carried out considering spectral accelerations as the IM, while in the last years more efficient intensity measures have been introduced for more accurate seismic structural assessment (e.g., Cordova et al. 2000; Bianchini et al. 2009; Bojórquez and Iervolino 2011). Furthermore, PSHA, as normally implemented, only refers to mainshocks (see next section) neglecting the effect of foreshocks and aftershocks on seismic hazard for a site. In other words, PSHA only considers the exceedance of the im threshold of interest due to prominent magnitude earthquakes within a cluster of events; i.e., the typical way earthquakes occur (e.g., Boyd 2012; Marzocchi and Taroni 2014). This is to take advantage of the ease of calibration and mathematical manageability of the homogeneous Poisson process (HPP) (e.g., Cornell 1968; McGuire 2004). Nevertheless, recently, a generalized hazard integral, able to account for the effect of aftershocks without losing the advantages of HPP, was developed and named sequence-based probabilistic seismic hazard analysis or SPSHA (Iervolino et al. 2014). Finally, in some situations, for example in the case of risk assessment of building portfolios or spatially-distributed infrastructure, hazard must account for exceedances at multiple sites jointly. In this case, which may be referred to as multi-site probabilistic seismic hazard analysis (MSPSHA), the key issue is to account for the stochastic dependence existing among the processes counting exceedances at each of the considered sites (e.g., Eguchi 1991; Giorgio and Iervolino 2016).

To provide an engineering-oriented tool including a number of state-of-the-art advances in probabilistic seismic hazard analysis, a stand-alone software named REgionAl, Single-SitE and Scenario-based Seismic hazard analysis (REASSESS V2.0), with a graphical user interface (GUI), has been developed and it is presented herein.¹ To this aim, the remainder of this paper is structured such that the hazard assessment methodologies considered are recalled first, along with the algorithms and numerical procedures developed for their implementation. Subsequently, REASSESS V2.0 is presented with the main input and output options. Finally, illustrative examples show the tools capabilities for earthquake engineering practice.

2 Single-site PSHA essentials

In classical PSHA, earthquakes on a seismic source are assumed to occur according to a HPP characterized by a rate, $\nu$. In other words, the probability of observing, in the time interval $\Delta T$, a number of earthquakes, $N\left( {\Delta T} \right)$, exactly equal to n is given by Eq. (1).

$$P\left[ {N\left( {\Delta T} \right) = n} \right] = \frac{{\left( {\nu \cdot \Delta T} \right)^{n} }}{n!} \cdot e^{ - \nu \cdot \Delta T}$$

(1)

The objective of PSHA is to compute the rate, $\lambda_{im}$, of seismic events exceeding the im threshold at a site of interest. Such a rate completely defines the HPP describing the occurrence of the events causing exceedance of im. In other words, the probability that, in the time interval $\Delta T$, the number of earthquakes causing exceedance of im at the site, $N_{im} \left( {\Delta T} \right)$, is equal to n, is given by Eq. (2).

$$P\left[ {N_{im} \left( {\Delta T} \right) = n} \right] = \frac{{\left( {\lambda_{im} \cdot \Delta T} \right)^{n} }}{n!} \cdot e^{{ - \lambda_{im} \cdot \Delta T}}$$

(2)

For a site subjected to earthquakes generated at $n_{s}$ seismic sources, the rate $\lambda_{im}$ can be computed as illustrated in Eq. (3), known as the hazard integral.

$$\lambda_{im} = \sum\limits_{i = 1}^{{n_{s} }} {\nu_{i} \cdot \int\limits_{M} {\int\limits_{X} {\int\limits_{Y} {P\left[ {IM > im\left| {m,x,y} \right.} \right]_{i} \cdot f_{M,X,Y,i} \left( {m,x,y} \right) \cdot dm \cdot dx \cdot dy} } } }$$

(3)

In the equation the i subscript indicates the ith seismic source; $\nu_{i}$ is the rate of earthquakes above a minimum magnitude of interest $\left( {m_{{\rm min} ,i} } \right)$ and below the maximum magnitude deemed possible for the source $\left( {m_{{\rm max} ,i} } \right)$; $f_{M,X,Y,i} \left( {m,x,y} \right)$ is the joint probability density function (PDF) of earthquake magnitude $M$ and location $\left\{ {X,Y} \right\}$; $P\left[ {IM > im\left| {m,x,y} \right.} \right]_{i}$, typically provided by a ground motion prediction equation (GMPE), is the exceedance probability conditional on the magnitude and location (via a source-to-site distance metric). GMPEs, usually, also account for soil type, rupture mechanism and other parameters that are not explicitly considered in the notation here for the sake of simplicity (see also Sect. 2.1).

It is also for simplicity that the location is defined in Eq. (3) by means of two horizontal coordinates that can represent, for example, the epicenter. This representation is typically used in the case of areal source zones; however, it is frequent that hazard assessments have to account for three-dimensional faults (see Sect. 5.1). Moreover, it also happens that the distance metric of the selected GMPE is not consistent with the way location is defined. In these cases, because the relationship between location and source-to-site distance is not necessarily deterministic, the hazard integral has to account for the probabilistic distribution of the distance metric of the GMPE, conditional to the considered location parameters (e.g., Scherbaum et al. 2004).

Magnitude and location of the earthquake are often considered stochastically independent, that is $f_{M,X,Y,i} \left( {m,x,y} \right) = f_{M,i} \left( m \right) \cdot f_{X,Y,i} \left( {x,y} \right)$. The distribution $f_{M,i} \left( m \right)$ is often modeled as an exponential distribution in the $\left( {m_{{\rm min} ,i} ,m_{{\rm max} ,i} } \right)$ interval; i.e., of Gutenberg–Richter (G–R) type (Gutenberg and Richter 1944); however, other choices are also considered by literature (e.g., Convertito et al. 2006). The distribution of earthquake location, $f_{X,Y,i} \left( {x,y} \right)$, typically reflects the hypothesis of uniformly-distributed probability on the source. For further details on classical PSHA, the interested reader is referred to, for example, Reiter (1990).

Equation (3) can be numerically solved via a matrix formulation approximating the integrals with summations. To this aim, MATHWORKS-MATLAB^® provides a simple computing environment that can be used to evaluate this expression. The domain of the possible realizations of the magnitude random variable (RV) is discretized via k magnitude bins represented by the values $\left\{ {m_{1} ,m_{2} , \ldots ,m_{k} } \right\}$, while the seismic source is discretized by means of s point-like seismic sources, $\left\{ {\left( {x,y} \right)_{1} ,\left( {x,y} \right)_{2} , \ldots ,\left( {x,y} \right)_{s} } \right\}$. Given these two vectors of size $1 \times k$ and $1 \times s$, Eq. (3) can be approximated by Eq. (4), where the row vector approximates $f_{X,Y,i} \left( {x,y} \right)$ by a mass probability function (MPF) described by a vector in a way that each element is repeated $k$ times; i.e., the first $k$ elements are the probabilities of $\left( {x,y} \right)_{1}$, the elements from $k + 1$ until $2k$ are for $\left( {x,y} \right)_{2}$ and so on, until $\left( {x,y} \right)_{s}$. Thus, the row vector has size $1 \times \left( {k \cdot s} \right)$. The first column vector of Eq. (4) is a $\left( {k \cdot s} \right) \times 1$ vector and accounts for the GMPE: each element represents the exceedance probability conditional to magnitude and location. The second column vector of the equation collects the finite $k$ probabilities of event’s magnitude, identically repeated s-times, as shown and it is, again, a $\left( {k \cdot s} \right) \times 1$ vector. Finally, in the equation, the pointwise multiplication between matrices of the same size (i.e., the Hadamard product, represented by the $\otimes$ symbol) results in a matrix of the size of those multiplied, and in which each element is the product of the corresponding elements of the original matrices.

$$\begin{aligned} \lambda_{im} & = \sum\limits_{i = 1}^{{n_{s} }} {\nu_{i} \cdot } \left\{ {\begin{array}{*{20}c} {P\left[ {\left( {x,y} \right)_{1} } \right]} & {P\left[ {\left( {x,y} \right)_{1} } \right]} & \ldots & {P\left[ {\left( {x,y} \right)_{1} } \right]} & \ldots & {P\left[ {\left( {x,y} \right)_{s} } \right]} & {P\left[ {\left( {x,y} \right)_{s} } \right]} & \ldots & {P\left[ {\left( {x,y} \right)_{s} } \right]} \\ \end{array} } \right\}_{i} \\ & \quad \cdot \left( {\left\{ {\begin{array}{*{20}c} {P\left[ {IM > im|m_{1} ,\left( {x,y} \right)_{1} } \right]} \\ {P\left[ {IM > im|m_{2} ,\left( {x,y} \right)_{1} } \right]} \\ \vdots \\ {P\left[ {IM > im|m_{k} ,\left( {x,y} \right)_{1} } \right]} \\ \vdots \\ {P\left[ {IM > im|m_{1} ,\left( {x,y} \right)_{s} } \right]} \\ {P\left[ {IM > im|m_{2} ,\left( {x,y} \right)_{s} } \right]} \\ \vdots \\ {P\left[ {IM > im|m_{k} ,\left( {x,y} \right)_{s} } \right]} \\ \end{array} } \right\}_{i} \otimes \left\{ {\begin{array}{*{20}c} {P\left[ {m_{1} } \right]} \\ {P\left[ {m_{2} } \right]} \\ \vdots \\ {P\left[ {m_{k} } \right]} \\ \vdots \\ {P\left[ {m_{1} } \right]} \\ {P\left[ {m_{2} } \right]} \\ \vdots \\ {P\left[ {m_{k} } \right]} \\ \end{array} } \right\}_{i} } \right) \\ \end{aligned}$$

(4)

Equation (4), as already discussed with respect to Eq. (3), is written in the case location can be defined by means of two coordinates and the distance metric of the GMPE is a deterministic function of the location. Otherwise, it is necessary to account for the non-deterministic transformation of the location in source-to-site distance, which can be done in the same framework presented herein.

To compute the hazard curve, that is the function providing $\lambda_{im}$ as a function of im, the hazard integral has to be computed for a number of values of $im$, say q in number, discretizing the domain of IM, that is $\left\{ {im_{1} ,im_{2} , \ldots ,im_{q} } \right\}$. The corresponding rates, $\left\{ {\lambda_{{im_{1} }} ,\lambda_{{im_{2} }} , \ldots ,\lambda_{{im_{q} }} } \right\}$, can be obtained via a single matrix operation conceptually equivalent to Eq. (4); see Iervolino et al. (2016a).

2.1 Disaggregation

Disaggregation of seismic hazard (e.g., Bazzurro and Cornell 1999) is a procedure that allows identification of the hazard contribution of one or more RVs involved in the hazard integral: e.g., magnitude and source-to-site distance, $R$, which, as discussed, is a function of the earthquake location. Another RV typically considered in hazard disaggregation is $\varepsilon$ (epsilon). It is the number of standard deviations that $\log \left( {im} \right)$ is away from the median of the GMPE considered in hazard assessment. In fact, classical GMPEs are of the type in Eq. (5), where $\log \left( {im} \right)$ is related to magnitude, distance and other parameters.

$$\log \left( {im} \right) = \mu \left( {m,r} \right) + \theta + \sigma \cdot \varepsilon$$

(5)

In the equation, $\sigma \cdot \varepsilon$ is a zero-mean Gaussian RV with standard deviation $\sigma$; often it is split in inter- and intra-event components in a way that $\sigma = \sqrt {\sigma_{\text{intra}}^{2} + \sigma_{\text{inter}}^{2} }$. The $\mu \left( {m,r} \right)$ term depends on magnitude and distance, θ represents one or more coefficients accounting, for example, for the soil site class. Ultimately, $\mu \left( {m,r} \right) + \theta$ is the mean, and the median, of the logarithms of IM given $\left\{ {m,r,\theta } \right\}$. (Note that, although the majority of the GMPEs is of the type in Eq. (5), see Douglas (2014), most of the recent models have soil factors that also change with magnitude and distance. This representation is considered herein to discuss some shortcuts implemented in REASSESS and that apply only in this case; see Sects. 2.3, 4.1.)

The result of disaggregation is the joint PDF of $\left\{ {M,R,\varepsilon } \right\}$ conditional to the exceedance of an IM threshold, $f_{{M,R,\varepsilon \left| {IM} \right.}}$, as per Eq. (6).

$$f_{{M,R,\varepsilon \left| {IM} \right.}} \left( {m,r,e} \right) = \frac{{\sum\nolimits_{i = 1}^{{n_{s} }} {\nu_{i} \cdot I\left[ {IM > im|m,r,e} \right]_{i} \cdot f_{M,R,\varepsilon ,i} \left( {m,r,e} \right)} }}{{\lambda_{im} }}$$

(6)

In the equation, $I$ is an indicator function that equals one if IM is larger than im for a given magnitude, distance and $\varepsilon$, while $f_{M,R,\varepsilon ,i} \left( {m,r,e} \right)$ is the marginal joint PDF obtained from the product $f_{M,R,i} \left( {m,r} \right) \cdot f_{\varepsilon } \left( e \right)$.

From the engineering perspective, hazard disaggregation is useful to identify the characteristics of the earthquake scenarios providing the largest contribution to the hazard being disaggregated and, consequently, for hazard-consistent seismic input selection for structural assessment (e.g., Lin et al. 2013). Moreover, it is a required information to compute the conditional hazard for secondary intensity measures, which is briefly recalled in the next section. Finally, note that disaggregation can also be obtained for the occurrence of im, that is $IM = im$, and REASSESS provides also this result; i.e., McGuire (1995). For a discussion on whether exceedance or occurrence disaggregation is needed in earthquake engineering, see, for example, Fox et al. (2016).

2.2 Conditional hazard

Vector-valued probabilistic seismic hazard analysis (VPSHA), originally introduced by Bazzurro and Cornell (2002), provides the rate of earthquakes causing joint occurrence (or exceedance) of the thresholds of two IMs at the site. VPSHA could improve the prediction of structural damage (e.g., Baker 2007). If one of the two intensity measures can be considered of primary importance with respect to the other, conditional hazard (Iervolino et al. 2010) can be considered an alternative to VPSHA. Conditional hazard provides the distribution of a secondary intensity measure $\left( {IM_{2} } \right)$, conditional to the occurrence (or exceedance) of a threshold of the primary one, that is $IM_{1} = im_{1}$ (or $IM_{1} > im_{1}$). In the hypothesis of bivariate normality of the logarithms of the two IMs, the conditional mean $\left( {\mu_{{\log IM_{2} \left| {IM_{1} ,M,R} \right.}} } \right)$ and standard deviation $\left( {\sigma_{{\log IM_{2} \left| {IM_{1} } \right.}} } \right)$ of $\log \left( {IM_{2} } \right)$, given $IM_{1}$, magnitude and distance, are reported in Eq. (7).

$$\left\{ {\begin{array}{*{20}l} {\mu_{{\log IM_{2} \left| {IM_{1} ,M,R} \right.}} = \mu_{{\log IM_{2} \left| {M,R} \right.}} + \rho \cdot \sigma_{{\log IM_{2} \left| {M,R} \right.}} \cdot \frac{{\log IM_{1} - \mu_{{\log IM_{1} \left| {M,R} \right.}} }}{{\sigma_{{\log IM_{1} \left| {M,R} \right.}} }}} \hfill \\ {\sigma_{{\log IM_{2} \left| {IM_{1} } \right.}} = \sigma_{{\log IM_{2} }} \cdot \sqrt {1 - \rho^{2} } } \hfill \\ \end{array} } \right.$$

(7)

In the equation, $\mu_{{\log IM_{2} \left| {M,R} \right.}}$ and $\sigma_{{\log IM_{2} \left| {M,R} \right.}}$ are the mean and standard deviation of $\log IM_{2}$; $\mu_{{\log IM_{1} \left| {M,R} \right.}}$ and $\sigma_{{\log IM_{1} \left| {M,R} \right.}}$ are the mean and standard deviation of $\log IM_{1}$ according to the selected GMPE (these terms are simply indicated as $\mu \left( {m,r} \right)$ and $\sigma$, respectively, in Sect. 2.1); $\rho$ is the correlation coefficient between residuals of $\log IM_{1}$ and $\log IM_{2}$ at the site (e.g., Baker and Jayaram 2008). Thus, the conditional distribution of the logarithm of the secondary IM is given by Eq. (8) in which $f_{{M,R,\varepsilon \left| {IM_{1} } \right.}}$ is from disaggregation and $f_{{\log IM_{2} \left| {IM_{1} } \right.,M,R,\varepsilon }}$ is the distribtion with the parameters in Eq. (7).

$$f_{{\log IM_{2} \left| {IM_{1} } \right.}} \left( {\log im_{2} \left| {im_{1} } \right.} \right) = \int\limits_{M} {\int\limits_{R} {\int\limits_{\varepsilon } {f_{{\log IM_{2} \left| {IM_{1} } \right.,M,R,\varepsilon }} \left( {\log im_{2} \left| {im_{1} ,m,r,e} \right.} \right) \cdot f_{{M,R,\varepsilon \left| {IM_{1} } \right.}} \left( {m,r,e\left| {im_{1} } \right.} \right) \cdot dm \cdot dr} } } \cdot d\varepsilon$$

(8)

Factually, the conditional hazard formulation of Eq. (8) allows VPSHA to be an output of REASSESS. This is because, for example, $f_{{\log IM_{2} \left| {IM_{1} } \right.}}$ multiplied by the absolute value of the derivative of the hazard curve from Eq. (3), $\left| {d\lambda_{im} } \right|$, calculated in $im_{1}$, allows to obtain the joint annual rate of $\left\{ {IM_{1} ,IM_{2} } \right\}$ for any pair of arbitrarily-selected realizations of the two IMs, $\lambda_{{IM_{1} = im_{1} ,IM_{2} = im_{2} }}$, as per Eq. (9).

$$\lambda_{{IM_{1} = im_{1} ,IM_{2} = im_{2} }} = \left| {d\lambda_{{im_{1} }} } \right| \cdot f_{{\log IM_{2} \left| {IM_{1} } \right.}} \left( {\log im_{2} \left| {im_{1} } \right.} \right).$$

(9)

2.3 Logic tree and shortcuts for GMPEs with additive soil factors

PSHA is often implemented considering a logic tree, which allows accounting for model uncertainty (e.g., McGuire 2004; Kramer 1996); indeed, it allows the use of alternative models, each of which is assigned a weighing factor that is interpreted as the probability of that model being the true one. When the logic tree of $n_{b}$ branches is of concern, $\lambda_{im}$ is computed through Eq. (10) in which $p_{j}$ and $\lambda_{im,j}$ are the weight and the result of each branch of the logic tree, respectively.

$$\lambda_{im} = \sum\limits_{j = 1}^{{n_{b} }} {\lambda_{im,j} \cdot p_{j} }$$

(10)

It should also be noted that, according to Eq. (5), and only in the case of GMPEs of this type, it can be easily demonstrated that, if PSHA is performed without logic tree: (1) hazard curves for the condition represented by $\theta$ (e.g., a specific site soil class) can be obtained shifting, in the logarithmic space, those for a reference condition when $\theta = 0$; and (2) disaggregation distribution does not depend on $\theta$ (i.e., disaggregation does not change with the soil site class). Moreover, if a logic tree featuring different GMPEs, with this same type of structures, is adopted, the discussed translation of hazard curves can be applied to the result of each branch, then re-applying Eq. (10) provides the hazard in the changed conditions (Iervolino 2016).

3 Sequence-based probabilistic seismic hazard analysis

Classical single-site PSHA discussed in the previous section neglects the effect of aftershocks on the exceedance rate. This descends from the fact that the rates $\nu_{i}$, $\left\{ {1,2, \ldots ,n_{s} } \right\}$ are obtained removing alleged foreshocks and aftershocks from earthquake catalogs; i.e., they refer to the so-called declustered catalogs. This is mainly because declustering is needed for the HPP to apply (Gardner and Knopoff 1974). Recently, Boyd (2012) discussed that mainshock–aftershock sequences occur, on each seismic source, with the same rate of the mainshocks; i.e., $\nu_{i}$ of Eq. (3). Then, Iervolino et al. (2014) demonstrated the possibility to include the effect of aftershocks in PSHA still working with HPP and declustered catalogs. On this premise, the SPSHA, was developed combining PSHA with the aftershock probabilistic seismic hazard analysis (APSHA) of Yeo and Cornell (2009). As a result, for any given im-value, SPSHA provides the annual rate, $\lambda_{im}$, of mainshock–aftershock sequences that cause exceedance of $im$ at the site, which can be computed via Eq. (11).

$$\lambda_{im} = \sum\limits_{i = 1}^{{n_{s} }} {\nu_{i} \cdot \left\{ {1 - \int\limits_{M} {\int\limits_{X} {\int\limits_{Y} P } } \left[ {IM \le im|m,x,y} \right]_{i} \cdot e^{{ - E\left[ {N_{A,im\left| m \right.} \left( {0,\Delta T_{A} } \right)} \right]}} \cdot f_{M,X,Y,i} \left( {m,x,y} \right) \cdot dm \cdot dx \cdot dy} \right\}}$$

(11)

In the equation, the terms: $\nu_{i}$, $P\left[ {IM \le im|m,x,y} \right]_{i} = 1 - P\left[ {IM > im|m,x,y} \right]_{i}$, and $f_{M,X,Y,i} \left( {m,x,y} \right)$ are the same defined in Eq. (3). The exponent $E\left[ {N_{A,im\left| m \right.} \left( {0,\Delta T_{A} } \right)} \right]$ refers to aftershocks, as indicated by the A subscript: it represents the average number of aftershocks that cause exceedance of im in a sequence triggered by the mainshock of magnitude and location $\left\{ {m,x,y} \right\}$, Eq. (12).

$$\begin{aligned} & E\left[ {N_{A,im\left| m \right.} \left( {0,\Delta T_{A} } \right)} \right] = E\left[ {N_{A\left| m \right.} \left( {0,\Delta T_{A} } \right)} \right] \\ & \quad \cdot \int\limits_{{M_{A} }} {\int\limits_{{X_{A} }} {\int\limits_{{Y_{A} }} {P\left[ {IM > im|m_{A} ,x_{A} ,y_{A} } \right]_{i} \cdot f_{{M_{A} ,X_{A} ,Y_{A} ,i\left| {M,X,Y} \right.}} \left( {m_{A} ,x_{A} ,y_{A} \left| {m,x,y} \right.} \right) \cdot dm_{A} \cdot dx_{A} \cdot dy_{A} } } } \\ \end{aligned}$$

(12)

The probability represented by the exponential term depends on $P\left[ {IM > im|m_{A} ,x_{A} ,y_{A} } \right]_{i}$, that is the probability that im is exceeded given an aftershock of magnitude and location identified by the vector $\left\{ {m_{A} ,x_{A} ,y_{A} } \right\}$; i.e., a GMPE for aftershocks (although in several applications those for mainshock are considered applicable). The term $f_{{M_{A} ,X_{A} ,Y_{A} ,i\left| {M,X,Y} \right.}}$ is the distribution of magnitude and location of aftershocks, which is conditional on the features, $\left\{ {m,x,y} \right\}$, of the mainshock. This distribution can be written as $f_{{M_{A} ,X_{A} ,Y_{A} ,i|M,X,Y}} = f_{{M_{A} ,i|M}} \cdot f_{{X_{A} ,Y_{A} ,i|M,X,Y}}$, where $f_{{M_{A} ,i|M}}$ is the PDF of aftershock magnitude of G–R type, and $f_{{X_{A} ,Y_{A} ,i|M,X,Y}}$ is the distribution of the location of the aftershocks and depends on the magnitude and location of the mainshock (e.g., Utsu 1970). $E\left[ {N_{A\left| m \right.} \left( {0,\Delta T_{A} } \right)} \right]$ is the expected number of aftershocks to the mainshock of magnitude $m$ in the $\Delta T_{A}$ and, according to Yeo and Cornell (2009), can be computed via Eq. (13) in which $m_{A,{\rm min} }$ is the minimum magnitude considered for aftershocks (often taken equal to the minimum magnitude considered for mainshocks) and $\left\{ {a,b,c,p} \right\}$ are parameters of the modified Omori Law.

$$E\left[ {N_{A|m} \left( {0,\Delta T_{A} } \right)} \right] = \frac{{10^{{a + b \cdot (m - m_{\text{A,min}} )}} - 10^{a} }}{p - 1} \cdot \left[ {c^{1 - p} - \left( {\Delta T_{A} + c} \right)^{1 - p} } \right]$$

(13)

Finally, note that $\lambda_{im}$ is still the rate of the HPP of the kind in Eq. (2), which now regulates the occurrence of sequences causing exceedance of im.

The matrix formulation presented in Eq. (4) for the numerical computation of PSHA, can be extended to the SPSHA case as reported in Eq. (14). In the latter, the vectors are arranged as discussed referring to Eq. (4), but a new column vector is introduced: it has the same $\left( {k \cdot s} \right) \times 1$ size and each element of it accounts for the probability that none of the aftershocks, after a mainshock of given magnitude and location, causes the exceedance of im.

$$\begin{aligned} \lambda_{im} & = \sum\limits_{i = 1}^{{n_{s} }} {\nu_{i} \cdot } \left[ {1 - \left\{ {\begin{array}{*{20}c} {P\left[ {\left( {x,y} \right)_{1} } \right]} & {P\left[ {\left( {x,y} \right)_{1} } \right]} & \ldots & {P\left[ {\left( {x,y} \right)_{1} } \right]} & \ldots & {P\left[ {\left( {x,y} \right)_{s} } \right]} & {P\left[ {\left( {x,y} \right)_{s} } \right]} & \ldots & {P\left[ {\left( {x,y} \right)_{s} } \right]} \\ \end{array} } \right\}_{i} } \right. \\ & \quad \left. { \cdot \left( {\left\{ {\begin{array}{*{20}c} {P\left[ {IM \le im|m_{1} ,\left( {x,y} \right)_{1} } \right]} \\ {P\left[ {IM \le im|m_{2} ,\left( {x,y} \right)_{1} } \right]} \\ \vdots \\ {P\left[ {IM \le im|m_{k} ,\left( {x,y} \right)_{1} } \right]} \\ \vdots \\ {P\left[ {IM \le im|m_{1} ,\left( {x,y} \right)_{s} } \right]} \\ {P\left[ {IM \le im|m_{2} ,\left( {x,y} \right)_{s} } \right]} \\ \vdots \\ {P\left[ {IM \le im|m_{k} ,\left( {x,y} \right)_{s} } \right]} \\ \end{array} } \right\}_{i} \otimes \left\{ {\begin{array}{*{20}c} {e^{{ - E\left[ {N_{{A\left| {m_{1} } \right.}} \left( {0,\Delta T_{A} } \right)} \right] \cdot P\left[ {IM_{A} > im|m_{1} ,\left( {x,y} \right)_{1} } \right]}} } \\ {e^{{ - E\left[ {N_{{A\left| {m_{2} } \right.}} \left( {0,\Delta T_{A} } \right)} \right] \cdot P\left[ {IM_{A} > im|m_{2} ,\left( {x,y} \right)_{1} } \right]}} } \\ \vdots \\ {e^{{ - E\left[ {N_{{A\left| {m_{k} } \right.}} \left( {0,\Delta T_{A} } \right)} \right] \cdot P\left[ {IM_{A} > im|m_{k} ,\left( {x,y} \right)_{1} } \right]}} } \\ \vdots \\ {e^{{ - E\left[ {N_{{A\left| {m_{1} } \right.}} \left( {0,\Delta T_{A} } \right)} \right] \cdot P\left[ {IM_{A} > im|m_{1} ,\left( {x,y} \right)_{s} } \right]}} } \\ {e^{{ - E\left[ {N_{{A\left| {m_{2} } \right.}} \left( {0,\Delta T_{A} } \right)} \right] \cdot P\left[ {IM_{A} > im|m_{2} ,\left( {x,y} \right)_{s} } \right]}} } \\ \vdots \\ {e^{{ - E\left[ {N_{{A\left| {m_{k} } \right.}} \left( {0,\Delta T_{A} } \right)} \right] \cdot P\left[ {IM_{A} > im|m_{k} ,\left( {x,y} \right)_{s} } \right]}} } \\ \end{array} } \right\}_{i} \otimes \left\{ {\begin{array}{*{20}c} {P\left[ {m_{1} } \right]} \\ {P\left[ {m_{2} } \right]} \\ \vdots \\ {P\left[ {m_{k} } \right]} \\ \vdots \\ {P\left[ {m_{1} } \right]} \\ {P\left[ {m_{2} } \right]} \\ \vdots \\ {P\left[ {m_{k} } \right]} \\ \end{array} } \right\}_{i} } \right)} \right]. \\ \end{aligned}$$

(14)

3.1 SPSHA disaggregation

Disaggregation of seismic hazard can be performed also in the case of SPSHA. Equation (15) provides the PDF of mainshock magnitude and distance $\left( R \right)$, given that the ground motion intensity of the mainshock, $IM$, or the maximum ground motion intensity of the following aftershock sequence $\left( {IM_{ \cup A} } \right)$ is larger than the im threshold. In the equation, similarly to what discussed in Sect. 2.1, $\left\{ {X,Y} \right\}$ and $\left\{ {X_{A} ,Y_{A} } \right\}$ vector RVs, are substituted by $R$ and $R_{A}$, respectively.

$$\begin{aligned} & f_{{M,R\left| {IM > im \cup IM_{ \cup A} > im} \right.}} \left( {m,r} \right) = \frac{{\sum\nolimits_{i = 1}^{{n_{s} }} {\nu_{i} } }}{{\lambda_{im} }} \\ & \quad \times \left\{ {1 - P\left[ {IM \le im|m,r} \right]_{i} \cdot e^{{ - E\left[ {N_{A\left| m \right.} \left( {0,\Delta T_{A} } \right)} \right] \cdot \int\limits_{{M_{A} }} {\int\limits_{{R_{A} }} {P\left[ {IM_{A} > im|m_{A} ,r_{A} } \right]_{i} \cdot f_{{M_{A} ,R_{A},i \left| {M,R} \right.}} \left( {m_{A} ,r_{A} \left| {m,r} \right.} \right) \cdot dm_{A} \cdot dr_{A} } } }} } \right\} \cdot f_{M,R,i} \left( {m,r} \right) \\ \end{aligned}$$

(15)

Moreover, it can be useful to quantify the probability that, given the $im$ exceedance, such exceedance is caused by an aftershock rather than by a mainshock. This probability, which quantifies the contribution of aftershocks to hazard, is recalled in Eq. (16).

$$\begin{aligned} & P\left[ {IM_{ \cup A} > im \cap IM \le im\left| {IM > im \cup IM_{ \cup A} > im} \right.} \right] = \sum\limits_{i = 1}^{{n_{s} }} {\frac{{\nu_{i} }}{{\lambda_{im} }}} \cdot \iint\limits_{M,R} {P\left[ {IM \le im|m,r} \right]_{i} } \\ & \quad \times \left( {1 - e^{{ - E\left[ {N_{A|m} \left( {0,\Delta T_{A} } \right)} \right] \cdot \int\limits_{{M_{A} }} {\int\limits_{{R_{A} }} {P\left[ {IM_{A} > im|m_{A} ,r_{A} } \right]_{i} \cdot f_{{M_{A} ,R_{A} ,i\left| {M,R} \right.}} \left( {m_{A} ,r_{A} \left| {m,r} \right.} \right) \cdot dm_{A} \cdot dr_{A} } } }} } \right) \cdot f_{M,R,i} \left( {m,r} \right) \cdot dm \cdot dr \\ \end{aligned}$$

(16)

In the equation, $P\left[ {IM_{ \cup A} > im \cap IM \le im\left| {IM > im \cup IM_{ \cup A} > im} \right.} \right]$ it is the probability that, given that exceedance of $im$ has been observed during the mainshock–aftershock sequence, $\left( {IM > im \cup IM_{ \cup A} > im} \right)$, it was in fact an aftershock to cause it, while the mainshock was below the threshold; i.e.,$\left( {IM_{ \cup A} > im \cap IM \le im} \right)$. All the terms of the equation have been already defined discussing Eq. (11); see Iervolino et al. (2018) for derivation of the equation.

4 Multi-site hazard

In the case of MSPSHA, for a set of spatially-distributed sites, say $n_{sts}$ in number, one can define a vector of thresholds, one for each site $\left\{ {im{}_{1},im_{2} ,. \ldots im_{{n_{sts} }} } \right\}$, of the IM of interest. Given a vector of thresholds, the sought outcomes of MSPSHA can be various, for example, the probabilistic distribution of the total number of exceedances collectively observed at the sites in the $\Delta T$ time interval. The main issue with MSPSHA is that, even if the process counting exceedances at each of the sites is an HPP, that is Eq. (2), these HPPs are (in general) not independent. Then, the process that counts the total number of exceedances observed at the ensemble of the sites over time is not a HPP. The nature and form of stochastic dependence, existing among the processes counting in time exceedances of ground motion thresholds at multiple sites, is related to the probabilistic characterization of the effects of a common earthquake at the different sites (e.g., Giorgio and Iervolino 2016).

The same reasoning discussed for one IM at multiple sites, can be applied when MPSHA involves multiple IMs. For example, if one considers as IMs two pseudo accelerations at two spectral periods, $IM_{1} = Sa\left( {T_{1} } \right)$ and $IM_{2} = Sa\left( {T_{2} } \right)$, it is generally assumed that, given an earthquake of m and $\left\{ {x,y} \right\}$ characteristics, the logarithms of IMs at the sites form a Gaussian random field (GRF), a realization of which is a $1 \times \left( {n_{sts} \cdot 2} \right)$ vector of the type $\left\{ {im{}_{1,1},im_{1,2} , \ldots ,im_{{1,n_{sts} }} ,im{}_{2,1},im_{2,2} , \ldots ,im_{{2,n_{sts} }} } \right\}$. This means that the logarithms of IMs have a multivariate normal distribution, where the components of the mean vector are given by the $E\left[ {\log IM_{1} \left| {m,} \right.r_{j} ,\theta } \right]$ and $E\left[ {\log IM_{2} \left| {m,} \right.r_{j} ,\theta } \right]$ terms; two for each j, being $r_{j}$ the distance between the site j and the location of the seismic event, and the covariance matrix, $\Sigma$, is given in Eq. (17). In the equation, $\sigma_{\text{inter,1}}$ and $\sigma_{\text{inter,2}}$ are the standard deviations of the inter-event residuals of the GMPEs of the two IMs, while $\sigma_{\text{intra,1}}$ and $\sigma_{\text{intra,2}}$ are the standard deviation of intra-event residuals of $Sa\left( {T_{1} } \right)$ and $Sa\left( {T_{2} } \right)$, respectively; $\rho_{\text{inter}} \left( {T_{1} ,T_{2} } \right)$ is the correlation coefficient between inter-event residuals at the two spectral periods in the same earthquake, while $\rho_{\text{intra}} \left( {T_{1} ,T_{2} ,h_{i,j} } \right)$ is the correlation coefficient between intra-event residuals of the GMPEs of $Sa\left( {T_{1} } \right)$ and $Sa\left( {T_{2} } \right)$ for sites $i$ and $j$; and $h_{i,j}$ is the inter-site distance. In this case, $\Sigma$ is the sum of two square matrices, each of $\left( {n_{sts} \cdot 2} \right) \times \left( {n_{sts} \cdot 2} \right)$ size. The first matrix accounts for the cross-correlation of inter-event residuals which is, by definition, independent on the inter-site distance; the second matrix accounts for the intra-event residuals spatial cross-correlation and is dependent on inter-site distance as well as the selected spectral periods. Assigning the mean vector and the covariance matrix completely defines the GRF in one earthquake (e.g., Baker and Jayaram 2008; Esposito and Iervolino 2012; Loth and Baker 2013; Markhvida et al. 2018).

$$\begin{aligned} \Sigma & = \left[ {\begin{array}{*{20}c} {\sigma_{\text{inter,1}}^{2} } & \cdots & {\sigma_{\text{inter,1}}^{2} } & {\rho_{\text{inter}} \left( {T_{1} ,T_{2} } \right) \cdot \sigma_{\text{inter,1}} \cdot \sigma_{\text{inter,2}} } & \ldots & {\rho_{\text{inter}} \left( {T_{1} ,T_{2} } \right) \cdot \sigma_{\text{inter,1}} \cdot \sigma_{\text{inter,2}} } \\ {} & \ddots & \vdots & \vdots & \ddots & \vdots \\ {} & {} & {\sigma_{\text{inter,1}}^{2} } & {\rho_{\text{inter}} \left( {T_{1} ,T_{2} } \right) \cdot \sigma_{\text{inter,1}} \cdot \sigma_{\text{inter,2}} } & \cdots & {\rho_{\text{inter}} \left( {T_{1} ,T_{2} } \right) \cdot \sigma_{\text{inter,1}} \cdot \sigma_{\text{inter,2}} } \\ {} & {} & {} & {\sigma_{\text{inter,2}}^{2} } & \ldots & {\sigma_{\text{inter,2}}^{2} } \\ {} & {} & {sym} & {} & \ddots & \vdots \\ {} & {} & {} & {} & {} & {\sigma_{\text{inter,2}}^{2} } \\ \end{array} } \right] \\ & \quad + \left[ {\begin{array}{*{20}c} {\sigma_{\text{intra,1}}^{2} } & \cdots & {\rho_{\text{intra}} \left( {T_{1} ,T_{1} ,h_{{1,n_{sts} }} } \right) \cdot \sigma_{\text{intra,1}}^{2} } & {\rho_{\text{intra}} \left( {T_{1} ,T_{2} ,h_{ 1 , 1} } \right) \cdot \sigma_{\text{intra,1}} \cdot \sigma_{\text{intra,2}} } & \ldots & {\rho_{\text{intra}} \left( {T_{1} ,T_{2} ,h_{{1,n_{sts} }} } \right) \cdot \sigma_{\text{intra,1}} \cdot \sigma_{\text{intra,2}} } \\ {} & \ddots & \vdots & \vdots & \ddots & \vdots \\ {} & {} & {\sigma_{\text{intra,1}}^{2} } & {\rho_{\text{intra}} \left( {T_{1} ,T_{2} ,h_{{n_{sts} , 1}} } \right) \cdot \sigma_{\text{intra,1}} \cdot \sigma_{\text{intra,2}} } & \ldots & {\rho_{\text{intra}} \left( {T_{1} ,T_{2} ,h_{{n_{sts} ,n_{sts} }} } \right) \cdot \sigma_{\text{intra,1}} \cdot \sigma_{\text{intra,2}} } \\ {} & {} & {} & {\sigma_{\text{intra,2}}^{2} } & \ldots & {\rho_{\text{intra}} \left( {T_{2} ,T_{2} ,h_{{ 1 ,n_{sts} }} } \right) \cdot \sigma_{\text{intra,2}}^{2} } \\ {} & {} & {sym} & {} & \ddots & \vdots \\ {} & {} & {} & {} & {} & {\sigma_{\text{intra,2}}^{2} } \\ \end{array} } \right] \\ \end{aligned}$$

(17)

To compute MPSHA representing the GRF with the discussed covariance structure, in REASSESS the Monte Carlo simulation approach has been chosen. In this framework, one possible algorithm is the two-step procedure of Fig. 1, which is described, for simplicity, with reference to a single seismic source where earthquakes occur as per Eq. (1) with assigned magnitude and location distributions.

• (a) The first step is addressed to simulate and collect realizations of the GRF conditional to the occurrence of an earthquake of generic magnitude and location. In other words, magnitudes and locations of the seismic events on the source are sampled according to their distributions and, then, the realizations of the IMs at the considered sites are simulated in accordance with the considered GMPEs and $\Sigma$. This step is described in Fig. 1, where $n_{m}$, $n_{xy}$ and $n_{\varepsilon }$ are the indices counting the number of simulations for magnitude, event location and GRF of residuals at the sites, respectively; capital letters of the indices, $N_{m}$, $N_{xy}$ and $N_{\varepsilon }$ are the total number of simulations for each of the three variables. Thus, the results of the first step are $N_{m} \cdot N_{xy} \cdot N_{\varepsilon }$ vectors, one for each simulation, collecting the IM-values simulated at the sites in each event. Each vector $\left\{ {\underline{im} } \right\} = \left\{ {im{}_{1},im_{2} , \ldots ,im_{{n_{sts} }} } \right\}$ represents realizations of the random field of IMs at the sites in one generic (i.e., considering all possible magnitudes and locations) earthquake and, therefore, it is time-invariant.

• (b) The realizations from step (a) are the input for the second step that consists of simulating the process of earthquakes affecting the sites, in any time interval $\Delta T$ of interest; i.e., the seismic history for the sites in $\Delta T$. In each run of the simulation of this step, indicated by the index z which varies from 1 to Z, the number of earthquake events on the source is sampled from a HPP with mean equal to $\nu \cdot \Delta T$. Then, a number of IM random fields, equal to the sampled number of events, is randomly selected among those generated in the first step of the procedure. These random fields collectively represent one realization of the seismic history at the sites in $\Delta T$. Therefore, repeating Z times this step, can provide a sample of histories of what could occur in $\Delta T$ at the sites.

The simulated seismic histories can be used to compute any MSPSHA result. For example, if one is interested in the distribution (i.e., the MPF) of the total number of exceedances collectively observed at the sites in $\Delta T$, it is sufficient to count in how many histories a specific number of total exceedances of the $\left\{ {im{}_{1},im_{2} , \ldots ,im_{{n_{sts} }} } \right\}$ vector has been observed and divide by the total number of simulated histories. For example, the probability that zero exceedances are observed collectively at the sites, in $\Delta T$ years, is equal to the number of histories in which none of the IM thresholds set for each of the sites is exceeded, divided by the number of simulated histories (i.e., Z).

Fig. 1

Flowchart of the simulation procedure for MSPSHA in the case of single seismic source

In the case of more than one seismic source, the first step is repeated for each of them to simulate the random field they individually produce. In the second step, the HPP describing the event occurrence on all the sources has mean equal to $\Delta T \cdot \sum\nolimits_{i} {\nu_{i} }$. This, similarly to the case of a single source, is used to sample the number of earthquakes in $\Delta T$ and to randomly select the random field realizations from those of each source; the number of realizations to be selected for each source is proportional to the probability that given that an earthquake occurs it is from source i, that is ${{\nu_{i} } \mathord{\left/ {\vphantom {{\nu_{i} } {\sum\nolimits_{i} {\nu_{i} } }}} \right. \kern-0pt} {\sum\nolimits_{i} {\nu_{i} } }}$. At this point the seismic history in $\Delta T$ for the sites is obtained in analogy to the case of a single source.

4.1 MSPSHA shortcuts for GMPEs with additive factors

In this section some helpful shortcuts for MSPSHA calculations that are implemented in REASSESS and that apply (only) in the case of GMPEs of the type in Eq. (5) are discussed. It should be noted that the covariance of two or more RVs does not change adding constant terms. Thus, to the aim of this section, it is required to recognize that Eq. (5) implies that the RV representing the logarithms of IM for a site with conditions represented by $\theta$, is obtained adding such a coefficient to the RV representing the logarithms of IM for a reference condition for which $\theta = 0$; this means that the covariance matrix of the GRF is also independent of $\theta$ (e.g., the soil class of each of the sites). As a consequence, the simulations described in Sect. 4 can be carried out considering a common site condition for all sites (e.g., rock). To obtain GRF realizations reflecting the different site conditions at the sites from those for the reference case, it is sufficient to add to the logarithms of the simulated IMs the site-specific coefficient, that is $\left\{ {\theta_{1} ,\theta_{2} , \ldots ,\theta_{{n_{sts} }} } \right\}$, from the GMPE. Equivalent, but even simpler, is to subtract the $\left\{ {\theta_{1} ,\theta_{2} , \ldots ,\theta_{{n_{sts} }} } \right\}$ vector from the vectors of logarithms of the IM thresholds for the sites. However, in closing this section, it has to be emphasized that, as mentioned, several recent GMPEs are not of the type in Eq. (5) for what concerns the soil term, and these shortcuts do not apply (see also Stafford et al. 2017). Nevertheless, this same reasoning holds in the case $\theta$ of Eq. (5) represents any other factor affecting the IMs, not only soil site class.

5 REASSESS V2.0

To implement the types of hazard assessment discussed above, REASSESS V2.0 is coded in MATLAB and profits of a graphical user interface (GUI). The GUI features one input panel and two output panels, one for PSHA/SPSHA and one for MSPSHA. In fact, the main GUI is complemented by secondary interfaces that pop up when needed (see Fig. 2). Note that, in the case of extended analyses (e.g., several seismic sources or sites), input can also be defined via dedicated MICROSOFT^®-EXCEL spreadsheets, as a shortcut.

Fig. 2

Principal and auxiliary GUIs of REASSESS V2.0

A schematic flowchart of the way REASSESS V2.0 operates is given in Fig. 3. First, the user is required to define the type of analysis to be performed; i.e., PSHA, SPSHA, or MSPSHA. Even in the case of single-site analysis (PSHA and SPSHA) the user is allowed to define more than one site of interest; in this case, REASSESS will run single-site PSHA or SPSHA separately for each of them according to Sects. 2 or 3. If MSPSHA is selected, more than one site must be defined, and the analyses are performed according to what discussed in Sect. 4. (When SPSHA or MSPSHA is selected, the corresponding PSHA is also performed for the considered sites, as it is considered a reference case.)

Fig. 3

REASSESS V2.0 flowchart showing single-site and multisite modules functionalities

The second step refers to the definition of the coordinates and soil condition of the sites. It can be carried out via the GUI or via an EXCEL spreadsheet, for which a template is given. The soil conditions can be defined in terms of shear wave velocity of the top 30 m of subsurface profile (Vs30) expressed in meter/second or in terms of the soil classes (A, B, C, D and E) according to the Eurocode 8 classification of sites (CEN 2004).

The third step is dedicated to the selection of the GMPE(s). A database of alternative GMPEs is included in the current release of REASSESS: Ambraseys et al. (1996), fitted on a European dataset, Akkar and Bommer (2010), which refers to data from southern Europe, North Africa, and active areas of the Middle East, Bindi et al. (2011), fitted on Italian dataset and Cauzzi et al. (2015), based on a worldwide dataset.² At this step, also the discretization of the domain of the intensity measure for single-site PSHA, which serves to lump the hazard curves, has to be defined in terms of minimum, maximum values and number of intermediate steps (constant in logarithmic scale). In the case of PSHA, the third step also allows the definition of a logic tree (Sect. 2.3) in terms of: (1) parameters of the magnitude distributions, (2) mean annual frequency of earthquake occurrence on the sources and (3) GMPEs (among those available).

The choice of the IMs to be considered (e.g., spectral pseudo-acceleration for different natural vibration periods) for all the types of analysis (PSHA, SPSHA or MSPSHA) is dependent on the IMs available per the selected GMPE (step 4). If a logic tree with different GMPE for each branch has been defined, the selection is among the IMs of the GMPE belonging to the branch with the largest weight. If different branches have the same (largest) weight, the selection is among the IMs of the GMPE selected for the first branch with that weight.

When PSHA is of concern, REASSESS also allows to perform analysis for advanced spectral-shape-based intensity measures such as $I_{Np}$ proposed by Bojórquez and Iervolino (2011) and reported in Eq. (18) in logarithmic terms. The $I_{Np}$ is a proxy of the pseudo-acceleration response $\left( {Sa} \right)$ spectral shape in a range of periods $\left( {T_{1} \ldots T_{N} } \right)$ and is dependent on a reference period $\left( {\bar{T}} \right)$ belonging to the $\left( {T_{1} \ldots T_{N} } \right)$ interval and an $\alpha$ parameter. In its analytical expression $Sa_{avg} \left( {T_{1} \ldots T_{n} } \right)$ appears; it is the geometric mean of the spectral acceleration in the $\left( {T_{1} \ldots T_{N} } \right)$ range of periods (Baker and Cornell 2006a). In the software, $\left( {T_{1} \ldots T_{N} } \right)$, $\bar{T}$ and $\alpha$ can be selected by the user (the periods can be chosen among those of the selected GMPE). It is easy to see that when the $\alpha$ parameter equals one, $I_{Np}$ corresponds to $Sa_{avg} \left( {T_{1} \ldots T_{n} } \right)$.

$$\log \left( {I_{Np} } \right) = \log \left[ {Sa\left( {\bar{T}} \right)} \right] + \alpha \log \left[ {\frac{{Sa_{avg} \left( {T_{1} \ldots T_{N} } \right)}}{{Sa\left( {\bar{T}} \right)}}} \right]$$

(18)

In the case of MSPSHA, when a single spectral ordinate is selected as IM, the user is allowed to choose the model of spatial correlation of intra-event residuals of Esposito and Iervolino (2012) or Loth and Baker (2013). On the other hand, when the IMs at the sites are spectral ordinates for several natural vibration periods, simulated (spatially) cross-correlated scenarios are computed adopting the models of (1) Loth and Baker (2013) for the spatial correlation of intra-event residuals and (2) Baker and Jayaram (2008) for the spectral correlation of inter-event residuals.

Step 5 is dedicated to the seismic source definition. In REASSESS V2.0, seismic source zones and/or finite three-dimensional faults can both be input of analysis. Faults are discussed in Sect. 5.1; for what concerns source zones, these are defined by the coordinates of the vertices of the zone, the annual rate of occurrence of earthquakes of Eq. (1) and the event’s magnitude distribution, which is assumed to be a truncated exponential distribution as discussed in Sect. 2; hence, the slope of the G–R relationship, together with minimum and maximum values of magnitude, is required. If known, a rupture faulting style can be associated to the seismic zone. As mentioned, all the required parameters can be alternatively given via GUI or EXCEL spreadsheet.

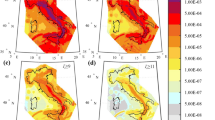
A number of literature databases of seismic zones are already embedded in the current version of the software. Referring to Italy, it is known that the seismic hazard study of Stucchi et al. (2011) lies at the basis of the hazard assessment for the Italian current building code and features a logic tree made of several branches; the branch named 921 is the one producing the results claimed to be the closest to those provided by the full logic tree. This branch considers the seismic source model of thirty-six areal zones of Meletti et al. (2008) and the GMPE by Ambraseys et al. (1996). It is implemented in REASSESS V2.0 and is named Meletti et al. (2008)—Magnitude rates from DPC-INGV-S1—Branch 921. It is the sole database selection which implies a specific GMPE (automatically selected). An alternative source model for Italy is named Meletti et al. (2008)—Magnitude rates from Barani et al. (2009) in which the same source model of Meletti et al. (2008) is considered, but the associated seismic characterization is from Barani et al. (2009). Other databases in REASSES are the one from the SHARE project, which covers the Euro-Mediterranean region, the one from the EMME project, which covers middle-east; i.e., Afghanistan, Armenia, Azerbaijan, Cyprus, Georgia, Iran, Jordan, Lebanon, Pakistan, Syria and Turkey. Moreover, included databases are: El-Hussain et al. (2012), Ullah et al. (2015) and Nath and Thingbaijam (2012), referring to the Sultanate of Oman, Kazakhstan, Kyrgyzstan, Tajikistan, Uzbekistan and Turkmenistan, and India, respectively. The area covered by the embedded databases is given in Fig. 4. For each of the cited databases, assuming a uniform earthquake location distribution in each seismic source, epicentral distance is converted into the metric required by the GMPE according to Montaldo et al. (2005). The style-of-faulting correction factors proposed by Bommer et al. (2003) are also applied to the Ambraseys et al. (1996) GMPE, in accordance with the rupture mechanism associated to each seismic zone (if any).

Fig. 4

Embedded databases of seismogenic sources

When SPSHA is performed, an additional step is required in the input definition. In particular, the model describing the aftershock occurrence has to be specified, that is the parameters of Eq. (13), providing the expected number of aftershock in any time interval given the magnitude of the mainshock. The available models are those of Reasenberg and Jones (1989, 1994), Lolli and Gasperini (2003) and Eberhart-Phillips (1998) which refer to generic California, Italian and New Zealand aftershock sequence, respectively. Such models, can be selected through a dedicated window (Fig. 5), automatically opened by REASSESS before running the SPSHA. In the current version of the software, the GMPE selected for PSHA is also applied to account for the evaluation of aftershock’s IM.

Fig. 5

Graphical interface window for calibration of the aftershock occurrence models

5.1 Finite faults

REASSESS also allows to compute hazard analysis (both PSHA and MSPSHA) in the case the seismic sources are represented by means of one or more finite faults. There are many alternative ways to define the characteristics of a fault for hazard assessment purposes (Scherbaum et al. 2004). In the current version of REASSESS a fault is defined by means of a point representing its center and the dip, rake, and strikes angles (Aki and Richards 1980). In the case of a finite fault in REASSESS, PSHA is carried out according to Eq. (19), which is an adaptation of Eq. (3).

$$\lambda_{im} = \nu \cdot \int\limits_{X} {\int\limits_{Y} {\int\limits_{M} {\int\limits_{A} {\int\limits_{S} {P\left[ {IM > im\left| {m,x,y} \right.} \right] \cdot f_{S\left| A \right.} \left( {s\left| a \right.} \right) \cdot f_{A\left| M \right.} \left( {a\left| m \right.} \right) \cdot f_{M} \left( m \right) \cdot f_{X,Y} \left( {x,y} \right) \cdot ds \cdot da \cdot dm \cdot dx \cdot dy} } } } }$$

(19)

In the equation: $\nu$ is the rate; $\left\{ {X,Y} \right\}$ is the position of the center of the rupture with respect to the center of the fault and its distribution $f_{X,Y} \left( {x,y} \right)$ is taken according to Mai et al. (2005); $f_{M} \left( m \right)$ is the magnitude distribution that can be defined as G–R or characteristic (e.g., Convertito et al. 2006); $f_{A\left| M \right.} \left( {a\left| m \right.} \right)$ is the distribution of the rupture size, conditional to the magnitude that is modelled according to Wells and Coppersmith (1994); finally, $f_{S\left| A \right.} \left( {s\left| a \right.} \right)$ is the aspect ratio (length-to-width ratio) of the rupture and is probabilistically modeled lognormally according to Iervolino et al. (2016b).³

6 Output of the analyses

At the end of the analysis, the outputs provided by the software can be consulted via the GUI in the format of figure or text files. Moreover, a compressed folder with all the input and output (figures and files) of the analyses can be saved by the user. In the following sub-sections, the available results are described.

6.1 PSHA and SPSHA results

When the analysis is finished, the hazard curves are plotted in the single-site output panel (see Fig. 2). If the analysis is performed for more than one site, the curves for each site of interest can be selected (via a dropdown menu). The uniform hazard spectrum (UHS) can be computed, and plotted in a dedicated panel, selecting any return period available (that depends on the range of IMs defined at the beginning).

In addition, REASSESS is able to provide disaggregation of PSHA, conditional mean spectrum (CMS; Lin et al. 2013) and conditional hazard (see Sects. 2.1, 2.2). The conditional hazard can be computed by REASSESS V2.0 profiting of the model of Bradley (2012), which provides correlation between peak ground velocity (PGV) and spectral accelerations and the model of Baker and Jayaram (2008), which provides the correlation among spectral acceleration values at different spectral periods. Therefore, the distribution of PGV or pseudo-acceleration response spectra at any vibration period conditional to the occurrence of any spectral ordinate can be computed.

Results of SPSHA are similar to those for PSHA; however, disaggregation is of two kinds (see Sect. 3.1). The first is the joint probability density function of magnitude and distance of the mainshock conditional to the exceedance, or the occurrence, of a chosen hazard threshold during the corresponding cluster (mainshock and subsequent aftershocks). This is equivalent to the classical hazard disaggregation, in terms of magnitude and distance, but computed in accordance with the approach of the SPSHA, Eq. (15). The second disaggregation provided represents the probability that, given that exceedance of $im$ has been observed during the mainshock–aftershock sequence, it was in fact an aftershock to cause it, Eq. (16).

6.2 MSPSHA results

MSPSHA can be performed on all or on a subset of the sites defined at the beginning of the analysis. It is performed through the two-steps procedure described in Sect. 4. At the end of the first step, the simulated scenarios of IM realizations at the sites, given the occurrence of an earthquake on the sources are available. As a reference, these results are also used to first provide single-site PSHA as per Eq. (2) (in fact, single-site PSHA can be viewed as a special case of MSPSHA; Giorgio and Iervolino 2016) and the results are reported in the single-site panel. Specifically referring to MSPSHA, REASSESS V2.0 provides three kinds of results:

• 1. the probability of observing an arbitrarily chosen number of exceedances at the sites in a given time interval;

• 2. the distribution of the total number of exceedances at the sites in a given time interval;

• 3. the distribution of the number of exceedances at the sites given the occurrence of an earthquake (a time-invariant results).

Results (1) and (2) are computed by REASSESS for any time interval without repeating the simulations of the first step of the analysis, thus reducing the required time of computation. Text files with the GRFs simulated (i.e., realizations) conditional to a generic event and in the selected time interval are also available at the end of the analyses.

It is to also highlight that, although the vector collecting sites threshold in MSPSHA can be completely defined by the user, REASSESS allows to define the threshold vector from the results of single-site PSHA. For example, the thresholds can be chosen as the values with the same exceedance return period at each site according to single-site PSHA, as illustrated in one of the examples below.

7 Illustrative examples

Some examples of the analyses REASSESS V2.0 enables are illustrated herein. To this aim five sites are considered; incidentally, they correspond to the five main hospitals of the health infrastructure for municipality of Naples (Italy): Ospedale del Mare, San Giovanni Bosco, Cardarelli, San Paolo and Fatebenefratelli (see Fig. 6 in which the sites and the municipality boundaries are highlighted). The inter-site distance ranges between 2 and 13 km.

Fig. 6

Geographical location of the sites within the municipality of Naples

The following sections refer to the results of PSHA, SPSHA and MSPSHA. For all of them, the Meletti et al. (2008)—Magnitude rates from DPC-INGV-S1—Branch 921 source model is used (see Sect. 5). For the aim of this paper, all the sites are assumed on rock soil conditions. In the case of SPSHA, the selected model defining parameters of Eq. (13) is Lolli and Gasperini (2003). All the data represented in the figures are taken from the texts files automatically saved by REASSESS (to assemble the figures of the paper, the format of the plots is slightly different from the one of the software).

7.1 Single-site PSHA

Because the considered sites can be considered close from the seismic hazard assessment point of view, differences in terms of single-site analysis, are minor. Thus, only one of the locations is considered for PSHA and SPSHA: 14.277°E, 40.873°N. Figure 7 summarizes the result of single-site PSHA computed for the site.

Fig. 7

a Geographic location of the site and areal sources contributing to the hazard, b hazard curves (grey lines) computed for all the spectral period provided by the GMPE and annual rate corresponding to the 475 return period (red line), c UHS’ with a 475 years return period, d hazard disaggregation distribution for the occurrence of the $Sa\left( {0.5\,{\text{s}}} \right)$ with a 475 years return period, e CMS and f conditional hazard distributions assuming as primary IM the $Sa\left( {0.5\,{\text{s}}} \right)$ with a 475 years return period

In Fig. 7a it is reported the location of the site (grey triangle) and the twelve seismic zones (out of the thirty-six in total, numbered from 901 to 936) of the model of Meletti et al. (2008) contributing to the hazard are plotted (these zones are automatically identified by REASSESS among those of the selected database). Figure 7b reports the hazard curves computed for the whole forty-seven spectral periods of the GMPE. In the same plot, the annual rate of exceedance equal to 0.0021, corresponding to the 475 return period $\left( {T_{R} } \right)$ of exceedance, is also plotted (red horizontal line). This return period is the one for which are computed the UHS’s in Fig. 7c (the three soil conditions allowed by the GMPE are considered; i.e., rock, stiff and soft soil). Such spectra have a peak ground acceleration (PGA) equal to about 0.2 g and are representative of a medium–high hazard site in Italy (see Stucchi et al. 2011).

Selecting as the IM the pseudo-acceleration response spectral ordinate at 0.5 s period, $Sa\left( {0.5\,{\text{s}}} \right)$, the occurrence disaggregation for a return period of 475 years is reported in Fig. 7d. Such a disaggregation (for the occurrence of im) is computed as per Eq. (6); however, because RVs are represented in a discretized way assuming bins of 10 km distance and 0.5 magnitude, the PDF, $f_{{M,R,\varepsilon \left| {IM} \right.}}$, is rendered in the plot by the corresponding discretized form, $P\left[ {m,r,\varepsilon \left| {(IM=im} \right.} \right]$. Disaggregation distribution is bi-modal, being the disaggregated hazard mainly affected by two seismic zones: the one in which the site is enclosed to (namely zone 928) and the zone 927 that, although is more distant than 928, is able to generate larger magnitude events and more frequently (see Iervolino et al. 2011, for a deeper discussion).

The CMS is reported in Fig. 7e: conditioning IM is maintained $Sa\left( {0.5\,{\text{s}}} \right)$ corresponding to $T_{R} = 475$ years. Finally, the conditional hazard distribution, Eq. (7), for four pseudo-spectral accelerations at 0 (PGA), 0.2 s, 0.6 s and 1.0 s conditional to the same primary IM are reported in Fig. 7f. (REASSESS also provides the conditional standard deviation for any IM.)

7.2 SPSHA

For the same site as Sect. 7.1, Fig. 8a shows the UHS’ corresponding to 475 years return period and computed via both SPSHA and PSHA. The latter case corresponds to classical hazard, while the former includes the effect of aftershocks. Sequence’s effect produces a maximum increase of UHS from PSHA equal to 12% which corresponds to a vibration period equal to 0.1 s. However, increments over the whole range of analysed periods are equal or higher than 7%; the minimum value is recorded at 1.5 s.

Fig. 8

a Comparison among UHS from PSHA and SPSHA for a 475 years return period, b hazard disaggregation distribution of PGA with a 475 years return period, c aftershock disaggregation for PGA, $Sa\left( {0.2\,{\text{s}}} \right)$ and $Sa\left( {0.6\,{\text{s}}} \right)$

Both kinds of sequence-based disaggregation are also computed. The mainshock magnitude and distance disaggregation distribution, that is Eq. (15), is shown for the PGA intensity measure and 475 years exceedance return period (Fig. 8b); it is interesting to note that, accounting for the sequence modifies the proportion between first and second modal values with respect to Fig. 7d (Chioccarelli et al. 2018).

Figure 8c provides the aftershock disaggregation, Eq. (16), performed for three IMs: PGA, $Sa\left( {0.2\,{\text{s}}} \right)$ and $Sa\left( {0.6\,{\text{s}}} \right)$. Aftershock disaggregation is here represented as a function of the increasing return period even if output text files provide them as function of both IM thresholds and return period. All these disaggregation distributions have a non-monotonic trend. In fact, they start from zero because it can be verified that when $im$ approaches zero, results of Eqs. (3) and (11) are equal, i.e., aftershock has no effect. The maximum value of disaggregation for PGA is 0.26 corresponding to a return period of about 4000 years; maximum disaggregation for $Sa\left( {0.2\,{\text{s}}} \right)$ is 0.26 and it occurs for a return period of about 2000 years; finally, maximum disaggregation for $Sa\left( {0.6\,{\text{s}}} \right)$ is 0.21 and correspond to $T_{R}$ of about 100 years. The non-monotonic trend of the plots indicates that the aftershock contribution to the hazard has a variable significance with the hazard threshold. Moreover, the different return period to which each disaggregation reaches its maximum suggests that aftershock effect is also dependent on the considered spectral period.

7.3 MSPSHA

Results of MSPSHA are reported in this section referring to the whole set of the five sites introduced above (Sect. 7). A set of five IMs has been selected for each of the site: PGA, $Sa\left( {0.2\,{\text{s}}} \right)$, $Sa\left( {0.5\,{\text{s}}} \right)$, $Sa\left( {0.6\,{\text{s}}} \right)$, $Sa\left( {1.0\,{\text{s}}} \right)$. Profiting of the REASSESS functionalities discussed in Sect. 6.3, the vector of IMs collecting the threshold values for each site, which is required for MSPSHA, is chosen in a way that the corresponding $T_{R}$, from single-site PSHA, are the same among all the sites: the common return period is, arbitrarily, 50 years.

The distribution of the number of exceedances at the sites given the occurrence of the event and the distribution of the number of exceedances collectively observed at the sites in a time window of 20 years are the output here, chosen among those available (see Sect. 6.2). Both types of distribution are computed referring to four different cases: in (1) at each of the five sites, PGA is the considered IM; in (2) and (3) the considered IM at the sites is $Sa\left( {0.5\,{\text{s}}} \right)$ and $Sa\left( {1.0\,{\text{s}}} \right)$, respectively; finally, in (4) a different intensity measure is selected at each site: PGA at site one, $Sa\left( {0.2\,{\text{s}}} \right)$ at site two, $Sa\left( {0.5\,{\text{s}}} \right)$ at site three, $Sa\left( {0.6\,{\text{s}}} \right)$ at site four and $Sa\left( {1.0\,{\text{s}}} \right)$ at site five. The MPF of the total number of exceedances given the occurrence of an earthquake is reported in the first line of panels of Fig. 9, from (a) to (d) corresponding to cases from 1 to 4, respectively.

Fig. 9

MPF of the total number of exceedances at the sites a given the event and b in 20 years

This result is representative of a specific case scenario which corresponds to the occurrence of a generic event. It appears that the most probable number of exceedances is zero while the exceedance probabilities at one, more than one, or all the sites are of the same order of magnitude. The second line of the figure, that is plots from (e) to (h), shows the MPF of the total number of exceedances in 20 years.

8 Final remarks

REASSESS V2.0, a MATLAB-coded tool for probabilistic seismic hazard analysis, has been presented. It is a standalone application which operates via GUI and/or template-based input files that has been developed to enable classical and advanced probabilistic seismic hazard assessment procedures. It is oriented towards earthquake engineering practice.

In the paper, the basics of probabilistic seismic hazard analyses embedded in the software have been recalled first, then implemented algorithms and the workflow of REASSESS have been discussed. The software allows the user to define the input of the analyses in terms of: site(s) coordinates, GMPEs (selected among an embedded database), intensity measures of interest, seismic sources (user-defined three-dimensional faults, seismic sources (areal) zones, or sources selected from embedded databases), and structure of logic tree, if any.

When single-site analyses are of concern, REASSESS is able to provide classical results of PSHA such as hazard curves, even in terms of spectral-shape-based (i.e., advanced) ground motion intensity measures. Moreover, uniform hazard and conditional mean spectra, together with disaggregation distributions given the occurrence or the exceedance of the IM threshold, can be computed. Conditional hazard can also be computed for PGV or pseudo-spectral accelerations selected as secondary intensity measures. Moreover, single-site analyses may also be performed accounting for the effect of the aftershocks. With this type of analysis, named SPSHA, available output is represented by: hazard curves, UHS, magnitude-distance disaggregation distribution and aftershock disaggregation. PSHA and SPSHA are implemented taking advantage of the accuracy and low computational demand allowed by matrix calculus of MATLAB.

For portfolio of sites that can be subjected to the same seismic sources, the software is able to perform the so-called MSPSHA providing, for a vector of IM thresholds, different probabilistic results all related to the exceedances possibly observed at the sites. A two-step simulation algorithm to carry out MSPSHA, allows to profit of random field simulations of IMs in generic earthquakes.

REASSES was optimized for accuracy of numerical computation, analysis time and ease of use, which was illustrated herein via a few applications, not exhaustive of the software capabilities. To this aim it also implements calculation shortcuts and provides a series of options of input/output management. It is finally to note that a practical user guide (tutorial) can be found online at http://wpage.unina.it/iuniervo/doc_en/REASSESS.htm, which is the same site where the software is available under a Creative Commons license: attribution—non-commercial—non derived.