1 Introduction

Considering the effects of underlying soil on the response of superstructure is the main purpose of geotechnical earthquake engineering (Bozorgnia and Bertero 2004). The available methods to model the foundation and underlying soil can be classified in two main categories: substructure and direct methods.

In the substructure method, the soil domain is completely replaced by appropriate elements in order to considering the effects of stiffness and damping of soil on the superstructure. Pais and Kausel (1988), Gazetas (1991), and Mylonakis et al. (2006) presented classical equations for stiffness and damping coefficients of surface and embedded rigid footings. Matlock (1970), Penzien (1970), Nogami et al. (1992), Boulanger et al. (1999), Yim and Chopra (1985), Allotey and El Naggar (2008), and Raychowdhury (2008) used different types of Beam on Nonlinear Winkler Foundation (BNWF) models for analyzing foundations and structures under static and dynamic loading conditions. Plasticity Based Macro-element (PBM) models are recently developed by a number of researchers to capture the nonlinear response of rigid foundations. Some recent versions of PBM models were developed by Cremer et al. (2001), Houlsby and Cassidy (2002), Gajan and Kutter (2008), Chatzigogos et al. (2009, 2011), and Figini et al. (2012).

Unlike the substructure method, the direct method includes modeling the soil domain and superstructure simultaneously and is an application of the finite element method (Gutierrez and Chopra 1978). Modeling the unbounded soil domain, its nonlinear behavior and an enormous computational effort are the most important challenges facing the direct finite element method. Nonlinear behavior of the soil domain can be simulated by different elastic or elastic–plastic constitutive models. Although elastic–plastic constitutive models are more accurate, they usually have many parameters and increase the computational cost. For example, Elgamal et al. (2008) studied three-dimensional (3D) seismic response of the Humboldt Bay Middle Channel Bridge. A nonlinear hysteretic material with a Von Mises multisurface kinematic plasticity model was used to model the foundation soil. They used a special sparse solver and reported 40 h of run time for analyzing the bridge model under a 25 s earthquake excitation. Nonlinear soil structure interaction can involve geometric and material nonlinearities such as structure nonlinearity, uplift, liquefaction etc. Addressing all these issues in the direct method considerably increases the analysis cost. Therefore, efforts have been made to simplify the direct method and make it more practical.

Researchers have shown that just a limited region in the vicinity of structure undergoes considerable plastic deformations; therefore it is not reasonable to use complicated constitutive models to simulate the behavior of the whole soil domain (Wolf and Song 1996). Accordingly, one can divide the soil domain into two parts: a part near the foundation experiencing large strains and nonlinear behavior (the near-field zone) and a remaining part with linear behavior (the far-field zone).

Different methods are available to analyze the near-field and far-field zones. The Boundary Element Method (BEM) can include wave radiation to infinity; therefore, it can be used to model the far-field zone (Von Estorff and Kausel 1989). It seems that using a coupled BEM–FEM method can eliminate the shortcomings of each individual method. Various researchers such as Von Estorff and Kausel (1989), Von Estorff and Firuziaan (2000), Yazdchi et al. (1999), Spyrakos and Xu (2004), Romero et al. (2013), Andersen and Jones (2006), and Vasilev et al. (2015) have presented coupled BEM–FEM methods for dynamic soil–structure interaction problems.

Wolf (2003) developed the Scaled Boundary Finite Element Method (SBFEM) for analyzing bounded and unbounded domains. He suggested that the unbounded far-field to be analyzed with SBFEM while the bounded near-field could be modeled with FEM having nonlinear material properties. Other researchers like Genes and Kocak (2005), Bazyar and Song (2006) and Chen et al. (2015) modified this method for layered and non-homogeneous unbounded domains.

Using the Equivalent Linear Method (ELM) is an effective approach to simplify the direct method and to enhance its efficiency and applicability. In this approach, the soil domain is assumed to behave linearly both in the near- and far-field zones and its dynamic properties are computed through an equivalent linear analysis (i.e. free-field analysis). An iterative procedure is used in the free-field analysis and the shear modulus and damping of each soil layer are readjusted in every iteration based on the effective shear strain in each different layer (Kramer 1996). When this procedure converges, strain-compatible shear modulus and damping values used for simulating the soil domain are calculated. These values are constant throughout the duration of the earthquake. Cubrinovski and Ishihara (2004), Casciati and Borja (2004) and Manna and Baidya (2010) employed ELM to approximate the nonlinear soil behavior in analyzing different types of structures. Since this method is only applicable for strain levels under approximately one percent (Ishihara 1996), using the equivalent linear properties in the near-field region, will not result in accurate results and it is the serious limitation of the ELM. On the other hand, in the conventional ELM the modified soil properties are obtained through a free-field analysis and therefore, the effects of large strains around the foundation are excluded. In a recently published paper, Ghandil and Behnamfar (2015) resolved this limitation and proposed the near-field method as a modified equivalent linear method with a further reduction of the soil shear modulus in the near-field of foundation resulting in validity of using the equivalent linear method throughout. They considered several 3D buildings resting on different soil types and proposed semi-analytical relations for calculating the shear modulus modification factors as functions of the fixed-base period of structures. Results showed that the near-field method, being more accurate than traditional ELM, can considerably reduce the computational cost of the direct method.

The present study is the continuation of the previous study by Ghandil and Behnamfar (2015). The main objective of this research is to propose an approach to include the nonlinear soil behavior in linear FE models and calculate maximum seismic displacements of building structures resting on shallow spread foundations. Here, the near-field method is generalized to be applicable for a wide range of building structures. To attain this goal, a set of dimensionless parameters representing relative properties of building structures and soil is selected and a comprehensive parametric study is carried out to determine the near-field zone dimensions and capture the variation of near-field properties, including the shear modulus and the damping ratio, with respect to these parameters.

2 Key dimensionless parameters

Soil–structure interaction and the effect of various parameters on this phenomenon have been the subject of many researches. Veletsos and Meek (1974), Veletsos and Nair (1975), Bielak (1975) and Wolf (1985) introduced dimensionless parameters that control response of a dynamic soil–structure system under a specific excitation. Table 1 lists these dimensionless parameters. In this table, h refers to structure height, V S is the shear wave velocity of the soil, T is the fixed-base period of the structure, a is a characteristic length of the foundation (i.e. half-width or radius of the foundation), ω S refers to structure’s angular frequency, m is the effective modal mass of structure and ρ S is the mass density of the soil.

Table 1 Dimensionless parameters that alter the soil–structure interaction effects
Full size table

Some researchers like Veletsos and Meek (1974) and Avilés and Pérez-Rocha (1996) studied the influence of the above mentioned parameters and concluded that the inertial SSI effects are more sensitive to the stiffness ratio (\(\bar{s}\)) and the slenderness ratio (\(\bar{h}\)) and sensitivity to the mass ratio (\(\bar{m}\)) is modest. In addition, it was concluded that neglecting other parameters such as linear and rotary inertia of the foundation may be permissible for deriving effective system parameters (Avilés and Pérez-Rocha 1996). Accordingly, \(\bar{s}\), \(\bar{h}\) and \(\bar{m}\) are considered as key dimensionless parameters in this research and the effects of these parameters on the properties of the near-field region are studied.

2.1 Dimensionless parameters for building structures

\(\bar{s}\), \(\bar{h}\) and \(\bar{m}\) are related to each other in building structures and arbitrary combinations of these parameters are not acceptable for this kind of structures. Therefore, the mathematical relations between dimensionless parameters and building structure properties should be determined at the first stage.

Consider an n-story building structure with a square foundation and assume that the story height is equal to h 1 and the foundation dimension is 2a. Thus the modal height of the mass center of structure may be calculated from the following equation:

$$h = b \cdot (n \cdot h_{1} ),\quad 0.1 \le b \le 0.8$$
(1)

where bis the height coefficient of the effective modal mass and may take the values between 0.1 and 0.8 according to the mode number for typical building structures.

If the half-side of the foundation has a relation with story height as Eq. 2:

$$a = d \cdot h_{1} \,$$
(2)

then the slenderness ratio can be defined as follows:

$$\bar{h} = \frac{h}{a} = \frac{{b \cdot n \cdot h_{1} }}{{d \cdot h_{1} }} = \frac{n \cdot b}{d}\,$$
(3)

For the models considered in this paper it is assumed that the range of d is from 1.5 to 8.

Now suppose that the modal period of the fixed base structure (T f ) is proportional to the number of stories as follows:

$$T_{f} = c \cdot n,\quad 0.02 \le c \le 0.20\,\,$$
(4)

Since ω f h quantifies the stiffness of the structure and V s is related to the stiffness of the soil, the structure to soil stiffness ratio can be expressed as Eq. 5:

$$\bar{s} = \frac{{\omega_{f} h}}{{V_{s} }} = \frac{2\pi \,h}{{T_{f} \cdot V_{s} }}$$
(5)

Stiffness ratio can be written as Eq. 6 after substituting Eqs. 1 and 4 in Eq. 5 and simplifying:

$$\bar{s} = \frac{{2\pi (b \cdot n \cdot h_{1} )}}{{c \cdot n \cdot V_{s} }} = \frac{{2\pi \,b \cdot h_{1} }}{{c \cdot V_{s} }}$$
(6)

The mass ratio is defined as the ratio of structure’s modal mass to the mass of soil in a specific volume below the foundation that extends to a depth equal to the structure modal height (equal to the soil mass filling the volume of structure). The following equations are used to calculate the mass ratio \(\bar{m}\):

$$m_{1} = 4\rho \,a^{2}$$
(7)
$$m = e \cdot n \cdot m_{1}$$
(8)
$$\bar{m} = \frac{m}{{\rho_{s} \cdot a^{2} \cdot h}}$$
(9)

After substituting Eqs. 1, 2, 7 and 8 in Eq. 9 and simplifying:

$$\bar{m} = \frac{{enm_{1} }}{{\rho_{s} \,d^{2} h_{1}^{2} (bnh_{1} )}} = \frac{{e(4\rho \,d^{2} h_{1}^{2} )}}{{\rho_{s} \,d^{2} h_{1}^{3} b}} = \frac{4\,e\rho }{{\rho {}_{s}\,bh_{1} }}$$
(10)

where ρ is the effective mass per unit area of the story, ρ s is the mass density of the soil and e is the coefficient of effective modal mass that may take a range of values from 0.1 to 1 according to the mode number.

2.2 Parametric study

There is a specific range of dimensionless parameters for a building in its different configurations and natural modes on various soils. Since these parameters are defined based on equivalent SDF system properties, the structure has to be idealized as an SDF stick model. The properties of this model such as mass, height and period are obtained from modal properties of the corresponding building and therefore each stick model is representing a mode of the same structure. Such a modeling makes it possible also to investigate the contribution level of different vibrational modes to SSI effects. Several structure and soil models are chosen on this basis. Table 2 represents these models and their corresponding dimensionless parameters. In this table, soft, medium and stiff soil conditions correspond to V s  ≤ 175 m/s, 175 m/s ≤ V s  ≤ 375 m/s and 375 m/s ≤ V s  ≤ 750 m/s respectively; low-, medium- and high-rise buildings correspond to 1 ≤ n ≤ 4, 5 ≤ n ≤ 15 and 16 ≤ n, respectively and values of the effective mass per unit area of each story varies from 500 kg/m2 for light weight to 1000 kg/m2 for heavy structures. Soil and structure conditions must be compatible in deriving the values of the parameters. Therefore, for example, it is considered that a shallow foundation is not appropriate for supporting mid-rise and tall buildings on soft soils. The last mode in this table represents the last important mode that has a significant effect on the dynamic response of structure.

Table 2 Selected models and the corresponding dimensionless parameters
Full size table

3 Procedure of this study

As mentioned in Sect. 1, ELM is based on free-field analysis and is not valid in the vicinity of the structure. Therefore, the near-field method is proposed to overcome this limitation by including the SSI effects and modifying soil properties around the foundation. The following three sets of analyses are conducted in turn, in order to develop the mathematical relations for the near-field’s mechanical and geometrical properties:

  1. a)

    Analyzing the rigorous models (plastic models):

In the rigorous models, the soil behavior is simulated by an elastic–plastic constitutive model that is accurate enough in general loading conditions. Each one of these models is analyzed under 10 different ground motions that are selected appropriately and are imposed to the base of the models. Dimensions of a region just below the foundation, or the near-field zone, where the soil has experienced on average larger strains at a larger rate compared with the far-field zone are determined. In other words, the rate of change in shear strains of the near-field zone is considerably greater than the far-field. It is the main criterion for determining the near-field dimensions. Figure 1 shows a schematic illustration of the mentioned region. In Fig. 1, 2a is the foundation width and L nf and H nf represent the near-field dimensions. Average of results obtained from 10 different ground motions is considered as the response of that model. More details about the soil domain, the superstructure modeling, and the boundary conditions are presented in Sect. 4.

Fig. 1
figure 1

Schematic illustration of the near and far-field regions

Full size image
  1. b)

    Analyzing models with the near-field approach

In this case, the soil is assumed to behave linearly and have equivalent linear characteristics. Properties of the soil in both the near- and far-field zones are first obtained by free-field analysis of the site (i.e. the traditional equivalent linear method) and kept unchanged for the soil in the far-field region in the rest of analysis. Then, characteristics (shear modulus and damping) of the near-field soil are modified through a trial and error process in order to achieve the same maximum structural drift obtained in the rigorous analyses. In other words, the near-field damping is determined based on the strain level of this region and then consecutive reductions are applied on the shear modulus of the soil in the near-field zone for the structural drift to be converged to that computed with the nonlinear soil modeling. Finally, these modified shear modulus and damping are collected as the near-field properties of the considered model.

  1. c)

    Regression analysis to develop mathematical relations

After obtaining the near-field properties for all of the models, regression analyses will be performed to develop mathematical relations for the near-field properties based on the dimensionless parameters of the SSI system, as introduced in Sect. 2.1.

Further explanation about modeling details and analysis steps are presented in the next sections.

4 Modeling details

The open source software framework OpenSees (Open System for Earthquake Engineering Simulation) (Mckenna 1997; Mazzoni et al. 2007) has been used to create and analyze the three dimensional FE models of this study in the time domain. The material and elements used for simulating both soil and superstructure are described in this section. In addition, the methodology used for applying gravitational and seismic loads is presented here.

4.1 Structure

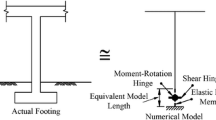
The structure is idealized as an SDF stick model with modal properties of the building structure as shown in Fig. 2. The lumped mass, m, and the height, h, of this SDF structure are corresponding to the effective modal mass and height of the building structure. Using such a simple model clears the path to investigate the effects of the modal properties of the structure without considering any specific type of structural system. The structure model is placed at the center of a square rigid mat foundation. As a main assumption, both the structure and its foundation are supposed to have a linear elastic behavior during analysis. Elastic beam-column and shell elements are used for modeling of the structure and mat foundation, respectively.

Fig. 2
figure 2

The idealized SDF structure and its square foundation

Full size image

4.2 Soil domain

The described SDF system is supported by a 3D soil domain and no uplift is allowed between the foundation and soil. Simulating the soil behavior is one of the major challenges in geotechnical earthquake engineering. In this study a Pressure Dependent Multi-Yield (PDMY) elastic–plastic constitutive model is used to model the soil behavior in the rigorous models. This constitutive model is capable of simulating the fundamental response characteristics (e.g. dilational behavior and cyclic mobility) of pressure sensitive soils under monotonic and cyclic loading conditions. The PDMY model has been developed by Yang et al. (2003) and was implemented in OpenSees. Values of the parameters of this model as recommended by its developers for typical soil conditions are presented in Table 3. In this table, the peak shear strain is an octahedral shear strain at which the maximum shear strength is reached; the reference pressure is a reference mean effective confining pressure at which the peak shear strain is attained; the pressure dependent coefficient is a positive constant defining variation of the shear modulus as a function of the effective confining pressure; the contraction is a non-negative constant used for defining the rate of contraction; and finally dilation 1 and dilation 2 are non-negative constants defining the rate of shear-induced volume increase (dilation). The dilational behavior of soil is controlled by dilation 1 and dilation 2 and larger values are used for denser sands and correspond to stronger dilation rates (Mazzoni et al. 2007). This material model is used to simulate the drained soil condition.

Table 3 Values of the constitutive parameters for the soils in this study
Full size table

As mentioned before, in the near-field model an equivalent linear elastic behavior is assumed for the soil and therefore a Rayleigh damping formulation should be used to include material damping in the soil domain. The full form of this formulation is expressed as Eq. 11.

$$\left[ C \right] = \alpha \left[ M \right] + \beta \left[ K \right]$$
(11)

where [M] is the mass matrix, [K] is the stiffness matrix and α and β are Rayleigh damping coefficients calculated to obtain desired damping ratios for two control frequencies (Phillips and Hashash 2009). Kwok et al. (2007) examined different frequencies and showed that using the first mode natural frequency of site and five times that frequency (presumably being equal to the third mode’s natural frequency of site) gives the best match to the exact solution. Because of its wide acceptability and accuracy, recommendation of Kwok et al. (2007) is followed for the purposes of this study.

The soil domain is discretized by 8 node solid elements. The maximum element length, ∆h, is calculated by Eq. 12 in order to avoid numerical damping (Jeremic et al. 2009).

$$\Delta h \le \frac{{\lambda_{\hbox{min} } }}{10} = \frac{{V_{s} }}{{10f_{\hbox{max} } }}$$
(12)

where V s is the shear wave velocity of the soil and f max and λ min are the highest frequency and the least wave length of the propagating waves, respectively. Typically, f max can be assumed to be equal to 10 Hz for seismic analysis. An example of the 3D FE mesh of the soil–foundation–structure (SFS) system of this study is illustrated in Fig. 3.

Fig. 3
figure 3

3D FE model of the SFS system

Full size image

4.3 Soil medium dimensions and boundary conditions

The soil domain is semi-infinite in dimension and just a bounded cut of it can be modeled in the FE analysis. The boundaries of such a model should be able to absorb impinging waves. The boundary condition developed by Lysmer and Kuhlmeyer (1969) is used as the absorbing boundary to simulate the radiation damping.

The sensitivity analysis of the structural response to the horizontal dimension (L) of the FE model shows that for the most critical cases, the horizontal dimension of the soil domain should be at least 4 times the foundation width. In practice the soil dimension is taken to be 5 times the foundation dimension. The depth of the soil layer on a rigid base is assumed to be 50 m. This is deep enough for the boundary condition at the bottom not to affect the structural response and the strain distribution under the foundation.

5 Ground motions

As shown in Table 2, four different soil types are considered for this research. A set of 10 ground motions are selected from the PEER Strong Motion Database (2010) and the European Strong Motion Database (2012) for each site based on the criteria mentioned in Table 4. Characteristics of the selected ground motions are summarized in Table 5.

Table 4 The criteria for ground motion selection
Full size table
Table 5 Selected ground motions for each site
Full size table

The selected earthquake records should be scaled to be strong enough to excite the structure more or less similarly. The ASCE7-10 (ASCE 2010) criteria and design spectrums with S S  = 1.5 g and S 1 = 0.6 g are used for this purpose. In the software, the ground motion is applied to the base of the model, but these records have been recorded on the ground surface. Therefore, a deconvolution analysis is performed beforehand to calculate the ground motion at the base level using the Shake91 software (Idriss and Sun 1992). As mentioned in Sect. 4.2, the PDMY model employs a power function to represent variation of the shear modulus as a function of the effective confining pressure. Same pattern is used to model different layers of the considered soil profile.

6 Solution procedure

Initial conditions are very important in simulating geotechnical phenomena; consequently a staged approach is employed in the rigorous analysis phase. The solution procedure is composed of the following three stages:

  1. a)

    The gravity load is applied to the linear soil model.

  2. b)

    The behavior of the soil elements is switched from linear elastic to elastoplastic constitutive behavior and the gravity analysis is continued until reaching equilibrium in this new state.

  3. c)

    The dynamic excitation is applied to the base of the model as an acceleration time history obtained from deconvolution analysis of the scaled ground motion.

An incremental-iterative procedure should be employed to integrate the equations of motion in the dynamic analysis phase. The Newmark method with the time integration parameters γ = 0.5 and β = 0.25 is used for conducting the transient analysis phase. As the previously described FE model has a large number of degrees of freedom (DOFs), the modified Newton–Raphson algorithm is utilized for decreasing the calculation cost.

The time step of the transient analysis phase (Δt) has to be limited in order to assure accuracy. The time step is selected not to be larger than the time step increment of the accelerogram. In addition, an accuracy criterion is set for considering higher mode effects as follows:

$$\Delta t < \frac{{T_{n} }}{10}$$
(13)

here, T n is the smallest natural period of the discretized SSI system (Jeremic et al. 2009). Another accuracy criterion arises from the nature of the FE analysis. When a wave propagates in the FE domain, it must reach one node after the previous one. With a too large time step, the wave may reach two successive nodes simultaneously. Providing for this condition ensures that the wave can propagate in the FE domain appropriately. This criterion can be expressed by Eq. 14:

$$\Delta t < \frac{\Delta h}{{V_{s} }}$$
(14)

where Δh is the minimum element size and V S is the shear wave velocity in the soil domain (Jeremic et al. 2009).

7 Time history analyses results

As mentioned in Sect. 3, 48 different SFS models are constructed for performing the parametric study and each model is subjected to 10 ground motions. Two sets of time history analyses including the rigorous (elastoplastic) and modified equivalent linear (near-field) are conducted to calculate the near-field region properties. These properties consist of the near-field dimensions, which are obtained from the rigorous analysis, and the shear modulus and damping ratio from the modified equivalent linear models analyzed with the near-field approach. Results of these analyses and their coefficients of variation (CV) are collected in Table 6. These results are the arithmetic means of the values obtained from applying 10 different ground motions to each model. Dispersion of these values is in an acceptable range because all of the ground motions are scaled to the same spectrum making them to have similar response spectrum amplitude levels. As mentioned in Sect. 3, shear strain variation around the foundation is the main criterion for determining the near-field dimensions. Therefore, shear strain distribution around the foundation is checked for each one of analyses and a region with high shear strain variation is specified as the near-field zone. For instance, the shear strain distribution and the near-field zone determination are shown for a cut of the soil domain in model No. 17 under Parkfield earthquake in Fig. 4a. The values shown in Fig. 4a are net numbers and the maximum shear strain is equal to 2.31 %. Figure 4b demonstrates variation of the normalized maximum seismic shear strain over the soil domain’s depth. As can be observed in this figure, the rate of shear strain variation near the foundation is considerably greater than other regions and the near-field zone can be distinguished from the far-field. Similar analyses are performed for each model under each earthquake and the average values of the near-field dimensions are calculated. In Table 6, H N.F. /2a and L N.F. /2a are ratios of the near-field’s depth and length to the foundation width, respectively, G/G Free-Field represents the shear modulus reduction factor which is defined as the ratio of the near-field shear modulus (obtained from the modified equivalent linear analysis) to the shear modulus of the same region calculated by the free-field analysis of Shake, i.e. the ELM analysis, and ξ is the damping ratio of near-field region. As seen in Table 6, variation of the dimensionless parameters considerably alters the seismic response of the SSI system. A regression analysis should be performed in order to derive mathematical relations between dimensionless parameters and the near-field properties as described in the next section.

Table 6 Time history analyses results: average of the results obtained from 10 different ground motions and coefficients of variation
Full size table
Fig. 4
figure 4

Seismic shear strain distribution and near-field zone determination for model No. 17 under Parkfield earthquake. a Shear strain contour. b Normalized maximum seismic shear strain along the soil domain depth

Full size image

8 Nonlinear regression analysis

Nonlinear regression analysis should be performed for deriving the near-field properties based on the SSI characteristics including \(\bar{s}\), \(\bar{h}\), and \(\bar{m}\). Studying the impact of each one of the dimensionless parameters shows that the near-field properties are significantly sensitive to \(\bar{s}\) variation and sensitivity to \(\bar{h}\) is slightly more than \(\bar{m}\). Moreover, based on the results presented in Table 6, it is concluded that while increase in \(\bar{s}\) and \(\bar{m}\) values increases the SSI effects, these effects decrease with increasing \(\bar{h}\). Therefore, inertial SSI effects are directly related to \(\bar{s}\) and \(\bar{m}\) (i.e. SSI effects vary with \(\bar{s}^{\alpha } \times \bar{m}^{\beta }\)) but they have an inverse relation with \(\bar{h}\) (i.e. SSI effects change with \(1/\bar{h}^{\gamma }\)). These conclusions are consistent with the results reported by Veletsos and Meek (1974), Wolf (1985), Avilés and Pérez-Rocha (1996) and Stewart et al. (1999a, b). Accordingly, a combination in the form of \(\left( {\bar{s}^{\alpha } \times \bar{m}^{\beta } /\bar{h}^{\gamma } } \right)\) can be considered as the key parameter playing a critical role in variation of the near-field properties. Therefore this ratio is treated as an independent variable in deriving the semi-analytical relations.

Nonlinear regression analysis is conducted to determine coefficients and powers of variables in the semi-analytical relations. After performing this analysis in a sample statistical software to obtain a preliminary estimation of the coefficients and powers, a manual adjustment is also necessary to arrive at smoothed values. As of powers \(\alpha , \beta\) and γ, several combinations are examined and eventually the values summarized in Table 7 are proposed. These powers clearly show the level of contribution of each parameter to the SSI effects.

Table 7 Powers of dimensionless parameters in the semi-analytical relations
Full size table

Therefore, the independent variable used for deriving all of the semi-analytical relations is \(\left( {\bar{s}^{1.5} \times \bar{m}^{0.10} /\bar{h}^{0.25} } \right)\). After adjusting the powers of the parameters, variation of each one of the near-field properties with respect to the considered independent variable is studied and a curve fitting technique is applied to derive the semi-analytical relations for estimating the near-field properties. More details about the proposed equations are presented in the next sections.

8.1 The shear modulus reduction factor

Applying the curve fitting technique to the shear modulus reduction factors leads to a function as Eq. 15.

$$\frac{{G_{Near{\text{-}}Field} }}{{G_{Free{\text{-}}Field} }} = \frac{0.6}{{\left( {\frac{{\bar{s}^{1.5}\,\times\,\bar{m}^{0.10} }}{{\bar{h}^{0.25} }}} \right) + 0.6}},\quad R^{2} = 0.934$$
(15)

where \(G_{Near{\text{-}}Field}\) is the final shear modulus of the near-field zone, \(G_{Free{\text{-}} Field}\) is the effective shear modulus for the top layer of soil obtained from ELM analysis of the free-field with Shake91 and R 2 is the coefficient of determination that indicates how well data fit the proposed semi-analytical model. The mathematical form of Eq. 15 is selected in such a way that it tends to unity and zero for decreasing and increasing \((\bar{s}^{\alpha } \times \bar{m}^{\beta } /\bar{h}^{\gamma } )\) respectively. Figure 5 illustrates the curve fitting for the shear modulus reduction factor of the near-field zone.

Fig. 5
figure 5

Curve fitting for the shear modulus reduction factor

Full size image

8.2 The damping ratio

The semi-analytical relation resulted from curve fitting for estimating damping ratio of near-field zone is as Eq. 16.

$$\xi = 18\,\left( {\frac{{\bar{s}^{1.5} \times \bar{m}^{0.10} }}{{\bar{h}^{0.25} }}} \right) + 3,\quad R^{2} = 0.969$$
(16)

where \(\xi\) is the damping ratio of the near-field zone in percent. Figure 6 demonstrates the curve fitting for the damping ratio of the near-field zone.

Fig. 6
figure 6

Curve fitting for the damping ratio of the near-field zone

Full size image

8.3 The near-field dimensions

Part of the horizontal dimension (length) of the near-field protruding from each side of the foundation (see Fig. 1), L NF , normalized to the foundation dimension is estimated by Eq. 17 with its curve fitting being presented in Fig. 7.

Fig. 7
figure 7

Curve fitting for the normalized near-field partial length

Full size image
$$\frac{{L_{N.F.} }}{2a} = \frac{{3.25\,\left( {\frac{{\bar{s}^{1.5}\,\times\,\bar{m}^{0.10} }}{{\bar{h}^{0.25} }}} \right)}}{{6\left( {\frac{{\bar{s}^{1.5}\,\times\,\bar{m}^{0.10} }}{{\bar{h}^{0.25} }}} \right) + 0.5}},\quad R^{2} = 0.496$$
(17)

Finally, a criterion for the depth of the near-field zone is set as:

$$H_{N.F.} = 0.25(2a) = 0.5a$$
(18)

where \(2a\) is the foundation width. Figure 8 illustrates the proposed equation for the near-field depths of all of the analyzed models. It should be noted that the slight discrepancies in the near-field dimensions will be shown to have no significant effects on the structural responses.

Fig. 8
figure 8

Curve fitting for the depth of the near-field zone

Full size image

9 Steps of employing the near-field method

In the previous sections details of the near-field method proposed in this study were explained. As mentioned before, this method is based on decomposition of the soil domain into near-field and far-field regions and proposes modified properties for modeling of the soil in the near-field zone. This section presents a step-by-step methodology for employing the near-field method in direct SSI analysis. The main steps of the near-field method can be summarized as follows: (1) modal analysis of the fixed-base structure; (2) determining the important modes based on modal participation factors; (3) calculating \(\bar{s},\bar{h}\) and \(\bar{m}\) values for important modes (Eqs. 3, 5, and 9); (4) using Eqs. 15 and 16 to calculate the shear modulus modification factor and damping ratio of the near-field region for important modes, (5) computing weighted average of the shear modulus modification factor and damping ratio using the modal mass participation factor as the weight; (6) using Eqs. 17 and 18 to determine the near-field region dimensions; (7) performing free-field analysis to calculate effective soil properties under the considered earthquake and assigning effective properties to the far-field zone; (8) modifying the effective properties of the near-field zone using the modification factors obtained in step 5 and the characteristics calculated in step 7.

More details about the numerical implementation and examples are given in a companion paper.

10 Comparison with other suggestions

There are other suggestions available in different references for modulus degradation and damping factors of the free-field soil under intensive shakings. In this section, results of the present study are compared with other available data.

10.1 Comparison with the building codes and references

Some of the building codes and references such as ASCE 7-10 (ASCE 2010), FEMA P-750 (2009) and NIST (2012) present the shear modulus modification factors in a tabular form for various site and excitation conditions to take the effect of large strains induced by the design earthquake motion into account, such as Table 8. These factors are used to modify average shear modulus of soil for calculating the foundation stiffnesses. The value of S DS /2.5 for considered site conditions of this research is equal to 0.4 and thus the middle column of the table is applicable for the sites of this study. On the other hand, different modulus reduction factors have been obtained by employing the near-field method for each one of the assumed site conditions and the average value of these values in each site is assumed to be a representative value for that site. Comparison between the code values and those of the near-field method is demonstrated in Table 9 and Fig. 9.

Table 8 Shear modulus modification factors suggested by ASCE 7-10 (ASCE 2010), FEMA P-750 (2009) and NIST (2012)
Full size table
Table 9 Comparison between modulus degradation values proposed by the near-field method and the codes
Full size table
Fig. 9
figure 9

Comparison between the modulus reduction factors suggested by the near-field method and the codes

Full size image

It is seen that the values of the near-field modification factors calculated in this study are smaller than those suggested by the codes. It is expected, because the code values are for the free-field conditions and no account has been given in their development for presence of a structure.

10.2 Comparison with Seed and Idriss modulus degradation and damping curves

Seed and Idriss (1970) used experimental data and proposed modulus degradation and damping ratio curves for sandy and clayey soils. The near-field modulus reduction and damping ratio values are compared with those suggested by Seed and Idriss in Figs. 10 and 11. It should be noted that Seed and Idriss curves are used in ELM analysis of the free-field with Shake91 and the horizontal axis represents the effective shear strain of soil in the near-field region obtained from these ELM analyses. Again, it is seen that to account for the large strains induced in the near-field, the shear modulus and damping ratios have to take smaller/larger values than those suggested by Seed and Idriss, respectively.

Fig. 10
figure 10

Comparison between the near-field and Seed and Idriss modulus reduction values

Full size image
Fig. 11
figure 11

Comparison between the near-field and Seed and Idriss damping ratios

Full size image

11 Conclusions

The main objective of this research was developing a simple model for the direct analysis of the soil–structure interaction including the effects of structure on the adjacent bearing soil. It was shown that a limited region in the vicinity of the foundation experiences large strains and a high level of nonlinearity to the extent that the equivalent linear method (ELM) was not accurate enough for this region. This region was called the near-field zone and it was suggested to modify its mechanical properties to resolve the limitation of ELM and take the effects of the large strains into account. The dimensionless parameters controlling the response of the dynamic soil–structure system were utilized to derive equations for the characteristics of the near-field zone. A comprehensive parametric study was conducted in a rigorous model using an elastoplastic (PDMY) constitutive relation for the underlying soil. 10 consistent ground motions were selected and applied to the model. In addition, in an equivalent linear parallel model, the characteristics of the near-field soil were tuned by trial and error to arrive at maximum structural responses equal to those of the rigorous model. After that, nonlinear regression analysis was performed and semi-analytical equations were derived for calculating the near-field properties as well as its dimensions. Comparing the reduction factors obtained in the present study with the recommendations of building codes such as ASCE 7-10 (ASCE 2010) and modulus degradation curves proposed by Seed and Idriss showed that the mechanical properties of the near-field zone have to be adopted as smaller than those of the nearby free-field zone because of the inertial effects of the structure. Inclusion of such an effect is the unique feature of the current study.

In this paper only the procedure and equations for further modification of the soil properties in the near field were given. In a companion paper (part II of the current paper), the structural responses are presented and effects of different approaches including the near-field method are discussed and compared with the available recorded data in real buildings.