1 Introduction

In the near-fault conditions, due to the effects of forward rupture directivity, most of the seismic energy in ground motions is concentrated in a single pulse of motion at the beginning of the record (Somerville et al. 1997). These ground motions, referred as “near-fault pulse-like ground motions”, may result in high seismic demands for buildings. Many investigations have studied the effects of the near-fault pulse-like ground motions on various structures (Alavi and Krawinkler 2004; Bertero et al. 1978; Park 2013; Phan et al. 2007; Sehhati et al. 2011). The results of these investigations demonstrated that the near-fault pulse-like ground motions can induce more severe damage on structures than the non-pulse-like ground motions (referred as “ordinary ground motions” here). Although several researchers (Kanee et al. 2013; Kennedy et al. 1981; Sankaranarayanan and Medina 2006) have investigated the effects of the near-fault pulse-like ground motions on nonstructural components established on inelastic supporting structures, their studies focused mainly on design response spectra for nonstructural components due to these ground motions. The near-fault pulse-like earthquake characteristics such as earthquake magnitude and rupture distance were less considered and not thoroughly investigated. Since failure of nonstructural components constitutes a major portion of economic losses (Filiatrault et al. 2002; McKevitt et al. 1995; Myrtle et al. 2005; Naeim 2000; Scholl 1984; Taghavi and Miranda 2003) and due to the need for performance-based seismic design of nonstructural components, it is, therefore, necessary to reconsider the effects of the near-fault pulse-like ground motions in the seismic design and performance evaluation of nonstructural components.

In the seismic design of nonstructural components, the amplification factors, defined as the floor response spectra (FRS) for an inelastic primary structure normalized by the FRS for the corresponding elastic primary structure, are a particularly appealing approach to obtain the design FRS of an inelastic primary structure. Many investigations have been conducted to study the characteristics of the amplification factors (Chen and Soong 1988; Gupta 1990; Lin and Mahin 1985; Phan and Taylor 1996; Sewell et al. 1986, 1987; Singh et al. 1993; Soong 1994; Toro et al. 1989; Villaverde 1997, 2004; Wesley and Hashimoto 1981). In some of these investigations, the amplification factors were computed by specifying target ductility values (Lin and Mahin 1985; Vukobratović and Fajfar 2015) or employing structural strength reduction method (Oropeza et al. 2010) to consider primary structure nonlinearity. Most other studies, such as (Sankaranarayanan and Medina 2007), quantified the reduction/increase in peak component acceleration demands due to structure nonlinearity through scaling the ground motion parameters, which is similar to the strength reduction method. Different from the preceding studies, the amplification factors in this study are calculated for primary structures suffering different levels of damage from ground motions. In comparison with the amplification factors based on primary structure ductility or strength reduction factor, the proposed amplification factors are more reasonable due to a more accurate evaluation of structural damage, which would facilitate the application of performance-based seismic design significantly.

It is well known that the damage of structures depends both on inelastic displacement demand and hysteretic energy dissipation (Fajfar 1992). Park-Ang damage index and its modified versions are good measures to quantify the structural damage and have been used extensively in the community of earthquake engineering because they account for the contribution of inelastic displacement demand and hysteretic energy dissipation to the damage of structures. Thus the modified Park–Ang damage index is adopted in this investigation to represent different damage levels of primary structures.

This manuscript studies the amplification factors, A DI , based on primary structure damage (represented by the modified Park–Ang damage index, DI) from 81 near-fault pulse-like ground motions. The analysis results are also compared with those of 573 ordinary ground motion records in some parts of the paper. The influences of damage index, earthquake magnitude, rupture distance, peak ground velocity (PGV), maximum incremental velocity (MIV), hysteretic behavior of structures, ultimate ductility factor, μ u, and damping of nonstructural components, ξ c, are evaluated and discussed statistically. Based on the parametric analysis, a predictive model is established for the application of the amplification factors in the seismic design of nonstructural components due to the near-fault pulse-like ground motions.

2 Amplification factors

In the seismic design of primary structures, the strength reduction method is widely used to account for structure nonlinearity since it allows engineers or researchers to compute the nonlinear responses of primary structures by scaling the elastic responses. In this study, a parameter denoted as amplification factor, A DI , is used to quantify the effect of primary structure nonlinearity on peak acceleration demands of nonstructural components. The A DI factor is defined as the ratio of the FRS for an inelastic primary structure to that for the corresponding elastic primary structure [Eq. (1)]. The terms ‘elastic’ and ‘inelastic’ in this equation refer to the behavior of the supporting structure:

$$A_{DI} = FRS_{\text{inelastic}} /FRS_{\text{elastic}}$$
(1)

where A DI is the amplification factor, FRS inelastic is the floor response spectra when the inelastic structure suffers damage (represented by the damage index, DI) from ground motions, FRS elastic is the floor response spectra when the elastic structure is excited by the same ground motion.

The inelasticity of a building modifies floor motions and forces which acceleration-sensitive nonstructural components are subjected to. In this investigation, the modified Park-Ang damage index (Kunnath et al. 1992) is selected to estimate the damage performance of primary structures. It removes the elastic portion of the displacement demand from both the numerator and denominator of the first term of the original Park-Ang damage index (Park and Ang 1985; Park et al. 1985), and is defined as:

$$DI = \frac{{x_{\text{m}} - x_{\text{y}} }}{{x_{\text{u}} - x_{\text{y}} }} + \beta \frac{{E_{\text{H}} }}{{x_{\text{u}} F_{\text{y}} }} = \frac{{\mu_{\text{m}} - 1}}{{\mu_{\text{u}} - 1}} + \beta \frac{{E_{\text{H}} }}{{F_{\text{y}} \mu_{\text{u}} x_{\text{y}} }}$$
(2)

where x m is the maximum displacement of the structure under the ground motion, and μ m is the corresponding ductility demand; x u is the ultimate deformation capacity under the monotonic loading, and μ u is the corresponding ultimate ductility capacity; E H is the hysteretic energy dissipation under the ground motion; F y is the yield strength, and x y is the yield displacement; β is a positive dimensionless parameter to scale the effect of hysteretic energy dissipation on the final damage of the structure. Referring to the investigations (Decanini et al. 2004; Panyakapo 2004; Warnitchai and Panyakapo 1999), β = 0.15 is used in this manuscript.

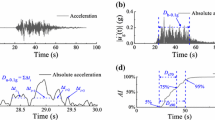
In this investigation, the amplification factors are computed for single-degree-of-freedom (SDOF) systems with the viscous damping ratio of ξ = 5 % for primary structures. Figure 1 shows the diagram for the computation of the amplification factors. As shown in Fig. 1b, c, the first step is to obtain the absolute accelerations of primary structures and these values can be computed according to Eq. (3).

$$m {\ddot{\textit{u}}} + c\dot{u} + r = - m{\ddot{\textit{u}}}_g$$
(3)

where m, c, and r represent mass, damping, and restoring force for the primary structure; c = 2 mξω; ω is the frequency of the primary structure; \({\ddot{\textit{u}}}\) and \(\dot{u}\) are the relative acceleration and velocity of the primary structure, while \({\ddot{\textit{u}}}_g\) represents ground motion acceleration; \({\ddot{\textit{u}}} + {\ddot{\textit{u}}}_g\) is the obtained absolute acceleration of the primary structure.

Fig. 1
figure 1

The diagram for the computation of the amplification factor, A DI : a 81 near-fault pulse-like ground motions; b absolute acceleration (response) of the inelastic primary structure; c absolute acceleration (response) of the elastic primary structure; d and e the obtained accelerations b and c are considered as ground motions for the subsystem and the obtained corresponding FRS; f obtained final results plotted in terms of FRS inelastic/FRS elastic versus T C/T B

Full size image

Then, as shown in Fig. 1d, e, the FRS can be computed by converting the obtained absolute acceleration into the format of pseudo-acceleration response spectra according to Eq. (4).

$$m_{\text{c}} {\ddot{\textit{u}}}_{\text{c}} + c_{\text{c}} \dot{u}_{\text{c}} + k_{\text{c}} u_{\text{c}} = - m_{\text{c}} \left( {\ddot{\textit{u}}} + {\ddot{\textit{u}}}_g \right)$$
(4)

where m c, c c, and k c represent mass, damping, and elastic stiffness for the subsystem; c c = 2m c ξ c ω c; ω c and ξ c are the frequency and damping ratio of the subsystem, respectively; k c = m c ω 2c ; \({\ddot{\textit{u}}}_{\text{c}}\), \(\dot{u}_{\text{c}}\), and \(u_{\text{c}}\) are the relative acceleration, velocity, and displacement of the subsystem, respectively.

In this paper, the FRS are expressed in terms of pseudo-spectral acceleration because subsystems are elastic and this completely describes the peak subsystem response values (Lin and Mahin 1985). Finally, the amplification factors can be obtained according to Eq. (1). It should be noted that the absolute accelerations for the inelastic primary structure are calculated by gradually reducing the applied strength of the SDOF system from the corresponding elastic strength demand until the specified DI is achieved within a tolerance (1 % is used in this manuscript). Besides, the nonlinearity of nonstructural components is not considered and the obtained results are valid for light components that do not offer dynamic feedback to the primary building.

The effects of various parameters on the amplification factors are studied. The primary structure period, T B, is between 0.3 s and 1.8 s with an interval of 0.3 s, and the component period, T C, is from 0.1 s to 6.0 s with an interval of 0.1 s. According to the comparison between the calculated DI and the real structural damage conducted by Park et al. (1987), four damage indices, DI = 0.1, 0.25, 0.4, and 0.8, which represent slight, minor, moderate, and severe damage, are selected to consider different damage performances of the primary structure, respectively. Three earthquake magnitude ranges, three rupture distance ranges, three peak ground velocity (PGV) ranges as well as three maximum incremental velocity (MIV) ranges are considered to indicate different characteristics of the near-fault pulse-like ground motions. Five ultimate ductility factors, μ u = 6, 8, 10, 12, and 14, are used to include structures with different ultimate ductility capacities. Four damping values of nonstructural components, ξ c = 0.01, 1, 2, and 5 % are employed to consider the effects of damping of nonstructural components. To investigate the influence of the hysteretic behavior of the primary structure, three different hysteretic models are used: (1) Elastic-Perfectly-Plastic (EPP) model, representing the non-degrading systems; (2) Modified Clough (MC) model (Mahin and Bertero 1975, 1976; Riddell and Newmark 1979), simulating the flexural behavior that exhibits stiffness degradation at reloading; and (3) Stiffness Strength Degradation (SSD) model based on the three-parameter model (Kunnath et al. 1990, 1992), representing global behavior of systems exhibiting stiffness degradation and strength deterioration during reloading branches. For the MC model, as shown in Fig. 2a, during loading, the response point follows the elastoplastic skeleton curve. The unloading stiffness after yielding is kept equal to the initial elastic stiffness. After unloading from point A, reloading along the same loading direction is towards the unloading point A, and after reaching this point further loading is directed towards point C. Several studies such as (Miranda and Ruiz-Garcia 2002) have concluded that the MC model is capable of reproducing the behavior of properly designed reinforced concrete structures where the behavior is primarily flexural and shear failure is avoided. However, it is not capable of capturing strength degradation caused by high shear stresses, slippage of steel bars or other phenomena. Different from the MC model, as shown in Fig. 2b, the SSD model assumes that the reloading is towards point C1, representing strength deterioration during cyclic analysis. The loss in strength, as indicated in Fig. 2b, is obtained from the following expression:

$$F_{\text{new}} = F_{\hbox{max} } (1.0 - \alpha \cdot E - \beta \cdot \mu )$$
(5)

where F new and F max are forces for C1 and C points, respectively; α and β are parameters that determine the amount of strength decay as a function of dissipated energy, E, and ductility, μ, respectively. In this study, as recommended by Kunnath et al. (1992), α and β are assigned to 1.0 and 0.0 due to test data being not readily available. Besides, no post-yield strain hardening is assumed in the above three models.

Fig. 2
figure 2

Load-deformation hysteretic models: a MC model; b SSD model

Full size image

3 Ground motions

Baker (2007) proposed a quantitative classification procedure of pulse-like ground motions, and 91 ground motions with large-velocity pulses in the fault-normal component of records were selected from approximately 3500 ground motions in the Next Generation Attenuation (NGA) project ground motion library. It is well known that for the near-fault pulse-like ground motions, the pulse-like signals of the fault-normal component are generally more pronounced than the fault-parallel component (Somerville et al. 1997). Therefore, 81 fault-normal ground motions are selected from Baker (2007) by excluding ground motions whose Joyner–Boore rupture distance is beyond 30 km. It should be noted that the epicentral distance is used to estimate the Joyner–Boore rupture distance when the Joyner–Boore rupture distance of a given ground motion is unavailable.

In order to quantitatively study the effects of the near-fault pulse-like ground motions on A DI , a total of 573 ordinary ground motions recorded in 38 earthquakes in the world is selected. These ordinary ground motions are generated from non-pulse-like ground motions, which do not differentiate between near-fault non-pulse-like and far-field ground motions because these two types of ground motions display virtually the same response behavior (Iervolino and Cornell 2008; Tothong and Cornell 2006). These ordinary ground motions are for magnitudes from 5.7 to 7.8, and rupture distances from 0.1 to 180 km and are obtained from the Pacific Earthquake Engineering Research Center (PEER) Next Generation Attenuation (NGA) relationships database (http://peer.berkeley.edu/nga/) and involve different site conditions [according to the United States Geological Survey (USGS) classification (Boore et al. 1993)]. The number of ground motions for site class A (>750 m/s), B (360–750 m/s), C (180–360 m/s), and D (0–180 m/s) is 111, 195, 180, and 87, respectively.

4 Statistical analyses

4.1 Mean amplification factors

A total of 8,748,000 amplification factors, A DI , is computed for 81 near-fault pulse-like ground motions, 6 primary structure periods, 60 vibration periods of components, 4 damage indices, 3 hysteretic behaviors, 5 ultimate ductility factors and 4 damping values of nonstructural components. Mean A DI values are then calculated by averaging results of 81 near-fault pulse-like ground motions for each primary structure period, each component period, each damage index, each hysteretic behavior, each ultimate ductility factor, μ u, and each component damping value, ξ c.

For the brevity of the paper, mean A DI values of the EPP system corresponding to μ u = 10 and ξ c = 0.05 are investigated and mainly the results for T B = 0.3 s and T B = 1.8 s are shown in this section. Figure 3 shows mean A DI values of the EPP system subjected to 81 near-fault pulse-like ground motions. The component periods are represented by the component period, T C, normalized by the primary structure period, T B, which is widely used in the preceding studies such as (Sankaranarayanan and Medina 2007). It can be seen that, in general, mean A DI values show the similar trend regardless of primary structure periods. In the short period region (T C ≤ 0.5 T B), mean A DI values are characterized by a significant reduction due to inelastic structural behavior, which is similar to the results (Lin and Mahin 1985; Vukobratovic and Fajfar 2015). In the fundamental period region (0.5 T B ≤ T C ≤ 1.5 T B), a substantial decrease in A DI is seen in the vicinity of T C/T B equal to 1.0 and mean A DI values decrease with the increase of DI. Take the mean A DI for primary structure period equal to 0.3 s as an example, the A DI for DI = 0.1 is 0.77 while the A DI for DI = 0.8 is 0.46 when T C/T B is equal to 1.0. Thus the inelasticity of primary structures would produce an obvious effect on the responses of nonstructural components when the period of components is close to that of the structure. Moreover, the decrease in the FRS is more significant when the structure suffers greater damage. In the long period region (1.5 T B ≤ T C ≤ 3.5 T B), mean A DI values increase very slightly with the increase of the component period and appear to be larger than one in some of the cases (e.g. Fig. 3a), implying that the FRS values for inelastic primary structures may be higher than those for elastic primary structures in this region. Amplification occurs in this region because the structure softens with higher DI values and the fundamental period of vibration lengthens. It is also noted that in the long period region, mean A DI values decrease with the increase of DI and the difference in the mean A DI between different DI values gradually reduces with the increase of the component period.

Fig. 3
figure 3

The mean A DI of the EPP system subjected to 81 near-fault pulse-like ground motions with μ u = 10 and ξ c = 0.05: a T B = 0.3 s; b T B = 1.8 s

Full size image

4.2 Dispersion of amplification factors

It is significant to quantify the level of dispersion in the amplification factors because the dispersion can reflect the diversity and uncertainty of ground motions. The coefficient of variation (COV), which is defined as the ratio of the standard deviation to the mean, is a common and effective parameter to quantify the dispersion.

The results of the EPP system for T B = 0.3 s and T B = 1.8 s corresponding to μ u = 10 and ξ c = 0.05 are given in this section. Figure 4 illustrates the COVs of A DI for two primary structure periods under the 81 near-fault pulse-like ground motions. It is clear from Fig. 4 that the COVs of A DI generally increase with the increase of T C/T B for T C/T B smaller than 1.0 while they decrease with the increase of T C/T B for T C/T B greater than 1.0. The peaking COVs of A DI occur in the vicinity of T C/T B equal to 1.0, indicating that the COVs are approximately period dependent. It is obvious that COVs are relatively sensitive to the damage index, DI, and increase with the increase of DI. For example, as shown in Fig. 4a, the COV for DI = 0.1 is about 0.13 when T C/T B is 1.0 while it increases to 0.30 for DI = 0.8.

Fig. 4
figure 4

COVs of A DI for the EPP system subjected to 81 near-fault pulse-like ground motions with μ u = 10 and ξ c = 0.05: a T B = 0.3 s; b T B = 1.8 s

Full size image

4.3 Comparison with the ordinary ground motions

To study the effect of the near-fault pulse-like ground motions, the ratios of the mean A DI of 81 near-fault pulse-like ground motions to the mean A DI of 573 ordinary ground motions are computed in this part for each primary structure period, each component period, each damage index, each hysteretic behavior, each ultimate ductility factor, μ u, and each damping of component, ξ c.

The case for the EPP system with μ u = 10 and ξ c = 0.05 is presented as an example in this part, and the results are shown in Fig. 5. It is clear that primary structures with different periods present similar results. In the short period region, the ratios of the mean A DI for different DI values just vary around 1.0, indicating that the near-fault pulse-like ground motions have a negligible effect on A DI . By contrast, the curves show obvious peaks in the fundamental period region and the ratios of the mean A DI tend to increase with the increase of DI. Most of the ratios are larger than 1.0 in this region. Take the 0.6 s building for example, the maximum ratios for DI = 0.1, 0.25, 0.4, and 0.8 are 1.03, 1.07, 1.10, and 1.15, respectively. It is therefore concluded that the near-fault pulse-like ground motions would increase A DI compared with the ordinary ground motions, and the magnitude of the increase can reach about 15 %. In the long period region, the ratios of the mean A DI decrease slightly when the component period or DI increases, and the ratios are just under 1.0. Hence, although the near-fault pulse-like ground motions can result in the reductions of A DI in the long period region, this effect is limited.

Fig. 5
figure 5

The ratios of the mean A DI of 81 near-fault pulse-like ground motions to the mean A DI of 573 ordinary ground motions for the EPP system with μ u = 10 and ξ c = 0.05: a T B = 0.3 s; b T B = 0.6 s; c T B = 0.9 s; d T B = 1.2 s; e T B = 1.5 s; f T B = 1.8 s

Full size image

4.4 Effect of earthquake magnitude

In this section, the 81 near-fault pulse-like ground motions are divided into three groups according to different earthquake magnitude (moment magnitude) ranges. The number of ground motions in each earthquake magnitude range can be seen in Table 1. Figure 6 shows the ratios of the mean A DI in each earthquake magnitude range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05. It is clear that ground motions with larger earthquake magnitude generally tend to induce greater A DI than the ground motions whose earthquake magnitude is relatively smaller. It is also indicated that the effect of earthquake magnitude on A DI becomes more obvious as DI increases. For the most T C/T B values, the ratios of the mean A DI in Fig. 6 are within the interval [0.8, 1.2], indicating the effect of earthquake magnitude on A DI is within 20 % for the near-fault pulse-like ground motions. However, the influence of earthquake magnitude on A DI is beyond 20 %, when both T B and DI are large (e.g. T B = 1.8 s and DI = 0.8).

Table 1 The number of ground motions in each earthquake magnitude, rupture distance, PGV, and MIV range
Full size table
Fig. 6
figure 6

The ratios of the mean A DI in each earthquake magnitude range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05: a T B = 0.3 s and DI = 0.1; b T B = 0.3 s and DI = 0.8; c T B = 1.8 s and DI = 0.1; d T B = 1.8 s and DI = 0.8

Full size image

4.5 Effect of rupture distance

Similar to the above section, the ground motion dataset is divided into three rupture distance ranges. The number of ground motions in each rupture distance range can be seen in Table 1. Figure 7 illustrates the ratios of the mean A DI in each rupture distance range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05. The ratios of the mean A DI tend to increase with the increase of DI, and the differences of the ratios of the mean A DI for different distance ranges in Fig. 7b, d are larger than the corresponding differences in Fig. 7a, c, respectively. These results reveal that the effect of rupture distance on A DI becomes more significant as DI increases. The ratios of the mean A DI in Fig. 7 are within the interval [0.8, 1.2], meaning that the effects of rupture distance on A DI are moderate for the near-fault pulse-like ground motions.

Fig. 7
figure 7

The ratios of the mean A DI in each rupture distance range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05: a T B = 0.3 s and DI = 0.1; b T B = 0.3 s and DI = 0.8; c T B = 1.8 s and DI = 0.1; d T B = 1.8 s and DI = 0.8

Full size image

4.6 Effect of peak ground velocity

Several investigations (Baez and Miranda 2000) have demonstrated that peak ground velocity (PGV) and maximum incremental velocity (MIV) are important ground motion parameters to characterize the near-fault pulse-like ground motions. It is necessary to investigate the effects of PGV and MIV on A DI . In this section, the ground motions are divided into three groups according to different PGV ranges, and the number of ground motions in each PGV range is summarized in Table 1. Figure 8 shows the ratios of the mean A DI in each PGV range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05. It is clear that in Fig. 8a, b the ground motions with larger PGVs tend to induce greater A DI than the ground motions whose PGV is relatively smaller, particularly in the fundamental period region. By contrast, Fig. 8c, d do not show the similar trend as compared to Fig. 8a, b. In addition, for the case of DI = 0.1 (i.e. Fig. 8a, c), the ratios of the mean A DI for different PGV ranges fluctuate around 1.0 in the whole component period region. For DI = 0.8 cases, as shown in Fig. 8b, d, the differences in the ratios of the mean A DI between different PGV ranges are more significant compared to the case of DI = 0.1 and tend to increase with the increase of primary structure period. It is concluded that the ratios of the mean A DI generally vary within the interval [0.9, 1.09], indicating that the effect of PGV on A DI is within 10 %.

Fig. 8
figure 8

The ratios of the mean A DI in each PGV range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05: a T B = 0.3 s and DI = 0.1; b T B = 0.3 s and DI = 0.8; c T B = 1.8 s and DI = 0.1; d T B = 1.8 s and DI = 0.8

Full size image

4.7 Effect of maximum incremental velocity

In this section, the ground motion dataset is divided into three groups according to different MIV ranges. The number of ground motions in each MIV range is summarized in Table 1. Figure 9 presents the ratios of the mean A DI in each MIV range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05. In general, the results for MIV show similarities with those of PGV. It is clear that for DI = 0.1 cases, the ratios of the mean A DI for three MIV ranges vary around 1.0 in the whole component period region, and the effect of MIV on A DI is insignificant. By contrast, the ratios of the mean A DI for DI = 0.8 cases deviate obviously from 1.0. The results show greater differences between different MIV ranges compared with the case of DI = 0.1 and are thus more significantly affected by MIV. The ratios of the mean A DI for different MIV ranges and DI values vary within the interval [0.92, 1.08], indicating that the effect of MIV on A DI is within 8 %.

Fig. 9
figure 9

The ratios of the mean A DI in each MIV range to the mean A DI of 81 near-fault pulse-like ground motions for the EPP system with μ u = 10 and ξ c = 0.05: a T B = 0.3 s and DI = 0.1; b T B = 0.3 s and DI = 0.8; c T B = 1.8 s and DI = 0.1; d T B = 1.8 s and DI = 0.8

Full size image

4.8 Effect of hysteretic behavior

In this part, the influence of stiffness degradation and strength deterioration is investigated by considering the MC and SSD models. The difference of A DI between the near-fault pulse-like ground motions and the ordinary ground motions is also researched. The ratios of A DI of MC and SSD systems normalized by A DI of EPP systems are calculated for each ground motion, each primary structure period, each component period, each damage index, each ultimate ductility factor, μ u, and each component damping, ξ c.

For the sake of simplicity, Fig. 10 presents the mean ratios of A DI of MC and SSD systems divided by A DI of EPP systems corresponding to μ u = 10 and ξ c = 0.05. The mean ratios of A DI are computed by averaging the results of 81 near-fault pulse-like ground motions or 573 ordinary ground motions. It is clear that MC and SSD systems show similar trends. For DI = 0.1 cases, the mean ratios of A DI for MC and SSD systems are close to 1.0 in the short and long period regions and tend to keep constant with the increase of the component period. While in the fundamental period region, a substantial decrease in the mean ratios of A DI can be observed for MC and SSD systems, being similar with the results (Lin and Mahin 1985), and the reduction for the ordinary ground motions is more significant than that for the near-fault pulse-like ground motions. For example, for the 1.8 s building, the mean ratio of A DI due to the near-fault pulse-like ground motions is about 0.86 for MC and SSD models when T C/T B being 1.0 while it has only 0.79 for the ordinary ground motions. It is concluded that the stiffness and strength degradation would result in a significant decrease of A DI in the fundamental period region, particularly for primary structures subjected to the ordinary ground motions.

Fig. 10
figure 10

The mean ratios of A DI of MC and SSD systems divided by A DI of the EPP system corresponding to μ u = 10 and ξ c = 0.05: a T B = 0.3 s and DI = 0.1; b T B = 0.3 s and DI = 0.8; c T B = 1.8 s and DI = 0.1; d T B = 1.8 s and DI = 0.8

Full size image

For DI = 0.8 cases, similar results can be found in the short period region when compared to the case for DI = 0.1. As the component period increases, the mean ratios of A DI for the two degrading systems experience a substantial decrease and the reduction region extends from the fundamental period region to the long period region, which is different from DI = 0.1 cases. In addition, the near-fault pulse-like ground motions result in larger mean ratios of A DI than the ordinary ground motions for two degrading systems, particularly in the fundamental period region. This suggests that for structures subjected to the ordinary ground motions, the effect (reduction) on A DI due to stiffness and strength degradation is more significant than that under the near-fault pulse-like ground motions. Hence, the near-fault pulse-like ground motions are more dangerous to components mounted on structures with degrading behavior than the ordinary ground motions.

4.9 Effect of ultimate ductility factor μ u

In order to quantitatively study the effect of ultimate ductility factor, μ u, on A DI , the mean ratios of A DI of the EPP system with μ u = 6, 8, 12, and 14 divided by A DI of the EPP system with μ u = 10 are calculated by averaging the results of 81 near-fault pulse-like ground motions or 573 ordinary ground motions.

Here, for the EPP system with ξ c = 0.05, the analysis results corresponding to μ u = 6 and 14 are presented in Fig. 11. For DI = 0.1 cases, it is clear from Fig. 11 that negligible difference can be found for the mean ratios of A DI between the near-fault pulse-like ground motions and the ordinary ground motions. The mean ratios of A DI with different μ u values vary around 1.0 in the short and long period regions, and thus the effect of ultimate ductility factor is not significant. In the fundamental period region, the mean ratios of A DI for two μ u values have significant differences and the mean ratios of A DI decrease with the increase of ultimate ductility factor in this period region.

Fig. 11
figure 11

The mean ratios of A DI of μ u = 6 and 14 normalized to A DI of μ u = 10 for the EPP system with ξ c = 0.05: a T B = 0.3 s and DI = 0.1; b T B = 0.3 s and DI = 0.8; c T B = 1.8 s and DI = 0.1; d T B = 1.8 s and DI = 0.8

Full size image

Although the mean ratios of A DI in the short period region show the similar trend for DI = 0.8 cases in comparison with DI = 0.1 cases, the effect of ultimate ductility factor on A DI becomes more significant in the fundamental and long period regions. Take the 0.3 s building subject to the near-fault pulse-like ground motions for instance, the mean ratio of A DI for μ u = 6 and DI = 0.8 reaches 1.15 when T C/T B is 1.0 while the value for μ u = 6 and DI = 0.1 has only 1.09. It is also clear that for DI = 0.8 cases, the differences in the mean ratios of A DI between different μ u values are more significant for the ordinary ground motions compared to the near-fault pulse-like ground motions in the fundamental period region. From Fig. 11, it is concluded that the effect of ultimate ductility factor, μ u, on A DI is within the interval [0.92, 1.17] and this effect is moderate for the design of nonstructural components.

4.10 Effect of damping of nonstructural components

In this section, the effect of damping of components, ξ c, on A DI is investigated. For the EPP system with μ u = 10, the ratios of A DI corresponding to ξ c = 0.01, 1, and 2 % divided by A DI of ξ c = 5 % are computed for each ground motion, each primary structure period, each component period, and each damage index. Then, the mean ratios of A DI are obtained by averaging the results of 81 near-fault pulse-like ground motions, as is shown in Fig. 12.

Fig. 12
figure 12

The mean ratios of A DI of ξ c = 0.01, 1, and 2 % divided by A DI of ξ c = 5 % for the EPP system subjected to 81 near-fault pulse-like ground motions with μ u = 10: a T B = 0.3 s and DI = 0.1; b T B = 0.3 s and DI = 0.8; c T B = 1.8 s and DI = 0.1; d T B = 1.8 s and DI = 0.8

Full size image

It is noted that the mean ratios of A DI for different ξ c values generally decrease with the increase of ξ c in the short and fundamental period regions. In the long period region, the mean ratios of A DI for different ξ c values basically tend to be close to 1.0 with the increase of T C, indicating that the effect of ξ c on A DI is negligible in this region. The above-obtained results are identical with the results (Vukobratovic and Fajfar 2015). Besides, the effect of ξ c on A DI in this region tends to increase with the decrease of primary structure period. It is also noted that the effect of damping of components becomes more significant when the structure suffers more severe damage. Take the 0.3 s building with ξ c = 0.01 % for example, the mean ratio of A DI for DI = 0.8 reaches 1.50 when T C/T B is equal to 0.46 while the value for DI = 0.1 has 1.10. From Fig. 12, the effect of ξ c on A DI is within the interval [0.98, 1.50]. Therefore, the damping of components can have a significant effect on component responses.

5 Predictive model

It is necessary and desirable to propose a predictive model of the mean A DI for the near-fault pulse-like ground motions. Based on the statistical results in Sect. 4, the predictive model to estimate the mean A DI for the near-fault pulse-like ground motions is developed and related parameters are established:

$$A_{DI} = a + b \cdot (T_{\text{C}} /T_{\text{B}} ) + c \cdot (T_{\text{C}} /T_{\text{B}} )^{2} + d/DI\quad (T_{\text{C}} /T_{\text{B}} \le 1)$$
(6)
$$A_{DI} = a + b/(T_{\text{C}} /T_{\text{B}} )^{2} + c \cdot \ln (DI )\quad (T_{\text{C}} /T_{\text{B}} \ge 1)$$
(7)

where T C is the vibration period of the component, T B is the primary structure period, DI is the damage index, a, b, c, and d are independent constants. Parameters a, b, c, and d are computed by a nonlinear least-square regression analysis using the Levenberg–Marquardt method for each hysteretic model. The resulting values of these parameters for T B = 0.3 s and ξ c = 0.05 are dependent on ultimate ductility factor, μ u, and the hysteretic model and summarized in Table 2. Figure 13 presents the comparison of the mean A DI computed using Eqs. (6) and (7) with the statistical results in this study for the three hysteretic models and all 81 ground motions. The correlation coefficient r (Ruiz-Garcia and Miranda 2004) is defined as:

$$r = \frac{{S(\bar{A}_{DI} ,\tilde{A}_{DI} )}}{{S(\bar{A}_{DI} )S(\tilde{A}_{DI} )}}$$
(8)

where \(\bar{A}_{DI}\) is the mean A DI computed by the nonlinear response history analysis, \(\tilde{A}_{DI}\) is the mean A DI computed using Eqs. (6) and (7), \(S(\bar{A}_{DI} ,\tilde{A}_{DI} )\) is the covariance between \(\bar{A}_{DI}\) and \(\tilde{A}_{DI}\), \(S(\bar{A}_{DI} )\) and \(S(\tilde{A}_{DI} )\) are the standard deviation of \(\bar{A}_{DI}\) and \(\tilde{A}_{DI}\), respectively. The r will approach 1.0 when the nonlinear regression model describes better the statistical data. In this investigation, r is used to measure the Goodness-of-Fit of Eqs. (6) and (7). Table 3 presents r for each hysteretic model and each ultimate ductility factor, μ u. All these data demonstrate that Eqs. (6) and (7) provides a good estimation of the mean A DI . For the application of the predictive model, users need to provide primary structure period, hysteretic behavior of the structure, ultimate ductility factor, and component damping to determine parameters used in the model. Then, according to the expected structural damage and component period, the amplification factor can be calculated using the predictive model. Note that the MC model and the SSD model can only be applied to properly designed reinforced concrete structures. For reinforced concrete structures with substantially increased strength and stiffness degradation, the established parameters for the predictive model need to be reconsidered and reevaluated.

Table 2 Parameters to be used in Eqs. (6) and (7) for T B = 0.3 s and ξ c = 0.05
Full size table
Fig. 13
figure 13

The comparison of the mean A DI computed using Eqs. (6) and (7) with the statistical results in this study: a EPP, μ u = 8; b EPP, μ u = 12; c MC, μ u = 8; d MC, μ u = 12; e SSD, μ u = 8; f SSD, μ u = 12

Full size image
Table 3 The correlation coefficients r of Eqs. (6) and (7) and statistical results for each hysteretic model and each ultimate ductility factor, μ u
Full size table

6 Conclusions

This manuscript investigates the amplification factors for the design of nonstructural components based on primary structure damage for the near-fault pulse-like ground motions. The amplification factors are computed with 81 near-fault pulse-like ground motions, and the corresponding statistical studies are presented. In some sections, the results for 573 ordinary ground motions are also given to make a comparison. Notice that the nonlinearity of the nonstructural component is not considered and the obtained results are valid for light components that do not offer dynamic feedback to the primary building. The following conclusions are drawn from this investigation:

  1. 1.

    The primary structure damage can lead to obvious reductions of the FRS in the short and fundamental period regions and this effect becomes more significant with the increase of primary structure period. In the long period region, the primary structure damage may result in amplifications of the FRS.

  2. 2.

    The peak COVs of A DI occur in the vicinity of T C/T B equal to 1.0 and the COVs on both sides of the peak decrease gradually with the distance from T C/T B equal to 1.0, indicating that the COVs are approximately period dependent. COVs are relatively sensitive to the damage index and increase with the increase of DI.

  3. 3.

    In comparison with the ordinary ground motions, the near-fault pulse-like ground motions can increase A DI in the fundamental period region, particularly for primary structures with higher DI values, and the maximum increase can reach about 15 %.

  4. 4.

    Ground motions with larger earthquake magnitude tend to induce greater A DI while the effect of rupture distance on A DI has no obvious regularity. Both the effects of earthquake magnitude and rupture distance on A DI become more significant as DI increases.

  5. 5.

    The PGV and MIV have similar effects on A DI , and ground motions with larger PGV or MIV do not necessarily induce greater A DI . The primary structure suffering greater damage from earthquakes would lead to larger differences in A DI between different PGV or MIV ranges, particularly for structures with higher periods.

  6. 6.

    The stiffness degradation and strength deterioration can cause obvious reductions in A DI in the fundamental period region, and the reduction region extends to the long period region with the increase of primary structure damage. Moreover, the decreases are more significant for the ordinary ground motions compared to the near-fault pulse-like ground motions, particularly for cases with higher DI values.

  7. 7.

    The ultimate ductility factor, μ u, can produce an obvious effect on A DI in the fundamental period region and the A DI decrease with the increase of μ u. Moreover, this effect becomes more significant with the increase of structural damage, which is especially true for the cases under the ordinary ground motions.

  8. 8.

    In the short and fundamental period regions, the effect of ξ c on A DI is significant. With the decrease of ξ c, the mean ratios of A DI generally increase in the whole period regions and the effect of ξ c on A DI becomes more significant for higher DI values. The effect of ξ c for different DI values is within the interval [0.98, 1.5].

  9. 9.

    In order to facilitate the application of the amplification factors, parameters for the predictive model under the near-fault pulse-like ground motions are established in this study. The parameters in the equation are dependent on primary structure period, structural hysteretic behavior, ultimate ductility factor, μ u, and damping of components, ξ c.

7 Data and resources

The 81 near-fault pulse-like ground motions and 573 ordinary ground motions used in this investigation can be downloaded from http://pan.baidu.com/s/1o8TfrBG. The parameters for the predictive model can also be downloaded from this site. In addition, the FORTRAN programming codes for conducting this statistical analysis are available from the authors upon request.