Preliminary ranking of alternative scalar and vector intensity measures of ground shaking

Abstract

In Performance-Based Earthquake Engineering, seismic demand in structures is predicted by building probabilistic seismic demand models that link measures of earthquake intensity (IMs) to measures of structural demand. Investigations are carried out herein for evaluating the predictive capability of a wide range of commonly-used scalar and vector-valued IMs for different peak-related demand parameters. To accomplish this goal, both efficiency and sufficiency of the candidate IMs are taken into account. The latter is evaluated with the recently-proposed “relative sufficiency measure”. This measure, which is derived based on information theory concepts, quantifies the amount of information gained (on average) by an IM relative to another about the demand parameter of interest. Evaluation of the IMs, herein, uses two sets of ground motions consisting of ordinary and pulse-like near-fault records. Two-dimensional RC frame structures, both fixed and isolated at the base, are selected. The most suitable IMs for predicting the considered different demand parameters and types of structure are identified in terms of both efficiency and sufficiency. The use of these most informative IMs is suggested to build improved probabilistic demand models.

1 Introduction

In the context of Performance Based Earthquake Engineering (PBEE, Cornell and Krawinkler 2000; Moehle and Deierlein 2004), seismic risk for a structure can be expressed in terms of the mean annual frequency (MAF) of exceeding a specified limit state, λ _LS . In this methodology, uncertainty in the ground motion intensity is described with a scalar parameter, or a low-dimensional vector of parameters, called intensity measure (IM) (Shome et al. 1998; Jalayer and Cornell 2003; Luco and Cornell 2007; Jalayer and Cornell 2009). This is a simplified way to represent ground motion uncertainty, which is alternative to the rigours approach consisting in a full probabilistic description of the ground-motion time history by means of a stochastic model (see e.g., Jalayer and Beck 2008). The IM serves as an intermediate variable between ground motion hazard and structural demand estimates, which are linked as follows:

$$ \lambda_{\,LS} = \int\limits_{im} {P\left[ {D > C_{LS} \left| {IM = im} \right.} \right]\left| {{\text{d}}\lambda_{\,IM} \left( {im} \right)} \right|} $$

(1)

where D denotes the structural demand (a.k.a. engineering demand parameter); C _LS is the capacity of the structure associated with the prescribed limit state LS; λ _IM is the seismic hazard expressed in terms of MAF of exceeding a certain level of IM at the site; and finally P[D > C _LS |IM] is the conditional probability that demand D exceeds the limit state capacity C _LS which is known as the structure fragility.

It is clear that in PBEE, the selection of a suitable IM for representing ground motion uncertainty is a major concern that has to be addressed. The stronger is the correlation between the predicted D and the adopted IM, the more accurate will be the result of the probabilistic risk assessment. Currently, the properties that are considered for measuring the suitability of an IM in representing the dominant features of ground shaking are the sufficiency, the efficiency, the scaling robustness, and the predictability through a probabilistic seismic hazard analysis (see Shome and Cornell 1999; Giovenale et al. 2004; Luco and Cornell 2007). Among these properties, the first two are of particular concern within the present study. An efficient IM leads to a relatively small variability of D|IM; consequently, a small number of ground motions and nonlinear dynamic analyses is required to estimate with adequate precision the conditional probability distribution P[D|IM]. A sufficient IM, on the other hand, is one that makes the probability distribution P[D|IM] independent of other ground motion characteristics; hence, using a sufficient IM implies that a detailed ground-motion record selection is not necessary while keeping the same accuracy in seismic structural performance estimation.

Efficiency and sufficiency of IMs have been the focus of attention of many researchers. For instance, Shome et al. (1998) demonstrated that the 5 %-damped pseudo-spectral acceleration at the first-mode period Sa(T ₁) is more efficient than the peak ground acceleration PGA. Nonetheless, for tall and long-period buildings as well as for structures subjected to near-source ground motions, Sa(T ₁) may not be neither efficient nor sufficient because of the limited spectral shape information (see Shome and Cornell 1999; Luco and Cornell 2007). This is in part due to the fact that Sa(T ₁) accounts neither for contribution of higher modes nor for period lengthening owing to structural nonlinearity.

Several alternative IMs were proposed as multiplicative adjustments of Sa(T ₁) in order to explicitly overcome the aforementioned drawbacks (Shome and Cornell 1999; Cordova et al. 2000; Mori et al. 2004; Luco and Cornell 2007; Bianchini et al. 2009; Lin et al. 2011). The objective of these proposals is not only to improve the predictive efficiency of the IM for all damage levels of a given structure, but also to account for the IM computability through a ground-motion hazard analysis without the need of any new attenuation relationships. Moreover, numerous spectrum-based scalar IMs including energy-derived ones were investigated, and studies showed that velocity-based IMs are in general better correlated to deformation demands especially in the case of medium rise frame structures (Akkar and Özen 2005; Riddell 2007; Yakut and Yilmaz 2008; Jayaram et al. 2010; Mollaioli et al. 2011). In Jayaram et al. (2010) and Mollaioli et al. (2011), the effect of near-fault ground motions and different soil types was also taken into account in evaluating predictive capabilities of the prescribed IMs.

As opposed to a scalar IM, a vector-valued one is a vector of more than one IM, which commonly comprises of two parameters. The vector-valued IM consisting of Sa(T ₁) and spectral values at other periods was shown to be a good predictor for ordinary ground motions (Luco et al. 2005; Vamvatsikos and Cornell 2005; Baker and Cornell 2008a) as well as for pulse-like ground motions (Baker and Cornell 2008b). The vector-valued IM consisting of Sa(T ₁) and ε (defined as the number of standard deviations by which lnSa(T ₁) differs from its predicted mean value obtained from a ground motion prediction model) was thoroughly investigated by Baker and Cornell (2006). The above mentioned vector-valued IMs provide more information about the shape of a record’s response spectrum.

This study aims at investigating the predictive capability of a wide range of scalar and vector-valued IMs by taking into account both ordinary and pulse-like near fault ground motions. In order to achieve this goal, efficiency and sufficiency of the considered IMs are assessed. Usually, logarithmic linear regression of the structural response parameter D conditioned on the considered scalar or vector-valued IM is carried out to define a probabilistic model for P[D|IM]. This probabilistic model is then used to evaluate efficiency and sufficiency of the prescribed IM. The standard error of regression σ _lnD|IM is considered as a measure of the IM efficiency, while a linear regression analysis of the residuals of lnD|IM relative to the ground motion parameters (e.g., magnitude M, distance R, and ε) is usually carried out for evaluating the IM sufficiency. Accordingly, the significance of having a linear trend implies the amount of insufficiency associated with the desired IM, which is usually measured by the p value of the estimated slope (see Luco and Cornell 2007).

Nevertheless, establishing sufficiency in an absolute sense is likely to require high-dimensional vector IMs since it involves independence of D|IM from other ground motion characteristics for all possible values of the IM. Hence, for a scalar or a low-dimensional vector IM, it is more reasonable to examine sufficiency in a relative sense. In this case, the suitability of one IM with respect to another could be evaluated in terms of the average difference in information provided about the predicted D. By using the concept of relative entropy from information theory, Jalayer et al. (2012) introduced a measure, called relative sufficiency measure (RSM). The RSM of IM ₁ with respect to IM ₂ quantifies on average how much more information IM ₁ relays to the designated structural response parameter D about the ground motion with respect to IM ₂.

This study intends to apply the RSM to measure the suitability of alternative IMs in predicting various demand parameters, and to provide a preliminary ranking of them. To fulfil this objective, two RC buildings consisting of a 4-story and a 6-story moment-resisting frame are employed. The frames are two-dimensional structures in order to avoid further concerns related to the study of IMs that explicitly account for possible torsional behaviors (for more details, see Lucchini et al. 2011). The two structures are designed according to a past Italian code (DM 96; 1996) and can be representative of regular existing RC buildings located in high seismic zones of the Mediterranean area. Both cases of the case-study structures being fixed and isolated at the base are considered herein. These buildings have been recently used by Mollaioli et al. (2013) and Ebrahimian et al. (2014) for a systematic evaluation of a large set of scalar IMs with respect to the seismic demand prediction of buildings. It is important to underline that in Mollaioli et al. (2013), the IM sufficiency is simply evaluated by measuring the independence of the conditional probability distribution P[D|IM] from magnitude and distance only. However, in this work the RSM is used as a robust measure of sufficiency. The set of IMs used in this study comprises those investigated by Mollaioli et al. (2013) in addition to other multi-parameter scalar and vector-valued IMs, which account for the period lengthening and/or higher mode effect. It should be noted that the RSM is particularly suitable for measuring the relative sufficiency of vector-valued IMs (e.g., vector IMs of more than two components). This provides the capability of studying candidate vector-valued IMs that are most suitable for pulse-like ground motion records.

As a result, this work provides sets of suitable IMs based on both efficiency and sufficiency criteria for different type of base fixities as well as different type of ground motions (i.e., ordinary and pulse-like). The outcomes reveal perfect correlation between relative sufficiency and efficiency of suitable IMs. It is shown that the results of the quantitative-evaluations of the sufficiency obtained by using the RSM agree quite well with the conclusions of Mollaioli et al. (2013). Findings and conclusions drawn in following sections are mainly applicable to buildings similar to those investigated in the present study, that is, existing medium-rise RC frames typical of high-intensity seismic zones of the Mediterranean area.

2 Intensity measures and demand parameters

The set of scalar and vector-valued IMs as well as the demand parameters used herein are summarized as follows. It is noteworthy that this paper focuses on the set of elastic IMs and the inelastic energy-based IMs (see e.g. Nurtuǧ and Sucuoǧlu 1995; Sucuoǧlu and Erberik 2004; Kalkan and Kunnath 2007) are not discussed herein.

2.1 Scalar IMs

Figure 1 outlines the general categorization of scalar IMs used in this study, which are summarized in Table 1. The set of scalar IMs includes those used in the comparative study by Mollaioli et al. (2013) for predicting seismic demands in base-isolated structures, which are composed of two general subsets: (1) 14 non-structure-specific IMs comprising of acceleration-, velocity-, and displacement-related IMs; (2) 13 structure-specific IMs dividing into spectral and integral ones. All the spectral values are estimated at 5 % damping. In addition, 5 structure-specific multi-parameter scalar IMs that account for the period lengthening and/or higher-mode effect are considered in this work (see Fig. 1 for a brief outline).

Fig. 1

Categorization of the set of scalar IMs

Table 1 IMs considered in this study

The set of IMs proposed by Mollaioli et al. (2013) is composed of most commonly used ones in literature together with new integral IMs, which were obtained by modifying the existing ones in order to get better correlation with the predicted demands. Integral-based structure-specified IMs (see Table 1) are evaluated by integration of the spectral values over a given period range in order to explicitly account for higher-mode effects as well as period lengthening due to structural softening. In this group, the so-called “modified” IMs are obtained from the existing IMs by changing the period range of integration. For the fixed-base buildings, Mollaioli et al. (2013) suggested the integration interval to be [0.2T ₁, 1.5T ₁] where T ₁ is the first-mode period of the structure. Similarly, the interval was set to [0.5T _ip , 1.25T _ip ] for base-isolated structures where T _ip is the isolation period. This period range was also suggested by Avsar and Özdenmir (2013). The aforementioned intervals are more-or-less used as a basis for defining the corresponding period-range in multi-parameter scalar IMs, which are defined as follows:

• (a) The IM proposed by Cordova et al. (2000) which is expressed as follows:

  $$ S^{ * } \left( {T_{1} ,C,\alpha } \right) = Sa\left( {T_{1} } \right)\left( {\frac{{Sa\left( {CT_{1} } \right)}}{{Sa\left( {T_{1} } \right)}}} \right)^{\alpha } $$

  (2)

  where CT ₁ (C > 1) accounts for period elongation which reflects softening of an inelastic structure. Cordova et al. (2000) suggested values of C = 2 and α = 0.5 by optimizing the efficiency of their proposed IM for a set of model structures and earthquake records. For the base-isolated structure herein, T _ip is used in place of T ₁, and C = 1.25.

• (b) The IM proposed by Bianchini et al. (2009):

  $$ Sa_{\text{avg}} \left( {{\mathbf{T}}^{ * } } \right) = Sa_{\text{avg}} \left( {T^{(1)} , \ldots ,T^{(n)} } \right) = \left( {\prod\limits_{i = 1}^{n} {Sa\left( {T^{(i)} } \right)} } \right)^{\frac{1}{n}} $$

  (3)

  where ${\mathbf{T}}^{*}$ = [T ⁽¹⁾,…,T ⁽ⁿ⁾] is the vector of n periods of interest, and Sa _avg is the geometric mean of Sa ordinates calculated at those periods. Bianchini et al. (2009) recommended that Sa _avg should be calculated at least at n = 10 logarithmically-spaced points (this treatment is more efficient than considering the same number of periods being arithmetically spaced). Accordingly, two different period-intervals were proposed: (1) ${\mathbf{T}}_{1}^{ * }$ = [T ₁,…,2T ₁] which was suggested for the first-mode dominant (low period structures), (2) ${\mathbf{T}}_{2}^{ * }$ = [0.2T ₁,…,2T ₁] suggested for structures with medium-to-long periods affected by higher modes. Comparably, for the base-isolated structures herein, the period-intervals are consistently set to ${\mathbf{T}}_{1}^{ * }$ = [T _ip ,…,1.25T _ip ] and ${\mathbf{T}}_{2}^{ * }$ = [0.5T _ip ,…,1.25T _ip ].

• (c) Two IMs proposed by Lin et al. (2011) are expressed as follows:

  $$ \begin{aligned} S_{\text{N1}} = Sa\left( {T_{1} } \right)^{\alpha } \cdot Sa\left( {CT_{1} } \right)^{1 - \alpha } \hfill \\ S_{\text{N2}} = Sa\left( {T_{1} } \right)^{\beta } \cdot Sa\left( {T_{2} } \right)^{1 - \beta } \hfill \\ \end{aligned} $$

  (4)

  These two IMs take into account the issues related to period elongation (i.e., S _N1) and the second mode effects considering T ₂ as the 2nd-mode period (denoted as S _N2), independently. By optimizing the efficiency, Lin et al. (2011) suggested C = 1.5, α = 0.5, and β = 0.75. Although these values are considered in this study for fixed-based frames, the IMs for the base-isolated frames (as mentioned previously) are modified by substituting T _ip for T ₁, 0.5T _ip for T ₂, and C = 1.25.

2.2 Vector-valued IMs

Four different vector-valued IMs are considered herein which are as follows:

• (a) [PGA, M] where M is the moment magnitude of the event generating the ground motion (Elefante et al. 2010). It is expected that this vector is a better predictor than PGA alone.

• (b) [Sa(T ₁), $R_{{T_{1} ,T^{*} }}$] where $R_{{T_{1} ,T^{*} }}$ = Sa($T^{*}$)/Sa(T ₁), and $T^{*}$ is another period chosen to capture important characteristics of the spectrum’s shape. Depending upon whether $T^{*}$ is smaller or larger than T ₁, this vector IM is able to provide information about excitation of higher modes or nonlinear response, respectively. Therefore, two values are taken for $T^{*}$, $T_{1}^{ * }$ = 2T ₁ and $T_{2}^{ * }$ = T ₂, which was suggested by Baker and Cornell (2008a) as an intuitive choice that agrees reasonably with their results. In a comparative study by Baker and Cornell (2008b), they demonstrated that 2T ₁ accounts also for the effect of velocity pulses in pulse-like ground motions with T _p /T ₁ > 2 where T _p denotes the measured pulse period. In an attempt to account for pulses that affect higher-mode response, i.e. those with 0.5 < T _p /T ₁ < 1.5, consideration was given to the choice T ₁/3 (which is approximately equal to T ₂ for medium-rise buildings). In case of base-isolated structure, T _ip is used in place of T ₁, and $T_{1}^{ * }$ = 1.25T _ip and $T_{2}^{ * }$ = 0.5T _ip .

• (c) [Sa(T ₁), ε(T ₁)] where ε is another measure for spectral shape (see Baker and Cornell 2006) defined as the number of standard deviations by which a given lnSa(T ₁) value differs from the mean predicted lnSa(T ₁) value for a given magnitude M, distance R, and other site-source properties denoted as φ. Mathematically, this is written as:

  $$ \varepsilon (T_{1} ) = \frac{{\ln \,Sa(T_{1} ) - \mu_{{\ln Sa(T_{1} )}} \left( {M,R,\varphi } \right)}}{{\sigma_{{\ln Sa(T_{1} )}} \left( {M,R,\varphi } \right)}} $$

  (5)

  where $\mu_{{\ln Sa\left( {T_{1} } \right)}}$ and $\sigma_{{\ln Sa\left( {T_{1} } \right)}}$ are the predicted mean and standard deviation, respectively, of lnSa at the given period T ₁. In this study, Campbell and Bozorgnia (2008) (referred as CB08 hereafter) ground-motion prediction equation is used for estimating mean and standard deviation of lnSa(T ₁). In order to account for pulse-like features while the suit of ground motions encounter observed pulses, the predicted mean and standard deviation of lnSa(T ₁) at the site are modified according to the observed pulses according to the provisions made by Shahi and Baker (2011) as follows:

  $$ \begin{aligned} \mu_{{\ln Sa(T_{1} ),{\text{pulse}}}} & = \mu_{\ln Af} + \mu_{{\ln Sa\left( {T_{1} } \right)}} \\ \sigma_{{\ln Sa(T_{1} ),{\text{pulse}}}} & = Rf \cdot \sigma_{{\ln Sa\left( {T_{1} } \right)}} \\ \end{aligned} $$

  (6)

  where $\mu_{{\ln Sa\left( {T_{1} } \right),{\text{pulse}}}}$ and $\sigma_{{\ln Sa\left( {T_{1} } \right),{\text{pulse}}}}$ are the predicted values of the ground motion model in the presence of pulses, and μ _lnAf is its predicted mean value of the amplification factor Af which allows to model the amplification due to the pulse-like feature. In addition, Rf is the reduction in standard deviation since the modified ground-motion model for pulse-like ground motions is expected to be lower than the standard deviation of the entire ground-motion library, which contains both pulselike and non-pulselike ground motions. The following mean amplification function and reduction factor are proposed (see Shahi and Baker 2011):

  $$ \mu_{\ln Af} = \left\{ {\begin{array}{*{20}c} {1.131\exp \left( { - 3.11\left[ {\ln \left( {{T \mathord{\left/ {\vphantom {T {T_{p} }}} \right. \kern-0pt} {T_{p} }}} \right) + 0.127} \right]^{2} } \right) + 0.058\quad \hbox{if}\;T \le 0.88T_{p} } \\ {0.896\exp \left( { - 2.11\left[ {\ln \left( {{T \mathord{\left/ {\vphantom {T {T_{p} }}} \right. \kern-0pt} {T_{p} }}} \right) + 0.127} \right]^{2} } \right) + 0.255\quad \hbox{if}\;T > 0.88T_{p} } \\ \end{array} } \right. $$

  (7)
  $$ Rf = \left\{ {\begin{array}{*{20}c} {1 - 0.20\exp \left( { - 0.96\left[ {\ln \left( {{T \mathord{\left/ {\vphantom {T {T_{p} }}} \right. \kern-0pt} {T_{p} }}} \right) + 1.56} \right]^{2} } \right)\quad {\hbox {if}} \;T \le 0.21T_{p} } \\ {1 - 0.21\exp \left( { - 0.24\left[ {\ln \left( {{T \mathord{\left/ {\vphantom {T {T_{p} }}} \right. \kern-0pt} {T_{p} }}} \right) + 1.56} \right]^{2} } \right)\quad {\hbox{if}}\;T > 0.21T_{p} } \\ \end{array} } \right. $$

  (8)

• (d) [Sa(T ₁), $R_{{T_{1} ,T^{*} }}$, ε(T ₁)] is a triple vector which can account for the spectral shape by considering both $R_{{T_{1} ,T^{*} }}$ and ε. Baker and Cornell (2008a) revealed that $R_{{T_{1} ,T^{*} }}$ does not fully account for the effect of ε. They investigated that neglecting ε results in conservative estimates of the demand hazard, especially at large levels of structural response.

2.3 Demand parameters

Alternative peak-related demand parameters (i.e., D’s) are considered for fixed-base and base-isolated structure as outlined in Table 3.

It is noteworthy that structural damage is reflected not only from maximum deformations or accelerations, but also by the amount of dissipated energy due to cyclic loading (cumulative damage). The energy-based demand parameters (see e.g. Benavent-Climent et al. 2002, López-Almansa et al. 2013) such as the normalized hysteretic energy, or the ratio of normalized hysteretic energy to normalized maximum displacement (also known as equivalent number of cycles) are then of major importance to be considered. In fact, they can be more effective than the displacement-based demand parameters especially in building designed according to old codes. However, energy-based demand parameters are not considered in this study (Table 2).

Table 2 Demand parameters considered in this study

3 Methodology

3.1 Efficiency of an IM

This study benefits considerably from an efficient nonlinear dynamic procedure referred to as the cloud analysis method (Jalayer and Cornell 2003; Jalayer et al. 2015). The cloud method can be employed in order to quantify the efficiency as well as the relative sufficiency of various IMs. The IM of interest is assumed to be, in general, a vector of m variables, i.e. IM = {IM _i , i = 1:m}. Accordingly, the structure is first subjected to a suite of n ground-motion wave-forms, and the associated structural response parameters is denoted as D = {y _k , k = 1:n}. By performing a multivariate linear regression in the logarithmic space on D versus the candidate IM, the statistical parameters corresponding to the lognormal distribution of D|IM can be extracted. The expected value is modeled as follows:

$$ {\mathbb{E}}\left[ {\ln D|{\mathbf{IM}}} \right] = \ln \eta_{{D|{\mathbf{IM}}}} = b_{0} + b_{1} \ln IM_{1} + b_{2} \ln IM_{2} + \cdots + b_{m} \ln IM_{m} $$

(9)

where η _{D| IM} is the conditional median, and the parameters b ₀ and b _i , i = 1,…,m, are the estimated regression coefficients. It is to note that Eq. (9) can have options where an IM _i , i = 1:m, is arithmetic (i.e., IM _i instead of ln IM _i ). The standard deviation is estimated by the standard error of the regression as:

$$ \sigma_{{\ln D|{\mathbf{IM}}}} = \beta_{{D|{\mathbf{IM}}}} \approx \sqrt {\frac{{\sum\nolimits_{k = 1}^{n} {\left( {\ln y_{k} - \ln \eta_{{D|{\mathbf{IM}}}} ({\mathbf{IM}}_{k} )} \right)^{2} } }}{n - (m + 1)}} $$

(10)

where σ _{lnD| IM} is the conditional standard deviation (or equivalently β _{D| IM} known as dispersion). It is obvious that in case of having scalar IMs, a simple logarithmic linear regression model can be applied (i.e., m = 1). As a result, the cloud analysis implements the non-linear dynamic analysis results in a (linear) regression-based probabilistic model. The estimated dispersion β _{D| IM} serves as quantitative measure for predictive efficiency of the candidate IMs; for instance, those resulting in standard errors in order of 0.20–0.30 are normally considered as those having a proper efficiency, while the range 0.30–0.40 is still considered as reasonably acceptable (see Mollaioli et al. 2013).

Another predictor that used herein for finding how well the sample regression line fits the data is called coefficient of determination or the R-square (R ²). This coefficient provides a relative measure (in percent) of the reduction in standard deviation due to the regression with respect to the marginal standard deviation of the dependent variable (herein, D). It is always between zero and one; an R-square equal to zero indicates zero reduction in variance with respect to that of the dependent data (very inefficient) and an R ² equal to 1 indicates 100 % reduction in variance due to regression (very efficient). Accordingly, the IM that best predicts the D is the one that provides the largest value of the R ² (around 1) among those considered.

3.2 Sufficiency of an IM

An IM is sufficient in its absolute sense if and only if the probability distribution for demand parameter D given IM is independent of the ground motion acceleration wave-forms denoted as a _g :

$$ p_{{D\left| {{\mathbf{IM}},{\mathbf{a}}_{g} } \right.}} \left( {y\left| {{\mathbf{IM}}({\mathbf{a}}_{g} ),{\mathbf{a}}_{g} } \right.} \right) = p_{{D\left| {{\mathbf{IM}}} \right.}} \left( {y\left| {{\mathbf{IM}}({\mathbf{a}}_{g} )} \right.} \right) $$

(11)

That is, knowing IM, there is no additional information that can be provided by the ground motion wave-form, a _g , necessary for prediction of demand D. ¹ This is clearly a very strong condition, and it is unlikely that any scalar or low-dimensional vector IM satisfies it. Furthermore, even if the equality holds for a certain IM, it is not at all straightforward to demonstrate that it holds. In order to overcome this obstacle, it seems definitely simpler to talk about the relative sufficiency of one IM with respect to another. In this regard, Jalayer et al. 2012 have used the concept of the relative entropy, also known as the Kullback–Leibler divergence (Kullback and Leibler 1951) in order to propose a measure of relative sufficiency of one IM with respect to another. The relative entropy provides the means of measuring the “distance” between two probability distributions.

The relative entropy $\boldsymbol{\mathcal{D}}$(p _{D|a g} ||p _D|IM ) between the two probability density functions (PDF) p _{D|a g} and p _D|IM can be calculated as:

$$ {\boldsymbol{\mathcal{D}}}\left( {p_{{D\left| {{\mathbf{a}}_{g} } \right.}} \left\| {p_{{D\left| {{\mathbf{IM}}} \right.}} } \right.} \right) = \int\limits_{{\Omega_{D} }} {p_{{D\left| {{\mathbf{a}}_{g} } \right.}} \left( {y|{\mathbf{a}}_{g} } \right)\log_{2} \frac{{p_{{D\left| {{\mathbf{a}}_{g} } \right.}} \left( {y|{\mathbf{a}}_{g} } \right)}}{{p_{{D\left| {{\mathbf{IM}}} \right.}} \left( {y|{\mathbf{IM}}({\mathbf{a}}_{g} )} \right)}}{\text{d}}y} $$

(12)

Note that the relative entropy $\boldsymbol{\mathcal{D}}$(p _{D|a g} ||p _D|IM ) in Eq. (12) is calculated as the expected value of information gain or entropy between the two PDF’s p _{D|a g} and p _D|IM (measured in “bits” of information). In other words, $\boldsymbol{\mathcal{D}}$(p _{D|a g} ||p _D|IM ) measures on average how much information is lost about demand D by adopting the intensity measure IM instead of the entire ground motion wave-form a _g . Based on this definition, the difference in relative entropies $\boldsymbol{\mathcal{D}}$(p _{D|a g} ||p _D|IM1) and $\boldsymbol{\mathcal{D}}$(p _{D|a g} ||p _D|IM2) can be written as:

$$ {\boldsymbol{\mathcal{D}}}\left( {p_{{D\left| {{\mathbf{a}}_{g} } \right.}} \left\| {p_{{D\left| {{\mathbf{IM}}_{1} } \right.}} } \right.} \right) - {\boldsymbol{\mathcal{D}}}\left( {p_{{D\left| {{\mathbf{a}}_{g} } \right.}} \left\| {p_{{D\left| {{\mathbf{IM}}_{2} } \right.}} } \right.} \right) = \int\limits_{{\Omega_{D} }} {p_{{D\left| {{\mathbf{a}}_{g} } \right.}} \left( {y|{\mathbf{a}}_{g} } \right)\log_{2} \frac{{p_{{D\left| {{\mathbf{IM}}_{2} } \right.}} \left( {y|{\mathbf{IM}}_{2} ({\mathbf{a}}_{g} )} \right)}}{{p_{{D\left| {{\mathbf{IM}}_{1} } \right.}} \left( {y|{\mathbf{IM}}_{1} ({\mathbf{a}}_{g} )} \right)}}{\text{d}}y} $$

(13)

Jalayer et al. (2012) have defined the relative sufficiency of two alternative IMs, IM ₁ and IM ₂ as the expected value of their relative entropies defined in Eq. (13) over all possible ground motion waveforms.

$$ {\text{I}}\left( {D\left| {{\mathbf{IM}}_{2} \left| {{\mathbf{IM}}_{1} } \right.} \right.} \right) = \int\limits_{{\Omega_{{{\mathbf{a}}_{g} }} }} {\left[ {\int\limits_{{\Omega_{D} }} {p_{{D\left| {{\mathbf{a}}_{g} } \right.}} \left( {y|{\mathbf{a}}_{g} } \right)\log_{2} \frac{{p_{{D\left| {{\mathbf{IM}}_{2} } \right.}} \left( {y|{\mathbf{IM}}_{2} ({\mathbf{a}}_{g} )} \right)}}{{p_{{D\left| {{\mathbf{IM}}_{1} } \right.}} \left( {y|{\mathbf{IM}}_{1} ({\mathbf{a}}_{g} )} \right)}}{\text{d}}y} } \right]} \,p_{{{\mathbf{a}}_{g} }} \left( {{\mathbf{a}}_{g} } \right)\,{\text{d}}{\mathbf{a}}_{g} $$

(14)

For a given a _g , y is known and is equal to y(a _g ); hence, the probability p _{D|a g} reduces to the Dirac delta function δ[y(a _g )]. Therefore, the equation can further be simplified as:

$$ \begin{aligned} {\text{I}}\left( {D\left| {{\mathbf{IM}}_{2} \left| {{\mathbf{IM}}_{1} } \right.} \right.} \right) & = \int\limits_{{\Omega_{{{\mathbf{a}}_{g} }} }} {\left[ {\int\limits_{{\Omega_{D} }} {\delta \left( {y({\mathbf{a}}_{g} )} \right)\log_{2} \frac{{p_{{D\left| {{\mathbf{IM}}_{2} } \right.}} \left( {y|{\mathbf{IM}}_{2} ({\mathbf{a}}_{g} )} \right)}}{{p_{{D\left| {{\mathbf{IM}}_{1} } \right.}} \left( {y|{\mathbf{IM}}_{1} ({\mathbf{a}}_{g} )} \right)}}{\text{d}}y} } \right]p_{{{\mathbf{a}}_{g} }} \left( {{\mathbf{a}}_{g} } \right){\text{d}}{\mathbf{a}}_{g} } \\ & = \int\limits_{{\Omega_{{{\mathbf{a}}_{g} }} }} {\log_{2} \frac{{p_{{D\left| {{\mathbf{IM}}_{2} } \right.}} \left( {y({\mathbf{a}}_{g} )|{\mathbf{IM}}_{2} ({\mathbf{a}}_{g} )} \right)}}{{p_{{D\left| {{\mathbf{IM}}_{1} } \right.}} \left( {y({\mathbf{a}}_{g} )|{\mathbf{IM}}_{1} ({\mathbf{a}}_{g} )} \right)}}p_{{{\mathbf{a}}_{g} }} \left( {{\mathbf{a}}_{g} } \right)\,{\text{d}}{\mathbf{a}}_{g} } \, \\ \end{aligned} $$

(15)

If I(D|IM ₂|IM ₁) is positive, this means that on average IM ₂ provides more information about D than IM ₁; hence, IM ₂ is more sufficient than IM ₁. Similarly, if I(D|IM ₂|IM ₁) is negative, IM ₂ is less sufficient than IM ₁. Jalayer et al. (2012) proposed a refined method for calculating the integral in Eq. (15) through Monte Carlo Simulation by adopting a stochastic ground motion model in conjunction with deaggregation of the seismic hazard at the site. In addition, they argued that the relative sufficiency measure (RSM) can be approximately calculated by replacing the expectation with an average over a suite of n real ground motion records:

$$ {\text{I}}\left( {D\left| {{\mathbf{IM}}_{2} \left| {{\mathbf{IM}}_{1} } \right.} \right.} \right) \approx \frac{1}{n}\sum\limits_{k = 1}^{n} {\log_{2} } \frac{{p_{{D\left| {{\mathbf{IM}}_{2} } \right.}} \left( {y_{k} \left| {{\mathbf{IM}}_{2} } \right.} \right)}}{{p_{{D\left| {{\mathbf{IM}}_{1} } \right.}} \left( {y_{k} \left| {{\mathbf{IM}}_{1} } \right.} \right)}} $$

(16)

where D = {y _k , k = 1:n} are the demand values for a suite of n ground motions (obtained from cloud analysis, see Sect. 3.1). This provides a preliminary ranking of candidate IM ₂ with respect to the reference IM ₁. Although the simplified and approximate formulation in Eq. (16) offers an efficient solution for comparing various IMs without the need to use a stochastic ground motion model, it may yield inaccurate results² (see also Jalayer et al. 2012).

The probability distribution function (PDF) p _D|IM (y|IM) can be calculated by considering a lognormal distribution with the parameters defined in Eqs. (9) and (10):

$$ p_{{D\left| {{\mathbf{IM}}} \right.}} \left( {y|{\mathbf{IM}}} \right) = \frac{ 1}{{y\beta_{{D\left| {{\mathbf{IM}}} \right.}} }}\phi \left( {\frac{{\ln y - \ln \eta_{{D|{\mathbf{IM}}}} }}{{\beta_{{D\left| {{\mathbf{IM}}} \right.}} }}} \right) $$

(17)

where ϕ(·) is the standardized Gaussian PDF. Hence, the relative sufficiency measure can approximately be expressed as:

$$ {\text{I}}\left( {D\left| {{\mathbf{IM}}_{2} \left| {{\mathbf{IM}}_{1} } \right.} \right.} \right) \approx \frac{1}{n}\sum\limits_{k = 1}^{n} {\log_{2} } \left( {\frac{{\beta_{{D\left| {{\mathbf{IM}}_{1} } \right.}} }}{{\beta_{{D\left| {{\mathbf{IM}}_{2} } \right.}} }}\frac{{\phi \left( {\frac{{\ln y_{k} - \ln \eta_{{D|{\mathbf{IM}}_{2} }} ({\mathbf{IM}}_{2,k} )}}{{\beta_{{D\left| {{\mathbf{IM}}_{2} } \right.}} }}} \right)}}{{\phi \left( {\frac{{\ln y_{k} - \ln \eta_{{D|{\mathbf{IM}}_{1} }} ({\mathbf{IM}}_{1,k} )}}{{\beta_{{D\left| {{\mathbf{IM}}_{1} } \right.}} }}} \right)}}} \right) $$

(18)

4 Numerical example

4.1 Ground motion database

In this study, 137 earthquake ground motions are selected from the next generation of attenuation (NGA) database (Chiou et al. 2008), and used as input for the cloud analysis methodology. The suite of wave-forms is divided into two subsets: (1) 78 ordinary ground motions with closest distance and magnitude ranging 0.64 km ≤ R _rup ≤ 87.87 km, and 5.74 ≤ M ≤ 7.90, respectively; (2) 56 pulse-like near-fault ground motions with 0.07 km ≤ R _rup ≤ 20.82 km and 5.0 ≤ M ≤ 7.62. Selected records are predominantly on soil type C or D according to the NEHRP site classification based on the preferred V _s30 values. It is noteworthy that current database is the one used previously by Mollaioli et al. (2013) with minor modifications implemented herein. Accordingly, ordinary ground motions are selected from one of the components of the corresponding NGA earthquakes while pulse-like ones are the specifically fault-normal rotated orientation of the two orthogonal components.

This classification of NGA records as pulse-like is originally based on the automated algorithm proposed by Baker (2007) which identifies pulse-like records using wavelet transforms. This algorithm uses the fault-normal component of ground motion for its classification. Nevertheless, pulses are often found in other orientations due to complex geometry of a real fault; thus, the velocity pulse can be present in orientations other than the computed fault-normal orientation. For this purpose, Shahi (2013) proposed an efficient algorithm that can acquire pulses at arbitrary orientations in multi-component ground motions. Based on this new algorithm, 44 out of 56 fault-normal components presented by Mollaioli et al. (2013) are classified as pulse-like ground motions. The details of each recording in both ordinary and pulse-like ground-motion sets together with the plot of their spectral accelerations are reported in the Appendix of the paper available as Online Resource.

4.2 Description of case-study buildings

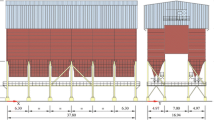
The case-study buildings are two three-bay 2-dimensional RC frames consisting of 4-story and 6-story structures dimensioned according to an Italian former code (DM 96, 1996), which lacks in specific capacity design rules. They are representative of existing buildings located in high seismic zones (i.e., “zone 1” according to the seismic hazard classification of DM 96). A schematic representation of the two frames is illustrated in Fig. 2 (for more details about the building structures, see Mollaioli et al. 2013). The periods of the first three modes of vibration of the fixed-base frames, obtained with a reduced cracked stiffness of the structural elements equal to half the initial elastic ones, are outlined in Table 3.

Fig. 2

Schematic representation of the case-study RC frame structures

Table 3 Periods of the first three modes of vibration of the fixed-base frames

The required non-linear dynamic analyses for the cloud analysis procedure are performed in OpenSees 2.2.2 (2010). The physical models of the two structures are built using Beam with Fibre-Hinges Elements for modelling beams and columns of the frames. The masses are concentrated at the nodes, and the stiffness of the floors is modelled with rigid diaphragm constraints. A Rayleigh damping proportional to the mass and tangent stiffness matrix is used, with coefficients calibrated to provide a 5 % damping at the first and second mode periods of the undamaged structures. The effects of geometric nonlinearities are not considered in the analyses.

In order to study the base-isolated systems in addition to ordinary fixed-based buildings, the same frames equipped with four different isolation properties are used in this study (see Mollaioli et al. 2013; Fig. 2). The considered isolation systems have bi-linear backbone curves with positive post-yield stiffness ratio and no stiffness degradation under cyclic loadings. To characterize four different isolation systems, the parameters of the backbone curve are defined as follows: (1) the characteristic strength is set F _d  = 0.03 W where W is the seismic weight of the corresponding structure; (2) the elastic limit displacement is D _y  = {0, 10, 25, 50 mm}, which are representative of different isolation systems (e.g., D _y  = 0 shows friction pendulum isolators, and D _y  > 0 correspond to lead rubber bearings with different initial stiffness); (3) the post-elastic stiffness is set so that the isolation periods T _ip outlined in Table 3 associated with the 4-story and 6-story buildings are attained.

4.3 Results in terms of efficiency

The logarithmic standard deviation of regression residuals, β _{D| IM} , as well as the R ² corresponding to the demand parameters MRDR, MIDR and MFA are obtained from the regression model (see Sect. 3.1) for both case-study fixed-base buildings (Fig. 3) and base-isolated buildings equipped with the isolation system having D _y  = 10 mm (Fig. 4). The structures are subjected to both ordinary and pulse-like ground motions. The efficiency results are illustrated in those figures for all 38 IMs (i.e., 32 scalar and 6 vector-valued). For scalar IMs, as explained formerly in Sect. 3.1, a simple linear regression in the logarithmic scale is performed on D versus the candidate IM. However, for the vector-valued IMs outlined in Table 1, the multi-linear regression models for η _D|IM , with reference to Eq. (9), have the following forms:

$$ \begin{aligned} \ln \eta_{D|[PGA,M]} & = b_{0} + b_{1} \ln PGA + b_{2} M \\ \ln \eta_{{D|[Sa(T_{1} ),R_{{T_{1} ,T_{1}^{ * } }} ]}} & = b_{0} + b_{1} \ln Sa(T_{1} ) + b_{2} \ln R_{{\,T_{1} ,T_{1}^{*} }} \\ \ln \eta_{{D|[Sa(T_{1} ),\varepsilon (T_{1} )]}} & = b_{0} + b_{1} \ln Sa(T_{1} ) + b_{2} \varepsilon (T_{1} ) \\ \ln \eta_{{D|[Sa(T_{1} ),R_{{T_{1} ,T_{1}^{ * } }} ,\varepsilon (T_{1} )]}} & = b_{0} + b_{1} \ln Sa(T_{1} ) + b_{2} \ln R_{{T_{1} ,T_{1}^{*} }} + b_{3} \varepsilon (T_{1} ) \\ \end{aligned} $$

(19)

Fig. 3

Logarithmic standard deviation of regression residuals, β _{D| IM} , and the R-squared, R ², corresponding to the demand parameters MRDR, MIDR and MFA, obtained from the cloud analysis of fixed-base buildings subjected to ordinary and pulse-like ground motions

Fig. 4

Logarithmic standard deviation of regression residuals, β _{D| IM} , and the R-squared, R ², corresponding to the demand parameters MRDR, MIDR, MBD, and MFA, obtained from the cloud analysis of base-isolated buildings equipped with isolation system having D _y  = 10 mm, subjected to ordinary and pulse-like ground motions

According to Figs. 3 and 4, the following general conclusions can be drawn for the fixed-based as well as base-isolated case-study frames:

• The dispersion values obtained from cloud regression for the MRDR are generally less sensitive to different types of buildings and ground motions with respect to those for MIDR. Nevertheless, these two demand parameters follow similar trend since inter-story drift demands are distributed almost uniformly within the structural height. This is likely to be interpreted by the fact that although the case-study frames are not ductile as modern designed structures, they are not characterized by any specific irregular behaviour which produces significant localization of seismic damages.

• The MRDR and MIDR are more efficiently predicted with ordinary ground motions rather than pulse-like ones. In other words, regression models are better fitted to data from ordinary ground motion set compared to pulse-like ones.

• The demand parameter MFA follows similar trends regarding different types of buildings and ground motions.

• The structure-specific and vector-valued IMs are generally more efficient, especially for MIDR, MRDR, and MBD.

• In predicting the MFA, both PGA and modified structure-specific IMs are more efficient than other considered IMs. However, the regression models associated with different IMs are generally less efficient for this demand parameter with respect to the other demand parameters.

• Sa is generally one of the efficient IMs for predicting MRDR and MIDR in fixed-base structures. This fact has been demonstrated by many researchers (see e.g. Shome et al. 1998; Shome and Cornell 1999). However, it does not hold for base-isolated buildings.

As an example of finding an efficient IM, consider the case of 6-story fixed-base building in Fig. 3 with the set of pulse-like ground motions, and demand parameter MIDR. For IM = CAD (Cumulative Absolute Displacement), the cloud regression is shown in Fig. 5a. It indicates that β _{D| IM}  = 0.55 (>0.40 according to the limits proposed by Mollaioli et al. 2013) and R ² = 0.054. Therefore, CAD is not an efficient IM for predicting the demand parameter MIDR using the proposed regression. On the other hand, for IM = S _N2 (multi-parameter intensity measure), the cloud regression (illustrated in Fig. 5b) indicates β _{D| IM}  = 0.18 and R ² = 0.90. Hence, this IM is efficient in predicting the desired demand parameter. As another example, consider the 4-story base-isolated building with D _y  = 10 mm, (see Fig. 4) considering set of ordinary ground motions, and demand parameter MIDR. The cloud regression is illustrated in Fig. 6a for IM = CAD and in Fig. 6b for IM = I _H (Housner intensity). Although β _{D| IM}  = 0.37 for IM = CAD is within the acceptable range (<0.40), the R ² is too small (R ² = 0.33) and the IM is not efficient. This is while IM = I _H with β _{D| IM}  = 0.17 and R ² = 0.85 is efficient.

Fig. 5

Comparison of cloud regression plots of alternative IMs a CAD, and b S _N2

Fig. 6

Comparison of cloud regression plots of alternative IMs a CAD, and b I _H

One of the objectives herein is to find the most efficient IMs (among those outlined in Table 1), which are capable of properly predicting the demand for the existing typical buildings designed according to older Italian building codes. To achieve this goal, the first 6 (in some cases up to 8) most efficient IMs, which ensure lowest β _{D| IM} and highest R ² (as explained in the above paragraphs), are selected. These IMs are tabulated for alternative demand parameters in Table 4 and Tables 5, 6, 7 and 8 corresponding to fixed-base and base-isolated building (equipped with four different isolation systems defined in previous section), respectively. The selection of the most efficient IMs is performed individually for the set of ordinary and pulse-like ground motions. It is worth noting that the orders of IMs in those Tables are compatible with their layout shown in Table 1.

Table 4 The most efficient IMs for fixed-base case-study buildings

Table 5 The most efficient IMs for base-isolated case-study buildings with D _y  = 0 mm

Table 6 The most efficient IMs for base-isolated case-study buildings with D _y  = 10 mm

Table 7 The most efficient IMs for base-isolated case-study buildings with D _y  = 25 mm

Table 8 The most efficient IMs for base-isolated case-study buildings with D _y  = 50 mm

With reference to Table 4 for fixed-based structures, it is particularly observed that:

• For demand parameters MRDR and MIDR, modified integral intensity MI _H (modified Housner intensity), the multi-parameter intensity S _N2, and all the suggested vector-valued IMs, except for [PGA, M], are all efficient with respect to the spectral acceleration at the first-mode period Sa, considering different sets of ground-motions.

• For demand parameter MFA, modified integral intensities MASI (modified acceleration spectrum intensity), and MAVI (modified velocity spectrum intensity), as well as the multi-parameter intensity Sa _avg (${\mathbf{T}}_{2}^{*}$) accounting for higher-mode effect are efficient for different sets of ground-motions.

• The scalar intensity PGA and the vector-valued [PGA, M] are sensitive to pulse-like ground motions for predicting the demad parameter MFA.

• Generally speaking, the vector-valued intensities [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$] and [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε], which account for higher-mode effect, are efficient with respect to all considered demand parameters.

With reference to Tables 5, 6, 7 and 8 for base-isolated frames, the following conclusions can be drawn:

• For MRDR and MIDR, quite the same trend in efficient IMs is shown among different isolation systems; that is, the set of integral IMs comprising V _EIa SI, V _EIr SI, MASI, MVSI, I _H , MI _H , MV _EIr SI (refer to Table 1 for their corresponding definitions) are proper IMs for predicting the aforementioned peak-related demand parameters regarding different set of ground-motions. Moreover, the vector-valued intensity [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] which account for both the spectral shape and the higher-mode effect is very efficient with respect to pulse-like ground-motions.

• For MBD, the list of efficient IMs is independent of the type of isolation system (i.e., D _y ) for the pulse-like ground-motion set; this is mainly for the reason that these records provide high bearing displacements. Moreover, as the yield displacement of the isolation system increases, the list of efficient IMs for the ordinary ground-motion set resembles more and more that of the pulse-like set. As a result, the modified integral intensity MI _H , the multi-parameter intensity Sa _avg (${\mathbf{T}}_{2}^{*}$), as well as the vector-valued intensities [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$], and [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] are efficient in case of MBD for various isolation systems and ground-motion sets.

• For MFA, the same trend (approximately) is observed among different isolation systems. As a result, the non-structure-specific IMs comprising of PGA, AI, I _a , I _c (see Table 1 for their corresponding definitions), the integral intensities ASI, VSI, and I _H , and finally the vector [PGA, M] are the most efficient ones.

• With refrence to the all previous observations, the modified integral intensity MI _H and the vector-valued intensity [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] are consistently efficient for displacement-based demand parameters and both types of fixity conditions. For the acceleration-based demand parameter MFA, the scalar intensity PGA and the vector [PGA, M] are commonly efficient.

An important issue that is raised while comparing the efficiency of various IMs associated with the pulse-like records, is mainly related to the pulse period T _p . Short-period pulses with small T _p /T ₁ ratio (i.e. < 1–1.5) are capable for affecting the structures for which the higher modes of vibration are contributing significantly to the response. Conversely, records with higher T _p /T ₁ values control the peak displacements associated with the first-mode dominant structures (see also Baker and Cornell 2008a). This issue can affect the regression models associated with multi-parameter as well as vector-valued IMs (see Table 1). Although these IMs are effective for a specific range of periods, the selected set of pulse-like ground-motion comprises records with both ranges of T _p /T ₁. This may reduce the efficiency of the candidate IMs. To further study this effect on both fixed-based and base-isolated structures, two subsets of pulse-like records are selected. The pulse-like records with T _p /T ₁ < 1 and those with T _p /T ₁ ≥ 1 are separated from the original set, and the cloud regression is performed separately on either of subsets. This distinction is expected to increase the efficiency of IMs.

Figure 7 illustrates β _{D| IM} and R ² of the regression model for Sa, multi-parameter, and vector-valued IMs corresponding to the demand parameters MIDR associated with the fixed-based structure.

Fig. 7

Logarithmic standard deviation of regression residuals, β _{D| IM} , and the R-squared, R ², obtained from the cloud analysis of fixed-based structures for the demand parameter MIDR and different pulse-like record sets

It is observed that for the 6-story building subjected to the set of pulse-like records with T _p /T ₁ < 1, the multi-parameter intensity S _N2, and the vector-valued intensities [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$] and [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] have a reduction in β _{D| IM} while their corresponding R ² remain unchanged. These IMs, which are sensitive to higher-mode effect, express higher efficiency with respect to the set of records with T _p /T ₁ < 1. However, the same reasoning does not apply for the 4-story building which is not affected by higher modes. It is to note that the set of records with T _p /T ₁ ≥ 1 has no superiority over the original set in terms of efficiency. This is mainly due to the fact that for the set of pulse-like ground motions, the number of records having T _p /T ₁ ≥ 1 are higher than those with T _p /T ₁ < 1. Therefore, no specific improvement in efficiency can be observed. The same experience is performed on the base-isolated structures with D _y  = 50 mm and for the demand parameter MBD, as illustrated in Fig. 8. For the 6-story structure, a more pronounced reduction in β _{D| IM} is observed with R ² remaining quite unchanged considering pulse-like records with T _p /T ₁ > 1 with respect to the multi-parameter intensities $S^{*}$, Sa _avg (${\mathbf{T}}_{1}^{*}$), S _N1, and vector-valued ones comprising [Sa(T ₁), $R_{{T_{1} ,T_{1}^{*} }}$], and [Sa(T ₁), $R_{{T_{1} ,T_{1}^{*} }}$, ε]. These IMs are sensitive to occurrence of nonlinearity in isolation system which is mainly reflected in MBD. As a result, separation of pulse-like ground motions based on the pulse-period can improve the efficiency for particulate IMs. In general, it can be observed that all these IMs except for [PGA, M] have a good efficiency. This can be attributed to the fact that they cover a range of periods and therefore they have a better possibility of capturing the predominant period of the structural response.

Fig. 8

Logarithmic standard deviation of regression residuals, β _{D| IM} , and the R-squared, R ², obtained from the cloud analysis of base-isolated structures equipped with isolation system having D _y  = 50 mm for demand parameter MBD and different pulse-like record sets

4.4 Results in terms of sufficiency

The RSM in this section is calculated in an approximate manner as explained previously in Sect. 3.2, in Eq. (16) through Eq. (18). Accordingly, the probability model for D|IM is calculated based on the lognormal model expressed in Eq. (17).

The reference intensity (i.e., IM ₁ in Eq. 18) is taken to be Sa for displacement-based demand parameters (i.e. MRDR, MIDR, and MBD), and PGA for acceleration-based demand parameter (i.e. MFA); this is mainly due to the fact that these reference intensities not only proved to be efficient, but also are well-known in engineering practice. The sufficiency is measured for each candidate IM relative to IM ₁. The relative sufficiency measures are shown in Fig. 9 for both case-study fixed-base buildings and in Fig. 10 for base-isolated buildings equipped with the isolation system D _y  = 10 mm. The results reveal that how many extra bits of information, on average, the candidate IM gives about the desired structural demand parameter compared to IM ₁. The positive value (above the red dashed line) shows that on average the candidate IM provides more information (i.e., is more sufficient) than IM ₁. Similarly, negative values indicates that the candidate IM provides on average less information (i.e., is less sufficient) compared to IM ₁ for predicting the demand parameter of interest.

Fig. 9

The RSM for alternative IMs corresponding to the demand parameters MRDR, MIDR and MFA, for fixed-base buildings subjected to ordinary and pulse-like ground motions

Fig. 10

The RSM for alternative IMs corresponding to the demand parameters MRDR, MIDR, MBD, and MFA, for base-isolated buildings with isolation system having D _y  = 10 mm subjected to ordinary and pulse-like ground motions

With reference to Fig. 9, the first eight IMs having highest RSM’s with respect to the reference IM ₁ are summarized in Table 9 for various demand parameters associated with the fixed-base structures. Selected IMs are followed by their RSM’s in terms of bits of information (>0). It is noteworthy that each outlined RSM in Table 9 is selected based on the maximum estimated values from 4-story and 6-story frames.

Table 9 The most relatively sufficient IMs for fixed-base case-study buildings (with respect to IM ₁)

Comparing Table 9 (i.e., most relatively sufficient IMs) with Table 4 (corresponding to the most efficient IMs) for the fixed-base structures reveals perfect harmony between associated results. Generally, for selecting the proper IMs for fixed-based buildings based on both efficiency and sufficiency criteria, it is concluded that:

• For displacement-based demand parameters, Sa is a proper IM for the case-study fixed-based buildings subjected to ordinary ground motions. For pulse-like ground motion record set, both vector-valued intensities [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$] and [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] and to a lower degree the multi-parameter intensity S _N2 are the most appropriate IMs.

• For MFA, PGA is a proper choice. However, for ordinary ground motions, the vector-valued intensities [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$] and [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε], the modified integral intensities MASI, MAVI, and MI _H , and finally the multi-parameter intensities S _N2 and Sa _avg (${\mathbf{T}}_{2}^{*}$) are recommended (see Table 1 for definition of these IMs). The vector [PGA, M] is the choice for pulse-like ground motions.

Consistently, the first eight IMs having the highest RSM’s are summarized in Tables 10, 11, 12 and 13 for the base-isolated structures with different isolation properties. Comparing Tables 5, 6, 7 and 8 with Tables 10, 11, 12 and 13 (corresponding to the most efficient IMs) reveals again very good agreement between efficient and sufficient IMs, respectively. Accordingly, the following conclusions can be drawn regarding the proper IMs for base-isolated structures:

Table 10 The most relatively sufficient IMs for base-isolated case-study buildings with D _y  = 0 mm (with respect to IM ₁)

Table 11 The most relatively sufficient IMs for base-isolated case-study buildings with D _y  = 10 mm (with respect to IM ₁)

Table 12 The most relatively sufficient IMs for base-isolated case-study buildings with D _y  = 25 mm (with respect to IM ₁)

Table 13 The most relatively sufficient IMs for base-isolated case-study buildings with D _y  = 50 mm (with respect to IM ₁)

• For demand parameters MRDR and MIDR, the most suitable IMs (i.e., are simultaneously sufficient and efficient) for all types of ground-motions are actually the integral scalar intensities comprising MASI, MVSI, V _EIa SI (see Table 1 for their definitions). Accordingly, for ordinary ground motions, it is suggested to use the integral scalar intensities V _EIr SI, and I _H , while for pulse-like ground motions, the modified integral intensities MV _EIr SI, MI _H , and the vector-valued intensity [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] pass the sufficiency and efficiency requirements. It is to note that other candidate IMs are more appropriate for a specific type of isolation system, while the aforementioned ones are applicable to all types of isolation properties.

• For demand parameter MBD, suitable IMs for all types of ground motions are the modified Housner intensity MI _H , the multi-parameter intensity Sa _avg (${\mathbf{T}}_{2}^{*}$), and vector-valued intensity [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] and to a lower degree [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$].

• For the acceleration-based demand MFA, proper IMs for all types of ground motions are PGA, [PGA, M] and to a lower degree the acceleration-related intensities AI, and I _c .

In order to find out the effect of separating pulse-like ground-motion records on the relative sufficiency measure (it has been already investigated for the efficiency results in Sect. 4.3), this measure is plotted in Fig. 11a for Sa, multi-parameter, and vector-valued IMs corresponding to the demand parameters MIDR associated with the 6-story fixed-based structure (see also Fig. 7 for comparison with the efficiency results). Accordingly, for pulse-like records with T _p /T ₁ < 1, the higher-mode sensitive IMs including S _N2, [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$], and [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] have higher sufficiency relative to Sa. Moreover, Fig. 11b illustrates the same approach applied to the 6-story base-isolated structures with D _y  = 50 mm considering the demand parameter MBD. Although no particular improvement in efficiency was previously observed in Fig. 8 for this case, the relative sufficiency, however, reveals an increase for pulse-like records with T _p /T ₁ > 1 with respect to $S^{*}$, Sa _avg (${\mathbf{T}}_{1}^{*}$), S _N1, [Sa(T ₁), $R_{{T_{1} ,T_{1}^{*} }}$], and [Sa(T ₁), $R_{{T_{1} ,T_{1}^{*} }}$, ε].³ It is noteworthy that, with respect to the results reported in terms of efficiency in Fig. 8, separating the pulse-like records based on the pulse period leads to a more significant increase of relative sufficiency in the interested IMs.

Fig. 11

Comparison of RSM of alternative IMs based on different pulse-like record sets corresponding to a MIDR associated with the fixed-based 6-story structure, b MBD associated with the base-isolated 6-story structure

5 Summary and conclusions

The relative capability of a wide range of intensity measures (IMs) in predicting the structural response of fixed-based and base-isolated buildings are investigated in terms of efficiency and sufficiency. Cloud analysis, a non-linear dynamic analysis procedure based on linear logarithmic regression of a response parameter versus the adopted IM, is employed herein in order to construct a probability model for the demand parameter conditional on the adopted IM. The estimated logarithmic standard deviation of the residuals serves as a quantitative measure for predicting the efficiency. The relative sufficiency of alternative IMs is calculated by measuring the approximate Relative Sufficiency Measure (RSM) derived earlier by Jalayer et al. (2012). The RSM quantifies the amount of information gained (on average) about a designated structural response parameter by adopting one IM instead of another.

The case-study buildings are two typical 4-story and 6-story existing RC moment-resisting frames which are designed according to a previous Italian code. Four alternative peak-related demand parameters, comprising of the maximum roof drift ratio (MRDR), maximum inter-story drift ratio (MIDR), maximum floor acceleration (MFA), and maximum bearing displacement (MBD, specifically for base-isolated buildings), together with 38 candidate IMs composed of 32 scalar and 6 vector-valued IMs, are considered herein. The investigations are made for both ordinary and pulse-like near-fault ground motion records.

In terms of both efficiency and sufficiency assessments, the most suitable IMs for predicting alternative demand parameters of fixed-based structures are summarized in Table 14 as follows. Furthermore, the most appropriate IMs for predicting alternative demand parameters of base-isolated buildings equipped with different isolation systems are listed in Table 15.

Table 14 The most suitable IMs for case-study fixed-based structures

Table 15 The most appropriate IMs for case-study base-isolated structures

With reference to Tables 14 and 15, it can be concluded that:

• The vector [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$, ε] and to a lower degree [Sa(T ₁), $R_{{T_{1} ,T_{2}^{*} }}$] are capable of predicting displacement-based demand parameters of buildings with different types of base fixity subjected to ordinary and pulse-like ground motions.

• The vector [PGA, M] is the nominated IM for predicting the MFA in fixed-base as well as base-isolated buildings.

• The modified Housner IM, i.e. MI _H , is a proper choice for alternative displacement-based demand parameters in base-isolated buildings.

• The most proper IMs for predicting the displacement-based demand parameters associated with pulse-like ground motions are generally those that are capable of considering a wide range of periods, i.e. vector-valued or modified IMs. This is mainly due to the fact that those IMs can better cover the range of pulse periods. Moreover, for acceleration-based demand parameter, MFA, the vector [PGA, M] seems to be the best choice for pulse-like ground motions since it can simultaneously account for the magnitude intensity and the PGA.

Furthermore, it is worth noting that the efficiency and especially the relative sufficiency of multi-parameter and vector-valued IMs (see Fig. 1) associated with pulse-like ground motions might be affected by the pulse period (or more specifically T _p /T ₁ ratio). Hence, in predicting demand parameters associated with pulse-like ground motions, separating the pulse-like records based on the pulse period leads to a more suitable choice of IMs in terms of relative sufficiency and efficiency.

It should be finally highlighted that since a large set of ground motions (ordinary and pulse-like) are selected, the efficiency-related findings are presumably not very sensitive to the choice of the ground-motion for the specific structures studied. However, the resulting relative sufficiency values are conditioned on the choice of the probability model for describing the demand parameter given the candidate IM. Moreover, this work employs an approximate RSM (from Eq. 18) as a simple screening tool for raking various candidate scalar and vector-valued IMs. The approximate expression presented in Eq. (18) is based on the assumption that various plausible ground motions are equally likely to take place. However, it should be emphasized that RSM is calculated more rigorously by resolving the integral in Eq. (15) by simulation. In this case, one needs to adopt an appropriate stochastic ground motion model in order to be able to simulate ground motions from a probability distribution (see Jalayer et al. 2012 for a comprehensive example). As a result, the ranking of IMs presented in this work in terms of their relative sufficiency should be regarded as a preliminary one. A more refined ranking can be established once suitable stochastic ground motion models for ordinary and near-source conditions are adopted.

As a final word for future developments, the investigations should also be carried out by implementing energy-based demand parameters and intensity measures. Elaborations on this study can lead towards identifying a pool of most suitable IMs for probabilistic seismic demand assessment for alternative classes of existing RC buildings (of course taking into account also their predictability through probabilistic seismic hazard analysis).