1 Introduction

Floor response spectra in terms of acceleration, which are also known as in-structure spectra, are usually used for the seismic design and evaluation of acceleration sensitive equipment installed in buildings. The floor response spectra concept is based on a separate (uncoupled) analysis of the structure and its equipment, which means that dynamic interaction between them is neglected. It is considered to be sufficiently accurate in cases of equipment whose mass is significantly smaller than that of the structure, by a factor of at least one thousand. If this factor is smaller, the floor response spectra are usually conservative (see e.g. Adam and Furtmüller 2008; Adam et al. 2013).

The main steps for the calculation of floor acceleration spectra are the following:

  1. 1.

    Response-history analysis of the structure by using a set of ground motions.

  2. 2.

    Determination of the response of a floor in terms of the absolute floor acceleration.

  3. 3.

    Generation of a floor acceleration spectrum corresponding to the absolute acceleration response-history determined in step (2).

An excellent state-of-the-art paper on the seismic design of secondary structures, which includes a historical overview of analysis methods, including the floor acceleration spectra, was prepared by Villaverde (1997).

The development of early floor response spectra methods was based on the assumption that, during earthquakes, structures and equipment remain in the linear elastic region. Even in the case of structures of great importance, such as nuclear power plants, it is justifiable to allow a moderate amount of inelastic behaviour during strong earthquakes. This fact is important, especially in the case of the evaluation of existing structures, since the neglecting of the influence of structural inelasticity on floor accelerations may lead to unrealistic results. In general, significant reductions in peak values of floor response spectra can be achieved if inelastic behaviour of the structure and/or equipment is taken into account. An early observation of this phenomenon was made by Lin and Mahin (1985), who defined an amplification factor which can be used for obtaining design floor response spectra for the inelastic primary structure from linear elastic floor response spectra. Several other researchers have also examined this problem and similarly concluded that inelasticity of the structure can have a strong influence on the accelerations of equipment (see e.g. Sewell et al. 1986; Igusa 1990; Fajfar and Novak 1995; Singh et al. 1996; Adam and Fotiu 2000; Rodriguez et al. 2002; Medina et al. 2006; Sankaranarayanan and Medina 2007; Politopoulos and Feau 2007; Adam and Furtmüller 2008; Chaudhuri and Villaverde 2008; Politopoulos 2010).

In order to avoid the extensive numerical integrations which are needed for the determination of floor response spectra, several researchers have proposed methods that enable the generation of simplified floor response spectra directly from the ground response spectra, using the dynamic properties of the structure. Examples of proposals which take into account the inelastic behaviour of structures are given in, e.g. Villaverde (1987, 2006), Rodriguez et al. (2002), Shooshtari et al. (2010), Novak and Fajfar (1994), Oropeza et al. (2010), and most recently Sullivan et al. (2013). The last three proposals are limited to single-degree-of-freedom (SDOF) primary structures, whereas the first four apply to multi-degree-of-freedom (MDOF) structures. It seems, however, that none of these proposals has yet been widely accepted in practice.

In this paper a simple practice-oriented approximate method is proposed for the direct determination of floor acceleration spectra from the design spectrum of the structure, taking into account inelastic structural behaviour. First, some results of an extensive parametric study which take into account inelastic behaviour of the structure and linear elastic behaviour of the equipment are presented. Both the structure and the equipment are modelled as SDOF systems. The main goal of the parametric study was to determine some general characteristics of the floor response spectra. The results mostly confirm the findings obtained by other researchers. Using the results of the parametric study, a method for direct determination of floor response spectra is proposed. The method is based on the method originally developed by Yasui et al. (1993) for elastic structures, as well as on the idea for the extension of this method to inelastic structures proposed by Novak and Fajfar (1994). The proposed method has a theoretical background because its development is based on the principles of structural dynamics. Empirical values obtained in the parametric study are used only in the resonance region in order to improve the accuracy of the peak values of the floor acceleration spectra. The method has been validated by comparing its results with floor response spectra obtained in the parametric study, i.e. obtained by response history analyses (RHA). Applications of the proposed method are limited to SDOF systems. It can, however, also be applied to MDOF systems if they are properly simulated by an equivalent SDOF system. Preliminary results of the study have already been presented in two conference papers (Vukobratović and Fajfar 2012, 2013).

2 Parametric study

2.1 Description of input parameters used in the study

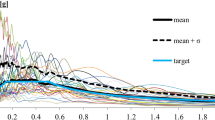
In the parametric study, several thousand floor response spectra were calculated by the procedure described in the Introduction. A SDOF model was used for both the inelastic structure and the elastic equipment, which were treated as uncoupled. The influences of natural period, hysteretic behaviour and ductility of the structure, as well as the influence of the damping of the equipment, were studied. The influence of the ground motion characteristics was also investigated. Two different sets, consisting of 30 ground records each, were used in the study. The records of each set were chosen so that their mean spectrum matched a target spectrum. The target spectrum was the elastic spectrum defined by Eurocode 8 (2004). Type 1 spectra for soil types B and D (each for one set of records) were used, with the peak ground acceleration PGA equal to 0.35 and 0.39 g, respectively. The characteristic periods of the ground motion \(\hbox {T}_{\mathrm{C}}\) (i.e. the periods corresponding to the boundary between the acceleration and velocity controlled ranges of the ground motion spectrum) are equal to 0.5 and 0.8 s for soil types B and D, respectively. The selection of ground records was made by using the REXEL program (Iervolino et al. 2010) in the case of soil type B, whereas the software developed by the Baker Research Group (Jayaram et al. 2011) was used in the case of soil type D. The target and mean spectra of the selected sets of records for both soil types are shown in Fig. 1. Note that the target spectra for 5 % damping were fitted between 0.15 and 2.5 s. The mean PGA values of 30 accelerograms representing soil types B and D amounted to 0.43 and 0.50 g, respectively.

Fig. 1
figure 1

Elastic acceleration spectra (5 % damping) of individual records, target and mean spectrum for a soil type B (target spectrum with PGA \(=\) 0.35 g) and b soil type D (target spectrum with PGA \(=\) 0.39 g)

Full size image

The natural periods of the structure, \(\hbox {T}_{\mathrm{p}}\), used in the parametric study, amounted to 0.2, 0.3, 0.5, 0.75, 1.0 and 2.0 s. In this paper, mainly the results for \(\hbox {T}_{\mathrm{p}}=0.3\) and \(\hbox {T}_{\mathrm{p}}=1.0\,\hbox {s}\) will be shown, which represent values of the \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}}\) ratio smaller and larger than 1, respectively. Three different hysteretic models were taken into consideration: elasto-plastic (EP), and stiffness degrading (Q) models with zero \((\hbox {Q}_{0})\) and 10 % hardening \((\hbox {Q}_{10})\). Structures with strength degradation were not considered in the study. In the case of the Q models (see Q-Hyst model by Saiidi and Sozen 1979), the unloading stiffness degradation coefficient was equal to 0.5. Typical hysteretic behaviour is shown in Fig. 2. A constant target ductility factor \(\upmu \) was assumed throughout the whole period range. It amounted to 2.0 and 4.0. “Mass-proportional” damping amounted to 5 % in the case of the structure, and to 1, 3, 5 and 7 % in the case of the equipment.

Fig. 2
figure 2

Hysteretic behaviour of a elasto-plastic (EP) and stiffness degrading (Q) model with b zero \((\hbox {Q}_{0})\) and c 10 % hardening \((\hbox {Q}_{10})\)

Full size image

2.2 Results of the parametric study

The results obtained in the parametric study provide the basis for the development of the method for the direct generation of floor response spectra for inelastic structures. They show some trends which can be considered as general characteristics of floor response spectra. In this section, some representative results are presented. The natural periods of the (primary) structure and of the equipment (the secondary structure) are denoted as \(\hbox {T}_{\mathrm{p}}\) and \(\hbox {T}_{\mathrm{s}}\), respectively. The floor acceleration spectra values are denoted as \(\hbox {A}_{\mathrm{s}}\) (or \(\hbox {A}_{\mathrm{se}}\) in the special case of an elastic structure). The peak acceleration of the structure is denoted as \(\hbox {A}_{\mathrm{p}}\). The results shown in Figs. 3, 4, 5, 6 and 7 were obtained for the sets of ground records which correspond to soil types B and D and for structures with natural periods of 0.3 and 1.0 s. In all cases the damping of the structure \((\upxi _{\mathrm{p}})\) amounted to 5 %, whereas damping of the equipment \((\upxi _{\mathrm{s}})\) amounted to 1 and 5 %. The results obtained for the EP model and the \(\hbox {Q}_{10}\) model are presented.

The floor response spectra shown in Figs. 3 and 4 represent mean values. In Fig. 5 the ratio of floor response spectra for an inelastic \((\hbox {A}_{\mathrm{s}})\) and the corresponding elastic structure \((\hbox {A}_{\mathrm{se}})\) are presented.

Fig. 3
figure 3

Mean values of the floor response spectra for soil type B, 5 % damping of the structure

Full size image
Fig. 4
figure 4

Mean values of the floor response spectra for soil type D, 5 % damping of the structure

Full size image

The period range of a floor response spectrum can be roughly divided into three regions, depending on the ratio \(\hbox {T}_{\mathrm{s}}/\hbox {T}_{\mathrm{p}}\): the pre-resonance region \((\hbox {T}_{\mathrm{s}}/\hbox {T}_{\mathrm{p}}<0.8)\), the resonance region \((0.8<\hbox {T}_{\mathrm{s}}/\hbox {T}_{\mathrm{p}}<1.25)\), and the post-resonance region \((\hbox {T}_{\mathrm{s}}/\hbox {T}_{\mathrm{p}}>1.25)\). It is clear that in the pre-resonance and in the resonance regions, the behaviour of the equipment is strongly influenced by the behaviour of the structure. Both regions are characterized by a significant reduction in \(\hbox {A}_{\mathrm{s}}\) due to inelastic structural behaviour. The shape of floor response spectra is influenced by the hysteretic behaviour of the structure. In the case of the EP model the peak values of \(\hbox {A}_{\mathrm{s}}\) occur close to the resonance \((\hbox {T}_{\mathrm{s}}\approx \hbox {T}_{\mathrm{p}})\), whereas in the case of the \(\hbox {Q}_{10}\) model the peak values of \(\hbox {A}_{\mathrm{s}}\) are shifted towards higher periods, due to increasing \(\hbox {T}_{\mathrm{p}}\) with increasing plastic deformations. In the post-resonance region, the floor response spectrum is controlled by the ground motion spectrum, and the inelastic structural behaviour has only a small influence on it. If \(\hbox {T}_{\mathrm{s}} \gg \hbox {T}_{\mathrm{p}}\), there is practically no reduction due to inelastic behaviour for the EP model. In the case of the \(\hbox {Q}_{10}\) model, some slight amplification can be observed. In the case of infinitely rigid equipment, \(\hbox {A}_{\mathrm{s}}\) is equal to \(\hbox {A}_{\mathrm{p}}\), whereas in the case of infinitely flexible equipment the value of \(\hbox {A}_{\mathrm{s}}\) is equal to zero.

Fig. 5
figure 5

The ratio of the floor response spectra of the inelastic and elastic structures (with 5 % damping)

Full size image
Fig. 6
figure 6

Floor response spectra normalized to the peak acceleration of the structure (with 5 % damping) for soil type B

Full size image

Figures 6 and 7 show the floor response spectra normalized to the peak acceleration of the structure \((\hbox {A}_{\mathrm{s}}/\hbox {A}_{\mathrm{p}})\). This ratio is mainly influenced by the damping value of the equipment. It can be observed that, in the pre-resonance and the resonance regions, the ratio \(\hbox {A}_{\mathrm{s}}/\hbox {A}_{\mathrm{p}}\) increases slightly with increasing ductility in the case of the EP model, whereas in the case of the \(\hbox {Q}_{10}\) model, in the resonance region, \(\hbox {A}_{\mathrm{s}}/\hbox {A}_{\mathrm{p}}\) decreases with increasing ductility.

Figure 8 presents a comparison between the floor response spectra obtained for the stiffness degrading Q models (\(\hbox {Q}_{0}\) and \(\hbox {Q}_{10}\)). The results were obtained for soil type B and a structure with \(\hbox {T}_{\mathrm{p}}=0.3\,\hbox {s}\). Damping of the structure \((\upxi _{\mathrm{p}})\) amounted to 5 %, whereas damping of the equipment \((\upxi _{\mathrm{s}})\) amounted to 1 and 5 %.

It can be seen from Fig. 8 that the floor response spectra \(\hbox {A}_{\mathrm{s}}\) obtained for the \(\hbox {Q}_{0}\) model are lower than the spectra obtained for the \(\hbox {Q}_{10}\) model. The reduction is smaller or even disappears in the case of the ratio \(\hbox {A}_{\mathrm{s}}/\hbox {A}_{\mathrm{p}}\), as shown in Fig. 9, because the acceleration of the structure \(\hbox {A}_{\mathrm{p}}\) is also smaller in the case of zero hardening (see Fig. 13a) as discussed later in Sect. 3.2.

Fig. 7
figure 7

Floor response spectra normalized to the peak acceleration of the structure (with 5 % damping) for soil type D

Full size image
Fig. 8
figure 8

A comparison between the floor response spectra obtained for different Q models of the structure (with 5 % damping), soil type B

Full size image
Fig. 9
figure 9

A comparison between the floor response spectra (normalized to the peak acceleration of the structure with 5 % damping) obtained for different Q models, soil type B

Full size image

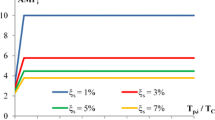
Figure 10 presents maximum values of the ratio \(\hbox {A}_{\mathrm{s}}/\hbox {A}_{\mathrm{p}}\), which will be hereinafter referred to as the amplification factor (AMP).

$$\begin{aligned} \hbox {AMP} = \max \left( \hbox {A}_\mathrm{s} /\hbox {A}_\mathrm{p}\right) \end{aligned}$$
(1)

The results obtained for both sets of ground motions indicate that the shape of the response spectrum characterized by the characteristic period of ground motion \(\hbox {T}_{\mathrm{C}}\) has only a small influence on the amplification factor, provided that the ratio \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}}\) is plotted on the x-axis instead of \(\hbox {T}_{\mathrm{p}}\).

Fig. 10
figure 10

The amplification factors AMP computed in the parametric study

Full size image

It is clear from Fig. 10 that, for both the EP model and the \(\hbox {Q}_{10}\) model of the structure, the main parameter that influences the amplitude of the factors AMP is the damping of the equipment \(\upxi _{\mathrm{s}}\). AMP reaches its peak value in the region \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}} \le 1\), and it then decreases with the increasing ratio \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}}\) if the ratio is larger than 1. Our study showed that the difference between the AMP factors obtained for two different Q models is insignificant, i.e. hardening practically does not influence them.

The influence of ground motion (soil type B versus type D) is negligible, provided that the period \(\hbox {T}_{\mathrm{p}}\) is normalized by the characteristic period of the ground motion \(\hbox {T}_{\mathrm{C}}\). In the case of the EP model, the influence of the ductility of the structure \((\upmu )\) is also small, whereas in the case of the Q model it is moderate. In the case of the EP model, the AMP values slightly increase with increasing ductility, whereas in the case of the Q model they decrease (ductility \(\upmu =1\) corresponds to the elastic case).

Figure 11 shows mean values of the AMP factors for the EP model and \(\hbox {Q}_{10}\) model for two characteristic cases, i.e. when the ratio \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}}\) is smaller, and larger than 1, respectively. Mean values were calculated for soil types B and D, and for natural periods of the structure \(\hbox {T}_{\mathrm{p}}\) equal to 0.2, 0.3, 0.5, 0.75, 1.0 and 2.0 s. In the case of the EP model, the mean values were computed taking into account the AMP values for ductility factors 1 (elastic structure), 2 and 4, whereas in the case of the \(\hbox {Q}_{10}\) model mean values were computed separately for ductility factors 2 and 4. In the case of \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}} \le 1\) coefficient of variation (COV) amounted to about 0.03–0.05, whereas in the case of \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}}>1\) it was in the range from 0.04 to 0.11.

Fig. 11
figure 11

The amplification factors AMP versus the damping of the equipment represented as mean values depending on the ratio \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}}\)

Full size image

3 Proposed direct method

3.1 The original method proposed by Yasui et al. (1993)

A very simple method for the direct determination of floor response spectra was proposed by Yasui et al. (1993), who derived an equation which is valid in the whole period range. Derivation was conducted for the case of linear elastic behaviour of both structure and equipment, which were modelled as SDOF systems. The equation was derived analytically, using the Duhamel integral for the response determination. Three responses in terms of absolute acceleration were analysed: the responses of the structure and of the equipment subjected to the ground motion, and the response of the equipment subjected to the absolute acceleration response-history of the structure. The maximum values of the responses were then combined with the Square Root of Sum of Squares (SRSS) combination rule in order to obtain the equation for the floor spectrum generation. The derivation was performed separately for the non-resonant and resonant cases. The two independent equations were then combined together into a single equation for the determination of the floor response spectrum

$$\begin{aligned} {\hbox {A}_{\mathrm{se}}} =\frac{1}{\sqrt{\left\{ {1-\left( {\hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{s}}\right) ^{2}}\right\} ^{2}+4\cdot \left( {\upxi _\mathrm{p} +\upxi _\mathrm{s}}\right) ^{2}\cdot \left( {\hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{s}}\right) ^{2}}}\sqrt{\left\{ \left( {\hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{s}}\right) ^{2}\cdot \hbox {S}_\mathrm{e} \left( {\hbox {T}_\mathrm{p}, {\upxi }_\mathrm{p}}\right) \right\} ^{2} +\hbox {S}_\mathrm{e} \left( {\hbox {T}_\mathrm{s}, {\upxi }_\mathrm{s}}\right) ^{2}} \end{aligned}$$
(2)

where \(\hbox {A}_{\mathrm{se}}\) is the value in the floor acceleration spectrum and \(\hbox {S}_{\mathrm{e}}\) is a value in the input elastic acceleration spectrum. \(\hbox {S}_{\mathrm{e}}(\hbox {T}_{\mathrm{p}}, \upxi _{\mathrm{p}})\) applies to the elastic primary structure (it was denoted as \(\hbox {A}_{\mathrm{p}}\) in the parametric study described in Sect. 2), whereas \(\hbox {S}_{\mathrm{e}}(\hbox {T}_{\mathrm{s}}, \upxi _{\mathrm{s}})\) applies to the equipment (the secondary system). The damping values of the structure and equipment are denoted as \(\upxi _{\mathrm{p}}\) and \(\upxi _{\mathrm{s}}\) respectively, whereas \(\hbox {T}_{\mathrm{p}}\) and \(\hbox {T}_{\mathrm{s}}\) are the natural periods of the structure and of the equipment, respectively.

Input data for the determination of floor response spectra (which represent absolute accelerations for equipment with a period \(\hbox {T}_{\mathrm{s}}\) and damping \(\upxi _{\mathrm{s}})\) according to Eq. 2 are the dynamic properties of the structure and the equipment and the elastic acceleration spectra (for different damping values) representing the ground motion.

The results of our analyses indicate that, outside of the resonance region, floor response spectra obtained by the direct method (Eq. 2) are in good agreement with the floor response spectra obtained by response-history analyses. In the resonance region, however, considerable inaccuracy of the direct method was observed in our studies (see Sect. 3.3).

3.2 Extension and modifications of the original method

In order to make the direct method applicable to the case of inelastic structures, and to improve its accuracy in the resonant region, some changes were made.

To allow the use of the method for inelastic structures, the elastic acceleration spectrum was replaced with an inelastic acceleration spectrum corresponding to the expected ductility demand, as originally proposed by Novak and Fajfar (1994). It should be noted that, in the proposed method, generally, any inelastic acceleration spectrum can be used. Inelastic acceleration spectra are discussed later in this section.

In order to improve the accuracy of the predicted floor response spectra, the spectral values in the resonant region \((\hbox {T}_{\mathrm{s}} \approx \hbox {T}_{\mathrm{p}})\) are determined by means of empirical equations which are based on the results of the parametric study, rather than on the original equation (Eq. 2). More details about this procedure are provided later in this section.

3.2.1 Inelastic spectra

Several proposals for inelastic spectra are available in the literature. For practical applications, the most convenient is the application of reduction factors due to ductility \(\hbox {R}_{\upmu }\), representing the ratio of elastic and inelastic strength demand (Vidic et al. 1994), i.e. the ratio of the elastic and the inelastic pseudo-acceleration spectra, where the inelastic pseudo-acceleration is related to the yield point of the bilinear force-deformation relationship. An early overview of various proposals for the reduction factor \(\hbox {R}_{\upmu }\) was presented by Miranda and Bertero (1994). The inelastic pseudo-acceleration spectrum, which is used for the analysis and design of the primary structure, can be obtained by reducing the elastic pseudo-acceleration spectrum by means of a reduction factor \(\hbox {R}_{\upmu }\). This spectrum can also be used in the process of the determination of floor response spectra, provided that there is no post-yield hardening of the force-deformation curve of the structure. In the case of post-yield hardening, the actual accelerations of the structure increase (compared to the acceleration at the yield point) with increasing plastic deformation (see Fig. 2c, and note that the acceleration is proportional to the force). The increase of acceleration due to hardening, normalized by the acceleration at the yield point, depends on the ductility factor \(\upmu \) and can be determined as \(\upalpha \cdot (\upmu -1)\), where \(\alpha \) is the ratio of the post-yield and the elastic stiffness. Thus, the following relation applies:

$$\begin{aligned} \hbox {A}_\mathrm{p}\, \hbox {(hardening)}/\hbox {A}_\mathrm{p}\, \hbox {(no hardening)} = 1+\upalpha \cdot (\upmu -1) \end{aligned}$$
(3)

where \(\hbox {A}_{\mathrm{p}}\) is the maximum acceleration of the primary structure.

In the validation of the proposed direct method, which is presented in this paper, the floor response spectra were first determined by using the “exact” inelastic acceleration spectra, in order to exclude the error introduced by using approximate inelastic spectra. The “exact” inelastic spectra are obtained by non-linear RHA. “Exact” inelastic spectra for the EP model and for the \(\hbox {Q}_{10}\) model are shown in Fig. 12. However, the use of “exact” inelastic spectra is not feasible in practical applications, so that, in practice, approximate inelastic spectra have to be used. This approximation introduces an additional error in the floor response spectra. In our study, we used the simplified form of the spectra proposed by Vidic et al. (1994) which has been implemented in Eurocode 8. This inelastic spectrum can be obtained by reducing the elastic acceleration spectrum by a reduction factor \(\hbox {R}_{\upmu }\), which is defined as

$$\begin{aligned} \hbox {R}_\upmu =\left\{ {\begin{array}{ll} {\frac{\hbox {T}_\mathrm{p}}{\hbox {T}_\mathrm{C}}\cdot (\upmu -1)+1,}&{} {\hbox {T}_\mathrm{p} <\hbox {T}_\mathrm{C}} \\ \upmu , &{} \hbox {T}_\mathrm{p} \ge \hbox {T}_\mathrm{C} \\ \end{array}}\right. \end{aligned}$$
(4)

where \(\hbox {T}_{\mathrm{p}}\) is the natural period of the structure, \(\upmu \) is ductility factor and \(\hbox {T}_{\mathrm{C}}\) is the characteristic period of the ground motion (see Sect. 2.1). The spectra apply for 5 % damping of the structure. As a conservative approximation, the spectra for 5 % damping can be used also for a lower damping percentage (Vidic et al. 1994).

Fig. 12
figure 12

“Exact” (solid lines) and approximate (dashed lines) inelastic spectra for soil types B and D (5 % damping of the structure)

Full size image

In the case of zero post-yield stiffness, approximate inelastic acceleration spectra of the structure can be obtained as \(\hbox {S}_{\mathrm{e}}/\hbox {R}_{\upmu }\), where \(\hbox {S}_{\mathrm{e}}\) is the elastic (pseudo-) acceleration spectrum. If a post-yield stiffness is included in the model, its influence on the absolute acceleration spectrum can be considered by dividing the reduction factor \(\hbox {R}_{\upmu }\) by \((1+\upalpha \cdot (\upmu -1))\), where \(\alpha \) is the ratio of the post-yield and the elastic stiffness (see Eq. 3)

$$\begin{aligned} \hbox {R}_\upmu =\frac{\hbox {R}_\upmu (\hbox {Eq. 4})}{1+\upalpha \cdot (\upmu -1)} \end{aligned}$$
(5)

In Fig. 12 the “exact” inelastic acceleration spectra obtained by nonlinear response-history analyses are compared with the approximate inelastic acceleration spectra obtained by reducing the target Eurocode 8 elastic (pseudo)-acceleration spectrum \(\hbox {S}_{\mathrm{e}}\) by means of the \(\hbox {R}_{\upmu }\) factor according to Eq. 4 in the case of the EP model with zero hardening, and according to Eq. 5 in the case of the \(\hbox {Q}_{10}\) model. The results for soil types B and D and the target ductility demands of 2.0 and 4.0 are shown. Damping of the structure \((\upxi _{\mathrm{p}})\) amounted to 5 %. A fair agreement between the “exact” and the approximate spectra can be observed, with some exceptions in the very short period range, where the approximate spectral values are quite conservative. Note that the results of the parametric study (see Sect. 2.2) are shown for cases when the natural periods of the structure amount to 0.3 and 1.0 s. The same natural periods will be used later in this paper for the validation of the direct method. Since the differences between the “exact” and the approximate inelastic acceleration spectra directly influence the accuracy of the proposed direct method, the errors of the approximate inelastic spectra are shown in Table 1, for structures with \(\hbox {T}_{\mathrm{p}}=0.3\) and \(\hbox {T}_{\mathrm{p}} =1.0\,\hbox {s}\). A negative value of the error indicates that the approximate spectral value is smaller than the corresponding “exact” value.

Table 1 Errors of the approximate spectra in comparison to the “exact” inelastic spectra
Full size table

In Fig. 13 “exact” and approximate inelastic spectra obtained for different Q models are compared, taking into account 5 % damping of the structure, target ductility demands of 2.0 and 4.0 and soil type B.

Fig. 13
figure 13

A comparison between a the “exact” and b the approximate inelastic acceleration spectra for the structure (with 5 % damping) obtained for two different Q models, soil type B. \(\hbox {Q}_{0}\) and \(\hbox {Q}_{10}\) represent the model with zero and 10 % hardening, respectively

Full size image

3.2.2 Empirical formula for the resonance region

In the resonance region, the formula provided in the original method provides too conservative results even in the elastic region (see Sect. 3.3). The amplification factors which are based on AMP values obtained in the parametric study (Figs. 10, 11) can be used in order to achieve a more realistic determination of the floor response spectra in the resonance region. In the following text a proposal for amplification factors is made, taking into account the results obtained in the parametric study.

The results of the parametric study suggest that the damping of the equipment has a major influence on the peak values of the floor response spectra. The frequency content of the ground motion (\(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{C}}\) ratio) and the ductility demand, which is more pronounced in the case of stiffness degrading Q model, have a moderate influence. Based on these observations, the first two influences were taken into account for both the EP and the Q model, whereas the influence of ductility was considered only for the Q model.

AMP, which represents the ratio between the peak value of the floor acceleration spectrum and the maximum acceleration of the structure (Eq. 1), can, in the case of the EP model of the structure, be determined approximately as (\(\upxi _{\mathrm{s}}\) should be entered as a percentage)

$$\begin{aligned} \hbox {AMP}=\left\{ {\begin{array}{ll} 18\cdot (1+\upxi _\mathrm{s})^{-0.60},&{} \hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{C} \le 1 \\ 18\cdot (1+\upxi _\mathrm{s})^{-0.60}\cdot (\hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{C})^{-0.20}, &{} \hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{C}>1\\ \end{array}}\right. \end{aligned}$$
(6)

In the case of the Q model, AMP is defined as (\(\upxi _{\mathrm{s}}\) should be entered as a percentage)

$$\begin{aligned} \hbox {AMP}=\left\{ {\begin{array}{ll} 18\cdot (1+\upxi _\mathrm{s})^{-0.60}\cdot (0.6+0.4\cdot \upmu )\cdot \upmu ^{-0.85}, &{} \hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{C}\le 1\\ 18\cdot (1+\upxi _\mathrm{s})^{-0.60}\cdot (\hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{C})^{-0.20}\cdot (0.6+0.4\cdot \upmu )\cdot \upmu ^{-0.85}, &{} \hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{C}>1 \\ \end{array}}\right. \end{aligned}$$
(7)

where \(\hbox {T}_{\mathrm{p}}\) is the natural period of the structure, \(\hbox {T}_{\mathrm{C}}\) is the characteristic period of the ground motion, \(\upxi _{\mathrm{s}}\) is the damping of equipment, and \(\upmu \) is the ductility factor.

Note that Eq. 6 is a special case of Eq. 7 for ductility \(\upmu =1\), i.e. for an elastic structure. The proposed amplification factors AMP for different values of the ductility demand, and damping of the equipment equal to 1 and 5 %, are presented in Fig. 14. They are compared with the mean AMP obtained in the parametric study (average for soil types B and D). In the case of the EP model, all the analysed ductilities, including the elastic structure, were taken into account when determining the mean values of AMP.

Fig. 14
figure 14

Proposed amplification factors and comparison with AMP obtained in the parametric study

Full size image

3.2.3 Simplification in the pre- and post-resonance regions

The summand in the denominator in Eq. 2, which contains the damping coefficients, is important in the resonance region whereas outside of this region it has a negligible effect. In the proposed approach, Eq. 2, adapted for inelastic primary structures, is used only outside of the resonance region, whereas in the resonance region the empirical values presented in the previous section are applied. For this reason it is possible to delete the summand in the denominator in Eq. 2, which contains the damping coefficients.

3.2.4 Summary of the proposed method

In the proposed direct approach, considering the changes explained above, floor response spectra can be computed for both the EP and Q models as follows:

  1. 1.

    In the pre- and the post-resonance regions, the spectral values are obtained as

$$\begin{aligned} \hbox {A}_\mathrm{s} =\frac{\sqrt{\left\{ (\hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{s})^{2}\cdot \displaystyle \frac{\hbox {S}_\mathrm{e} (\hbox {T}_\mathrm{p}, {\upxi }_\mathrm{p})}{\hbox {R}_\upmu }\right\} ^{2}+\hbox {S}_\mathrm{e}(\hbox {T}_\mathrm{s}, \upxi _\mathrm{s})^{2}}}{\left| 1-(\hbox {T}_\mathrm{p}/\hbox {T}_\mathrm{s})^{2}\right| } \end{aligned}$$
(8)

where \(\hbox {A}_{\mathrm{s}}\) is the value in the floor acceleration spectrum, and \(\hbox {S}_{\mathrm{e}}\) is a value in the input elastic acceleration spectrum. \(\hbox {S}_{\mathrm{e}}(\hbox {T}_{\mathrm{p}}, \upxi _{\mathrm{p}})/\hbox {R}_{\upmu }\) applies to the inelastic primary structure, whereas \(\hbox {S}_{\mathrm{e}}(\hbox {T}_{\mathrm{s}}, \upxi _{\mathrm{s}})\) applies to the linear elastic equipment. The damping values of the structure and of the equipment are denoted by \(\upxi _{\mathrm{p}}\) and \(\upxi _{\mathrm{s}}\) respectively, whereas \(\hbox {T}_{\mathrm{p}}\) and \(\hbox {T}_{\mathrm{s}}\) are the natural periods of the structure and the equipment, respectively.

In the case of the stiffness degrading Q model, in the post-resonance region, the ratio \(\hbox {T}_{\mathrm{p}}/\hbox {T}_{\mathrm{s}}\) in Eq. 8 should be replaced by the ratio \(\hbox {T}_{\mathrm{p},\upmu }/\hbox {T}_{\mathrm{s}}\), where \(\hbox {T}_{\mathrm{p},\upmu }\) represents the effective natural period of the structure. It depends on the inelastic deformation, which is expressed in terms of ductility. It can be defined by Eq. 9, as proposed by Akiyama (1985).

$$\begin{aligned} \hbox {T}_{\mathrm{p},\upmu } =\hbox {T}_\mathrm{p} \cdot \sqrt{\frac{1+\sqrt{\upmu }+\upmu }{3}} \end{aligned}$$
(9)
  1. 2.

    In the resonance region, the spectral values are limited to the value obtained by Eq. 10. The amplification factors AMP are defined by Eqs. 6 and 7.

$$\begin{aligned} \hbox {A}_\mathrm{s} =\hbox {AMP}\cdot \frac{\hbox {S}_\mathrm{e} \left( \hbox {T}_\mathrm{p}, \upxi _\mathrm{p}\right) }{\hbox {R}_\upmu } \end{aligned}$$
(10)

Note that \(\hbox {S}_{\mathrm{e}}(\hbox {T}_{\mathrm{p}}, \upxi _{\mathrm{p}})/\hbox {R}_{\upmu }\) represents the value in the inelastic acceleration spectrum, i.e. the maximum acceleration of the inelastic primary structure denoted in the parametric study as \(\hbox {A}_{\mathrm{p}}\). \(\hbox {R}_{\upmu }\) should be determined according to Eq. 4 in the case of zero post-yield stiffness or according to Eq. 5 when the influence of hardening needs to be taken into account (i.e. non-zero post-yield stiffness). Note also that the simplified inelastic spectrum used in this paper can be replaced by any other simplified spectrum available in the literature, or by the “exact” inelastic spectrum also used in this paper.

3.3 Comparison of the original and the proposed direct method for elastic structures

In this section, a comparison of the floor response spectra determined by the original direct method proposed by Yasui et al. (1993) and those obtained by the direct method proposed in this paper is presented (see Fig. 15) for elastic structures with \(\hbox {T}_{\mathrm{p}}\) equal to 0.3 and 1.0 s (soil type B). In both of the direct approaches a target spectrum of the chosen set of accelerograms was used as the seismic input, representing the acceleration of the structure and the equipment. In the resonance region, proposed values of the AMP were used in the case of the proposed method. The mean values of floor response spectra determined in the parametric study (described in Sect. 2) are also shown (denoted as RHA). Additionally, broadened mean floor response spectra are plotted (denoted as RHA broadened). Broadening of the peaks of the floor response spectra is a standard procedure, which is intended to take into account the uncertainties related to the determination of the natural periods of the structure. For instance, according to USNRC (1978), the frequency region where the spectrum should be broadened is obtained by considering a \(\pm \)15 % variation in the frequencies associated with the spectral peaks. A similar approach (15 % broadening of the period) has been used for the broadening of spectral peaks in our study. More information on broadening is provided in Sect. 4.

The comparison presented in Fig. 15 shows that the original method proposed by Yasui et al. (1993) provides very conservative results in the resonance region. In the pre- and the post-resonance regions, however, the results of the original method are in good agreement with the mean floor response spectra obtained by response-history analyses.

Fig. 15
figure 15

Comparison of the floor response spectra for elastic structures for soil type B, 5 % damping of the structure

Full size image

The proposed direct method eliminates conservatism in the resonance region, where a fair agreement with the results of the parametric study can be observed. In the pre- and the post-resonance regions, the original and the proposed methods yield almost the same results.

4 Validation of the proposed direct method

The proposed direct method was validated by comparing its results with the floor response spectra obtained in the parametric study. Selected results shown in this section were obtained for sets of ground records which corresponded to the soil types B and D, for structures with natural periods equal to 0.3 and 1.0 s. The EP model and the \(\hbox {Q}_{10}\) model were taken into account, and two different values of \(\upmu \) were considered. Damping of the structure amounted to 5 %, whereas damping of the equipment amounted to 1 and 5 %.

Figures 16, 17 and 18 show the mean (denoted as RHA), the mean plus standard deviation (denoted as RHA + \(\upsigma \)), and the broadened mean (denoted as RHA broadened) values of the floor response spectra obtained in the parametric study (i.e. by using the response-history analysis), as well as the spectra computed by the proposed direct method. In the direct method, both the “exact” inelastic acceleration spectra (obtained by nonlinear response-history analyses), and the approximate inelastic acceleration spectra (obtained by reducing the target Eurocode 8 elastic pseudo-acceleration spectrum by the factor \(\hbox {R}_{\upmu }\)) were used as the seismic input for the structure. In the case of the equipment, mean elastic acceleration spectra of the chosen sets of accelerograms were used in the case of the “exact” approach, whereas target Eurocode 8 elastic pseudo-acceleration spectra were used in the case of the approximate approach. By using the “exact” approach, approximations related to the inelastic spectrum and the difference between the mean and the target ground motion spectra are eliminated, which allows an evaluation of the basic features of the proposed direct method. On the other hand, by using the approximate approach these approximations are involved in the results. In both cases the proposed values of AMP were used (Eqs. 6, 7). In Figs. 16, 17 and 18, the results obtained with the “exact” spectra are denoted as “direct “exact””, whereas those obtained with the approximate spectra are denoted as “direct approx.”

Fig. 16
figure 16

Floor response spectra for the EP model of the structure with 5 % damping, soil type B

Full size image
Fig. 17
figure 17

Floor response spectra for the \(\hbox {Q}_{10}\) model of the structure with 5 % damping, soil type B

Full size image
Fig. 18
figure 18

Floor response spectra for the \(\hbox {Q}_{10}\) model of the structure with 5 % damping, soil type D

Full size image

As mentioned above, in the comparisons of the floor response spectra, the broadened mean floor response spectra are also shown (RHA broadened). Due to uncertainties related to the determination of the natural period of the structure, the floor response spectra are, in practice, broadened in order to allow moderate shifts (typically \(\pm \)15 %) of the frequency or the period of the structure. The existing provisions (e.g. ASCE 4-98 2000) consider structures with linear elastic behaviour. In the case of the EP model of the structure, where peak values of floor response spectra always occur close to the resonance \((\hbox {T}_{\mathrm{s}} \approx \hbox {T}_{\mathrm{p}})\), it is also reasonable to apply the same the \(\pm \)15 % rule. In the case of the Q model, the peaks of the floor response spectra are shifted towards higher periods. The size of the shift depends on the ductility demand of the structure, i.e. larger shifts are a consequence of a higher ductility demand. In some cases, though, mean floor response spectra have multiple peaks. The question is: what kind of peak broadening makes sense in the case of the Q model? It seems reasonable that both the original and the modified natural periods of the structure (\(\hbox {T}_{\mathrm{p}}\) and \(\hbox {T}_{\mathrm{p},\upmu }\), respectively) should be taken into account in the peak broadening procedure. For this reason the plateau of the broadened spectra shown in this paper extends from \(\hbox {T}_{\mathrm{s}}/\hbox {T}_{\mathrm{p}}=0.85\) to \(\hbox {T}_{\mathrm{s}}/\hbox {T}_{\mathrm{p},\upmu }=1.15\). In this way, a quite wide broadened spectrum is obtained, especially in the case of structures with a higher ductility demand.

It is clear from Figs. 16, 17 and 18 that the proposed direct method in general provides a fair estimate of the broadened floor acceleration spectra, throughout the whole period range, for all of the analysed hysteretic models, natural periods of the structure, levels of ductility and equipment damping. The differences are mainly due to the approximations in the inelastic spectra. This source of errors (see Table 1) is eliminated if “exact” inelastic spectra are used.

5 Conclusions

An extensive parametric study of floor acceleration spectra, taking into account inelastic behaviour of the structure and linear elastic behaviour of the equipment was performed. The structure and the equipment were modelled as SDOF systems. The influences of input ground motion, ductility, hysteretic behaviour, and the natural period of the structure, as well as the damping of the equipment were studied. The results of the study confirmed the well-known fact that inelastic behaviour of the structure can significantly reduce floor acceleration spectra, especially their peak values.

Based on the results obtained in the parametric study, a simple approximate practice-oriented method for the generation of floor response spectra for inelastic structures, directly from the design response spectrum, has been proposed. The proposed method is based on the method originally developed by Yasui et al. (1993) for elastic structures. Using the proposed method, approximate floor acceleration spectra can be obtained as a function of the input acceleration spectra and the dynamic characteristics of the structure and the equipment. Input acceleration spectra represent the elastic and inelastic response of a SDOF system to the ground motion. The elastic spectra provided in codes can be used. Approximate inelastic spectra can be obtained from elastic spectra by using the reduction factors \(\hbox {R}_{\upmu }\) which are provided in the literature. The dynamic characteristics of the structure are its natural period and its damping (which, in our study, was set to 5 %). By replacing the elastic acceleration spectra with inelastic acceleration spectra, it was possible to extend the applicability of the original Yasui et al. method (1993), from elastic to inelastic structures. The method is based on the principles of dynamics. In order to improve the accuracy, in the proposed method the peak value in the floor acceleration spectrum is determined based on empirical results obtained in the parametric study, rather than by the original (conservative) approach. The floor response spectra obtained by the proposed method show reasonable agreement with the broadened floor response spectra obtained by the standard approach by means of response-history dynamic analysis.

The application of the proposed method is limited to the case of SDOF structures without strength degradation, or MDOF structures which can be approximated as equivalent SDOF systems. The method can be used for a quick estimation of the floor response spectra, e.g. in conceptual design, or when checking the results.