Adaptive sampling of cumulus clouds with UAVs

Abstract

This paper presents an approach to guide a fleet of Unmanned Aerial Vehicles (UAVs) to actively gather data in low-altitude cumulus clouds with the aim of mapping atmospheric variables. Building on-line maps based on very sparse local measurements is the first challenge to overcome, for which an approach based on Gaussian Processes is proposed. A particular attention is given to the on-line hyperparameters optimization, since atmospheric phenomena are strongly dynamical processes. The obtained local map is then exploited by a trajectory planner based on a stochastic optimization algorithm. The goal is to generate feasible trajectories which exploit air flows to perform energy-efficient flights, while maximizing the information collected along the mission. The system is then tested in simulations carried out using realistic models of cumulus clouds and of the UAVs flight dynamics. Results on mapping achieved by multiple UAVs and an extensive analysis on the evolution of Gaussian processes hyperparameters is proposed.

1 Introduction

Context Atmospheric models still suffer from a gap between ground-based and satellite measurements. As a consequence, the impact of clouds remain one of the largest uncertainties in the climate General Circulation Model (GCM): for instance the diurnal cycle of continental convection in climate models predicts a maximum of precipitation at noon local time, which is hours earlier compared to observations—this discrepancy being related to insufficient entrainment in the cumulus parameterizations (Genio and Wu 2010). Despite the continual efforts of cloud micro-physics modelers to increase the complexity of cloud parameterization, uncertainties continue to persist in GCMs and numerical weather prediction (Stevens and Bony 2013). To alleviate these uncertainties, adequate measurements of cloud dynamics and key micro-physical parameters are required. The precision of the instruments matters for this purpose, but it is the way in which samples are collected that has the most important impact. Fully characterizing the evolution over time of the various parameters (namely pressure, temperature, radiance, 3D wind, liquid water content and aerosols) within a cloud volume requires dense spatial sampling for durations of the order of 1 h: a fleet of autonomous lightweight Unmanned Aerial Vehicles (UAVs) that coordinate themselves in real time could fulfill this purpose.

The objective of the SkyScanner project,¹ which gathers atmosphere and drone scientists, is to conceive and develop a fleet of micro UAVs to better assess the formation and evolution of low-altitude continental cumulus clouds. The fleet should collect data within and in the close vicinity of the cloud, with a spatial and temporal resolution of respectively about $10\,$m and $1\,$Hz over the cloud lifespan. In particular, by reasoning in real time on the data gathered so far, an adaptive data collection scheme that detects areas where additional measures are required can be much more efficient than a predefined acquisition pattern: this article focuses on the definition of such adaptive acquisition strategies.

Challenges The overall control of the fleet to map the cloud must address the two following problems:

• It is a poorly informed problem. On the one hand the UAVs perceive the variables of interest only at the positions they reach (contrary to exteroceptive sensors used in robotics, all the atmosphere sensors perform pointwise measures at their position), and on the other hand these parameters evolve dynamically. The mapping problem in such conditions consists in estimating a 4D structure with a series data acquired along 1D manifolds. Furthermore, even though the coarse schema of air currents within cumulus clouds is known (Fig. 1), the definition of laws that relate the cloud dimensions, the inner wind speeds, and the spatial distribution of the various thermodynamic variables is still a matter of research—for which UAVs can bring significant insights.

• It is a highly constrained problem. The mission duration must be of the order of a cumulus lifespan, that is about 1 h, and the winds considerably affect both the possible trajectories of the UAVs and their energy consumption—all the more since we are considering small sized motor gliders aircrafts (maximum take off weight of $2.0\,$kg). Since winds are the most important variables that influence the definition of the trajectories and are mapped as the fleet evolves, mapping the cloud is a specific instance of an “explore vs. exploit” problem.

Exploring cloud with a fleet of UAVs is therefore a particularly complex problem. The challenge to overcome is to develop non-myopic adaptive strategies using myopic sensors, that define UAV motions that maximize both the amount of gathered information and the mission duration.

Fig. 1

Schematic representation of a cumulus cloud. The arrows represent wind velocities, the orange blobs denote areas where mixing is occurring between the cloud and the surrounding atmosphere. This representation is very coarse: for instance the updrafts in the center of the cloud are known to behave as “bubbles” when the cloud is young. The cloud dimensions can vary from one to several hundreds of meters (Color figure online)

Related work Atmospheric scientists have been early users of UAVs,² thanks to which significant scientific results have rapidly been obtained in various contexts: volcanic emissions analysis (Diaz et al. 2010), polar research (Holland et al. 2001; Inoue et al. 2008) and naturally climatic and meteorological sciences (Ramanathan et al. 2007; Corrigan et al. 2008; Roberts et al. 2008). UAVs indeed bring forth several advantages over manned flight to probe atmospheric phenomena: low cost, ease of deployment, possibility to evolve in high turbulence (Elston et al. 2011), etc. An in-depth overview of the various fixed-wing airframes, sensor suites and state estimation approaches that have been used so far in atmospheric science is provided in Elston et al. (2015).

In these contexts, UAVs follow pre-planned trajectories to sample the atmosphere. In the robotics literature, some recent works have tackled the problem of autonomously exploring or exploiting atmospheric phenomena. The possibility of using dynamic soaring to extend the mission duration for sampling in supercell thunderstorms has been presented in Elston and Argrow (2014). In this case, only the energetic consumption is optimized, and the gathered information does not drive the planning. Lawrance and Sukkarieh (2011a, b) present an approach where a glider explores a wind field trying to exploit air flows to augment flight duration. The wind field is mapped using a Gaussian Process Regression framework (GPR), and the wind currents are simulated using combinations of sines and cosines and a toroidal model for updrafts, and a constant lateral drift is added to introduce dynamicity. The authors propose a hierarchic approach for the planning, where a target point is firstly selected and then a trajectory to reach it is generated for every planning cycle. In a similar scenario, a reinforcement learning algorithm to find a trade-off between energy harvesting and exploration is proposed in Chung et al. (2015). Autonomous soaring has also been studied, as in Nguyen et al. (2013), where a glider has to search for a target on the ground. The goal here is to maximize the probability of detecting the target traveling between thermals with known location. The problem of tracking and mapping atmospheric phenomena with a UAV is also studied in Ravela et al. (2013). The authors use GPR to map the updraft created by a smoke plume. Even though the mapped currents are not taken into account for the navigation, it is worth to remark that contrary to the previous contributions, here experiments with a real platform are presented. This shows the possibility of online mapping of atmospheric phenomena by a fixed-wing UAV using GPR. An other significant contribution on wind-field mapping is presented in Langelaan et al. (2012): aiming at autonomous dynamic soaring with a small UAV, the authors present and approach in which the wind field is modelled by polynomials, which parameters are estimated with a Kalman Filter. Experiments in which the mapped wind-field is compared to an “air-truth” obtained by tracking lighter than air balloons small are presented. Finally, autonomous exploration of current fields is not exclusively related to aerial applications: the use of Autonomous Underwater Vehicles for oceanographic studies has been recently investigated (Das et al. 2013; Michini et al. 2014).

Besides in Michini et al. (2014), in all the aforementioned work only the use of a single vehicle to achieve the mission is considered, and no multi-UAV systems are proposed.

Contributions and outline The work presented in this article tackles the following problem: a fleet of a handful of UAVs is tasked to autonomously gather information in a specified area of the cloud. The UAVs trajectories are optimized using an on-line updated dense model of the variables of interest. The dense model is built on the basis of the gathered data with a Gaussian Processes Regression, and is exploited to generate trajectories that minimize the uncertainty on the required information, while steering the vehicles within the air flows to save energy. The results presented here significantly extend the preliminary work depicted in Renzaglia et al. (2016): they use a realistic dynamic aircraft model, and extensive simulation in dynamic clouds models are analyzed. The main contributions of this work with respect to the state of the art are:

• The mapped phenomenon varies a lot in time and space, and the ability to build proper wind maps is essential, as it conditions the ability to derive optimal adaptive sampling schemes. The hyperparameters of the GP are hence learned online (Sect. 2), and an analysis of their evolution is proposed (Sect. 4).

• An original exploration technique based on a stochastic optimization scheme is proposed to plan feasible trajectories in the mapped current field (Sect. 3). The approach aims at optimizing possibly contradictory goals: augmenting the information gathered so far, while minimizing energy consumption.

• Realistic simulations based on a cumulus cloud model produced by realistic large-eddy simulations and a realistic motor glider flight dynamics model are presented (Sect. 4). Some exploration tasks are depicted, varying the criteria to optimize, and we show the ability of our approach to perform the specified mission in a realistic setting.

A discussion concludes the paper and proposes further research and development directions to explore, so as to effectively deploy adaptive fleets of drones within atmospheric phenomena.

2 Mapping clouds

Maintaining a reliable map of the environment is of course of utmost importance for exploration tasks, as it is necessary to assess both the feasibility of trajectories and the relevant sampling locations. In the case of atmospheric phenomena, there are numerous variables of interest to the meteorologist. Of particular interest is the 3D wind vector: it is both one of the most dynamic atmospheric variables and an essential information for planning feasible and energy efficient paths. We therefore focused our work on the mapping of dynamic 3D wind currents.

Due to the sparsity of the sampling process in a dynamic 3D environment, the GPR probabilistic framework is particularly adapted for this mapping problem, as shown by related work (Lawrance and Sukkarieh 2011a, b; Ravela et al. 2013; Das et al. 2013). Being statistical in nature, GPR allows to estimate the quality of predictions. This is naturally exploited in active perception tasks, such as in Souza et al. (2014), where the authors derives exploration strategies for outdoor vehicles, and in Kim and Kim (2015), where a GP framework is used to drive surface reconstruction and occupancy mapping.

The mapping framework used in this paper is similar to the one presented in Lawrance and Sukkarieh (2011a), where three independent GP models are used to map the components of the 3D wind vector, but we propose an online hyperparameter optimization, which is activated between each planning iteration. We have also focused efforts on deriving interesting and fast to compute information metrics from the model to drive the exploration strategies.

2.1 Gaussian process regression model

We introduce here briefly the usage of Gaussian processes for regression tasks. We refer the reader to the work of Rasmussen and Williams (2006) for an in-depth view of the subject.

Gaussian process regression is a very general statistical framework, where an underlying process $y=f(x){:}~\mathbb {R}^n \rightarrow \mathbb {R}$ is modeled as “a collection of random variables, any finite number of which have a joint Gaussian distribution” (Rasmussen and Williams 2006). One can view this as a way to set a Gaussian prior over the set of all admissible functions: given a location $x \in \mathbb {R}^n$, the values y taken by all admissible functions are distributed in a Gaussian manner. Under the Gaussianity assumption, the process is fully defined by its mean and covariance:

$$\begin{aligned} \begin{aligned}&m(\mathbf {x}) = \mathbb {E}[f(\mathbf {x})]\,,\\&k(\mathbf {x},\mathbf {x}') = \mathbb {E}[(f(\mathbf {x})-m(\mathbf {x})(f(\mathbf {x}')-m(\mathbf {x}'))]\,. \end{aligned} \end{aligned}$$

(1)

In this model, the mean m and covariance k are not learned directly from the data, but given as parameters. In most cases, the process is assumed to have zero mean, so that the only parameter is the covariance function or kernel. We currently do not use any particular prior information and adopt a zero mean process: this is a matter of further work, that will explicitly define the relations between the higher level coarse cloud model and the dense GP-based model, as well as the relations between the various variables of interest.

The kernel encodes the similarity of the target process f at a pair of given inputs and so describes the spatial correlations of the process. Given a set of n samples (X, Y) and assuming zero mean, the GP prior is fully defined by the $n \times n$ Gram matrix $\Sigma _{X,X}=[k(X_i,X_j)]$ of the covariances between all pairs of sample locations. Inference of the processes value $y_\star$ at a new location $x_\star$ is then done by conditioning the joint Gaussian prior distribution on the new samples:

$$\begin{aligned} \begin{aligned}&\bar{y}_\star = \Sigma _{\mathbf {x}_\star ,\mathbf {X}}\Sigma _{X,X}^{-1}\mathbf {Y},\\&\mathbb {V}[y_\star ] = k(\mathbf {x}_\star ,\mathbf {x}_\star ) - \Sigma _{\mathbf {x}_\star ,\mathbf {X}}\Sigma _{X,X}^{-1}\Sigma _{\mathbf {x}_\star ,\mathbf {X}}^{\top } \end{aligned} \end{aligned}$$

(2)

The posterior Gaussian distribution at location $x_\star$ of the values of all admissible functions in the GP model therefore has mean $\bar{y}_\star$ and variance $\mathbb {V}[y_\star ]$, which can be used both to predict the value of the function and to quantify the uncertainty of the model at this location.

Thanks to the Gaussianity assumption, inference has a closed form solution involving only linear algebraic equations. Computing the model is done in $\mathcal {O}(n^3)$, due to the cost of inversion of the $\Sigma$ matrix and subsequent computation of the posterior are done in $\mathcal {O}(n^2)$. This can be done online using optimized linear algebra software for models of up to a few hundreds of samples.

2.2 Learning hyperparameters

The choice of the expression of the kernel function k is central: it sets a prior on the properties of f such as its isotropy, stationarity or smoothness. The only requirement for the kernel function is that it has to be positive semidefinite, which means the covariance matrix $\Sigma$ of any set of inputs must be positive semidefinite and therefore invertible. In practice, one selects a family of kernels, whose so called hyperparameters are learned to fit the data. We selected the most widely used squared exponential kernel with additive Gaussian noise:

$$\begin{aligned} k_{SE}(\mathbf {x_i},\mathbf {x_j}) = \sigma _f^2 e^{-\frac{1}{2}|\mathbf {x_i}-\mathbf {x_j}|M|\mathbf {x_i}-\mathbf {x_j}|} + \delta _{ij} \sigma _n^2 \end{aligned}$$

(3)

where $\delta _{ij}$ is the Kronecker delta function, $M=\mathbf {l}^{-2}I$ is a diagonal matrix that defines the characteristic anisotropic length scales $\mathbf {l}$ of the process, and $\sigma _f^2$ and $\sigma _n^2$ are respectively the process variance and the Gaussian noise variance over the measures. The squared exponential kernel is stationary, anisotropic and infinitely smooth.

Fig. 2

Illustration of the GP-based mapping process applied in a realistic wind field. The left pictures represent the ground truth of the vertical wind velocity, pictures in the middle show the computed maps on the basis of the measures taken at the positions denoted by a black dot (the measure standard deviation $\sigma _n$ is equal to 0.25 m), and the right images show the predicted variances of the map. Unit of all depicted values is m s$^{-1}$. The sequences of measures are defined by the planning approach presented in Sect. 3. From top to bottom, a time lapse of 20 s separates each line of pictures, the altitude shown is the one of the first UAV, respectively 800, 825 and 850 m

The kernels hyperparameters $\theta = (\sigma _f,\mathbf {l},\sigma _n)$ are chosen by maximizing the Bayesian log marginal likelihood criterion:

$$\begin{aligned} \log p(\mathbf {Y}|\mathbf {X},\theta ) = -\frac{1}{2}\mathbf {Y}^\top \Sigma ^{-1}\mathbf {Y} -\frac{1}{2}\log |\Sigma | -\frac{n}{2}\log 2 \pi \end{aligned}$$

(4)

This is a non-convex optimization problem: the optimization function may be subject to local maxima, and therefore may not always converge in finite time. Optimizing the kernel hyperparameters is computationally demanding: although the partial derivative of Eq. (4) with respect to $\theta$ can be computed in $\mathcal {O}(n^3)$, convergence to a local optimum may involve a great number of steps. Usually the optimization of hyperparameters is therefore done offline.

In our context, the input space is the four dimensional space-time location of the UAVs, and the estimated variables are the three components of the 3D wind vector. Therefore we train three GP models separately, making the simplifying assumption that there is no correlation between the three components. The optimization of hyperparameters is done online: indeed the underlying atmospheric process’s length scales may vary from one cloud to the other, and the stationarity assumption may not hold during the course of the mission. To alleviate computational issues we keep only the most relevant samples. This is done by setting a tolerance value $h_{tol}$, so that when comparing the newest sample $x_n$ to an older one $x_o$, and setting all spatial coordinates to zero, the older one is discarded if $k(x_n,x_o) < h_{tol}$. Using this criteria on the covariance instead of the age of the samples lets the amount of retained samples adapt to the the temporal length scale of the process. In order to avoid dropping all data if the optimization produces very short length scale on the time dimension, we also specify a minimum amount of time it has to stay in the model, which was set to 1 min in our experiments.

Figure 2 illustrates the mapping of the wind vertical component, by virtually gathering wind data in a realistically simulated wind field (see Sect. 4.1.1).

2.3 Computing information metrics on trajectories

As the task at hand is an exploration one, it is crucial to be able to properly evaluate the quantity of information a set of new samples add to the current map, so as to enable a planning process to select informative trajectories. Since the GP framework encodes probability distributions, the resulting maps are particularly well adapted for this purpose: the variance of the GP as defined by Eq. (2), which represents the uncertainty of the current model at each point in space, is a natural candidate to evaluate the utility of new measurements.

The problem of selecting the best possible future measurements to estimate a statistical model has been extensively studied. The idea is to minimize the variance of the estimator using a statistical criterion. Chung et al. (2015) integrate the variance of the GP over the region to be mapped and derive a measure of the quality of the model. Unfortunately, a closed-from expression of this integral does not exist in general. The integration criterion defined in Chung et al. (2015) is an instance of I-optimality. Other classical criteria directly seek to minimize the covariance matrix:

• D-optimality aims to maximize the differential Shannon entropy of the statistical model, which comes to maximizing the determinant of the information matrix (the inverse of the covariance matrix).

• T-optimality aims to maximize the trace of the information matrix.

We have found very few differences between these two criteria in previous work (Renzaglia et al. 2016), so we used the T-optimality criterion in the experiments, which it is slightly faster to compute.

To efficiently evaluate the information gain of a new set of measurement points, we define the conditional covariance $\Sigma _{\mathbf {X}_{new}|\mathbf {X}}$ of the set of m new points $\mathbf {X}_{new}$ against $\mathbf {X}$, the points already included in the regression model:

$$\begin{aligned} \Sigma _{\mathbf {X}_{new}|\mathbf {X}} = \Sigma _{\mathbf {X}_{new},\mathbf {X}_{new}} - \Sigma _{\mathbf {X}_{new},\mathbf {X}}\Sigma _\mathbf {X,X}^{-1}\Sigma _{\mathbf {X}_{new},\mathbf {X}}^\top \end{aligned}$$

(5)

The $\Sigma _{\mathbf {X}_{new}|\mathbf {X}}$ matrix is of fixed size $m \times m$, independent of the size of the model, which yield swift computations. The matrix itself is computed in $\mathcal {O}(nm^2+mn^2)$, subsequent inversion or computation of the determinant are performed in $\mathcal {O}(m^3)$. The value $v_T$ of the T-optimality criterion is thus defined as:

$$\begin{aligned} v_T(\Sigma _{\mathbf {X}_{new}|\mathbf {X}})&=tr([\Sigma _{\mathbf {X}_{new}|\mathbf {X}}+\sigma ^2_nI]^{-1}) \end{aligned}$$

(6)

This criterion does not yield absolute values, not even positive ones. The scale will depend on the kernel function and on the number of samples in the model. Therefore it is only useful for comparing trajectories generated using the same model (and with the same amount of new samples). To be able to integrate this information measure in a multi-criteria optimization framework, it is necessary to normalize it. We introduce here an empirical way of normalizing the information measure.

Assuming a fixed sampling rate, the feasible trajectory maximizing the information measure in a completely empty model is a straight line in the spatial direction where the covariances length scale is the shortest. Computing the utility measure $v_{Tb}$ for such a trajectory gives an upper bound for a best set of samples. Driving the UAV along a straight line in the direction of the longest length scale would still provide a passable utility $v_{Tp}$ (as the model is still empty). Setting absolute utilities for $v_{Tb}$ and $v_{Tp}$ then enables to define a normalization for the information measure. This normalized value is not relative anymore, it takes into account the current state of the model: if the model is very dense, with low variances everywhere, then the normalized utility will be very low (depending on the normalization function) because we compare it to an ideal empty model. Note that these ideal trajectories must be feasible for the UAV, at least in a windless environment. As we use fixed wing UAVs, it is not realistic to drive them along a strictly vertical trajectory. Therefore when the shortest length scale is the vertical one, we assume a trajectory at maximum climb rate, with the horizontal component along the second shortest length scale.

3 Energy-efficient data gathering

The regression model presented in the previous section is the basis on which the energy-efficient data gathering strategy is developed. The local map built with the GPs is indeed the source of two fundamental information to plan the trajectories: generate feasible trajectories, and predicting the information gain their execution will bring. The optimization problem to solve can be then formulated as follows: generating safe and feasible trajectories which minimize the total energy consumption according to the mapped wind field, while maximizing the information collected along the paths.

Planning in currents fields is a challenging problem even in standard start-to-goal problems, where a robot moves in a static two-dimensional flow and assuming a perfect knowledge of the map (Petres et al. 2007; Soulignac 2011). Our scenario is deeply different, since the field is changing over time, is initially unknown and sensed during the mission and it is not possible to identify an optimal final goal to reach in order to reduce the problem complexity. Furthermore, even though we do not consider large swarm of UAVs, the deployment of a small number of aircrafts (typically around 3–4) is crucial for the success of the mission, leading to larger planning spaces. All these complex issues, combined with strong computational constraints imposed by the requirements of on-line planning, make this multi-criteria optimization problem particularly challenging. As a result, obtaining a global optimal solution is not feasible and we limit our convergence requirements to local optimal solutions.

For the trajectory generation and evaluation, we consider short-time horizons (typically in the order of $\sim$20 s). This choice is motivated by two main reasons: firstly, the reliability of our local models significantly decreases in time, making unrealistic any long-term prediction; secondly, the computational constraints would be harder to respect with larger optimization spaces. Each planning horizon $\varDelta T$ is then divided in m sub-intervals of duration dt in which the optimization variables (controls) are constant. As a result, the trajectory for the UAV j during $\varDelta T$ is described by the sequence $u_i^{(j)}$, with $i\in \{1,\ldots ,m\}$, and a given initial condition $u_0^{(j)}$.

3.1 Trajectory evaluation

The first criterion to evaluate the trajectories is the energy consumption. Flying within currents leads indeed to energy costs which strongly depend on the planning: flying against strong wind can hugely increase the amount of required energy, while optimally exploiting these currents (and especially ascending air flows) can on the other hand allow the UAVs to significantly extend their flight duration. To take into account this phenomenon in the trajectory evaluation, we explicitly consider the total energy consumed by the fleet over a planning horizon $\varDelta T$. This value is simply represented by the sum over time of the input power $P_{in}(t)$, which is one of the controls on which the trajectories are optimized. Introducing normalization terms, for the aircraft j, we have:

$$\begin{aligned} U_{E}^{(j)}(t_0,\varDelta T) = 1 - \frac{1}{P_{in}^{max}\varDelta T} \sum _{t=t_0}^{t_0+\varDelta T} P_{in}^{(j)}(t)dt. \end{aligned}$$

(7)

The total fleet energetic utility $U_E$ is given by average this value over the UAVs. Note that this criterion is strictly local and does not take into account the total amount of energy stored in the batteries: this is rather a concern for the higher-level decision process, that must for instance make sure every UAV can come back the ground station. It is also independent of the trajectory of the UAVs. Indeed exploitation of the wind field is an indirect result of the combination of minimization of the energetic expense with other goals. For example when trying to reach a higher altitude, trajectories that traverse updrafts will need less energy for the same climb rate and therefore will be preferred over trajectories outside the updraft.

The second criterion for the trajectory evaluation is the information gain $U_I$. To predict the information utility acquired by a given set of trajectories we use the T-information metric: after sampling the planned trajectories at at fixed sampling rate, we compute the relative utility of the $X_{new}$ samples $v_T(\Sigma _{\mathbf {X}_{new}|\mathbf {X}})$ using (6). A linear normalization is obtained using $U_I(v_{Tb})=1$ and $U_I(v_{Tp})=0.5$, subsequently clipping values above one and below zero:

$$\begin{aligned} U_I(v) = max \left( 0,\; min \left( 1,\; \frac{v + v_{Tb}- 2v_{Tp}}{2(v_{Tb}-v_{Tp})} \right) \right) . \end{aligned}$$

(8)

As discussed in Sect. 2.3, $v_{Tb}$ and $v_{Tp}$ are respectively the best and worst expected information gains for an ideal rectilinear trajectory that is not influenced by winds, on an empty model with current hyperparameters. This way we are able to compute an absolute measure for the information gain, that takes into account both the current samples in the model and the hyperparameters. As the model fills up with samples, the information gain lowers in already visited areas. The choice of $U_I(v_{Tp})$ influences what is considered a good sampling: setting it to a low value degrades the utility of sampling along dimensions with a longer length scale, whereas setting it to a value close to one would not favor any particular sampling direction. The values $U_I(v_{Tb})=1$ and $U_I(v_{Tp})=0.5$ have been empirically chosen.

The third considered criterion, $U_G$, is strictly dependent on the specific goal of each mission. The acquisition of information within a given area is one of the essential task issued by the higher planning level. Formally, defining a rectangular box b, the utility of a given trajectory for this task is defined as:

$$\begin{aligned} U_{G}^{j}(t_0,\varDelta T) = \frac{d_b(X^{j}_{t_0 + \varDelta T})- d_b(X^{j}_{t_0})}{V_{zmax} \varDelta T}, \end{aligned}$$

(9)

where $X^{j}_{t}$ is the position of the j-th UAV at time t and $d_{b}(X)$ is the distance between the UAV and the closest point of the box boundary ($d_{b}(X)=0$ if the UAV is inside the box). The total utility for the fleet is the mean value over all UAVs.

To tackle this centralized multi-criteria optimization problem we consider a linear combination of the three criteria:

$$\begin{aligned} U_{tot} = w_E U_E + w_I U_I + w_G U_G. \end{aligned}$$

(10)

In Sect. 4.2 we analyze in details the effects on the mission of different choices of the weights $w_x$. In future work it is our intention to explore also different methods to tackle this multi-criteria optimization problems, e.g using multi criteria decision making approaches (Basilico and Amigoni 2011).

3.2 Trajectory optimization

For every $\varDelta T$, we can now formulate the trajectory optimization problem, which consists in maximizing a global utility function $U_{tot}(\varvec{u})$ as a function of the control variables $\varvec{u}$, subject to some constraints:

$$\begin{aligned} |u_i^{(j)}-u_{i-1}^{(j)} |\le \varDelta u_{max} \quad \forall \, i,j. \end{aligned}$$

(11)

As defined in details in “Appendix 1”, our controls inputs are the turn radius R and the motor power input $P_{in}$. To tackle this optimization problem, we propose a centralized two-step approach³: a first phase based on a blind random search in order to have a good trajectories initialization, followed by a gradient ascent algorithm to optimize them.

3.2.1 Trajectory initialization

The first phase of the optimization process, based on a blind random search, is achieved creating a set of feasible trajectories obtained by a constrained random sampling of controls $u_t$, and exploiting the approximated field generated by the GP regression. The trajectories are then evaluated using the utility function $U_{tot}$ and the best set of $N_r$ trajectories is the initial configuration for the gradient ascent phase. The presence of the first sampling step is due to the strong dependence of the gradient-based solution on the initial configuration. In this way, even though we only have local convergence guarantees, the probability of getting stuck in local maxima far from the global optimal trajectories is reduced.

3.2.2 Stochastic gradient approximation

To perform the gradient ascent we adopt a constrained version of the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm (Spall 2005; Sadegh 1997). This algorithm is based on successive evaluations of the utility function to obtain a numerical approximation of the gradient. At every algorithm iteration k, the optimization variables $\varvec{u}$ are hence updated as follows:

$$\begin{aligned} \varvec{u}_{k+1} = \varPi (\varvec{u}_k + a_k \hat{g}(\varvec{u}_k)), \end{aligned}$$

(12)

where $\varPi$ is a projection operator to force $\varvec{u}$ to stay in the feasible space, and $\hat{g}$ is the gradient approximation, for which we used the two-sided version:

$$\begin{aligned} \hat{g}_k(\varvec{u}_k) = \left[ \begin{array}{c} \frac{U(\varvec{u}_k + c_k\varDelta _k) - U(\varvec{u}_k - c_k\varDelta _k)}{2c_k\varDelta _{k1}}\\ \vdots \\ \frac{U(\varvec{u}_k + c_k\varDelta _k) - U(\varvec{u}_k - c_k\varDelta _k)}{2c_k\varDelta _{kN}} \end{array} \right] , \end{aligned}$$

(13)

Fig. 3

Illustration of the trajectory generation process in a realistic wind field, for a planning horizon $\varDelta T=20\,$s. Projections on the xy plane for the random sampling initialization, optimized trajectory and final trajectory executed by the UAV are shown. The red star represents the initial position and the map colors shows the vertical component of the wind—with no particular units, the redder being the highest (Color figure online)

where $\varDelta$ is a random vector. Note that, due to the simultaneous perturbation of all the optimization variables, every iteration requires only two evaluations of U, regardless of the optimization space dimension. This is in contrast with other popular stochastic gradient approximation algorithms, such as the Finite Difference Stochastic Approximation (FDSA), which require 2p evaluations, where p is the dimension of the vector $\varvec{u}$. At the same time, under reasonable general conditions, these algorithms achieve the same level of statistical accuracy for a given number of iterations (Spall 2005). This point may be crucial for real-time applications and when the optimization function evaluation is time consuming, as in our case. To ensure the convergence of the algorithm, a simple and popular distribution for the random perturbation vector $\varDelta _k$ is the symmetric Bernoulli $\pm 1$ distribution, and the conditions on the gain sequences $a_k, c_k$ are:

$$\begin{aligned} a_k>0, \,\, c_k>0, \,\, a_k\rightarrow 0, \,\, c_k\rightarrow 0, \nonumber \\ \sum _{k=0}^\infty a_k=\infty , \quad \sum _{k=0}^\infty \frac{a_k^2}{c_k^2} <\infty . \end{aligned}$$

(14)

A standard choice which satisfies the previous conditions is:

$$\begin{aligned} a_k = \frac{a}{(k+1)^\alpha } \quad c_k = \frac{c}{(k+1)^\gamma }. \end{aligned}$$

(15)

Practically effective and theoretically valid values for the decay ratings $\alpha$ and $\gamma$ are 0.602 and 0.101 (Spall 1998). The coefficients a and c are more dependent on the particular problem and their choice significantly affects the optimization result. The parameter c represents the initial magnitude of the perturbations on the optimization variables and, for every variable, we fixed it at $\sim$5% of its maximum range. Lower values would increase the number of required iterations to converge, while higher values would result in instability of the algorithm since the perturbation would not be local anymore. The coefficient a is instead chosen as a function of the desired variation in these variables after the update at early iterations, which can be set at same order of the perturbations. To do this reliably, we use few initial iterations to have a good estimation of the gradient $\hat{g}_k(\varvec{u}_0)$ and we then exploit Eq. (12) to fix a.

3.3 Illustrative examples

Figure 3 shows the different phases of the trajectory generation for one UAV in one planning horizon within a realistic wind field. An xy projection of the trajectories is shown, including the vertical wind prediction at the starting altitude and time. The random sampled trajectories are shown in black, with the best one in blue. The SPSA algorithm then locally optimizes the best trajectory, resulting here in a loop more tightly closed around the center of the updraft (in green). The open-loop executed trajectory is shown in red, following closely the planned trajectory. Only a portion of the optimal trajectory is actually executed before the next planning phase. The utility function in this case is given by $U_{tot}$, with no information term. Its maximization as a function of SPSA iterations is shown in Fig. 4.

Fig. 4

Behavior of $U_{tot}$ over a planning horizon $\varDelta T$ as a function of SPSA iterations

Figure 5 shows some trajectories obtained after a few iterations of the trajectory planning process, in an illustrative two-dimensional case where fictitious current fields and utility maps have been defined so as to ease results visualization and understanding. Here the utility is defined as a scalar map and the optimization function is given by the sum of the utility collected along the trajectory. The figures show the results for both a single and a multi-UAV case. It is clear how the algorithm forces the UAVs to spread to avoid visiting the same locations in the three-UAVs case. When possible, currents are also exploited in order to visit more locations, and so collect more utility, in the same amount of time.

Fig. 5

a one UAV is moving in a 2D environment where a scalar utility map and a wind field are defined. The trajectories initialized by a blind search at every planning-horizon $\varDelta T$ are shown in magenta, and the final trajectories provided by the SPSA algorithm are in red. b 3 UAVs are steered in the same environment to maximize the total utility (only the final trajectories are shown)

4 Integrated simulations

The final objective of the SkyScanner project to experiment the flight of a fleet of drones within actual cumulus clouds is yet to be achieved. Beforehand, intensive simulations are required to assess the validity of the proposed solutions. This section depicts a first integrated simulation architecture, which aims at validating the mapping and planning algorithms. Various results are depicted, focusing in particular on the mapping performance and the learning of the GPR hyperparameters.

4.1 Simulation setup

4.1.1 Cloud model

To validate the mapping and planning algorithms, realistic cloud simulations are required: this is provided by atmospheric models, that can simulate the microphysical, dynamical, optical and radiative properties of clouds.

The atmospheric model used for the current study is Meso-NH (Lafore et al. 1998). This model is the result of the joint collaboration between the national center of meteorological research (CNRM, Météo-France) and Laboratoire d’Aéorologie (LA, UPS/CNRS). Meso-NH is a non-hydrostatic model with the flexibility to simulate atmospheric phenomena at a wide range of resolutions that extends from 1 m up to 10 km. For this work, non-precipitating shallow cumulus clouds over land are simulated with the large-eddy simulations (LES) version of Meso-NH, with resolutions down to 10 m. The simulation was driven by realistic initial conditions obtained on June 21, 1997 from meteorological measurements at the Southern Great Plains site in Oklahoma, USA (Brown et al. 2002). This site is the first field measurement site established by the Atmospheric Radiation Measurement (ARM) Program.

To capture more details about clouds and their surroundings, it is preferable to set the atmospheric model at its highest resolution. The considered simulation domain is a cube of $400\times 400\times 161$ grid points representing a volume of $4\,\text {km} \times 4\,\text {km} \times 4\,\text {km}$ with horizontal resolutions of $dx = dy = 10\,$m, vertical resolutions from $dz = 10$–100 m and a time-step of $0.2\,$s. This setup is a compromise between the desired high resolutions and a reasonable simulation computation time.⁴

The 161 vertical levels have a high resolution of $10\,$m in both convective cloud and surface layers; in the upper cloud-free troposphere, the domain has stretched resolutions from 10 up to 100 m. The upper five layers of the simulation domain act as a sponge layer to prevent wave reflection. In addition, the horizontal boundary conditions are cyclic with a periodicity equal to the horizontal width of the simulation domain. The simulation estimates the following atmospheric variables: cloud liquid water content, water vapor, pressure, temperature, and the three components of wind. Figure 6 illustrates the 3D cloud water content of convective cumulus clouds at a given time. The overall simulation covers a time period of 15 h, but variables of interest have been saved every second only during 1 h that corresponds to the maximum of surface fluxes.

Fig. 6

Meso-NH LES simulation: liquid cloud water content of the cumulus formed at 1h30 PM (ARM Southern Great Plains, June 21, 1997 conditions)

4.1.2 UAV control

For the trajectory planning we choose a simplified aircraft model which, whilst being computationally light, captures the essential characteristics of the flight dynamics necessary to simulate realistic trajectories. The considered UAV is a Mako aircraft, 1.3 m wingpsan tail-less fixed wing airframe (Fig. 7), which model is depicted in “Appendix 1”. The realism of the model relies on two hypotheses. The first one is that the UAVs evolve in wind fields of moderate strength and turbulence, such as in the fair weather conditions in which cumulus clouds form. The second hypothesis is that the trajectories of the UAVs are not overly dynamic, which is consistent with the general design of the UAVs sent by meteorologist for such missions and the selected UAV for the project: dynamic maneuvers indeed degrade the measurements quality, and are not energy efficient.

Fig. 7

Mako aircraft used as a model for the simulations

We assume a constant total airspeed V: the fixed pitch propeller that is used on the aircraft yields a small flight envelope where it works efficiently, and the Paparazzi controls are designed for a fixed airspeed. Trajectories consists of a series of command pairs $(R, P_{in})$, which correspond to time slices during which the commands are constant. Their computation is depicted in “Appendix 2”: R defines the turn radius and direction of the UAV, and $P_{in}$ the power drawn by the motor from the battery. As V is kept constant, all other parameters are bound. To further simplify the dynamics, changes in turn radius and direction between planned steps are assumed to happen instantaneously. Changes in climb rate as a result of a change of propulsive power $P_{in}$ are linear. The key parameters and coefficients are estimated from the analysis of the Mako aircraft selected for field experiments in the SkyScanner project.

Fig. 8

Simulation architecture

4.1.3 Simulation architecture

We tested our planning and mapping framework using a fairly simple simulation architecture, depicted Fig. 8. The planning algorithm optimizes the joint trajectory of all UAVs using the predictions of the GP mapping framework. The resulting control sequences are then sent to the UAVs, which execute them with the dynamic model used to plan the trajectories in open-loop: no trajectory tracking is applied, but the wind ground truth influences the UAV actual motions, which then differ slightly from the planned motions.⁵

A wind sampling process is simulated by adding zero mean and fixed variance Gaussian noise on the wind ground truth. This constant noise model is a simplification of the actual errors made by processes that estimate the wind on board micro UAVs (in Langelaan et al. 2011; Condomines et al. 2015, the errors are indeed Gaussian, but depend of the airspeed—yet in our simulations the aispeed is kept constant).

These wind samples are then fed to the three GP models, each modeling one component of the 3D wind vector. The GP hyperparameter optimization step is performed before each planning iteration.

The whole simulation loop is not real-time, as all steps happen in sequence and no particular attention has been paid to optimize the computing time. In fact, whilst the planning algorithm runs faster than real-time, the hyperparameter optimization step can last up to a few minutes. This costly step has not been finely tuned, and its implementation has not been optimized—all computations were performed using only one core on a i7 3.60 GHz CPU. The simulation framework is implemented in Python, with the exception of the UAV model and the GP mapping framework which are implemented in Cython and C${++}$ for speed purposes. The GP hyperparameter optimization is performed using the basin-hopping algorithm implementation of the SciPy package, with the ‘L-BFGS-B’ algorithm for local bound constrained optimization. Ten local optimization steps are achieved each time. Bounding the hyperparameters allows avoiding completely incoherent solutions, particularly in the beginning of the simulations, and quickens the convergence.

4.1.4 Scenarios

We conducted three sets of simulations corresponding to three different optimization scenarios:

$$\begin{aligned}&\text {All: } U_{tot} = \frac{1}{3}U_E + \frac{1}{3}U_I + \frac{1}{3}U_G\\&\text {No information: } U_{tot} = \frac{1}{2}U_E + \frac{1}{2}U_G\\&\text {No energy: } U_{tot} = \frac{1}{2}U_I + \frac{1}{2}U_G \end{aligned}$$

These scenarios have been chosen to show the possibilities and versatility of the proposed framework, even with simple linear combinations of criteria. For each scenario, a set of 80 simulations were run, with all other parameters remaining the same. The task to achieve is the exploration of an area defined as a box, that spans 400 m in the x and y axes, and which is $20\,$m thick along the z axis and centered at an altitude $z=1.0\,$km. Three identical UAVs start the mission from a unique position located under the center of the box, at an altitude of $800\,$m. The total simulation duration is 5 min. Although all simulations share the same starting point for the UAVs, the initial direction is chosen at random. This, coupled to the fact that the initial map starts empty, results in completely different trajectories and maps after a few dozen of seconds of simulation. Also, we picked a single cloud in the weather simulation to carry our experiments, but the whole weather simulation shares the same properties, and clouds of similar size are very similar. To generate cloud with different properties, one would have to run the weather simulations again with other initial conditions and models, which was not within our reach.

We choose a planning horizon of $\varDelta T=20\,$s with a $dt=1\,$s resolution, but a re-planning is done each $10\,$s, so that only the first half of each planned trajectory is executed. The UAVs airspeed V is set to $15\,$m s$^{-1}$. Planning is done by sampling 200 random perturbations, then performing 400 SPSA algorithm steps. The mapping algorithm tolerance on the time dimension is set to 0.1 or $60\,$s, whichever the longest (see Sect. 2.2). Spatio-temporal length scale hyperparameters $\mathbf {l}=(l_x,l_y,l_z,l_t)$ are bounded between 1 and $e^5 \approx 150\,$m (respectively seconds) and the $\sigma _f$ and $\sigma _n$ parameters are bounded between $\mathrm {e}^{-10}$ and $\mathrm {e}^{10}\,$m (values are expressed as exponentials because GP library optimizes the logarithm of the hyperparameters). In the absence of a precise prior on the $\sigma _f$ and $\sigma _n$ parameters, we chose an interval wide enough to let the hyperparameters optimization step scale them as needed.

Fig. 9

Examples of 3D trajectories of the three UAVs from $t=0\,$s to $t=150\,$s in the ‘No information’ scenario. The vertical wind component ground truth is shown in colors. All UAVs start on the bottom at altitude $0.8\,$km at the beginning of the simulation (Color figure online)

4.2 Results

Figure 9 shows typical trajectories for the three UAVs up to $150\,$s of simulation, in the ‘No Information’ scenario that favors the reduction of energetic expense. A first interesting result is that the planning algorithm allows the UAVs to benefit from updrafts by circling in high vertical wind regions, thus climbing with a lesser energy expense up to the target altitude. The UAVs then manage to stay around the desired altitude: the trajectories are less characteristic here, as the information gathering utility is disabled. The planned trajectories seem quite natural, avoiding unnecessary changes in heading.

4.2.1 Performance of the wind prediction for trajectory planning

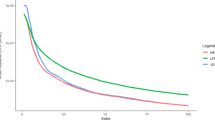
We analyze results for the vertical component of the wind, as it is both the most relevant information for the planning algorithm and the one with the largest amplitude in the Meso-NH simulation. Over all the simulated flights, the sampled values span from −2.8 to $5.0\,$m s$^{-1}$. Figure 10 shows the RMSE of the wind prediction during the planning iterations as a function of time, computed along all the executed trajectories. After an initial stabilization period of about five iterations ($50\,$s), the mean error converges towards $0.5\,$m s$^{-1}$ ($6\%$ relative error), which is quite a good estimate considering the sensors additive Gaussian noise of standard deviation $0.25\,$m s$^{-1}$ (3% relative error). It is also interesting to note that the scenario does not impact significantly the mean error of the GP regression, when considering the mean value over the trajectory. The prediction of the error is also quite good, the standard deviation estimated by the GPP follows a similar pattern as the RMSE (Fig. 11).

Fig. 10

RMSE of the up wind prediction $y_\star$ along the executed trajectory at each iteration, computed over all the iterations of the three scenarios

Fig. 11

Mean of the standard deviation of the up wind prediction $\sqrt{\mathbf {V}[y_\star ]}$ along the executed trajectory at each iteration, computed over all the iterations of the three scenarios

Fig. 12

Mean and variance of the standard normal deviate $\frac{y-y_\star }{\sqrt{\mathbb {V}[y_\star ]}}$ of the up wind prediction along the executed trajectory at each iteration, computed over all the iterations of the three scenarios

Fig. 13

Mean of the standard error of the up wind prediction along the planned trajectory from the current planning time up to 20 s in the future, computed over all the instances of the three scenarios. Top current planning time is $\text {t}=100\,\text {s}$. Bottom current planning time is $\text {t}=290\,\text {s}$

We can further investigate the quality of the prediction by looking at the standard normal deviate, obtained by dividing the (signed) prediction error by the predicted standard deviation (Fig. 12). Here again there is not much difference between the three scenarios: the standard deviation remains approximately constant at $\approx$1.4 $\sigma$, meaning the model has a slight tendency to under-estimate the variance (e.g. the error). In contrast, the mean decreases constantly: at the beginning of the simulations the GP model has a tendency to under-estimate the wind and at the end to slightly over-estimate it. If the first behavior is expected whilst the hyperparameters are being learned with only a few samples, the over-estimation of the wind at the end of the simulations is not expected. This bias may be due to the two following factors: first the time and altitude covariance estimation is relatively poor (see Sect. 4.2.2), and second the vertical wind values below and at $1\,$km are very different, as can be seen Fig. 9. Hence samples gathered at altitudes lower than the final plateau may still influence the prediction of the GP, resulting in a slight positive bias.

Fig. 14

Position error after 10 s of open-loop following of the planned trajectory with respect to the planned end position. Top error on the z axis. Bottom error on the xy axis

Although very little difference can be observed when looking at the average error over the whole planned trajectory for each iteration (Fig. 10), we can see more differences when zooming in on single planning iterations. Figure 13 shows how the prediction error evolves in average along a single planned trajectory as the points are predicted both farther from the current location and, more importantly, farther in the future. Here we can clearly see that the ‘No energy’ scenario comes ahead of the other, especially in the middle of the simulation. However as we are replanning every 10 s, and as the highest difference is on the points farther in the future, the effect is minimal when computing the mean over the first half of the planned trajectories (such as in Figs. 10, 14).

Another indirect way to assess the quality of the mapping is to look at the position error induced by the wind prediction error at the end of each planning iteration. Indeed, as we execute the planned trajectories computed over the predicted wind in open loop, the wind prediction is the sole source of error in the final position of the aircraft. The up wind prediction error induces error in predicting the altitude of the UAV, while the horizontal wind prediction contributes to the horizontal xy position error (Fig. 14). The xy and z position errors are of the same order of magnitude, with an average around $2.5\,$m in both cases, with a standard deviation of about $2.5\,$m, over a constant trajectory length of $150\,$m. The key importance of a good prediction of the up wind is clear: at the start of the simulations, the mean error in altitude is about ten times more than at the end of the simulation, whereas the xy error is only about $1.5\,$m. This is due to the nature of our Meso-NH simulations, which are initialized without advection (that is, no horizontal wind). In real-life cases, one should also estimate independently the mean horizontal wind, even if it varies only very slowly across space and time.

4.2.2 Hyperparameters optimization

The evolution of the hyperparameter values of the GP model are also an indication of the quality and stability of the model. Figure 15 shows 2D histograms of the hyperparameter values, for all simulation scenarios combined, during the course of the simulation. The type of scenario does not impact much the hyperparameter optimization, but all parameters are not estimated equally well. The estimation of the parameter $\sigma _n$ is particularly good and stable, with a median slightly above its actual value (set to $0.25\,$m s$^{-1}$), and a narrow distribution. It is not surprising as the additive noise added to the samples is a pure Gaussian one, and modeled as such. The process variance $\sigma _f$ starts quite high at about 4 to end around 0.5, with the distribution narrowing around the median rapidly as simulation time passes. Considering the GP posterior variance in Eq. (2), we see that the maximal posterior variance is $k(\mathbf {x}_\star ,\mathbf {x}_\star )=\sigma _f^2$. Therefore the process variance indicates the maximum possible predictive uncertainty of the model. As the amplitude of the measurements does not decrease so drastically through time, it seems to indicate that it is not directly the process variance that is optimized. Indeed, as in the second half of the flights the UAVs gather samples in the same area (the plateau at $1\,$km altitude), the type II maximum likelihood [Eq. (4)] used to optimize the hyperparameters overfits the data, which leads to the model being overconfident.

Fig. 15

2D histograms of the values of all GP parameters through time. The median is plotted as a black line

The evolution of the spatio-temporal length scales also exhibits some discrepancies. The length scales in the x and y directions are quite precisely estimated, and seem stable. The $l_x$ hyperparameter converges in most cases to a value between 30 and 40 m, the $l_y$ parameter distribution being a bit wider, with the median around 40–50. Both hyperparameters show distributions peeking around the median and densely packed, indicating convergence towards a common value. On the other hand the vertical length scale $l_z$ and the temporal length scale $l_t$ exhibit a completely different behavior. The distributions remain very spread out in both cases. For a significant proportion of the simulations, the values are set to the upper bound given to the optimizer, indicating that the GP model is unable to estimate them properly. Even after 5 min, about $2\%$ of the simulations still have a maximum value for the $l_t$ parameter, and more than $20\%$ of the simulations exhibit this behavior for the $l_z$ parameter. This failure to estimate properly the time and altitude correlations is most probably caused by a problem of observability. As a matter of fact, the UAVs rapidly explore the x and y axis, and change altitude much slower. In addition, the time correlations are more difficult to estimate because time is the only dimension upon which the UAVs have no control: good estimation of this parameter is dependent on the frequency at which UAVs go back to a similar location in space. It is also possible that temporal correlations cannot be well fitted with our choice of model.

It should be noted that, as we have seen, the failure to extract some of the underlying processes parameter does not induce bad prediction performances: on the contrary, the model adapts the parameters to keep a good predictive accuracy. This problem could be mitigated by keeping more samples in the model, or more interestingly by defining utility measures that lead to a more informative sampling for the hyperparameter optimization (as opposed to gathering information for map exploration purpose only). Finally, one could modify the GP model to account for the particular nature of the temporal dimension, either by developing a more appropriate kernel or by encoding the temporal dimension within a meta-model.

4.2.3 Impact of weights in the utility function

While the definition of the scenario does not affect much the GP prediction, it strongly impacts the way the mission is achieved.

Starting with the “explore-box” objective, the UAVs have no trouble staying in the xy bounds of the box, but the choice of weights on the combination affects how they reach and stay in the z bounds (Fig. 16). When the optimization of energy is disabled (‘No energy’ scenario), the UAVs go faster to a mean altitude of $1\,$km (the center of the box), staying until the end of the simulation a bit above. Standard deviation lies equally on both sides of the $1\,$km mark. On the contrary when the information gain utility is disabled (‘No information’ scenario), the $1\,$km altitude is reached later and the mean altitude then starts to slowly decrease until the end of the simulation: the UAVs have difficulties maintaining their altitude because of the associated energy expense. We see the same effect when all utilities are equally weighted, although the mean altitude is a bit higher, allowing the UAVs to explore a larger portion of the box. Interestingly, when the energy utility is turned on, the mean altitude’s variance starts decreasing after the first half of the simulation. It can be explained by the fact that, once the box is sufficiently explored, the absolute value of the information gain decreases up to a point where it does not counterbalance the energetic expense anymore, forcing the UAVs to lose altitude.

The impact of the energy optimization on the battery level is shown in Fig. 17. Optimizing the energy saves on average 4% percent of the battery level at the end of the simulation in the ‘All’ scenario and 5% in the ‘No information’ scenario as opposed to the ‘No energy’ one. Considering that the ‘No information’ scenario consumes just under 20% of the battery on average, the relative gain is respectively 20 and 25%. When looking at the progression of the battery level throughout the simulation, it is clear that even though the difference in battery savings is higher during the ascension phase (0–1 min), optimizing energy consumption is helpful throughout the whole mission to save battery.

Fig. 16

Mean altitude of the UAVs through time for all three scenarios. The standard deviation is plotted in dashed lines of the same color (Color figure online)

Fig. 17

Evolution of the battery level. Top Mean of the battery level through the simulation, over all instances of the three scenarios. The standard deviation is plotted in dashed lines of the same color. Bottom Box and violin of the battery level at the end of the simulation, for all three scenarios. Whiskers at 9th and 91th percentiles, the red square mark indicates the mean (Color figure online)

The information gain is more difficult to assess: we have already seen that optimizing this utility impacts only a little the predictive power of the GP for the planning purpose and not at all the quality of the hyperparameter optimization. Also, as old samples are discarded in the model and the observed process is dynamic, it is difficult to compute a total amount of gathered information. Nevertheless one can look at the RMSE of the prediction computed on the whole “mission-box” at the end of the simulation (Fig. 18). Unsurprisingly there is little difference between the three scenarios: at the end of the mission, they all perform well enough. The limited temporal validity of the samples (due to the weather dynamics) and the instability of some hyper-parameters weigh heavily on the results. However the “No energy” is still indubitably statistically better than the other two scenarios, even if the absolute difference remains small (under 0.1 m s$^{-1}$ between medians).

Fig. 18

Box and violin plot of the RMSE of the prediction over the box defining the mission, at the end of the simulation ($\text {t}=300\,\text {s}$), over all instances of the three scenarios. The box is sampled at a spatial resolution of 10 m, and the GP predictions on the samples at $\text {t}=300\,\text {s}$ are compared with the ground truth

Fig. 19

Top Cumulative distributions of values in the covariance matrices of all three scenarios between 50 and $100\,$s, in percents. Bottom distances between the cumulative distributions of values in the covariance matrices of the ‘no information’ and the other scenarios. Values smaller than $10^{-2}$ represent respectively 10 and 20% more space in the covariance matrices of ‘All’ and ‘No energy’ scenarios than the in the ‘No information’ scenario (note the abscissas have a logarithmic scale)

Another way to approach this is to look directly at the covariance matrices. Figure 19 illustrates the differences in density of the covariance matrices of the GP models by plotting the cumulative distribution of values in the matrices in each scenario. The smaller the values, the more information the matrices contain (the more the samples are considered independent). It is clear that optimizing the information gain utility has a direct effect on the density of the matrix: when we plot the distance of the other distributions to the one of the “No information” scenario, there is up to $10\%$ more values smaller than $10^{-2}$ in the “All” scenario, and $20\%$ for the “No energy” one. In other words, the “No energy” scenario has half of the values in the covariance matrix under $10^{-2}$ whereas the “No information” one has only thirty percent, which is about a 65% relative increase. This result is also interesting to speed up the GP regression. Indeed if one were to use compact support kernels, the resulting matrices would become sparser with the information gathering utility, thus potentially speeding up the linear algebra computations.

5 Discussion

5.1 Summary

We have presented an approach to drive a fleet of information gathering UAVs to optimize the acquisition of information in a given area, while minimizing the energy expenses. The approach generates flight patterns that properly exploit the updrafts and generate accurate wind maps.

In particular, we have shown how a GPR framework can be used online to faithfully map wind fields corresponding to realistic cloud simulations. The resulting predictions are accurate enough to drive the team of UAVs during the course of the mission. A careful inspection of the resulting GP model, in particular of its hyperparameters, has shown its strengths and weaknesses. The predictive error of the GP model is quite low during the mission, resulting in negligible positional errors after the execution of the planned trajectories, and regardless of failures to estimate properly the underlying hyperparameters of the process. The proposed simulations exploit realistic wind and aircraft models, address the main task that atmosphere scientists expect from a fleet of UAVs, and exhibit the properties of the approach.

5.2 Future work

Numerous improvements remain to be addressed in order to define an efficient operational system.

The mapping framework would certainly benefit from better priors. A prior on the mean could in particular be provided by a macroscopic model of the cumulus cloud, which relates high level variables such as mean updraft as a function of the cloud base diameter for instance. The macroscopic model could also exhibit various regions in the cloud, within which priors on the hyperparameters could help to learn them more rapidly and more precisely. Furthermore, one should be able to explicit and exploit the correlations between the various atmosphere variables that the UAVs can measure, correlations that are pretty well known by atmosphere scientists (e.g. between the liquid water content and the vertical wind). One would need to resort to multi-task GPR for this purpose (Chai 2010). Finally the temporal dimension should be more carefully accounted for, either by using a more appropriate kernel or as a parameter of a separate meta-model.

We have seen that the hyperparameter estimation can suffer from lack of observability. Deriving a utility measure aiming at maximizing information gain for their estimation would certainly improve the accuracy of the model. Another way to stabilize the hyperparameters would have the UAVs perform predefined synchronized measurements, for instance at different altitude levels, when the system detects a too important variability of the parameters.

As for trajectory planning, using more complex utility measure definition than a simple linear combination would allow the UAVs to achieve more complex tasks and to take into account specific preferences defined by the user. Additional criteria and constraints (such as anti-collision) should also be considered. Finally, there remain various free parameters in the system (planning horizon, planning resolution, sampling rate...), that have been manually set: they could be learned online during the mission.

Finally, an overall integrated system architecture is yet to be defined. We foresee an approach that casts the problem in a hierarchy of two modeling and decision stages. A macroscopic parametrized model of the cloud, updated from the gathered data, would provide to the ground operator a coarse description akin to Fig. 1. He would then tasks the fleet with information gathering goals such as “map the top of the cloud”, “assess updraft currents over the whole cloud height”, “quantify the convection flux at the cloud base”, “monitor the liquid water content within a given area and time lapse”, etc. Given the required tasks and the current fleet situation (the UAVs positions, their on-board energy level, and their sensing capacities), a high-level decision process allocates UAVs to each task. This two tier approach would break the overall complexity of the problem, and allows the operator to task the fleet with high level goals, which are then achieved autonomously and independently by sub-teams of UAVs, using the mapping and trajectory planning approaches proposed in this paper.

We believe that deploying such a fleet within a distributed architecture remains far-fetched, and that a centralized architecture would provide more benefits than drawbacks. GP regression and hyperparameter learning are intensive computing tasks, that can for now hardly be embedded on-board lightweight UAVs. An approach in which all the gathered data are sent down to a powerful ground station that executes both the mapping and fleet control processes is a realistic option: only a very low bandwidth data link would be required for both the data reception and command transmission. Furthermore, the overall system would benefit from the use of a ground atmosphere radar, that would provide real-time estimations of some global cloud parameters such as its geometry, which directly conditions the amplitude of updrafts for instance. Such a system would also allow to update the position of the cloud: indeed most cumulus clouds develop in conditions with significant advective (lateral) wind.⁶ The cloud simulations we exploited have been generated in the absence of such advective wind, and the cloud map is built in a geo-referenced frame, whereas in real flights one should map the cloud in a cloud relative reference frame, which evolution would be provided by the radar.

Appendices

Appendix 1: Aircraft model

In this Appendix, we provide the details of the flight dynamics model adopted for this work. We consider a simplified aircraft model to enable fast trajectory computations, but still able to capture the essential characteristics of the flight mechanics for a realistic trajectory optimization simulation. The key parameters and coefficients used for the analytical calculations are estimated from a modified vortex-lattice analysis (Bronz et al. 2013) of the aircraft.

In particular, we consider the Mako aircraft shown in Fig. 7, which will be employed for future experiments within the SkyScanner project. Table 1 shows its general aerodynamic and geometrical specifications.

Table 1 General aerodynamic and geometrical specifications of the Mako aircraft

The trajectory computation is based on two control inputs: the power input $P_{in}$ and the turn radius R. The airspeed V is considered constant, therefore the angle of attack is kept fixed for simplification. The trajectory optimization mainly requires the drag force evaluation, which has to be compensated by the input power. Note the air density is kept constant during the simulations, again for the sake of simplicity.

In order to calculate the performance within the flight envelope, the flight phases are isolated as steady banked turn and constant climb. The climb calculations derived from energy equations, the pull-up and down transition phases are approximated according to the maximum lift capability limit.

Fig. 20

Forces applied during the steady banked turn phase (left) during the steady climb phase (right)

1.1 Steady banked turn phase

During the steady banked turn phase, the vertical component of the lift force $L_v$ is equal to the weight of the aircraft and its lateral component $L_h$ compensates the centrifugal force as shown in Fig. 20.

$$\begin{aligned} \sum F_z = 0 \Rightarrow W = L_v = L \cos \phi \end{aligned}$$

(16)

For a given bank angle $\phi$, the load factor n, given by

$$\begin{aligned} n&= \frac{L_v}{W} = \frac{L}{L \cos \phi } = \frac{1}{\cos \phi }, \end{aligned}$$

(17)

has to be accounted for in the lift force, which can then be expressed as:

$$\begin{aligned} L = \frac{1}{2} \rho V^2S_{ref}(nC_L) \; [C_{L_{max}} > nC_L], \end{aligned}$$

(18)

with drag coefficient and resultant drag force being

$$\begin{aligned}&C_D = C_{D_0} + k(nC_L)^2 \quad \quad \text {where} \quad \quad k = \frac{1}{\pi AR e} \end{aligned}$$

(19)

$$\begin{aligned}&D =\frac{1}{2}V^2S_{ref}C_D \end{aligned}$$

(20)

in oder to take into account the additional drag contribution coming from the induced lift force.

1.2 Rate of Climb (ROC) and power consumption

To maintain level flight, the required aerodynamic power is

$$\begin{aligned} P_{aero} = DV \end{aligned}$$

(21)

Incorporating the thrust, we can calculate the climb rate of the aircraft as:

$$\begin{aligned} ROC = V_{climb} = V\frac{(T-D)}{W} = \frac{P_{prop} - P_{aero}}{W} \end{aligned}$$

(22)

The maximum propulsive power is limited according to the specifications of the propulsion system used, whose efficiency $\eta _p$ results in a higher power drawn from battery: ${P_{prop} = \eta _p P_{in}}$, where $P_{in}$ is the input power drawn from the battery. The resulting $V_{climb}$ is then:

$$\begin{aligned} V_{climb} = \frac{\eta _p \times P_{in} - P_{aero}}{W}. \end{aligned}$$

(23)

The total propulsion system efficiency varies, as it is related to the flight speed and generated thrust force: a fine modeling of these variations would be required for a precise propulsion model. However, comparing electrical power input $P_{in}$ versus aerodynamic power output $P_{aero}$ shows that a linear relation is a fairly accurate model for the considered flight speeds range, as shown in Fig. 21. This fact is exploited to define the total propulsion efficiency $\eta _p$ in our simulation model.

Fig. 21

Resultant propeller aerodynamic power from battery input power for three different flight speeds

1.3 Pull-up and pull-down

The transition from level flight to steady climb is achieved by a short pull-up flight maneuver. Likewise, a pull-down flight maneuver is used to transition from level flight to steady descend phase. In our simplified aircraft model, as the flight angle of attack is assumed constant at all times, the distinction between climb and descent transitions is defined by the given power input $P_{in}$: if $P_{in} \times \eta _{p}$ is higher than the required level flight aerodynamic power $P_{aero}$, then the aircraft climbs.

The pitch turn radius can be calculated as:

$$\begin{aligned} R_{up} = \frac{V^2}{g (n-1)}, \quad R_{down} = \frac{V^2}{g (n+1)} \end{aligned}$$

(24)

where the contribution of the total aircraft weight is in the $(n-1)$ and $(n+1)$ terms. As the angle of attack is constant, the pitch rate $\dot{\gamma }$ is given by:

$$\begin{aligned} \dot{\gamma }= \pm \frac{V}{ R_{up/down}} \end{aligned}$$

(25)

Appendix 3: Trajectory computation

Assuming a fixed airspeed V, a steady turn radius R and input power $P_{in}$, the trajectory can be computed by separating it in a pull-up (or pull-down) phase and a steady phase. Pull-up and pull-down phases are executed assuming a maximal allowed bank angle, thus assuring that the maximal allowable load factor will not be exceeded. First we compute the maximum allowed load factor $n_{max}$:

$$\begin{aligned} C_L&= \frac{2 * W}{\rho V^2 S_{ref} } \end{aligned}$$

(26)

$$\begin{aligned} n_{max}&= \frac{C_{Lmax}}{C_L} \end{aligned}$$

(27)

Using Eq. (23), $V_{climb}$ can be obtained from $P_{aero}$ and $P_{in}$. This value represents the target value for vertical velocity for given $P_{in}$ and R. The climb rate $\gamma (t)$ can then be computed as:

$$\begin{aligned}&\varDelta _\gamma = \text {arcsin}(V_{climb}/V) - \gamma (0) \end{aligned}$$

(28)

$$\begin{aligned}&u = \text {sign}(\varDelta _\gamma )\end{aligned}$$

(29)

$$\begin{aligned}&R_{up/down} = \frac{V^2}{g*(n_{max}-u)} \end{aligned}$$

(30)

$$\begin{aligned}&\dot{\gamma }= \frac{uV}{R_{up/down}} \end{aligned}$$

(31)

$$\begin{aligned}&\varDelta _{tpull}(t) = min(t, \frac{ \varDelta _\gamma }{ \dot{\gamma }}) \end{aligned}$$

(32)

$$\begin{aligned}&\gamma (t) = \gamma (0) + \dot{\gamma }\varDelta _{tpull}(t) \, \end{aligned}$$

(33)

where $\varDelta _{tpull}(t)$ represents the duration of the pull up or pull down phase. Finally we can compute the projection on the z axis of the path on the $R_{up/down}$ circle during the pull phase, and assume a constant vertical velocity during the remaining time:

$$\begin{aligned}&\varDelta _{zpull}(t) = u R_{up/down}(\cos \gamma (0) - \cos \gamma (\varDelta _{tpull}(t))) \end{aligned}$$

(34)

$$\begin{aligned}&z(t)= \varDelta _{zpull}(t) + V_{climb}(t-\varDelta _{tpull}(t)) \end{aligned}$$

(35)

Knowing the vertical velocity, and assuming a constant total velocity V and turn radius R, we finally compute x(t) and y(t) using the change in the heading $\psi$ to project the position on a circle of radius R tangent to the horizontal velocity vector. We first compute the heading $\psi (t)$:

$$\begin{aligned} \dot{\psi }(t)&= \frac{V_H(t)}{R} \end{aligned}$$

(36)

$$\begin{aligned}&= \frac{V}{R}\cos \gamma (t) \end{aligned}$$

(37)

$$\begin{aligned} \varDelta _{\psi }(t)&= \int _0^{t} \dot{\psi }(x) dx \end{aligned}$$

(38)

$$\begin{aligned}&= \frac{V}{R}(\sin \gamma (\varDelta _{tpull}) - \sin \gamma (0)) + \gamma (\varDelta _t)(t-\varDelta _{tpull}) \end{aligned}$$

(39)

$$\begin{aligned} \psi (t)&= \psi _0 + \varDelta _\psi (t) \end{aligned}$$

(40)

Using $\psi (t)$ we deduce the xy position of the aircraft:

$$\begin{aligned} \begin{pmatrix} x \\ y \end{pmatrix} (t)&= \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + R\begin{pmatrix} -\sin (\psi _0) + \sin (\psi (t))\\ +\cos (\psi _0) - \cos (\psi (t)) \end{pmatrix} \end{aligned}$$

(41)

Finally, the remaining capacity of the battery J(t) (in joules) is:

$$\begin{aligned} J(t)&= J(0) - \int _0^t P_{in}(x)dx = J(0) - P_{in}t. \end{aligned}$$

(42)