1 Introduction

Since 1998, we have a strong belief that our universe experiences an accelerated expansion. The various astronomical data obtained from SNe Ia (Perlmutter et al. 1999), WMAP (Bennett et al. 2003), SDSS (Tegmark et al. 2004) and X-ray (Allen et al. 2004) experiments support this cosmic acceleration. In the framework of standard cosmology, a dark energy component with negative pressure is necessary for this acceleration. The dark energy scenario is one of the most popular research areas in modern cosmology. Up to now many theoretical models have been suggested to interpret the treatment of dark energy. The earliest and simplest one is the Einstein’s cosmological constant with the time—independent equation of state w Λ=−1. The cosmological constant suffers from tow deep theoretical problems namely the “fine-tuning” and “cosmic coincidence”. In addition to cosmological constant, dynamical dark energy model with time-varying equation of state have been investigated to interpret the cosmic acceleration. The scalar field models such as quintessence (Wetterich 1988; Ratra and Peebles 1988), phantom (Caldwell 2002; Nojiri and Odintsov 2003a, 2003b), quintom (Elizalde et al. 2004; Nojiri et al. 2005; Anisimov et al. 2005), K-essence (Chiba et al. 2000; Armendáriz-Picón et al. 2000, 2001), tachyon (Sen 2002; Padmanabhan 2002; Padmanabhan and Choudhury 2002) and dilaton (Gasperini et al. 2002; Arkani-Hamed et al. 2004; Piazza and Tsujikawa 2004) together with interacting dark energy models such as holographic (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006, 2007a, 2007b, 2007c, 2007d, 2007e) and agegraphic (Cai 2007; Wei and Cai 2008) models are the examples of dynamical dark energy models.

The interesting approach of the nature of dark energy is considering it as an issue of quantum gravity (Witten 2000). The holographic dark energy (HDE) is constructed based on the holographic principle in quantum gravity (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006, 2007a, 2007b, 2007c, 2007d, 2007e). In holographic principle, a short distance ultra-violet (UV) cut-off is related to the long distance infra-red (IR) cut-off, due to the limit set by the formation of a black hole (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006, 2007a, 2007b, 2007c, 2007d, 2007e). Based on the holographic principle, Cohen et al., indicated that the zero-point energy of a system with size L should not be exceed from the mass of black hole with the same size, i.e.,

(1)

where L is the UV cut-off and m p is the reduced plank mass. From the above relation, the energy density of HDE in cosmology can be described as

(2)

where c 2 is a numerical constant of order unity. The HDE model has been constrained by various astronomical observation (Huang and Gong 2004; Zhang and Wu 2005; Wu et al. 2008; Ma and Gong 2009; Enqvist et al. 2005; Shen et al. 2005; Kao et al. 2005) and also investigated widely in Huang and Li (2004), Ito (2005), Enqvist and Sloth (2004), Huang and Li (2005), Pavon and Zimdahl (2005), Wang et al. (2005), Kim et al. (2006), Nojiri and Odintsov (2006), Elizalde et al. (2005), Hu and Ling (2006), Li et al. (2006), Setare (2006, 2007f), Saridakis (2008a, 2008b, 2008c), Setare and Vagenas (2008, 2009). If we consider L as a Hubble length H −1, in this case, the accelerated expansion of the universe can not be achieved and we get a wrong equation of state for HDE model (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006, 2007a, 2007b, 2007c, 2007d, 2007e). However, by considering the interaction between dark matter and dark energy, one can derive the accelerated expansion of the universe and solve the coincidence problem for HDE model under Hubble length scale H −1 Pavon and Zimdahl (2005), Zimdahl and Pavon (2007). In the case of particle horizon, the HDE model can not also obtain the cosmic acceleration (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006, 2007a, 2007b, 2007c, 2007d, 2007e), but this model with event horizon can derive the accelerated expansion of the universe (Li 2004). Therefor we consider the event horizon as an IR cut-off for HDE model as

(3)

The coincidence problem has been solved in HDE model with event horizon (Li 2004). This model also stable from the view point of perturbational theory (Li et al. 2008, 2010a, 2010b; Hogan 2007a, 2007b; Lee et al. 2007, 2009; Li and Wang 2010). The parameter c 2 in HDE model has an essential rule in characterizing the properties of HDE model. For example, the HDE model can behave as a phantom or quintessence dark energy models at the future for the values of c 2 bigger or smaller than 1, respectively. In the standard HDE model the parameter c 2 is constant respect with cosmic time. However there are no strong evidences telling us that c should be a constant parameter. In general the term c 2 can be assumed as a function of time. By slowly vary function with time, \(\dot{(c^{2})}/c^{2}\) is upper bounded by the Hubble expansion rate, i.e.,

(4)

In this case the time scale of the evulsion of c 2 is shorter than H −1 and one can be satisfied to consider the time dependency of c 2 (Radicella and Pavon 2010). Also, it has been shown that the parameter c 2 can not be constant for all times during the evolution of the universe (Radicella and Pavon 2010). The holographic dark energy with time varying c 2 at the Hubble length has been studied in Duran and Parisi (2012). It has been shown that the interacting model of dark energy in which the coincidence problem is alleviated can be recast as a noninteracting model in which the holographic parameter c 2 evolves slowly with time (Duran and Parisi 2012). The HDE model with time varying c 2, the so-called generalized holographic dark energy (GHDE), has been constrained by astronomical data (Zhang et al. 2012). In GHDE with event horizon, the energy density od dark energy is given by

(5)

It has been shown that the GHDE model can interpret the phantom, quintessence and cosmological constant models, depending on the parameter c(z). This generalization has also been done for holographic Ricci dark energy model (Wi 2009).

Motivated by the above studies, we consider the GHDE model described by event horizon and obtain the cosmological evolution of the model in FRW cosmology. Also we apply the statefinder diagnostic for GHDE model. Since the Hubble parameter, \(H=\dot{a}/a\), (first time derivative) and the deceleration parameter \(q=-\ddot{a}H^{2}/a\) (second time derivative) can not discriminate the model, we need a higher order of time derivative of scale factor. Sahni et al. (2003) and Alam et al. (2003), by using the third time derivative of scale factor, introduced the statefinder pair {s,r} in order to diagnostic the treatment of dark energy models. The statefinder pair in spatially flat universe is given by

(6)

The statefinder parameters s and r are the geometrical parameters, because they only depend on the scale factor. Up to now, different dark energy models have been investigated from the viewpoint of statefinder diagnostic. These models have different evolutionary trajectories in {s,r} plane, therefore the statefinder tool can discriminate these models. The well known ΛCDM model corresponds to the fixed point {s=0,r=1} in the s–r plane (Sahni et al. 2003). The distance of the current value of statefinder pair {s 0,r 0} of a given dark energy model from the fixed point {s=0,r=1} is a valuable criterion to examine of model.

Here we list the following dark energy models which have been studied from the viewpoint of statefinder diagnostic: the quintessence DE model (Sahni et al. 2003; Alam et al. 2003), the interacting quintessence models (Zimdahl and Pavon 2004; Zhang 2005a), the holographic dark energy models (Zhang 2005b; Zhang et al. 2008), the holographic dark energy model in non-flat universe (Setare et al. 2007), the phantom model (Chang et al. 2007), the tachyon (Shao and Gui 2008), the generalized Chaplygin gas model (Malekjani et al. 2011a), the interacting new agegraphic DE model in flat and non-flat universe (Zhang et al. 2010; Khodam-Mohammadi and Malekjani 2010), the agegraphic dark energy model with and without interaction in flat and non-flat universe (Wei and Cai 2007; Malekjani and Khodam-Mohammadi 2010), the new holographic dark energy model (Malekjani et al. 2011b), the interacting polytropic gas model (Malekjani and Khodam-Mohammadi 2012a) and the interacting ghost dark energy model (Malekjani and Khodam-Mohammadi 2012b).

In this work first we study the cosmological evolution of GHDE model by calculating the evolution of cosmological quantities EoS and deceleration parameters. Then we investigate this model from the viewpoint of statefinder diagnostic.

2 GHDE model in FRW cosmology

In the context of flat Friedmann-Robertson-Walker (FRW) cosmology, the Friedmann equation is given by

(7)

where H and m p are the Hubble parameter and the reduced Planck mass, respectively.

By using the dimensionless energy densities

(8)

the Friedmann equation (7) can be written as

(9)

The conservation equations for dark matter and dark energy are given by

(10)
(11)

Taking the time derivative of Friedmann equation (7) and using (9), (10), (11), one can obtain

(12)

Taking the time derivative of (5) and using (12), \(\dot{R_{h}}=1+HR_{h}\), from (11), we obtain the equation of state for GHDE model as follows

(13)

where prime is derivative with respect to x=lna. In terms of cosmic redshift, we have d/dx=−(1+z)d/dz. Taking the derivative with respect to x=lna, we obtain

(14)

where c (2)=d 2 c/dx 2. Also, taking the time derivative of \(\varOmega_{d}=\rho_{d}/\rho_{c}=\frac{1}{H^{2}R_{h}^{2}}\) we obtain the evolutionary equation for dark energy density for GHDE as follows

(15)

Using (12)and (13), the deceleration parameter q which represents the decelerated or accelerated phase of the expansion of the universe, for GHDE model can be calculated as

(16)

In the limiting case of constant parameter c (i.e., c′=0) all of the above equations reduce to those obtained for original holographic dark energy (OHDE) model in Zhang (2005b).

For complexness, we now derive the statefinder parameters {s,r} in GHDE model. For this aim, by time derivative of (12), we first obtain

(17)

Inserting (12)and (17) in \(r=\ddot{H}/H^{3}+3\dot{H}/H^{2}+1\), we obtain the following equation for the parameter r:

(18)

The statefinder parameter \(s=(1-r)/(9/2+3\dot{H}/H^{2})\) is also obtained as follows

(19)

Putting (13), (14) and (15) in (18) and (19) yields the following relations for statefinder parameters of GHDE model:

(20)

and

(21)

where c (2)=d 2 c/dx 2.

In the next section we give a numerical description of the evolution of GHDE model by solving (13), (15), (14), (16), (20), (21). Here we consider the model parameter c(z) of GHDE as a function of redshift as follows

(22)

The above choice for c(z) is inspired by the parameterizations known as Chevallier-Polarski-Linder (CPL) (Chevallier and Polarski 2001; Linder 2003). At the early time (z→∞), we have c→c 0+c 1 and at the present time (z→0), c→c 0. Therefore the model parameter c varies smoothly from c 0+c 1 to c 0 from past to present. By the above choice, the first and second derivative of c, i.e., c′ and c (2) are

(23)

respectively. Assuming the positive energy density of GHDE model at any time yields the following conditions for c 0 and c 1:

(24)

3 Numerical results

Here we calculate the evolutionary behavior of GHDE model in FRW cosmology. We first obtain the evolution of EoS parameter as well as the deceleration parameter. Then we perform the statefinder diagnosis and w−w′ analysis for this model. In numerical procedure we set Ω m =0.30 and Ω d =0.70.

3.1 EoS parameter

By solving (13) and using (22), (23) for different model parameters c 0 and c 1, we show the evolution of EoS parameter of GHDE as a function of redshift in Fig. 1. In upper panel we fix the parameter c 1=0.10 and vary the parameter c 0=0.25, 0.5, 0.75 corresponds to the solid-blue, dashed-black and dotted-dashed-red curves, respectively. Here we see that the GHDE model enters the phantom regime without a need for interaction between dark matter and dark energy. Also, it is worthwhile to mention that the GHDE model crosses that phantom line (w d =−1) from up (w d >−1) to below (w d <−1). This behavior of GHDE model is in agreement with recent observations (Alam et al. 2004; Huterer and Cooray 2005; Wang and Tegmark 2005). By increasing the parameter c 0 the phantom regime can be achieved later. In lower panel, by fixing c 0=0.70, we vary the parameter c 1=−0.10,0.00,0.10 corresponds to dashed-black, solid-blue and dotted-dashed-red curves, respectively. The solid-blue curve indicates the original holographic dark energy model (OHDE). One can conclude that for c 1<0 the GHDE model can cross the phantom line earlier and for c 1>0 cross the phantom line later compare with OHDE model. It should be noted that the above illustrative values for c 0 and c 1 should satisfy the conditions in (24).

Fig. 1
figure 1

The evolution of EoS parameter of GHDE model, w d , versus redshift parameter z for different values of model parameters c 0 and c 1. In upper panel, by fixing c 1, we vary c 0 as indicated in legend. In lower panel, by fixing c 0 we vary the parameter c 1 as described in legend

Full size image

3.2 Energy density

Here we calculate the evolution of energy density of GHDE model as a function of redshift parameter from the early time up to late time by solving (15). The evolution of parameters c and c′ are given by (22) and (23), respectively. In Fig. 2, we plot the evolution of energy density Ω d versus of redshift for different values of model parameters c 0 and c 1. We see that at the early times Ω d →0 and at the late times Ω d →1, means the dark energy dominated universe at the late time. In upper panel by fixing c 1=0.10 the parameter c 0 is varied as illustrative values 0.25, 0.50, 0.75 corresponding to solid-blue, dashed-black and dotted-dashed-red curves, respectively. We see that in the past times the dark energy becomes more dominant for larger values of c 0 and at the late times the dark energy dominated universe can be achieved sooner for lower values. In lower panel by fixing c 0=0.70 the parameter c 1 is varied as illustrative values −0.10,0.00,0.10 corresponding to dashed-black, solid-blue and dotted-dashed-red curves, respectively. It has been seen that the dark energy becomes more dominant for positive values of c 1 and less dominant for negative values compare with OHDE model.

Fig. 2
figure 2

The evolution of dark energy density of GHDE model as a function of redshift z. In upper panel, by fixing c 1, we vary c 0 as indicated in legend. In lower panel, by fixing c 0 we vary the parameter c 1 as described in legend

Full size image

3.3 Deceleration parameter

Here we study the expansion phase of the universe by calculating the evolution of deceleration parameter q in GHDE model. By solving (16) and using (15), we plot the evolution of q versus redshift parameter z in Fig. 3. In both panels we see that the parameter q start from q=0.50, representing the CDM model at the early time. Then the parameter q becomes negative, representing the accelerated expansion phase of the universe at recent epochs. Therefore the GHDE model can interpret the decelerated phase of the expansion of the universe at the early times and accelerated phase later. In upper panel we fix the parameter c 1=0.1 and vary the parameter c 0=0.25,0.50,0.75 corresponding to solid-blue, dashed-black and dotted-dashed-red curves, respectively. By increasing c 0, the accelerated expansion can be achieved sooner. In lower panel, we fix c 0=0.70 and vary c 1=−0.10, 0.0, 0.10, corresponding to dashed-black, solid-blue and dotted-dashed-red curves, respectively. The solid-blue curve indicate the OHDE model. We see that negative values of c 1 result the larger accelerated expansion at the present time and positive values of c 1 obtain the smaller accelerated expansion, compare with standard OHDE model.

Fig. 3
figure 3

The evolution of deceleration parameter q in the context of GHDE model as a function of redshift parameter z for different illustrative values of model parameters c 0 and c 1. In upper panel, by fixing c 1, we vary c 0 as indicated in legend. In lower panel, by fixing c 0 we vary the parameter c 1 as described in legend

Full size image

3.4 Statefinder diagnosis

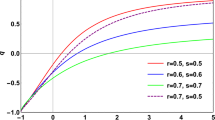
The statefinder pair {s,r} for GHDE model is given by (20) and (21). In statefinder plane, the horizontal axis is defined by the parameter s and vertical axis by the parameter r. In Fig. 4, by solving (21) and (20) and using (22), (23), (24), we obtain the evolutionary trajectories of GHDE model in s–r plane. In both panels, by expanding the universe, the evolutionary trajectories evolve from right to left. The parameter r increases and the parameter s decreases. The trajectories cross the ΛCDM fixed point {s=0,r=0} at the middle of evolution. In upper panel we fix the parameter c 1=0.10 and vary the parameter c 0=0.25,0.50,0.75 corresponding to the solid-blue, dashed-black and dotted-dashed-red curves, respectively. We see that different values of model parameter c 0 result different trajectories in s–r plane. Therefore the GHDE model in s–r plane is discriminated for different values of model parameter c 0. The colored circles on the curves represent the today’s value of statefinder parameters {s 0,r 0} of the model. We also see that for larger values of c 0, the distance of {s 0,r 0} from the ΛCDM fixed point is shorter. In lower panel, the parameter c 0 is fixed by c 0=0.70 and the parameter c 1 is varied by c 1=−0.10, 0.00, 0.10, respectively, corresponding to the dashed-black, solid-blue and dotted-dashed-red curves. Same as upper panel the GHDE model mimics the ΛCDM model at the middle of evolution. The GHDE model can be discriminated by model parameter c 1 in s–r plane. Different values of c 1 result different evolutionary trajectories. The solid blue curve indicate the OHDE model. We see that for positive values of c 1, the distance of {s 0,r 0} from ΛCDM fixed point is shorter and for negative values of c 1 is longer than standard OHDE model.

Fig. 4
figure 4

The evolutionary trajectories of GHDE model in s–r plane for different values of model parameters c 0 and c 1 as indicated in legend

Full size image

4 Conclusion

Summarizing this work, we studied the new version of holographic dark energy model, the so-called generalized holographic dark energy (GHDE), in which the model parameter c 2 is considered as a time-varying function. Here we considered the CPL parameterizations in which c(z)=c 0+c 1 z/(1+z) (Chevallier and Polarski 2001; Linder 2003). We first investigated the cosmological evolution of GHDE model by calculating the evolution of EoS and deceleration parameters. We showed that for negative values of c 1 the phantom regime can be achieved sooner and for positive values later compare with original holographic model (OHDE). In agreement with recent observation (Alam et al. 2004; Huterer and Cooray 2005; Wang and Tegmark 2005), we show that the phantom line is crossed from quintessence regime (w d >−1) to phantom regime (w d <−1). The evolution of dark energy density in terms of model parameter c 2 has been investigated. We showed that the dark energy becomes more dominant for positive values of c 1 and less dominant for negative values compare with OHDE model. It has been shown that the transition from decelerated to the accelerated expansion depends on the time-varying function c 2(z). Increasing the parameter c 0 causes that the transition tacks place sooner. Also positive values of c 1 result larger accelerated expansion and negative values obtain smaller accelerated expansion compare with OHDE. Eventually we performed the statefinder diagnostic tool in this model. Different values of c 0 and c 1 give different evolutionary trajectories for GHDE model in s–r plane. Hence the GHDE model can be discriminated by parameter c 2(z). Since the standard ΛCDM model is still a standard model of dark energy, therefore a distance of present value {s 0,r 0} from ΛCDM fixed point {s 0=0,r 0=1} is valuable criterion to examine a given dark energy model in s–r plane. The distance of {s 0,r 0} from {s 0=0,r 0=1} is shorter for c 1>0 and longer for c 1<0 in comparison with OHDE model (c 1=0). Increasing the parameter c 0 yields the shorter distance of {s 0,r 0} from ΛCDM fixed point {s 0=0,r 0=1}.