1 Introduction

Support vector machine (SVM) [2, 36, 39] has been extensively used in the past few decades for solving classification and regression problems in many applications [31, 33, 44, 45]. It gives a global solution to the optimization problem by solving a convex optimization problem using quadratic programming and provides a relatively robust and sparse solution. Other techniques like artificial neural networks (ANNs) are based on empirical risk minimization (ERM) principle which suffer from the problem of local minima. SVM has been used in various applications such as face recognition [11, 27, 29], pattern recognition [10, 21], speaker verification [23], intrusion detection [20], sentiment classification [38] and various other classification problems [6, 7, 19].

SVM has its roots in statistical learning theory and it is based on the principle of structural risk minimization (SRM). It finds the optimal hyperplane separating the different classes using a set of data points known as support vectors. Due to this it has a very low Vapnik-Chervonenkis (VC) dimension as compared to other techniques like ANN. One of the drawbacks of SVM is that its training cost is very high i.e. O(m3) where m is the total number of training samples [14]. Recently, an efficient approach twin support vector machine (TWSVM) is proposed by Jayadeva and Chandra [14] to decrease the training cost of SVM. In TWSVM two quadratic programming problems (QPPs) of smaller size are solved to find the classifying hyperplane rather than solving a single large problem as in standard SVM. A least squares variant of SVM has been proposed by Suykens and Vandewalle [15] to decrease the training cost, called as least squares support vector machine (LSSVM). In LSSVM one solves a set of system of linear equation instead of a QPP of large size. To further reduce the training cost, a twin version of LSSVM is proposed by Kumar and Gopal [21], termed as least square twin support vector machine (LS-TWSVM) where it solves a pair of set of linear equations.

In the training of SVM, same importance is given to all the training points in constructing the classifier. Due to this, the hyperplane gets biased towards the majority class samples. Since, the class of interest is the minority class so more weight needs to be given to the minority class samples to generate the unbiased classifier. In applications like fault detection, disease detection and many other related applications, the task is to correctly identifying the faults and disease from the data. Usually the data contains a lot less number of data samples with the abnormality. For assigning the weights many fuzzy based membership techniques have been proposed in the recent years. Lin and Wang [3] have proposed support vector machine based on fuzzy membership values (FSVM). Similar to SVM, FSVM also suffers in accuracy in case of class imbalanced data. To handle the problem of class imbalance, Batuwita and Palade [32] have presented a new model as FSVMs for class imbalance learning (FSVM-CIL). FSVM-CIL reduces the effect of outliers and noise in the training data. Here, the smaller fuzzy membership values are assigned to support vectors to reduce the effect of support vectors on the resultant decision surface based on class centres. Similarly, a new efficient approach fuzzy support vector machine for non-equilibrium data is proposed [9] to reduce the misclassification accuracy of positive class as compared to the negative class in FSVM. Bilateral-weighted FSVM (B-FSVM) is proposed [45] where membership of each sample is calculated by considering the samples on the basis of membership values for the positive and negative class. To solve bankruptcy prediction problem, a new fuzzy SVM is proposed by Chaudhuri and De [1]. In weighted least squares support vector machines (WLSTSVM) [16] the authors have obtained a sparse model for least squares support vector machine which is obtained by a pruning method where weights are given to the data points based on the error distribution to take care of the non-gaussian distributions which results in better accuracy.

For multiclass problems, a fuzzy least squares support vector machine is proposed by Tsujinishi and Abe [8]. In a similar way, Zhang et al. [37] have proposed a fuzzy least squares support vector machine for object tracking. Least squares recursive projection twin support vector machine (LSPTSVM) is proposed in Shao et al. [42] for classification. It generates projection planes for better classification on the basis of projection twin support vector machine (PTSVM) [40] by solving two modified primal problems in the form of linear equations whereas PTSVM needs to solve two quadratic programming problems along with two systems of linear equations. Weighted linear loss twin support vector machine (WLTSVM) for large-scale classification is proposed in Shao et al. [43] where the authors have considered twin support vector machine with weighted linear loss function to construct the two hyperplanes and use the weights on the linear loss function to take care of the differences in the data distribution. It is solved by using conjugate gradient algorithm to deal with large-scale datasets. Mehrkanoon and Suykens [22] have developed a method to solve partial differential equations using least squares support vector machine (LS-SVM). The partial differential equations are solved using LS-SVM using a set of linear equations rather than by non-linear equations as in ANN.

To further reduce the training cost of SVM, fuzzy least squares twin support vector machine is proposed by Sartakhti et al. [18] to deal with class imbalance datasets. Recently, Rastogi and Saigal [34] have proposed a new approach termed as tree-based localized fuzzy twin support vector clustering with square loss function. Further, Chen and Wu [40] have proposed a new fuzzy twin support vector machine (NFTWSVM) for pattern classification. For the work on the variants of TWSVM, we refer the reader to Shao et al. [41], Tanveer et al. [24] and Balasundaram et al. [35].

Entropy is used by Chen and Wu [40] to get the uncertainty measurement in neighbourhood systems. The information entropy based weights are more suited to imbalance problems as they take into account the probability distribution of the data which helps in determining the weights according to the class certainty. Further, it helps in giving less weight to the noisy data points which have less class certainty. Recently, Fan et al. [30] have proposed an entropy based fuzzy support vector machine (EFSVM) for class imbalance problem in which fuzzy membership is computed based on the entropy of the class samples where it solves a large size QPP to find the final decision classifier. Motivated by the work of Fan et al. [30], Lin and Wang [3] and Suykens and Vandewalle [15], we have proposed a new approach termed as entropy based fuzzy least squares support vector machine (EFLSSVM-CIL) for class imbalanced data. In EFLSSVM-CIL, we solve a set of linear equations through matrix operations resulting in less training time as compared to SVM where a large size QPP is solved to find the resultant classifier. Further, we have also proposed another method called entropy based fuzzy least squares twin support vector machine (EFLSTWSVM-CIL) to further improve the generalization ability and reduce the training cost. To justify the usability and applicability of our proposed methods, we have performed numerical experiments on several real-world datasets and compared the results with twin support vector machine (TWSVM), fuzzy twin support vector machine (FTWSVM), entropy based fuzzy support vector machine (EFSVM) and new fuzzy twin support vector machine (NFTWSVM) in terms of accuracy and training cost. One can notice that the proposed method EFLSTWSVM-CIL has outperformed the other existing fuzzy based techniques by a significant margin.

In this paper, all vectors are taken as column vectors. The inner product of two vectors is denoted as: xtz where x and z are the vector of n −dimensional real spaceRn and xt is the transpose of x. ||x|| and ||Q|| will be the 2-norm of a vector x and a matrix Q respectively. The vector of ones of dimension m and the identity matrix of appropriate size is denoted by e and I respectively.

The paper is organized as follows: Section 2 is to give a review on the work related to variants of support vector machine like Least squares support vector machine (LSSVM), Twin support vector machine (TWSVM), Least squares twin support vector machine (LSTWSVM), Fuzzy twin support vector machine (FTWSVM) and New fuzzy twin support vector machine (NFTWSVM) for pattern classification. The proposed methods EFLSSVM-CIL and EFLSTWSVM-CIL are discussed in Sections 3 and 4 respectively. Several numerical experiments have been performed on well known real world datasets to check the effectiveness and applicability of proposed methods in Section 5. In Section 6, we have concluded the paper with future work.

2 Related work

In this section, we have briefly discussed the formulations of least squares support vector machine (LSSVM), twin support vector machine (TWSVM), least squares twin support vector machine (LSTWSVM), fuzzy twin support vector machine (FTWSVM) and new fuzzy twin support vector machine (NFTWSVM).

2.1 Least squares support vector machine (LSSVM)

Least squares support vector machine (LSSVM) is proposed by Suykens and Vandewalle [15] where the formulation of LSSVM is given by the following optimization problem

$$\min\frac{1}{2}\vert \vert w\vert \vert^{2}+\frac{C}{\text{2}}\left( {\sum\limits_{i = 1}^{m} {\xi_{i}^{2}}} \right)$$

subject to

$$ y_{i} (\varphi (x_{i} )^{t}w+b)= 1-\xi_{i},\;\forall i = 1,2,.....m $$
(1)

where the input parameters C > 0; the vectors of slack variables ξ1 = (ξ11,...,ξ1m)t ∈ Rm and φ(xi) is the non-linear mapping which map the input example xi in higher dimensional space.

We introduce the Lagrangian multipliers λ = (λ1,...,λm)t such that λi ≥ 0 ,∀i = 1,...,m and take the gradient of Lagrangian function with respect to the primal variables w, b and ξ to zero. By eliminating w and ξ from the Lagrangian function, the solution is obtained by solving the following set of linear equations as

$$ \left[ {\begin{array}{l} 0\quad\quad\quad\quad Y^{t} \\ Y\quad\quad QQ^{t}+\frac{I}{C} \end{array}} \right] \left[ {\begin{array}{l} b \\ \lambda \end{array}} \right]=\left[ {\begin{array}{l} 0 \\ \vec{1} \end{array}} \right] $$
(2)

where Q = [φ(x1)ty1;...;φ(xm)tym],Y = [y1;...;ym] and \(\vec {1} =[1;...;1]\).

The decision function is given by

$$f(x)=sign (\sum\limits_{i = 1}^{m} {\lambda_{i} y_{i}} \varphi (x_{i} \mathbf{)}^{t}\varphi (x\mathbf{)}+b\mathbf{)} $$

By applying the kernel trick [4, 25, 26], the non-linear decision function for any x ∈ Rn,f(.) is given as:

$$ f(x)=sign\mathbf{ } (\mathbf{ } \sum\limits_{i = 1}^{m} {\lambda_{i} y_{i}} \mathbf{ } k(x_{i} ,x)+b) $$
(3)

where k(xi, x) = φ(xi)tφ(x) is the kernel function.

2.2 Twin support vector machine (TWSVM)

In TWSVM [14], two non parallel hyperplanes are obtained instead of one hyperplane such that each of them is nearer to one of the class and as far as possible from the other class. Let us consider the input matrices X1 and X2 of size p × n and q × n where p is the number of data point belonging to ‘Class 1’ and q denotes the number of data points belonging to ‘Class 2’ such that total number of data samples m = p + q and n is the dimension of each data point. In non-linear case, twin support vector machine finds a pair of non parallel hyperplanes f1(x) = K(xt, Dt)w1 + b1 = 0 and f2(x) = K(xt, Dt)w2 + b2 = 0 from the solution of the following QPPs as

$$\min\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +e_{1} b_{1} \vert \vert^{2}+C_{1} {e_{2}^{t}} \xi $$

subject to

$$ -(K(X_{2} ,D^{t})w_{1} +e_{2} b_{1} )+\xi \ge e_{2}, \quad \xi \ge 0 $$
(4)
$$\min\frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +e_{2} b_{2} \vert \vert^{2}+C_{2} {e_{1}^{t}} \eta $$

subject to

$$ (K(X_{1} ,D^{\text{\textbf{t}}})w_{2} +e_{1} b_{2} )+\eta \ge e_{1} , \quad \eta \ge 0 $$
(5)

where ξ, η represent slack variables; C1, C2 are penalty parameters; D = [X1;X2]; e1, e2 are vectors of suitable dimension having all values as 1’s and K(xt,Dt) = (k(x, x1),...,k(x, xm)) is a row vector in Rm.

The Lagrangian functions of problems (4) & (5) are written as

$$\begin{array}{@{}rcl@{}} L_{1} &=&\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +e_{1} b_{1} \vert \vert^{2}+C_{1} {e_{2}^{t}} \xi\\ &&+{\alpha_{1}^{t}} ((K(X_{2} ,D^{t})w_{1} +e_{2} b_{1} )-\xi +e_{2} )-{\beta_{1}^{t}} \xi \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} L_{2} &=&\frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +e_{2} b_{2} \vert \vert^{2}+C_{2} {e_{1}^{t}} \eta\\ &&+{\alpha_{2}^{t}} ((-K(X_{1} ,D^{t})w_{2} -e_{1} b_{2} )-\eta +e_{1} )-{\beta_{2}^{t}} \eta \end{array} $$
(7)

where the vectors of Lagrangian multipliers α1 = (α11,...,α1q)t ∈ Rq,β1 = (β11,...,β1q)t ∈ Rq,α2 = (α21,...,α2p)t ∈ Rp and β2 = (β21,...,β2p)t ∈ Rp. The Wolfe dual of (6) and (7) is written by applying the Karush-Kuhn-Tucker (K.K.T) necessary and sufficient conditions [25] as

$$ \max {e_{2}^{t}} \alpha_{1} -\frac{1}{2}{\alpha_{1}^{t}} T(S^{t}S)^{-1}T^{t}\alpha_{1} $$
(8)

subject to

$$0\le \alpha_{1} \le C_{1} $$
$$ \max {e_{1}^{t}} \alpha_{2} -\frac{1}{2}{\alpha_{2}^{t}} S(T^{t}T)^{-1}S^{t}\alpha_{2} $$
(9)

subject to

$$0\le \alpha_{2} \le C_{2} $$

where S = [K(X1, Dt) e1] and T = [K(X2, Dt) e2].

We compute the value of w1, w2, b1 and b2 using the following equations as

$$ \left[ {\begin{array}{l} w_{1} \\ b_{1} \end{array}} \right]=-(S^{t}S+\delta I)^{-1}T^{t}\alpha_{1} $$
(10)
$$ \left[ {\begin{array}{l} w_{2} \\ b_{2} \end{array}} \right]=(T^{t}T+\delta I)^{-1}S^{t}\alpha_{2} $$
(11)

Each new test data point x ∈ Rn is assigned to a given class ’i′ by using the following formula

$$ class\;i=\min \vert K(x^{t},\,D^{t})w_{i} +b_{i} \vert \, \text{for}\, i = 1,2. $$
(12)

2.3 Least squares twin support vector machine (LSTWSVM)

Kumar and Gopal [21] have proposed a new efficient approach which is known as least squares twin support vector machine (LSTWSVM) where non-parallel hyperplanes are constructed by solving a pair of two linear equations instead of solving a pair of quadratic programming problems in case of TWSVM. To find the kernel generated surfaces K(xt,Dt)w1 + b1 = 0 and K(xt,Dt)w2 + b2 = 0, the optimization problem for non-linear LSTWSVM is formulated as

$$\min\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +eb_{1} \vert \vert^{2}+\frac{C_{1}} {2}\xi^{t} \xi $$

subject to

$$ -(K(X_{2} ,D^{t})w_{1} +eb_{1} )+\xi =e $$
(13)

and

$$\min \frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +eb_{2} \vert \vert^{2}+\frac{C_{2}} {2}\eta^{t} \eta $$

subject to

$$ (K(X_{1} ,D^{t})w_{2} +eb_{2} )+\eta =e $$
(14)

where ξ, η represent slack variables, C1, C2 > 0 are penalty parameters and e is the vector of ones of suitable dimension.

Using the inequality constraints of (13) & (14) in its objective function, we get

$$ \min\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +eb_{1} \vert \vert^{2}+\frac{C_{1}} {2}\vert \vert K(X_{2} ,D^{t})w_{1} +eb_{1} +e\vert \vert^{2} $$
(15)

and

$$ \min\frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +eb_{2} \vert \vert^{2}+\frac{C_{2}} {2}\vert \vert -K(X_{1} ,D^{t})w_{2} -eb_{2} +e\vert \vert^{2} $$
(16)

Taking the gradient of (15) with respect to primal variables w1 and b1and equating to zero, we get

$$\begin{array}{@{}rcl@{}} &&K(X_{1} ,D^{t})^{t} (K(X_{1} ,D^{t})w_{1} +eb_{1})\\&+& C_{1} K(X_{2} ,D^{t})^{t} (K(X_{2} ,D^{t})w_{1} +eb_{1} +e)= 0e \end{array} $$
(17)
$$ e^{t}(K(X_{1} ,D^{t})w_{1} +eb_{1} )+C_{1} e^{t}(K(X_{2} ,D^{t})w_{1} +eb_{1} +e)= 0 $$
(18)

Combining (17) and (18) in matrix form and solving for w1 and b1 as

$$ \left[ {\begin{array}{l} w_{1} \\ b_{1} \end{array}} \right]=-\text{ } \left( {V^{t}V+\frac{1}{C_{1}} U^{t}U} \right)^{-1}V^{t}e $$
(19)

where U = [K(X1, Dt)e] and V = [K(X2, Dt)e]. Similarly, for the other hyperplane the unknowns are computed by the following formula

$$ \left[ {\begin{array}{l} w_{2} \\ b_{2} \end{array}} \right]=\text{ } \left( {U^{t}U+\frac{1}{C_{2}} V^{t}V} \right)^{-1}U^{t}e $$
(20)

To predict the class of new data samplex ∈ Rn, we find the perpendicular distances from the hyperplanes K(xt,Dt)w1 + b1 = 0 and K(xt,Dt)w2 + b2 = 0 and assign the class label of the minimum distance hyperplane to the data sample. For more details, see [21].

2.4 Fuzzy twin support vector machine (FTWSVM)

Like FSVM, in FTWSVM weights are given to the different data samples on the basis of fuzzy membership values and the training gets biased towards the samples of interest. To calculate the fuzzy membership we have considered the centroid measure for the data samples of each class where the membership values are assigned based on the distance of the data points from the centroid of that class [32]. The membership values are used as a basis for giving weights to the error tolerance i.e. C for every data point.

The fuzzy membership function for centroid based membership is written as

$$mem= 1-\frac{d_{cen}} {\max (d_{cen} )+\delta} $$

where dcen is the Euclidean distance of each data point from the centroid of its class, δ is a small positive integer value for making the denominator non-zero.

The formulation of FTWSVM in primal is written as

$$\min\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +e_{1} b_{1} \vert \vert^{2}+C_{1} {s_{2}^{t}} \xi $$

subject to

$$ -(K(X_{2} ,D^{t})w_{1} +e_{2} b_{1} )+\xi \ge e_{2} \quad , \quad \xi \ge 0 $$
(21)
$$\min\frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +e_{2} b_{2} \vert \vert^{2}+C_{2} {s_{1}^{t}} \eta $$

subject to

$$ (K(X_{1} ,D^{t})w_{2} +e_{1} b_{2} )+\eta \ge e_{1} , \quad \eta \ge 0 $$
(22)

where ξ, η represent slack variables; C1, C2 are penalty parameters; s1, s2 are vectors having the membership values of the data samples of the other class.

The Lagrangian function of the problems (21) & (22) are written as

$$\begin{array}{@{}rcl@{}} L_{1} &=&\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +e_{1} b_{1} \vert \vert^{2}+C_{1} {s_{2}^{t}} \xi\\&& +{\alpha_{1}^{t}} ((K(X_{2} ,D^{t})w_{1} +e_{2} b_{1} )-\xi +e_{2} )-{\beta_{1}^{t}} \xi \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} L_{2} &=&\frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +e_{2} b_{2} \vert \vert^{2}+C_{2} {s_{1}^{t}} \eta\\ &&+{\alpha_{2}^{t}} ((-K(X_{1} ,D^{t})w_{2} -e_{1} b_{2} )-\eta +e_{1} )-{\beta_{2}^{t}} \eta \end{array} $$
(24)

where α1 = (α11,...,α1q)t, β1 = (β11,...,β1q)t,α2 = (α21,...,α2p)t and β2 = (β21,...,β2p)t are the vectors of Lagrange multipliers.

Now, we apply the Karush-Kuhn-Tucker (K.K.T) necessary and sufficient conditions to find the Wolfe dual of (21) and (22) as

$$\min\frac{1}{2}{\alpha_{1}^{t}} T(S^{t}S)^{-1}T^{t}\alpha_{1} -{e_{2}^{t}} \alpha_{1} $$
$$ \text{subject to}\qquad \qquad 0\le \alpha_{1} \le s_{2} C_{1} $$
(25)
$$\min\frac{1}{2}{\alpha_{2}^{t}} S(T^{t}T)^{-1}S^{t}\alpha_{2} -{e_{1}^{t}} \alpha_{2}$$
$$ \text{subject to}\qquad\qquad 0\le \alpha_{2} \le s_{1} C_{2} $$
(26)

where S = [K(X1, Dt) e1] and T = [K(X2, Dt) e2].

We compute the non-linear hyperplanes K(xt,Dt)w1 + b1 = 0 and K(xt,Dt)w2 + b2 = 0 by computing the values of w1, w2, b1 and b2 by using the following equations as

$$ \left[ {\begin{array}{l} \!w_{1} \\ \!b_{1} \end{array}} \!\right]\,=\,-(S^{t}S+\delta I)^{-1}T^{t}\alpha_{1} \, \text{and} \,\left[ {\begin{array}{l} \!w_{2} \\ \!b_{2} \end{array}} \!\right]\,=\,(T^{t}T+\delta I)^{-1}S^{t}\alpha_{2} $$
(27)

The resultant classifier is obtained by using (12).

2.5 New fuzzy twin support vector machine (NFTWSVM)

Recently, Chen and Wu [40] have proposed a fuzzy based variant of SVM named as new fuzzy twin support vector machine for pattern classification (NFTWSVM). It employs a fuzzy membership function based on Keller and Hunt [17] to give the weights to the data points where the fuzzy 2-partition is formed

The fuzzy membership function for a positive sample is written as

$$m_{1} (x_{i} )= 0.5+\frac{\exp (C_{0} (d_{-1} (x_{i} )-d_{1} (x_{i} ))/d)-\exp (-C_{0} )}{2(\exp (C_{0} )-\exp (-C_{0} ))} $$
$$m_{-1} (x_{i} )= 1-m_{1} (x_{i} ) $$

For a negative sample,

$$m_{-1} (x_{i} )= 0.5+\frac{\exp (C_{0} (d_{1} (x_{i} )\,-\,d_{-1} (x_{i} ))/d)\,-\,\exp (-C_{0} )}{2(\exp (C_{0} )-\exp (-C_{0} ))} $$
$$m_{1} (x_{i} )= 1-m_{-1} (x_{i} ) $$

where the Euclidean distance between xi and the mean of the negative class is represented by d− 1, the distance between xi and the mean of the positive class is represented by d1, d is the distance between the means of the positive and negative classes and to control the membership function C0 is used as a constant.

The formulation of NFTWSVM in primal is written as

$$\min\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +e_{1} b_{1} \vert \vert^{2}+\frac{1}{2}C_{1} ({w_{1}^{2}} +{b_{1}^{2}} )+C_{2} {e_{2}^{t}} \eta_{2} $$

subject to

$$ Y_{2} (K(X_{2} ,D^{t})w_{1} +e_{2} b_{1} )\ge {Y_{2}^{2}} e_{2} -{Y_{2}^{2}} \eta_{2} ~~ , ~~ \eta_{2} \ge 0 $$
(28)
$$\min\frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +e_{2} b_{2} \vert \vert^{2}+\frac{1}{2}C_{3} ({w_{2}^{2}} +{b_{2}^{2}} )+C_{4} {e_{1}^{t}} \eta_{1} $$

subject to

$$ Y_{1} (K(X_{1} ,D^{t})w_{2} +e_{1} b_{2} )\ge {Y_{1}^{2}} e_{1} -{Y_{1}^{2}} \eta_{1} , ~~ \eta_{1} \ge 0 $$
(29)

where η1, η2 represent slack variables; C1, C2, C3 and C4 are penalty parameters; Y 1 = diag(y1, y2,...,yp),Y 2 = diag(y1, y2,...,yq) for p positive samples and q negative samples with yi = 2mi − 1.

After applying the Karush-Kuhn-Tucker (K.K.T) necessary and sufficient conditions to find the Wolfe dual of (21) and (22), we get

$$\min\frac{1}{2}{\alpha_{1}^{t}} Y_{2} T(S^{t}S+C_{1} I)^{-1}T^{t}Y_{2}^{T}\alpha_{1} -{e_{2}^{t}} {Y_{2}^{T}}\alpha_{1} $$
$$ \text{subject to}\qquad \qquad0\le \alpha_{1} \le C_{2} ({Y_{2}^{2}})^{-1}e_{2} $$
(30)
$$\min\frac{1}{2}{\alpha_{2}^{t}} Y_{1} S(T^{t}T+C_{3} I)^{-1}S^{t}Y_{1}^{T}\alpha_{2} -{e_{1}^{t}} {Y_{1}^{T}}\alpha_{2} $$
$$ \text{subject to}\qquad\qquad 0\le \alpha_{2} \le C_{4} ({Y_{1}^{2}})^{-1}e_{1} $$
(31)

where S = [K(X1, Dt) e1] and T = [K(X2, Dt) e2].

The non-linear hyperplanes K(xt,Dt)w1 + b1 = 0 and K(xt,Dt)w2 + b2 = 0 are obtained by computing the values of w1, w2, b1 and b2 by using the following equations as

$$ \left[ {\begin{array}{l} w_{1} \\ b_{1} \end{array}} \right]\,=\,(S^{t}S\,+\,C_{1} I)^{-1}T^{t}{Y_{2}^{t}}\alpha_{1} \, \text{and} \,\left[ {\begin{array}{l} w_{2} \\ b_{2} \end{array}} \right]\,=\,(T^{t}T\,+\,C_{3} I)^{-1}S^{t}{Y_{1}^{T}}\alpha_{2} $$
(32)

For more details, see [40].

3 Proposed entropy based fuzzy least squares support vector machine for class imbalance learning (EFLSSVM-CIL)

To enhance the training speed of SVM for imbalanced data, we propose a new approach i.e. least squares version of entropy based fuzzy support vector machine which uses the information entropy of data samples. Recently, Fan et al. [30] have proposed a novel approach for fuzzy membership evaluation based on information entropy of the data samples. Entropy is helpful in giving less weight to the data points at the boundary of the classes, so it is used to solve the problem of class imbalance. Hence, one can assign the fuzzy membership to the data points by using the information entropy as the weighted parameter. The class of interest is given highest membership value and the other class is given membership values based on its entropy. The samples of majority class with high entropy are given less membership value and with low entropy are given higher membership values. This is done so as to increase the participation of lower entropy data points of the majority class in constructing the classifier and decreasing the role of high entropy data points of the majority class which are near the boundary of the classes. The entropy of any sample xi is given as:

$$ E_{i} =-P_{pos\mathunderscore x_{i}} \ast \text{ } \ln (P_{pos\mathunderscore x_{i}} )\text{ } -\text{ }P_{neg\mathunderscore x_{i}} \ast \text{ } \ln (P_{neg\mathunderscore x_{i}} ) $$
(33)

where \(P_{pos\mathunderscore x_{i}} \) and \(P_{neg\mathunderscore x_{i}} \) are the probability of positive class and negative class of sample xi respectively. Further, we calculate the K −nearest neighbors of sample xi and assign the values to \(P_{pos\mathunderscore x_{i}} \) and \(P_{neg\mathunderscore x_{i}} \) based on count of total positive and negative class neighbors.

Further, the data points of the negative class are divided into l subsets based on increasing order of entropy. The fuzzy membership of each samples in each subset are calculated as

$$F_{q} = 1.0-\beta \ast (q-1), q = 1,2,...,l $$

where Fq is the fuzzy membership for samples distributed in qth subset with fuzzy membership parameter \(\beta \in \left ({0,\frac {1}{l-1}} \right ]\) which control the scale of fuzzy membership of samples. The fuzzy membership function is given as

$$ s_{i} =\left\{ {\begin{array}{l} 1-\beta \ast (q-1), if\;y_{i} =-1 \\ 1, if\;y_{i} = 1 \end{array}} \right.{\begin{array}{*{20}c} {and\;x_{i} \in q^{th}subset} \hfill \\ { } \hfill \end{array}} $$
(34)

The majority class samples are given a membership of 1 and the minority class samples are given the membership based on the above formula.

In this paper, motivated by the work of Fan et al. [30] and Suykens and Vandewalle [15], we have proposed a new least squares version of entropy based fuzzy support vector machine based on information entropy for class imbalance learning where information entropy is used to compute the weights for fuzzy membership.

EFLSSVM-CIL finds a class separating hyperplane that maximizes the margin between the two classes from the formulations of EFSVM by modifying inequality constraints to equality constraints and considered the 2-norm slack variables with C/2 instead of 1-norm slack variable with C. Further, one can find the solution of the optimization problem by solving the system of linear equations instead of solving it by QPP which takes less computational time and applicable to large imbalance data. To classify the non-linear separable data points, the non-linear entropy based fuzzy least squares support vector machine for class imbalance learning (EFLSSVM-CIL) is formulated in primal form as

$$\min\frac{1}{2}\vert \vert w\vert \vert^{2}+ \frac{C}{2} \left( {\sum\limits_{i = 1}^{m} {s_{i} {\xi_{i}^{2}}}} \right)$$

subject to

$$ y_{i} (\varphi (x_{i} )^{t}w+b)= 1-\xi_{i},\;\forall i = 1,2,.....m $$
(35)

where input sample xi is transformed to φ(xi) in higher dimensional space.

By introducing the Lagrangian multipliers λ = (λ1,...,λm)t such that λi ≥ 0,∀i = 1,...,m, the Lagrangian function can be written as

$$ L=\frac{1}{2}\vert \vert w\vert \vert^{2}+ \frac{C}{2}\left( {\sum\limits_{i = 1}^{m} {s_{i} {\xi_{i}^{2}}}} \!\right)-\sum\limits_{i = 1}^{m} {\lambda_{i}} (y_{i} (\varphi (x_{i} )^{t}w+b)-1+\xi_{i} ) $$
(36)

Making the gradient of L with respect to the primal variables w, b, ξ and λ to zero, we obtain

$$\frac{\partial L}{\partial w}= 0\Rightarrow w=\sum\limits_{i = 1}^{m} {\lambda_{i} y{}_{i} \varphi (x_{i} )} $$
$$\frac{\partial L}{\partial b}= 0\Rightarrow \sum\limits_{i = 1}^{m} {\lambda_{i} y{}_{i}= 0} $$
$$\frac{\partial L}{\partial \xi_{i}} = 0\Rightarrow \lambda_{i} =C\text{ } s_{i} \xi_{i} $$
$$\frac{\partial L}{\partial \lambda_{i}} = 0\Rightarrow y_{i} \left( {\varphi (x_{i} )^{t}w+b} \right)-1+\xi_{i} = 0, $$

where i = 1,2,.....m.

Further, the solution of primal EFLSSVM can be formulated in its dual form and solved by eliminating w and ξ which results to the following set of linear equations as

$$ \left[ {\begin{array}{l} 0 \quad\quad\quad\quad Y^{t}\\ Y\quad\quad QQ^{t}+\frac{I}{sC} \end{array}} \right] \left[ {\begin{array}{l} b \\ \lambda \end{array}} \right]=\left[ {\begin{array}{l} 0 \\ \vec{1} \end{array}} \right] $$
(37)

where s is the vector containing the membership values of majority class.

For any data sample x ∈ Rn, the non-linear decision function is given by (3).

4 Proposed entropy based fuzzy least squares twin support vector machine for class imbalance learning (EFLSTWSVM-CIL)

To further improve the generalization ability and reduce the training cost of fuzzy based LSSVM [8], we have proposed a twin version of fuzzy based least squares support vector machine using the information entropy which has good generalization performance and improved computational cost. Since there is not much work done with least squares twin support vector machine for class imbalance problem, motivated by the work of Fan et al. [30], we have proposed a entropy based fuzzy least squares twin support vector machine (EFLSTWSVM-CIL) for class imbalance.

The problem formulation of non-linear EFLSTWSVM is written as

$$\min\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +eb_{1} \vert \vert^{2}+\frac{s_{2} C_{1}} {2}\xi^{t} \xi $$
$$ \text{subject to }\qquad\qquad-(K(X_{2} ,D^{t})w_{1} +eb_{1} )+\xi =e, $$
(38)

and

$$\min \frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +eb_{2} \vert \vert^{2}+\frac{s_{1} C_{2}} {2}\eta^{t} \eta $$
$$ \text{subject to}\, (K(X_{1} ,D^{t})w_{2} +eb_{2} )+\eta =e, $$
(39)

where ξ, η represent slack variables, C1, C2 > 0 are penalty parameters, e is the vector of ones of suitable dimension and s1 and s2 are the vectors containing the membership values of positive class and negative class respectively which are computed in the same manner as in proposed EFLSSVM-CIL.

Using the equality constraints of (38) & (39) with its objective function, we get

$$ \min\frac{1}{2}\vert \vert K(X_{1} ,D^{t})w_{1} +eb_{1} \vert \vert^{2}+\frac{s_{2} C_{1}} {2}\vert \vert K(X_{2} ,D^{t})w_{1} +eb_{1} +e\vert \vert^{2} $$
(40)

and

$$ \min\frac{1}{2}\vert \vert K(X_{2} ,D^{t})w_{2} +eb_{2} \vert \vert^{2}+\frac{s_{1} C_{2}} {2}\vert \vert -K(X_{1} ,D^{t})w_{2} -eb_{2} +e\vert \vert^{2} $$
(41)

Taking the gradient of (40) with respect to primal variables w1 and b1 and equate to zero, we get

$$\begin{array}{@{}rcl@{}} &&K(X_{1} ,D^{t})^{t} (K(X_{1} ,D^{t})w_{1} +eb_{1})\\ &+& s_{2} C_{1} K(X_{2} ,D^{t})^{t} (K(X_{2} ,D^{t})w_{1} +eb_{1} +e)= 0e \end{array} $$
(42)
$$ e^{t}(K(X_{1} ,D^{t})w_{1} +eb_{1} )+s_{2} C_{1} e^{t}(K(X_{2} ,D^{t})w_{1} +eb_{1} +e)= 0 $$
(43)

Combining (42) and (43) in matrix form and solving for w1 and b1

$$\left[ {\begin{array}{l} w_{1} \\ b_{1} \end{array}} \right]=\left[ {\left[ {\begin{array}{l} K(X_{2} ,D^{t})^{t} \\ e^{t} \end{array}} \right]\left[ {K(X_{2} ,D^{t}) e} \right]+\frac{1}{s_{2} C_{1}} \left[ {\begin{array}{l} K(X_{1} ,D^{t})^{t} \\ e^{t} \end{array}} \right] \left[ {K(X_{1} ,D^{t}) e} \right]} \right]^{-1} \left[ {\begin{array}{l} -K(X_{2} ,D^{t})^{t} e \\ - q \end{array}} \right] $$
(44)

One can write (44) in the following form

$$ \left[ {\begin{array}{l} w_{1} \\ b_{1} \end{array}} \right]=- \left( {H^{t}H+\frac{1}{s_{2} C_{1}} G^{t}G} \right)^{-1}H^{t}e $$
(45)

where G = [K(X1, Dt)e] and H = [K(X2, Dt)e].

Similarly for the other hyperplane the parameters are computed by the following formula

$$ \left[ {\begin{array}{l} w_{2} \\ b_{2} \end{array}} \right]=\text{ } \left( {G^{t}G+\frac{1}{s_{1} C_{2}} H^{t}H} \right)^{-1}G^{t}e $$
(46)

Using Sherman–Morrison–Woodbury (SMW) [12] formula, we rewrite the (45) and (46) so that we have to solve inverses of smaller dimension which leads increase in computation speed.

Below we discuss the solution of nonlinear EFLSTWSVM-CIL for two cases.

  1. Case 1:

    p < q

$$ \left[ {\begin{array}{l} w_{1} \\ b_{1} \end{array}} \right]=-\text{ } \left( {Y-YG^{t}\left( {C_{I} s_{1} +GYG^{t}} \right)^{-1}GY} \right)H^{t}s_{2} $$
(47)
$$ \left[ {\begin{array}{l} w_{2} \\ b_{2} \end{array}} \right]=\text{ C}_{\text{2}} \left( {Y-YG^{t}\left( {\frac{s_{1}} {C_{2}} +GYG^{t}} \right)^{-1}GY} \right)G^{t}s_{1} $$
(48)

where Y = (HtH)− 1.

Using the regularization term εI, where ε > 0 for the possible ill conditioning of (HtH)− 1 and rewritten as

$$Y=\frac{1}{\varepsilon} \left( {I-H^{t}\left( {\varepsilon I+HH^{t}} \right)^{-1}H} \right) $$
  1. Case 2:

    q < p

$$ \left[ {\begin{array}{l} w_{1} \\ b_{1} \end{array}} \right]=-\text{ } C_{1} \left( {Z-ZH^{t}\left( {\frac{s_{2}} {C_{I}} +HZ^{t}H} \right)^{-1}HZ} \right)H^{t}s_{2} $$
(49)
$$ \left[ {\begin{array}{l} w_{2} \\ b_{2} \end{array}} \right]=\text{ } \left( {Z-ZH^{t}\left( {C_{2} s_{2} +HZH^{t}} \right)^{-1}HZ} \right)G^{t}s_{1} $$
(50)

where Z = (GtG)− 1 which is rewritten using SMW formula as

$$Z=\frac{1}{\varepsilon} \left( {I-G^{t}\left( {\varepsilon I+GG^{t}} \right)^{-1}G} \right) $$

To predict the class of new data sample x ∈ Rn, find the perpendicular distances from the hyperplanes K(xt,Dt)w1 + b1 = 0 and K(xt,Dt)w2 + b2 = 0 and assign the class label of minimum distance hyperplane.

5 Numerical experiments

To check the performance of the proposed methods, we have experimented on various linear and non-linear imbalanced datasets which are taken from KEEL imbalanced datasets [13] and UCI repository [28] for binary classification. The proposed EFLSSVM-CIL and EFLSTWSVM-CIL are compared with NFTWSVM, EFSVM, FTWSVM and TWSVM. All computations are carried-out on a PC running on Windows 7 OS with 64 bit, 3.20 GHz Intel®;coreTM i5-2400 processor having 2 GB of RAM under MATLAB R2008b environment. We have used MOSEK optimization toolbox to solve the quadratic programming problems which is taken from http://www.mosek.com. Gaussian kernel is used for non-linear classifier, defined as k(a, b) = exp(−μ||a − b||2) where vector a, b ∈ Rmand μ is the kernel parameter.

The value of the parameter C = C1 = C2 is taken from the set {10− 7,...,107} and μ is chosen from the range {2− 5,...,25} for all the cases. For FTWSVM, δ is taken as 0.5. For EFSVM, EFLSSVM-CIL and EFLSTWSVM-CIL, β is considered as 0.05, l is taken as 10, the value of K is chosen from the set {5,8,11}. For, NTWSVM the value of C1 = C2, C3 = C4 are taken from the set {10− 5,...,105} and C0 is selected from the set {0.5,1,1.5,2,2.5}.

All the results for the proposed method EFLSSVM-CIL and EFLSTWSVM-CIL with NFTWSVM, EFSVM, FTWSVM and TWSVM are shown in terms of prediction accuracy and training time both for linear and Gaussian kernel in Tables 1 and 3 respectively. One can observe from Tables 1 and 3 that EFLSTWSVM-CIL is much superior to TWSVM, FTWSVM, EFSVM, NFTWSVM and EFLSSVM-CIL in terms of better prediction accuracy for unknown samples. Also, our proposed method EFLSTWSVM-CIL takes very less training time in comparison with EFSVM, TWSVM, FTWSVM and EFLSSVM-CIL. EFLSTWSVM-CIL solves two systems of linear equations instead of a pair of QPP as in TWSVM and FTWSVM. In similar manner, EFLSSVM solves a system of linear equation instead of a QPP as in case of EFSVM which results in less computation time.

Table 1 Performance comparison of EFLSTWSVM-CIL and EFLSSVM-CIL with TWSVM, FTWSVM, EFSVM and NFTWSVM using linear kernel for classification on imbalance datasets. Time is in seconds. The values shown in bold represent the highest AUC values [30]
Full size table

For linear kernel, note that the total number of times the best accuracy obtained by TWSVM, FTWSVM, EFSVM, NFTWSVM, EFLSSVM-CIL and EFLSTWSVM-CIL are 4, 0, 4, 6, 3 and 10 respectively from Table 1. This indicates the supremacy of proposed EFLSTWSVM-CIL. It is concluded from Table 1 that for all the datasets our proposed EFLSSVM-CIL and EFLSTWSVM-CIL have not performed better. So, we analyze the comparative performance of EFLSSVM-CIL and EFLSTWSVM-CIL with TWSVM, FTWSVM, EFSVM and NFTWSVM based on the average rank of all the methods which are shown in Table 2. One can clearly observe from Table 2 that the average rank of proposed EFLSTWSVM-CIL is 2.18 which is lowest among all the methods. Further, for statistical comparison on the performance of 6 algorithms using 25 datasets, we have performed the Friedman test with the corresponding post-hoc test [5]. We assume that all the methods are equivalent under null hypothesis, the Friedman statistic is computed from Table 2 as

$$\begin{array}{@{}rcl@{}} {\chi_{F}^{2}} \!&=&\!\frac{12\times 25}{6\times (6 + 1)}\left[ {\vphantom{\frac{6\times (6 + 1)^{2}}{4}}}\!(\text{3}.08^{2}\,+\,\text{3}.66^{2}\,+\,4\text{.16}^{2}\,+\,\text{ 3.56}^{2}\,+\,4.36^{2}\,+\,\text{2.18}^{2})\right.\\&&\quad\quad\quad\quad\quad\quad-\left.\frac{6\times (6 + 1)^{2}}{4} \right]\cong 22.3086 \end{array} $$
(51)
$$F_{F} =\frac{(25-1)\times 22.3086}{25\times (6-1)-22.3086}\cong 5.2137 $$

where FF is distribution according to the F-distribution with (6 − 1, (6 − 1) × (25 − 1)) = (5, 120) is degree of freedom with 6 methods and 25 datasets. The critical value of F(5,120) is 2.2898 for the level of significance at α = 0.05. Since the value of FF = 5.3938 > 2.2898, so we reject the null hypothesis. Further, Nemenyi post-hoc test is performed for pair-wise comparison of methods and the significant difference between them is checked by computing the critical difference (CD) at p = 0.10 which should differ by at least \(2.589\sqrt {\frac {6\times (6 + 1)}{6\times 25}} \approx 1.37\).

Table 2 Average ranks of TWSVM, FTWSVM, EFSVM, NFTWSVM, EFLSSVM-CIL and EFLSTWSVM-CIL using linear kernel for classification on imbalance datasets
Full size table

The difference between the average ranks of NFTWSVM, EFSVM, FTWSVM and EFLSSVM-CIL with EFLSTWSVM-CIL are (3.56 − 2.18 = 1.38), (4.16 − 2.18 = 1.98),(3.66 − 2.18 = 1.48), and (4.36 − 2.18 = 2.18) respectively, which are greater than 1.37. So we conclude that EFLSTWSVM-CIL is significantly better than EFSVM, FTWSVM and EFLSSVM-CIL. Since the difference of average rank of TWSVM with EFLSTWSVM-CIL is (3.08 − 2.18 = 0.9) which is less than 1.37 that shows that there is no significant difference between EFLSTWSVM-CIL and TWSVM.

In non-linear case, the accuracy values are shown with the training time for the proposed EFLSSVM-CIL and EFLSTWSVM-CIL with TWSVM, FTWSVM, EFSVM and NFTWSVM in Table 3. It can be observed from Table 3 that the number of times the best accuracy obtained by TWSVM, FTWSVM, EFSVM, NFTWSVM, EFLSSVM-CIL and EFLSTWSVM-CIL are 4, 5, 9, 6, 5 and 19 respectively which indicates the supremacy of proposed EFLSTWSVM-CIL in terms of generalization performance. The learning speed of our proposed EFLSTWSVM-CIL is better than EFSVM and EFLSSVM-CIL in all the cases. It is noticeable from the table that the proposed EFLSTWSVM-CIL is not always better in terms of accuracy for all the datasets, so we compute the average rank of all the methods based on accuracy values which are shown in Table 4. One can conclude that among all the methods our proposed EFLSTWSVM-CIL has lowest average rank. Further, we have performed the Friedman statistical test with the post-hoc tests.

Table 3 Performance comparison of EFLSTWSVM-CIL and EFLSSVM-CIL with TWSVM, FTWSVM, EFSVM and NFTWSVM using Gaussian kernel for classification on imbalance datasets. Time is in seconds. The values shown in bold represent the highest AUC values [30]
Full size table
Table 4 Average ranks of TWSVM, FTWSVM, EFSVM, NFTWSVM, EFLSSVM-CIL and EFLSTWSVM-CIL using Gaussian kernel for classification of imbalance datasets
Full size table

Now the Friedman statistic is computed for nonlinear kernel under null hypothesis by using Table 4:

$$\begin{array}{@{}rcl@{}} {\chi_{F}^{2}}\! &=&\!\frac{12\!\times\! 39}{6\times (6\,+\,1)}\!\left[\vphantom{\frac{6\times (6 + 1)^{2}}{4}} \!(4.0641^{2}+ 3.74359^{2}+ 3\text{.29487}^{2}+\text{3}.73077^{2}\right.\\ &&\qquad\qquad~~\left.+ 3.98718^{2}\,+\,2.17949^{2})\,-\,\frac{6\!\times\! (6 + 1)^{2}}{4} \right]\!\cong 27.3442 \end{array} $$
$$F_{F} =\frac{(39-1)\times 27.3442}{39\times (6-1)-27.3442}\cong 6.1977 $$

The critical value of F(5,190) i.e. 2.2616 for the level of significance α = 0.05 is less than the value of FF. Thus, it rejects the null hypothesis. Further, the Nemenyi post-hoc test is used to find the significant difference between the pair-wise comparisons. We computed the critical difference (CD) at p = 0.10 which should differ by at least \(2.589\sqrt {\frac {6\times (6 + 1)}{6\times 39}} \approx 1.0969\).

The difference between the average ranks of EFLSTWSVM-CIL with TWSVM, FTWSVM, EFSVM, NFTWSVM and EFLSSVM-CIL are (4.0641 − 2.17949 = 1.88461), (3.74359 − 2.17949 = 1.5641),(3.29487 − 2.17949 = 1.11538), (3.73077 − 2.17949 = 1.55128) and (3.98718 − 2.17949 = 1.80769) respectively, which are greater than 1.0969. Hence, proposed EFLSTWSVM-CIL is significantly better than TWSVM, FTWSVM, EFSVM, NFTWSVM and EFLSSVM-CIL.

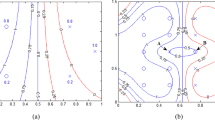
One can verify that the performance of our proposed EFLSSVM-CIL and EFLSTWSVM-CIL are not very sensitive to the values of its parameters C, μ and K. To illustrate this result, the sensitivity is shown for user defined parameters C and K for proposed EFLSSVM-CIL on Ecoli0137vs26, Monk2, Vehicle2 and Yeast-0-3-5-9_vs_7-8 datasets are shown in Fig. 1a, b, c and d respectively and for proposed EFLSTWSVM-CIL on Ecoli-0-1_vs_2-3-5, Monk2, Vehicle2 and Yeast-0-3-5-9_vs_7-8 datasets are shown in Fig. 3a, b, c and d respectively. In similar manner, the sensitivity analysis for user defined parameters μ and K for proposed EFLSSVM-CIL on Ecoli-0-6-7_vs_3-5, Pima, Vowel and Yeast-0-2-5-6_vs_3-7-8-9 are shown in Fig. 2a, b, c and d respectively and for proposed EFLSTWSVM-CIL on Cleveland, Ecoli2, Ecoli-0-3-4-6_vs_5 and Ecoli-0-1-4-7_vs_2-3-5-6 datasets are shown in Fig. 4a, b, c and d respectively. Also from the figures, note that better accuracy could be achieved for larger values of C and smaller values of μ in case of EFLSSVM-CIL (Figs. 1 and 2) and in case of EFLSTWSVM-CIL, the better accuracy could be achieved for smaller values of C and larger values of μ (Figs. 3 and 4).

Fig. 1
figure 1

Insensitivity performance of EFLSSVM-CIL for classification to the user specified parameters (C, K) on imbalance datasets using Gaussian kernel

Full size image
Fig. 2
figure 2

Insensitivity performance of EFLSSVM-CIL for classification to the user specified parameters (μ, K) on imbalance datasets using Gaussian kernel

Full size image
Fig. 3
figure 3

Insensitivity performance of EFLSTWSVM-CIL for classification to the user specified parameters (C, K) on imbalance datasets using Gaussian kernel

Full size image
Fig. 4
figure 4

Insensitivity performance of EFLSTWSVM-CIL for classification to the user specified parameters (μ, K) on imbalance datasets using Gaussian kernel

Full size image

6 Conclusions and future work

In this paper, we have proposed new efficient variants of SVM as EFLSSVM-CIL and EFLSTWSVM-CIL to solve class imbalance problem in binary class datasets where the fuzzy membership is calculated based on entropy values of samples. Here, our proposed EFLSSVM-CIL and EFLSTWSVM-CIL solve the set of linear equations rather than solving the QPPs as in case of EFSVM, TWSVM and FTWSVM to find the decision surface. We have carried out the experiments to analyze our proposed methods against TWSVM, FTWSVM, EFSVM and NFTWSVM. It can be concluded from the results that EFLSTWSVM-CIL shows better generalization performance as compared to TWSVM, FTWSVM, EFSVM, NFTWSVM and EFLSSVM-CIL which clearly illustrates its efficacy and applicability. It has been found that EFLSTWSVM-CIL outperforms in terms of learning speed in comparison to EFSVM and EFLSSVM-CIL for both linear and non-linear case. Some heuristic approaches can be used to improve the method for parameter selection which may result in better performance.