1 Introduction

Solving muli-objective problems is one of the big challenges in different applications such as power and energy [1], Robotics [2,3,4], bioinformatics [5], mechanical engineering [6], and chemoinformatics [7, 8]. In the multi-objective problem, there is no single optimal solution, but rather a set of alternative solutions represent the optimal solutions. These solutions are optimal when no other solutions in the search space are superior to them when all objectives are considered; these solutions are known as Pareto Optimal (PO) solutions [9]. This problem can be handled by combining the objectives into one single objective with a set of weights. These weights represent the importance of each objective. However, the distribution of the weights does not guarantee finding the optimal solution [10]. A multi-objective formulation of the multi-objective problems is capable of exploring the behavior of the problems across a range of parameters and operating conditions [11]. In the multi-objective optimization algorithm, there is no single objective and the goal is to optimize different objectives. Hence, a set of solutions including the optimal solutions represents various trade-offs between different objectives [12,13,14].

Evolutionary algorithms were introduced by David Schaffer for optimizing multi-objective problems [15,16,17]. Since then, a significant number of studies have been introduced for developing multi-objective evolutionary algorithms. The evolutionary algorithms are gradient-free and they can escape from local optima traps. The literature shows that the evolutionary algorithms can approximate the true Pareto optimal solutions of multi-objective problems effectively. Many evolutionary algorithms were employed for optimizing multi-objective problems such as Non-dominated Sorting Genetic Algorithm (NSGA-I) [18], Non-dominated Sorting Genetic Algorithm version 2 (NSGA-II) [19], Strength-Pareto Evolutionary Algorithm (SPEA) [20], Multi-Objective Particle Swarm Optimization (MOPSO) [21,22,23], Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) [24], and Pareto-frontier Differential Evolution (PDE) [25]. According to the No Free Lunch (NFL) theorem [26], the superior performance of an optimization algorithm on a class of problems or applications cannot guarantee the similar performance on other problems.

Grasshopper Optimization Algorithm (GOA) was proposed recently and it has been proven to benefit from its high exploration while showing very fast convergence speed toward the optimal solutions [27]. In GOA, the special adaptive mechanism smoothly balances the exploration and exploitation phases which makes the GOA potentially able to cope with the difficulties of multi-objective problems and outperform other optimization algorithms. As reported in [27], the computational complexity of GOA is better than the complexity of many other optimization algorithms. These reasons motivated our attempts to propose a multi-objective optimizer inspired from the GOA. In this paper, we introduce a multi-objective variant of GOA, termed MOGOA, and employed it for optimizing constrained and unconstrained testing functions. A distinguishing feature of MOGOA is that an external archive which was integrated to the GOA algorithm to store non-dominated solutions. Moreover, the multi-objective version of the GOA has been proposed using the features of original GOA.

The rest of the paper is organized as follows. Section 2 presents some of the related work. Definitions and preliminaries of optimization algorithm, i.e., GOA, in a multi-objective search space were introduced in Section 3. In Section 4, the proposed algorithm MOGOA was introduced. Experimental results and discussions are presented in Section 5. Concluding remarks and future work are provided in Section 6.

2 Related work

The main goal of multi-objective optimization algorithms is to search for an accurate approximation of the exact or true Pareto optimal solutions. This problem was solved by aggregating the objectives into a single objective by using weight factors as follows, \(F={\sum }_{i = 1}^{N}w_{n}f_{n}\), where N indicates the number of objective functions, w n is the weighting factors, and f n represent the objective functions [28, 29]. In single-objective problems, the problem has one point as the global optimal solution; therefore, the solutions can be compared easily [30]. However, finding a set of solutions can be solved by using a wide variety of weight factors which is extremely time-consuming [31]. Moreover, the distribution of the weights does not guarantee finding Pareto optimal solutions [32].

There are some studies that tried to improve this method. For example, two dynamic weighted aggregations were used to adjust the weights over time [33]. However, the main problems were not completely solved using this method. Moreover, it needs to run for several times to approximate the whole Pareto solutions. Deb reported that the metaheuristics were used with the multi-objective optimization problem to overcome some difficulties such as local fronts, infeasible area, isolation of optimum, and diversity of solutions [34].

Recently, multi-objective optimization algorithms were used to approximate the whole Pareto optimal front in a single run. These algorithms address the conflicting objectives and allow the exploration of the behavior of problems across the operating conditions and a range of design parameters. Most of the well-known meta-heuristic optimization such as Genetic Algorithm (GA) [34] and Particle Swarm Optimization (PSO) [12] were used for solving the multi-objective problems.

A modified version of the GA was called Non-dominated Sorting GA (NSGA-II) and it was used for solving multi-objective problems [35]. This algorithm was proposed to solve the problems of the first version NSGA-I [18] such as the high computational cost of non-dominated sorting and lack of considering elitism. In NSGA-II, the solutions are grouped based on the non-dominating sorting method and the fitness for the individuals are defined based on its non-domination level. MOPSO was proposed by Coello et al. [12]. The MOPSO is inspired from PSO [36] and it starts by placing all particles randomly in the problem space. These particles’ positions were updated using their own non-dominated solutions, i.e., previous best positions, and the non-dominated solution the swarm has obtained so far, i.e., global best position. The MOPSO is terminated by satisfying of a stopping criterion. MOPSO has a fast convergence speed which makes it prone to parameter termination without finding the Pareto optimal front [37]. In MOPSO, an external archive was utilized for storing and retrieving the obtained Pareto optimal solutions. This external archive was also introduced in [38] to design the adaptive grid in Pareto Archived Evolution Strategy (PAES). In PAES, the archive controller component was used for deciding if a solution should be added to the archive or not. In other words, if a new solution is not dominated by the archive members, it should be added as a new member to the archive. Moreover, in PAES, the grid component is responsible for making the archive solutions diversified.

Recently, many multi-objective optimization algorithms have been proposed. For example, the Multi-Objective Cat Swarm Optimization (MOCSO) algorithm was proposed in [39] and the results were compared with MOPSO and NSGA-II. Shi Xiangui and Kong Dekui introduced the Multi-Objective Ant Colony Optimization (MOACO) algorithm [40]. Multi-objective Artificial Bee Colony (MOABC) algorithm was proposed in [41], and the proposed algorithm was used for feature selection using fuzzy mutual information. In another research, Multi-objective Gravitational Search Algorithm (MOGSA) was introduced and it outperformed the NSGA-II and MOACO algorithms [42]. Multi Objective Differential Evolution algorithm was proposed and it was compared with NSGA-II and PAES algorithms [43]. In addition, Multi-Objective Cuckoo Search Optimization (MOCSO) was proposed in [44] and Multi-Objective Gray-Wolf Optimization (MOGWO) was introduced in [45]. Further, Multi-objective Teaching Learning-Based Optimization (MOTLO) algorithm was applied for scheduling in turning processes for minimizing makespan and carbon footprint [46]. The recent studies show the ability of the metaheuristic optimization algorithms in handling multi-objective problems. However, all mentioned algorithms are not able to solve all optimization problems according to the NFL theorem. Hence, it is very likely that a new optimization algorithm solves a problem that cannot be solved by one of the existing techniques in the literature. In the next section, a novel multi-objective version of GOA is introduced as an alternative to the current optimization algorithms in the literature for solving multi-objective optimization problems.

3 Preliminaries

3.1 Multi-objective optimization

In Multi-objective Optimization Problem (MOP), the problem has two or more objective functions and it can be formulated as follows:

$$\begin{array}{@{}rcl@{}} \text{Minimize} \;\;&& F(x)=[f_{1}(x),f_{2}(x),\dots,f_{m}(x)]^{T}, \\ \text{Subject to}&& : \; g_{i}(x)\geq 0, \; i = 1,2,\dots,n, \\ &&\;\;\;\;h_{i}(x)= 0, \; i = 1,2,\dots,o, \\ &&\;\;\;\;L_{i}\leq x_{i}\leq U_{i}, \; i = 1,2,\dots,p, \end{array} $$
(1)

where \(x = [x_{1}, x_{2}, {\dots } , x_{d}]\) represents a vector of design variables, d represents the number of variables, m is the number of objective functions, g i represents the i th inequality constraint, n is the number of inequality constraints, h i (x) is the i th equality constraint, o is the number of equality constraints, and [L i ,U i ] are the boundaries for the variable x i . In MOP, the problem can be solved by storing a set of best solutions in an external archive (\(\mathcal {A}\)). This archive stores a historical record that is created for the non-dominated solutions found along the search phases. In the initialization phase, the archive is initialized and it is updated iteratively, and the best solutions are defined as non-dominated solutions or Pareto optimal solutions [47]. In multi-objective problems, the solutions cannot be compared using relational operators. This is due to multi-criterion comparison metrics. In this case, a solution can be considered as a non-dominated solution if it satisfies the following conditions:

  1. 1.

    Pareto dominance: Given two vectors \(W = (w_{1}, w_{2},{\dots } , w_{n})\) and \(V = (v_{1}, v_{2}, \dots , v_{n})\). W dominates V if and only if W is partially less than V in the objective space as follows:

    $$ \left\{\begin{array}{llll} f_{i}(W)\leq f_{i}(V)& \forall \; i\;,\; i = 1,2,\dots,m, \\ f_{i}(W)< f_{i}(V)& \exists \; i, \end{array}\right. $$
    (2)

    where m represents the number of objective functions [48].

  2. 2.

    Pareto optimal solution: vector W represents a Pareto optimal solution if and only if any other obtained solutions cannot dominate W.

A set of Pareto optimal solutions is called a Pareto (Optimal Front) P F O p t i m a l and it consists of a set of non-dominated solutions. The goal for any optimization algorithm is finding the most accurate approximation of true Pareto optimal solutions, i.e., convergence, with uniform distributions across all objectives [49].

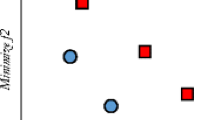
Figure 1 shows an overview of non-dominated solutions in MOP. As shown, the problem is multi-objective and it has two objective functions, i.e. the space is two-dimensional, and the goal is to find a solution that minimizes the objective functions. In the figure, the values for f 1 and f 2 of the C solution are higher than the A and B solutions. Hence, C is dominated by A and B. On the other hand, the A and B solutions are considered as non-dominated solutions because neither of them dominates the other.

Fig. 1
figure 1

Illustrative example of the optimal Pareto solution in two-dimensional space, i.e., two objective functions. The solution C is dominated by the A and B solutions

Full size image

3.1.1 Performance metric parameters

For fair comparisons among different types of multi-objective evolutionary algorithms, in this study, three well-known assessment measures are used to evaluate the performance of metaheuristic algorithms. The details of each measure are explained below.

Metric of spacing

The goal of this metric is to show the distribution of non-dominated solutions which are obtained by a specific algorithm [34]. This metric is defined as follows:

$$ S=\sqrt{\frac{1}{n_{pf}-1}\sum\limits_{i = 1}^{n_{pf}}(d_{i}-\hat{d})^{2}} $$
(3)

where S is the metric of spacing, d i represents the Euclidean distance between the i th member in P F g and nearest member in P F g , P F g is the generated Pareto front (see Fig. 2), and \(\hat {d}\) is the average of all distances. The Euclidean distance is defined in (4). A small value of S gives the best uniform distribution in P F g , and the value of S will be zero when \(d_{i}=\hat {d}\), i.e., all non-dominated solutions are uniformly distributed.

$$ d(a,b)=d(b,a)=\sqrt{\sum\limits_{i = 1}^{n}(f_{ia}-f_{ib})^{2}} $$
(4)

where \(a = (f_{1a}, f_{2a}, f_{3a},\dots , f_{na})\) and \(b = (f_{1b}, f_{2b}, f_{3b}, \dots , f_{nb})\) represents two points on the P F g .

Fig. 2
figure 2

Illustration of the metric of spacing for MOPs

Full size image

Metric of spread

The spread metric (Δ) was proposed by Deb, and it determines the extent of spread attained by the non-dominated solutions which are obtained from a specified algorithm [34]. Hence, this metric can analyze how the obtained solution is extended across the Pareto optimal fronts, and it is defined as follows:

$$ {\Delta}=\frac{d_{f}+d_{l}+\sum\limits_{i = 1}^{n_{pf}}|d_{i}-\hat{d}|}{d_{f}+d_{l}+(n_{pf}-1)\hat{d}} $$
(5)

where d f and d l represent the Euclidean distances between the extreme solutions in P F O p t i m a l and P F g , respectively, as shown in Fig. 3, d i indicates the Euclidean distance between each point in P F g and the closest point in P F O p t i m a l , n p f is the total number of members in P F g , and \(\hat {d}\) is the average of all distances. As indicated in (5), the value of Δ is always greater than or equal to zero, and a small value of Δ indicates better spread of the obtained solution; Δ = 0 is the best solution indicating that extreme solutions of P F O p t i m a l have been found and \(d_{i}=\hat {d}\) for all non-dominated points.

Fig. 3
figure 3

Illustration of the spread metric (Δ) for MOPs

Full size image

Generational distance metric

The generational distance (GD) metric was first introduced by Veldhuizen and Lamont, and the goal of this metric is to show the capability of different problems which are used for finding a set of non-dominated solutions having the lowest distance with the P F O p t i m a l [50]. Therefore, the algorithm with the minimum GD results has the best convergence to P F O p t i m a l [51]. The definition of GD is as follows:

$$ GD=\frac{1}{n_{pf}}\sqrt{\sum\limits_{i = 1}^{n_{pf}}{d_{i}^{2}}} $$
(6)

where n p f represents the number of members in the generated Pareto front or the obtained Pareto front P F g and d i is the Euclidean distance between i th member in P F g and the nearest member in P F O p t i m a l .

Figure 4 displays an illustration of the GD metric in two-dimensional space. In GD metric, the best obtained value is equal to zero which corresponds to P F g exactly covers the P F O p t i m a l [52].

Fig. 4
figure 4

Illustration of the GD metric for MOPs

Full size image

3.2 Grasshopper optimization algorithm (GOA)

Grasshopper Optimization Algorithm (GOA) is a new nature-inspired algorithm that was proposed by Mirjalili et al. [27]. This algorithm as many optimization algorithms has two phases: exploration and exploitation. In the exploration phase, the search agents are encouraged to move for searching or exploring different regions in the search space. While in the exploitation phase, the agents move locally to enhance the current solutions. These two phases can be implemented using GOA.

Mathematically, the GOA simulates the swarming behavior as follows:

$$ X_{i}= S_{i}+G_{i}+ A_{i} $$
(7)

where X i is the position for the i th grasshopper, S i is the social interaction for the i th grasshopper, G i represents the gravity force for the i th grasshopper, and A i represents the wind advection for the i th grasshopper. The random behavior of the GOA can be written as follows, X i = r 1 S i + r 2 G i + r 3 A i , where r 1, r 2, and r 3 are random numbers in [0, 1].

The social interaction is given by:

$$ S_{i}=\sum\limits_{\begin{array}{c} j = 1\ \\ j\ \neq i \end{array} }^{N} {s (d_{ij})} \hat{d_{ij}} $$
(8)

where N is the total number of grasshoppers, d i j refers to the distance between the i th and the j th grasshoppers as follows, d i j = |x j − x i |, s is a function that defines the strength of social forces and it is defined as in (9), and \(\hat {d_{ij}}\) represents a unit vector from the i th grasshopper to the j th grasshopper as follows, \(\hat {d_{ij}}= \frac {x_{j}- x_{i}}{d_{ij}}\).

$$ s(r)=fe^{\frac{-r}{l}}-e^{-r} $$
(9)

where f is the intensity of attraction and l represents the attractive length scale. GOA has three different zones, namely, comfort, attraction, and repulsion zones; and the values of f and l change the comfort zone or comfortable distance which results in different social behaviors in artificial grasshoppers (see Fig. 5). It is worth mentioning that the attraction or repulsion regions are very small for some values, e.g., l = 1.0 and f = 1.0. In this study, we have chosen l = 1.5 and f = 0.5 as in the original paper of GOA [27]. Moreover, the function s divides the space between two grasshoppers into attraction region, comfort zone, and repulsion region.

Fig. 5
figure 5

Behavior of the function s with different values of l and f

Full size image

The G i component in (7) is defined as follows:

$$ G_{i}=-g\hat{e_{g}} $$
(10)

where g indicates the gravitational constant and \(\hat {e_{g}}\) is a unit vector toward the center of earth.

The third component in (7), i.e., A i , is defined as follows:

$$ A_{i}=u\hat{e_{w}} $$
(11)

where u is a constant drift and \(\hat {e_{w}}\) represents a unit vector in the direction of wind.

Substituting the S, G, and A components in (7) as follows:

$$ X_{i}=\sum\limits_{\begin{array}{c} j = 1\ \\ j\ \neq i \end{array} }^{N}{s (\left|x_{j}- x_{i}\right|)} \frac{x_{j}- x_{i}\ }{d_{ij}}-g\hat{e_{g}} + u\hat{e_{w}} $$
(12)

As reported in [27], (12) was not used in swarm simulation and optimization. This is because the grasshoppers quickly reach the comfort zone; hence, the swarm does not converge to the optimal solution. Therefore, (12) prevents the GOA from exploring and exploiting the search space around the current solutions. Some modifications were added to (12) to solve this problem as follows [27]:

$$ {X_{i}^{d}}= c \left( \sum\limits^{N}_{\begin{array}{c} j = 1 \\ j\ \neq i \end{array} } c \frac{ub_{d}-lb_{d}}{2} s (|{x_{j}^{d}}- {x_{i}^{d}}|) \frac{x_{j}- x_{i}}{d_{ij}} \right) + \hat{T_{d}} $$
(13)

where u b d and l b d represent the upper and lower bounds, respectively, in the d th dimension, \(\hat {T_{d}}\) indicates the target value in the d th dimension and it also represents the best solution found, c represents a decreasing coefficient and this parameter is used to shrink the attraction zone, comfort zone, and repulsion zone. In (13), S is similar to S component in (12) but the G and A components are not found and the wind direction is always toward the target \(\hat {T_{d}}\).

The parameter c has been used twice in (13) for the following reasons:

  • The first c from the left is similar to inertia weight w in PSO [36], loudness in Bat algorithm [53], or \(\vec {a}\) in Grey Wolf Optimization [54]. The goal of c is to reduce the movements of the grasshoppers around the target. Thus, it balances between exploration and exploitation of the GOA. The value of c is given by:

    $$ c = c_{max} - t \frac{c_{max}-c_{min}}{t_{max}} $$
    (14)

    where c m a x is the maximum value of c, c m i n represents the minimum value of c, t is the current iteration, and t m a x is the maximum number of iterations. In this study, the values of c m i n and c m a x were 0.00001 and 1, respectively. Hence, \(c\rightarrow c_{min}\), where \(t\rightarrow \infty \) .

  • The goal of the second c is to decrease the comfort zone, repulsion zone, and attraction zone between grasshoppers. Hence, using this term (c), the repulsion/attraction forces between different grasshoppers decrease proportionally with the number of iterations.

Generally, in GOA, the search agents moved based on their current positions, global best, and the position of all other search agents. While in one of the well-known optimization algorithms PSO, the positions are updated based on the current position, personal best, and global best. Hence, in PSO, none of the other particles contribute to modifying the position of a particle; on the other hand, in GOA, all search agents are required to get involved in finding next position of each search agent. In other words, GOA increases the social capabilities of its agents which reflects how the GOA is more social than PSO, and this will help the GOA to escape from local minima traps.

4 Multi-objective grasshopper optimization algorithm (MOGOA)

Our proposed multi-objective optimization algorithm has two main goals. First, an accurate approximation for the true Pareto optimal solutions should be obtained. Second, the obtained solution should be well-distributed across all objectives.

Comparing different solutions in multi-objective algorithms cannot be achieved using regular relational operators, instead, a Pareto optimal dominance is utilized. The best Pareto optimal solutions are saved in an external archive. The main difference between the MOGOA and GOA is the process of updating the target which guides the search agents toward promising regions of the problem space. This target can be easily chosen in a single-objective problems by selecting the best solution. In MOGOA, the Pareto optimal solutions are added to the archive and the target is chosen from these solutions to improve the distribution of the current solutions in the archive. This can be achieved through calculating the distance between each solution and a number of neighboring solutions. Next, the number of neighboring solutions is counted and it is used to measure the crowdedness of regions in the Pareto optimal front. Equation (15) defines the probability of choosing the target (P i ) from the current solutions in the archive.

$$ P_{i}=\frac{1}{N_{i}}, $$
(15)

where N i represents the number of solutions in the neighborhood of the i th solution. Based on P i , a roulette wheel is used to select the target from the archive. This improves the distribution of less distributed regions of the search space.

The archive has a limitation, i.e., maximum number of solutions, that can be stored in the archive. Increasing the size of the archive increases the computational cost. On the other hand, decreasing the size of the archive may lead to the issue of a full archive. Hence, to solve this problem, solutions in a crowded neighborhood are removed. This will give a chance for a new solution to be stored in less populated regions.

The content of the archive should be updated regularly. This can be achieved by comparing the solution in the archive with a new external solution. In MOGOA, there are two cases:

  • when the external solution is dominated by at least one of the archive solutions, the external solution should be thrown away.

  • when the external solution is non-dominated with respect to all solutions inside the archive. Thus, a non-dominated solution, i.e., external solution, should be added to the archive. However, if the external solution dominates a solution inside the archive, it should be replaced with it.

Generally, the MOGOA is capable of finding the Pareto optimal solutions, save them in the archive, and their distribution are improved. The steps of the proposed MOGOA algorithm are summarized in Algorithm 1.

figure f

It is worth mentioning that the computational complexity of the MOGOA algorithm is O(M N 2), where M and N represent the number of objectives and the number of solutions, respectively, while the computational complexity of NSGA [19] and SPEA [20] algorithms are O(M N 3). This reflects how the proposed MOGOA is faster for finding the optimal or near optimal solutions than some of the state-of-the-art algorithms.

5 Experimental results and discussion

In this section, we describe the results we obtained from a set of experiments for evaluating the proposed MOGOA algorithm. The aim of the first set of experiments is to test our algorithm using unconstrained testing functions (see Section 5.2). In the second set of experiments, the aim was to evaluate our algorithm using constrained functions (see Section 5.3). In all experiments, to see how the proposed algorithm performs in comparison with other algorithms, the results of MOGOA algorithm were compared with MOPSO [49], NSGA-II [49], and MOALO [55] algorithms.

5.1 Experimental setup

In order to get an unbiased comparison of CPU times, all the experiments are performed using the same PC with the detailed settings as shown in Table 1.

Table 1 The detailed settings
Full size table

In this section, 12 test problems were selected to evaluate the performance of the proposed MOGOA algorithm. The benchmark functions were divided into two groups, namely, Constrained and Unconstrained. Each group has six testing functions. In both experiments, the testing functions with diverse characteristics and especially different Pareto optimal Front (PF) were chosen to test the performance of MOGOA from different perspectives. The details of the unconstrained functions are listed in Table 2, while the details of the constrained testing functions are summarized in Section 5.3. For each algorithm, the optimization task was run 10 times for all benchmark problems, and the obtained results are illustrated in the form of average ± standard deviation. Moreover, the maximum number of iterations was 100 and the search of agents was 100.

Table 2 Unconstrained test functions
Full size table

Different assessment methods have been used to evaluate the performance of the proposed algorithm such as: (1) metric of spacing [56], (2) metric of spread [57], and (3) generational distance (GD) [50]. Moreover, for comparison between multiple algorithms and multiple test functions, the average ranks were used. For each given testing function, the algorithms are sorted from best to worst, and the best algorithm receives rank 1, the second best algorithm receives rank 2, and so on. The average ranks are assigned in case of a tie, e.g. if two algorithms tie for the top rank, they both receive rank 1.5. Average ranks of all testing functions are then calculated. Moreover, we used the non-parametric Wilcoxon signed rank test for all of the testing functions to compare different algorithms [58].

5.2 Unconstrained test functions

The goal of this experiment is to evaluate the proposed MOGOA algorithm and compare it with three well-known algorithms MOPSO [49], NSGA-II [49], and MOALO [55]. In this experiment, six unconstrained testing functions were used (ZDT1, ZDT2, ZDT3, ZDT4, ZDT6, and Linear ZDT1 or simply LZDT1); these testing functions are well-known ZDT test suite and it was used in [59]. The first five test functions in this study are identical to those in the original ZDT suite, another last test function is slightly different in the same manner similar to [49]. The details of these functions are summarized in Table 2. Figure 6 shows the obtained Pareto optimal solutions of all algorithms using unconstrained functions. The results of this experiment are summarized in Tables 3, 4, and 5.

Fig. 6
figure 6

Obtained Pareto optimal solutions by the MOGOA, MOALO, MOPSO, and NSGA-II algorithms with unconstrained functions

Full size image
Table 3 Statistical results of metric of spacing with unconstrained testing functions
Full size table
Table 4 Statistical results of metric of spread with unconstrained testing functions
Full size table
Table 5 Statistical results of generation distance metric with unconstrained testing functions
Full size table

Tables 3, 4, and 5 allow us to draw the following conclusions:

  • In terms of the metric of spacing, the MOGOA achieved results better than all the other algorithms in most cases. As shown in Table 3, the MOGOA achieved the best results with all testing functions and it achieved the second best results with ZDT3. In addition, the MOALO and MOPSO obtained the second and third best solutions, respectively. Moreover, from the table, the results with ∗ sign means that the p-value for this algorithm is larger than the predicted statistical significance level of 0.005. As shown, the p-value for ZDT3 with MOPSO algorithm and ZDT4 with MOALO algorithm were greater than the predicted statistical significance level of 0.005, but the other p-values are smaller than the significance level of 0.005. Further, Fig. 7 shows the average ranks for all algorithms and as shown, the MOGOA achieved the lowest, i.e., best, rank.

    Fig. 7
    figure 7

    Average ranking of the comparison between the proposed MOGOA algorithm and the other three algorithms, i.e., MOALO, MOPSO, and NSGA-II, with the unconstrained testing functions

    Full size image

  • In terms of metric of spread results, as shown in Table 4, the MOGOA achieved the best results with all testing functions except with ZDT2 the MOGOA obtained the second best results. Moreover, the MALO obtained the second best results and NSGA-II obtained the worst results. These results are in agreement with Fig. 7. As shown, the MOGOA algorithm obtained the best rank. Additionally, from the table, the p-value for ZDT2 with MOALO algorithm was greater than the predicted statistical significance level of 0.005, but the other p-values are smaller than the significance level of 0.005.

  • In terms of GD results, as shown in Table 5, the MOGOA algorithm outperformed the other three algorithms in most cases. As shown, with the ZDT3 and ZDT4 testing functions the MOGOA obtained the second best results and obtained the best results with the other testing functions. Moreover, the MOALO achieved the second best results and the NSGA-II obtained the worst results. Figure 7 shows that the MOGOA algorithm obtained results better than the other algorithms. Further, from Table 5 the p-values for ZDT3 (with MOALO and MOPSO) and ZDT4 (with MOALO) testing functions were greater than the predicted statistical significance level of 0.005, but the other p-values are smaller than the significance level of 0.005.

Figure 6 illustrates the best PF obtained (in one run) by MOGOA, MOALO, MOPSO, and NSGA-II algorithms with the unconstrained functions. As shown, the NSGA-II shows the worst convergence which is in agreement with the obtained results. Moreover, the MOGOA, MOALO, and MOPSO algorithms provide a very good convergence toward all true Pareto-optimal fronts.

To conclude, compared with the MOPSO, MOALO, and NSGA-II algorithms, the proposed MOGOA algorithm achieved the best results and a better convergence toward all the true Pareto optimal fronts.

5.3 Constrained test functions

The aim of this experiment is to evaluate the performance of the proposed MOGOA algorithm when six constrained testing functions were used (CONSTR, TNK, SRN, BNH, OSY, and KITA). The results of the MOGOA were compared with MOPSO, NSGA-II, and MOALO algorithms. The details of these functions are summarized in this section. Figure 8 shows the obtained Pareto optimal solutions for all optimization algorithms with all constrained functions. The results of this experiment are summarized in Tables 6, 7, and 8.

Fig. 8
figure 8

Obtained Pareto optimal solutions by the MOGOA, MOALO, MOPSO, and NSGA-II algorithms with constrained functions

Full size image
Table 6 Statistical results of metric of spacing with constrained testing functions
Full size table
Table 7 Statistical results of metric of spread with constrained testing functions
Full size table
Table 8 Statistical results of generation distance metric with constrained testing functions
Full size table

The details of the constrained testing functions that were used in our experiments are as follows:

  1. 1.

    CONSTR: This function represents a mathematical problem and it has two design variables [34]. The Pareto optimal front for this function is convex and the function is defined as follows:

    $$\begin{array}{@{}rcl@{}} Minimize \;\;&& F(f_{1}(x),f_{2}(x)), \text{where} \\ &&f_{1}(x) = x_{1}, \\ &&f_{2}(x) =\frac{(1+x_{2})}{(x_{1})}, \end{array} $$
    (16)

    Subject to:

    $$\begin{array}{@{}rcl@{}} g_{1}(x)= 6 - (x_{2} + 9x_{1})\leq 0, \\ g_{2}(x)= 1 + x_{2}- 9x_{1} \leq 0, \\ 0.1 \le x_{1} \le 1, 0 \le x_{2} \le 5 \end{array} $$
    (17)
  2. 2.

    TNK: This function has two design variables and it is defined as in (18). This function has some convex regions and it has discontinuous Pareto optimal front which lies on the boundary of the first constraint [60].

    $$\begin{array}{@{}rcl@{}} Minimize && : F(f_{1}(x),f_{2}(x)), \text{where} \\ && \;\;\;f_{1}(x) = x_{1}, \\ && \;\;\;f_{2}(x) = x_{2}, \end{array} $$
    (18)

    Subject to:

    $$\begin{array}{@{}rcl@{}} && g_{1}(x)\,=\,- {x^{2}_{1}} - {x^{2}_{2}} \,+\, 1 \,+\,0.1 Cos(16 arctan (\frac{x_{1}}{x_{2}}))\leq 0, \\ && g_{2}(x) \,=\, 0.5 \!- (x_{1} \!- 0.5)^{2}\!-(x_{2} \!- 0.5)^{2}\leq 0, \\ && 0.1 \!\le x_{1} \!\le \pi, 0 \!\le x_{2}\!\le\pi \end{array} $$
    (19)
  3. 3.

    SRN: This function is introduced by Srinivas and Deb in [57]. It has two design variables with a continuous Pareto optimal front. It is given by:

    $$\begin{array}{@{}rcl@{}} Minimize && : F(f_{1}(x),f_{2}(x)), \text{where} \\ &&\;\;\;f_{1}(x) = 2 + (x_{1} - 2)^{2}+ (x_{2} - 1)^{2}, \\ &&\;\;\;f_{2}(x) = 9x_{1} - (x_{2} - 1){2}, \end{array} $$
    (20)

    Subject to:

    $$\begin{array}{@{}rcl@{}} &&g_{1}(x) = {x^{2}_{1}}+ {x^{2}_{2}}-255\leq 0, \\ &&g_{2}(x) = x_{1} - 3x_{2} + 10\leq 0, \\ && -20 \le x_{1}\le 20, - 20 \le x_{2}\le 20 \end{array} $$
    (21)
  4. 4.

    BNH: This function was first introduced by Binh and Korn in [61], and it is defined as follow:

    $$\begin{array}{@{}rcl@{}} Minimize: &&\;\; F(f_{1}(x),f_{2}(x)), \text{where} \\ && \;\;\;f_{1}(x) = 4{x^{2}_{1}}+ 4{x^{2}_{2}}, \\ && \;\;\;f_{2}(x) = (x_{1}- 5)^{2} + (x_{2}-5)^{2}, \end{array} $$
    (22)

    Subject to:

    $$\begin{array}{@{}rcl@{}} && g_{1}(x) = (x_{1} -5)^{2} + {x^{2}_{2}}- 25\leq 0, \\ && g_{2}(x) = 7.7 - (x_{1}- 8)^{2}-(x_{2} + 3)^{2}\leq 0, \\ && 0 \le x_{1} \le 5, 0 \le x_{2} \le 3 \end{array} $$
    (23)
  5. 5.

    OSY: The OSY function has five separated regions and it was proposed by Osyczka and Kundu [62]. Moreover, it has six constraints and six design variables. The definition of this variable is as follows:

    $$\begin{array}{@{}rcl@{}} Minimize: && F(f_{1}(x),f_{2}(x)), \text{where} \\ && \;f_{1}(x)= {x^{2}_{1}}+ {x^{2}_{2}}+ {x^{2}_{3}}+ {x^{2}_{4}}+ {x^{2}_{5}}+ {x^{2}_{6}}, \\ && \;f_{2}(x)=[25(x_{1} -2)^{2}+ (x_{2}- 1)^{2}+(x_{3}- 1) \\ && \;+(x_{4}- 4)^{2} + (x_{5}- 1)^{2}], \end{array} $$
    (24)

    Subject to:

    $$\begin{array}{@{}rcl@{}} &&g_{1}(x) = 2- x_{1}- x_{2}\leq 0, \\ &&g_{2}(x) = -6 + x_{1} + x_{2}\leq 0, \\ &&g_{3}(x) = -2 - x_{1} + x_{2}\leq 0, \\ &&g_{4}(x) =-2 + x_{1}- 3x_{2}\leq 0, \\ &&g_{5}(x) =-4 + x_{4} + (x_{3}- 3)^{2}\leq 0, \\ &&g_{6}(x) = 4 - x_{6}- (x_{5}- 3)^{2}\leq 0, \\ &&0 \le x_{1}\le 10, 0 \le x_{2} \le 10, 1 \le x_{3}\le 5, \\ &&0 \le x_{4}\le 6, 1 \le x_{5}\le 5, 0 \le x_{6} \le 10 \end{array} $$
    (25)
  6. 6.

    KITA: This function was introduced by Kita et al. [63], and it has been widely used. The mathematical formula for this function is as follows:

    $$\begin{array}{@{}rcl@{}} Maximize && : \;F(f_{1}(x),f_{2}(x)), \text{where} \\ &&\;\;\;f_{1}(x) = -{x^{2}_{1}}+ x_{2}, \\ &&\;\;\;f_{2}(x) = \frac{1}{2}x_{1}+x_{2}+ 1, \end{array} $$
    (26)

    Subject to:

    $$\begin{array}{@{}rcl@{}} && g_{1}(x) = \frac{1}{6} x_{1}+x_{2} - \frac{13}{2} \le 0 \\ && g_{2}(x) = \frac{1}{2} x_{1}+x_{2}- \frac{15}{2} \le 0 \\ && g_{3}(x) = 5x_{1}+x_{2}-30 \le 0 \\ && 0 \le x_{1} , x_{2} \le 7 \end{array} $$
    (27)

From Tables 6, 7, and 8, the following notes can be remarked:

  • In terms of the metric of spacing, the MOGOA obtained results better than all the other algorithms in most cases. As shown in Table 6, the MOGOA achieved the best results with all testing functions and it achieved the second best results with the CONSTR and TNK functions. Additionally, the MOALO and MOPSO obtained the second and third best solutions, respectively. Moreover, from the table, the results with ∗ sign means that the p-value for this algorithm is larger than the predicted statistical significance level of 0.005 (as in the first experiment). As shown, the p-value for CONSTR, TNK, and KITA with MOALO algorithm were greater than the predicted statistical significance level of 0.005, but the other p-values are smaller than the significance level of 0.005. Further, Fig. 9 shows the average ranks for all algorithms and as shown the MOGOA achieved the lowest, i.e., best, rank, and the NSGA-II algorithm was the worst one.

    Fig. 9
    figure 9

    Average ranking of the comparison between the proposed MOGOA algorithm and the other three algorithms, i.e., MOALO, MOPSO, and NSGA-II, with the constrained testing functions

    Full size image

  • In terms of metric of spread results, as shown in Table 7, the MOGOA obtained the best results with all testing functions except with SNR function the MOGOA obtained the second best results. Moreover, the MOALO obtained the second best results in most cases and the NSGA-II algorithm obtained the worst results. These results are in agreement with Fig. 9. As shown, the MOGOA algorithm obtained the best rank and the NSGA-II attained the highest, i.e., worst, rank. Additionally, from the table, the p-value for SRN and BNH testing functions with MOALO algorithm was greater than the predicted statistical significance level of 0.005, but the other p-values are smaller than the significance level of 0.005.

  • In terms of GD results, as shown in Table 8, the MOGOA algorithm outperformed the other three algorithms in all cases, and the MOALO achieved the second best results, while the MOPSO and NSGA-II algorithms obtained the worst results. Figure 9 displays that the MOGOA algorithm obtained results better than the other algorithms. Further, from Table 8 the p-values for SNR and BNH testing functions with MOALO algorithm were greater than the predicted statistical significance level of 0.005, but the other p-values are smaller than the significance level of 0.005.

Figure 8 displays the PF obtained (in one run) by MOGOA, MOALO, MOPSO, and NSGA-II algorithms with the constrained functions. As shown, the constrained test functions have very different Pareto fronts compared with the unconstrained test functions, such as CONSTR, BNH, and OSY. CONSTR function has a concave front attached to a linear front. As shown, the MOGOA and MOALO managed to approximate the CONSTR function successfully. The OSY function is slightly similar to CONSTR function but with multiple linear regions with different slopes. Moreover, the TNK function has a wave-shaped front. As shown in Fig. 8, the MOGOA and MOALO algorithms provide a very good convergence toward most of the true Pareto-optimal fronts.

Generally, the proposed MOGOA algorithm obtained the best results and a competitive convergence toward all the true Pareto optimal fronts compared with the MOPSO, MOALO, and NSGA-II algorithms.

6 Conclusions

This paper proposed a multi-objective version of the recently proposed Grasshopper optimization algorithm (GOA) called MOGOA. The proposed algorithm was designed by integrating the GOA with an external archive and grasshopper selection mechanism based on Pareto optimal dominance. The goal of the external archive is to keep non-dominated solutions. The proposed MOGOA utilized the same features of the GOA. The MOGOA was verified by 12 testing functions including six unconstrained functions and six constrained functions. In our experiments, three assessment methods were used: generational distance metric, metric of spacing, and metric of spread. The findings of our experiments proved that the proposed MOGOA was able to find the optimal Pareto front (PF) and provide a superior quality of solutions in comparison with a variety of other algorithms such as Multi-Objective Particle Swarm Optimization (MOPSO), Multi-Objective Ant Lion Optimizer (MOALO), and Non-dominated Sorting Genetic Algorithm version 2 (NSGA-II). In general, according to the reported results, the MOGOA offers competitive solutions compared with the other multi-objective algorithms and it offers a wider range of non-dominated solutions.

For future studies, we are planning to employ the MOGOA algorithm in machine learning-related applications. In this area, some applications have many problems with different objectives such as feature selection, parameter optimization, i.e., parameter tuning, and data preprocessing. Our next goal is to employ the MOGOA in such problems. Moreover, different modifications will be added to the MOGOA such as using Chaotic maps, this is called Chaotic optimization, for generating values for c parameter. This modification can help the MOGOA to converge to the optimal solution faster than standard stochastic search as reported in [64].