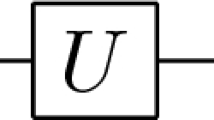An introduction to variational quantum algorithms for combinatorial optimization problems

Abstract

Noisy intermediate-scale quantum computers are now readily available, motivating many researchers to experiment with Variational Quantum Algorithms. Among them, the Quantum Approximate Optimization Algorithm is one of the most popular one studied by the combinatorial optimization community. In this tutorial, we provide a mathematical description of the class of Variational Quantum Algorithms, assuming no previous knowledge of quantum physics from the readers. We introduce precisely the key aspects of these hybrid algorithms on the quantum side (parametrized quantum circuit) and the classical side (guiding function, optimizer). We devote a particular attention to QAOA, detailing the quantum circuits involved in that algorithm, as well as the properties satisfied by its possible guiding functions. Finally, we discuss the recent literature on QAOA, highlighting several research trends.

1 Introduction

This tutorial, which is an updated version of Grange et al. (2023), aims at providing the operational research community with some background knowledge of quantum computing and explore the particular branch of heuristic quantum algorithms for combinatorial optimization. Today, the quantum information theory community is excited by the emergence of quantum computers first theorized in the 1980 s. Indeed, since then, some theoretical advantages of quantum algorithms compared with classical algorithms have been proved for several problems. For instance, the Quantum Phase Estimation (Kitaev, 1995), which is the subroutine of Shor’s algorithm (Shor, 1994), enables the latter to solve the integer factorization problem efficiently. Moreover, Grover Search (Grover, 1996) finds an element in an unstructured base with a quadratic speedup compared with classical algorithms. This algorithm is also used as a subroutine in dynamic programming algorithms to improve their exponential complexity for problems such as the Travelling Salesman Problem and the Minimum Set Cover (Ambainis et al., 2019). More recently, a polynomial speedup that relies on a Quantum Interior Point Method (Kerenidis & Prakash, 2020) applies to Linear Programming, Semi-Definite Programming, and Second-Order Cone Programming (Kerenidis et al., 2021). Furthermore, a quantum subroutine for the Simplex also provides a polynomial speedup (Nannicini, 2021). One can also mention the subroutine that quantum walks represent in backtracking algorithms (Montanaro, 2015), themselves used in quantum Branch-and-Bound achieving an almost quadratic speedup (Montanaro, 2020). Other problems or methods in optimization going beyond combinatorial optimization are studied with a quantum approach as presented in Abbas et al. (2023).

These algorithms prove quantum advantages on numerous problems, but their implementations require a lot of quantum resources with high quality. Specifically, they need quantum computers with many qubits that can interact two by two and quantum operations that can be applied in a row on qubits without generating noise, namely they can support deep-depth quantum circuits. Such quantum computers are believed to be built in the medium term but current devices are noisy intermediate-scale quantum computers, usually referred to as NISQ computers (Preskill, 2018). Therefore, NISQ computers cannot handle the implementations of such algorithms. These physical limitations encouraged quantum algorithm theory to look into lighter quantum algorithms to implement them on quantum computers today. It consists of hybrid algorithms that require both quantum and classical resources. Indeed, the classical part overcomes the limited and noisy quantum resources, whereas the quantum part still takes partial advantage of quantum information theory. This tutorial focuses on a particular type of hybrid algorithm, that is the class of Variational Quantum Algorithms (VQAs).

Variational Quantum Algorithms are heuristic algorithms that alternate between a quantum circuit and a classical optimizer. They tackle optimization problems of the form

$$\begin{aligned} \min _{x\in \{0,1\}^n} f(x), \end{aligned}$$

(1)

where f is any function defined on $\{0,1\}^n$. VQAs are of great interest to the quantum information theory community today because they have the convenient property of an adjustable quantum circuits’ depth, making them implementable on the current NISQ computers. The variational approach of VQAs (Cerezo et al., 2021) consists of probing the initial search space $\{0,1\}^n$ with a relatively small set of parameters optimized classically. Specifically, these parameters describe a probability distribution over the search space. This description results from a sequence of quantum logic gates: this is a quantum circuit. VQAs take advantage of the quantum computing principle (Nielsen & Chuang, 2022) that prepares a probability distribution over an exponential search space in a short sequence of quantum gates. The choice of the quantum circuit, and in particular the number of parameters, is a huge stake for VQAs (Nannicini, 2019). On the one hand, the more parameters, the more precise the search space probing. On the other hand, too many parameters can harden the classical optimization part. The function that drives this optimization, which depends on the probability distribution and f, is also a non-trivial choice and worth investigating (Barkoutsos et al., 2020).

In this tutorial, we provide a mathematical description of Variational Quantum Algorithms and focus on one of them, specifically the Quantum Approximate Optimization Algorithm (QAOA) (Farhi et al., 2014). We shall also devote particular attention to problems in which f is a polynomial function. In Sect. 2, we give a brief introduction to the basics of quantum computing for combinatorial optimization. Notice that the model of quantum computation considered is the gate-based model, also called the circuit model. Then, in Sect. 3, we describe the general class of VQAs, starting by defining the different parts that constitute and define a VQA, namely the quantum circuit (also called ansatz in the literature), the classical optimizer, and the guiding function driving the classical optimization. Then, we characterize each part with properties that should be valid for potential theoretical guarantees. Eventually, in Sect. 4, we focus on a particular case of VQAs, the Quantum Approximate Optimization Algorithm. We describe the necessary reformulation of the initial problem (1) into a Hermitian matrix (also called Hamiltonian in the literature) to be solved by QAOA and analyze this algorithm in light of the previous properties of Sect. 3. We also provide a universal decomposition of the QAOA quantum circuit for the general case where f is polynomial while, as far as we know, only the quadratic f case had been treated in the literature so far. Finally, we give a condensed overview of empirical trends and theoretical limitations of QAOA. We remind some helpful basic notions of linear algebra in Appendix A. Furthermore, the proofs of technical properties of the function optimized in VQAs and specific constructions of the quantum circuit in QAOA are deferred to Appendices B.1 and B.2, respectively.

2 Basics of quantum computing for combinatorial optimization

This section aims at providing the basic notions of quantum computing necessary for the understanding of the quantum resolution of combinatorial problems.

2.1 Quantum bits

Let $|0\rangle$ and $|1\rangle$ denote the basic states of our quantum computer (the counterpart of states 0 and 1 in classical computers). The first building block of quantum algorithms is the quantum bit, also called qubit.

Definition 1

(Qubit) We define a qubit as

$$\begin{aligned} |q\rangle =q_0|0\rangle +q_1|1\rangle , \end{aligned}$$

(2)

where $(q_0,q_1)\in \mathbb {C}^2$ is a pair of complex numbers that satisfies the normalizing condition

$$\begin{aligned} |q_0|^2 +|q_1|^2 = 1. \end{aligned}$$

We say that $q_0$ and $q_1$ are the coordinates of $|q\rangle$ in the basis $(|0\rangle , |1\rangle )$.

It is often convenient to use the matrix representation of $|0\rangle$ and $|1\rangle$, namely

$$\begin{aligned} |0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \text{ and } |1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}. \end{aligned}$$

With this matrix representation, the qubit $|q\rangle$ defined in (2) is equal to

$$\begin{aligned} |q\rangle = \begin{pmatrix} q_0\\ q_1 \end{pmatrix}. \end{aligned}$$

Example 2

Important examples of one-qubit states are $\frac{|0\rangle + |1\rangle }{\sqrt{2}}$ and $\frac{|0\rangle - |1\rangle }{\sqrt{2}}$. These are usually denoted as $|+\rangle$ and $|-\rangle$, respectively.

The algorithms studied in this paper typically manipulate quantum states of larger dimension. Specifically, let n denote the number of qubits that our quantum computing device is able to manipulate simultaneously. An n-qubit state is defined by $2^n$ complex numbers that satisfy the normalizing condition and represent the normal decomposition in the canonical basis.

Definition 3

(Canonical basis) The canonical basis of an n-qubit state is the set

$$\begin{aligned} \mathcal{C}\mathcal{B}_n= \left( \bigotimes _{k=1}^n|i^{(k)}\rangle , (i^{(1)},\ldots ,i^{(n)}) \in \{0,1\}^n\right) , \end{aligned}$$

where $i^{(k)}$ represents the state of the k-th qubit and $\otimes$ is the tensor product defined in Appendix A. The canonical basis is the set of all possible combinations of tensor products of n one-qubit basis states, $|0\rangle$ and $|1\rangle$. Thus, in the matrix representation, each canonical basis state is a column vector of $2^n$ components with one component equal to 1 and the rest equal to 0. It directly results that the size of the canonical basis of an n-qubit state is $2^n$. For more readability, we omit to write the tensor product between qubits, i.e., we refer to the canonical basis as

$$\begin{aligned} \mathcal{C}\mathcal{B}_n= (|i\rangle , i \in \{0,1\}^n). \end{aligned}$$

The matrix representation of canonical basis states results from the definition above. We illustrate it for the canonical basis of two qubits:

$$\begin{aligned} |00\rangle = \begin{pmatrix} 1\\ 0 \end{pmatrix}\otimes \begin{pmatrix} 1\\ 0 \end{pmatrix} = \begin{pmatrix} 1\\ 0\\ 0\\ 0 \end{pmatrix}, ~~ ~~ |01\rangle = \begin{pmatrix} 1\\ 0 \end{pmatrix}\otimes \begin{pmatrix} 0\\ 1 \end{pmatrix} = \begin{pmatrix} 0\\ 1\\ 0\\ 0 \end{pmatrix}, \\ |10\rangle = \begin{pmatrix} 0\\ 1 \end{pmatrix}\otimes \begin{pmatrix} 1\\ 0 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 1\\ 0 \end{pmatrix},~~ ~~ |11\rangle = \begin{pmatrix} 0\\ 1 \end{pmatrix}\otimes \begin{pmatrix} 0\\ 1 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix}. \end{aligned}$$

Definition 4

(n-qubit state) An n-qubit state $|\psi \rangle$ is a normalized linear combination of the basis states in $\mathcal{C}\mathcal{B}_n$,

where $(\psi _i)_{i\in \{0,1\}^n} \in \mathbb {C}^{2^n}$ are its coordinates, which satisfy the normalizing condition

$$\begin{aligned} \langle \psi \rangle =\sum _{i \in \{0,1\}^n}|\psi _i|^2 = 1. \end{aligned}$$

(3)

For $n = 1$, we find the definition of a qubit (Definition 1), as expected.

Example 5

For instance, $\frac{|00\rangle +|11\rangle }{\sqrt{2}}$, called $|\Phi ^+\rangle$, is a two-qubit state. Its matrix representation is:

$$\begin{aligned} |\Phi ^+\rangle&= \frac{|00\rangle +|11\rangle }{\sqrt{2}} \\&= \frac{1}{\sqrt{2}}\left( \begin{pmatrix} 1\\ 0 \end{pmatrix}\otimes \begin{pmatrix} 1\\ 0 \end{pmatrix} + \begin{pmatrix} 0\\ 1 \end{pmatrix}\otimes \begin{pmatrix} 0\\ 1 \end{pmatrix}\right) \\&= \frac{1}{\sqrt{2}}\left( \begin{pmatrix} 1\\ 0\\ 0\\ 0 \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix}\right) \\&= \frac{1}{\sqrt{2}}\begin{pmatrix} 1\\ 0\\ 0\\ 1 \end{pmatrix}. \end{aligned}$$

Remark 6

Our notation $(\psi _i)_{i\in \{0,1\}^n} \in \mathbb {C}^{2^n}$ for the coordinates of $|\psi \rangle$ in basis $\mathcal{C}\mathcal{B}_n$ is used to simplify the presentation throughout. It is, however, uncommon in the quantum computing literature where different bases may be used.

2.2 Quantum gates

In the model of gate-based quantum computation, qubits are manipulated with quantum gates. Mathematically speaking, these quantum gates are modeled by unitary matrices. More precisely, a quantum gate that manipulates n-qubit states is a matrix in $\mathcal {M}_{2^n}(\mathbb {C})$ that modifies the $2^n$ complex coefficients of a quantum state such that they still satisfy the normalizing condition (3).

Definition 7

(Unitary matrix) A matrix $U\in \mathcal {M}_{2^n}(\mathbb {C})$ is unitary if its inverse is equal to its conjugate transpose (denoted by the dagger symbol $\dagger$):

$$\begin{aligned} UU^{\dagger } = U^{\dagger }U= I. \end{aligned}$$

Notice that the application of a quantum gate is logically reversible.

We easily see that a unitary matrix $U$ preserves the normalizing condition since, denoting $|\psi '\rangle =U|\psi \rangle$, we have

$$\begin{aligned} \langle \psi '\rangle =\langle \psi |U^{\dagger }U|\psi \rangle =\langle \psi \rangle . \end{aligned}$$

As an illustration, we describe below all the possible one-qubit gates, i.e., all the unitary matrices in $\mathcal {M}_{2}(\mathbb {C})$.

Example 8

(Generic one-qubit gate) A generic one-qubit gate $U= \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \mathcal {M}_{2}(\mathbb {C})$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} |a|^2+|b|^2 = 1 \\ a\bar{c} + b\bar{d}= 0\\ \bar{a}c + \bar{b}d = 0\\ |c|^2+|d|^2 = 1 \end{array}\right. } \end{aligned}$$

Its application on a qubit $|q\rangle = q_0|0\rangle + q_1|1\rangle$ is:

$$\begin{aligned} U|q\rangle = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \end{pmatrix} = \begin{pmatrix} aq_0 + bq_1 \\ cq_0 + dq_1 \end{pmatrix} = (aq_0 + bq_1)|0\rangle + (cq_0 + dq_1)|1\rangle = |q'\rangle \end{aligned}$$

(4)

We introduce next the circuit representation of a quantum gate, which is a useful formalism to represent unitary matrices. Specifically, Fig. 1 represents the application of the quantum gate U to the one-qubit state $|q\rangle$, as in (4), by:

Fig. 1

Circuit of gate U applying to $|q\rangle$

This representation easily generalizes to n-qubit quantum gates, where each horizontal line is associated with a qubit.

2.3 Quantum circuits

We can manipulate quantum gates to build other quantum gates in two different ways. The first one is the composition, and the other one is the tensor product.

Definition 9

(Composition of quantum gates) The composition of gates only operates between gates acting on the same qubits. Let k be the number of involved qubits. The composition of $U_1\in \mathcal {M}_{2^k}(\mathbb {C})$ and $U_2 \in \mathcal {M}_{2^k}(\mathbb {C})$ consists of the application of $U_1$ followed by the application of $U_2$. The matrix representation of this composition is the product $U_2U_1$. The circuit representation of this composition is illustrated on Fig. 2 for $k = 3$.

Fig. 2

Composition of $U_1$ and $U_2$

It can be seen as a series sequence of gates.

Notice that we read from right to left in the matrix representation, and from left to right in the circuit representation. Moreover, in the circuit representation, qubits are numbered in ascending order from top to bottom which is important for the tensor product circuit representation that follows.

Definition 10

(Tensor product of quantum gates) The tensor product of gates only operates between gates acting on different qubits. Suppose $U_1\in \mathcal {M}_{2^k}(\mathbb {C})$ applies on the first k qubits and $U_2\in \mathcal {M}_{2^{k'}}(\mathbb {C})$ applies on the $k'$ following ones. Their tensor product is the application of $U_1$ and $U_2$ on respective qubits in parallel. The matrix representation of this tensor product is $U_1\otimes U_2$ (Definition 40). The circuit representation is depicted on Fig. 3 for $k = 3$ and $k'=2$.

Fig. 3

Tensor product of $U_1$ and $U_2$

Notice that when we apply a quantum gate on k qubits of an n-qubit system, it supposes that we apply identity gate $I = \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}$ on the qubits not concerned. For instance, let us consider a 3-qubit system on which we apply $U\in \mathcal {M}_{2}(\mathbb {C})$ on qubit number 2. The matrix representation of the resulting 3-qubit gate is $I\otimes U\otimes I$, and its circuit representation is illustrated on Fig. 4, where the application of I is usually replaced by a simple wire.

Fig. 4

Application of U to qubit number 2

One readily verifies that both composition and tensor product transform unitary matrices into a resulting unitary matrix.

Throughout, we consider that a quantum algorithm is a quantum circuit acting on n qubits, that is, a sequence of quantum gates’ compositions and/or tensor products. These quantum gates can be k-qubit gates, for $k\in [n]$. However, quantum gates involving many qubits are typically not implementable natively on quantum computers and need to be decomposed into smaller and simpler gates. This set of small gates can be considered as the quantum counterpart of the elementary logic gates used in classical circuit computing to assess the circuit complexity of a classical algorithm. Thus, an n-qubit quantum algorithm is described by a unitary matrix in $\mathcal {M}_{2^n}(\mathbb {C})$, and we decompose it as a sequence of universal gates (Definition 11) to obtain the complexity of the quantum algorithm.

Definition 11

(Set of universal gates) A set of quantum gates $PU$ is universal if we can decompose any n-qubit quantum gate through a circuit composed solely of the gates in PU.

Fortunately, there exist different universal sets of quantum gates. We introduce below such a set formed of four types of gates. First, we consider the three following families of one-qubit gates, each of which is parametrized by a real number $\theta \in \mathbb {R}$:

$$\begin{aligned} R_X(\theta )&= \begin{pmatrix} \cos {\frac{\theta }{2}} & -i\sin {\frac{\theta }{2}} \\ -i\sin {\frac{\theta }{2}} & \cos {\frac{\theta }{2}} \end{pmatrix} \end{aligned}$$

(5)

$$\begin{aligned} R_Y(\theta )&= \begin{pmatrix} \cos {\frac{\theta }{2}} & -\sin {\frac{\theta }{2}} \\ \sin {\frac{\theta }{2}} & \cos {\frac{\theta }{2}} \end{pmatrix} \end{aligned}$$

(6)

$$\begin{aligned} R_Z(\theta )&= \begin{pmatrix} e^{-i\frac{\theta }{2}} & 0 \\ 0 & e^{i\frac{\theta }{2}} \end{pmatrix}\,. \end{aligned}$$

(7)

Notice that these gates are often referred to as rotation gates because they correspond to rotations in a certain representation of qubits, known as the Bloch sphere (Mosseri & Dandoloff, 2001). Second, we consider the two-qubit gate $CX$:

$$\begin{aligned} CX= \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix}. \end{aligned}$$

(8)

$CX$ applies gate $X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$ on the second qubit if and only if the first qubit is in state $|1\rangle$. Indeed, for instance, we have

$$\begin{aligned} CX|01\rangle = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = |01\rangle \,, \end{aligned}$$

and

$$\begin{aligned} CX|11\rangle = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} = |10\rangle \,. \end{aligned}$$

In other words, we can define $CX$ on the canonical basis as

$$\begin{aligned} CX|a,b\rangle = |a,b\oplus a\rangle , \end{aligned}$$

for $a,b\in \{0,1\}$, where $\oplus$ is the addition modulo 2.

Remark 12

(Notation on gates indexes) Henceforth, we use the notation $R_{X,i}$ for the application of $R_X$ on qubit i (and the application of identity matrix on the remaining qubits). We do the same with $R_{Y,i}$ and $R_{Z,i}$. We note $CX_{i,j}$ the application of $CX$ gate to qubits i and j: X is applied to qubit j if and only if qubit i is in state $|1\rangle$.

Theorem 13

(Universal gates (Nielsen & Chuang, 2022)) The set of one-qubit gates and the $CX$ gate (8) is universal. Thus, because any one-qubit gate is the composition of rotation gates (5)–(7), the set $PU= \{R_X(\alpha ), R_Y(\beta ), R_Z(\gamma ), CX: \alpha , \beta , \gamma \in \mathbb {R}\}$ is universal.

In comparison, the sets of gates {NAND}, {NOR}, {NOT, AND} and {NOT, OR} are universal for classical computation. Indeed, we can compute any arbitrary classical function with them. In view of the above, we typically consider that the quantum counterpart of the classical number of elementary operations is the number of universal gates used to decompose the circuit. Of course, this decomposition depends on the set of universal gates $PU$ considered, but the number of gates required is the same with any set, modulo a multiplicative constant (Nielsen & Chuang, 2022). Thereafter, we only consider the set $PU$ defined in Theorem 13. This choice is motivated by the algorithms we study in this paper, as it will be convenient to express them with this set. Furthermore, if we consider the family of circuits $(\mathcal {C}_n)_{n\in \mathbb {N}}$ where $\mathcal {C}_n$ is a circuit on n qubits and is decomposed on $\mathcal {O}(poly(n))$ universal quantum gates, then this family is said to be efficient.

2.4 Non-classical behaviors

The quantum algorithms we present in this paper rely on three characteristics of quantum states with no classical equivalent: measurement, superposition, and entanglement. Let us present these notions through the bare minimum mathematical background.

2.4.1 Measurement

We need to measure a quantum state $|\psi \rangle$ to get information from it. Otherwise, no information is accessible. The peculiar property of measurement is that it only extracts partial information from the quantum state: the single measurement output of $|\psi \rangle$ is a bitstring.

Definition 14

(Measurement) In the gate-based quantum model, the measurement $\mathcal {M}$ of an n-qubit state outputs the n-bitstring i with probability $|\psi _i|^2$. After having been measured, state $|\psi \rangle$ no longer exists: it has been replaced by the state $|i\rangle$.

For example, measuring qubit $|q\rangle = q_0|0\rangle + q_1|1\rangle$ outputs 0 with probability $|q_0|^2$ and 1 with probability $|q_1|^2$, and changes the state $|q\rangle$ to $|0\rangle$ and $|1\rangle$, respectively. A measurement appears as a loss of information. Indeed, we describe an n-qubit state by $2^n$ normalized complex coefficients, but we only extract an n-bitstring after measuring it. The perfect knowledge of the probabilities representing a given quantum state $|\psi \rangle$, namely the square module of each of its coordinates $(|\psi _i|^2)_{i\in \{0,1\}^n} \in [0,1]^{2^n}$, can be obtained only if we measure $|\psi \rangle$ an infinite number of times. Notice that it requires resetting state $|\psi \rangle$ after each measurement.

Remark 15

(Sampling of quantum states) In reality we are limited to approximating a given quantum state through sampling. In particular, if $|\psi \rangle$ is the result of an algorithm, this means we have to repeat the same algorithm for every measurement of $|\psi \rangle$ we wish to perform.

2.4.2 Superposition

Classically, the state of an n-bit computer is given by a bitstring in $\{0,1\}^n$. We have seen so far that the state of an n-qubit quantum computer is given by its coordinates $(\psi _i)_{i\in \{0,1\}^n} \in \mathbb {C}^{2^n}$, which satisfy . In general, more than one of the coordinates are different from 0, meaning that measuring $|\psi \rangle$ may result in different bitstring $i \in \{0,1\}^n$.

Definition 16

(Superposition) A quantum state $|\psi \rangle$ is said in superposition if where there are at least two terms with non-zero coefficients in the sum. A quantum state that is not a basis state is in superposition.

The following Hadamard gate is the usual one-qubit gate that produces superposition starting from a canonical basis state.

Example 17

(Hadamard gate) The Hadamard gate $H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}$ is essential in quantum computing because it creates superposition starting from a basis state. We obtain the state $|+\rangle$, respectively $|-\rangle$, of Example 2 by applying H on $|0\rangle$, respectively $|1\rangle$:

$$\begin{aligned} H|0\rangle&= \frac{|0\rangle + |1\rangle }{\sqrt{2}} = |+\rangle \,,\\ H|1\rangle&= \frac{|0\rangle - |1\rangle }{\sqrt{2}} = |-\rangle \,. \end{aligned}$$

Example 18

(Uniform superposition) The two states $|+\rangle$ and $|-\rangle$ are in uniform superposition because both have the same probability of being measured as 0 or 1. In general, an n-qubit state uniformly superposed is equal to , with $\alpha _j \in [0, 2\pi [$, $\forall j \in \{0,1\}^n$. In what follows, we shall often use the uniformly superposed n-qubit state .

Notice that applying an n-qubit quantum gate $U$ to $|\psi \rangle$ possibly modifies the $2^n$ coordinates of $|\psi \rangle$ since

$$\begin{aligned} U|\psi \rangle = \sum _{i\in \{0,1\}^n}\psi '_i|i\rangle , \end{aligned}$$

where possibly each $\psi '_i$ differs from $\psi _i$. This is the case, for instance, when applying the tensor product of n Hadamard gates, each applied to a qubit initially in state $|0\rangle$, specifically

(9)

Equation (9) illustrates the potential benefit of quantum circuits: applying $\mathcal {O}(n)$ universal one-qubit gates impacts the exponentially many coefficients of $|\psi \rangle$. Indeed, one readily verifies that $H = R_X(\pi )R_Y(\frac{\pi }{2})$ modulo a global phase¹, so $H^{\otimes n}$ amounts to applying 2n universal one-qubit gates.

2.4.3 Entanglement

Each quantum state is either a product state or an entangled state. Entanglement has the peculiar and helpful property that we can apply a circuit only on a part of the n-qubit system, and as a result, the whole system is affected.

Definition 19

(Product state) An n-qubit state is a product state if it is the tensor product of n one-qubit states. In other words, an n-qubit state $|\psi \rangle$ is a product state if it exists 2n complex coefficients $(q_0^{(j)}, q_1^{(j)})_{j \in [n]}$ such that

$$\begin{aligned} |\psi \rangle = \bigotimes _{j = 1}^{n}(q_0^{(j)}|0\rangle + q_1^{(j)}|1\rangle ), \text { with } |q_0^{(j)}|^2+|q_1^{(j)}|^2 = 1, \forall j \in [n]. \end{aligned}$$

Thus, each state of a qubit that composes $|\psi \rangle$ can be described independently of the states of the other.

If an n-qubit state is not a product state, it is an entangled state.

Definition 20

(Entangled state) An n-qubit state is entangled if the numerical values of its coordinates $(\psi _i)_{i\in \{0,1\}^n} \in \mathbb {C}^{2^n}$ admit no solution $(q_0^{(j)}, q_1^{(j)})_{j \in [n]} \in \mathbb {C}^{2n}$ to the system

It means that operations performed on some coordinates of the entangled state can affect the other coordinates without direct operations on them.

Notice that when an n-qubit system is entangled, it makes no sense to speak about qubit number $k \in [n]$ because isolated qubits are not defined. Notice also that there is a difference between superposition and entanglement. A state is in superposition if at least two non-zero coefficients are in its basis decomposition. A state is entangled if it cannot be written as a tensor product of independent qubits, implying that it is in superposition.

To illustrate the notion of entanglement, we consider the following quantum circuit on Fig. 5. Starting from a two-qubit product state $|00\rangle$, it results an entangled state.

Fig. 5

Entangling circuit

This circuit is the application of Hadamard gate on qubit 1, followed by $CX_{1,2}$. The quantum state that results is $|\Phi ^+\rangle$ of Example 5:

$$\begin{aligned} \begin{aligned} CX_{1,2}(H\otimes I)|00\rangle&= CX_{1,2}\left( \frac{1}{\sqrt{2}}(|00\rangle + |10\rangle )\right) \\&= \frac{1}{\sqrt{2}}\left( CX_{1,2}|00\rangle + CX_{1,2}|10\rangle \right) \\&= \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle )\\&= |\Phi ^+\rangle . \end{aligned} \end{aligned}$$

We prove now by contradiction that $|\Phi ^+\rangle$ is entangled. Suppose that $|\Phi ^+\rangle$ is a product state. Thus, there exists $(q_0^{(0)},q_1^{(0)})\in \mathbb {C}^2$ such as $|q_0^{(0)}|^2 + |q_1^{(0)}|^2 = 1$ and $(q_0^{(1)},q_1^{(1)})\in \mathbb {C}^2$ such as $|q_0^{(1)}|^2 + |q_1^{(1)}|^2 = 1$, satisfying:

$$\begin{aligned} |\Phi ^+\rangle&= (q_0^{(0)}|0\rangle + q_1^{(0)}|1\rangle )\otimes (q_0^{(1)}|0\rangle + q_1^{(1)}|1\rangle )\\&= q_0^{(0)}q_0^{(1)}|00\rangle +q_0^{(0)}q_1^{(1)}|01\rangle + q_1^{(0)}q_0^{(1)}|10\rangle +q_1^{(0)}q_1^{(1)}|11\rangle \,. \end{aligned}$$

Because the decomposition of a quantum state’s coordinates is unique in the canonical basis, it follows by identification:

$$\begin{aligned} {\left\{ \begin{array}{ll} q_0^{(0)}q_0^{(1)} & = \frac{1}{\sqrt{2}} \\ q_0^{(0)}q_1^{(1)} & = 0 \\ q_1^{(0)}q_0^{(1)} & = 0 \\ q_1^{(0)}q_1^{(1)} & = \frac{1}{\sqrt{2}} \end{array}\right. } \end{aligned}$$

This equation system admits no solution. We deduce that $|\Phi ^+\rangle = \frac{|00\rangle + |11\rangle }{\sqrt{2}}$ is not a product state, hence it is entangled.

3 Variational Quantum Algorithms for optimization

Some of the quantum algorithms that tackle combinatorial optimization problems are Variational Quantum Algorithms (VQAs) (Cerezo et al., 2021). They are hybrid algorithms because they require both quantum and classical computations. VQAs are studied today because they represent an alternative approach that reduces the quality and quantity of the quantum resources needed (Peruzzo et al., 2014). Specifically, they are designed to run on the NISQ era (Preskill, 2018) where quantum computers are noisy with few qubits: for instance, they harness low-depth quantum circuits.

In this section, we consider optimization problems of the form

$$\begin{aligned} \underset{x\in \{0,1\}^n}{\min }f(x), \end{aligned}$$

(1)

where f is any function defined on $\{0,1\}^n$. We note $\mathcal {F}$ the set of optimal solutions.

3.1 General description

Variational Quantum Algorithms (VQAs) are hybrid algorithms that, given an input $|0\rangle ^{\otimes n}$, alternate between a quantum and a classical part. Henceforth, we note $|0_n\rangle$ the state $|0\rangle ^{\otimes n}$ to ease the reading. Let us first provide a high-level description of the key elements of VQAs that are detailed in this section. Let $d\in \mathbb {N}$, the three key elements of VQAs are:

• A parametrized quantum circuit, $U: \mathbb {R}^d \rightarrow \mathcal {M}_{2^n}(\mathbb {C}),$

• A guiding function, $g: \mathbb {R}^d \rightarrow \mathbb {R},$

• And a classical optimizer, which is an algorithm $\mathcal {A}$ that optimizes g over space $\mathbb {R}^d.$

These elements, the parametrized quantum circuit and the two others, are detailed and illustrated in Subsections 3.2 and 3.3, respectively. Before that, we provide a general overview of VQAs in Algorithm 1.

The main idea of a VQA is as follows. The main loop of the algorithm executes the following steps until the classical optimizer stops according to a given stopping criterion. First, given $\theta \in \mathbb {R}^d$, the quantum part executes the parametrized quantum circuit $U(\theta )$ for several times to sample the quantum state (see Remark 15). It results in a distribution probability over $\{0,1\}^n$ that we note $\{p_\theta (x): x\in \{0,1\}^n\}$. Second, the classical part computes the cost of this state through the evaluation of the guiding function according to the sampling results, specifically, $g(\theta ) = G(p_\theta , f)$ for a given function G that is constructed from f and $p_\theta$. More precisely, for a given $\theta$, the computation of G requires only the values f(x) for x such that $p_\theta (x) > 0$. Eventually, this cost value is given to the classical optimizer $\mathcal {A}$, which outputs a new parameter in order to minimize g. Notice that, between the two parts the best-found solution is possibly updated by a classical computer.

Algorithm 1

Variational Quantum Algorithm

In the following subsections, we detail each part of VQAs and show how specific choices of g and U ensure that VQAs optimize f. Let us begin with the quantum part.

3.2 Quantum part

The quantum part of VQAs applies a quantum circuit on the n-qubit system that constitutes the quantum computer. Importantly, variational in VQAs stands for the parametrization of the quantum circuit. Let $d \in \mathbb {N}$ be the number of parameters.

Definition 21

A parametrized quantum circuit is a continuous function $U:\mathbb {R}^d\rightarrow \mathcal {M}_{2^n}(\mathbb {C})$ mapping any $\theta \in \mathbb {R}^d$ to unitary matrix $U(\theta )$.

As defined in Subsection 2.3, a quantum circuit is a sequence of universal quantum gates’ compositions and/or tensor products. Thus, all coefficients of matrix $U(\theta )$ are continuous functions on $\mathbb {R}^d$.

Example 22

A simple example of a parametrized quantum circuit for $n=3$ and $d=3$ is depicted in Fig. 6.

The expression of $U(\theta )$ for this circuit is as follows: $\forall \theta = (\theta _1, \theta _2, \theta _3) \in \mathbb {R}^3$,

$$\begin{aligned} U(\theta )&= R_Y(\theta _1)\otimes R_Y(\theta _2)\otimes R_Y(\theta _3)\\&= \begin{pmatrix} \cos {\frac{\theta _1}{2}} & -\sin {\frac{\theta _1}{2}} \\ \sin {\frac{\theta _1}{2}} & \cos {\frac{\theta _1}{2}} \end{pmatrix} \otimes \begin{pmatrix} \cos {\frac{\theta _2}{2}} & -\sin {\frac{\theta _2}{2}} \\ \sin {\frac{\theta _2}{2}} & \cos {\frac{\theta _2}{2}} \end{pmatrix} \otimes \begin{pmatrix} \cos {\frac{\theta _3}{2}} & -\sin {\frac{\theta _3}{2}} \\ \sin {\frac{\theta _3}{2}} & \cos {\frac{\theta _3}{2}} \end{pmatrix}\\&= \begin{pmatrix} c_1 c_2 c_3 & -c_1 c_2 s_3 & -c_1 s_2 c_3 & c_1 s_2 s_3 & -s_1 c_2 c_3 & s_1 c_2 s_3 & s_1 s_2 c_3 & -s_1 s_2 s_3 \\ c_1 c_2 s_3 & c_1 c_2 c_3 & -c_1 s_2 s_3 & -c_1 s_2 c_3 & -s_1 c_2 s_3 & -s_1 c_2 c_3 & s_1 s_2 s_3 & s_1 s_2 c_3\\ c_1 s_2 c_3 & -c_1 s_2 s_3 & c_1 c_2 c_3 & -c_1 c_2 s_3 & -s_1 s_2 c_3 & s_1 s_2 s_3 & -s_1 c_2 c_3 & s_1 c_2 s_3\\ c_1 s_2 s_3 & c_1 s_2 c_3 & c_1 c_2 s_3 & c_1 c_2 c_3 & -s_1 s_2 s_3 & -s_1 s_2 c_3 & -s_1 c_2 s_3 & -s_1 c_2 c_3 \\ s_1 c_2 c_3 & -s_1 c_2 s_3 & -s_1 s_2 c_3 & s_1 s_2 s_3 & c_1 c_2 c_3 & -c_1 c_2 s_3 & -c_1 s_2 c_3 & c_1 s_2 s_3 \\ s_1 c_2 s_3 & s_1 c_2 c_3 & -s_1 s_2 s_3 & -s_1 s_2 c_3 & c_1 c_2 s_3 & c_1 c_2 c_3 & -c_1 s_2 s_3 & -c_1 s_2 c_3\\ s_1 s_2 c_3 & -s_1 s_2 s_3 & s_1 c_2 c_3 & -s_1 c_2 s_3 & c_1 s_2 c_3 & -c_1 s_2 s_3 & c_1 c_2 c_3 & -c_1 c_2 s_3\\ s_1 s_2 s_3 & s_1 s_2 c_3 & s_1 c_2 s_3 & s_1 c_2 c_3 & c_1 s_2 s_3 & c_1 s_2 c_3 & c_1 c_2 s_3 & c_1 c_2 c_3 \end{pmatrix}\,, \end{aligned}$$

where $c_i = \cos {\frac{\theta _i}{2}}$ and $s_i = \sin {\frac{\theta _i}{2}}$ for $i\in [3]$.

Fig. 6

Quantum circuit parametrized by $(\theta _1, \theta _2, \theta _3) \in \mathbb {R}^3$

Remark 23

The use of the generalized circuit to n qubits amounts to a continuous relaxation of the $\{0,1\}$-problem (1), where each decision variable $x_i \in [0,1]$ is represented by a rotation angle $\theta _i\in [0,2\pi ]$ as follows:

$$\begin{aligned} x_i = \left( \cos {\frac{\theta _i}{2}}\right) ^2. \end{aligned}$$

3.3 Classical part

The classical part of VQAs consists of a classical optimization over the parameters $\theta \in \mathbb {R}^d$. The classical optimizer essentially aims at finding the optimal parameters $\theta ^*$ that lead to optimal solutions of the initial problem (1) with high probability, specifically, such that

$$\begin{aligned} \sum _{s\in \mathcal {F}}|\langle s|U(\theta ^*)|0_n\rangle |^2 \ge 1-\epsilon , \end{aligned}$$

(10)

for small $\epsilon >0$. Henceforth, we use notation $|x\rangle$ instead of $|i\rangle$ to efficiently recall that we deal with solutions of optimization problems.

The classical part is characterized by two aspects: the function that guides the optimization and the optimizer itself.

3.3.1 Guiding function

Let $g: \mathbb {R}^d \rightarrow \mathbb {R}$ be the guiding function, formally defined in Definition 24 below, that the classical optimizer minimizes. The function g acts as a link between the quantum and classical parts. For a given $\theta \in \mathbb {R}^d$, we evaluate $U(\theta )|0_n\rangle$ according to f as we will exemplify below. Notice that f and g are distinct since g is defined on $\mathbb {R}^d$ and outputs a quality measure of an n-qubit quantum state whereas f is defined on $\{0,1\}^n$. Let us denote as the set of quantum states that are superpositions of optimal solutions of problem (1). Naturally, we would like to define g such that minimizing g tends to minimize f.

Definition 24

(Guiding function) Let $g: \mathbb {R}^d \rightarrow \mathbb {R}$ be a function and $\mathcal {G}$ be its set of minimizers. We call g a guiding function for f with respect to U if g is continuous and

$$\begin{aligned} \{U(\theta )|0_n\rangle : \theta \in \mathcal {G}\} \subseteq \mathcal {F}_\text {quant}. \end{aligned}$$

(11)

In other words, optima of a guiding function g must lead to optima of f or superpositions of optima of f. Indeed, Equation (11) implies that measuring the quantum state $U(\theta ^*)|0\rangle ^{\otimes n}$ for $\theta ^*\in \mathcal {G}$ outputs with probability 1 an optimal solution of the initial problem $s\in \mathcal {F}$. Thus, minimizing g amounts to minimizing f, and finding $\mathcal {F}$ is done by finding $\mathcal {G}$. The latter is found with the classical optimizer. Without any information on $\mathcal {F}$, we need to choose a quantum circuit U such that any optimal solution $s\in \mathcal {F}$ is reachable, specifically,

$$\begin{aligned} \{U(\theta )|0_n\rangle : \theta \in \mathbb {R}^d\} \supseteq \mathcal{C}\mathcal{B}_n. \end{aligned}$$

(12)

Notice that this condition is weak and easily satisfied. For instance, the circuit depicted in Fig. 6 satisfies this condition. If ever one is interested in finding all optimal solutions of problem (1), the circuit and the guiding function should satisfy instead the stronger condition

$$\begin{aligned} \{U(\theta )|0_n\rangle : \theta \in \mathcal {G}\} = \mathcal {F}_\text {quant}. \end{aligned}$$

(13)

In that case, U satisfying (12) is not enough. Without any information on $\mathcal {F}$, we need to choose U that can reach any n-qubit quantum states, specifically,

A popular choice for the guiding function in the literature is the mean function

$$\begin{aligned} g_{\text {mean}}(\theta ) = \sum _{x\in \{0,1\}^n} p_\theta (x)f(x), \end{aligned}$$

(14)

where $p_\theta (x) = |\langle x|U(\theta )|0_n\rangle |^2$ is the probability of finding x when $U(\theta )|0_n\rangle$ is measured. We show next that $g_{\text {mean}}$ is indeed a guiding function according to Definition 24, see Appendix B.1.1 for a proof.

Proposition 25

Function $g_{\text {mean}}$ is a guiding function.

Example 26

We illustrate the mean function on the 3-qubit quantum circuit $U(\theta )$ depicted in Fig. 6. The generalization of its computation for n qubits is trivial since it needs to replace 3 by n. The single application of rotation gate $R_Y$ (6) of angle $\theta _i$ on a qubit initially on state $|0\rangle$ is

$$\begin{aligned} R_Y(\theta _i)|0\rangle&= \cos \frac{\theta _i}{2}|0\rangle + \sin \frac{\theta _i}{2}|1\rangle \\&= \sum _{j\in \{0,1\}} \cos \frac{\theta _i - j\pi }{2}|j\rangle \,, \end{aligned}$$

since $\sin (\phi ) = \cos (\phi - \frac{\pi }{2})$ for $\phi \in \mathbb {R}$. Eventually, the quantum state resulting from $U(\theta )$ is

$$\begin{aligned} U(\theta )|0_3\rangle&= \bigotimes _{i=1}^3 R_{Y,i}(\theta _i)|0\rangle \\&= \sum _{j_1,j_2,j_3\in \{0,1\}}\left( \prod _{i=1}^3 \cos \frac{\theta _i - j_i\pi }{2}\right) |j_1j_2j_3\rangle \,. \end{aligned}$$

Thus, the probability to measure $x = (x_1,x_2,x_3) \in \{0,1\}^3$ is

$$\begin{aligned} p_\theta (x) = \left( \prod _{i=1}^3 \cos \frac{\theta _i - x_i\pi }{2}\right) ^2, \end{aligned}$$

(15)

and the expression of $g_{\text {mean}}$ of equation (14) directly results from it.

Other functions are compatible with Definition 24. One of these functions encountered in the literature is the Gibbs function (Li et al., 2020) which stems from statistical mechanics. Let $\eta >0$ be a parameter to be set. The Gibbs function is defined as

$$\begin{aligned} g_{G,\eta }(\theta ) = -\ln \left( {\sum _{x\in \{0,1\}^n}p_\theta (x)e^{-\eta f(x)}} \right) . \end{aligned}$$

(16)

The choice of this function is motivated by the exponential shape that highly rewards the increase of probabilities of low-cost states. Notice that for small $\eta$, minimizing the Gibbs function is essentially equivalent to minimizing the mean function in the sense that the Taylor series of $g_{G,\eta }$ at first order in $\eta = 0$ gives $g_{G,\eta } = \eta g_\text {mean}$. We show next that $g_{G,\eta }$ is indeed a guiding function according to Definition 24, see Appendix B.1.2 for a proof.

Proposition 27

Let $\eta >0$. Function $g_{G,\eta }$ is a guiding function.

One might suggest other guiding functions, such as the minimum function

$$\begin{aligned} g_{\text {min}}(\theta )=\underset{x \hspace{0.5mm}:\hspace{0.5mm} p_\theta (x) > 0}{\min } f(x). \end{aligned}$$

(17)

However, $g_{\text {min}}$ does not verify (11), and is not even continuous, hardening its optimization and excluding its choice for the guiding function.

Example 28

Let us illustrate that $g_{\text {min}}$ is not a guiding function. For that, we consider the circuit of Fig. 6 and the following function $f: \{0,1\}^3 \mapsto \mathbb {R}$ to minimize,

$$\begin{aligned} {\left\{ \begin{array}{ll} f(0,0,0) & = 1 \\ f(x) & = 0,~~\forall x \ne (0,0,0) \end{array}\right. } \end{aligned}$$

where $f^* = 0$ is the optimal value. Function $g_{\text {min}}$ reaches its optimal value $g_{\text {min}}^* = 0$ on the set of its optimizers

$$\begin{aligned} \mathcal {G}= \mathbb {R}^3\setminus \{(2k\pi , 2k\pi , 2k\pi ): k\in \mathbb {Z}\}. \end{aligned}$$

However,

$$\begin{aligned} \forall \theta \in \mathcal {G}\setminus \{((2k+1)\pi , (2k+1)\pi , (2k+1)\pi ): k\in \mathbb {Z}\},U(\theta )|0_n\rangle \notin \mathcal {F}_\text {quant}, \end{aligned}$$

because there is a non-zero probability of sampling (0, 0, 0). Thus, $g_{\text {min}}$ violates (11). Moreover, $g_{\text {min}}$ is not continuous. Indeed, $g_{\text {min}}(0,0,0) = 1$, whereas $\forall \epsilon >0\,, g_{\text {min}}(\epsilon ,0,0) = 0$.

The above observation motivated (Barkoutsos et al., 2020) to suggest another function, the CVaR (Conditional Value-at-Risk) function. The CVaR function is the average on the lower $\alpha$-tail of values of f encountered, where $\alpha \in ]0,1]$ is a parameter to be set. Let $(x_1,\ldots ,x_{2^n})$ be the n-bitstrings sorted in non decreasing order, namely $f(x_i) \le f(x_{i+1})$ for any $i\in [2^n - 1]$. Let $N_\alpha$ be the index that delimits the $\alpha$-tail elements of the distribution, specifically,

$$\begin{aligned} N_\alpha = \min \left\{ N \ge 1: \sum _{i=1}^{N} p_\theta (x_i) \ge \alpha \right\} . \end{aligned}$$

Then, the CVaR function is

$$\begin{aligned} g_{C,\alpha }(\theta ) = \frac{1}{\sum _{i=1}^{N_\alpha }p_\theta (x_i)}\sum _{i=1}^{N_\alpha } p_\theta (x_i)f(x_i). \end{aligned}$$

(18)

The special case $\alpha = 1$ implies $g_\alpha = g_{\text {mean}}$, whereas when $\alpha$ approaches zero, we find $g_{\text {min}}$.

The CVaR function is an alternative to the non-smooth minimum function. While CVaR does not verify (11) either, it keeps continuity and still focuses on the best solutions that appear on the probability distribution.

Example 29

Let us illustrate the violation of (11) by the CVaR function, for any $\alpha \in ]0,1[$. For that, we consider function f of Example 28 with the same quantum circuit of Fig. 6. Let $\alpha \in ]0,1[$. Let us find $\theta \in \mathcal {G}$ such that $U(\theta )|0_n\rangle \notin \mathcal {F}_\text {quant}$. In other words, we search $\theta \in \mathbb {R}^3$ such that

$$\begin{aligned} g_{C,\alpha }(\theta ) = 0\,\text { and }\,p_\theta (0,0,0) > 0. \end{aligned}$$

Let us look at $\theta = (\pi - \epsilon , 0, 0)$, where $\epsilon \in ]0,\pi [$. According to (15), we have

$$\begin{aligned} p_\theta (0,0,0) = \cos ^2\left( \frac{\pi - \epsilon }{2}\right) >0. \end{aligned}$$

It remains to choose $\epsilon$ to ensure $g_{C,\alpha }(\theta ) = 0$. Namely, we want $\epsilon$ such that

$$\begin{aligned} \sum _{x\ne (0,0,0)}p_\theta (x) \ge \alpha , \end{aligned}$$

meaning

$$\begin{aligned} 1 - \cos ^2\left( \frac{\pi - \epsilon }{2}\right) \ge \alpha . \end{aligned}$$

This holds for any $\epsilon \le \pi - 2\arccos {(\sqrt{1-\alpha })}$.

Even if CVaR does not verify (11), it can be seen as a pseudo-guiding function, defined just below. Notice that in practice, using the CVaR function seems appropriate because it accepts a probability of measuring optimal solutions after optimizing to be lower than one, such as expressed in (10).

Definition 30

(Pseudo-guiding function) Let $g: \mathbb {R}^d \rightarrow \mathbb {R}$ be a function and $\mathcal {G}$ be its set of minimizers. We call g a pseudo-guiding function for f with respect to U if g is continuous and if there exists $\alpha \in ]0,1[$ such that optima of g can lead to non-optimal solutions of f with a probability strictly lower than $1-\alpha$. Specifically, let $\theta \in \mathcal {G}$. Thus, either $U(\theta )|0_n\rangle \in \mathcal {F}_\text {quant}$ or .

We show next that $g_{C,\alpha }$ is indeed a pseudo-guiding function according to Definition 30, see Appendix B.1.3 for a proof.

Proposition 31

Let $\alpha \in ]0,1[$. Function $g_{C,\alpha }$ is a pseudo-guiding function.

3.3.2 Classical optimizer

The role of the classical optimizer is to minimize the guiding function. The function g is continuous and is usually differentiable but not convex. Any unconstrained optimization algorithm can be used to minimize g, such as local search, descent gradient method, or any black-box optimization algorithm.

To speak in terms of stochastic optimization, the classical optimizer aims at solving the stochastic programming model under endogenous uncertainty

$$\begin{aligned} \min _\theta \{g(\theta ) = \mathbb {E}[ G(\theta , \xi _\theta )]\}, \end{aligned}$$

(19)

where the definition of G depends on the choice of a specific guiding function, and $\xi _\theta$ is an endogenous vector that depends on $\theta$. Specifically, $\xi _\theta$ is a discrete random variable, with the set of possible outcomes $\{0,1\}^n$ and the following distribution probability:

$$\begin{aligned} \mathbb {P}(\xi _\theta = x) = p_\theta (x),~~\forall x\in \{0,1\}^n. \end{aligned}$$

Thus, this problem falls into the class of stochastic dependent-decision probabilities problems (Hellemo et al., 2018). In practice, the classical optimizer approximates the function by a Monte Carlo estimation as follows:

$$\begin{aligned} \hat{g}_N(\theta ) = \frac{1}{N}\sum _{j=1}^{N} G(\theta , \xi _{\theta }^j), \end{aligned}$$

where $\{\xi ^j_\theta \}_{j\in [N]}$ is a sample of size N from the distribution of $\xi _\theta$. Notice that for a given $\theta$, the quantity $\hat{g}_N(\theta )$ itself is a random variable since its value depends on the sample that has been generated, which is random. In contrast, the value of $g(\theta )$ is deterministic. In practice, the classical optimizer iterates the loop that consists of, given a sampling distribution of size N of the quantum state $U(\theta )|0_n\rangle$ (Remark 15), outputs a $\theta '$. This $\theta '$ is then transmitted to the quantum part. Eventually, the aim is to output $\theta ^*$ such that $U(\theta )|0_n\rangle \subseteq \mathcal {F}_\text {quant}$. In each iteration, the value of $\hat{g}_N(\theta )$ is computed. Notice that according to the Law of Large Numbers (Shapiro, 2003), $\hat{g}_N(\theta )$ converges with probability one to $g(\theta )$ as $N\rightarrow \infty$.

For instance, for the case of $g=g_\text {mean}$, we have

$$\begin{aligned} G(\theta , \xi _\theta ) = f(\xi _\theta ). \end{aligned}$$

Hence, for each $\xi _\theta ^j\in \{0,1\}^n$ sampled, either we compute classically $f(\xi _\theta ^j)$ and store it if not already computed, or we get its value. Thus, we can compute $\hat{g}_N(\theta )$. Notice that for the CVaR function, we compute the empirical mean only on the best $\lceil \alpha N \rceil$ values $f(\xi _\theta )$ found by sampling.

The solution returned by the VQA is the minimum value of f and the associated minimizer x encountered while the algorithm runs.

4 Quantum approximate optimization algorithm

We assume throughout this section that the function f to be minimized is polynomial. First, we reformulate problem (1) to a more suitable form for quantum optimization. This reformulation is motivated by the quantum adiabatic evolution (Farhi et al., 2000) that, for a given Hermitian matrix,² approximates the eigenvector with the lowest eigenvalue under certain conditions. For that, we interpret the objective function of problem (1) as an Hermitian matrix $H_f$ such that each eigenvector $|u_x\rangle$ is matching a classical solution $x\in \{0,1\}^n$ with an eigenvalue equal to f(x), specifically,

$$\begin{aligned} H_f|u_x\rangle = f(x)|u_x\rangle . \end{aligned}$$

Thus, the solutions of problem (1) are the solutions corresponding to the lowest eigenvalues of $H_f$. The Quantum Approximate Optimization Algorithm (QAOA) (Farhi et al., 2014) presented in this section aims at finding the lowest eigenvalue of $H_f$.

4.1 Problem reformulation

The construction of $H_f$ is as follows. First, we transform the $\{0,1\}$-problem (1) into a $\{-1,1\}$-problem. For that, we apply the following linear transformation: for $x=(x_1,\ldots ,x_n)\in \{0,1\}^n$, we define $z=(z_1,\ldots ,z_n)\in \{-1,1\}^n$ where

$$\begin{aligned} z_i = 1-2x_i, \forall i \in [n]. \end{aligned}$$

(20)

This leads to the problem

$$\begin{aligned} \underset{z \in \{-1,1\}^n}{\min } f_{\pm }(z), \end{aligned}$$

where, for $z\in \{-1,1\}^n$,

where $h_{\alpha } \in \mathbb {R}, \forall \alpha \in \{0,1\}^n$. Second, we define $H_f$ as

where $Z = \begin{pmatrix}1& 0\\ 0& -1\end{pmatrix}$, $Z^0 = I$ and $Z^1 = Z$. We note $Z_i$ the application of Z to qubit i. Notice that Z is equal to the universal gate $R_{Z}(\pi )$ modulo a global phase (see (7)). This construction of $H_f$ leads to the following property.

Proposition 32

The eigenvectors of $H_f$ are the canonical basis $|x\rangle \in \mathcal{C}\mathcal{B}_n$ with eigenvalues that are the cost of the solutions f(x), specifically,

$$\begin{aligned} \forall |x\rangle \in \mathcal{C}\mathcal{B}_n,\hspace{2mm} H_f|x\rangle = f(x)|x\rangle . \end{aligned}$$

(21)

Proof

First, the eigenvectors of $H_f$ are the canonical basis states. Indeed, each term of the sum that constitutes $H_f$ is a tensor product of n matrices I or Z, both diagonal. Thus, $H_f$ is a $2^n$ diagonal matrix. Second, let us find the eigenvalues associated with the eigenvectors. Let $|x\rangle = |x_1 \ldots x_n\rangle$ be in $\mathcal{C}\mathcal{B}_n$. Let $z=(z_1,\ldots ,z_n)$ be the result of transformation (20). Thus, we can easily show that $Z|x_i\rangle = z_i|x_i\rangle ,\forall i\in [n]$ and

$\square$

Example 33

We illustrate this transformation on a small example with $n=2$. Let us consider the problem

$$\begin{aligned} \min _{x\in \{0,1\}^2} f(x) = x_1 + 2x_2 -3x_1x_2. \end{aligned}$$

Using (20), the equivalent $\{-1,1\}$-problem is

$$\begin{aligned} \min _{z\in \{-1,1\}^2} f_{\pm }(z) = \frac{1}{4}z_1 - \frac{1}{4}z_2 - \frac{3}{4}z_1z_2 + \frac{3}{4}. \end{aligned}$$

Thus, the Hermitian matrix associated with the problem is

$$\begin{aligned} H_f = \frac{1}{4}Z\otimes I - \frac{1}{4}I\otimes Z - \frac{3}{4}Z\otimes Z +\frac{3}{4}I \otimes I. \end{aligned}$$

To illustrate (21), we compute the eigenvalue of the canonical basis state $|10\rangle$.

$$\begin{aligned} H_f|10\rangle&= \frac{1}{4}(Z\otimes I)|10\rangle - \frac{1}{4}(I\otimes Z)|10\rangle - \frac{3}{4}(Z\otimes Z)|10\rangle +\frac{3}{4}(I \otimes I)|10\rangle \\&= -\frac{1}{4}|10\rangle - \frac{1}{4}|10\rangle + \frac{3}{4}|10\rangle +\frac{3}{4}|10\rangle \\&= |10\rangle \\&= f(1,0)|10\rangle \,, \end{aligned}$$

because $f(1,0) = 1$.

Notice that most of the problems solved with QAOA in the literature are QUBO (Quadratic Unconstrained Binary Optimization) problems. Thus, $H_f$ has the specific form

$$\begin{aligned} H_f = \sum _{i}h_{ii}Z_i + \sum _{i<j}h_{ij} Z_i\otimes Z_j, \end{aligned}$$

where $h_{ij}\in \mathbb {R},\,\forall i\le j$. It is justified by the fact that solving QUBO problems to optimality is already NP-hard, and the quantum gates of the circuit are easier to implement on hardware in that case.

4.2 Quantum part

QAOA is a Variational Quantum Algorithm where the quantum part derives from the Hamiltonian $H_f$. This quantum part consists of a quantum circuit with 2p parameters $({\gamma },{\beta }) = (\gamma _1,\ldots ,\gamma _p, \beta _1,\ldots ,\beta _p) \in \mathbb {R}^{2p}$, where p is called depth. The quantum circuit $U({\gamma },{\beta })$ is the sequence of p layers of two blocks, initially applied to the uniform superposition $|+\rangle ^{\otimes n}$ (see Example 18). The first block is of the form $Exp (H_f, \gamma )$, for $\gamma \in \mathbb {R}$, which is the unitary operator (see Definition 43) associated with the Hamiltonian $H_f$. The second block is of the form $Exp (H_B, \beta )$, for $\beta \in \mathbb {R}$, which is the unitary operator associated with the Hamiltonian . Thus, the quantum circuit is

$$\begin{aligned} U({\gamma },{\beta }) = Exp (H_B, \beta _p)Exp (H_f, \gamma _p)\ldots Exp (H_B, \beta _1)Exp (H_f, \gamma _1)H^{\otimes n}, \end{aligned}$$

(22)

where the first gates applied in this circuit are $H^{\otimes n}$ to then apply the p layers to state $|+\rangle ^{\otimes n}$. The three propositions that follow express the quantum circuit of QAOA with the set of universal gates (see Theorem 13). We give first the general decomposition of the QAOA quantum circuit defined in (22), see Appendix B.2.1 for a proof.

Proposition 34

The first block $Exp (H_f, \gamma )$ parametrized by $\gamma \in \mathbb {R}$ is

$$\begin{aligned} Exp (H_f, \gamma ) = \prod _{\alpha \in \{0,1\}^n}Exp (\bigotimes _{i=1}^n Z_i^{\alpha _i}, h_\alpha \gamma ). \end{aligned}$$

The second block $Exp (H_B, \beta )$ parametrized by $\beta \in \mathbb {R}$ is

$$\begin{aligned} Exp (H_B, \beta ) = \bigotimes _{i=1}^n R_{X,i}(2\beta ). \end{aligned}$$

The particular case of QUBO is mainly considered in the literature. Thus, we propose next a decomposition of the QAOA quantum circuit for this specific case, see Appendix B.2.2 for a proof.

Proposition 35

For the case of QUBO, the expression of $Exp (H_f, \gamma )$ simplifies in

$$\begin{aligned} Exp (H_f, \gamma ) = \left( \bigotimes _{i=1}^n R_{Z,i}(2h_{ii}\gamma )\right) \prod _{i<j}CX_{i,j} R_{Z,j}(2h_{i,j}\gamma )CX_{i,j}, \end{aligned}$$

and is rather easily implemented with universal quantum gates.

The decomposition in universal quantum gates of the term $Exp (Z_i\otimes Z_j, t)$ for the specific case of QUBO (see Proposition 35) is mainly used in the literature. We propose in Proposition 37 a generalization of such a decomposition for the term $Exp (\bigotimes _{i=1}^n Z^{\alpha _i}, t)$, where the number of Z gates in effect can be bigger than two, namely, $|\{\alpha _i,\, i\in [n]: \alpha _i = 1\}| \ge 2$. This proposition enables us to overtake the QUBO problems, namely, to deal with a polynomial function f with a degree strictly larger than two. We introduce next a technical result that will be necessary to derive the subsequent proposition, see Appendix B.2.3 for a proof.

Lemma 36

$\forall n\in \mathbb {N}^*$,

$$\begin{aligned} (I^{\otimes n-1}\otimes X)e^{-itZ^{\otimes n}}(I^{\otimes n-1}\otimes X) = e^{itZ^{\otimes n}}. \end{aligned}$$

The proposition that follows enables a decomposition in universal quantum gates of any quantum circuit of QAOA, see Appendix B.2.4 for a proof.

Proposition 37

Let us consider the subsystem composed of the N qubits to which the Z gate is applied. Specifically, $N = |\{\alpha _i\, i\in [n]: \alpha _i = 1\}|$, and we renumber the qubits in question in [N]. Thus, for $N\ge 2$, the term $Exp (\bigotimes _{i=1}^n Z^{\alpha _i}, t)$ on this subsystem simplifies in

$$\begin{aligned} Exp (Z^{\otimes N}, t) = \prod _{j=0}^{N-2} CX_{1,N-j} R_{Z,N}(2t) \prod _{j=0}^{N-2} CX_{1,N-j}. \end{aligned}$$

We represent this decomposition on Fig. 7.

Fig. 7

Decomposition of $Exp (Z^{\otimes N}, t)$ on the N-qubit subsystem

Example 38

We illustrate the construction of the quantum circuit with the problem of Example 33 where $n=2$, for the case $p=1$. Thus,

$$\begin{aligned} U(\gamma , \beta ) = Exp (H_B, \beta )Exp (H_f, \gamma )|+\rangle ^{\otimes 2},~~\forall \gamma , \beta \in \mathbb {R}. \end{aligned}$$

The circuit is detailed in Fig. 8.

Notice that we do not take into account the term $\frac{3}{4}I\otimes I$ of $H_f$ in this circuit. More generally, the term $h_{0\ldots 0}I^{\otimes n}$ of $H_f$ never appears on the quantum circuit because it represents a constant term and does not influence the optimization.

Fig. 8

QAOA circuit of Example 33 for $p=1$

Notice that the choice of QAOA circuit does not ensure (12). For example, one can show that the probability of measuring 00 at the end of the circuit depicted in Fig. 8 never reaches 1. Specifically,

$$\begin{aligned} p_{(\gamma , \beta )}(00) = |\langle 00|Exp (H_B, \beta )Exp (H_f, \gamma )|+\rangle ^{\otimes 2}|^2 < \frac{1}{2},~~\forall \gamma , \beta \in \mathbb {R}. \end{aligned}$$

However, QAOA satisfies another important property: it uses entangling gates. Each gate $Exp (Z_i\otimes Z_j, t)$, for $t\in \mathbb {R}\setminus \{k\pi : k\in \mathbb {Z}\}$, entangles the qubits i and j. Indeed, $Exp (Z_i\otimes Z_j, t) = CX_{i,j} R_{Z,j}(2t)CX_{i,j}$, and unless $R_{Z,j}(2t) = I$, namely $t\in \{k\pi : k\in \mathbb {Z}\}$, the CNOT gate operates³ and creates entanglement as mentioned in Subsection 2.4.3. The other gates, which are one-qubit gates, do not have this power. Entanglement is not necessary to (12). However, Remark 23 can justify the use of entanglement gate. Indeed, without it, it seems unlikely to achieve better results than pure classical optimization because the optimizer essentially solves a classical continuous relaxation.

In fact, the popularity of QAOA originates essentially from the fact that it mimics the adiabatic schedule (Wurtz & Love, 2022). The n-qubit system verifies the adiabatic condition when $p\rightarrow \infty$ and ensures that for a particular set of parameters, the quantum circuit gives the exact solution. However, quantum computers’ quality today makes implementations on large instances impossible. But because the number of gates of the quantum circuit is $\mathcal {O}(pn^2)$, for small depth d, QAOA, and more generally VQAs, can already be implemented on current NISQ computers.

5 Literature review for QAOA

Many papers have recently addressed the empirical evaluation of QAOA, some also comparing it with specific implementations of VQA. We present below a non-exhaustive list of these trends, we mention several theoretical limitations for specific cases known up to now and we end with the different leverages that are at stake to improve QAOA performances. This section does not provide a complete, up-to-date overview of QAOA performances, but rather aims at illustrating trends on combinatorial problems of interest to the operations research community.

5.1 Empirical and theoretical trends on QAOA

Let us begin with the numerical trends of QAOA performances. All the empirical experiments are presented on small instances because quantum computers’ quality today makes implementations on large instances impossible, leading to difficult conclusions. Thus, many experiments are done on classical simulators of quantum computers. Most of the empirical results of QAOA apply to the MAX-CUT problem because it was initially the first application of QAOA (Farhi et al., 2014).

Definition 39

(MAX-CUT problem) Let $G=(V,E)$ be a undirected graph. A cut in G is a subset $S\subseteq V$. We define its cost as the number of edges with one node in S and one node in $V\setminus S$. The MAX-CUT problem aims at finding a cut with maximum cost. A version with weighted edges can also be defined.

Notice that for the MAX-CUT problem, with the notations of Sect. 4, the objective function is

$$\begin{aligned} f(x) = -\sum _{(i,j)\in E} \left( x_i(1 - x_j) + x_j(1-x_i)\right) , \end{aligned}$$

where $x_i$ is 1 if node i is in the cut, 0 otherwise. The Hermitian matrix that corresponds to this problem is

$$\begin{aligned} H_f = -\frac{1}{2}\sum _{(i,j)\in E} (1 - Z_i Z_j). \end{aligned}$$

The approximation ratio r mainly quantifies the performance of QAOA as follows:

$$\begin{aligned} r = \frac{f^\text {QAOA}}{f^*}, \end{aligned}$$

where $f^\text {QAOA}$ is the value returned by QAOA, and $f^*$ is the optimal value. Papers often compare this ratio with the best-known guaranteed ratio of Goemans-Williamson algorithm (Goemans & Williamson, 1995), specifically, $r=0.87856$. The seminal paper of QAOA (Farhi et al., 2014) provides a lower bound of r for the specific class of 3-regular graphs for $p=1$ that is $r=0.6924$. More precise analytical expressions of the lower bound of the ratio for $p=1$ and for some other typical cases are given in Wang et al. (2018). In addition, the authors of Wurtz and Love (2021) provide lower bounds of the ratio for larger depth for uniform 3-regular graphs (under specific assumptions implying the absence of large cycles in the graph): $r \ge 0.7559$ for $p=2$ and $r \ge 0.7924$ for $p=3$.

Several empirical results on MAX-CUT spotlight patterns of optimal parameters and enable QAOA to exceed Goemans-Williamson bound for some specific instances. Some classes of MAX-CUT instances studied reveal patterns of optimal parameters. Thus, it seems to offer efficient heuristics for parameter selection and initialization. For example, the authors of Crooks (2018) look at the class of Erdös-Rényi graphs (random graphs where an edge appears between two nodes with probability 0.5) of size up to 17 nodes, where the classical optimizer is an automatic differentiation with stochastic gradient descent. The authors of Lotshaw et al. (2021) examine the exhaustive set of graphs with $n\le 9$ nodes, with the gradient-based search BFGS (Broyden-Fletcher-Goldfarb-Shanno algorithm (Fortran et al., 1992)) for the classical optimizer. Both exhibit instances that exceed the bound of Goemans-Williamson for small depth, $p\le 8$ and $p\le 3$, respectively. The sets of unweighted and weighted 3-regular graphs also lead to patterns in Zhou et al. (2020) for graphs of a maximum size of 22 nodes, also detected in the parameter space of the Job Shop Scheduling problem (Kurowski et al., 2023). But even if the performance of QAOA sometimes exceeds the Goemans-Williamson bound for the low-depth circuits, it is believed that p must grow with the instance size to have a chance to outperform the best classical algorithms. Indeed, for random large-girth d-regular graphs, QAOA with depth $p=11$ presents better performances than any known classical algorithms, in the case where the optimal parameters are found and where d goes to infinity (Basso et al., 2021). Notice that the authors of the nominal paper of QAOA (Farhi et al., 2014) tackle also the Sherrington-Kirkpatrick model, well-known in the spin glass theory. The Hamiltonian of this model represents the energy of n spins with random coefficients, specifically,

$$\begin{aligned} H_f = \frac{1}{\sqrt{n}} \sum _{i<j}h_{ij}Z_iZ_j, \end{aligned}$$

where the coefficients $h_{ij}$ are chosen independently from a distribution centered in 0 and with a variance equal to 1. In Farhi et al. (2022), it is shown that, for $p=11$, QAOA outperforms asymptotically with n the standard semidefinite programming algorithm and the spectral relaxation.

Some theoretical limits of QAOA are displayed, where the shape of the quantum state produced by the quantum circuit is at stake. The authors of Bravyi et al. (2020) point out that the symmetry and locality of this resulting variational state fund amentally limit the performances of QAOA. Indeed, they show that Goemans-Williamson outperforms QAOA for several instances of the MAX-CUT problem for any fixed depth p. Consequently, this paper suggests a non-local version of QAOA to overcome these limitations. The limits of the locality also appear when solving the problem of the Maximum Independent Set (MIS). In Farhi et al. (2020), MIS instances are random graphs of n vertices, with a fixed average degree $\bar{d}$. Thus, it proves that for depth $p\le C\log (n)$, where C is a constant depending on $\bar{d}$, QAOA cannot return an independent set better than 0.854 times the optimal for $\bar{d}$ large. Due to this locality issue, the author of Hastings (2019) compares QAOA with local classical algorithms which also have this locality notion: at each step, the value of a variable is updated depending on the values of its neighbors, i.e., the variables that share the same term within the objective function. Namely, after t steps, the value of a variable depends on all information gathered in its t-neighborhood. Yet, these classical algorithms still outperform QAOA. A single step of these algorithms outperforms, resp. achieves the same performance as, a single step of QAOA ($p=1$) for MAX-CUT instances, resp. MAX-3-LIN-2 instances. Notice that given binary variables and a set of linear equations modulo 2 with exactly three variables, the MAX-3-LIN-2 problem aims at finding a variable value assignment that maximizes the number of satisfied equations. Several other canonical combinatorial optimization problems have been tackled with QAOA in recent years. While these examples are limited to numerical tests on toy instances and do not include comparisons of performance with classical resolutions, we mention some of them to illustrate the growing interest in solving reference combinatorial problems with Variational Quantum Algorithms. For instance, in Radzihovsky et al. (2019), the authors reformulate the Traveling Salesman Problem (TSP) as an appropriate Hamiltonian matrix and test it on small instances of three and four cities. The authors of Tabi et al. (2020) reformulate and solve the Graph Coloring problem for a dozen of nodes. The authors of Kurowski et al. (2023) study the Job Shop Scheduling problem, find a suitable formulation, and implement it on an artificial instance with three machines and three jobs, each of them containing one or two operations. We end by citing a benchmark provided in Khumalo et al. (2022), that compares classical techniques, among them the Simulated Annealing, and quantum techniques including VQAs on NISQ quantum computers. It applies to the TSP and the Quadratic Assignment problem and shows that in terms of running time and quality solution, the classical methods significantly outperform the quantum ones. Notice that besides the latter paper, the mention of the computation time for VQAs in literature is rare. It could be explained by the fact that most of the experiments are tested on trivial instances and solved with quantum algorithms simulated on classical high-performance computers due to the noise on current quantum hardware (De Palma et al., 2023).

5.2 Improvements and adaptations of QAOA

Despite the theoretical limitations displayed above, QAOA has leverages (guiding function, parametrized quantum circuit, classical optimizer, etc.) that are still of interest in the literature. We display some of these studies on different choices of leverages that empirically improve QAOA performances.

First, the guiding function is mainly the mean function (14) as in the seminal paper of QAOA. However, both the CVaR function (18) and the Gibbs function (16) give an alternative to the mean function and show empirical improvements. For the former, several optimization problems, such as MAX-CUT, Maximum Stable Set, MAX-3SAT, etc., are solved with QAOA in Barkoutsos et al. (2020) and show better results with faster convergence. For the latter, the authors of Li et al. (2020) display better results solving MAX-CUT with this guiding function. Notice that comparing these improvements is hard because they use different classical optimizers. A different method to guide the optimization, presented in Amaro et al. (2022) as a Filtering Variational Quantum Algorithm, substitutes the guiding function for filtering functions. A filtering function is a function associated with a filtering operator that, given a Hamiltonian matrix and a quantum state, essentially modifies the latter by increasing the probability of eigenvectors with low eigenvalues and decreasing the probability of eigenvectors with high eigenvalues. Empirical results show improvements in the quality solution and the speed of convergence for the weighted Max-Cut problem.

Second, the choice of the quantum circuit is challenged in the literature. The underlying question is whether the quantum circuit of QAOA (see Subsection 4.2) is a good choice for finite depth p. Several papers suggest better circuits based on empirical results for small depth and small instances. For example, VQA with the circuit proposed in Barkoutsos et al. (2020) has better performances than QAOA, or with the Bang-Bang circuit described in Yang et al. (2017). The benefit of entanglement gates in the circuit is also discussed in Nannicini (2019) without giving a clear advantage. One can refer to the survey (Blekos et al., 2024) for other variants of quantum circuits. Notice that the authors of Egger et al. (2021) suggest to warm-start QAOA with either a continuous relaxation or a randomized rounding. This consists of initializing the quantum circuit with a solution of a continuous relaxation (Quadratic Programming or Semi Definite Programming), respectively with a randomly rounded solution of a continuous relaxation, instead of the state $|+\rangle ^{\otimes n}$. In both cases, QAOA performances for small p are better with a warm-start. Other initialization techniques are proposed in the literature. Among them, the annealing-inspired method (Sack & Serbyn, 2021) shows that a random parameters initialization on random graphs for the MAX-CUT problem is outperformed by the use of a Trotterized Quantum Annealing initialization. Another proposition is to initialize the parameters by using Machine Learning models (Alam et al., 2020). Specifically, looking for Machine Learning models that enable the prediction of parameters close to the optimal is relevant because there is an observed correlation between parameters of low-depth and high-depth circuits for some problems. For instance, this type of initialization empirically reduces the number of iterations of the classical optimizer of 44.9% on average for MAX-CUT problems.

The choice of the classical optimizer represents another leverage, where both gradient-based and gradient-free optimizers can be used. The most encountered gradient-based methods used in VQAs in the literature are the Gradient Descent (Ruder, 2016), the Broyden-Fletcher-Goldfarb-Shanno algorithm (Fortran et al., 1992), and the stochastic optimization algorithm ADAM (Kingma & Ba, 2014). As gradient-free methods, we can find the constrained optimization with linear approximation algorithm COBYLA (Powell, 1994), the simplex-based algorithm Nelder-Mead (Nelder & Mead, 1965), and the simultaneous perturbation stochastic approximation algorithm SPSA (Spall, 1992). The authors of Nannicini (2019) advise the choice of a global optimizer rather than a local optimizer to avoid numerous local optima. In Soloviev et al. (2022), the authors choose the gradient-free evolutionary algorithm called Estimation of Distribution Algorithm as the classical optimizer. This algorithm generates new solutions from a probabilistic model that depends on the best solutions of the previous iterations. They empirically show that it improves the results compared to traditional optimizers as mentioned above. The expression of the quantum circuit can also produce barren plateaus, hardening the optimization (McClean et al., 2018; Holmes et al., 2022). However, the authors of Mastropietro et al. (2023) indicate that re-starting the optimization when reaching barren plateaus, where the new parameters are chosen using a stochastic process, improves QAOA performances on MAX-CUT problems. Notice that the classical optimization loop is not always required. Indeed, the authors of Brandao et al. (2018) express that for some classes of QUBO problems, the (near) optimal parameters do not depend on the instance, allowing to train parameters before executing the quantum circuit only once. This is called the concentration of parameters and is numerically illustrated on random 3-regular graphs of 20 nodes for low-depth circuits regarding the MAX-CUT objective function. We do not list all the possible choices of VQA leverages. The surveys (Cerezo et al., 2021; Blekos et al., 2024) propose other possibilities.

In parallel, several algorithms derived from QAOA are appearing in the literature. An adaptation of QAOA is the Recursive-QAOA (Bravyi et al., 2022), also called RQAOA. It applies first several times QAOA to the problem in order to reduce its size, namely the number of variables, according to the correlation that appears between some variables. Then, it solves with classical brute force the resulting smaller problem. This algorithm seems to be competitive compared to QAOA for problems such as MAX-k-CUT. The authors of Zhu et al. (2022) propose another algorithm, the Adaptive-QAOA, that converges faster than QAOA on some instances of MAX-CUT. It consists of applying recursively QAOA, increasing step by step the depth of the quantum circuit.

Eventually, there is ongoing work on the formulation and implementation of the QAOA circuit to ease and lighten QAOA implementation. For instance, the authors of Nüßlein et al. (2022) present an algorithmic method to reduce the growth of the QUBO matrix size with the problem size for the k-SAT problem and the Hamiltonian Cycles problem. Besides that, the authors of Herrman et al. (2021) expose a global variable substitution method that, given an initial linear formulation of a 3-SAT problem, exploits the advantage of product representation in QAOA and, thus, minimizes the circuit depth.⁴ The shallower depth, the more efficient the implementation of the quantum circuit for NISQ computers. A different approach is proposed in Nagarajan et al. (2021), that is, given a quantum circuit, minimizes the circuit depth by solving a Mixed-Integer Program, with an optimality guarantee on the quantum circuit produced (it can find up to 57% reduction of the number of gates). It applies to any gate-based quantum algorithm and thus, can be applied to QAOA and, more generally, to VQAs.

Notice that solving combinatorial optimization problems using QAOA involves first formulating them into unconstrained problems, and more precisely into QUBO for easier circuits. There are essentially two types of formulation. The first and most common one is to integrate constraints as suitable penalty terms into the objective function. For instance, in Lucas (2014) we find formulations of Karp’s 21 NP-complete problems, and the authors of Oh et al. (2019) tackle the k-coloring graph problem with the same method. The tutorial (Glover et al., 2019) addresses more general cases for this formulation problem methodology. The second type of formulation is to change the expression of the mixing Hamiltonian (referred to as $H_B$ in Sect. 4). Initially presented in Hadfield et al. (2019), the main idea is to make this Hamiltonian varying the quantum state only in the feasible search space. Some problems have been specifically studied with this method, such as the Traveling Salesman problem (Ruan et al., 2020; Radzihovsky et al., 2019). Notice that there exists a third way to deal with constrained problems, which relies on the quantum Zeno dynamics. This consists of a generic method that essentially projects the quantum states into the feasible space (Herman et al., 2023). This requires auxiliary qubits which are measured in the middle of VQA or QAOA circuit. This shows improvements of QAOA’s performances, compared to the method with penalty terms, for the portfolio optimization problem numerically assessed on instances with less than ten assets.

6 Conclusion

In this tutorial, we have provided a mathematical description of VQAs and how they are translated into quantum algorithms. There has been a growing interest in VQAs, and more particularly QAOA, mostly because of their compatibility with NISQ computers. We have described how VQAs raise interesting questions regarding the choice of guiding functions and quantum circuits, among others. They also raise many technical questions that we did not address in this work, such as the noise at the implementation level (Lao et al., 2019).

Since its inception, researchers have argued about the potential advantages of QAOA over classical optimization algorithms (Farhi & Harrow, 2016; Lotshaw et al., 2021; Marwaha & Hadfield, 2022). This research seems to indicate that there is currently no scientific evidence that QAOA will soon beat classical heuristics. The available results even suggest the opposite, such as Hastings (2019) showing that local search algorithms can do better at low depth. Moreover, the current numerical results are hard to assess because they are run on small instances for which optimal or near-optimal solutions can be obtained easily with classical algorithms. Hopefully, the quickly growing capabilities of quantum computers will soon lead to a better understanding of the numerical efficiency of such algorithms (Guerreschi & Matsuura, 2019).

Appendices

Basics of linear algebra

This section provides some basic notions of linear algebra used throughout the tutorial. Notice that some specific definitions, such as unitary and Hermitian matrices, are introduced together with their use in quantum computing.

Definition 40

(Tensor product) Let $A = \begin{pmatrix} a_{11} & \dots & a_{1\,m}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nm} \end{pmatrix} \in \mathcal {M}_{n,m}(\mathbb {C})$ and $B = \begin{pmatrix} b_{11} & \dots & b_{1q}\\ \vdots & \ddots & \vdots \\ b_{p1} & \dots & b_{pq} \end{pmatrix} \in \mathcal {M}_{p,q}(\mathbb {C})$ be two complex matrices. Then, we define their tensor product, a bilinear operation, as

$$\begin{aligned} A \otimes B = \begin{pmatrix} a_{11}B & \dots & a_{1m}B\\ \vdots & \ddots & \vdots \\ a_{n1}B & \dots & a_{nm}B \end{pmatrix} \in \mathcal {M}_{np,mq}(\mathbb {C}). \end{aligned}$$

where $a_{ij}B = \begin{pmatrix} a_{ij}b_{11} & \dots & a_{ij}b_{1q}\\ \vdots & \ddots & \vdots \\ a_{ij}b_{p1} & \dots & a_{ij}b_{pq} \end{pmatrix} \in \mathcal {M}_{p,q}(\mathbb {C})$.

Proposition 41

(Tensor product properties) We draw attention to some useful properties of the tensor product:

• $A\otimes B \ne B\otimes A$

• $(A \otimes B) \otimes C = A \otimes (B \otimes C) = A \otimes B \otimes C$

• $A\otimes (cB) = (cA)\otimes B = c(A\otimes B)$, for $c\in \mathbb {C}$

Definition 42

(Braket notation) We also introduce the braket notation used in quantum computing. Let $\psi = \begin{pmatrix} \psi _1\\ \vdots \\ \psi _{2^n} \end{pmatrix} \in \mathbb {C}^{2^n}$ be a column vector. We note $|\psi \rangle$, said ket $\psi$, the vector $\psi$ itself. Thus, we define $\langle \psi |$, said bra $\psi$, the conjugate transpose of $|\psi \rangle$. Specifically,

$$\begin{aligned} |\psi \rangle&= \psi = \begin{pmatrix} \psi _1 \\ \vdots \\ \psi _{2^n} \end{pmatrix}\,,\\ \langle \psi |&= \bar{\psi }^T = \begin{pmatrix} \bar{\psi _1} & \ldots & \bar{\psi _{2^n}}\\ \end{pmatrix}\,. \end{aligned}$$

Thus, ket vectors are always column vectors whereas bra vectors are row vectors. With this notation, the norm of the vector $\psi$ is

We also consider the complex inner product

$$\begin{aligned} \psi , \phi \mapsto \langle \psi \rangle {\phi }, \end{aligned}$$

where we use the notation $\langle \psi |\cdot |\phi \rangle = \langle \psi \rangle {\phi }$. Notice that it is not commutative. Indeed, for $\psi = \begin{pmatrix} \psi _1 \\ \vdots \\ \psi _{2^n} \end{pmatrix} \in \mathbb {C}^{2^n}$ and $\phi = \begin{pmatrix} \phi _1 \\ \vdots \\ \phi _{2^n} \end{pmatrix} \in \mathbb {C}^{2^n}$, we have:

Definition 43

(Unitary operator associated with Hermitian matrix) Given a Hermitian matrix A, we define its associated quantum gate $Exp (A, t)$ parametrized by the parameter $t\in \mathbb {R}$ as:

Because A is Hermitian, $Exp (A,t)$ is a unitary matrix.

Omitted proofs

1.1 Guiding function properties

1.1.1 Proof of Proposition 25

Proposition 25

Function $g_{\text {mean}}$ is a guiding function.

Proof

Let us prove that $g_{\text {mean}}$ is continuous. Let $x\in \{0,1\}^n$. The function $\theta \mapsto p_\theta (x) = |\langle x|U(\theta )|0_n\rangle |^2$ is continuous, because each coefficient of $U(\theta )$ is continuous. Thus, because multiplication and addition preserve continuity, $g_{\text {mean}}$ is continuous.

We prove by contradiction that (11) holds. Let $\theta \in \mathcal {G}$ and let us consider the quantum state $|\psi (\theta )\rangle = U(\theta )|0_n\rangle$. Its decomposition in the canonical basis is $|\psi (\theta )\rangle = \sum _{x \in \{0,1\}^n}\psi _x|x\rangle$.

Assume that $|\psi (\theta )\rangle \notin \mathcal {F}_\text {quant}$. By definition, there exists $x_0\in \{0,1\}^n$ such that $x_0\notin \mathcal {F}$ and $|\psi _{x_0}|\ne 0$. Thus,

$$\begin{aligned} g_{\text {mean}}(\theta )&= \sum _{x \in \{0,1\}^n} |\psi _x|^2f(x)\\&= \sum _{x \in \mathcal {F}} |\psi _x|^2f(x) + \sum _{x \notin \mathcal {F}} |\psi _x|^2f(x)\\&= \left( \sum _{x \in \mathcal {F}} |\psi _x|^2\right) f^* + \sum _{x \notin \mathcal {F}} |\psi _x|^2f(x)\,, \end{aligned}$$

where $f^*$ is the optimal value of f, reached on $\mathcal {F}$. By definition, $f(x) > f^*, \forall x\notin \mathcal {F}$, and because we assume that $|\psi _{x_0}|\ne 0$, thus the second term of the sum is bounded below as follows: $\sum _{x \notin \mathcal {F}} |\psi _x|^2f(x) > \left( \sum _{x \notin \mathcal {F}} |\psi _x|^2\right) f^*$, where $\sum _{x \notin \mathcal {F}} |\psi _x|^2 \ge |\psi _{x_0}|^2 > 0$. Thus,

$$\begin{aligned} g_{\text {mean}}(\theta )&> \left( \sum _{x \in \mathcal {F}} |\psi _x|^2\right) f^* + \left( \sum _{x \notin \mathcal {F}} |\psi _x|^2\right) f^* = f^*\,. \end{aligned}$$

This contradicts the previous statement that $\theta \in \mathcal {G}$, as one readily verifies that the minimum of $g_{\text {mean}}$ is $g_{\text {mean}}^* = f^*$. $\square$

1.1.2 Proof of Proposition 27

Proposition 27

Let $\eta >0$. Function $g_{G,\eta }$ is a guiding function.

Proof

Let us prove that $g_{G,\eta }$ is continuous. Let $x\in \{0,1\}^n$. The function $\theta \mapsto p_\theta (x) = |\langle x|U(\theta )|0_n\rangle |^2$ is continuous, because each coefficient of $U(\theta )$ is continuous. Thus, because multiplication, addition, and composition preserve continuity, $g_{G,\eta }$ is continuous.

Let $\eta >0$. Let us prove by contradiction that (11) holds. As before, let $\theta \in \mathcal {G}$ and let us consider the quantum state $|\psi (\theta )\rangle = U(\theta )|0_n\rangle$. Its decomposition in the canonical basis is $|\psi (\theta )\rangle = \sum _{x \in \{0,1\}^n}\psi _x|x\rangle$. Assume that $|\psi (\theta )\rangle \notin \mathcal {F}_\text {quant}$. Thus, there exists $x_0\in \{0,1\}^n$ such that $x_0\notin \mathcal {F}$ and $|\psi _{x_0}|\ne 0$. Thus,

$$\begin{aligned} g_{G,\eta }(\theta )&= -\ln \left( {\sum _{x\in \{0,1\}^n}|\psi _x|^2e^{-\eta f(x)}} \right) \\&= -\ln \left( {\sum _{x \in \mathcal {F}} |\psi _x|^2e^{-\eta f(x)} + \sum _{x \notin \mathcal {F}} |\psi _x|^2e^{-\eta f(x)}} \right) \\&= -\ln \left( {\left( \sum _{x \in \mathcal {F}} |\psi _x|^2\right) e^{-\eta f^*} + \sum _{x \notin \mathcal {F}} |\psi _x|^2e^{-\eta f(x)}}\right) \,, \end{aligned}$$

where $f^*$ is the optimal value of f, reached on $\mathcal {F}$. By definition, $f(x) > f^*, \forall x\notin \mathcal {F}$, and because $\eta >0$, we have $e^{-\eta f(x)} < e^{-\eta f^*}$. Moreover, we assume that $|\psi _{x_0}|\ne 0$, thus the second term of the sum in the logarithm is bounded above as follows: $\sum _{x \notin \mathcal {F}} |\psi _x|^2e^{-\eta f(x)} < \left( \sum _{x \notin \mathcal {F}} |\psi _x|^2\right) e^{-\eta f^*}$, where $\sum _{x \notin \mathcal {F}} |\psi _x|^2 \ge |\psi _{x_0}|^2 > 0$. Thus, because $y \mapsto -\ln (y)$ is a decreasing function,

$$\begin{aligned} g_{G,\eta }(\theta )&> -\ln \left( {\left( \sum _{x \in \mathcal {F}} |\psi _x|^2\right) e^{-\eta f^*} + \left( \sum _{x \notin \mathcal {F}} |\psi _x|^2\right) e^{-\eta f^*}}\right) = \eta f^*\,. \end{aligned}$$

This contradicts the previous statement that $\theta \in \mathcal {G}$. Indeed, we can easily verify that the minimum of $g_{G,\eta }$ is $g_{G,\eta }^* = \eta f^*$. $\square$

1.1.3 Proof of Proposition 31

Proposition 31

Let $\alpha \in ]0,1[$. Function $g_{C,\alpha }$ is a pseudo-guiding function.

Proof

For the same reason as for $g_\text {mean}$, $g_{C,\alpha }$ is continuous.

Let $\alpha \in ]0,1[,\theta \in \mathcal {G}$ and let us consider the quantum state $|\psi (\theta )\rangle = U(\theta )|0_n\rangle$. Its decomposition in the canonical basis is $|\psi (\theta )\rangle = \sum _{x \in \{0,1\}^n}\psi _x|x\rangle$.

Let us prove that either $|\psi (\theta )\rangle \in \mathcal {F}_\text {quant}$ or that , where $N_\mathcal {F}$ is the index that delimits $\mathcal {F}$, specifically,

$$\begin{aligned} \mathcal {F}= \{x_i, i\in [N_\mathcal {F}]\}. \end{aligned}$$

There are two cases for $N_\alpha$ (we recall that $N_\alpha$ depends on $\theta$):

• If $N_\alpha \le N_\mathcal {F}$, thus

  

  where $f^*$ is the optimal value of f, reached on $\mathcal {F}$. This contradicts (11) but the probability of sampling non-optimal solutions when measuring $|\psi (\theta )\rangle$ is strictly lower than $1 - \alpha$. Indeed, by definition of $N_\alpha$,

  

• Otherwise, $N_\alpha > N_\mathcal {F}$. Let us prove by contradiction that $|\psi (\theta )\rangle \in \mathcal {F}_\text {quant}$. Assume that $|\psi (\theta )\rangle \notin \mathcal {F}_\text {quant}$. Thus, there exists $k>N_\mathcal {F}$ such that $|\psi _k|\ne 0$. We can show that $g_{C,\alpha }(\theta ) > f^*$ using essentially the same proof as that of Proposition 25 for $x_0 = \min \{k > N_\mathcal {F}: |\psi _k|\ne 0\}$. This contradicts the statement that $\theta \in \mathcal {G}$, because the minimum of $g_{C,\alpha }$ is $g_{C,\alpha }^* = f^*$. $\square$

1.2 Quantum circuit of QAOA

1.2.1 Proof of Proposition 34

Proposition 34

The first block $Exp (H_f, \gamma )$ parametrized by $\gamma \in \mathbb {R}$ is

$$\begin{aligned} Exp (H_f, \gamma ) = \prod _{\alpha \in \{0,1\}^n}Exp (\bigotimes _{i=1}^n Z_i^{\alpha _i}, h_\alpha \gamma ). \end{aligned}$$

The second block $Exp (H_B, \beta )$ parametrized by $\beta \in \mathbb {R}$ is

$$\begin{aligned} Exp (H_B, \beta ) = \bigotimes _{i=1}^n R_{X,i}(2\beta ). \end{aligned}$$

Proof

Let $\gamma \in \mathbb {R}$ and let us consider the first block $Exp (H_f, \gamma )$. By Definition 43, and because each pair of matrices of the family $\{\bigotimes _{i=1}^n Z_i^{\alpha _i}: \alpha = (\alpha _1,\ldots ,\alpha _n)\in \{0,1\}^n\}$ commutes two by two,

$$\begin{aligned} Exp (H_f, \gamma )&= e^{-i(\sum _{\alpha = (\alpha _1,\ldots ,\alpha _n) \in \{0,1\}^n} h_{\alpha }\bigotimes _{i=1}^n Z_i^{\alpha _i})\gamma } \end{aligned}$$

(23)

$$\begin{aligned}&= \prod _{\alpha = (\alpha _1,\ldots ,\alpha _n)\in \{0,1\}^n} e^{-ih_{\alpha }\bigotimes _{i=1}^n Z_i^{\alpha _i}\gamma } \end{aligned}$$

(24)

$$\begin{aligned}&= \prod _{\alpha = (\alpha _1,\ldots ,\alpha _n)\in \{0,1\}^n}Exp (\bigotimes _{i=1}^n Z_i^{\alpha _i}, h_{\alpha }\gamma ) \,. \end{aligned}$$

(25)

Let $\beta \in \mathbb {R}$ and let us consider the second block $Exp (H_B, \beta )$. For more readability, we write $X_i=R_{X,i}(\pi )$ the application of matrix $X=\begin{pmatrix} 0& 1\\ 1& 0 \end{pmatrix}$ on qubit i. With the same development as above, and because each pair of matrices of the family $\{X_i: i\in [n]\}$ commutes two by two,

$$\begin{aligned} Exp (H_B, \beta ) = \prod _{i=1}^nExp (X_i, \beta ). \end{aligned}$$

Let $i\in [n]$. Thus,

(26)

(27)

(28)

(29)

$$\begin{aligned}&= \cos (t)I -i\sin (t)X_i \end{aligned}$$

(30)

$$\begin{aligned}&= R_{X,i}(2\beta )\,, \end{aligned}$$

(31)

where line (27) exploits the fact that $X^2 = I$, implying $X^{2k} = I$ and $X^{2k+1} = X$. Moreover, line (28) applies the definition of the complex number i, and one can recognize the power series of cosinus and sinus functions. $\square$

1.2.2 Proof of Proposition 35

Proposition 35

For the case of QUBO, the expression of $Exp (H_f, \gamma )$ simplifies in

$$\begin{aligned} Exp (H_f, \gamma ) = \left( \bigotimes _{i=1}^n R_{Z,i}(2h_{ii}\gamma )\right) \prod _{i<j}CX_{i,j} R_{Z,j}(2h_{i,j}\gamma )CX_{i,j}, \end{aligned}$$

and is rather easily implemented with universal quantum gates.

Proof

Let $\gamma \in \mathbb {R}$. The application of (23)–(25) to the case of QUBO gives

$$\begin{aligned} Exp (H_f, \gamma )&= e^{-i(\sum _{i=1}^n h_{ii}Z_i + \sum _{i<j}h_{ij} Z_i\otimes Z_j)\gamma }\\&= \prod _{i=1}^n e^{-iZ_i h_{ii}\gamma }\prod _{i<j}e^{-i Z_i\otimes Z_j h_{ij}\gamma }\\&= \prod _{i=1}^n Exp (Z_i, h_{ii}\gamma )\prod _{i<j}Exp (Z_i\otimes Z_j, h_{ij}\gamma )\,. \end{aligned}$$

Then, let us prove that, for $i\in [n]$ and $t\in \mathbb {R}$, $Exp (Z_i, t) = R_{Z,i}(2t)$. The same development as above (27)–(30), replacing X by Z that have the same property $Z^2 = I$, gives

$$\begin{aligned} Exp (Z_i,t)&= \cos (t)I -i\sin (t)Z_i \end{aligned}$$

(32)

$$\begin{aligned}&= R_{Z,i}(2t) \,. \end{aligned}$$

(33)

Eventually, line (32) is the application of the gate $\begin{pmatrix} e^{-it} & 0\\ 0 & e^{it} \end{pmatrix} = R_Z(2t)$ on qubit i, and the identity on the others.

It remains to prove that, for $i<j \in [n]$ and $t\in \mathbb {R}$, $Exp (Z_i\otimes Z_j, t) = CX_{i,j} R_{Z,j}(2t)CX_{i,j}$. Following the same developments as above, we have

$$\begin{aligned} Exp (Z_i\otimes Z_j, t) = \cos (t)I -i\sin (t)Z_i\otimes Z_j. \end{aligned}$$

(34)

We consider the two-qubit system that corresponds to the qubit i as the first qubit and the qubit j as the second qubit (the others are unchanged by the transformation). Thus, it remains to prove the equality of the two circuits depicted on Fig. 9.

Fig. 9

Decomposition of $Exp (Z_1\otimes Z_2, t)$ into universal gates

On the one hand, (34) is the application of the gate $= \begin{pmatrix} R_Z(2t) & 0\\ 0 & R_Z(-2t) \end{pmatrix}$ to this system. Indeed,

$$\begin{aligned} \cos (t)I -i\sin (t)Z_1\otimes Z_2&= \cos (t)\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1& 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} -i\sin (t)\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1& 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \\&= \begin{pmatrix} e^{-it} & 0 & 0 & 0 \\ 0 & e^{it} & 0 & 0 \\ 0 & 0 & e^{it} & 0 \\ 0 & 0 & 0 & e^{-it} \end{pmatrix} \\&= \begin{pmatrix} R_Z(2t) & 0\\ 0 & R_Z(-2t) \end{pmatrix}\,. \end{aligned}$$

On the other hand, the composition of gates $CX_{1,2} R_{Z,2}(2t)CX_{1,2}$ on this system amounts to

$$\begin{aligned} CX_{1,2}R_{Z,2}(2t)CX_{1,2}&= \begin{pmatrix} I & 0 \\ 0 & X \end{pmatrix}\begin{pmatrix} R_Z(2t) & 0 \\ 0 & R_Z(2t) \end{pmatrix}\begin{pmatrix} I & 0 \\ 0 & X \end{pmatrix}\\&= \begin{pmatrix} R_Z(2t) & 0 \\ 0 & XR_Z(2t)X \end{pmatrix}\\&= \begin{pmatrix} R_Z(2t) & 0 \\ 0 & R_Z(-2t) \end{pmatrix}\,. \end{aligned}$$

Thus, the proof results from replacing t by appropriate values $h_{ii}\gamma$ for $i\in [n]$ and $h_{ij}\gamma$ for $i< j$. $\square$

1.2.3 Proof of Lemma 36

Lemma 36

$\forall n\in \mathbb {N}^*$,

$$\begin{aligned} (I^{\otimes n-1}\otimes X)e^{-itZ^{\otimes n}}(I^{\otimes n-1}\otimes X) = e^{itZ^{\otimes n}}. \end{aligned}$$

Proof

Let $P_n$ be the statement

$$\begin{aligned} (I^{\otimes n-1}\otimes X)e^{-itZ^{\otimes n}}(I^{\otimes n-1}\otimes X) = e^{itZ^{\otimes n}}. \end{aligned}$$

Let us prove by induction that $P_n$ holds for all integer $n\in \mathbb {N}^*$.

Base case: Let us prove $P_1$. According to (33), $e^{-itZ} = R_Z(2t)$, thus,

$$\begin{aligned} Xe^{-itZ}X&= \begin{pmatrix} 0& 1\\ 1& 0 \end{pmatrix}\begin{pmatrix} e^{-it}& 0\\ 0& e^{it} \end{pmatrix}\begin{pmatrix} 0& 1\\ 1& 0 \end{pmatrix}\\&= \begin{pmatrix} e^{it}& 0\\ 0& e^{-it} \end{pmatrix}\\&= e^{itZ}\,. \end{aligned}$$

Induction step: Let $n\ge 1$ be given and suppose $P_n$. Let us prove $P_{n+1}$. According to (35), we have $e^{-itZ^{\otimes n+1}} = \begin{pmatrix} e^{-itZ^{\otimes n}}& 0\\ 0 & e^{itZ^{\otimes n}} \end{pmatrix}$. Thus,

$$\begin{aligned}&(I^{\otimes n}\otimes X)e^{-itZ^{\otimes n+1}}(I^{\otimes n}\otimes X) = (I\otimes I^{\otimes n-1}\otimes X)e^{-itZ^{\otimes n+1}}(I\otimes I^{\otimes n-1}\otimes X)\\&= \begin{pmatrix} I^{\otimes n-1}\otimes X& 0\\ 0& I^{\otimes n-1}\otimes X \end{pmatrix}\begin{pmatrix} e^{-itZ^{\otimes n}}& 0\\ 0 & e^{itZ^{\otimes n}} \end{pmatrix} \begin{pmatrix} I^{\otimes n-1}\otimes X& 0\\ 0& I^{\otimes n-1}\otimes X \end{pmatrix}\\&= \begin{pmatrix} (I^{\otimes n-1}\otimes X)e^{-itZ^{\otimes n}}(I^{\otimes n-1}\otimes X)& 0\\ 0& (I^{\otimes n-1}\otimes X)e^{itZ^{\otimes n}}(I^{\otimes n-1}\otimes X) \end{pmatrix}\,. \end{aligned}$$

By induction hypothesis $P_n$,

$$\begin{aligned} (I^{\otimes n}\otimes X)e^{-itZ^{\otimes n+1}}(I^{\otimes n}\otimes X)&= \begin{pmatrix} e^{itZ^{\otimes n}}& 0\\ 0& e^{-itZ^{\otimes n}} \end{pmatrix}\\&= e^{itZ^{\otimes n+1}}\,. \end{aligned}$$

$\square$

1.2.4 Proof of Proposition 37

Proposition 37

Let us consider the subsystem composed of the N qubits to which the Z gate is applied. Specifically, $N = |\{\alpha _i\, i\in [n]: \alpha _i = 1\}|$, and we renumber the qubits in question in [N]. Thus, for $N\ge 2$, the term $Exp (\bigotimes _{i=1}^n Z^{\alpha _i}, t)$ on this subsystem simplifies in

$$\begin{aligned} Exp (Z^{\otimes N}, t) = \prod _{j=0}^{N-2} CX_{1,N-j} R_{Z,N}(2t) \prod _{j=0}^{N-2} CX_{1,N-j}. \end{aligned}$$

We represent this decomposition on Fig. 7.

Fig. 10

Circuit representation of

Proof

Let $P_n$ be the statement

$$\begin{aligned} Exp (Z^{\otimes n}, t) = \prod _{j=0}^{n-2} CX_{1,n-j} R_{Z,n}(2t) \prod _{j=0}^{n-2} CX_{1,n-j}. \end{aligned}$$

Let us prove by induction that $P_n$ holds for all integer $n\ge 2$.

Base case: Proposition 35 proves $P_2$.

Induction step: Let $n\ge 2$ be given and suppose $P_n$. Let us prove $P_{n+1}$.

On the one hand,

$$\begin{aligned} Exp (Z^{\otimes n+1}, t) = e^{-itZ^{\otimes n+1}} = e^{-itZ\otimes Z^{\otimes n}} \end{aligned}$$

where $Z\otimes Z^{\otimes n} = \begin{pmatrix} Z^{\otimes n}& 0\\ 0 & -Z^{\otimes n} \end{pmatrix}$. This latter matrix is diagonal, thus,

$$\begin{aligned} Exp (Z^{\otimes n+1}, t) = \begin{pmatrix} e^{-itZ^{\otimes n}}& 0\\ 0 & e^{itZ^{\otimes n}} \end{pmatrix}. \end{aligned}$$

(35)

On the other hand, we compute the term

$$\begin{aligned} & \prod _{j=0}^{n-1} CX_{1,n+1-j} R_{Z,n+1}(2t) \prod _{j=0}^{n-1} CX_{1,n+1-j} \\ & = CX_{1,n+1}\left( \prod _{j=1}^{n-2} CX_{1,n+1-j} R_{Z,n+1}(2t) \prod _{j=1}^{n-2} CX_{1,n+1-j}\right) CX_{1, n+1} \end{aligned}$$

that is represented on Fig. 10, where $e^{-itZ^{\otimes n}}$ applies on the qubits 2 to n by induction hypothesis.

Thus,

$$\begin{aligned}&\prod _{j=0}^{n-1} CX_{1,n+1-j} R_{Z,n+1}(2t) \prod _{j=0}^{n-1} CX_{1,n+1-j} = CX_{1,n+1}(I\otimes e^{-itZ^{\otimes n}})CX_{1,n+1} \\&= \begin{pmatrix} I^{\otimes n}& 0\\ 0& I^{\otimes n-1}\otimes X \end{pmatrix}\begin{pmatrix} e^{-itZ^{\otimes n}}& 0\\ 0& e^{-itZ^{\otimes n}} \end{pmatrix}\begin{pmatrix} I^{\otimes n}& 0\\ 0& I^{\otimes n-1}\otimes X \end{pmatrix}\\&= \begin{pmatrix} e^{-itZ^{\otimes n}}& 0\\ 0& (I^{\otimes n-1}\otimes X)e^{-itZ^{\otimes n}}(I^{\otimes n-1}\otimes X) \end{pmatrix}\\&= \begin{pmatrix} e^{-itZ^{\otimes n}}& 0\\ 0& e^{itZ^{\otimes n}} \end{pmatrix}\,, \end{aligned}$$

where the last line comes from the application of Lemma 36. Thus,

$$\begin{aligned} Exp (Z^{\otimes n+1}, t) = \prod _{j=0}^{n-1} CX_{1,n+1-j} R_{Z,n+1}(2t) \prod _{j=0}^{n-1} CX_{1,n+1-j}, \end{aligned}$$

proving $P_{n+1}$. $\square$