The COVID-19 pandemic and the performance of healthcare supply chains

Abstract

Recent pandemic outbreaks, including the COVID-19 and SARS, have revealed that supply chains (SCs) are unable to respond to such disasters. To mitigate the destructive impacts and improve the performance of SCs, Operations Research (OR) techniques have been applied to address the issues over the last two decades. The objective of this paper is to develop a network data envelopment analysis (NDEA) model to measure the resilience and sustainability of healthcare SCs in response to the COVID-19 pandemic outbreak. In the proposed NDEA model, for the first time, outputs’ weak disposability, chance-constrained programming (CCP), the convexity assumption, and the semi-oriented radial approach are aggregated. Moreover, a modified directional distance function (DDF) measure is developed to measure the overall and divisional efficiency scores. Furthermore, the proposed model can deal with different types of data such as integer-valued data, negative data, stochastic data, ratio data, and undesirable outputs. Also, several useful and interesting properties of the novel efficiency measure are presented. Finally, we measure the performance of 28 healthcare SCs to demonstrate the applicability and capability of our proposed approach.

1 Introduction

The recent outbreak of COVID-19 was first diagnosed in late 2019 in the Chinese city of Wuhan (Belhadi et al., 2021). The World Health Organization (WHO) in March 2020 officially declared COVID-19 as a global pandemic (Nagurney, 2021). The pandemic rapidly spread all over the world and has caused devastating damages to the global community. The WHO officially reported 1,831,703 death tolls and 83,326,479 cases by 3 January 2021 owing to the COVID-19 pandemic.¹ The number of death tolls and new cases are increasing dramatically, particularly in the US, Brazil, and the UK. The pandemic also has resulted in irreparable economic consequences around the globe. International financial institutes report that the global economic growths in advanced and developing economies have decreased by 6% and 1%, respectively (Karmaker et al., 2021). The COVID-19 epidemic has negatively affected over 94% of the top 1,000 firms. The unprecedented increase in unemployment rate, considerable reductions in income, and huge disruptions in goods and services are among the serious consequences of the COVID-19 outbreak (Pak et al., 2020).

Preventive and precautionary measures taken by countries to control the spread of the coronavirus virus have resulted in severe disruptions of supply chains (SCs) (Tang et al., 2020). Managing disruptions of SCs due to unexpected events such as natural disasters and man-made disasters has been an interesting research topic over the last few decades (Ivanov & Das, 2020). The disruptions caused by Covid-19 epidemic and other global epidemics, including SARS and Influenza, have highlighted the strategic importance of SCs to supply goods and services. The COVID-19 outbreak is testing the resilience SCs in terms of flexibility, robustness, and recovery (Ivanov & Dolgui, 2020). Furthermore, the pandemic has shown that the triple-bottom-line of sustainable SCs (economic, social, and environmental dimensions) are associated with one another (Karmaker et al., 2021; Sarkis, 2020). Disruptions in providing goods and services across industries reveal the economic aspect of sustainable SCs. Also, the source of the virus (sales markets of animal products) and new social norms such as social distancing reveal the environmental and social dimensions of sustainable SCs (Sarkis, 2020). As such, the recent unprecedented crisis has prompted and compelled many organizations to adopt strategies to tackle the sustainability issues in their SCs (Ivanov & Dolgui, 2020).

Pandemic diseases outbreaks such as Influenza, SARS, and the recent COVID-19 have been a major issue for policymakers, managers, and decision-makers in the healthcare strategic sector over the two last decades (Sharma et al., 2020). Disruptions of hospital SCs are mostly owing to demand increase in the necessary equipment, resulting in huge shortages of such equipment, causing considerable surge in the number of infected people and death toll, as well as healthcare costs (Chakrabarty & Roy, 2021). As such, the performance of healthcare systems is negatively affected by such pandemic outbreaks for an uncertain period. To decrease the negative impacts of epidemic outbreaks, healthcare SCs need to be resilient and sustainable (Govindan et al., 2020). In response to patients’ needs during epidemic outbreaks, the healthcare SC plays a key role in healthcare systems. Therefore, there is an essential need to develop apposite approaches and frameworks to measure the performance of healthcare systems, especially during pandemic outbreak periods (Göleç & Karadeniz, 2020).

Management Science (MS) and Operations Research (OR) methods and techniques are of considerable importance to address epidemic outbreaks problems such as scare resource allocation, increased demand forecast, and SC risk management (Ivanov & Dolgui, 2020). Data envelopment analysis (DEA) derived from OR is a powerful nonparametric method for assessing the performance of a set of decision-making units (DMUs) in many strategic and key sectors such as healthcare, education, and services (Buffa & Ross, 2011; Kaffash et al., 2020; Min & Ahn, 2017; Muir et al., 2019; Su et al., 2018). Since the performance of healthcare SCs has been affected by the recent pandemic, it is crucial to develop and apply advanced OR approaches such as network DEA to measure the performance of healthcare SCs. To this end, in this paper, the resilience and sustainability of healthcare SCs are assessed. This paper makes the following contributions:

• A novel network DEA model is proposed to deal with different types of data such as integer-valued data, negative data, stochastic data, ratio data, and undesirable outputs.

• Ideas of outputs’ weak disposability, chance-constrained programming (CCP), the convexity assumption, and the partitioning approach of the semi-oriented radial model (SORM) are aggregated in a unified framework.

• A modified directional distance function (DDF) is developed to derive both the overall and divisional efficiency scores.

• Several interesting properties of the new efficiency measure are presented.

• A case study is presented to measure the resilience and sustainability of healthcare SCs under the COVID-19 pandemic crisis.

The rest of this paper is organized as follows: In Sect. 2 we present the related works. The proposed method is presented in Sect. 3. Next, we present the case study in Sect. 4. Finally, conclusions and future researches are provided in Sect. 5.

2 Literature review

2.1 Epidemic diseases and healthcare supply chains

Healthcare SCs play a strategic and pivotal role in supplying medical devices and providing the required services to patients (Leite et al., 2020). If a pandemic disease occurs, healthcare SCs cannot act efficiently due to the increased demands in medical devices and services (Hoyos et al., 2015). Weak efficiency management may lead to considerable shortages in crucial medical devices and services.

2.2 Performance assessment in healthcare SCs

Al-Saa'da et al. (2013) assessed different dimensions of healthcare SCs, including standards, requirements, compatibility, relationship with vendors, and delivery of quality healthcare services. Chen et al. (2013) evaluated the impact of the hospital-supplier collaboration on the efficiency of healthcare SCs. Nyaga et al. (2015) examined the effect of internal and external indicators on the efficiency of healthcare SCs. Supeekit et al. (2016) applied the analytic network process (ANP) to assess the performance of hospital SCs. Leksono et al. (2019) adopted the balanced scorecard (BSC) and ANP to measure the efficiency of sustainable healthcare SCs. Chorfi et al. (2019) proposed a DEA model for evaluating the performance of healthcare SCs in the presence of interval data. Göleç and Karadeniz (2020) developed a fuzzy model for analyzing the performance of healthcare SCs.

2.3 Data envelopment analysis (DEA)

DEA is the most popular approach for evaluating the relative efficiency of a set of decision-making units (DMUs) (Kazemi Matin et al., 2022; Mahmoudi et al., 2019; Saeedi et al., 2019; Uludağ, 2020; Visani et al., 2016) To derive the relative efficiency of DMUs, DEA forms an efficiency frontier using combinations of inputs and outputs (Emrouznejad et al., 2010a, 2010b). The Charnes et al. (1978) (CCR) and Banker et al. (1984) (BCC) models are two basic DEA models. Owing to its numerous advantages, DEA has been used in many decision-making areas over the last two decades (Izadikhah et al., 2022). DEA assumes that the DMUs that produce more outputs with fewer inputs are more efficient compared with the other DMUs. However, this assumption is not valid to measure the efficiency of DMUs if there are some undesirable outputs such as pollution and noise (Halkos & Petrou, 2019). Färe et al. (1989) presented a DEA model to address both undesirable outputs and desirable outputs. Seiford and Zhu (2002) proposed a DEA model for increasing the efficiency of DMUs in the existence of both good outputs and bad outputs. Jahanshahloo et al. (2005) developed a non-radial DEA model for addressing bad outputs in the performance evaluation of DMUs. Yang and Pollitt (2010) presented a DEA model for distinguishing the weak and strong disposability assumptions among different bad outputs, considering some of their technical features. Mahdiloo et al. (2014) developed a game-theoretic method to decompose the efficiency score in DEA. Liu et al. (2017) developed a DEA cross-efficiency model for dealing with bad outputs. Mozaffari et al. (2021) proposed a two-stage DEA model to measure the efficiency of DMUs in the existence of fuzzy data and undesirable outputs. For more discussions on undesirable outputs in DEA, the reader may refer to the review by Halkos and Petrou (2019).

The presence of ratio data presents another challenge to deploy the conventional DEA model. To tackle this challenge, Emrouznejad and Amin (2009) proposed the convexity assumption for the DEA structure. Olesen et al. (2015) proposed production technologies for handling ratio data. To cope with ratio data, Hatami-Marbini and Toloo (2019) modified the proposed approach of Emrouznejad and Amin (2009). The traditional DEA models also are unable to deal with integer data for measuring the efficiency of DMUs. In the traditional DEA model, it is assumed that the inputs and outputs take only real values. However, there might be inputs and outputs that only take integer-valued data. Lozano and Villa (2006), for the first time, presented integer-valued DEA. Kazemi Matin and Kuosmanen (2009) revised their model by developing an axiomatic foundation for DEA models in the existence of integer values. Over the last decade, various researchers have addressed integer data in DEA (e.g., Azadi & Saen, 2014; Chen et al., 2012; Khoveyni et al., 2019; Kordrostami et al., 2019; Wu & Zhou, 2015).

The classical DEA model assumes that the inputs and outputs are deterministic. However, there are many situations in which the inputs and outputs can be stochastic. Sengupta (1982) developed the first stochastic DEA model. Cooper et al. (2002) developed the CCP version of DEA models for determining efficient and inefficient resources. Tavana et al. (2014) presented the chance-constrained DEA (CCDEA) model in the presence of random inputs and outputs. Chen and Zhu (2019) investigated the computational tractability of CCDEA models using optimization models. There are studies on stochastic DEA models (e.g., Cooper et al., 1998, 2004; Huang & Li, 2001; Morita & Seiford, 1999; Olesen & Petersen, 1995).

Another pitfall of the traditional DEA model is that it is unable to deal with negative data. For example, profit as an output may take positive and negative values. Scheel (2001) addressed the negative values by considering negative outputs as inputs. Sharp et al. (2007) modified the slacks-based measure (SBM) model to deal with negative outputs and inputs. Over the last decade, researchers have addressed the negative data in DEA (e.g., Allahyar & Rostamy-Malkhalifeh, 2015; Emrouznejad et al., 2010a, 2010b; Izadikhah & Saen, 2016; Lin & Chen, 2018; Tavana et al., 2020; Tavassoli & Saen, 2019; Tavassoli et al., 2015). Tavassoli et al. (2014) developed a super-efficiency DEA model in the existence of undesirable outputs.

Ignoring the internal transactions of DMUs is another major drawback of the classical DEA model. In other words, in real-world applications, many DMUs such as SCs deal with network structures. Nevertheless, the classical DEA models treat DMUs as black boxes and do not take into account the internal transactions of DMUs. Färe and Grosskopf (2000) proposed network DEA to measure the efficiency in network structures. Liang et al. (2008) developed a two-stage DEA model based on game theory. Tone and Tsutsui (2009) presented a network SBM model to evaluate the performance of electric power companies. Kao and Hwang (2010) developed a network DEA model to investigate inefficiency in the banking sector. Fathi and Saen (2018) presented a bidirectional network DEA model to assess the sustainability of SCs in the transport sector. Shi et al. (2021) introduced a network DEA model for two-stage processes. For a review of the most important studies on network DEA, the reader may refer to Chang et al. (2020), Chen et al. (2020), and Chen and Zhu (2020).

2.4 Research gap

The literature review shows that despite the significance of performance measurement of healthcare SCs, it has not been sufficiently addressed. Moreover, resilience and sustainability issues have not been considered simultaneously in the performance evaluation of healthcare SCs. Besides, none of the existing DEA and network DEA models can deal with integer-valued data, ratio data, stochastic data, negative data, and undesirable data, simultaneously. To address the above-mentioned shortcomings, we propose a novel network DEA model with several distinctive features, which are discussed in the next section.

3 Proposed method

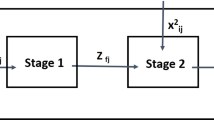
Suppose that there are $n$ observed DMUs, where $DM{U}_{j}$ ($j=1,\dots ,n$) consists of $p$ divisions (sub-processes). The kth division $(k=1,\dots , p)$ consumes external inputs ${{\varvec{x}}}_{i}^{(k)} (i={m}^{\left(k-1\right)}+1,\dots ,{m}^{(k)})$ and the intermediate inputs ${{\varvec{z}}}_{g}^{(k-1)} \left(g={h}^{(k-2)}+1,\dots ,{h}^{(k-1)}\right)$ to produce final output ${{\varvec{y}}}_{r}^{\left(k\right)}\left(r={s}^{(k-1)}+1,\dots ,{s}^{(k)}\right)$ and intermediate product ${{\varvec{z}}}_{g}^{(k)} (g={h}^{\left(k-1\right)}+1,\dots ,{h}^{\left(k\right)})$. Note that the first division consumes only the external inputs and the last division produces only the final outputs. As shown in Fig. 1, the divisions are connected by the intermediate products.

Fig. 1

General series network

3.1 Production set

Following Färe and Grosskopf (2000), the production technology set for general series production systems under variable returns to scale assumption is as follows:

$$T=\{\left({\varvec{x}},{\varvec{z}},{\varvec{y}}\right)\in {\mathbb{R}}_{+}^{{m}^{\left(p\right)}+{h}^{\left(p\right)}+{s}^{\left(p\right)}}|$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{x}_{ij}^{\left(k\right)}\le {x}_{i}^{\left(k\right)}, i={m}^{\left(k-1\right)}+1, \dots , {m}^{\left(k\right)}$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{z}_{gj}^{\left(k\right)}\ge {z}_{g}^{\left(k\right)}, g={h}^{\left(k-1\right)}+1, \dots , {h}^{\left(k\right)}$$

$${z}_{g}^{\left(k\right)}\ge {\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k+1\right)}{z}_{gj}^{\left(k\right)}, g={h}^{\left(k-1\right)}+1, \dots , {h}^{\left(k\right)}$$

$${y}_{r}^{\left(k\right)}\le {\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{\left(k\right)}, k=1,\dots ,p, r={s}^{\left(k-1\right)}+1, \dots , {s}^{\left(k\right)}$$

$$\sum_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}=1, k=1,\dots ,p$$

$${\lambda }_{j}^{\left(k\right)}\ge 0, k=1,\dots ,p, j=1,\dots ,n \},$$

(1)

where ${\lambda }_{j}^{\left(k\right)}$ denotes the intensity weight of $DM{U}_{j}$ in division $k$.

3.2 Modelling different types of data

The conventional DEA model assumes that the data in the production processes are positive real values. However, in many real applications, the inputs, intermediates, and outputs may not be positive real values. Here, without loss of generality and in line with our case study, we assume the following types of data:

• Non-integer ($NI$) and integer ($I$) inputs

• Deterministic ($D$) and stochastic ($S$) intermediates

• Desirable or good ($G$) and undesirable or bad ($B$) outputs

• Positive ($P$) and negative ($N$) desirable outputs

• Absolute ($A$) and ratio ($R$) positive outputs

Now, the inputs, intermediate products, and outputs are decomposed as follows:

$Inputs= NI\cup I,$

$Intermediates=D\cup S,$

$Outputs=G\cup B=\left(P\cup N\right)\cup B=\left(\left(A\cup R\right)\cup N\right)\cup B.$

The associated partitioning of the input, intermediate, and output vectors are as follows:

$${\varvec{x}}=\left({{\varvec{x}}}^{{\varvec{N}}{\varvec{I}}},\boldsymbol{ }{{\varvec{x}}}^{{\varvec{I}}}\right),{\varvec{z}}=\left({{\varvec{z}}}^{{\varvec{D}}},\boldsymbol{ }{{\varvec{z}}}^{{\varvec{S}}}\right),{\varvec{y}}=\left({{\varvec{y}}}^{G}{,{\varvec{y}}}^{B}\right),{{\varvec{y}}}^{G}=\left({{\varvec{y}}}^{P}, {{\varvec{y}}}^{N}\right),and {{\varvec{y}}}^{P}=\left({{\varvec{y}}}^{A}, {{\varvec{y}}}^{R}\right).$$

(2)

For simplicity, assume that all the divisions have the same data structure. Extending to the case of a hybrid index in which integer, stochastic, undesirable, negative, and ratio data co-exist in any specific division is straightforward. Here, we discuss our proposed strategies for modelling different types of data, including integer-valued, ratio, negative, stochastic, and undesirable.

• (a) Note that in the presence of integer-valued inputs, i.e., ${{\varvec{x}}}^{{\varvec{I}}(k)}\in {\mathbb{Z}}_{+}^{|I|}$, the reference technology is a non-convex set of disconnected points in the input space. Therefore, a modified version of traditional efficiency measures is needed. To deal with this case, the proposed approach of Kuosmanen and Kazemi Matin (2009) and Kuosmanen, Keshvari & Kazemi Matin (2015) is followed, in which the integer-valued targets are imposed on efficiency analysis of the observed production units. This approach gauges the efficiency score relative to the monotonic hull of the production technology set in the input space and requires integer variables for computing the efficiency scores and target setting.

• (b) The stochastic intermediate products ${\widetilde{{\varvec{z}}}}_{g}^{S(k)}$ follow the normal distribution. The CCP proposed by Charnes and Cooper (1959) is one of the most commonly used approaches for modelling stochastic data in DEA. In this study, we adopt the CCP approach developed by Cooper et al., (2002, 2004). The associated deterministic constraints are used in the efficiency evaluation of DMUs.

• (c) To deal with the undesirable outputs, the weak disposability (WD) approach is used in this study. The WD axiom implies that any radial feasible contraction of undesirable outputs requires contraction of desirable outputs with the same rate, i.e., $\left({\varvec{x}},{\varvec{z}},{{\varvec{y}}}^{G}{,{\varvec{y}}}^{B}\right)\in T$ implies that $\left({\varvec{x}},{\varvec{z}},{\alpha {\varvec{y}}}^{G}{,\alpha {\varvec{y}}}^{B}\right)\in T$ for all $\alpha \in [\mathrm{0,1}]$. Kuosmanen (2005) introduced the production technology set to satisfy the underlying axioms, including WD of desirable and undesirable outputs. Kuosmanen & Kazemi Matin (2011) discussed the economic interpretations of WD technology from a duality viewpoint. Note that modelling the undesirable outputs using the WD approach requires different abatement factors associated with individual DMUs. This requires some variable substitutions to avoid non-linear constraints in the production technology set.

• (d) The SORM proposed by Emrouznejad et al., (2010a, 2010b) is used for modelling negative desirable outputs. This approach can be applied in the case where the outputs have both positive and negative values. SORM suggests a partitioning approach for this type of outputs as ${{\varvec{y}}}^{N(k)}={{\varvec{y}}}^{1(k)}-{{\varvec{y}}}^{2(k)}$, where the non-negative vectors ${{\varvec{y}}}^{1(\mathrm{k})}$ and ${{\varvec{y}}}^{2(\mathrm{k})}$ are defined as follows:

  $${y}_{rj}^{1(k)}=\left\{\begin{array}{ll}{y}_{rj}^{N(k)} &\quad {\it if} {y}_{rj}^{N(k)}\ge 0 \\ 0&\quad {\it otherwise}\end{array}\right.\quad {\it and}\quad {y}_{rj}^{2(k)}=\left\{\begin{array}{ll}{y}_{rj}^{N(k)}&\quad {\it if} {y}_{rj}^{N(k)}<0 \\ 0 & \quad {\it otherwise}\end{array}.\right.$$

  (3)

As a result, the output constraints associated with ${{\varvec{y}}}^{N(k)}$ are needed to replace the two different sets of constraints for ${{\varvec{y}}}^{1(k)}$ and ${{\varvec{y}}}^{2(k)}$.

• (e) For modelling the desirable positive ratio outputs ${{\varvec{y}}}^{R}$, note that such data do not satisfy the standard production assumptions like convexity. In this study, we follow the idea of using the ratio measure as is, without any transformation or use of the underlying volume measures proposed by Oleson et al. (2015). Under the variable returns to scale (VRS) assumption for the production technology set, the axiom of selective convexity introduced by Podinovski (2005) is used. This allows the convex combination of feasible DMUs, provided that the ratio outputs have equal values. As a result, the condition ${{\lambda }_{j}^{\left(k\right)}y}_{r}^{R\left(k\right)}\le {\lambda }_{j}^{\left(k\right)}{y}_{rj}^{R\left(k\right)}$ is imposed on the constraints of the VRS production technology set. This means that the observed DMUs in the convex combinations of inputs and outputs are not allowed to be more than ${y}_{r}^{R\left(k\right)}$ in all the ratio outputs.

Given the above discussions, the production technology set is as follows:

$${T}_{WD-SORM}^{Int-Ratio-Sto}=\{\left({({\varvec{x}}}^{{\varvec{N}}{\varvec{I}}},\boldsymbol{ }{{\varvec{x}}}^{{\varvec{I}}}),({{\varvec{z}}}^{{\varvec{D}}},\boldsymbol{ }{\widetilde{{\varvec{z}}}}^{{\varvec{S}}}),({{\varvec{y}}}^{A}, {{\varvec{y}}}^{R}, {{\varvec{y}}}^{1},{{{\varvec{y}}}^{2},{\varvec{y}}}^{B})\right)|$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{x}_{ij}^{NI\left(k\right)}\le {x}_{i}^{NI\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{x}_{ij}^{\left(k\right)}\le {x}_{i}^{I\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{z}_{gj}^{D\left(k\right)}\ge {z}_{g}^{D\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k+1\right)}{z}_{gj}^{D\left(k\right)}\le {z}_{g}^{D\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{\widetilde{z}}_{gj}^{S\left(k\right)}\ge {\widetilde{z}}_{g}^{S\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k+1\right)}{\widetilde{z}}_{gj}^{S\left(k\right)}\le {\widetilde{z}}_{g}^{S\left(k\right)},$$

$${y}_{r}^{A\left(k\right)}\le {\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{A\left(k\right)},$$

$${{\lambda }_{j}^{\left(k\right)}y}_{r}^{R\left(k\right)}\le {\lambda }_{j}^{\left(k\right)}{y}_{rj}^{R\left(k\right)},$$

$${\begin{array}{c} \\ y\end{array}}_{r}^{1\left(k\right)}\le {\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{1\left(k\right)},$$

$${y}_{rj}^{2\left(k\right)}\ge {\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{2\left(k\right)},$$

$${y}_{r}^{B\left(k\right)}={\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{B\left(k\right)},$$

$$\sum_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}=1,$$

$${\lambda }_{j}\ge 0, 0\le {\alpha }_{j}\le 1, \forall k, \forall i, \forall r, \forall g\}$$

(4)

By applying the CCP approach, the production set can be stated as follows:

$${T}_{WD-SORM}^{Int-Ratio-Sto}=\{\left({({\varvec{x}}}^{{\varvec{N}}{\varvec{I}}},\boldsymbol{ }{{\varvec{x}}}^{{\varvec{I}}}),({{\varvec{z}}}^{{\varvec{D}}},\boldsymbol{ }{\widetilde{{\varvec{z}}}}^{{\varvec{S}}}),({{\varvec{y}}}^{A}, {{\varvec{y}}}^{R}, {{\varvec{y}}}^{1},{{{\varvec{y}}}^{2},{\varvec{y}}}^{B})\right)|$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{x}_{ij}^{NI\left(k\right)}\le {x}_{i}^{NI\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{x}_{ij}^{\left(k\right)}\le {x}_{i}^{I\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{z}_{gj}^{D\left(k\right)}\ge {z}_{g}^{D\left(k\right)},$$

$${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k+1\right)}{z}_{gj}^{D\left(k\right)}\le {z}_{g}^{D\left(k\right)},$$

$$Pr\left\{{\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{\widetilde{z}}_{gj}^{S\left(k\right)}\ge {\widetilde{z}}_{g}^{S\left(k\right)}\right\}\ge 1-\alpha ,$$

$$Pr\left\{{\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k+1\right)}{\widetilde{z}}_{gj}^{S\left(k\right)}\le {\widetilde{z}}_{g}^{S\left(k\right)}\right\}\ge 1-\alpha ,$$

$${y}_{r}^{A\left(k\right)}\le {\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{A\left(k\right)},$$

$${{\lambda }_{j}^{\left(k\right)}y}_{r}^{R\left(k\right)}\le {\lambda }_{j}^{\left(k\right)}{y}_{rj}^{R\left(k\right)},$$

$${\begin{array}{c}\\ y\end{array}}_{r}^{1\left(k\right)}\le {\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{1\left(k\right)},$$

$${\begin{array}{c} \\ y\end{array}}_{r}^{2\left(k\right)}\ge {\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{2\left(k\right)},$$

$${y}_{r}^{B\left(k\right)}={\sum }_{j=1}^{n}{\alpha }_{j}{\lambda }_{j}^{\left(k\right)}{y}_{rj}^{B\left(k\right)},$$

$$\sum_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}=1,$$

$${\lambda }_{j}^{\left(k\right)}\ge 0, 0\le {\alpha }_{j}\le 1, \forall k, \forall i, \forall r, \forall g\},$$

(5)

where $Pr$ denotes “probability” and $"\sim "$ denotes random data following the normal distribution. $\alpha \in (\mathrm{0,1}]$ shows a pre-defined value of allowable chance of failing constraints to satisfy.

3.3 Computational issues

• (i) By assuming the normal distribution for the stochastic intermediate products ${\widetilde{z}}_{gj}^{S\left(k\right)}$, the probability constraint $Pr\left\{{\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{\widetilde{z}}_{gj}^{S\left(k\right)}\ge {\widetilde{z}}_{g}^{S\left(k\right)}\right\}\ge 1-\alpha$ can be stated as ${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}{z}_{gj}^{S\left(k\right)}+{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k\right)}\ge {z}_{g}^{S\left(k\right)}$, with ${\left({u}_{g}^{\left(k\right)}\right)}^{2}={\sum }_{j=1}^{n}{\sum }_{l=1}^{n}{\lambda }_{j}^{\left(k\right)}{\lambda }_{l}^{\left(k\right)}Cov\left({\widetilde{z}}_{gj}^{S\left(k\right)}, {\widetilde{z}}_{gl}^{S\left(k\right)}\right)+Var\left({\widetilde{z}}_{g}^{S\left(k\right)}\right)-2{\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k\right)}Cov\left({\widetilde{z}}_{gj}^{S\left(k\right)}, {\widetilde{z}}_{g}^{S\left(k\right)}\right)$, where ${E\left({\widetilde{z}}_{gj}^{S\left(k\right)}\right)=z}_{gj}^{S\left(k\right)}$ and ${E\left({\widetilde{z}}_{g}^{S\left(k\right)}\right)=z}_{g}^{S\left(k\right)}$ denote the expected values. ${\Phi }^{-1}$ is the inverse of the cumulative distribution function (CDF). $Var(.)$ and $Cov(.,.)$ are the variance and covariance operators, respectively. Similarly, the stochastic inequality constraint $Pr\left\{{\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k+1\right)}{\widetilde{z}}_{gj}^{S\left(k\right)}\le {\widetilde{z}}_{g}^{S\left(k\right)}\right\}\ge 1-\alpha$ can be transformed into ${\sum }_{j=1}^{n}{\lambda }_{j}^{\left(k+1\right)}{z}_{gj}^{S\left(k\right)}-{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k+1\right)}\le {z}_{g}^{S\left(k\right)}$. See Cooper et al., (2002, 2004) for more details.

• (ii) In ${T}_{WD-SORM}^{Int-Ratio-Sto},$ ${\alpha }_{j}$ denotes the individual abatement factor associated with the WD axiom for the undesirable outputs of $DM{U}_{j}$. Note that these factors should be considered for all the outputs, including positive and negative outputs. Due to the multiplication of the abatement factors ${\alpha }_{j}$ by the intensity weights ${\lambda }_{j}^{\left(k\right)}$, the associated output constraints in ${T}_{WD-SORM}^{Int-Ratio-Sto}$ are nonlinear. To overcome this issue, we use the following variable substitutions $\forall j, \forall k: {\alpha }_{j}{\lambda }_{j}^{\left(k\right)}={\delta }_{j}^{(k)}$, $(1-{{\alpha }_{j})\lambda }_{j}^{\left(k\right)}={\mu }_{j}^{(k)}$, ${\lambda }_{j}^{(k)}={\delta }_{j}^{(k)}+{\mu }_{j}^{(k)}$ (see Kuosmanen (2005) for more details).

Finally, the production technology set takes the following form:

$${T}_{WD-SORM}^{Int-Ratio-Sto}=\{\left({({\varvec{x}}}^{{\varvec{N}}{\varvec{I}}},\boldsymbol{ }{{\varvec{x}}}^{{\varvec{I}}}),({{\varvec{z}}}^{{\varvec{D}}},\boldsymbol{ }{\widetilde{{\varvec{z}}}}^{{\varvec{S}}}),({{\varvec{y}}}^{A}, {{\varvec{y}}}^{R}, {{\varvec{y}}}^{1},{{{\varvec{y}}}^{2},{\varvec{y}}}^{B})\right)|$$

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){x}_{ij}^{NI\left(k\right)}\le {x}_{i}^{NI\left(k\right)},$$

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){x}_{ij}^{\left(k\right)}\le {x}_{i}^{I\left(k\right)},$$

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){z}_{gj}^{D\left(k\right)}\ge {z}_{g}^{D\left(k\right)},$$

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k+1\right)}+{\mu }_{j}^{\left(k+1\right)}\right){z}_{gj}^{D\left(k\right)}\le {z}_{g}^{D\left(k\right)},$$

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){z}_{gj}^{S\left(k\right)}+{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k\right)}\ge {z}_{g}^{S\left(k\right)},$$

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k+1\right)}+{\mu }_{j}^{\left(k+1\right)}\right){z}_{gj}^{S\left(k\right)}-{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k+1\right)}\le {z}_{g}^{S\left(k\right)},$$

$${\left({u}_{g}^{\left(t\right)}\right)}^{2}={\sum }_{j=1}^{n}{\sum }_{l=1}^{n}\left({\delta }_{j}^{\left(t\right)}+{\mu }_{j}^{\left(t\right)}\right)\left({\delta }_{l}^{\left(t\right)}+{\mu }_{l}^{\left(t\right)}\right)Cov\left({\widetilde{z}}_{gj}^{S\left(t\right)}, {\widetilde{z}}_{gl}^{S\left(t\right)}\right)+Var\left({\widetilde{z}}_{g}^{S\left(t\right)}\right)-2{\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(t\right)}+{\mu }_{j}^{\left(t\right)}\right)Cov\left({\widetilde{z}}_{gj}^{S\left(t\right)}, {\widetilde{z}}_{g}^{S\left(t\right)}\right), t\in \left\{k,k+1\right\},$$

$${ y}_{r}^{A\left(k\right)}\le {\sum }_{j=1}^{n}{\delta }_{j}^{\left(k\right)}{y}_{rj}^{A\left(k\right)},$$

$${\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right)y}_{r}^{R\left(k\right)}\le \left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){y}_{rj}^{R\left(k\right)},$$

$${\begin{array}{c} \\ y\end{array}}_{r}^{1\left(k\right)}\le {\sum }_{j=1}^{n}{\delta }_{j}^{\left(k\right)}{y}_{rj}^{1\left(k\right)},$$

$${\begin{array}{c} \\ y\end{array}}_{r}^{2\left(k\right)}\ge {\sum }_{j=1}^{n}{\delta }_{j}^{\left(k\right)}{y}_{rj}^{2\left(k\right)},$$

$${y}_{r}^{B\left(k\right)}={\sum }_{j=1}^{n}{\delta }_{j}^{\left(k\right)}{y}_{rj}^{B\left(k\right)},$$

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right)=1,$$

$${\delta }_{j}^{\left(k\right)}\ge 0, {\mu }_{j}^{\left(k\right)}\ge 0 \forall k, \forall i, \forall r, \forall g.\}$$

(6)

4 Efficiency measurement: a modified DDF

Based on the introduced production technology set ${T}_{WD-SORM}^{Int-Ratio-Sto}$, the efficiency scores of DMUs are assessed. The traditional DDF for the performance evaluation of $DM{U}_{o}$ (the DMU under evaluation) concerning the known production possibility set $T$ can be represented as $Max\{\varphi |\left({{\varvec{x}}}_{o},{{\varvec{z}}}_{{\varvec{o}}},{{\varvec{y}}}_{o}\right)+\varphi (-{{\varvec{x}}}_{o},0,{{\varvec{y}}}_{o})\in T\}$, where the uniform distance parameter $\varphi$ is used in the natural directional vector $\left({\mathbf{g}}^{\mathbf{x}},{\mathbf{g}}^{\mathbf{z}},{\mathbf{g}}^{\mathbf{y}}\right)=(-{{\varvec{x}}}_{o},0,{{\varvec{y}}}_{o})$. For more details, see Chambers et al. (1996).

To incorporate both the overall and stage efficiency scores in ${T}_{Network-SORM}^{WD-Integer}$, we introduce a modified version of DDF in which the natural improvement direction $\left({\mathbf{g}}^{{\mathbf{x}}^{{\varvec{N}}{\varvec{I}}}},\boldsymbol{ }{\mathbf{g}}^{{\mathbf{x}}^{{\varvec{I}}}},{\mathbf{g}}^{\mathbf{z}},{\mathbf{g}}^{{\mathbf{y}}^{{\varvec{A}}}},\boldsymbol{ }{\mathbf{g}}^{{\mathbf{y}}^{{\varvec{R}}}},{\mathbf{g}}^{{\mathbf{y}}^{1}},\boldsymbol{ }{\mathbf{g}}^{{\mathbf{y}}^{2}},{\mathbf{g}}^{{\mathbf{y}}^{{\varvec{B}}}}\right)=\left(-{{\varvec{x}}}_{\mathrm{o}}^{NI},-{{\varvec{x}}}_{\mathrm{o}}^{I},0,{{\varvec{y}}}_{o}^{A}, 0,{{\varvec{y}}}_{o}^{1},{-{\varvec{y}}}_{o}^{2},-{{\varvec{y}}}_{o}^{B}\right)$ is used for evaluating the DMUs in which different distance parameters are applied for different stages. Let ${\varphi }^{(k)}$ denote the distance parameters for division $k$. Also, let ${w}^{\left(k\right)}$ denote the associated predefined positive weights corresponding to the $k$th division in which $\sum_{k=1}^{p}{w}^{\left(k\right)}=1$. For the performance assessment of $DM{U}_{o}:\left({{\varvec{x}}}_{\mathrm{o}}^{NI},{{\varvec{x}}}_{\mathrm{o}}^{I},{{\varvec{z}}}_{o}^{{\varvec{D}}},\boldsymbol{ }{{\widetilde{{\varvec{z}}}}_{o}}^{{\varvec{S}}},{{\varvec{y}}}^{A}, {{\varvec{y}}}^{R}, {{\varvec{y}}}^{1},{{{\varvec{y}}}^{2},{\varvec{y}}}^{B}\right)$, we suggest the following modified DDF model:

$$\underset{\varphi , \delta , \mu ,\overline{x} }{max }\sum_{k=1}^{p}{w}^{\left(k\right)}{\varphi }_{o}^{\left(k\right)}$$

(7)

subject to

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){x}_{ij}^{NI\left(k\right)}\le \left(1-{\varphi }_{o}^{\left(k\right)}\right){x}_{io}^{NI\left(k\right)}, i\in NI$$

(7.1)

$${\sum }_{j=1}^{n}({\delta }_{j}^{(k)}+{\mu }_{j}^{(k)}){x}_{ij}^{\left(k\right)}\le {{\overline{x} }_{io}}^{\left(k\right)}\le \left(1-{\varphi }_{o}^{\left(k\right)}\right){x}_{io}^{I\left(k\right)}, i\in I$$

(7.2)

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){z}_{gj}^{D\left(k\right)}\ge {z}_{go}^{D\left(k\right)}, g\in D$$

(7.3)

$${\sum }_{j=1}^{n}({\delta }_{j}^{(k+1)}+{\mu }_{j}^{(k+1)}){z}_{gj}^{D\left(k\right)}\le {z}_{go}^{D\left(k\right)}, g\in S$$

(7.4)

$${\sum }_{j=1}^{n}({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}){z}_{gj}^{S\left(k\right)}+{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k\right)}\ge {z}_{go}^{S\left(k\right)}, g\in S$$

(7.5)

$${\sum }_{j=1}^{n}({\delta }_{j}^{(k+1)}+{\mu }_{j}^{(k+1)}){z}_{gj}^{S\left(k\right)}-{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k+1\right)}\le {z}_{go}^{S\left(k\right)}, g\in S$$

(7.6)

$${\left({u}_{g}^{\left(t\right)}\right)}^{2}={\sum }_{j=1}^{n}{\sum }_{l=1}^{n}({\delta }_{j}^{\left(t\right)}+{\mu }_{j}^{\left(t\right)})({\delta }_{l}^{(t)}+{\mu }_{l}^{(t)})Cov\left({\widetilde{z}}_{gj}^{S\left(t\right)}, {\widetilde{z}}_{gl}^{S\left(t\right)}\right)+Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)-2{\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(t\right)}+{\mu }_{j}^{\left(t\right)}\right)Cov\left({\widetilde{z}}_{gj}^{S\left(t\right)}, {\widetilde{z}}_{go}^{S\left(t\right)}\right), t\in \left\{k,k+1\right\},g\in S$$

(7.7)

$${\sum }_{j=1}^{n}{\delta }_{j}^{\left(k\right)}{y}_{rj}^{A\left(k\right)}\ge \left(1+{\varphi }_{o}^{\left(k\right)}\right){ y}_{ro}^{A\left(k\right)} , r\in A$$

(7.8)

$${({\delta }_{j}^{(k)}+{\mu }_{j}^{(k)})y}_{ro}^{R\left(k\right)}\le \left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){y}_{rj}^{R\left(k\right)},r\in R$$

(7.9)

$${\sum }_{j=1}^{n}{\delta }_{j}^{\left(k\right)}{y}_{rj}^{1\left(k\right)}\ge \left(1+{\varphi }_{o}^{\left(k\right)}\right){\begin{array}{c} \\ y\end{array}}_{ro}^{1\left(k\right)}, r\in N$$

(7.10)

$${\sum }_{j=1}^{n}{\delta }_{j}^{(k)}{y}_{rj}^{2\left(k\right)}\le \left(1-{\varphi }_{o}^{\left(k\right)}\right){\begin{array}{c} \\ y\end{array}}_{ro}^{2\left(k\right)},r\in N$$

(7.11)

$${\sum }_{j=1}^{n}{\delta }_{j}^{(k)}{y}_{rj}^{B\left(k\right)}=(1-{\varphi }_{o}^{\left(k\right)}){y}_{ro}^{B\left(k\right)}, r\in B$$

(7.12)

$${\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right)=1,$$

(7.13)

$${{\overline{x} }_{io}}^{(k)}\in {\mathbb{Z}}_{+}, 0\le {\varphi }_{o}^{\left(k\right)}\le 1, {\delta }_{j}^{\left(k\right)}\ge 0, {\mu }_{j}^{\left(k\right)}\ge 0 \forall k, \forall i, \forall r, \forall g.$$

(7-14)

Remark 1

In Model (7), new integer variables ${\overline{x} }_{i}$ are used to avoid non-integer targets for integer-valued factors. Thus, a subset of the variables is restricted to integer values (see Kuosmanen, Keshvari & Matin, 2015).

Remark 2

If we assume that the intermediate products among the different production units are independent, then $Cov\left({\widetilde{z}}_{gj}^{S\left(k\right)}, {\widetilde{z}}_{gl}^{S\left(k\right)}\right)=0$ for $j\ne l$. This independence assumption leads to the following relation: ${\left({u}_{g}^{\left(t\right)}\right)}^{2}={\sum }_{j=1}^{n}{\left({\delta }_{j}^{(t)}+{\mu }_{j}^{(t)}\right)}^{2}Var\left({\widetilde{z}}_{gj}^{S\left(t\right)}\right)+(1-2({\delta }_{o}^{(t)}+{\mu }_{o}^{(t)}))Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)$.

Theorem 1

Model (7) is always feasible and bounded.

Proof

For all $k,$ let ${\varphi }_{o}^{(k)}=0$, ${\delta }_{o}^{\left(k\right)}={\delta }_{o}^{\left(k+1\right)}=$ 1, ${\delta }_{j}^{\left(k\right)}={\delta }_{o}^{\left(k+1\right)}=0 (\forall j\ne o)$, and ${\mu }_{j}^{\left(k\right)}={\mu }_{j}^{\left(k+1\right)}=0 (\forall k \forall j)$. Furthermore, let ${\overline{{x }_{i}}}^{(k)}={x}_{io}^{I\left(k\right)}(\forall i\in I)$. It is easy to verify that these values satisfy all the constraints of Model (7). Note that with these values, we have

$${\left({u}_{g}^{\left(t\right)}\right)}^{2}={\left({\delta }_{o}^{\left(t\right)}+{\mu }_{o}^{\left(t\right)}\right)}^{2} Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)+Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)-2\left({\delta }_{o}^{\left(t\right)}+{\mu }_{o}^{\left(t\right)}\right)Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)=Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)+Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)-2 Var\left({\widetilde{z}}_{go}^{S\left(t\right)}\right)=0.$$

Therefore, the model is feasible. To prove the boundedness, given the constraints of the inputs, undesirable, and second part of the negative outputs, we conclude that ${\varphi }_{o}^{\left(k\right)}\le 1$. Thus, we have $\forall k: 0\le {\varphi }_{o}^{\left(k\right)}\le 1$, which shows the objective value is bounded. □

Theorem 2

Model (7) has a global optimal solution for $\alpha \le 0.5$.

Proof

For $\alpha \le 0.5$, we have ${\Phi }^{-1}\left(\alpha \right)\le 0$. In this case, $-{\sum }_{j=1}^{n}\left({\delta }_{j}^{\left(k\right)}+{\mu }_{j}^{\left(k\right)}\right){z}_{gj}^{S\left(k\right)}-{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k\right)}+{z}_{go}^{S\left(k\right)}$ and ${\sum }_{j=1}^{n}({\delta }_{j}^{(k+1)}+{\mu }_{j}^{(k+1)}){z}_{gj}^{S\left(k\right)}-{\Phi }^{-1}\left(\alpha \right){u}_{g}^{\left(k+1\right)}-{z}_{go}^{S\left(k\right)}$ are convex functions as ${u}_{g}^{\left(k\right)}$ and ${u}_{g}^{\left(k+1\right)}$ are convex functions. All the other linear constraints of Model (7) are also convex functions, as well as the objective function. In solving this optimization model, due to the existence of integer variables ${\overline{x} }_{i}$ for $i\in I$, any created branches would be a convex programming problem, which has a global optimal solution. Therefore, the model has the global optimal solution. □

In optimality, the overall and division efficiency scores of $DM{U}_{o}$ are suggested as follows, which are inspired from the hyperbolic measure introduced by Färe et al. (1989):

$$Ef{f}_{Overall }\left(DM{U}_{o}\right)=\frac{1-\sum_{k=1}^{p}{w}^{\left(k\right)}{\varphi }_{o}^{*\left(k\right)}}{1+\sum_{k=1}^{p}{w}^{\left(k\right)}{\varphi }_{o}^{*\left(k\right)}},$$

(8)

$$Ef{f}_{k }\left(DM{U}_{o}\right)=\frac{1-{\varphi }_{o}^{\left(k\right)}}{1+{\varphi }_{o}^{*\left(k\right)}} \left(k=1,\dots ,p\right),$$

(9)

where ${\varphi }_{o}^{*\left(k\right)}$ shows the maximum percentage of proportional improvements of the inputs and outputs of division $k$.

Theorem 3

For $\alpha \le 0.5$, the objective value of Model (7) is an increasing function of $\alpha$.

Proof

Let ${\alpha }_{2}>{\alpha }_{1}$ and $({\overline{\varphi } }_{o}^{\left(k\right)}, {\overline{\delta }}_{j}, {\overline{\mu }}_{j},{\overline{x} }_{i}, {\overline{u} }_{g}^{\left(k\right)})$ for all $k, j$, $i\in I$ and $g\in S$, be a feasible solution of Model (7) at probability level ${\alpha }_{1}$. Since ${\alpha }_{2}>{\alpha }_{1}$, $0<{-\Phi }^{-1}\left({\alpha }_{2}\right)<-{\Phi }^{-1}\left({\alpha }_{1}\right)$, and from the constraints of Model (7) associated with the stochastic intermediate products, we have

$${z}_{go}^{S\left(k\right)}\le {\sum }_{j=1}^{n}\left({\overline{\delta }}_{j}^{\left(k\right)}+{\overline{\mu }}_{j}^{\left(k\right)}\right){z}_{gj}^{S\left(k\right)}+{\Phi }^{-1}\left({\alpha }_{1}\right){\overline{u} }_{g}^{\left(k\right)}\le {\sum }_{j=1}^{n}\left({\overline{\delta }}_{j}^{\left(k\right)}+{\overline{\mu }}_{j}^{\left(k\right)}\right){z}_{gj}^{S\left(k\right)}+{\Phi }^{-1}\left({\alpha }_{2}\right){\overline{u} }_{g}^{\left(k\right)}$$

$${\sum }_{j=1}^{n}({\overline{\delta }}_{j}^{(k+1)}+{\overline{\mu }}_{j}^{(k+1)}){z}_{gj}^{S\left(k\right)}-{\Phi }^{-1}\left({\alpha }_{2}\right){\overline{u} }_{g}^{\left(k+1\right)}\le {\sum }_{j=1}^{n}\left({\overline{\delta }}_{j}^{\left(k+1\right)}+{\overline{\mu }}_{j}^{\left(k+1\right)}\right){z}_{gj}^{S\left(k\right)}-{\Phi }^{-1}\left({\alpha }_{1}\right){\overline{u} }_{g}^{\left(k+1\right)}\le {z}_{go}^{S\left(k\right)}.$$

This shows that $({\overline{\varphi } }_{o}^{\left(k\right)}, {\overline{\delta }}_{j}, {\overline{\mu }}_{j},{\overline{x} }_{i}, {\overline{u} }_{g}^{\left(k\right)})$ for all $k, j$, $i\in I$ and $g\in S$ is a feasible solution of Model (7) at ${\alpha }_{2}$ probability level. Therefore, at optimality, we have $\sum_{k=1}^{p}{w}^{\left(k\right)}{\varphi }_{o, {\alpha }_{1}}^{*\left(k\right)}\le \sum_{k=1}^{p}{w}^{\left(k\right)}{\varphi }_{o, {\alpha }_{2}}^{*\left(k\right)}$. This completes the proof. □

Remark 3

The new proposed model satisfies the following properties, the proofs of which are straightforward:

• P1. $0<Ef{f}_{Overall }\le 1$ and $0< Ef{f}_{k }\le 1$ for all $k$.

• P2. $Ef{f}_{Overall }=1$ if and only if $Ef{f}_{k }=1$ for all $k$.

• P3. $Ef{f}_{Overall}$ and $Ef{f}_{k}$($k=1,\dots ,p$) are unit invariant.

• P4. $Ef{f}_{Overall}$ and $Ef{f}_{k}$($k=1,\dots ,p$) are monotonic in the inputs and outputs.

• P5. $Ef{f}_{Overall}$ and $Ef{f}_{k}$($k=1,\dots ,p$) are decreasing functions of the $\alpha$ values.

5 Case study

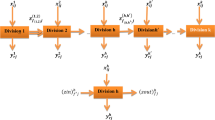
Iran is one of the most vulnerable countries due to the COVID-19 pandemic with 1,320,000 total cases and over 56,000 death tolls by January 2021. To mitigate the devastating effects of the COVID-19 pandemic, resilience and sustainability assessment of healthcare SCs have attracted considerable attention from healthcare managers. In this study, the healthcare SC is comprised of suppliers (division 1) and hospitals (division 2). The suppliers produce COVID-19 testing kits. The kits can detect infected people, which are one of the most important medical devices.

In this study, several meetings were held with managers and experts of suppliers and hospitals for identifying the most significant indicators to assess the resilience and sustainability of healthcare SCs. Table 1 provides the dataset of 28 healthcare SCs. The dataset dates back to August 2020 till November 2020, which is extracted by observing the documents of the suppliers and hospitals of healthcare SCs. The external inputs of division 1 are raw material cost (${x}_{1}^{(1)})$, environmental costs (${x}_{2}^{(1)}$), and personnel costs (${x}_{3}^{(1)}$). The number of produced COVID-19 testing kits ${(z}_{1}^{I(1)})$ and the average inventory $({\widetilde{z}}_{2}^{S\left(1\right)})$ are intermediate measures, which exit from division 1 and enter division 2. The external inputs of division 2 include employees’ health and safety costs (${x}_{1}^{(2)}$), the number of personnel ${(x}_{2}^{I(2)}$), the personnel costs (${x}_{3}^{(2)}$), the number of patients (${x}_{4}^{I(2)}$), and the number of beds (${x}_{5}^{I(2)}$). The outputs of stage 2 are the number of errors in diagnosing COVID-19 disease (${y}_{1}^{UD(2)}$), the number of discharged patients (${y}_{2}^{R(2)}$), and profit (${y}_{3}^{N(2)}$). Figure 2 shows the network structure of the healthcare SC.

Table 1 The factors used to measure resilience and sustainability of healthcare SCs

Fig. 2

The healthcare SC

The following model is based on Model (7), which is customized for this case study. Assume that the intermediate stochastic variables are independent.

$$\underset{\varphi ,\lambda , \delta , \mu , \overline{x },\mathit{ }\overline{y}}{\mathrm{Max}}\mathit{ }{w }^{(1)}{\varphi }_{o}^{\left(1\right)}+{w}^{(2)}{\varphi }_{o}^{\left(2\right)}$$

(10)

subject to

$${\sum }_{j=1}^{28}{\lambda }_{j}^{\left(1\right)}{x}_{ij}^{\left(1\right)}\le (1-{\varphi }_{o}^{\left(1\right)}){x}_{io}^{(1)}, i=\mathrm{1,2},3$$

(10.1)

$$\begin{array}{cc}\sum_{j=1}^{28}{\lambda }_{j}^{\left(1\right)}{z}_{1j}^{I\left(1\right)}\ge {z}_{1o}^{I(1)}& \end{array}$$

(10.2)

$$\begin{array}{cc}\sum_{j=1}^{28}{\lambda }_{j}^{\left(2\right)}{z}_{1j}^{I\left(1\right)}\le {z}_{1o}^{I(1)}& \end{array}$$

(10.3)

$${\sum }_{j=1}^{28}{\lambda }_{j}^{\left(1\right)}{z}_{2j}^{S\left(1\right)}+{\Phi }^{-1}\left(\alpha \right){u}_{2}^{\left(1\right)}\ge {z}_{2o}^{S\left(1\right)},$$

(10.4)

$${\left({u}_{2}^{\left(1\right)}\right)}^{2}={\sum }_{j=1}^{28}{({\lambda }_{j}^{\left(1\right)})}^{2}Var\left({\widetilde{z}}_{2j}^{S\left(1\right)}\right)+(1-2{\lambda }_{O}^{\left(1\right)})Var\left({\widetilde{z}}_{2o}^{S\left(1\right)}\right)$$

(10.5)

$${\sum }_{j=1}^{28}({\delta }_{j}^{(2)}+{\mu }_{j}^{(2)}){z}_{2j}^{S\left(1\right)}-{\Phi }^{-1}\left(\alpha \right){u}_{2}^{\left(2\right)}\le {z}_{2o}^{S\left(1\right)},$$

(10.6)

$${\left({u}_{2}^{\left(2\right)}\right)}^{2}={\sum }_{j=1}^{28}{\left({\delta }_{j}^{(2)}+{\mu }_{j}^{(2)}\right)}^{2}Var\left({\widetilde{z}}_{2j}^{S\left(1\right)}\right)+(1-2({\delta }_{o}^{(2)}+{\mu }_{o}^{(2)}))Var\left({\widetilde{z}}_{2o}^{S\left(1\right)}\right)$$

(10.7)

$$\sum_{j=1}^{28}({\delta }_{j}^{(2)}+{\mu }_{j}^{(2)}){x}_{ij}^{\left(2\right)}\le (1-{\varphi }_{o}^{\left(2\right)}){x}_{io}^{(2)}, i=\mathrm{1,3}$$

(10.8)

$$\sum_{j=1}^{28}({\delta }_{j}^{(2)}+{\mu }_{j}^{(2)}){x}_{ij}^{\left(2\right)}\le {{\overline{x} }_{io}}^{\left(2\right)}\le (1-{\varphi }_{o}^{\left(2\right)}){x}_{io}^{I(2)}, i={2,4},5$$

(10.9)

$$\begin{array}{cc}\sum_{j=1}^{ 28}{\delta }_{j}^{\left(2\right)}{y}_{1j}^{I,UD\left(2\right)}={{\overline{y} }_{1o}}^{(2)}\le (1-{\varphi }_{o}^{\left(2\right)}){y}_{1o}^{I,UD\left(2\right)}& \end{array}$$

(10.10)

$${({\delta }_{j}^{(2)}+{\mu }_{j}^{(2)})y}_{2o}^{R\left(2\right)}\le \left({\delta }_{j}^{\left(2\right)}+{\mu }_{j}^{\left(2\right)}\right){y}_{2j}^{R\left(2\right)}, j=1,...,28$$

(10.11)

$$\sum_{j=1}^{28}{\delta }_{j}^{\left(2\right)}{y}_{3j}^{1\left(2\right)}\ge (1+{\varphi }_{o}^{\left(2\right)}){y}_{3o}^{1\left(3\right)}$$

(10.12)

$$\sum_{j=1}^{28}{\delta }_{j}^{\left(2\right)}{y}_{3j}^{\left(2\right)}\le (1-{\varphi }_{o}^{\left(2\right)}){y}_{3o}^{2\left(3\right)}$$

(10.13)

$$\sum_{ j=1}^{ 28}{\lambda }_{j}^{\left(1\right)}=1$$

(10.14)

$$\sum_{ j=1}^{ 28}{(\delta }_{j}^{\left(2\right)}+{\mu }_{j}^{\left(2\right)})=1$$

(10.15)

$${\lambda }_{j}^{\left(1\right)}, {\delta }_{j}^{\left(2\right)},{\mu }_{j}^{\left(2\right)},\ge 0,\quad j=1,..,28,$$

(16)

$${\overline{x} }_{io}^{(2)},\,\,{{\overline{y} }_{1o}}^{(2)}\in\,{\mathbb{Z}}_{+}, i={2,4},5$$

(10.17)

$$0\le {\varphi }_{o}^{\left(k\right)}\le 1, k={1,2}.$$

(10.18)

Table 2 shows the dataset. Table 3 reports the results given Model (8). Table 3 shows the results for the 28 healthcare SCs. We ran Model (8) with different $\alpha$ values, including $\alpha =$ 0.001, $\alpha =$ 0.01, $\alpha =$ 0.05, $\alpha =$ 0.1, $\alpha =$ 0.3, and $\alpha =$ 0.5. The $\alpha$ is a pre-determined acceptable risk, which is determined by the decision-maker. ${\varphi }_{o}^{1}$ and ${\varphi }_{o}^{2}$ imply the maximum percentages of proportional improvements of inputs and outputs of divisions 1 and 2, respectively. The resilience and sustainability scores of division 1 and division 2 with $\alpha =$ 0.001 are shown in column 4 and column 5 of Table 3, respectively. As shown, while 22 out of the 28 healthcare SCs are resilient and sustainable in division 1, all the 28 healthcare SCs are resilient and sustainable in division 2. Only six out of the 28 healthcare SCs are not overall resilient and sustainable. By increasing $\alpha$, the results change. For $\alpha =$ 0.5, only 15 and 16 out of the 28 healthcare SCs are resilient and sustainable in division 1 and division 2, respectively. As shown, for $\alpha =$ 0.001, 22 healthcare SCs are resilient and sustainable, and for $\alpha =$ 0.5, seven healthcare SCs are resilient and sustainable. Note that for α = 0.5, we have ${\Phi \left(\alpha \right)}^{-1}=0$ and deterministic efficiency is computed.

Table 2 The dataset

Table 3 Divisional and overall resilience and sustainability at different $\alpha$ levels

5.1 Managerial implications

Performance assessment and management of healthcare systems are key challenges for healthcare researchers to deal with in disasters such as the COVID-19 pandemic. The proposed approach determines the divisional and overall resilience and sustainability of healthcare SCs in face of crises such as the pandemic COVID-19. Given $\alpha$=0.5 (deterministic efficiency), Fig. 3 summarizes the results. As is seen, healthcare SCs 1, 4, 13, 17, 19, 20, and 27 are overall resilient and sustainable.

Fig. 3

Summary of the results at $\alpha$=0.5

Moreover, being able to reasonably and accurately assess the sustainability and resilience of healthcare SCs, healthcare SC managers can better mitigate the pressure from public opinions and social media to address the sustainability issues of healthcare systems. This study shows how well the resilience and sustainability of healthcare SCs can be estimated using apposite DEA models. Specifically, the proposed method can address different types of data in the network DEA structure. This, in turn, assists researchers to develop a variety of DEA and network DEA models in different settings.

6 Conclusions and future research

Disasters such as the COVID-19 epidemic outbreak result in devastating damages to human lives and causing huge economic losses. Pandemic diseases also lead to a large number of infected people, as well as an extraordinary increase in the demand for limited health care resources. As such, the resilience and sustainability of healthcare SCs are major challenges of healthcare managers. In this regard, OR approaches and techniques are very useful address the challenges arising from such crises.

In this paper, we propose a novel network DEA model for assessing the resilience and sustainability of healthcare SCs in face of the COVID-19 pandemic outbreak. Our proposed network DEA model can deal simultaneously with different types of data such as negative, stochastic, ratio, integer, and undesirable. In the proposed approach, the outputs’ WD, CCP approach, the convexity assumption, and SORM are aggregated. Furthermore, a modified DDF model is developed to measure the overall and divisional resilience and sustainability of healthcare SCs. Moreover, we present several significant and interesting properties of the proposed model. Through a case study, we apply the developed method to evaluate the resilience and sustainability of 28 healthcare SCs in response to the COVID-19 pandemic outbreak.

For future research, we suggest two directions. One direction is to develop a new network DEA model to deal with the dual-role factors. The other direction is to propose a dynamic network DEA model for assessing healthcare SCs in several periods.