Post-disaster multi-period road network repair: work scheduling and relief logistics optimization

Abstract

We develop a multi-period bi-level programming model for the post-disaster road network repair work scheduling and relief logistics problem. A maximum relative satisfaction degree-based steady-state parallel genetic algorithm is designed to solve this model. In order to validate and test the effectiveness of the presented mathematical model and method, we use a network generator to create numerical examples with different scales and characteristics of road network. Our numerical analysis of the solutions shows that the proposed mathematical model and method can effectively assist the decision-makers to deal with the road network repair work scheduling and relief logistics optimization problem during the emergency response phase. This mathematical model and the approach being developed are applied to deal with the case of Wenchuan earthquake in China. The results show that the required CPU time is short enough such that it meets the time limitation in the emergency response phase, and the strategy of road network repair scheduling will allow repair of the damaged roads to be completed before the end of the planning time horizon by 14.93%. Furthermore, the strategy of relief logistics can provide an efficient relief allocation and transportation path.

1 Introduction

Earthquake is one of the most destructive natural disasters, causing the death of tens of thousands of people and loss of billions of dollars over the past two decades in the world (Mimura et al. 2011). An important observation is that the number of casualties is usually related to the availability of relief materials, such as food, clean water, adequate medical care and shelters during the aftermath (PAHO 2000). Therefore, effective logistic response to a disaster is critically important (Sheu 2007). It was conjectured that 80 percent of the disaster relief effort is on logistics (Trunick 2005). Therefore, as first approximation, disaster relief is logistics.

However, the conditions of the road network in natural disaster areas are the main factors, influencing the delivery of relief materials to the affected regions. In many cases, the deaths are not due to the lack of supplies of relief materials. The inability of transporting these relief materials to the people in need is the main cause. The devastating Wenchuan earthquake, that was occurred on May 12, 2008, was the strongest earthquake in China for the past 100 years. Due to the extensive media coverage, a large excess stock of relief materials was being donated. However, distributing these relief materials to the affected villages was found extremely difficult as road network had been destroyed or damaged (Beresford and Pettit 2012; Cho et al. 2014). Therefore, repairing this damaged road network timely and efficiently is critical to relief logistics.

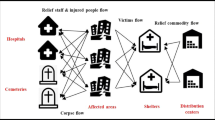
In this paper, we consider the issues of road network restoration and relief logistics together. This problem is referred to as the road network repair work scheduling and relief logistics problem, abbreviated as NRWSRLP, where two problems are being addressed: (i) the scheduling and routing of the repair crews for the repair of the damaged nodes; and (ii) relief logistics for materials allocation and delivery. To proceed further, we note that the strategy for the road network restoration is being planned by the emergency command center (ECC) in the upper level. The administrators of distribution centers, which are in the lower level, are required to make relief logistics decisions according to the given strategy. The relationships between the road network repair work scheduling in the upper level and the relief logistics of allocating and delivering in the lower level are shown in Fig. 1.

Fig. 1

The relationships between road network repair work scheduling and relief logistics

The main task of this problem is to periodically create a road network repair work scheduling for the repairs of the damaged nodes in the upper level so that the demand and supply nodes of relief logistics can be connected in a timely manner in the lower level. Meanwhile, the road network status would be changed in line with the progress of the repair process. Consequently, the strategy of logistics activities in the lower level will need to be adjusted accordingly. Therefore, we model the NRWSRLP as a multi-period problem (MP-NRWSRLP), where road network repair work scheduling is to be worked out at the beginning of each period (e.g. a day, or a shift of eight or 12 h) subject to the availability of the limited number of repair crews and amount of resources. The work plan of relief logistics in the lower level is made according to the road network repair work scheduling in the upper level.

The problem is a multi-period bi-level programming problem. It is highly complex, making it impractical to obtain exact solution in real life situations. In order to overcome this difficulty, we introduce the concept of maximum relative satisfaction degree (MRSD) and then use it to solve the relief allocation problem in the lower level, where the steady-state parallel genetic algorithm (SSPGA) (Berger and Barkaoui 2004; Altiparmak et al. 2009) is being incorporated in the upper level to plan the cumulative accessibility of the road network. This approach is referred to as MRSD-based SSPGA, named as hybrid steady-state parallel genetic algorithm (HSSPGA).

The contributions of this paper are fourfold: (1) we develop a multi-period bi-level programming model, which aims to maximize the cumulative accessibility of road network in the upper level and to maximize the satisfaction of relief allocation, while minimizing the total required time for delivering the relief materials at the lower level; (2) we design a HSSPGA to cater for different types of road network topology (e.g. “grid/ring” in urban or “sparse” in rural) and medium- to large-scale instances that are generated by GNETGEN; (3) we carry out the required sensitivity analysis so as to gain managerial insights into this problem. On this basis, we can make useful suggestions to decision-makers; and (4) this mathematical model and the approach being developed are applied to deal with the case of Wenchuan earthquake in China.

The remainder of this paper is organized as follows. In Sect. 2, we review the literature related to road network repair work scheduling and relief logistics problems. The introduction of MP-NRWSRLP, notations, and assumptions are given in Sect. 3. The evaluation method of cumulative accessibility and the mathematical model of MP-NRWSRLP are presented in Sect. 4. The HSSPGA is introduced in Sect. 5, and the solution approach is proposed and numerical examples are given to validate the mathematical model in Sect. 6. A case study is presented in Sect. 7. Some concluding remarks and suggestions for future research are made in Sect. 8.

2 Literature review

In the post-disaster emergency response stage, the two most important intervention activities are the evacuation of residents and the delivery of relief materials. Evacuation takes place during the initial phase of emergency response, for which the injured people are transferred out of the affected areas. Delivery of materials (relief logistics) activities is a continuing process for a longer period of time to provide necessary relief materials to the people who remaining in the affected areas. Clearly, the effectiveness of these two activities depend critically on the situations of the road networks. This is particularly more critical in rural areas because the road network in these areas are usually much easier to be damaged by natural disasters, such as earthquakes, floods, and landslides.

There are many useful results on road network repair work schedules and relief logistics. For road network repair work schedules, we categorize the relevant references into three classes: (I) repair work assignment problem (RWAP), (II) repair crew routing problem (RCRP), and (III) repair work scheduling problem (RWSP), including repair work assignment problem and repair crew routing problem. Each classification is divided into five groups according to the characteristics of the mathematical model: (1) single-objective (SO), (2) multi-objective (MO), (3) multi-period (MP), (4) Robust, and (5) bi-level programming (BLP). The results obtained in the relevant references on road network repair work schedules are categorized in Table 1, in which the references and adopted approaches are listed in each grid. For relief logistics, we categorize the relevant references into seven classes: (I) facility location problem or facility layout problem (FLP), (II) facility location-allocation problem or facility location-transportation problem (FLAP/FLTP), (III) facility location-routing problem (FLRP), (IV) relief allocation problem (RAP), (V) relief vehicle routing problem (RVRP), (VI) relief allocation-routing problem (RARP), and (VII) facility location-allocation-routing problem (FLARP). Each category is also split into five items in accordance with the characteristics of the mathematical model: (1) SO, (2) MO, (3) MP, (4) Robust, and (5) BLP. The results obtained in these references on relief logistics are categorized in Table 2, where the references and adopted methods are shown in each grid. Note that Table 2 only lists the references from the year of 2012, for relevant references before 2012, the readers can refer to the survey paper on facility location problem in Boonmee et al. (2017) and to the review paper on models, solutions and enabling technologies of relief logistics in Özdamar and Ertem (2015).

From Tables 1 and 2, we can see that these references are mainly focused on mathematical models from the perspective of SO, MO, and MP. Only one paper considers the mathematical model for road network repair work schedule from the view point of BLP. The proposed methods include heuristics algorithm, such as genetic algorithm (GA) or hybrid genetic algorithm (HGA), simulated annealing (SA), tabu search (TS), and $\epsilon$-constraint ($\epsilon$-C), and exact algorithm, such as LINGO, CPLEX, Lagrangian relaxation (LR). In recent years, much attention has been shifted to disaster management and humanitarian logistics (Çelik 2016).

Table 1 Literature review for road network repair work schedules

Table 2 Literature review for relief logistics from the year of 2012

There are some studies, where road network repair work schedules and relief logistics are being incorporated within the same framework. For example, Yan and Shih (2009) proposed a model to minimize the time required for both the road network repair work scheduling and relief logistics, which was based on two time-space networks (one is for road network repair work scheduling, and the other is for relief logistics). Duque and Sörensen (2011) considered allocating scarce resources to repair the rural road network that was damaged by natural/man-made disaster so as to improve the accessibility to a set of vertices in the network. A solution approach is then proposed based on greedy randomized adaptive search procedure (GRASP) and variable neighborhood search (VNS). Duque et al. (2013) extended the road network repair work scheduling problem through analyzing the complexity of specific cases based on the work reported in Duque and Sörensen (2011). On this basis, a linear integer programming model and two heuristics approaches (the GRASP and VNS) were proposed. Liberatore et al. (2014) developed a hierarchical optimization model to balance the objective functions between relief logistics and road network restoration. Vahdani et al. (2018) developed an integer nonlinear multi-objective, multi-period, and multi-commodity model to locate the distribution centers for timely delivering vital relief materials to affected areas (demand nodes, e.g., towns and villages) and road network restoration operations. They employed non-dominated sorting genetic algorithm-II (NSGA-II) and multi-objective particle swarm optimization (MOPSO) to solve this model. It is well-known that this kind of problem is extremely complex. For this reason, the validation of the mathematical model and the proposed approaches are only carried out through solving a small-scaled example.

Note the studies that are mentioned above have ignored the fact that road network repair work schedules and relief logistics should have appeared as an upper-lower hierarchical form of structure (see Fig. 1). In our MP-NRWSRLP, a road network repair work schedule is periodically created in the upper level. Meanwhile, the relief logistics in the lower level is required to adjust their policy timely in the course of road network restoration. This model has the potential of being extended to other networks, such as power distribution network.

In this paper, the road network repair work scheduling problem in the upper level is a combinational optimization problem, which is known to be an NP-hard problem. By adding the relief logistics problem in the lower level, the resulting problem becomes a bi-level programming problem which is generically non-convex and non-differentiable. It is an extremely difficult problem to solve. Even the “simplest” instance, the linear-linear bi-level programming problem, was shown to be NP-hard (Colson et al. 2007). From the literature, see, for example, Teo and Yang (2001), portfolio selection problems are usually formulated as multi-stage stochastic programming problems. However, it should be noted that the multi-period problems are different from the multi-stage stochastic programming problems. From Tables 1 and 2, we see that those methods, which are used to solve the bi-level programming model of road network repair work scheduling and routing problem, are heuristic algorithms, such as GA or DEA. They can be extended to be implemented as parallel algorithms for solving large scale realistic problems (Berger and Barkaoui 2004). Therefore, we use the parallel genetic algorithm (PGA) that was introduced in Berger and Barkaoui (2004) to solve the repair work scheduling and routing problem in the upper level and the emergency vehicle routing problem in the lower level. On the other hand, a MRSD heuristic algorithm is introduced to deal with the relief allocation problem in the lower level to ensure the fairness of relief allocation. To maintain the diversity of the population of PGA and to overcome the PGA being trapped into the basins of local solutions, we adopt a steady-state chromosome coding and decoding strategy (Altiparmak et al. 2009). The HSSPGA possesses the strengths of GA, such as parallelization, robustness, efficiency, and it can solve large-scale realistic problems, compared with CPLEX and LR (Berger and Barkaoui 2004). However, this type of approach usually needs more than one computer node rather than a computer node with multi-threads. For example, CPLEX can run 8/16 threads on one computer node. Even though the HSSPGA can run on one computer node and use more than one thread, the size of population of genetic algorithm is usually set as 80/100. Thus, the efficiency of calculation will suffer, depending critically on the number of cores or threads of CPU. For the HSSPGA to run on more than one computer node, the efficiency of calculation will be influenced by the required bandwidth of internet/intranet network, the number of computer nodes and the buffer size of network interface card.

3 Problem formulation, notations and assumptions

3.1 Problem formulation

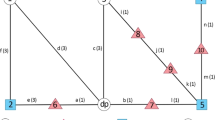
The problem is defined on an undirected graph $G=(N,A)$ (see Fig. 2, which presents an example and solution for the MP-NRWSRLP, generally, it is not necessary for the repair crews to visit all damaged nodes in a given planning time horizon T), where N denotes the set of nodes, consisting of: (1) Damaged nodes (or blocks) requiring repair ($N_{r}$), $d, b, k \in N_{r}$, each of such nodes has a repair time $s_{d}$ (for damaged node d) that repair crew spends on its first visit (every time the repair crew encounters a damaged node that has not been visited previously, it repairs the node and incurs the associated repair time. On subsequent visits, the repair crews can pass that node without incurring any additional time). Note that without loss of generality, we represent a damaged road link by a node located in the middle of the corresponding edge. Therefore, repairing a road connection is equivalent to repairing a node, and we use two terms interchangeably. (2) Demand nodes ($N_{q}$), $n \in N_{q}$, which correspond to the locations (affected areas) that need relief materials. The degree of urgency of an affected area (node n) is represented by demand (i.e., a weight factor $D_{n}$), which might, for example, correspond to traffic demand. (3) Distribution centers or supply depots ($N_{s}$), $m \in N_{s}$, which correspond to the depots from which the materials are supplied to repair crews, damaged nodes and demand nodes etc. (4) Workstation nodes ($N_{w}$) denote depots from which the repair crews depart from, each of the workstation nodes has $C_{w} \subset C$ (for node $w\in N_{w}$) repair crews, where C denotes the set of repair crews. In addition, without loss of generality, we do not distinguish between demand nodes and transshipment nodes, i.e., cross points where two or more roads come together since such nodes can be modeled as demand nodes without demand or traffic analysis zones without attracting or generating traffic flows. Each link $a= (i, j) \in A$ represents a road that connects two nodes $i, j \in N$, $i \ne j$. A travel time $t_{a}$ is defined for each link $a \in A$ to represent the time taken to travel over the link.

Fig. 2

Example of repair crews scheduling and relief logistics for MP-NRWSRLP

The aim of this problem is twofold: (I) to determine the damaged nodes to be assigned to repair crews and the optimal sequence, which is worked out by ECC in the upper level; and (II) to make the plan based on this sequence of repairing for relief logistics so as to reduce the losses, which is usually sorted out within the administrations of distribution centers in the lower level.

In addition, when some damaged nodes have been repaired, the accessibility of road network would be improved. In this paper, we set the golden “72” hours as the whole planning time horizon. Let $\eta$ denote the length of an interval time, namely $T=\lceil 72/\eta \rceil$, where $\lceil \cdot \rceil$ denotes the smallest integer equal to or greater than $72/\eta$.

3.2 Notations and assumptions

For ease of description, other notations that we use throughout the remainder of this paper are defined in Table 3.

Table 3 Notations

In addition, some reasonable assumptions are made in the following.

• 1. The planning time horizon T is considered to be the period during which the basic function of the road network is improved to a sufficiently usable condition for delivering relief materials and evacuation activities during the post-disaster response phase, it is not focused on the long-term road network rehabilitation.

• 2. The locations of all types of nodes (e.g., damaged nodes, distribution centers/supply depots, and affected areas) are known before making a decision in each period.

• 3. A damaged nodes can be accessed by only one repair crew. Furthermore, each repair crew must finish the current assignment before going to the next. The tools (e.g., excavators), fuel oil and other equipments are supplied by the workstation or distribution centers without the need for the repair crew to return to the workstation or distribution centers to collect them.

• 4. The residents always choose the available shortest path. If no path exist, we set the required travel time for this pairs of origin-destination to planning time horizon T until there are some damaged nodes lying on the available shortest path have been repaired.

4 Cumulative accessibility and modeling

4.1 Cumulative accessibility evaluation method

The travel time of the edge is determined by traversed traffic flows which are dependent on traffic demand and network topology. During the post-disaster, the changes of the network structure and the traversed traffic flows on edges are time varying in accordance to the implementation of road network restoration (Maya-Duque et al. 2016). Therefore, in this paper, based on the definitions and inaccessibility measured method proposed by Özdamar et al. (2014), the method is appropriately modified so that it can be used to measure the cumulative accessibility generated by road network restoration. We assume that there is an undirected graph, see Fig. 2 for example, the shortest path of $\forall i, j \in N^{\tau }$ and $i \ne j$ is $sp_{ij}$ and the required travel time for this path is $t_{ij}$ during the pre-earthquake. After an earthquake, the road network was damaged, and there exists a network repair strategy, $\varvec{X}$, to improve the damaged network status for emergency search-and-rescue. When the strategy is implemented $\tau =0,1,2,\ldots ,T$ periods, the shortest path of $\forall i, j \in N^{\tau }$ and $i \ne j$ is $sp_{ij}(\varvec{X},\tau )$ and the required travel time for this path is $t_{ij}(\varvec{X},\tau )$. Therefore, the accessibility between i and j during the period $\tau$ after the strategy $\varvec{X}$ has been implemented can be calculated as follows:

$$\begin{aligned} A_{ij}(\varvec{X},\tau ) = \frac{t_{ij}}{t_{ij}(\varvec{X},\tau )} \end{aligned}$$

(1)

Based on Eq. (1), the accessibility of any node i during the period $\tau$ after the strategy $\varvec{X}$ has been executed is given by the following equation,

$$\begin{aligned} A_{i}(\varvec{X},\tau ) = \frac{\sum _{j=1,i \ne j}^{|N^{\tau }|}{t_{ij}}}{\sum _{j=1,i \ne j}^{|N^{\tau }|}{t_{ij}(\varvec{X},\tau )}} \end{aligned}$$

(2)

where $|N^{\tau }|$ denotes the number of nodes involved in the set $N^{\tau }$. Therefore, for the whole of road network nodes, the accessibility during the period $\tau$ after the strategy $\varvec{X}$ has been executed can be calculated as shown below:

$$\begin{aligned} A(\varvec{X},\tau ) = \frac{1}{|N^{\tau }|} \sum _{i=1}^{|N^{\tau }|}{w_{i} \cdot A_{i}(\varvec{X},\tau )} \end{aligned}$$

(3)

Referring to Özdamar et al. (2014) and Chang and Nojima (2001), Eq. (3) can be transformed into the form given by

$$\begin{aligned} A(\varvec{X},\tau ) = \frac{\sum _{i=1}^{|N^{\tau }|}{w_{i} \cdot \sum _{j=i+1}^{|N^{\tau }|}{t_{ij}}}}{\sum _{i=1}^{|N^{\tau }|}{w_{i} \cdot \sum _{j=i+1}^{|N^{\tau }|}{t_{ij}(\varvec{X},\tau )}}} \end{aligned}$$

(4)

However, this formulation does not identify the difference between relief logistics and normal users traffic flows. How to balance the relief logistics and normal users traffic flows is one of the most important problems facing administrators of ECC during the emergency response phase. In order to overcome this hurdle, we introduce a weighting factor $\rho \in [0,1]$ for relief logistics. If $\rho \le 0.5$, it means that the relief logistics is not the main consideration, indicating that we are now at the recovery phase. This usually denotes the time from one month after the disaster to two years. In this paper, we assume that the weighting factor $\rho \ge 0.5$, which means that the relief logistics traffic flows are equal or more important than normal users traffic flows, such as during the emergency response phase. Therefore, Eq. (4) can be divided into two parts, one is the accessibility of relief logistics and the other is the accessibility of normal users, and their weighting factors are $\rho$ and $1-\rho$, respectively, as shown below:

$$\begin{aligned} A(\varvec{X},\tau ) = \frac{\rho \sum _{n=1}^{|N_{q}^{\tau }|}{D_{n}^{\tau } \sum _{m=1}^{|N_{s}^{\tau }|}{t_{mn}}}}{\sum _{n=1}^{|N_{q}^{\tau }|}{D_{n}^{\tau } \sum _{m=1}^{|N_{s}^{\tau }|}{t_{mn}(\varvec{X},\tau )}}} + \frac{ (1-\rho ) \sum _{s=1}^{|D^{\tau }|}{Q_{rs}^{\tau } \sum _{r=1}^{|O^{\tau }|}{t_{rs}}}}{\sum _{s=1}^{|D^{\tau }|}{Q_{rs}^{\tau } \sum _{r=1}^{|O^{\tau }|}{t_{rs}(\varvec{X},\tau )}}} \end{aligned}$$

(5)

Therefore, during the planning horizon T, the cumulative accessibility generated by the strategy $\varvec{X}$ can be calculated by the following formula.

$$\begin{aligned} Z(\varvec{X},T) = \sum _{\tau =1,2\ldots ,T}{(A(\varvec{X},\tau )-A(\varvec{X},\tau -1))(T-\tau )\eta } \end{aligned}$$

(6)

4.2 Modeling

In this section, we develop a multi-period bi-level programming mathematical model with the following bi-level objectives: (i) planning a network repair work scheduling $\varvec{X}$ to maximize the cumulative accessibility during the planning horizon T in the upper level; and (ii) working out a plan so as to maximize the satisfaction of relief allocation while minimizing the total required time of delivering relief materials under the policy $\varvec{X}$ in the lower level. The flow chart of modeling is as shown in Fig 3.

Fig. 3

Schematics of the decision making process and modeling procedure

4.2.1 Road network repair work scheduling in the upper level

The purpose of the upper level is to construct a policy $\varvec{X}$ so as to maximize the cumulative accessibility during the planning time horizon T as shown below:

$$\begin{aligned} Z_{1}=\max Z(\varvec{X},T) \end{aligned}$$

(7)

subject to

$$\begin{aligned}&\sum _{c \in C^{\tau }}{x_{cd}^{\tau }} = 1,~\forall d \in N_{r}^{\tau } \end{aligned}$$

(8)

$$\begin{aligned}&\sum _{c \in C^{\tau }}{\sum _{d \in N_{r}^{\tau }, d \ne b}{y_{cdb}^{\tau }}} = 1 \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{c \in C^{\tau }}{\sum _{b \in N_{r}^{\tau }, d \ne b}{y_{cdb}^{\tau }}} = 1 \end{aligned}$$

(10)

$$\begin{aligned}&\sum _{c \in C^{\tau }}{\sum _{d \in N_{r}^{\tau }}{\sum _{b \in N_{r}^{\tau }}{y_{cdb}^{\tau }}}} - \sum _{c \in C^{\tau }}{\sum _{b \in N_{r}^{\tau }}{\sum _{k \in N_{r}^{\tau }}{y_{cbk}^{\tau }}}} = 0 \end{aligned}$$

(11)

$$\begin{aligned}&\sum _{w \in N_{w}^{\tau }}{s_{cw1}^{1}} = 1,~\forall c \in C^{\tau } \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{d \in N_{r}^{\tau }}{\sum _{b \in N_{r}^{\tau }}{y_{cdb}^{\tau }}} \le |H(\varvec{X},c,\tau )| - 1,~\forall c \in C^{\tau },~2 \le |H(\varvec{X},c,\tau )| \le \sum _{d \in N^{\tau }}{x_{cd}^{\tau }} \end{aligned}$$

(13)

$$\begin{aligned}&\sum _{r \in O^{\tau }}{\sum _{s \in D^{\tau }}{\sum _{j:(i,j) \in A^{\tau }}{f_{(i,j)}^{\tau } \delta _{rs}^{(i,j),\tau ,p} z_{rs}^{\tau ,p}}}} \nonumber \\&\quad - \sum _{r \in O^{\tau }}{\sum _{s \in D^{\tau }}{\sum _{j:(j,i) \in A^{\tau }}{f_{(j,i)}^{\tau } \delta _{rs}^{(j,i),\tau ,p} z_{rs}^{\tau ,p}}}} = \left\{ \begin{array}{ll} Q_{rs}^{\tau }, &{} \quad i=r\\ 0, &{} \quad i \notin {r} \cup {s} \\ -Q_{rs}^{\tau }, &{} \quad i=s\\ \end{array} \right. \; \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{r \in O^{\tau }}{\sum _{s \in D^{\tau }}{\sum _{j:(i,j) \in A^{\tau }}{f_{(i,j)}^{\tau } \delta _{rs}^{(i,j),\tau ,p}}}} \nonumber \\&\quad -\sum _{r \in O^{\tau }}{\sum _{s \in D^{\tau }}{\sum _{j:(j,i) \in A^{\tau }}{f_{(j,i)}^{\tau } \delta _{rs}^{(j,i),\tau ,p}}}} = \left\{ \begin{array}{ll} f_{(i,j)}^{\tau },&{} \quad i=r\\ 0, &{} \quad i \notin {r} \cup {s} \\ -f_{(i,j)}^{\tau },&{} \quad i=s\\ \end{array} \right. \; \end{aligned}$$

(15)

$$\begin{aligned}&\sum _{r \in O^{\tau }}{\sum _{s \in D^{\tau }}{\sum _{j:(i,j) \in A^{\tau }}{\delta _{rs}^{(i,j),\tau ,p}}}}\nonumber \\&\quad - \sum _{r \in O^{\tau }}{\sum _{s \in D^{\tau }}{\sum _{j:(j,i) \in A^{\tau }}{\delta _{rs}^{(j,i),\tau ,p}}}} = \left\{ \begin{array}{ll} 1, &{} \quad i=r\\ 0, &{} \quad i \notin {r} \cup {s} \\ -1,&{} \quad i=s\\ \end{array} \right. \; \end{aligned}$$

(16)

$$\begin{aligned}&\sum _{i:(i,j) \in A^{\tau }}{\delta _{rs}^{(i,j),\tau ,p}} = 1 \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{j:(j,i) \in A^{\tau }}{\delta _{rs}^{(j,i),\tau ,p}} = 1 \end{aligned}$$

(18)

$$\begin{aligned}&\tau = 1,2,\ldots ,T \end{aligned}$$

(19)

Here, the constraint sets defined by Eqs. (8)–(10) ensure that each repair operation to be carried out by repair crews is preceded and succeeded by only one repair operation during each period $\tau$. Equation (11) ensures that if a repair operation is assigned to a repair crews, then its predecessor and successor are also assigned to the same repair crew. Thus, the route followed by each repair crew to complete the repair operation is defined by this constraint set. Equation (12) specifies that the repair crew must depart from one repair workstation to go to their first repair operation. Equation (13) represents the fact that damaged edges that have been repaired do not needed to be repaired again. Equations (14) and (15) request that traffic flow on nodes and links are balanced. Equations (16)–(18) represent that the travel path is continuous. Equaion (19) denotes period $\tau =1,2,\ldots ,T$.

4.2.2 Relief logistics decision in the lower level

The objective in the lower level is to plan and carry out the relief logistics such that the satisfaction of allocation is maximized, while minimizing the total required time to delivery these relief materials under the policy $\varvec{X}$ that was worked out in the upper level. They are represented by the following two equations, respectively.

$$\begin{aligned} Z_{2}= & {} \max \min \left\{ \sum _{m \in N_{s}^{\tau }}{A_{mn}^{\tau }} / D_{n}^{\tau },~\forall n \in N_{q}^{\tau } \right\} \end{aligned}$$

(20)

$$\begin{aligned} Z_{3}= & {} \min \sum _{m \in N_{s}^{\tau }}{\sum _{n \in N_{q}^{\tau }}{\sum _{v \in V^{\tau }}{{SUS}_{mnv}^{\tau } T_{mnv}^{\tau } w_{mnv}^{\tau }}}} \end{aligned}$$

(21)

subject to

$$\begin{aligned}&\sum _{m \in N_{s}^{\tau }}{A_{mn}^{\tau }} = \sum _{m \in N_{s}^{\tau }}{\sum _{v \in V^{\tau }}{{SUV}_{mnv}^{\tau } {SUS}_{mnv}^{\tau } Q_{v} z_{m}^{\tau } }},~\forall n \in N_{q}^{\tau } \end{aligned}$$

(22)

$$\begin{aligned}&0 < \sum _{m \in N_{s}^{\tau }}{A_{mn}^{\tau }} \le D_{n}^{\tau },~\forall n \in N_{q}^{\tau } \end{aligned}$$

(23)

$$\begin{aligned}&0 < \sum _{n \in N_{q}^{\tau }}{A_{mn}^{\tau }} \le S_{m}^{\tau },~\forall m \in N_{s}^{\tau } \end{aligned}$$

(24)

$$\begin{aligned}&T_{mnv}^{\tau } = \sum _{m \in N_{s}^{\tau }}{\sum _{n \in N_{q}^{\tau }}{\sum _{(i,j) \in A^{\tau }}{\delta _{mn}^{(i,j),\tau ,p} z_{mn}^{\tau ,p} t_{(i,j)}^{\tau } w_{mnv}^{\tau }}}},~\forall v \in V^{\tau } \end{aligned}$$

(25)

$$\begin{aligned}&\sum _{m \in N_{s}^{\tau }}{\sum _{m \in N_{q}^{\tau }}{\sum _{j:(i,j) \in A^{\tau }}{f_{(i,j)}^{\tau } \delta _{mn}^{(i,j),\tau ,p} z_{mn}^{\tau ,p} w_{mnv}^{\tau }}}} \nonumber \\&\quad - \sum _{m \in N_{s}^{\tau }}{\sum _{n \in N_{q}^{\tau }}{\sum _{j:(j,i) \in A^{\tau }}{f_{(j,i)}^{\tau } \delta _{mn}^{(j,i),\tau ,p} z_{mn}^{\tau ,p} w_{mnv}^{\tau }}}} = \left\{ \begin{array}{ll} A_{mn}^{\tau } w_{mnv}^{\tau },&{} \quad i=m\\ 0,&{} \quad i \notin {m} \cup {n} \\ -A_{mn}^{\tau } w_{mnv}^{\tau },&{} \quad i=n\\ \end{array} ,\right. \forall v \in V^{\tau } \end{aligned}$$

(26)

$$\begin{aligned}&\sum _{m \in N_{s}^{\tau }}{\sum _{m \in N_{q}^{\tau }}{\sum _{j:(i,j) \in A^{\tau }}{f_{(i,j)}^{\tau } \delta _{mn}^{(i,j),\tau ,p} w_{mnv}^{\tau }}}} \nonumber \\&\quad - \sum _{m \in N_{s}^{\tau }}{\sum _{n \in N_{q}^{\tau }}{\sum _{j:(j,i) \in A^{\tau }}{f_{(j,i)}^{\tau } \delta _{mn}^{(j,i),\tau ,p} w_{mnv}^{\tau }}}} = \left\{ \begin{array}{ll} f_{(i,j)}^{\tau } w_{mnv}^{\tau },&{} \quad i=m\\ 0, &{} \quad i \notin {m} \cup {n} \\ f_{(i,j)}^{\tau } w_{mnv}^{\tau }, &{} \quad i=n\\ \end{array} ,\right. ~\forall v \in V^{\tau } \end{aligned}$$

(27)

$$\begin{aligned}&\sum _{m \in N_{s}^{\tau }}{\sum _{n \in N_{q}^{\tau }}{\sum _{j:(i,j) \in A^{\tau }}{\delta _{mn}^{(i,j),\tau ,p} w_{mnv}^{\tau }}}} \nonumber \\&\quad - \sum _{m \in N_{s}^{\tau }}{\sum _{n \in N_{q}^{\tau }}{\sum _{j:(j,i) \in A^{\tau }}{\delta _{mn}^{(j,i),\tau ,p} w_{mnv}^{\tau }}}} = \left\{ \begin{array}{ll} w_{mnv}^{\tau },&{} \quad i=m\\ 0, &{} \quad i \notin {m} \cup {n} \\ -w_{mnv}^{\tau }, &{} \quad i=n\\ \end{array} ,\right. ~\forall v \in V^{\tau } \end{aligned}$$

(28)

$$\begin{aligned}&\sum _{i:(i,j) \in A^{\tau }}{\delta _{mn}^{(i,j),\tau ,p} w_{mnv}^{\tau }} = 1 \end{aligned}$$

(29)

$$\begin{aligned}&\sum _{j:(j,i) \in A^{\tau }}{\delta _{mn}^{(j,i),\tau ,p} w_{mnv}^{\tau }} = 1 \end{aligned}$$

(30)

$$\begin{aligned}&\tau = 1,2,\ldots ,T \end{aligned}$$

(31)

Here, Eq. (22) is to cater for the total relief materials allocated to each of the affected areas. Equation (23) specifies that the total allocated relief materials must not be more than the required relief materials for each of the affected areas. This is due to the fact that the amount of relief materials is limited during the emergency response phase. Equation (24) ensures that the allocated relief materials are less than the supply that the depot can provide. Equation (25) is the formula for the computation of the required travel time from supply depot $m \in N_{s}^{\tau }$ to affected area $n \in N_{q}^{\tau }$ using vehicle $v \in V^{\tau }$. Equations (26) and (27) ensure that relief materials flow on nodes and links are balanced. Equations (28)–(30) represent that the delivery path is continuous. Equation (31) denotes period $\tau =1,2,\ldots ,T$.

From the above mentioned mathematical model, Eqs. (8)–(13) in the upper level is the vehicle routing problem (VRP) model, which has been shown to be an NP-hard problem (Lenstra and Kan 1981). In this paper, we use a parallel genetic algorithm to solve this problem, and its complexity is $O(|N_{r}|)$, where $N_{r}$ denotes the number of damaged nodes for all periods. Equations (14)–(18) is a traffic flow balance problem, requiring to calculate the shortest path for each OD pair. The main algorithm for calculating the shortest path is Floyd–Warshall, which has a complexity of $O(|N|^{3})$ Floyd (1962), where |N| denotes the number of nodes in this road network. For lower level, the relief allocation problem is determined by MRSD, which has a complexity of $log(|N_{d}|)$, where $N_{d}$ denotes the number of demand nodes for all periods. The complexity for the scheduling of distribution of relief materials is $O((|N_{d}|\cdot |N_{s}|\cdot |V|)log(|N_{d}|\cdot |N_{s}|\cdot |V|))$. Therefore, the whole complexity of this problem is $O(|N|^{3}+|N_{r}|+(|N_{d}|\cdot |N_{s}|\cdot |V|)log(|N_{d}|\cdot |N_{s}|\cdot |V|))$, which is less than $O(|N|^{3}+|N|+|N|^{2}log(|N|^{2})) \le O((|N|+1)^3)$.

In addition, we can see that the constraint sets defined by Eqs. (26)–(30) in the lower level are, respectively, the subsets of the constraint sets defined by Eqs. (14)–(18) in the upper level. Furthermore, the formulation of Eq. (25) is determined by the required travel time of the links lying on the path from the supply depot to the affected area. Clearly, these results are affected by relief allocation strategy in the lower level and the traffic flow distribution in the upper level. To solve this problem, we first introduce MRSD to allocate the relief materials as the objective $Z_{2}$. Secondly, we incorporate the strategy of relief materials delivering into the traffic flow distribution in the upper level to compute the required travel time for each OD pairs, including the required travel time from supply depots to affected areas, $T_{mnv}^{\tau }$. Finally, we employ the steady-state parallel genetic algorithm (SSPGA) to plan the policy of network work repair scheduling.

5 Solution methods

Although the MRSD can allocate the relief materials fairly for the whole of the affected areas, the administrators of distribution centers are still required to determine the amount of the relief materials that are to be allocated to which affected areas. To overcome this difficult, we employ the parallel genetic algorithm (PGA) to deal with it, where the MRSD is incorporated to provide an upper bound for relief materials that can be received and for emergency relief vehicles that can be assigned from supply depots for each affected area. Then it is possible to determine either one or more supply depots are required to provide the relief materials or emergency relief vehicles to each of the affected areas. Therefore, in this section, we present a HSSPGA to deal with this model, which is shown in Fig. 4.

Fig. 4

The flow chart of HSSPGA

Fig. 5

Example of a chromosome

5.1 The rule of HSSPGA coding

In this section, we present the rule of coding for HSSPGA. For ease of description, we assume that there are 10 damaged edges, and there are 5 repair crews belonging to 2 distribution centers/work stations. These 2 distribution centers provide relief materials to 3 affected areas with 2 types of vehicle. Therefore, we use three sections to denote a chromosome, where section one denotes the sequence of road network restoration, the length of this section is $|N_{r}^{\tau }|$, and the value of each position (gene) is random taking value from a non-repeated integer number from 1 to $|N_{r}^{\tau }|$. Section two is matched with section one to decide the repair crew for each damaged edge, the length of this section is also $|N_{r}^{\tau }|$, the value of each position is random taking value from an integer number from 1 to $|C^{\tau }|$. Section three denotes the relief allocation strategy, the length of this section is $|N_{s}^{\tau }| \cdot |N_{q}^{\tau }| \cdot |V^{\tau }|$, and the value of each position is random taking value from a non-repeated integer number from 1 to $|N_{s}^{\tau }| \cdot |N_{q}^{\tau }| \cdot |V^{\tau }|$. Figure 5 illustrates an example of a chromosome.

In Fig. 5, the damaged edges 3 and 5 in section one match the repair crew 1 in section two, and the sequence is 3–5. The other is also decoded similarly to confirm the assignment and repair sequence for each repair crew.

5.2 MRSD-based relief allocation

We note that the relief materials are usually not enough to meet the demand of affected areas during the emergency response phase. Therefore, we first employ MRSD to allocate relief materials to ensure fair distribution, which is regarded as an upper bound. Secondly, through decoding section three to identify which supply depot will distribute the allocated relief materials to which affected area. The rule of decoding section three is shown as follows.

Algorithm I: MRSD-based Relief Allocation Approach
Step 1:	Initialize by setting ${SUS}_{mnv}^{\tau } \leftarrow 0$, ${SUV}_{mnv}^{\tau } \leftarrow 0$, $w_{mnv}^{\tau } \leftarrow 0$, ${AD}_{n}^{\tau } \leftarrow 0$, ${AV}_{nv}^{\tau } \leftarrow 0$, where $\forall m \in N_{s}^{\tau }$, $\forall n \in N_{q}^{\tau }$, $\forall v \in V^{\tau }$, ${AD}_{n}^{\tau }$ denotes the amount of relief materials that is predicted to be allocated to affected area $n \in N_{q}^{\tau }$, which is also an upper bound for relief allocation, ${AV}_{nv}^{\tau }$ denotes the amount of $v \in V^{\tau }$ vehicles that is predicted to be allocated to affected area $n \in N_{q}^{\tau }$.
Step 2:	Use $TD=\sum _{n=1}^{|N_{q}^{\tau }|}{D_{n}^{\tau }}$ to represent the total demand and $TS=\sum _{m=1}^{N_{s}^{\tau }}{S_{m}^{\tau }}$ to denote the total relief materials that can be provided. Allocate allthe relief materials that can be supplied by MRSD. Firstly, allocate the total amount of relief materials TS equally, i.e.,${AD}_{n}^{\tau } = \left\lfloor D_{n}^{\tau } \cdot \frac{TS}{TD} \right\rfloor$. Use $\widetilde{L}$ to denote the residual relief materials, which means that $\widetilde{L} = TS - \sum _{n=1}^{|N_{q}^{\tau }|}{{AD}_{n}^{\tau }}$.
Step 3:	If $\widetilde{L}=0$, then go to next step, else, do the following to allocate the residual relief materials. Allocate one more relief material to affected areas and compute the relative satisfaction. Then, choose the affected area with the minimum relative satisfaction, namely $n^{*} = argmin \{({AD}_{n}^{\tau }+1)/D_{n}^{\tau }\}$, where $argmin\{\cdot \}$ denotes a function that returns the index with the minimal value. Therefore, we allocate one relief material to this affected area $n^{*}$, namely ${AD}_{n^{*}}^{\tau } = {AD}_{n^{*}}^{\tau } + 1$. Set $\widetilde{L} = \widetilde{L} - 1$, if $\widetilde{L} \ne 0$, then go to Step 3, else go to next step.
Step 4:	Similarly, we employ the MRSD to allocate the vehicle. The average amount of vehicles allocated to affected area $n \in N_{q}^{\tau }$ is $AV_{nv}^{\tau } = \left\lfloor {NUM}_{v}^{\tau } \cdot \frac{D_{n}^{\tau }}{TD} \right\rfloor$ for each type of vehicle $v \in V^{\tau }$. Use $\widetilde{V_{v}}$ to denote the residual vehicles of the type of vehicle $v \in V^{\tau }$, which means $\widetilde{V_{v}} = {NUM}_{v}^{\tau }-\sum _{n \in N_{q}^{\tau }}{{AV}_{nv}^{\tau }}$.
Step 5:	If $\widetilde{V_{v}} = 0$, then $v=v+1$. If $v \le |V^{\tau }|$, then go to Step 4, else go to next step, else do as follows: Add one vehicle of type $v \in V^{\tau }$ to every affected areas and compute the relative satisfaction. Choose the affected area with minimum relative satisfaction, i.e., $n^{'} = argmin\{ ({AV}_{n}^{\tau } + 1)/\left\lceil D_{n}^{\tau }/Q_{v} \right\rceil \}$, Then, allocate one vehicle of type $v \in V^{\tau }$ to the affected area $n^{'}$, which means ${AV}_{n^{'}v}^{\tau } = {AV}_{n^{'}v}^{\tau } + 1$. Set $\widetilde{V_{v}} = \widetilde{V_{v}} - 1$. If $\widetilde{V_{v}} > 0$, then go to Step 5, else $v=v+1$. If $v \le |V^{\tau }|$, then go to Step 4, else go to next step.
Step 6:	Find $\lambda ^{*} = argmax \{Section~three(\lambda ),~\lambda = 1,2,\cdots , |N_{s}^{\tau }| \cdot |N_{q}^{\tau }| \cdot |V^{\tau }|\}$, where $argmax\{\cdot \}$ denotes a function which returns the index with the maximal value. If $Section~three(\lambda ^{*}) = 0$, then go to end step, Step 12, else go to next step.
Step 7:	Compute the parameters $v^{*}$, $m^{*}$ and $n^{*}$, where $v^{*} = \left\lceil \lambda ^{*}/(|N_{s}^{\tau }| \cdot |N_{q}^{\tau }|) \right\rceil$, $m^{*} = \left\lceil [\lambda ^{*} - (v^{*}-1) \cdot |N_{s}^{\tau }| \cdot |N_{q}^{\tau }|]/|N_{q}^{\tau }| \right\rceil$, and $n^{*} = \lambda ^{*} - (v^{*}-1) \cdot |N_{s}^{\tau }| \cdot |N_{q}^{\tau }| - (m^{*}-1) \cdot |N_{q}^{\tau }|$. Set $w_{m^{*}n^{*}v^{*}}^{\tau } = 1$.
Step 8:	Set ${TS}_{m^{*}n^{*}}^{*} = \min \{S_{m^{*}}^{\tau }, {AD}_{n^{*}}^{\tau }\}$, update $S_{m^{*}}^{\tau } = S_{m^{*}}^{\tau } - {TS}_{m^{*}n^{*}}^{*}$ and ${AD}_{n^{*}}^{\tau } = {AD}_{n^{*}}^{\tau } - {TS}_{m^{*}n^{*}}^{*}$.
Step 9:	If $S_{m^{*}}^{\tau } = 0$, then set $Section~three((v-1) \cdot |N_{s}^{\tau }| \cdot |N_{q}^{\tau }| + (m^{*}-1) \cdot |N_{q}^{\tau }| + j) = 0$, where $v=1,2,\cdots ,|V^{\tau }|$ and $j=1,2,\cdots ,|N_{q}^{\tau }|$. Else if ${AD}_{n^{*}}^{\tau } = 0$, then set $Section~three(\lambda ^{*}) = 0$ and $Section~three(n^{*} + (v-1) \cdot |N_{s}^{\tau }| \cdot |N_{q}^{\tau }| + (m-1) \cdot |N_{q}^{\tau }|) = 0$, where$v=1,2,\cdots ,|V^{\tau }|$ and $m = 1,2,\cdots ,|N_{s}^{\tau }|$.
Step 10:	Set ${SUV}_{m^{*}n^{*}v^{*}}^{\tau } = \min \{ \left\lceil {TS}_{m^{*}n^{*}}/Q_{v^{*}} \right\rceil , {AV}_{n^{*}v^{*}}^{\tau }\}$, update ${AV}_{n^{*}v^{*}} = {AV}_{n^{*}v^{*}} - {SUV}_{m^{*}n^{*}v^{*}}^{\tau }$.
Step 11:	If ${SUV}_{m^{*}n^{*}v^{*}}^{\tau } \ne 0$, then to compute the required travel times ${SUS}_{m^{*}n^{*}v^{*}}^{\tau }= \left\lceil {AD}_{n^{*}}^{\tau }/({SUV}_{m^{*}n^{*}v^{*}}^{\tau } \cdot Q_{v^{*}}) \right\rceil$, else, set ${SUS}_{m^{*}n^{*}v^{*}}^{\tau } = 0$. Go to Step 6.
Step 12:	End and output ${AD}_{n}^{\tau }$, ${AV}_{nv}^{\tau }$, ${SUS}_{mnv}^{\tau }$, ${SUV}_{mnv}^{\tau }$, and $w_{mnv}^{\tau }$.

After the relief allocation process, we will re-compute the shortest path for each OD pair to compute the network accessibility during each period $\tau$. After that, the cumulative network accessibility can be computed by Eq. (6), and hence meeting the objective in the upper level.

5.3 Fitness

In this study, we employ the following equation to compute the fitness of chromosome.

$$\begin{aligned} Fit(Pos) = (2-SP) + \frac{2 (SP-1) (Pos-1)}{Popsize-1} \end{aligned}$$

(32)

where Pos denotes the position of the chromosome in the sort, $SP \in [1.0,2.0]$ denotes the strength for the selection, and Popsize is population size.

5.4 Genetic operators

• 1. In this study, we adopt the selection strategy based on roulette of genetic algorithm.

• 2. In order to avoid generating repeat gene during the crossover operation, in this study, we adopt two-point crossover operation for Section one and Section three because these sections use the natural number to encode. For Section two, single-point crossover is adopted.

• 3. Similarly, for Section one and Section three, we adopt the inverse transcription variation mutation strategy, while using interchange variation strategy for Section two.

5.5 The rule of ending the algorithm

We end the algorithm when the number of iterations reaches the maximum number of iterations, which is denoted as Maxgen.

6 Numerical examples

In this section, we evaluate the solution approach that we propose for the MP-NRWSRLP through solving several randomly generated instances. The HSSPGA is coded in OpenMPI+Fortran and ran on the Pawsey Supercomputing Centre, with 5 compute nodes, each compute node has two sockets each housing one 2.6GHz Intel Xeon E5-2690 v3 “Haswel” chip. Each Xeon has 12 hardware cores, making a total of 24 cores per node. The same compute system is provided by the Laboratory High-Performance Computring and Stochastic Information Processing (HPCSIP) of Hunan Normal University to develop and test the code and calculate the samll-scale instances.

6.1 Instance generation

To generate the instances necessary for the experiments, we use the network generator GNETGEN (netlib, http://www.netlib.org/lp/generators/gnetgen), which is a modification of the widely used NETGEN generator proposed in Klingman et al. (1974). The generator creates a minimum cost flow network for given numbers of nodes |N| and edges |A|. In the generated network, there are $|N_{s}| = \sum _{\tau = 1}^{T}{|N_{s}^{\tau }|}$ and $|N_{q}| =\sum _{\tau = 1}^{T}{|N_{q}^{\tau }|}$ nodes associated with supply value and demand value, respectively, where the supplies equal to the total demand, and each edge has a cost for being traversed. In our case, this cost represents the required travel time under free flow $t_{(i, j)}^{0}$ between the two nodes i and j, connected by edge $a=(i, j) \in A$, and it is a variable within the interval [0, 30]. This network is transformed into a network repair instance using the following procedure.

First, the number of edges |A| is determined. We use a parameter $\gamma$ to specify the multiplier of the number of nodes of the network, i.e., the average of the number of edges in the network that each node is connected to these edges. Thus, the number of edges is $|A|=\left\lceil \gamma \cdot |N| \right\rceil$. Furthermore, the capacity of each edge is a variable within the interval [1000, 3000]. We use the multiplier $\gamma$ to denote different types of road network, when $\gamma =3$, means the maximum average number of edges in that road network each node is connected is three, which is sparse. Hence, this type of road network is referred to as rural network. If $\gamma =5$, this type of road network is defined as urban network, which is also a grid/ring network. Finally, we use $\gamma =4$ to denote the mixed area, which is between the rural network and the urban network.

Next, the number of damaged edges $|N_{r}| = \sum _{\tau = 1}^{T}{|N_{r}^{\tau }|}$ is determined. We use a parameter $\vartheta$ to specify the percentage of damage of the network, i.e., the percentage of the edges in the network that are damaged in a disaster. Therefore, the number of damaged edges is $|N_{r}| = \left\lceil \vartheta \cdot |A|\right\rceil$. We randomly select $|N_{r}|$ damaged edges. For each selected edge $a = (i,~j)$, the repair time $s_{d}$ for the damaged edge is set as a random variable uniformly distributed in the interval [10, 60].

Thirdly, we set the number of repair crews for each instance, in this paper, which is determined by the formulation $\left\lceil |N|/30\right\rceil +1$.

Finally, we fix the length of interval time. The interchange/update time for network structure information is denoted by $\eta$, which is determined by the update time or the planning horizon T. In our case, we set “72” hours as the whole interval time, which is recognized as the “golden” hours for emergency search-and-rescue.

Four sets of instances are considered for the computational experiments. First, we consider a set $S_{1}$, small size instances, $S_{2}$, medium size instances, $S_{3}$, large size instances, and $S_{4}$, xlarge size instances, which are used to test the performance of the HSSPGA. Note that using each one of the minimum cost flow networks generated by GNETGEN, several instances can be created by using different combinations of the parameters $\gamma$, which is used to determine the number of arcs by multiplying the number of nodes, $\vartheta$, which denotes the damaged ratio of this network, and $\eta$, which is set to the interval time of updating information. Table 4 shows the number of nodes considered in each instance, the values used for parameters $\gamma$, $\vartheta$, and $\eta$, and the total number of instances in each set.

Table 4 Sets of instances generated for the computational experiments

6.2 Parameter tuning

The HSSPGA approach we propose in this paper has six parameters that can be tuned: the size of populations $Popsize = 100$, the maximum number of iterations $Maxgen = 300$, the probability of crossover operator $p_{c} = 0.9$, the probability of mutation operator $p_{m} = 0.1$, the strength for selection $SP=1.2$, the weighting factor of traffic flow $\rho =0.5$.

6.3 Numerical results for the set of instances

To evaluate the performance of HSSPGA, we solve the four scales of instances $S_{1}$, $S_{2}$, $S_{3}$, and $S_{4}$ and compare the solutions found by the HSSPGA. Due to the random nature of our instances and algorithm, we perform 30 independent runs of HSSPGA with random start over the set of instances $S_{1}$, $S_{2}$, $S_{3}$, and $S_{4}$, we call each of these runs as a repetition. The HSSPGA performance is assessed based on two metrics: (1) algorithm computation runtime, (2) consistency of the algorithm performance among multiple repetitions.

The average computing time for HSSPGA after running 300 iterations is less than 25.35s for small instances. As the scale of instances increase, the computing time of HSSPGA increases considerably. The computing time increases for larger values of $\gamma$, $\vartheta$ and smaller value of $\eta$, i.e., when the network is severely affected by the disaster (the number of damaged edges also affected by the value of $\gamma$, because the higher value of $\gamma$, the greater number of edges of this network has) and the time to make a new strategy for network repair and relief logistics is short. Note that the effect of the parameter $\eta$ is significantly larger than the effect of the parameter $\vartheta$. Tables 5 and 6 present the average and standard deviation of the computing time for each combination of the number of nodes and values of the parameters $\vartheta$ and $\eta$, respectively.

Table 5 Average (and standard deviation) CPU time (in seconds) with reference to the instance size and values of $\vartheta$ with $\gamma =5$ and $\eta =4$

Table 6 Average (and standard deviation) CPU time (in seconds) with reference to the instance size with $\vartheta =50\%$

To evaluate whether our HSSPGA approach consistently finds good solutions among multiple repetitions, we analyze the variability of the solutions found over the 30 repetitions. We compute the coefficient of variation (CV) for the objective functions values, defined as the ratio of the standard deviation of the mean. Averaged over all scales instances, the CV is 0.97 percent. Table 7 shows the average coefficient of variation with respect to the instance size and values of $\gamma$, $\vartheta$ and $\eta$. Results show that the variability of the solutions obtained by our approach is predominantly affected by the network characteristics (higher connectivity) ($\gamma$), the damaged level ($\vartheta$) of the network, and the interval time ($\eta$) for making a new strategy.

Table 7 CV (percent) with reference to the instance size and values of $\gamma$, $\vartheta$, $\eta$

6.4 Solution analysis and insights

In this section, we analyze the structure of the solutions found with the goal to validate our optimization model and obtain some managerial insights. The discussion in this section is restricted to the solution found by the HSSPGA for four levels instances. However, it should be mentioned that not all solutions found using HSSPGA are guaranteed to be optimal.

Several observations from the policy and planning perspective are listed below:

• (1) The CPU time (in second) is determined by the level of network connectivity ($\gamma$), the length of interval time ($\eta$) and the damaged level ($\vartheta$) (see Table 5 and Table 6). As expected, the CPU time increases as the value of $\vartheta$ increases, since this corresponds to the situation where there are more requirements for the repair of the damaged nodes accessibility. On the other hand, the CPU time decreases as the value of $\eta$ is increased, since this corresponds to fewer update times. However, the relationship between CPU time and $\gamma$ is not clear, since the CPU time depends mainly on the number of nodes |N|.

• (2) The percentage of damaged nodes, which have been repaired to ensure accessibility for the entire network, is determined by the level of network connectivity ($\gamma$), the length of interval time ($\eta$) and the damaged level ($\vartheta$) (see Tables 8, 9, 10, 11). As expected, the percentage increases in accordance to the increase of update times, namely decreasing value of $\eta$, since this corresponds to more relaxed requirements for a damaged node to be repaired along with the change of the road network. On the other hand, the percentage is decreased as the value of $\gamma$ is increased, since this corresponds to more damaged nodes being repaired under fixed and limited resources (e.g. repair crews). Furthermore, the percentage decreases as the value of $\vartheta$ increases, since this corresponds to a higher damaged level of this road network, meaning that more damaged nodes are required to be repaired within the limited planning time horizon.

Table 8 Percentage of repaired damaged nodes for small scale with node $|N|=50$

Table 9 Percentage of epaired damaged nodes for medium scale with node $|N|=100$

Table 10 Percentage of repaired damaged nodes for large scale with node $|N|=200$

Table 11 Percentate of repaired damaged nodes for xlarge scale with node $|N|=800$

From Tables 8, 9, 10 and 11, we can calculate the average of the percentage of repaired damaged nodes under different damaged levels and length of interval time (or road network status update times (is $\lceil T/ \eta \rceil$)), which are shown in Figs. 6 and 7, from which we can obtain another three advanced managerial insights based on the former two managerial insights.

• (3) The percentage of repaired damaged nodes is decreasing with the damaged level increasing, as shown in Fig. 6. The main tendency is as shown in Fig. 7. The difference between the CPU time for different damaged levels for small- to media-scale instances is tiny. There is a bigger gap between the CPU time for large- to xlarge-scale instances than small- to media-scale ones, as shown in Table 5 (e.g., for $|N|=1000$, the gap of CPU time for the damaged level between 5 and 50% is 5.81%).

• (4) The update times (or the length of interval time) not only cause the CPU time to increase, but also impact on the percentage of repaired damaged nodes. Hence, we have to balance the percentage of the repaired damaged nodes and CPU time during the emergency response phase when making a road network restoration decision for ECC. According to the results recorded above, the optimal length of interval time $\eta \in [8,12]$ can give rise to a satisfied road network restoration decision within the limited CPU time.

• (5) The different characteristics of road network ($\gamma =3$ denotes the rural road network, $\gamma =5$ denotes the urban road network, and $\gamma =4$ denotes the mixed area road network) will influence on the percentage of repaired damaged nodes as shown in Fig. 8. Moreover, the percentage of the repaired damaged nodes in the rural area is lower than the urban area, and the urban area is lower than the mixed area. By analyzing the results of the experiments carefully, we can see that the main reason is that there is lack of redundancy in the road network in the rural area. In the urban area, there are sufficiently many arcs/roads which are linked to a node, and hence, the number of arcs/roads may become more than what are needed in demand. When there is a huge damage to this road network, the number of arcs/roads required repaired would become dramatic, especially the number of repair crews is determined by the number of nodes as being observed in the experiments, and subsequently, the percentage of repaired damaged nodes will be smaller. Therefore, there should have some reasonable redundancy of road network in the rural area. On the other hand, the number of road repair crews should be increased in the urban area, as shown in Table 12.

Fig. 6

Average % repaired damaged nodes for the length of interval time and different characteristics road network under % edges blocked

Fig. 7

Average % repaired damaged nodes for different characteristics road network and % edges blocked under varying length of interval time

Table 12 Percentage repaired damaged nodes by increasing the number of repair crews in urban areas

Fig. 8

Average % repaired damaged nodes for the length of interval time and % edges blocked under different characteristics of road network

7 Case study

7.1 Case construction

In this section, we use the mathematical model and algorithm developed in previous sections to deal with the case that is derived from the Wenchuan earthquake of magnitude 8.0 on the Richter scale. The disaster area we consider in this case is shown in Fig. 9. We choose the Dujiangyan, Pengzhou, and Shifang as repair workstation nodes and also supply nodes, which are shown in Fig. 9 with triangle. There are 35 demand nodes, which are labeled by circle in Fig. 9. The demands information for demand nodes, the required travel time from each OD pair nodes, the supply information for supply nodes, and the number of repair crews in repair workstation nodes are shown in “Appendix A”. There are 16 damaged nodes, which are labeled by plus circle in Fig. 9. The required repair time for damaged nodes are shown in “Appendix A”.

Fig. 9

The Case of Wenchuan earthquake

7.2 Case study results

We use the HSSPGA approach to obtain the strategy of road network repair work scheduling, $\varvec{X}$. Then we calculate for each period the routing of repair crews, relief allocation, and the path for delivering relief materials. In this case study, we set $\eta =8$ in accordance with the discussion in Sect. 6. After running 104.7 s on laptop with 8 threads, the results of each period of the repair crews routing are shown in Table 13, the results of relief allocation are shown in Table 14, and the results for each period of the path for delivering relief materials are shown in Table 15. Due to the space limitation, we only show three paths for relief delivery, which are from node 1 to node 8, from node 2 to node 17, and from node 3 to node 38.

Table 13 Repair crews routing for each period

From Table 13, we can see that the HSSPGA can work out the assignment schedule of the damaged nodes to repair crews in the upper level and the relief allocation strategy for each supply nodes in the lower level. It can provide for each period the repair crews routing in the upper level and the path for delivery relief materials in the lower level. These results are useful for helping the ECC and the administrators of distribution centers for decision making. The strategies that are obtained by HSSPGA can repair the damaged nodes 100%, and the required repair time is shortened by 14.93% (645.07 min). Hence, the proposed mathematical model and solution approaches are useful to help decision-makers to plan the road network restoration strategy during the post-disaster.

Table 14 The relief allocation and satisfy level (SL (%))

From Table 14, we can see that the satisfy level (SL) for each of the affected areas is closed to 79.73%, which is the average satisfy level for total relief supplies divided by whole demands. The results show that the maximum related satisfy degree approach is really efficient to allocate the relief materials in the lower level.

Table 15 Part path of emergency relief vehicle for delivering relief materials

From Table 15, We can conclude that the vehicles for delivering relief materials can’t pass these damaged roads that are not repaired in the first three periods, if there are no other alternative paths, such as from node 1 to node 8, or from node 3 to node 38. Once some damaged roads have been repaired, the roads for delivering the relief materials become connected, and the path for delivery the relief materials will be changed at the same time. However, with more and more damaged roads are having been repaired, the traffic flow assignment schedule will need to be changed accordingly. Some roads will become crowded, and hence, the required travel time will be longer, such as from node 2 to node 17, the period from $\tau =1$ to $\tau =6$. We can see that the main cause for this phenomenon is that the required travel time from node 16 to node 13 and from node 13 to node 17 are becoming longer, which means that it is necessary to adopt appropriate traffic control for these roads to ensure that the relief materials can arrive the affected areas as soon as possible.

8 Conclusions and future research

In this paper, we considered a multi-period road network repair work scheduling and relief logistics problem in post-disaster (MP-NRWSRLP) with two main objectives: (1) to optimize the scheduling and routing of repair crews during each period to improve the accessibility of road network timely and efficiently; and (2) to maximum the satisfaction of relief materials allocation, while minimizing the total required time for transferring the relief materials to affected areas. Given the impact that a functioning road network has on providing the accessibility for the relief materials to be transferred to the affected areas, it is clear that MP-NRWSRLP is an important problem. This paper extends the traditional network upgrading problems by considering not only the emergency repair (the selection of the damaged edges needed to be repaired or upgraded, the time dependency, and the routing of repair crews) but also the relief logistics which is regarded as a main activity during the post-disaster emergency response phase.

A MRSD-based steady-state parallel genetic algorithm is developed to solve the MP-NRWSRLP, which allows us to find good solutions for different instance sizes and road network topologies under limited CPU time. We observe that the CPU time increases as update times and damaged level of road network are increasing, namely the values of $\eta$ and $\vartheta$ are decreasing, but the relationships between CPU time and road network types is not clear. On the other hand, the percentage of road network repaired is increasing as the values of $\eta$, $\gamma$ and $\vartheta$ are decreasing. Furthermore, it is required to set a balance between the update times and the percentage of damaged nodes being repaired and the CPU time during the emergency response phase. In this paper, we conclude that the best update times are equal to two or three times a day, namely 8 h or 12 h for an interchange or update, this interval time appears highly realistic. In addition, the different characteristics of road network will influence on the percentage of repaired damaged nodes. The percentage of the repaired damaged nodes in the rural area is lower than the urban area, and the urban area is lower than the mixed area. By analyzing the results of the experiments carefully, there should have some reasonable redundancy of road network in the rural area. On the other hand, the number of road repair crews should be increased in the urban area.

From our study of the MP-NRWSRLP, we see that this work can be extended by covering more complex and realistic settings, such as integrating optimized evacuations. For this extended model, different organizations or relief entities are involved in the emergency reconstruction operations of the road network repair. In addition, the collaboration and coordination aspects should also be taken into consideration, such as how to deal with the situation when two or more repair crews are able to work simultaneously to repair a single damaged node. Furthermore, the relief operations/scheduling can be carried out not only through vehicles. The relief materials can also be transferred by helicopters during the emergency response phase. Clearly, this multi-mode feature of the relief operations/scheduling during the emergency response phase should not be ignored. Therefore, we shall tackle, in our future research, the realistic problem where more than one repair crews can work on a single damaged node simultaneously under multi-mode relief operations/scheduling. In regards of the computational issue, a comparison study on the performance analysis of the proposed GA based algorithm with other existing heuristic algorithms is to be carried out in our future research.

Appendix A: Detail information for case study

The detail information for supply depots and demand nodes are shown in Table 16, where $S_{m}^{\tau }$ is determined by the capacity of the distribution center $m \in N_{s}^{\tau }$ and $D_{n}^{\tau }$ is determined by the number of people in accordance with the Statistical Yearbook 2008, Sichuan, and the percentage of the collapsed houses that can be predicted by satellite images, infrared and aerial photography technology. In addition, the traverse time for each road/link is available from google earth.

Table 16 Supply nodes and demand nodes

The damaged nodes detail information are shown in Table 17, where $s_{d}, d \in N_{r}^{\tau }$ is the required repair time in minutes, which is forecasted using the technology of infrared or aerial photography. Namely, we first get the length of destroyed roads/links each of the damaged nodes by using the technology of infrared or aerial photography, then it is divided by the capability of each repair crew. In this paper, we assume that the capability of each of the repair crew is the same and equals to 0.5 Km/h.

Table 17 The damaged nodes detail information

In Table 18, the number of vehicles and the occupied OD are obtained from the data of Public Road Bureau, Department of Transportation of Sichuan Province, China.

Table 18 Emergency relief vehicle information