Measuring the risk of European carbon market: an empirical mode decomposition-based value at risk approach

Abstract

Unlike common financial markets, the European carbon market is a typically heterogeneous market, characterized by multiple timescales and affected by extreme events. The traditional Value-at-Risk (VaR) with single-timescale fails to deal with the multi-timescale characteristics and the effects of extreme events, which can result in the VaR overestimation for carbon market risk. To measure accurately the risk on the European carbon market, we propose an empirical mode decomposition (EMD) based multiscale VaR approach. Firstly, the EMD algorithm is utilized to decompose the carbon price return into several intrinsic mode functions (IMFs) with different timescales and a residue, which are modeled respectively using the ARMA–EGARCH model to obtain their conditional variances at different timescales. Furthermore, the Iterated Cumulative Sums of Squares algorithm is employed to determine the windows of an extreme event, so as to identify the IMFs influenced by an extreme event and conduct an exponentially weighted moving average on their conditional variations. Finally, the VaRs of various IMFs and the residue are estimated to reconstruct the overall VaR, the validity of which is verified later. Then, we illustrate the results by considering several European carbon futures contracts. Compared with the traditional VaR framework with single timescale, the proposed multiscale VaR–EMD model can effectively reduce the influences of the heterogeneous environments (such as the influences of extreme events), and obtain a more accurate overall risk measure on the European carbon market. By acquiring the distributions of carbon market risks at different timescales, the proposed multiscale VaR–EMD estimation is capable of understanding the fluctuation characteristics more comprehensively, which can provide new perspectives for exploring the evolution law of the risks on the European carbon market.

1 Introduction

Over the past few years, carbon markets have been advanced as an efficient solution for tackling climate change at the lowest cost. Following the 2008 sub-primes crisis and the 2011 European debt crisis, carbon prices have been witnessing violent fluctuations, and increasingly dominant uncertainties (Zhang and Wei 2010). From this perspective, accurately measuring the risk on the carbon markets can not only help investors favorably avoiding market risks and achieving maximum profits, but also help the governments constantly improving the pricing system, implementing pilot phases, and even constructing the future unified Chinese carbon market.

Although measuring the risks on carbon markets appears as a central research question, the related literature lies still in its infancy. Previous studies have mainly focused on the fluctuations of carbon prices. Only a few studies have measured the risk of carbon market. Chevallier (2013) has proposed a new methodology to measure the volatility of CO₂ assets—computed as the difference between model-free implied volatility from option prices and model-free realized volatility from high-frequency intraday data—coined as ‘variance risk-premia’. The author found that (1) variance risk-premia are equal to a daily sample average of 0.79 for European Union Allowances (EUA) and 0.18 for Certified Emissions Reductions (CER), and (2) variance risk-premia are time-varying, and can be used as strong predictors for forecasting CO₂ returns. However, the author did not account for the Value-at-Risk (VaR) on carbon markets. Feng et al. (2012) have used the extreme value theory (EVT) to measure the VaR for the European carbon market. The authors found that (1) the downside risk is higher than the upside risk especially during the first phase (June 2005–December 2007) and the second phase (February 2008–December 2009) for both the spot and futures markets; (2) the EVT–VaR is more effective for measuring the EU ETS market risk than the traditional VaR methods, which can reduce the risks for market participants. Jiang et al. (2015) have developed an integrated GARCH–EVT–VaR model for the carbon market risk measurement of the EU ETS. They found that (1) the GARCH–EVT–VaR model makes more accurate risk measurement of the carbon market than the traditional VaR models; (2) the EUA and CER are exposed to the same level of market price, and that market risks of EUA and CER are significantly correlated, in spite of differences in their policy risk, legal risk and credit risk. During the latest years, more and more studies have explored the risks between carbon market and other financing markets (Balcilar et al. 2016; Luo and Wu 2016; Zhang and Sun 2016).

Although existing findings can provide an important reference for estimating the risks on the carbon markets, there are still some shortcomings to be further improved. The EU ETS trades by spot, futures and options, and is therefore endowed with the financial commodity attribute, which is influenced by market mechanisms as well. Its volatility characteristics have been documented, among others, by Tang et al. (2017) in the operations research literature. The VaR, as a widely used approach for measuring the risks on traditional financial markets, is also applicable to estimate the risk of carbon market. As a traded commodity, there are different strategies for different market transactions to evade the fluctuation risks of the carbon price, and their influences on carbon markets are also different (Zhu et al. 2014a, b). Speculators of short timescales determine their trading strategies based on the short-term fluctuations of the carbon price, and therefore they make frequent transactions, which exert short-term influences on the carbon price and limited influences on the carbon market. Speculators of long timescales are concerned by the long-term trend of the carbon price. Thus, they produce a low transaction frequency, which exerts a long-term influence on the carbon price, and a strong penetrability and great influence on the carbon market. Speculators of medium timescales focus both the short-term fluctuations and the long-term trend of the carbon price. Their transaction behaviors have a moderate influence on the carbon market. Therefore, all factors influencing carbon market are endowed with different roles from the perspective of the speculators of different timescales. As a result, their transaction behaviors induced by these factors are also different. The sum of their mutual influences and interactions between market behaviors with different timescales is finally reflected in the overall carbon price, which leads to a multi-timescale characteristic of fluctuations of carbon price changes (Zhu et al. 2015).

The VaR as a downside risk measure in the Carbon market also exhibits a multi-timescale characteristic. As a matter of fact, investors’ risk concerns on the carbon market are influenced by different timescales. On the one hand, the investors of long timescale pay more attention to the influences of large timescale fluctuations on the investment income and ignore that of short timescale fluctuations. On the other hand, the investors of short timescale concentrate on the risk of short timescale fluctuations. However, the existing studies only measure the overall VaR of the carbon market from single-timescale instead of multi-timescale, which ignore the multi-timescale characteristics. As a result, they fail to acquire the distributions of carbon market risks at different timescales, and thereby cannot understand the multiscale characteristic of carbon price fluctuations. Consequently, they are unable to accurately measure the VaR of the carbon market, which is unfavorable for the comprehensive understanding on the evolution law of carbon market risks.

Unlike other commodity markets, the European carbon market is fundamentally determined by compliance issues (Alberola et al. 2008). The supply of allowances is set by the European Commission, which also controls the allocation, bankability and size of the program through the number of participants and allowances. These elements of the EU ETS have differed between the first phase (2005–2007) and the second phase (2008–2012). They will also change again, in the third phase (2013–2020), as the cap tightens and the size of the market increases with the extension to more polluters. Uncertainty over a global climate agreement, the size of the future cap and market, the eligibility and number of some types of offsets allowable in the scheme are key factors impacting the carbon price now and in the future. It is observed that the institutional information disclosures can enlarge the volatility of carbon price, so as to enhance the risk of carbon market. Therefore, carbon market is a typical heterogeneous market, and extreme events tend to give rise to the violent fluctuations of carbon price in a short period. The VaR estimation based on the efficient market hypothesis (EMH) in existing studies can result in the overestimation on the VaR of carbon market. This approach cannot accurately measure the risk of carbon market, and is unable to provide an effective information support for the investors’ decisions.

This article aims at filling the gaps identified in the literature above regarding financial risk management for the carbon markets, and the central issue of the correct VaR measure. As a novel adaptive data decomposition method, empirical mode decomposition (EMD) can decompose nonlinear and nonstationary carbon price return into several simple modes with different timescales, called intrinsic mode functions (IMFs) and a residue (Wu and Huang 2009), which cannot only capture the multiscale characteristic of the risks in carbon market, but also provide an easy access for measuring their VaRs. Therefore, the aim of this study is to accurately measure the VaR of carbon market from the multi-timescale perspective.

The main objective of this paper is to assess the risk exposure for investors operating in the carbon market. We examine Value-at-Risk (VaR) risk measurement for the EU ETS ECX (European Climate Exchange) carbon market. We use ECX EUA daily futures prices from April 25, 2005 to July 28, 2017. To complement the existing empirical literature with regard to risk assessment in carbon markets, we suggest a multi-timescale VaR framework taking into account the impact of extreme events on the risk. Evidence shows that the VaR measure outperforms other traditional VaR methods.

The main contributions are twofold: (1) an EMD-based multiscale VaR is constructed for measuring the risks on the European carbon market. Firstly, the EMD algorithm is utilized to decompose the carbon price return into several IMFs with different timescales and a residue, which are modeled respectively using the ARMA–GARCH model to obtain their conditional variances at different timescales. Furthermore, the Iterated Cumulative Sums of Squares algorithm (ICSS) by Inclan and Tiao (1994) is employed to determine the windows of an extreme event, so as to identify the IMFs influenced by an extreme event and conduct an exponentially weighted moving average (EWMA, Lowry et al. 1992) on their conditional variations. Finally, the VaRs of various IMFs and the residue are estimated to reconstruct the overall VaR, the validity of which is verified later.

(2) Compared with the traditional VaR estimation with single timescale, the empirical results demonstrate that the proposed multiscale VaR–EMD approach can effectively reduce the influences of the heterogeneous environments (such as the influences of extreme events on the risk of carbon market), and obtain a more accurate overall risk measure. Meanwhile, the proposed multiscale VaR–EMD estimation strategy can acquire the distributions of carbon market risks at different timescales. So, it is capable of understanding the fluctuation characteristics of carbon prices more comprehensively, which can provide a new perspective for exploring the evolution law of the risks on the European carbon market.

The remainder of the article is structured as follows. Section 2 details the methodology. Section 3 contains the empirical analysis. Section 4 briefly concludes.

2 Methodology

This section develops the several steps to implement the newly introduced VaR–EMD approach. By doing so, we build on the latest developments by Zhu et al. (2016).

2.1 VaR

VaR is one of the main downside risk measures in the financial industry (Iglesias 2015; Youssef et al. 2015; Karmakar and Paul 2016), and has been proved recently to be an effective way to measure carbon market risks. VaR represents the maximum expected loss of a single asset or a portfolio over a given holding period at a specified confidence level. To measure the downside risk exposure, VaR is defined based on the particular quantile of the data distribution. Generally, it is defined as follows. In the general case of a single asset worth $X$ at the confidence level $cl$, VaR is defined as (Szegö 2002; Dowd 2005; Jorion 1997):

$$ VaR_{a} = - F_{x}^{ - 1} \left( a \right) $$

where $\alpha = 1 - cl,\,Z_{\alpha }$ is the quantile value of the inverse Cumulative Density Function. $F_{x}^{ - 1}$ is the inverse of the distribution function $F_{x}$.

The original VaR only defines the general framework to measure downside risk, but not the specific estimation models. There are many classifications of estimation methods for VaR. Duffie and Pan (1997) classified VaR estimation method based on different ways to estimate returns and volatility. They are classified into jumps, stochastic volatility, etc. In Jorion (1997), VaR estimation main is classified into parametric and non-parametric, etc. Dowd (2005) further added the semi-parametric category as the third classification to include the recent techniques such as extreme value theory. In all these different classifications, when the Gaussian distribution is assumed for the return data, the parametric specification of VaR can be calculated with the mean and variances. The Parametric approach requires explicitly specific statistical distribution. Mainstream parametric models include Isometrics’ Exponential Weighted Moving Average (EWMA) and Generalized Autoregressive Conditional Heteroscedasticity (GARCH), EGARCH, and ARMA–EGARCH models (Duffie and Pan 1997). The Non-parametric approach includes Historical Simulation (HS) and Monte Carlo Simulation (MCS). HS is a histogram-based approach which is easy to understand and implement. However, it largely depends on historical record and the choice of the time window length. MCS repeatedly draws samples from specified distributional to simulate the real scenarios and then estimate the VaR accordingly. It is very flexible to implement but difficult to replicate the extreme event scenario thus could lead to VaR overestimation. Recently, new VaR estimation models are constructed to take advantage of both parametric and non-parametric approach (Dowd 2005). New techniques introduced have been introduced, ranging from Copula theory, Extreme Value theory to multiscale models such as wavelet analysis and EMD models. Compared with the Fourier analysis and wavelet analysis, EMD is especially suitable to deal with nonlinear and non-stationary data which is a self-adaptive data processing method (Huang et al. 1998; Wu and Huang 2009).

2.2 EMD

As an adaptive data analysis method, empirical mode decomposition (EMD) can decompose nonlinear and nonstationary carbon price return into a set of IMFs and a residue (Huang et al. 1998; Wu and Huang 2009). Following the decomposition-ensemble methodology, EMD model can be used to analyze and model the hidden data characteristics (Yu et al. 2015). An IMF must meet two requirements: (1) the amount of maximum and minimum values is same as, or differs up to one by that of zero-crossings. (2) The upper envelop shaped by the local maximum values is symmetrical with the lower envelop shaped by the local minimum values in terms of zero. Setting the original carbon price return as x(t), the processes of EMD are following:

• 1. Determining all local maximum points and local minimum points of $X(t)$;

• 2. Connecting all local maximum points and minimum points respectively by utilizing cubic spline so as to form the envelopes $e_{\hbox{max} 1} (t),\,e_{\hbox{min} 1} (t);$

• 3. Obtaining the average envelop value between the maximum envelop and minimum envelop;

  $$ m_{ 1} (t) = \frac{{e_{\hbox{max} 1} (t) + e_{\hbox{min} 1} (t)}}{2}. $$

• 4. Calculating the difference between $X(t)$ and $m_{1} (t)$:

  $$ d_{1} (t) = X(t) - m_{1} (t). $$

• 5. Judging whether or not $d_{1} (t)$ satisfies IMF’s conditions. If it does, it is regarded as the first IMF; otherwise, it is considered as the original sequence. After obtaining average envelop $m_{11} (t)$ of the maximum and minimum of $d_{1} (t)$, whether or not $d_{11} (t) = d_{1} (t) - m_{11} (t)$ meets conditions of IMF is determined. If it cannot meet the conditions, the cycle is repeated for $k$ times until $d_{1k} (t) = d_{1(k - 1)} (t) - m_{1k} (t)$ is obtained to make $d_{1k} (t)$ meet the IMF’s conditions. In case $C_{1} (t) = d_{1k} (t)$, $C_{1} (t)$ is the first IMF of the $X(t)$, namely IMF₁ = $C_{1} (t)$

• 6. Separating $C_{1} (t)$ from $X(t)$, the residue $r_{ 1} (t) = X(t) - C_{1} (t)$ is regarded as the original series. Then repeat steps (1)–(5), IMF_j = $C_{j} (t)$, and $m$ IMFs and one residue $r(t)$ can be obtained. Under such circumstance, the original carbon price return is equal to the sum of all IMFs and the final residue:

  $$ X(t) = \sum\limits_{j = 1}^{m} {C_{j} (t) + r(t)} . $$

For the convenience, we denote $r(t)$ as $c_{m + 1} (t)$. IMFs have nice properties: stationary; IMFs contains most information of local characteristic in different timescale. Meanwhile $r(t)$ represent the trend.

The performance of EMD is sensitive to the stoppage criterion for the sifting process. There are many stoppage criteria, such as the standard deviation by Huang et al. (1998), threshold method by Rilling et al. (2003), etc. Threshold method has been developed as an improvement over the original standard deviation method to avoid over-iteration or over-decomposition during the sifting process due to locally large excursions and globally small fluctuations in means (Huang et al. 1998; Rilling et al. 2003).

2.3 ARMA–EGARCH model

ARMA–EGARCH model can favorably capture the autocorrelation and conditional variance of carbon price returns, especially having the advantage in deal with lever effect, nonlinear problem, and the complex fluctuation. Thus, the model has been widely employed to measure the risk of financial market. The ARMA (m, n)–EGARCH (p, q) model is defined as:

$$ \left\{ {\begin{array}{*{20}l} {y_{t} = \mu + \sum\limits_{i = 1}^{m} {\omega_{i} y_{t - i} + \sum\limits_{j = 1}^{n} {\gamma_{j} \varepsilon_{t - j} + \varepsilon_{t} } } } \hfill \\ {\varepsilon_{t} = N_{t} \sqrt {h_{t} } } \hfill \\ {ln(h_{t} ) = \alpha_{0} + \sum\limits_{i = 1}^{q} {\alpha_{i} \frac{{\left| {\varepsilon_{t - i} } \right|}}{{\sqrt {h_{t - i} } }}} + \sum\limits_{j = 1}^{p} {\beta_{j} \ln (h_{t - j} ) + \sum\limits_{l = 1}^{q} {\lambda_{l} \frac{{\varepsilon_{t - l} }}{{\sqrt {h_{t - l} } }}} } } \hfill \\ \end{array} } \right. $$

where, t, μ are time, constant term respectively, $y_{t}$ is time series. ε is the residue or error term, while m and n are the orders of autoregressive process and moving average process separately. $h_{t}$ is the conditional variance, while $N_{t}$ is an independent and identically distributed random variable which is independent with $\sqrt {h_{t} }$. $\alpha_{0}$, p and q are the constant term, ARCH order and GARCH order respectively. Meanwhile, $\alpha_{i}$, $\beta_{j}$ and $\lambda_{l}$ are the coefficients of ARCH, GARCH and leverage, respectively. If lever effect is not significant, $\lambda_{l}$ is 0.

The conditional mean $\hat{\mu }$ and conditional variance $\hat{h}_{\text{t}}$ of carbon price return can be obtained by the ARMA–EGARCH model, and then the VaR based on ARMA–EGARCH model is acquired:

$$ VaR_{a} = - \left( {\hat{\mu } - Z_{a} \sqrt {\hat{h}_{t} } } \right){\text{P}} $$

where $\alpha = 1 - cl$, $Z_{\alpha }$ is the quantile value, or the inverse Cumulative Density Function value, at the particular probability of standard normal distribution. $\sigma$ is the volatility of the carbon price return, $l$ is the holding period, and $P$ is the value of carbon price. In a special case when zero mean can be assumed, VaR can be calculated using the conditional variance.

2.4 ARMA–EGARCH–EWMA model

Although the ARMA–EGARCH model can effectively capture the volatility clustering of carbon price return, the presence of extreme events on the carbon market can lead to the violent fluctuations of carbon price in a short period, which can give rise to the overestimation of the VaR. EWMA is introduced to perform a smooth processing on the conditional variances of carbon price return within the windows of an extreme event, so as to take away the overestimation on VaR to a certain degree.

As is well known, EWMA, firstly proposed by Morgan (1996), places different significance on each return observation within the sample window and the weights decline exponentially over time. That is to say, EWMA gives greater weight to more recent observations and less weight to more distant ones. Formally, EWMA is defined as:

$$ \sigma_{t}^{2} = \lambda \sigma_{t - 1}^{2} + (1 - \lambda )r_{t - 1}^{2} $$

where $\lambda \in (0,1)$ is the decay factor, $\sigma_{t}^{2}$ is the volatility at time $t$, $\sigma_{t - 1}^{2}$ is the volatility at time $t - 1$, and $r_{t - 1}^{2}$ is carbon price the return at time $t - 1$. The EWMA estimate daily volatility based on the most recent daily return. A high $\lambda$ means that the weight declines slowly and vice versa. Inspired by the RiskMetrics Technical Document (1996) and Boucher et al. (2014), we can take $\lambda = 0.94$ here.

The conditional mean $\hat{\mu }$ and conditional variance $\hat{h}_{et}$ of carbon price returns can be calculated by the ARMA–EGARCH–EWMA model. In this way, the VaR based on ARMA–EGARCH–EWMA model is obtained:

$$ VaR_{a} = - \left( {\hat{\mu } - Z_{a} \sqrt {\hat{h}_{et} } } \right){\text{P}} . $$

2.5 VaR backtesting

For backtesting, VaR failures as defined by Kupiec (1995) are utilized to verify the validity (reliability) and accuracy of VaR. T is the sample size, namely, the length of carbon price return. N is the number of failure times for the actual loss exceeding the VaR value, and the failure rate is expressed as $P = {N \mathord{\left/ {\vphantom {N T}} \right. \kern-0pt} T}$. Assuming that the confidence of VaR is cl, the expected probability for each failure is $P_{0} = 1 - cl$. If the failures rate is greater than P₀, the VaR calculation is erroneous. Otherwise, the calculation has succeeded. Therefore, the null hypothesis and alternative hypothesis can be established: H₀: $P \ge P_{0}$, H₁: $P < P_{0}$. In this way, the VaR accuracy test is converted into the hypothesis test for investigating whether or not the failure rate P is significantly lower than the expected probability in each failure P₀. Therefore, the z-statistics is constructed as:

$$ z = \frac{{P - P_{0} }}{{\sqrt {\frac{{P_{0} (1 - P_{0} )}}{T}} }}\sim\,N(0,1) $$

where, $N(0,1)$ is the standard normal distribution. Particularly, in case $cl = 95\%$ and $z < - 1.645$, the null hypothesis is denied. Otherwise, the null hypothesis is accepted.

2.6 VaR–EMD based estimation for the European carbon market

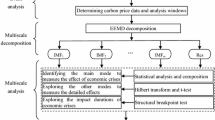
The overall process of the proposed EMD based VaR Estimation is shown in Fig. 1, and the specific processes are described as follows:

Fig. 1

The process of EMD based VaR estimation methodology

Firstly, we use EMD algorithm to decompose the in-sample carbon price return into m IMFs and one residue.

Secondly, we use ARMA–EGARCH model to obtain the conditional variance of each IMF and the residue at any timescale.

Thirdly, we use the ICSS algorithm applied for instance by Zhu et al. (2014a, b) and Bai–Peeron test to identify the structural breakpoints of the original carbon price return, and determine the time window of each extreme event. We assume the IMFs with the bigger volatility as the extreme event components, which is affected by the extreme event, while the other IMFs are assumed to the normal market behaviors, which are not affected by the extreme event. This is based on the assumption that extreme events have a more significant impact on carbon price than the normal market behaviors. In addition, to remove the effect of the extreme event from the original carbon price return, the EWMA approach is used to estimate the volatilities of those IMFs identified as the extreme event components (IMF₁–IMF_i) in the period of time window.

Fourthly, since different IMFs are orthogonal (Huang et al. 1998; Wu and Huang 2009), the aggregated volatility can be reconstructed from the volatility of all the IMFs and the residue as:

$$ \sigma_{\text{agg}} (t) = \sqrt {\sum\limits_{i = 1}^{m} {\sigma_{IMF(i)}^{2} (t) + \sigma_{RES}^{2} (t)} } $$

where $\sigma_{\text{agg}} (t)$ is the aggregated volatility at time t. $\sigma_{IMF(i)}^{2}$ (t) and $\sigma_{RES}^{2} (t)$ are the volatilities of the ith IMF and residue at time t respectively.

Fifthly, suppose the holding period is 1 day, VaR at time t is estimated as:

$$ aggVaR(\alpha ,t) = Z_{\alpha } \sigma_{agg} P $$

where $z_{\alpha }$ is the quantile value, or the inverse Cumulative Density Function value, at the particular probability of standard normal distribution. $\alpha$ takes the value of $1 - cl$, and $cl$ is the confidence level.

Sixthly, we repeat the above steps with the out-of-sample carbon price return and make one-step-ahead forecasts.

Seventhly, we choose a particular evaluation criterion: the number of the exceedances for backtesting to test the accuracy of the proposed approach.

3 Empirical analysis

This section develops the empirical application of the VaR–EMD based estimation strategy in the context of the European carbon market.

3.1 Data

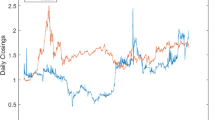
The European Climate Exchange (ECX) is the largest carbon market under the EU ETS, with its daily trading volume of carbon futures generally accounting for more than 70% of that of global carbon markets, which can reflect the overall state of global carbon market. For the purpose of our illustrative empirical application, we select the ECX EUA futures price from April 25, 2005 to July 28, 2017, including 3141 daily transaction prices in total as a sample. The first 2512 daily transaction prices (about 80% of all data) from April 25, 2005 to February 16, 2015 are applied as in-sample data to construct the model. The remaining 629 daily transaction prices (20% of all data) from February 17, 2015 to July 28, 2017 are used as the out-of-sample data to verify the robustness of the established model. EUA futures is selected as one of the representative mainstream contracts in current futures trading of ECX. Carbon price return is defined as $R_{t} = \ln P_{t} - \ln P_{t - 1}$, where $P_{t}$ and $P_{t - 1}$ are the EUA futures prices in the day $t$ and $t - 1$ respectively. Figure 2 illustrates the daily carbon price of EUA FUTURES with unit of €/t and its return.

Fig. 2

The daily carbon price of EUA futures and its t return from 2005/04/25 to 2017/7/28

3.2 EMD decomposition of carbon price return

The Matlab R2014a platform, developed by the Mathworks Inc, is utilized to perform the EMD decomposition on the in-sample EUA futures return using the EMD algorithm. The parameters for the stoppage criterion in EMD model is as follows. $\upalpha = 0.05$, $\theta_{1} = 0.05$, $\theta_{2} = 10\theta_{1}$. This gives rise to nine IMFs with different timescales and one residue, as shown in Fig. 3. IMF1, IMF2, …, IMF9 are plotted from the top to the bottom in Fig. 3, and the last item Res at the bottom is the residue. The frequencies and amplitudes of all the IMFs change over time. The frequencies of those components are arranged in a descending order: IMF1 > IMF2 > IMF3 > IMF4 > IMF5 > IMF6 > IMF7 > IMF8 > IMF9 > Res. With the gradual decrease of frequency of an IMF, the amplitude and the volatility are reduced accordingly. Furtherly, the variance ratio contribution of the first three IMFs, IMF1, IMF2 and IMF3, reach 87.13%.

Fig. 3

The IMFs and residue from 2005/04/25 to 2015/2/16 through EMD

3.3 VaR estimation of carbon price returns

3.3.1 ARMA–EGARCH modeling

The Eviews 8.0 software package, developed by Quantitative Micro Software Corporation, is used for modeling ARMA–EGARCH. The principle for determining the order of ARMA model is that the residue $\varepsilon_{t}$ is not autocorrelated, while $\varepsilon_{t}^{2}$ is autocorrelation. At first, EGARCH, TGARCH and EGARCH are performed and compared, and according to AIC and likelihood, we eventually choose EGARCH to deal with variance. EGARCH model is set as EGARCH (1, 1). The modeling results of ARMA–EGARCH are shown in Tables 1 and 2. $C_{j} (t),j = 1,2, \ldots ,10$ are the IMF₁–IMF₉ and Res respectively, and ln − r is original carbon price return without EMD. Here Ln − r is modeled to calculate VaR without EMD for comparison in part 3.5 and part 3.6. ARMA (1,0) model is employed to estimate IMF6, IMF7, IMF8 and IMF9 and ARMA (1,1) for the other series. All of parameters of AR and MA are significantly not 0 at the significance level of 1%. As demonstrated in the ARCH test of the residue $\varepsilon_{j} \left( t \right)$ of each $C_{j} \left( t \right)$ in the mean equation, all IMFs present significant conditional heteroscedasticity, and the statistics of Durbin–Watson (DW) are all close to 2, indicating that the residues exhibit a poor self-correlation. In the variance equation, the coefficients (α and β) of ARCH and GARCH for each component are significantly not 0 at the significance level of 1% so is coefficients of leverage for ln − r, which indicates that original carbon price return have significant lever effect. Needs to point out, for all of nine IMFs and one residue, their coefficients of leverage is 0 at the significance level of 10%, which means there are not lever effect, though original carbon price return has. The possible reason is that EMD decomposition algorithm will eliminate lever effect. This worth further research and beyond the discussion of this study. As indicated in various test results, the established ARMA–EGARCH (1, 1) model is effective, and can be used for the subsequent VaR calculation.

Table 1 Parameters of the ARMA model

Table 2 Parameters of the EGARCH (1, 1) model

3.3.2 VaR estimation based on EMD–ARMA–EGARCH

Firstly, the confidence level is set as $cl = 95\%$, and the VaRs of all IMFs are calculated, as seen in Fig. 4. The failures backtesting is carried out to test the accuracy of the estimated VaRs, and the results are illustrated in Table 3. It can be found that al the VaRs of IMFs and residue pass the test at the significance level of 5%, which proves that all the calculated VaRs are accurate. As observed in Fig. 4, with increasing frequency of IMF, VaR shows a gradually smooth variation. This is because the investors of long timescale are more concerned about the long-term returns, while those of short timescale pay more attention to the short-term fluctuations. Therefore, the adjustment range of conditional risks undertaken by the investors of long timescale is certainly greater than that undertaken by the investors of short timescale.

Fig. 4

VaRs of IMFs and residue with EMD–ARMA–EGARCH

Table 3 EMD–ARIMA–EGARCH based VaR failures backtesing

Secondly, the aggregated volatility $\sigma_{\text{agg}}$ is calculated, which is then used to calculate $aggVaR$. The calculated results are reported in Table 3. As indicated in Table 3, the aggVaR passes the test at the significance level of 5%, and therefore is accurate. As shown in Table 4, the proportion that the actual return exceeds aggVaR is 2.74 from April 25, 2005 to February 16, 2015 at the confidence level of 95%, it is far below 5% and z has reach − 5.18. This indicates that the actual return will not surpass the estimated aggVaR for all investigated days.

Table 4 aggVaR with EMD–ARMA–EGARCH

3.3.3 VaR estimation based on EMD–ARMA–EGARCH–EWMA

As shown in Fig. 2, EUA futures return shows violent fluctuations in several trading periods, which means extreme events occur. According to the fluctuations, actual carbon market, Bai–Peeron Test and ICSS algorithm, the trading periods No. 230-282 (March 20, 2006–June 05, 2006), No. 865-1020 (September 10, 2008–April 22, 2009), No. 1666-1790 (October 25, 2011–April 23, 2012), No. 1969-2085 (January 02, 2013–June 17, 2013), and No. 2270-2320 (March 06, 2014–May 19, 2014), are identified as the windows of extreme events. The first three event windows are relevant to information leakage of verified emission in 2006, Financial crisis in 2008, and continuation of the European debt crisis in 2011 respectively. The last two events respectively correspond to the backloading scheme voted against, and passed by the European Parliament. According to the backloading scheme, the allocation of 0.9 billion tons of EUA is expected to be delayed by the end of 2020, so as to alleviate the dilemma of the surplus EUA in carbon market (Morgan 1996). In every event window, breakpoint can be identified by both Bai–Peeron Test and ICSS algorithm. For instance, in the first event window, No. 253 (4/24/2006) is identified as breakpoint by ICSS algorithm and No. 262(5/5/2006) is identified as breakpoint by Bai–Peeron Test.

As discovered in Fig. 3, IMF₁, IMF₂ and IMF₃ exhibit great fluctuations, while the others present little fluctuations in the five event windows. Further analysis shows that, in five event windows, the first three IMFs contribute 99% of increase in $\sigma_{agg}$. Thus, it can be found that the influences of the five extreme events on carbon price are mainly reflected in IMF₁, IMF₂ and IMF₃. Therefore, the ARMA–EGARCH model can be utilized to acquire the conditional standard deviations (CSD) of IMF₁, IMF₂, and IMF₃ within the two event windows. Furthermore, the EWMA method is used to conduct a smooth processing on the obtained CSDs, so as to eliminate the abnormal influences of extreme events on the fluctuations of EUA futures return to some extent and avoid the overestimation of VaRs.

The confidence level is set as $cl = 95\%$. Figure 5 provides the VaRs of IMFs and residue after the two event windows are processed by EWMA, and the corresponding failure backtesting results are reported in Table 5. Therefore, it can be found that all the VaRs of IMFs and Res pass the test at the significance level of 5%, which indicates that all the calculated VaRs are accurate. The $aggVaR$ listed in Tables 5 and 6 as well pass the test at the significance level of 5%, and therefore is proven to be accurate. As shown in Table 5, the proportion that the real return fluctuation exceeds aggVaR is 3.5% during April 25, 2005–February 16, 2015 at the confidence level of 95%. This suggests that the real return fluctuations will not surpass the estimated aggVaR for 96.5% of the investigated days. After EWMA, both the average aggVaR and the Maximum aggVaR decreased, especially the Maximum aggVaR. Therefore, it is concluded that the ARMA–EGARCH–EWMA based VaR can accurately measure the risks of components with different timescales of EUA futures return.

Fig. 5

VaRs of IMFs and residue with EMD–ARMA–EGARCH–EWMA

Table 5 ARMA–EGARCH–EWMA based VaR failures backtesing

Table 6 aggVaR with EMD–ARMA–EGARCH–EWMA

3.4 A comparison of aggVaR before and after being processed by EWMA

The confidence level is set as $cl = 95\%$. Figures 6, 7, 8, 9 and 10 and Table 7 illustrate the comparison of VaRs respectively in the five event windows before and after being processed by EWMA. As displayed in the comparison results, there are 291 days when aggVaR before being processed by EWMA is higher than aggVaR after being processed by EWMA in five event windows, occupying 57.97% (291/502). More specifically, in first four windows, each one have more than half of days, whose aggVaR have decreased after being processed by EWMA, and in the fifth window, the proportion is 47.06%, nearly half. Meanwhile, both the average aggVaR and the Maximum aggVaR decline obviously. For instance, in the event window of March 20, 2006–June 05, 2006, average aggVaR is lowered from 1.529 to 1.184 and Maximum aggVaR is lowered from 4.853 to 2.072, respectively. Thus, it can be found that EWMA smoothing can effectively reduce the overestimated amplitude of VaR caused by extreme events.

Fig. 6

Comparison of aggVaRs before and after EWMA smoothing in the event window of March 20, 2006–June 05, 2006

Fig. 7

Comparison of aggVaRs before and after EWMA smoothing in the event window of September 10, 2008–April 22, 2009

Fig. 8

Comparison of aggVaRs before and after EWMA smoothing in the event window of October 25, 2011–April 23, 2012

Fig. 9

Comparison of aggVaRs before and after EWMA smoothing in the event window of January 2, 2013–June17, 2013

Fig. 10

Comparison of aggVaRs before and after EWMA smoothing in the event window of March 06, 2014–May 19, 2014

Table 7 Comparison of aggVaRs before and after EWMA smoothing in five event windows

3.5 A comparison of VaR based on ARMA–EGARCH without EMD preprocessing

The original carbon price return ln − r is modeled with ARMA–EGARCH (1,1) in Sect. 3.3.1, by which, the VaR of ln − r, namely VaRs based on ARMA–EGARCH without EMD, can be calculated. The results are reported in Table 8. The proportion that the real return fluctuation exceeds aggVaR is 3.90%. Although it passes the failure backtesing, the VaRs are obviously higher than that estimated by EMD–ARMA–EGARCH–VaR and EMD–ARIMA–EGARCH–EWMA–VaR. Moreover, despite higher VaRs, the failure rate is higher than that estimated by EMD–ARMA–EGARCH–VaR (2.74%) and EMD–ARIMA–EGARCH–EWMA–VaR (3.5%). Therefore, it can be concluded that the proposed multiscale VaRs based on EMD is dramatically superior to the traditional single VaRs based on ARMA–EGARCH.

Table 8 Comparison of VaRs by three methods

3.6 A prediction of out-of sample VaRs

In this study, 629 daily transaction prices (20% of all data) from February 17, 2015 to July 28, 2017 are used as the out-of-sample data. During this period, Paris Agreement was negotiated at COP 21 in 2015 and signed later, and U.S. position have changed, both of which may have large impact on carbon prices. Therefore, it is necessary to check these extreme events before prediction. We check the total sample from April 25, 2005 to July 28, 2017(No. 1-3141), with Bai–Peeron Test and ICSS algorithm, however there is no single day that can be identified as breakpoint by either algorithm during period from February 17, 2015 to July 28,2017. The possible reasons are as follows: there are no binding force and no strong mechanism to force any country to set specific target by a specific date in Paris Agreement, and COP21 do not change the downturn situation of carbon market actually; new policy of U.S. have limited impact on European carbon market.

Since there are no structural breakpoints of out-of sample, we only use EMD–ARMA–EGARCH and ARMA–EGARCH to estimate the out-of-sample VaRs, and the obtained results are listed in Table 9. It can be discovered that VaR based on EMD–ARMA–EGARCH passes the failure backtesting at the confidence level of 95%.

Table 9 Comparison between out-of-sample VaRs with EMD–ARMA–EGARCH and ARMA–EGARCH

There are 23 days when the actual return fluctuations surpass the VaRs estimated by EMD–ARMA–EGARCH, accounting 3.66% of the total days, which suggests that the real return fluctuations will not surpass the estimated aggVaR for 96.34% of the investigated days. VaR based on ARMA–EGARCH without EMD fails to pass the failure backtesing at the confidence level of 95%, but succeeds at the confidence level of 90%, where there are 20 days with the actual return fluctuations higher than the VaRs based on ARMA–EGARCH, accounting for 3.18% of the total days. This indicates that the real return fluctuations will not surpass the estimated VaRs based on ARMA–EGARCH for 96.82% of the investigated days.

4 Conclusions

This paper proposes a new modelling of conditional volatility, which dissects the data into sub-samples (intrinsic mode functions or IMFs), which take into consideration different time scales. Then we use the volatility estimates of each IMF to construct an aggregated measure of variance, which is then used to estimate the Value at Risk (VaR) on different time horizons.

We apply this modelling on the European Carbon Futures Market (EU ETS) and find that the new approach provides an estimate of VaR that consistently covers potential losses, even when extreme events are considered. The new approach outperforms the conventional conditional VaR approach with no time-scaling, in terms of number of days that market losses exceed VaR.

As a heterogeneous market, carbon market risk is characterized by multi-timescale and affected by heterogeneous environments. To accurately measure the risk of carbon market, an EMD-based multiscale VaR estimation is proposed for measuring carbon market risk. Taking the European allowance futures price with maturity in December 2015 under the EU ETS as an example, the empirical results demonstrate that the proposed multiscale VaR estimation can achieve a higher precision than the traditional VaR estimation without EMD.

The proposed method can not only accurately measure the overall risk of carbon market, but also capture the distributions of carbon market risks at different timescales. Through the EWMA smooth processing, the proposed method can effectively reduce the influences of heterogeneous environments such as extreme events on the risk of carbon market, so as to avoid the overestimation of VaR and make VaR estimation more objective and accurate.

The proposed method can provide a new perspective for exploring the evolution law of carbon market risk. How to further improve the performance of EMD algorithm and the precision of VaR estimation based on data characteristics of carbon price returns is one of our future tasks.