Analysis and design of low noise transconductance amplifier for selective receiver front-end

Abstract

Analysis and design of a low-noise transconductance amplifier (LNTA) aimed at selective current-mode (SAW-less) wideband receiver front-end is presented. The proposed LNTA uses double cross-coupling technique to reduce noise figure (NF), complementary derivative superposition, and resistive feedback to achieve high linearity and enhance input matching. The analysis of both NF and IIP3 using Volterra series is described in detail and verified by SpectreRF ^® circuit simulation showing NF < 2 dB and IIP3 = 18 dBm at 3 GHz. The amplifier performance is demonstrated in a two-stage highly selective receiver front-end implemented in 65 nm CMOS technology. In measurements the front-end achieves blocker rejection competitive to SAW filters with noise figure 3.2–5.2 dB, out of band IIP3 >+17 dBm and blocker P_1dB >+5 dBm over frequency range of 0.5–3 GHz.

1 Introduction

For a multi-standard radio receiver the wideband RF front-end circuit is essential. It is well known that a low-noise amplifier (LNA) as the first front-end stage largely decides the receiver performance in terms of noise figure (NF) and linearity. With relaxed requirements on RF filters the demands placed on the front-end linearity are usually increased according to intermodulation or cross-modulation effects evoked by strong interferers. While the nonlinear contribution of the following receiver stages is raised by the LNA gain, the overall NF is reduced. As a consequence a reasonable balance between linearity and noise performance of the LNA, mixer, and to some extent the baseband stages must be attained. One possible solution to this problem is a current-mode front-end where LNA is a transconductance amplifier (LNTA) followed by a passive mixer [1–7]. Since current rather than a voltage is applied, the mixer design is simplified and also the effect of 1/f noise is diminished. Most of those designs implement the concept of so called SAW-less front-end making use of N-path filtering [8]. In fact, it is the high output impedance of LNTA that jointly with low impedance of the N-path circuitry enables significant blocker attenuation at offset frequencies. In this case the demands for the input range (up to 0 dBm, i.e. 632 mV_pp), and respectively for the linearity and compression of the LNTA, are exacerbated since the attenuation is achieved at the output rather than at the input of the amplifier. Additionally, such an LNTA is challenged by the requirement of wideband (WB) operation typical of the contemporary multi-band radios.

The LNTA nonlinearity originates from two major sources: nonlinear transconductance which converts linear input voltage to nonlinear output drain current, and nonlinear output conductance, the effect of which is evident under large output voltage swing. The latter can be avoided using a low impedance output load that is usually achieved using a passive mixer followed by a transimpedance amplifier (TIA) [1–6].

Several techniques exist to improve linearity of LNAs [9]. The optimization of gate bias voltages can fairly improve linearity of LNA [10] but it leads to reduced range of the input amplitudes and increased sensitivity to process variation. The WB negative feedback by resistive source degeneration also improves linearity but limits the voltage headroom of the devices and adds extra noise. Superposition of an auxiliary transistor to cancel nonlinearity of the main device, called derivative superposition (DS), extends fairly the linear gain range [11, 12]. Its variant referred to as the complementary DS also improves the second order nonlinearity of the amplifier [13]. More recently, this technique has been also presented in [7, 14, 15]. Unlike DS, in the post-distortion technique (PD) the auxiliary device operates in saturation and is controlled by the output voltage. The PD advantage is in superior PVT robustness as demonstrated e.g. in [16].

Other critical concerns in LNA/LNTA design i.e., the input matching and noise figure (NF) usually cannot be compromised. A popular wideband matching technique exploits the common gate (CG) circuit with its input impedance approximated by the inverse of the front device transconductance (1/g_m). Since in this case g_m is virtually bound to 20 mS, achieving larger effective values of the amplifier transconductance requires an extra amplification stage. To guarantee NF of the CG amplifier below 3 dB extra mechanisms are necessary, such as negative/positive feedback [17, 18], output noise cancellation using an auxiliary amplifier [19] (also called feed forward cancellation), or capacitive cross coupling when a balanced circuit is used [20]. Another WB matching technique providing a low NF is based on the reactive feedback which requires on-chip RF transformers [21].

A combination of a low noise figure with high linearity for wideband LNTA applications in CMOS was presented in [1–6, 13, 22, 23]. In particular, the noise cancelling receiver demonstrated in [4] extends the noise cancelling to the N-path filter/mixer resulting in the superior NF, but it consumes more power than the circuits using conventional noise cancellation [1–3, 5, 6].

In this paper we present analysis and design of LNTA suitable for current-mode wideband front-end with RF N-path filtering in 0.5–3 GHz frequency range. The LNTA design combines two linearization techniques, namely the derivative superposition and resistive feedback, with NF reduction by double capacitive cross-coupling which results in superior noise performance. The resistive feedback also helps to attain good input matching without sacrificing gain of the common gate input stage. By using elevated supply voltage the LNTA can tolerate blockers up to 0 dBm without compression. The mathematical analyses of NF and IIP3 are described in detail and the achieved estimates are verified by SpectreRF ^® simulation. The LNTA is implemented and measured in a two-stage highly selective receiver front-end, integrated using 65 nm CMOS technology [7].

The paper is arranged as follows. In Sect. 2 we derive the LNTA circuit architecture combining various mechanisms to achieve the intended performance. In Sect. 3 we analyze the noise figure and verify the attained estimate by simulation. The Volterra series based analysis of IIP3 and verification is presented in Sect. 4. In Sect. 5 the LNTA implementation as a part of the receiver front-end with RF N-path filtering is presented. Conclusion is provided in the last section.

2 LNTA design

Based on our preliminary work [15], here, we describe the LNTA design in detail, including a complete noise and linearity analysis.

For high linearity we refer to the complementary DS technique, which due to the reusing of current, gives also significant power savings. The complementary common gate (CG) architecture has been preferred over its counterpart, common source (CS) (Fig. 1), for the ease in achieving wideband input matching and low noise figure.

Fig. 1

LNTA complementary DS architectures, a common source, b common gate

By using appropriate bias voltages the nonlinear third order g _m terms can be cancelled providing a high value of IIP3 [13, 14, 22, 24]. In this case the pMOS is an auxiliary transistor with g _m much smaller than that of nMOS. Large off-chip inductors L ₁, L ₂ rather than resistors are used to guarantee maximum bias voltage V _ds and thereby to reduce the g _ds nonlinearity that is increasingly pronounced in deep submicron CMOS.

The input impedance and noise factor for the DS-CG circuit can be estimated from

$$Z_{in} = \frac{1}{{g_{mn} + g_{mp} }}$$

(1)

$$F \cong 1 + \frac{\gamma }{{\alpha \left( {{g_{mn}} + {g_{mp}}} \right){R_{so}}}}$$

(2)

where R _so is the source resistance, γ is the excess channel thermal noise coefficient, and α = g _m /g _d0 , with g _m as the device transconductance and g _d0 as zero-biased channel conductance.

Clearly, for perfect matching we have F ≈ 1 + γ/α. In deep submicron CMOS γ/α > 2/3, and to reduce its effect on F we use a differential (balanced) variant of this circuit where the capacitive cross-coupling technique is adopted [20, 25]. In this case, F can be estimated from

$$F \cong 1 + \frac{\gamma }{{2\alpha }}$$

(3)

according to partial noise cancellation achieved in this circuit. We observe that for γ/α ≈ 1, the expected noise figure is NF = 10log(1.5) ≈ 1.75 dB.

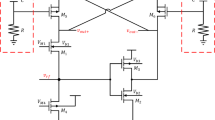
Further noise factor improvement as we proposed in [15] can be achieved by using double capacitive cross-coupling circuit shown in Fig. 2 (to be discussed in detail in Sect. 3).

Fig. 2

Differential LNTA implementing DS and capacitive cross-coupling technique (simplified schematic)

By sizing up the transistors the LNTA transconductance can be increased to some extent, but the input impedance is decreased accordingly and the reflection coefficient S11 is largely deteriorated. One solution to mitigate this tradeoff is based on the source degeneration technique. Acting as a local negative feedback it additionally improves circuit linearity. With a resistance R _sn as shown in Fig. 3 the LNTA input impedance can be restored as demonstrated by (4) for the n-MOS part of the circuit. Knowing that g _m /C _gs  = 2πf _T where f _T  ≈ 100 GHz, for simplicity we can assume ωC _gs /g _m  = f /f _T  ≈ 0. Then for the nMOS part of the circuit we find

Fig. 3

S11 and linearity improvement by resistive source degeneration

$$Z_{{in}}^{{(n)}} \cong \frac{{1 + Z_{L} Y_{{dsn}} + R_{{sn}} \left( {g_{{mn}} + Y_{{dsn}} } \right)}}{{g_{{mn}} + Y_{{dsn}} /2}}$$

(4)

where Y _dsn is the drain-source admittance and Z _L is the loading impedance while the inductor reactance goes to infinity. A similar formula can be derived for the pMOS part (Z ^(p) _in ) and assuming the drain-source admitances are small enough we find the LNTA input impedance as Z ^(p) _in ‖Z ⁽ⁿ⁾ _in .The LNTA transconductance is inversely proportional to Z _in that is

$$G_{m} = \frac{1}{{Z_{{in}}^{{(p)}} (\omega )}} + \frac{1}{{Z_{{in}}^{{(n)}} (\omega )}}$$

(5)

Hence, there is a tradeoff between the input matching and LNTA gain. For perfect matching no increase in G _m is achieved. In practice, however, the requirement is S11 < −10 dB. To meet this condition the corresponding boundaries of Z _in can be found: $Z_{in} \in \left( {0.67,\;{\kern 1pt} 2} \right)\,R_{so}$, where R _so is the matching resistance. In an extreme case, when Z _in  = 2R _so and R _s  = 0 we have G _m  ≈ 2/2R _so . Next, the transistors are sized up and by using R _s we obtain Z _in  = 0.67R _so with the corresponding G _m  ≈ 3/R _so . This means 3× increase in G _m (9.5 dB) is feasible while S11 = −10 dB. Clearly, larger values of R _s should be avoided here to preserve a sufficient V _ds voltage headroom. Also the noise factor is traded for S11 as the R _s resistors add noise. Moreover, when the loading impedance Z _L is selective (as for N-path filters), its impedance goes down at offset frequencies and the input impedance (4) is reduced accordingly providing thereby attenuation of blockers at the amplifier input.

The proposed final LNTA circuit, designed in 65 nm CMOS is shown in Fig. 4. It combines the discussed above techniques to achieve high linearity and a low noise figure over a wide frequency range. Four off-chip inductors providing reactance of a few hundred Ohms each are large enough to guarantee S11 < −10 dB also at lower frequencies. Similarly, the coupling capacitances C _s  > 10 pF should be chosen (X _s  < 2 Ω) to avoid reduction of LNTA transconductance gain. Four of them (connected to transistor gates) must be integrated at the expense of the silicon area overhead. After choosing the bias voltages (to be discussed in Sec. IV) and the output DC equal to VDD/2 the sizes of the MOS transistors Mp, Mn were chosen to achieve the best third-order g _m cancellation with 29 μm/65 nm and 48 μm/65 nm, respectively. The source degeneration resistors providing correction of S11 are R _sp  = 17 Ω and R _sn  = 111 Ω.

Fig. 4

Circuit schematic of proposed wideband LNTA

3 LNTA noise analysis

The circuit model for noise analysis is shown in Fig. 5. In each half of the circuit there are five noise sources to be considered: v _ns (source noise), v _nM1 (of M1), v _nM3 (of M3), v _nRsp (of R _sp ) and v _nRsn (of R _sn ), using the following equations

$$\begin{aligned} v_{{_{ns} }}^{2} &= 4kTR_{so} , \\ v_{{_{nM1} }}^{2} &= \frac{{4kT\gamma_{1} }}{{\alpha_{1} g_{m1} }},\;v_{{_{nM3} }}^{2} = \frac{{4kT\gamma_{3} }}{{\alpha_{3} g_{m3} }}, \\ v_{{_{nRsn} }}^{2}& = 4kTR_{sn} ,\;v_{{_{nRsp} }}^{2} = 4kTR_{sp} ,\\ \end{aligned}$$

(6)

where k is Boltzmann’s constant, T is the absolute temperature in Kelvin. The differential noise current at the output i _{n_out} = i _y − i _x can calculated using superposition principle. In particular for v _ns the currents i ₁,…, i ₄ as shown in Fig. 5 can be found as

$$i_{{1,\,3}} = \left( {\nu _{y} - \nu _{x} } \right)g_{{m1,\,3t}} ,\quad i_{{2,\,4}} = \left( {\nu _{y} - \nu _{x} } \right)g_{{m2,\,4t}},$$

(7)

with $g_{m1,2t} = \frac{1}{{R_{sn} \left( {1 + \frac{{sC_{gsn} }}{{g_{m1,2} }}} \right) + \frac{1}{{g_{m1,2} }}}}$

$$g_{m3,4t} = \frac{1}{{R_{sp} \left( {1 + \frac{{sC_{sgp} }}{{g_{m3,4} }}} \right) + \frac{1}{{g_{m3,4} }}}}$$

(8)

Fig. 5

LNTA circuit for noise analysis

Using Kirchhoff’s Voltage Law (KVL) for the loop from v _x to v _y through v _ns and Kirchhoff’s Current Law (KCL) at nodes v _x , v _y we have

$$\begin{aligned} v_{x} - v_{y} &= v_{ns} + R_{so} \left[ {i_{1} \left( {1 + \frac{{2sC_{gsn} }}{{g_{m1} }}} \right) + i_{3} \left( {1 + \frac{{2sC_{sgp} }}{{g_{m3} }}} \right)} \right] \\ &\quad -\, R_{so} \left[ {i_{2} \left( {1 + \frac{{2sC_{gsn} }}{{g_{m2} }}} \right) + i_{4} \left( {1 + \frac{{2sC_{sgp} }}{{g_{m4} }}} \right)} \right] \hfill \\ \end{aligned}$$

(9)

Substituting (7) into (9), the voltage of v _x  − v _y can be found as

$$v_{x} - v_{y} = \frac{{v_{ns} }}{{1 + R_{so} \sum\nolimits_{k = 1}^{4} {g_{mktz} } }}$$

(10)

with $g_{m1,2tz} = g_{m1,2t} \left( {1 + \frac{{2sC_{gsn} }}{{g_{m1,2} }}} \right)$,

$$g_{m3,4tz} = g_{m3,4t} \left( {1 + \frac{{2sC_{sgp} }}{{g_{m3,4} }}} \right)$$

(11)

The output differential noise current i _{ns_out}  = i _y  − i _x due to noise source of v _ns can be calculated as

$$i_{ns\_out} = \frac{{ - v_{ns} \sum\nolimits_{k = 1}^{4} {g_{mkt} } }}{{1 + R_{so} \sum\nolimits_{k = 1}^{4} {g_{mktz} } }}$$

(12)

With similar procedure, we can calculate the output differential noise currents i _{nM1_out} , i _{nM3_out} , i _{nRsp_out} , i _{nRsn_out} due to v _nM1, v _nM3, v _nRsp and v _nRsn respectively

$$\begin{aligned} i_{nM3\_out} &= \frac{{ - R_{so} v_{nM3} \left[ {g_{m3tz} \left( {1 + R_{sp} sC_{sgp} } \right) - 2sC_{sgp} } \right]\sum\nolimits_{k = 1}^{4} {g_{mkt} } }}{{1 + R_{so} \sum\nolimits_{k = 1}^{4} {g_{mktz} } }} \\& \quad + \, v_{nM3} g_{m3t} \left( {1 + R_{sp} sC_{sgp} } \right) \hfill \\ \end{aligned}$$

(13)

$$\begin{aligned} i_{nM1\_out} &= \frac{{ - R_{so} v_{nM1} \left[ {g_{m1tz} \left( {1 + R_{sn} sC_{gsn} } \right) - 2sC_{gsn} } \right]\sum\nolimits_{k = 1}^{4} {g_{mkt} } }}{{1 + R_{so} \sum\nolimits_{k = 1}^{4} {g_{mktz} } }} \\ & \quad + \, v_{nM1} g_{m1t} \left( {1 + R_{sn} sC_{gsn} } \right) \hfill \\ \end{aligned}$$

(14)

$$i_{nRsn\_out} = \frac{{R_{so} v_{nRsn} g_{m1t} \left( {1 + \frac{{2sC_{gsn} }}{{g_{m1} }}} \right)\sum\nolimits_{k = 1}^{4} {g_{mkt} } }}{{1 + R_{so} \sum\nolimits_{k = 1}^{4} {g_{mktz} } }} - v_{nRsn} g_{m1t}$$

(15)

$$i_{nRsp\_out} = \frac{{R_{so} v_{nRsp} g_{m3t} \left( {1 + \frac{{2sC_{sgp} }}{{g_{m3} }}} \right)\sum\nolimits_{k = 1}^{4} {g_{mkt} } }}{{1 + R_{so} \sum\nolimits_{k = 1}^{4} {g_{mktz} } }} - v_{nRsp} g_{m3t}$$

(16)

The same noise contribution will be achieved from the other half of the circuit. The noise factor (F) and noise figure (NF) will be calculated based on (12–16) as

$$F = \frac{{2i_{ns\_out}^{2} + 2i_{nM1\_out}^{2} + 2i_{nM3\_out}^{2} + 2i_{nRsn\_out}^{2} + 2i_{nRsp\_out}^{2} }}{{2i_{ns\_out}^{2} }}$$

(17)

$$NF = 10\log_{10} (F)$$

(18)

In order to compare NF of the proposed circuit to the one with conventional cross-coupling, the equivalent circuit can be simplified by ignoring the gate-source capacitances. The noise factor in this case will be

$$\begin{aligned} F &= 1 + \frac{{\gamma_{1} g_{{_{m1t} }}^{2} }}{{\alpha_{1} g_{m1} R_{so} \left( {\sum\nolimits_{k = 1}^{4} {g_{mkt} } } \right)^{2} }} + \frac{{\gamma_{3} g_{{_{m3t} }}^{2} }}{{\alpha_{3} g_{m3} R_{so} \left( {\sum\nolimits_{k = 1}^{4} {g_{mkt} } } \right)^{2} }} \\& \quad \, + \frac{{g_{m1t}^{2} }}{{\left( {\sum\nolimits_{k = 1}^{4} {g_{mkt} } } \right)^{2} }}\frac{{R_{sn} }}{{R_{so} }} + \frac{{g_{m3t}^{2} }}{{\left( {\sum\nolimits_{k = 1}^{4} {g_{mkt} } } \right)^{2} }}\frac{{R_{sp} }}{{R_{so} }} \hfill \\ \end{aligned}$$

(19)

The input impedance of the differential circuit ideally should be Z _in  = 2R _so . Then for matching we need

$$Z_{in} = 2R_{so} = \frac{2}{{\sum\nolimits_{k = 1}^{4} {g_{mkt} } }}$$

(20)

For brevity we can assume that the differential circuit is perfectly balanced having the same γ, α values for all transistors. Then (19) can be simplified to

$$F = 1 + \frac{{\gamma \left( {\frac{{g_{{_{m1t} }}^{2} }}{{g_{m1} }} + \frac{{g_{{_{m3t} }}^{2} }}{{g_{m3} }}} \right)}}{{4\alpha R_{so} (g_{m1t} + g_{m3t} )^{2} }} + \frac{{\left( {R_{sn} g_{{_{m1t} }}^{2} + R_{sp} g_{{_{m3t} }}^{2} } \right)}}{{4R_{so} (g_{m1t} + g_{m3t} )^{2} }}$$

(21)

It should be noted that the double cross-coupling results in ¼ coefficient for the (γ/α) contribution as compared to ½ for the traditional cross-coupling. Moreover, the noise factor contribution by the source degeneration resistors (the 3rd term in (21)) appears less than the one by transistors for (γ/α) > 1. A comparison between NF of the proposed circuit and the conventional one (3) for g _m1 = g _m2 = 30 mS, g _m3 = g _m4 = 13.6 mS, R _so  = 50 Ω, R _sn  = 111 Ω, R _sp  = 17 Ω, is shown in Table 1. With technology scaling the ratio (γ/α) is increasingly large so the NF improvement is more pronounced. For example with (γ/α) = 1.5 the proposed LNTA can improve NF from 2.43 dB down to 1.34 dB.

Table 1 NF versus (γ/α) comparison of (3) and (21)

The NF comparison of the presented analytical model and SpectreRF^® circuit simulation including the gate-source capacitances according to (12-16) is shown in Fig. 6. In this verification we use specifications captured from the designed chip: g _m1 = g _m2 = 30 mS, g _m3 = g _m4 = 13.6 mS, R _so  = 50 Ω, R _sp  = 17.2 Ω, R _sn  = 110.8 Ω, C _gsn  = 30 fF, C _gsp  = 20 fF. As seen the respective differences remain within 0.08 dB that can be considered negligible.

Fig. 6

NF comparison of analytical model (12–18) and SpectreRF^® circuit simulation for proposed LNTA (transistor level)

4 Linearity analysis using Volterra Series

The simulation environment using a conventional inverter, here, also considered as common-source complementary DS circuit, with output bias voltage was proposed in [13] as shown in Fig. 7(a). This circuit can achieve high linearity due to subtraction of the nonlinear current components of the transistors M _p and M _n . Both the second and third order terms can be partly cancelled if the circuit is appropriately biased. However, the useful input range is very narrow as shown for g ₃ in Fig. 7(b) where g ₃ = ∂³ i _o /∂(V _in )³. In effect the possible blockers are not well tolerated by this circuit, still resulting in significant distortion.

Fig. 7

a Schematic of conventional inverter, b Simulation of third-order transconductances of PMOS g _3p , NMOS g _3n and output g ₃

A possible way to overcome this problem is using different bias voltages for M _p and M _n in combination with the resistive source degeneration applied to the both transistors as presented in Fig. 8(a) [15]. In Fig. 8(b), the input voltage range can be significantly increased comparing the previous case in Fig. 7(b). The combined g ₃ is less than its components g _n3 and g _p3 in the operating range as seen in the zoom view. Moreover, it should be noted that R _sp is much less than R _sn in order to maintain the output bias voltage at V _dd /2 while M _n is larger than M _p . Should we increase the size of M _p and the resistance of R _sp , the effective g ₃ would be less, but its range would shrink degrading the linearity for large blockers.

Fig. 8

a Schematic of resistive-feedback technique, b Simulation of third-order transconductances of PMOS g _3p , NMOS g _3n and output g ₃

The following analysis aims at describing IIP3 and third-order gain H ₃ of LNTA using the Volterra series approach. Figure 9 shows the small-signal model for linearity analysis where the differential circuits are assumed to be identical for simplicity. The drain current of M _p and M _n can be modelled up to 3rd-order as

$$i_{dp} = g_{1p} v_{sgp} + g_{2p} v_{sgp}^{2} + g_{3p} v_{sgp}^{3}$$

(22)

$$i_{dn} = g_{1n} v_{gsn} + g_{2n} v_{gsn}^{2} + g_{3n} v_{gsn}^{3}$$

(23)

where g _ip and g _in are the ith-order coefficients of M _p and M _n , accordingly, obtained by taking the derivative of the drain DC current I _SD /I _DS with respect to the gate-source voltage V _SG /V _GS at the DC bias point

$$g_{1p} = \frac{{\partial I_{SDP} }}{{\partial V_{SGP} }},g_{1n} = \frac{{\partial I_{DSN} }}{{\partial V_{GSN} }}$$

(24)

$$g_{2p} = \frac{1}{2!}\frac{{\partial^{2} I_{SDP} }}{{\partial V_{SGP}^{2} }},g_{2n} = \frac{1}{2!}\frac{{\partial^{2} I_{DSN} }}{{\partial V_{GSN}^{2} }}$$

(25)

$$g_{3p} = \frac{1}{3!}\frac{{\partial^{3} I_{SDP} }}{{\partial V_{SGP}^{3} }},g_{3n} = \frac{1}{3!}\frac{{\partial^{3} I_{DSN} }}{{\partial V_{GSN}^{3} }}$$

(26)

Fig. 9

Equivalent circuit of a proposed wideband LNTA

Applying the Volterra series to the output voltage

$$v_{outn} = G_{1} \circ v_{in} + G_{2} \circ v_{in}^{2} + G_{3} \circ v_{in}^{3}$$

(27)

$$v_{in} = A_{1} \circ v_{so} + A_{2} \circ v_{so}^{2} + A_{3} \circ v_{so}^{3}$$

(28)

$$v_{out} = H_{1} \circ v_{so} + H_{2} \circ v_{so}^{2} + H_{3} \circ v_{so}^{3}$$

(29)

where v _in  = v _inp  − v _inn and v _out  = v _outp  − v _outn . If circuits are completely symmetric v _out can be calculated as

$$v_{outp} = - G_{1} \circ v_{in} + G_{2} \circ v_{in}^{2} - G_{3} \circ v_{in}^{3}$$

(30)

$$v_{out} = - 2G_{1} \circ v_{in} - 2G_{3} \circ v_{in}^{3}$$

(31)

From (27) and (57) from Appendix 1, we have

$$G_{1} = \frac{{ - \hat{Z}_{L} \left\{ {\frac{{\left( {g_{1p} + \frac{1}{{r_{dp} }}} \right)n_{p} }}{{\left( {1 + k_{p} } \right)m_{p} }} + \frac{{\left( {g_{1n} + \frac{1}{{r_{dn} }}} \right)n_{n} }}{{\left( {1 + k_{n} } \right)m_{n} }}} \right\}}}{{\eta_{L} }}$$

(32)

$$G_{2} = \frac{{\hat{Z}_{L} \left\{ {\frac{{g_{2p} G_{1p}^{2} }}{{\left( {1 + k_{p} } \right)^{3} m_{p}^{2} }} - \frac{{g_{2n} G_{1n}^{2} }}{{\left( {1 + k_{n} } \right)^{3} m_{n}^{2} }}} \right\}}}{{\eta_{L} }}$$

(33)

$$\begin{aligned} G_{3} &= \frac{{\frac{{\hat{Z}_{L} G_{1p} }}{{\left( {1 + k_{p} } \right)^{3} m_{p}^{2} }}\left\{ {2g_{2p} \frac{{R_{sp} }}{{r_{dp} }}G_{2} + \frac{{G_{1p}^{2} }}{{\left( {1 + k_{p} } \right)m_{p} }}\left[ {g_{3p} - \frac{{2R_{sp} g_{2p}^{2} }}{{\left( {1 + k_{p} } \right)m_{p} }}} \right]} \right\}}}{{\eta_{L} }} \\& \quad \frac{{ - \frac{{\hat{Z}_{L} G_{1n} }}{{\left( {1 + k_{n} } \right)^{3} m_{n}^{2} }}\left\{ {2g_{2n} \frac{{R_{sn} }}{{r_{dn} }}G_{2} + \frac{{G_{1n}^{2} }}{{\left( {1 + k_{n} } \right)m_{n} }}\left[ {g_{3n} - \frac{{2R_{sn} g_{2n}^{2} }}{{\left( {1 + k_{n} } \right)m_{n} }}} \right]} \right\}}}{{\eta_{L} }} \hfill \\ \end{aligned}$$

(34)

where

$$\eta_{L} = 1 - \hat{Z}_{L} \left\{ {\frac{{\left( {g_{1p} + \frac{1}{{r_{dp} }}} \right)R_{sp} }}{{\left( {1 + k_{p} } \right)m_{p} r_{dp} }} + \frac{{\left( {g_{1n} + \frac{1}{{r_{dn} }}} \right)R_{sn} }}{{\left( {1 + k_{n} } \right)m_{n} r_{dn} }}} \right\}$$

(35a)

$$G_{1p} = - n_{p} + \frac{{R_{sp} }}{{r_{dp} }}G_{1} ,G_{1n} = n_{n} - \frac{{R_{sn} }}{{r_{dn} }}G_{1}$$

(35b)

Substituting (59–64), (45), (51–55), (22–23) into (58) and comparing with (28), we can find A ₁, A ₂ and A ₃

$$A_{1} = \frac{1}{{1 + 2R_{so} \left\{ {\frac{1}{2}\left( {\frac{1}{{sL_{p} }} + \frac{1}{{sL_{n} }} - \frac{1}{{r_{dp} }} - \frac{1}{{r_{dn} }}} \right) + G_{1} \left( {\frac{1}{{r_{dp} }} + \frac{1}{{r_{dn} }}} \right) + G_{1p} \left[ {\frac{{ - 2sC_{gsp} - \frac{1}{{r_{dp} }} + \frac{{m_{p} }}{{R_{sp} }}}}{{\left( {1 + k_{p} } \right)m_{p} }} - \frac{1}{{R_{sp} }}} \right] + G_{1n} \left[ {\frac{{2sC_{gsn} + \frac{1}{{r_{dn} }} - \frac{{m_{n} }}{{R_{sn} }}}}{{\left( {1 + k_{n} } \right)m_{n} }} + \frac{1}{{R_{sn} }}} \right]} \right\}}}$$

(36)

$$A_{2} = 2R_{so} A_{1}^{3} \left\{ {\frac{{R_{sp} g_{2p} }}{{\left( {1 + k_{p} } \right)^{3} m_{p}^{3} }}\left( {\frac{1}{{r_{dp} }} - \frac{{m_{p} }}{{R_{sp} }}} \right)\left( { - n_{p} + \frac{{R_{sp} }}{{r_{dp} }}G_{1} } \right)^{2} - \frac{{R_{sn} g_{2n} }}{{\left( {1 + k_{n} } \right)^{3} m_{n}^{3} }}\left( {\frac{1}{{r_{dn} }} - \frac{{m_{n} }}{{R_{sn} }}} \right)\left( {n_{n} - \frac{{R_{sn} }}{{r_{dn} }}G_{1} } \right)^{2} } \right\}$$

(37)

$$\begin{aligned} A_{3}& = 2R_{so} A_{1}^{2} \frac{{sC_{gsp} }}{{\left( {1 + k_{p} } \right)^{{}} m_{p}^{{}} }}\left\{ {\left[ {\frac{{R_{sp} }}{{r_{dp} }}G_{3} A_{1}^{2} - \frac{{2A_{2}^{{}} R_{sp} g_{2p} }}{{\left( {1 + k_{p} } \right)^{2} m_{p}^{2} }}G_{1p}^{2} } \right] + \frac{{R_{sp} A_{1}^{2} }}{{\left( {1 + k_{p} } \right)^{3} m_{p}^{3} }}\left[ {\left( {\frac{{2g_{2p}^{2} R_{sp} }}{{\left( {1 + k_{p} } \right)^{{}} m_{p}^{{}} }} - g_{3p} } \right)G_{1p}^{3} } \right]} \right\} \\&\quad -\, 2R_{so} A_{1}^{2} \frac{{\left( {sC_{gsp} + \frac{1}{{r_{dp} }} - \frac{{m_{p} }}{{R_{sp} }}} \right)}}{{\left( {1 + k_{p} } \right)^{{}} m_{p}^{{}} }}\left\{ {\left[ {\frac{{ - R_{sp} }}{{r_{dp} }}G_{3} A_{1}^{2} - \frac{{2A_{2}^{{}} R_{sp} g_{2p} }}{{\left( {1 + k_{p} } \right)^{2} m_{p}^{2} }}G_{1p}^{2} } \right] - \frac{{R_{sp} A_{1}^{2} }}{{\left( {1 + k_{p} } \right)^{3} m_{p}^{3} }}\left[ {\left( {\frac{{2g_{2p}^{2} R_{sp} }}{{\left( {1 + k_{p} } \right)^{{}} m_{p}^{{}} }} - g_{3p} } \right)G_{1p}^{3} } \right]} \right\} \\& \quad -\, 2R_{so} A_{1}^{2} \frac{{sC_{gsn} }}{{\left( {1 + k_{n} } \right)^{{}} m_{n}^{{}} }}\left\{ {\left[ {\frac{{ - R_{sn} }}{{r_{dn} }}G_{3} A_{1}^{2} - \frac{{2A_{2}^{{}} R_{sn} g_{2n} }}{{\left( {1 + k_{n} } \right)^{2} m_{n}^{2} }}G_{1n}^{2} } \right] + \frac{{R_{sn} A_{1}^{2} }}{{\left( {1 + k_{n} } \right)^{3} m_{n}^{3} }}\left[ {\left( {\frac{{2g_{2n}^{2} R_{sn} }}{{\left( {1 + k_{n} } \right)^{{}} m_{n}^{{}} }} - g_{3n} } \right)G_{1n}^{3} } \right]} \right\} \\& \quad +\, 2R_{so} A_{1}^{2} \frac{{\left( {sC_{gsn} + \frac{1}{{r_{dn} }} - \frac{{m_{n} }}{{R_{sn} }}} \right)}}{{\left( {1 + k_{n} } \right)^{{}} m_{n}^{{}} }}\left\{ {\left[ {\frac{{R_{sn} }}{{r_{dn} }}G_{3} A_{1}^{2} - \frac{{2A_{2}^{{}} R_{sn} g_{2n} }}{{\left( {1 + k_{n} } \right)^{2} m_{n}^{2} }}G_{1n}^{2} } \right] - \frac{{R_{sn} A_{1}^{2} }}{{\left( {1 + k_{n} } \right)^{3} m_{n}^{3} }}\left[ {\left( {\frac{{2g_{2n}^{2} R_{sn} }}{{\left( {1 + k_{n} } \right)^{{}} m_{n}^{{}} }} - g_{3n} } \right)G_{1n}^{3} } \right]} \right\} \\ \end{aligned}$$

(38)

If two single-ended circuits are identical, we substitute (28, 29) into (31) and have

$$H_{1} (\omega_{1} ) = -2G_{1}(\omega_{1} )A_{1} (\omega_{1} )$$

(39)

$$H_{2} (\omega_{1} ,\,\omega_{2}) = -2G_{1}(\omega_{1} \pm \omega_{2} )A_{2} (\omega_{1},\omega_{2} )$$

(40)

$$\begin{aligned} H_{3} (\omega_{1} ,\omega_{2} ,\omega_{3} ) &= - 2\left[ {G_{1} (\omega_{1} \pm \omega_{2} \pm \omega_{3} )A_{3} (\omega_{1} ,\omega_{2} ,\omega_{3} )} \right. \\& \quad +\, \left. {G_{3} (\omega_{1} ,\omega_{2} ,\omega_{3} )A_{1}^{3} (\omega_{1} \pm \omega_{2} \pm \omega_{3} )} \right] \\ \end{aligned}$$

(41)

From [16, 23], IIP3 can be estimated as

$$IIP_{3,dBm} = 20\log_{10} \left( {\sqrt {\left| {\frac{4}{3}\frac{{H_{1} (\omega_{1} )}}{{H_{3} (\omega_{1} ,\omega_{2} ,\omega_{3} )}}} \right|} } \right) + 10$$

(42)

DS technique has been used to cancel the third-order transconductance distortion g ₃ well [9] but the operating range of input voltage V _gs is not wider than 200 mV. In this design, we propose a technique that can cancel the third-order voltage gain (41) in larger operating range up to 650 mV shown in Fig. 10. From that figure, the bias voltages can be chosen as V_gsn = 570 mV and V_sgp = V_gsn + 190 mV = 760 mV. Therefore IIP3 of LNTA is not sensitive to the bias voltages and can tolerate large blockers up to 0 dBm.

Fig. 10

The third-order voltage gain H ₃ (41) versus the bias voltage V _gsn

The IIP3 obtained by the Volterra series model (42) and by SpectreRF™ simulations are depicted in Fig. 11 for two RF frequencies with the following parameters g _1n  = 30 mS, g _1p  = 13.6 mS, g _2n  = 57 (mA/V²), g _2p  = 8.2 (mA/V²), g _3n  = −70.3 (mA/V³), g _3p  = −9.6 (mA/V³), r _dn  = 339 Ω, r _dp  = 843 Ω at VDD = 2.5 V with R _so  = 50 Ω, L _p  = 30 nH, L _n  = 70 nH, R _sp  = 17.2 Ω, R _sn  = 110.8 Ω, C _gsn  = 30 fF, C _gsp  = 20 fF.

Fig. 11

IIP3 comparison of analytical expression (42) and SpectreRF^® simulation for LNTA, using two-tone 40 MHz spacing (transistor level)

As shown, IIP3 is rising with the loading capacitance due to the reduced output voltage swing. For the same reason larger IIP3 values are attained at the higher operating frequency. It should be noted that the increment of IIP3 for C _load increased from 0.2 pF to 1 pF (5×) at f _RF  = 520 MHz is almost the same as the one achieved for the frequency change from 520 MHz to 3 GHz (~5× as well) for C _load  = 0.2 pF.

In post-layout simulation with pad and bonding wire parasitics the IIP3 estimate at f _RF  = 3 GHz with 40 MHz spacing is reduced by 4 dB, i.e. from 22 dBm at transistor level to 18 dBm for 2.5 V supply. The Monte-Carlo post-layout simulation under process variation with fixed bias is shown in Fig. 12. The mean value is 17.9 dBm while the standard variation is only 0.24 dB. To see the separate contributions to IIP3 by the different mechanisms used we found IIP3 to be reduced by 3 dB, down to 15 dBm, for supply voltage changed to the standard value, 1.2 V. The circuit will lose 6 dB more when the derivative superposition technique is excluded resulting in IIP3 = 9 dBm. Finally, by removing the resistive degeneration, IIP3 = 5 dBm is attained.

Fig. 12

Monte-Carlo simulation of LNTA IIP3 obtained with 50 iterations at f _RF  = 3 GHz, 40 MHz spacing, C _L  = 1 pF

Using a linear model also the LNTA transconductance estimate can be verified against the analytical model (5). From simulations over the operating frequency range with Z _L  ≪ r _ds , G _m varying between 17 and 17.7 mS can be found whereas from (5) it is around 18 mS. To reduce the effect of r _ds on G _m in this simulation a larger C _L  = 4 pF has been chosen.

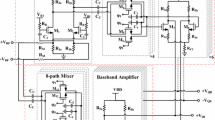
5 Implementation of a selective receiver front-end

The proposed LNTA is used in a selective two-stage RF front-end [7] shown in Fig. 13. In order to tolerate blockers up to 0 dBm (632 mV_pp) we have used elevated supply voltage of 2.5 V for LNTA1 and the standard supply of 1.2 V for the LNTA2. To prevent loading of the first stage, which could degrade the filter transfer function, a simple CMOS buffer is added in front of LNTA2 as shown in Fig. 14. The schematic topology of LNTA2 is similar to LNTA1 except for the values of bias voltages, resistances and sizes of transistors. The design was fabricated in 65 nm CMOS technology and the chip photo is shown in Fig. 15. A significant portion of the chip area is occupied by the banks of baseband capacitors C _BB , which allow for bandwidth programming. The maximum power consumption at 3 GHz amounts for 113 mW and it drops to 46 mW at 0.5 GHz.

Fig. 13

Architecture of selective two-stage RF front-end

Fig. 14

Circuit schematic of LNTA2

Fig. 15

Chip photo [7]

With N-path filter as a load the LNTA noise figure is raised by approximately 1 dB that can be attributed to noise folding as devised in [7]. In effect, the two-stage front-end NF varies between 3.2 dB and 5.2 dB for frequencies between 500 MHz and 3 GHz, respectively. The NF at 2 GHz under 0 dBm blocker with 100 MHz offset is 12 dB that is below the 3GPP limit. Similarly, the in-band IIP3 is only less than 0 dBm due to large loading impedance (large voltage swing). On the contrary, the out-of-band IIP3 is as large as +20 dBm in the lower frequency range and +17 dB at 3 GHz. Additionally, superior blocker rejection of 44 dB is attained for frequencies up to 2 GHz and 38 dB at 3 GHz owing to the two-stage filtering [7]. Measured S11 for different LO frequencies is shown in Fig. 16. Within the whole frequency range 0.5–3 GHz, S11 is below −10 dB in the bandwidth of interest.

Fig. 16

Measured S₁₁ around LO frequencies for C _BB  = 40 pF

A comparison of the state-of-the-art and the presented LNTA design as well as the respective RF front-end based on N-path filtering is given in Table 2. In simulations the stand-alone amplifier compares favorably to the other work. Clearly, the LNTA design is critical for the performance of the measured front-end which, while superior in terms of blocker rejection, can be found well in line with the remaining state-of-the-art specifications.

Table 2 Performance comparison

6 Conclusions

In this paper we have presented LNTA design suitable for current-mode wideband front-end in CMOS technology. The amplifier architecture has been derived from the common gate circuit making use of complementary DS technique, which enables highly linear amplification. The tradeoff between the input matching and the transconductance of transistors (g _m ) has been mitigated by resistive source degeneration. As a negative feedback it also supported the amplifier linearity. On the other hand, a suitable impedance mismatch at the input was useful to achieve a larger amplifier gain (G _m ).

Superior noise performance has been attained by the double capacitive cross-coupling technique in a differential setup as proposed in this work. In effect, the LNTA compares favorably with the state-of-the-art designs both in terms of NF and linearity.

We have presented a complete NF analysis and Volterra series based IIP3 analysis of the amplifier. The obtained estimates were shown compliant with the circuit simulation results. The LNTA was implemented in 65 nm CMOS as a part of a tunable RF front-end using two-stage N-path filtering technique that provided blocker rejection competitive to SAW filters. Owing to the LNTA design the front-end linearity and noise performance have been placed well in line with the state-of-the-art.

Appendices

Appendix 1: Derivation of the Volterra operators for the proposed LNTA: G1, G2 and G3

For the circuit shown in Fig. 9 the respective currents and voltages can be expressed as

$$v_{sgp} = \frac{{ - n_{p} v_{in} - R_{sp} (i_{dp} - \frac{{v_{outn} }}{{r_{dp} }})}}{{m_{p} }}$$

(43)

$$v_{gsn} = \frac{{n_{n} v_{in} - R_{sn} (i_{dn} + \frac{{v_{outn} }}{{r_{dn} }})}}{{m_{n} }}$$

(44)

$$v_{sp} = v_{sgp} + \frac{{v_{in} }}{2},v_{sn} = \frac{{v_{in} }}{2} - v_{gsn}$$

(45)

$$v_{outn} = k_{loadn} (i_{dp} - i_{dn} + \frac{{v_{sp} }}{{r_{dp} }} + \frac{{v_{sn} }}{{r_{dn} }})$$

(46)

where

$$m_{p} = 1 + R_{sp} (C_{gsp} s + \frac{1}{{r_{dp} }}),m_{n} = 1 + R_{sn} (C_{gsn} s + \frac{1}{{r_{dn} }})$$

(47)

$$n_{p} = 1 + \frac{{R_{sp} }}{{2r_{dp} }},n_{n} = 1 + \frac{{R_{sn} }}{{2r_{dn} }}$$

(48)

$$k_{p} = \frac{{g_{1p} R_{sp} }}{{m_{p} }},k_{n} = \frac{{g_{1n} R_{sn} }}{{m_{n} }}$$

(49)

$$\hat{Z}_{L} = \frac{{Z_{L} }}{{1 + Z_{L} (\frac{1}{{r_{dp} }} + \frac{1}{{r_{dn} }})}}$$

(50)

Substituting (22, 23) into (43, 44) with maximum 3rd order of v _in , we have

$$v_{sgp}^{3} = \frac{{B_{p}^{3} }}{{m_{p}^{3} (1 + k_{p} )^{3} }},v_{gsn}^{3} = \frac{{B_{n}^{3} }}{{m_{n}^{3} (1 + k_{n} )^{3} }}$$

(51)

$$v_{sgp}^{2} = \frac{{B_{p}^{2} }}{{m_{p}^{2} (1 + k_{p} )^{2} }}\left( {1 - \frac{{2R_{sp} g_{2p} B_{p} }}{{m_{p}^{2} (1 + k_{p} )^{2} }}} \right)$$

(52)

$$v_{gsn}^{2} = \frac{{B_{n}^{2} }}{{m_{n}^{2} (1 + k_{n} )^{2} }}\left( {1 - \frac{{2R_{sn} g_{2n} B_{n} }}{{m_{p}^{2} (1 + k_{p} )^{2} }}} \right)$$

(53)

$$v_{sgp}^{{}} = \frac{1}{{m_{p}^{{}} (1 + k_{p} )^{{}} }}\left\{ {B_{p}^{{}} - \frac{{R_{sp} g_{2p} B_{p}^{2} }}{{m_{p}^{2} (1 + k_{p} )^{2} }}\left( {1 - \frac{{2R_{sp} g_{2p} B_{p} }}{{m_{p}^{2} (1 + k_{p} )^{2} }}} \right) - \frac{{R_{sp} g_{3p} B_{p}^{3} }}{{m_{p}^{3} (1 + k_{p} )^{3} }}} \right\}$$

(54)

$$v_{gsn}^{{}} = \frac{1}{{m_{n}^{{}} (1 + k_{n} )^{{}} }}\left\{ {B_{n}^{{}} - \frac{{R_{sn} g_{2n} B_{n}^{2} }}{{m_{n}^{2} (1 + k_{n} )^{2} }}\left( {1 - \frac{{2R_{sn} g_{2n} B_{n} }}{{m_{n}^{2} (1 + k_{n} )^{2} }}} \right) - \frac{{R_{sn} g_{3n} B_{n}^{3} }}{{m_{n}^{3} (1 + k_{n} )^{3} }}} \right\}$$

(55)

where

$$B_{p} = - n_{p} v_{in} + \frac{{R_{sp} }}{{r_{dp} }}v_{outn} ,B_{n} = n_{n} v_{in} - \frac{{R_{sn} }}{{r_{dn} }}v_{outn}$$

(56)

Substituting (22, 23), (45, 51–55) into (46), we have

$$\begin{aligned} v_{outn} &= \frac{{\hat{Z}_{L} B_{p} (g_{1p} + \frac{1}{{r_{dp} }})}}{{(1 + k_{p} )m_{p} }} + \frac{{\hat{Z}_{L} B_{p}^{2} }}{{m_{p}^{2} (1 + k_{p} )^{3} }}\left\{ {g_{2p} \left( {1 - \frac{{2R_{sp} g_{2p} B_{p} }}{{m_{p}^{2} (1 + k_{p} )^{2} }}} \right) + \frac{{g_{3p} B_{p}^{{}} }}{{m_{p}^{{}} (1 + k_{p} )^{{}} }}} \right\} \\ &\quad- \,\frac{{\hat{Z}_{L} B_{n} (g_{1n} + \frac{1}{{r_{dn} }})}}{{(1 + k_{n} )m_{n} }} - \frac{{\hat{Z}_{L} B_{n}^{2} }}{{m_{n}^{2} (1 + k_{n} )^{3} }}\left\{ {g_{2n} \left( {1 - \frac{{2R_{sn} g_{2n} B_{n} }}{{m_{n}^{2} (1 + k_{n} )^{2} }}} \right) + \frac{{g_{3n} B_{n}^{{}} }}{{m_{n}^{{}} (1 + k_{n} )^{{}} }}} \right\} \hfill \\ \end{aligned}$$

(57)

Appendix 2: Derivation of the Volterra operators for the proposed LNTA: A1, A2, A3, H1, H2 and H3

For the circuit of Fig. 9 the current and voltage equations follow

$$v_{in} = v_{so} - 2R_{so} i_{so}$$

(58)

$$\begin{aligned} i_{so} &= - sC_{gsp} v_{sgp1} + sC_{gsn} v_{gsn1} + v_{inp} (\frac{1}{{sL_{p} }} + \frac{1}{{sL_{n} }}) + i_{dp2} - i_{dn2} \\ & \quad +\, sC_{gsp} v_{sgp2} - sC_{gsn} v_{gsn2} + \frac{{v_{sp2} - v_{outp} }}{{r_{dp} }} - \frac{{v_{outp} - v_{sn2} }}{{r_{dn} }} \hfill \\ \end{aligned}$$

(59)

where

$$v_{{sgp_{1} }} = v_{{sgp}} \left( {v_{{in}} ,v_{{out}} } \right),v_{{sgp_{2} }} = v_{{sgp}} \left( { - v_{{in}} , - v_{{out}} } \right)$$

(60)

$$v_{{gsn_{1} }} = v_{{gsn}} \left( {v_{{in}} ,v_{{out}} } \right),v_{{gsn_{2} }} = v_{{gsn}} \left( { - v_{{in}} , - v_{{out}} } \right)$$

(61)

$$v_{{sp_{2} }} = v_{{sp}} \left( { - v_{{in}} , - v_{{out}} } \right),v_{{sn_{2} }} = v_{{sn}} \left( { - v_{{in}} , - v_{{out}} } \right)$$

(62)

$$i_{{dp_{2} }} = i_{{dp}} \left( { - v_{{in}} , - v_{{out}} } \right),i_{{dn_{2} }} = i_{{dn}} \left( { - v_{{in}} , - v_{{out}} } \right)$$

(63)

For differential mode, the single voltages should be

$$v_{inp} = - v_{inn} = \frac{{v_{in} }}{2},v_{outp} = - v_{outn} = \frac{{v_{out} }}{2}$$

(64)