Inference on a distribution function from ranked set samples

Abstract

Consider independent observations $(X_i,R_i)$ with random or fixed ranks $R_i$, while conditional on $R_i$, the random variable $X_i$ has the same distribution as the $R_i$-th order statistic within a random sample of size k from an unknown distribution function F. Such observation schemes are well known from ranked set sampling and judgment post-stratification. Within a general, not necessarily balanced setting we derive and compare the asymptotic distributions of three different estimators of the distribution function F: a stratified estimator, a nonparametric maximum-likelihood estimator and a moment-based estimator. Our functional central limit theorems generalize and refine previous asymptotic analyses. In addition, we discuss briefly pointwise and simultaneous confidence intervals for the distribution function with guaranteed coverage probability for finite sample sizes. The methods are illustrated with a real data example, and the potential impact of imperfect rankings is investigated in a small simulation experiment.

1 Introduction

Ranked set sampling and judgment post-stratification are both sampling strategies in situations in which ranking several observations is possible and relatively easy without referring to exact values, whereas obtaining complete observations is much more involved. For instance, this occurs often in agriculture or forestry when the quantities of interest are yields on different plots or of different trees. Good overviews of theory and applications of ranked set sampling are given by Wolfe (2004, 2012) and Chen et al. (2004). Let us explain the two sampling schemes just mentioned in a simple hypothetical example: Suppose we want to estimate the distribution of body heights among all men of age 20–25 in a certain population. Whenever we have obtained a precise measurement $X_i$ of such a man, we could compare him to $k-1$ additional young men and note the rank $R_i \in \{1,2,\ldots ,k\}$ of $X_i$ within this small group without measuring the heights of the additional men precisely. This sampling scheme is called judgment post-stratification (JPS), see MacEachern et al. (2004). Alternatively, for each observation we could recruit a group of k young men, rank them with respect to their heights and then obtain the precise body height $X_i$ of the person with rank $R_i \in \{1,\ldots ,k\}$ only. Here the ranks $R_1, R_2, \ldots , R_n$ have been specified in advance. This sampling scheme, called ranked set sampling (RSS), was introduced by McIntyre (1952). If the empirical distribution of the ranks $R_i$ is (approximately) uniform on $\{1,\ldots ,k\}$, one talks about balanced RSS, otherwise unbalanced RSS. For instance, if we are mainly interested in the upper tail of the distribution of body heights, we could favor larger ranks $R_i$.

In general, we consider independent random pairs $(X_1,R_1)$, $(X_2,R_2)$, ..., $(X_n,R_n)$ with fixed or random ranks $R_i \in \{1,2,\ldots ,k\}$. Conditional on $R_i = r$, the random variable $X_i$ has the same distribution as the r-th order statistic of a random sample of size k from F. That means, $X_i$ has distribution function

$$\begin{aligned} F_r(x) := \ \mathop {\mathrm {I\!P}}\nolimits (X_i \le x \,|\, R_i = r) \ = \ B_r(F(x)) , \end{aligned}$$

where $B_r : [0,1] \rightarrow [0,1]$ denotes the distribution function of the beta distribution with parameters r and $k+1-r$. Thus for $p \in [0,1]$,

$$\begin{aligned} B_r(p) \ = \ \sum _{i=r}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) p^i (1 - p)^{k-i} \ = \ \int _0^p \beta _r(u) \, \mathrm{d}u \end{aligned}$$

with

$$\begin{aligned} \beta _r(u) \ = \ C_r u^{r-1} (1 - u)^{k-r} \quad \text {and}\quad C_r \ = \ k \left( {\begin{array}{c}k-1\\ r-1\end{array}}\right) \ = \ k \left( {\begin{array}{c}k-1\\ k-r\end{array}}\right) , \end{aligned}$$

see David and Nagaraja (2003). The vector $\varvec{N}_{\!n}= (N_{nr})_{r=1}^k$ of stratum sizes

$$\begin{aligned} N_{nr} \ := \ \sum _{i=1}^n 1_{[R_i = r]} \end{aligned}$$

plays a key role. In RSS, the ranks $R_1, R_2, \ldots , R_n$ and thus the whole vector $\varvec{N}_{\!n}$ are fixed. In JPS, the $R_i$ are independent and uniformly distributed on $\{1,\ldots ,k\}$, whence $\varvec{N}_{\!n}$ follows a multinomial distribution $\mathrm {Mult}\, (n; 1/k, \ldots , 1/k)$.

Several estimators of the c.d.f. F have been proposed. Of course one could just ignore the rank information and compute the empirical c.d.f. $\widehat{F}_n$,

$$\begin{aligned} \widehat{F}_n(x) \ := \ \frac{1}{n} \sum _{i=1}^n 1_{[X_i \le x]}. \end{aligned}$$

In the JPS setting, this estimator is unbiased and $\sqrt{n}$-consistent. However, the stratified estimator

$$\begin{aligned} \widehat{F}_n^\mathrm{S}\ := \ \frac{1}{\#\{r : N_{nr}> 0\}} \sum _{r \,:\, N_{nr} > 0} \widehat{F}_{nr} \end{aligned}$$

with the empirical c.d.f.

$$\begin{aligned} \widehat{F}_{nr}(x) \ := \ \frac{1}{N_{nr}} \sum _{i = 1}^n 1_{[R_i = r, \, X_i \le x]} \end{aligned}$$

within stratum $\{i : R_i = r\}$ is usually more efficient. It has been introduced and analyzed in a balanced RSS setting by Stokes and Sager (1988). Refinements and modifications of this estimator $\widehat{F}_n^\mathrm{S}$ in the JPS setting have been proposed by Frey and Ozturk (2011) and Wang et al. (2012). In particular, these authors consider situations with small or moderate sample sizes so that some stratum sizes $N_{nr}$ may be zero or the empirical c.d.f.s $\widehat{F}_{nr}$ may fail to satisfy order relations which are known for their theoretical counterparts $F_r$.

A second approach to estimating the c.d.f. F which can also handle empty strata was introduced by Kvam and Samaniego (1994). They propose to estimate F(x) by maximizing the conditional log-likelihood function

$$\begin{aligned} L_n(x,p)&:= \ \sum _{i=1}^n \Big [ 1_{[X_i \le x]} \log B_{R_i}(p) + 1_{[X_i > x]} \log (1 - B_{R_i}(p)) \Big ] \\&= \ \sum _{r=1}^k N_{nr} \Big [ \widehat{F}_{nr}(x) \log B_r(p) + (1 - \widehat{F}_{nr}(x)) \log (1 - B_r(p)) \Big ] \end{aligned}$$

of the indicator vector $(1_{[X_i \le x]})_{i=1}^n$, given the rank vector $\varvec{R}_{n}= (R_i)_{i=1}^n$. The resulting estimator $\widehat{F}_n^\mathrm{L}$ is given by

$$\begin{aligned} \widehat{F}_n^\mathrm{L}(x) \ := \ \mathop {\mathrm {arg\,max}}_{p \in [0,1]} L_n(x,p). \end{aligned}$$

Huang (1997) provides a detailed asymptotic analysis of this estimator $\widehat{F}_n^\mathrm{L}$ in the special setting when $n = k\ell$, $N_{nr} = \ell$ for $1 \le r \le k$, and $\ell \rightarrow \infty$.

A third approach, introduced by Chen (2001), is to estimate F by a moment equality for the naive empirical c.d.f. $\widehat{F}_n$. Note that

$$\begin{aligned} \mathop {\mathrm {I\!E}}\nolimits \bigl ( n \widehat{F}_n(x) \,\big |\, \varvec{R}_{n}\bigr ) \ = \ \sum _{r=1}^k N_{nr} B_r(F(x)). \end{aligned}$$

Hence, one can estimate F(x) by the unique number $\widehat{F}_n^\mathrm{M}(x) \in [0,1]$ such that

$$\begin{aligned} n \widehat{F}_n(x) \ = \ \sum _{r=1}^k N_{nr} B_r\Big (\widehat{F}_n^\mathrm{M}(x)\Big ). \end{aligned}$$

(1)

In the RSS setting with proportions $N_{nr}/n$ converging to fixed numbers $\pi _r > 0$ as $n \rightarrow \infty$, Chen (2001) proves asymptotic normality of $\sqrt{n} \bigl ( \widehat{F}_n^\mathrm{M}(x) - F(x) \bigr )$ for finitely many points x and shows that the supremum norm of $\widehat{F}_n^\mathrm{M}- F$ converges to zero in probability. (Note that Chen (2001) formulates the moment equality (1) with $n \pi _r$ in place of $N_{nr}$, but this would introduce an unnecessary estimation bias.)

In Sect. 2, we present some elementary properties of the estimators $\widehat{F}_n^\mathrm{S}$, $\widehat{F}_n^\mathrm{L}$ and $\widehat{F}_n^\mathrm{M}$ and comment briefly on the computation of the latter two. In addition, we describe two methods to obtain pointwise and simultaneous confidence intervals for F, respectively. The former procedure is just an adaptation of a method by Terpstra and Miller (2006) and closely related to the estimator $\widehat{F}_n^\mathrm{M}$. Inverting the underlying tests yields honest confidence intervals for any given quantile of F as proposed by Balakrishnan and Li (2006) for balanced RSS. The confidence bands are a generalization of the confidence bands described by Stokes and Sager (1988). Here it turns out that the estimator $\widehat{F}_n^\mathrm{M}$ is particularly convenient to work with.

Section 3 provides a detailed analysis of the asymptotic distribution of the estimators $\widehat{F}_n^\mathrm{S}$, $\widehat{F}_n^\mathrm{L}$ and $\widehat{F}_n^\mathrm{M}$ as $n \rightarrow \infty$ while k is fixed and $N_{nr}/n \rightarrow _p \pi _r > 0$ for $1 \le r \le k$. Our analyses provide linear stochastic expansions and functional central limit theorems for the processes $\sqrt{n}(\widehat{F}_n^\mathrm{Z} - F)$, $\mathrm{Z} = \mathrm{S}, \mathrm{L}, \mathrm{M}$. These results generalize the findings of Stokes and Sager (1988) about $\widehat{F}_n^\mathrm{S}$, of Huang (1997) about $\widehat{F}_n^\mathrm{L}$ in balanced RSS and of Chen (2001) and Ghosh and Tiwari (2008) about $\widehat{F}_n^\mathrm{M}$. We obtain explicit expressions for the asymptotic covariance functions of $\sqrt{n}(\widehat{F}_n^\mathrm{Z} - F)$ which enable efficiency considerations. The most important findings are that (i) the estimator $\widehat{F}_n^\mathrm{L}$ is always superior to the other two, (ii) the estimators $\widehat{F}_n^\mathrm{S}$ and $\widehat{F}_n^\mathrm{M}$ are asymptotically equivalent in case of $\pi _1 = \cdots = \pi _k = 1/k$ and (iii) in unbalanced settings the estimator $\widehat{F}_n^\mathrm{S}$ can be substantially worse than the other two estimators. Moreover, the efficiency gain of $\widehat{F}_n^\mathrm{L}$ over $\widehat{F}_n^\mathrm{M}$ is bounded and typically rather small. In addition, we analyze the estimators’ asymptotic behavior in the tails of the distribution F where they turn out to be essentially equivalent.

A detailed analysis of a real data example is presented in Sect. 4. It involves population sizes of Swiss municipalities and illustrates that sampling from finite populations without replacement may render our confidence regions conservative, even if the rankings are not perfect. The impact of imperfect rankings itself is investigated in a small simulation study based on the model of Dell and Clutter (1972).

The main proofs are deferred to an appendix. Further technical details and additional material, including references to computer code in R (R Core Team 2013), are collected in a supplement.

2 Computation of the estimators and exact inference

Computations In what follows let $X_{(1)}< X_{(2)}< \cdots < X_{(n)}$ be the order statistics of $X_1, X_2, \ldots , X_n$, augmented by $X_{(0)} := -\infty$ and $X_{(n+1)} := \infty$. One can easily verify that for $\mathrm {Z} = \mathrm {S}, \mathrm {M}, \mathrm {L}$, the estimator $\widehat{F}_n^\mathrm{Z}$ is constant on each interval $[X_{(y)}, X_{(y+1)})$, $0 \le y \le n$, where $\widehat{F}_n^\mathrm{Z}\equiv 0$ on $[X_{(0)}, X_{(1)})$ and $\widehat{F}_n^\mathrm{Z}\equiv 1$ on $[X_{(n)}, X_{(n+1)})$.

While the computation of the stratified estimator $\widehat{F}_n^\mathrm{S}$ is straightforward, the estimators $\widehat{F}_n^\mathrm{M}$ and $\widehat{F}_n^\mathrm{L}$ may be computed numerically by running a suitable bisection algorithm $n-1$ times. Concerning $\widehat{F}_n^\mathrm{M}$, note that $\sum _{r=1}^k N_{nr} B_r(p)$ is continuous and strictly increasing in $p \in [0,1]$ with boundary values 0 and 1. Hence for $1 \le y < n$ and $X_{(y)} \le x < X_{(y+1)}$, the estimator $\widehat{F}_n^\mathrm{M}(x)$ is the unique solution $p \in (0,1)$ of $\sum _{r=1}^k N_{nr} B_r(p) = y$.

As to $\widehat{F}_n^\mathrm{L}$, the next lemma provides some essential properties of the log-likelihood function $L_n(\cdot ,\cdot )$. Its proof is given in the supplement.

Lemma 1

For any $x \in \mathbb {R}$, the function $L_n(x,\cdot ) : [0,1] \rightarrow [-\infty ,0]$ is continuous and continuously differentiable on (0, 1). Its derivative $L_n'(x,p) := \partial L_n(x,p)/\partial p$ is strictly decreasing in $p \in (0,1)$ and equals

$$\begin{aligned} L_n'(x,p) \ = \ \sum _{r=1}^k N_{nr} w_r(p) \bigl [ \widehat{F}_{nr}(x) - B_r(p) \bigr ] \end{aligned}$$

with the auxiliary function

$$\begin{aligned} w_r(p) \ = \ \frac{\beta _r}{B_r(1 - B_r)}(p) \ = \ \frac{\beta _r(p)}{B_r(p) B_{k+1-r}(1-p)}. \end{aligned}$$

Moreover, in case of $X_{(1)} \le x < X_{(n)}$, the limits of $L_n'(x,\cdot )$ at the boundary of (0, 1) are equal to $L_n'(x,0) = \infty$ and $L_n'(x,1) = -\infty$.

According to this lemma, for $y \in \{1,\ldots ,n-1\}$ and $X_{(y)} \le x < X_{(y+1)}$, the value of $\widehat{F}_n^\mathrm{L}(x)$ is the unique number $p \in (0,1)$ such that

$$\begin{aligned} \sum _{r=1}^k N_{nr} w_r(p) \bigl [ \widehat{F}_{nr}(X_{(y)}) - B_r(p) \bigr ] \ = \ 0. \end{aligned}$$

The computation of $\widehat{F}_n^\mathrm{M}$ and $\widehat{F}_n^\mathrm{L}$ for one single data set is of similar complexity. There is, however, an important difference: The vector $\bigl ( \widehat{F}_n^\mathrm{M}(X_{(y)}) \bigr )_{y=1}^{n-1}$ depends solely on the vector $\varvec{N}_{\!n}= (N_{nr})_{r=1}^k$ of stratum sizes. Hence, if we want to simulate the conditional distribution of $\widehat{F}_n^\mathrm{M}$, given $\varvec{R}_{n}$, we have to compute the vector $\bigl ( \widehat{F}_n^\mathrm{M}(X_{(y)}) \bigr )_{y=1}^{n-1}$ only once. By way of contrast, the vector $\bigl ( \widehat{F}_n^\mathrm{L}(X_{(y)}) \bigr )_{y=1}^{n-1}$ depends on the whole matrix $(N_{nry})_{1 \le r \le k, 1 \le y \le n}$ of frequencies $N_{nry} = N_{nr} \widehat{F}_{nr}(X_{(y)}) = \sum _{i=1}^n 1_{[R_i = r, \, X_i \le X_{(y)}]}$. For given $\varvec{N}_{\!n}$, there are

$$\begin{aligned} \frac{n!}{N_{n1}! \, N_{n2}! \, \cdots \, N_{nk}!} \end{aligned}$$

possibilities for that matrix, and this number grows exponentially with n, unless $\varvec{N}_{\!n}$ is extremely unbalanced. As a consequence, for each new data set we have to compute $\widehat{F}_n^\mathrm{L}$ anew, even if $\varvec{N}_{\!n}$ remains unchanged.

Basic distributional properties From now on, we condition on the rank vector $\varvec{R}_{n}= (R_i)_{i=1}^n$. Hence the vector $\varvec{N}_{\!n}= (N_{nr})_{r=1}^k$ of stratum sizes is viewed as a fixed vector, and all probabilities, expectations and distributional statements refer to the conditional distribution of $\varvec{X}_{\!n}= (X_i)_{i=1}^n$, given $\varvec{R}_{n}$.

All estimators $\widehat{F}_n$, $\widehat{F}_n^\mathrm{S}$, $\widehat{F}_n^\mathrm{M}$ and $\widehat{F}_n^\mathrm{L}$ are distribution-free in the following sense: Let $\widehat{B}_n$, $\widehat{B}_n^\mathrm{S}$, $\widehat{B}_n^\mathrm{M}$ and $\widehat{B}_n^\mathrm{L}$ be defined analogously with raw observations from the uniform distribution on [0, 1]. That means, we replace the random variables $X_1, X_2, \ldots , X_n$ with random variables $\widetilde{X}_1, \widetilde{X}_2, \ldots , \widetilde{X}_n \in [0,1]$ which are independent, and $\widetilde{X}_i$ has (conditional) distribution function $B_r$ if $R_i = r$. Then

$$\begin{aligned} \bigl ( \widehat{F}_n^\mathrm{Z}(x) \bigr )_{x \in \mathbb {R}} \quad \text {has the same distribution as} \quad \bigl ( \widehat{B}_n^\mathrm{Z}(F(x)) \bigr )_{x \in \mathbb {R}} , \end{aligned}$$

where $\mathrm{Z} = \mathrm{S}, \mathrm{M}, \mathrm{L}$. Consequently, it suffices to analyze the distribution of the random processes $\bigl ( \widehat{B}_n^\mathrm{Z}(t) \bigr )_{t \in [0,1]}$.

Pointwise confidence intervals Recall that the estimator $\widehat{F}_n^\mathrm{M}(x)$ was defined by matching $n \widehat{F}_n(x)$ to its (conditional) mean. Comparing $n \widehat{F}_n(x)$ with its distribution function yields exact confidence bounds for F(x). This approach has been used by Terpstra and Miller (2006) in the framework of balanced ranked set sampling. In the present general framework, this method works as follows: The (conditional) distribution of $n \widehat{F}_n(x)$ depends only on $\varvec{N}_{\!n}$ and F(x). Precisely, in case of $F(x) = p$, it has the same distribution as $\sum _{r=1}^k Y_{r,p}$ with independent random variables $Y_{1,p}$, $Y_{2,p}$, ..., $Y_{k,p}$, where

$$\begin{aligned} Y_{r,p} \ \sim \ \mathrm {Bin}(N_{nr}, B_r(p)). \end{aligned}$$

Let $G_{\varvec{N}_{\!n},p}$ be the corresponding distribution function, i.e.,

$$\begin{aligned} G_{\varvec{N}_{\!n},p}(y) \ := \ \mathop {\mathrm {I\!P}}\nolimits \left( \sum _{r=1}^k Y_{r,p} \le y \right) . \end{aligned}$$

This is not a standard distribution but a convolution of binomial distributions which can be computed numerically quite easily. Elementary considerations reveal that for any $y \in \{0,1,\ldots ,n-1\}$, the distribution function $G_{\varvec{N}_{\!n},p}(y)$ is continuous and strictly decreasing in $p \in [0,1]$ with boundary values $G_{\varvec{N}_{\!n},0}(y) = 1$ and $G_{\varvec{N}_{\!n},1}(y) = 0$. Further, $G_{\varvec{N}_{\!n},p}(n) = 1$ and $G_{\varvec{N}_{\!n},p}(-1) = 0$ for all $p \in [0,1]$. Consequently, non-asymptotic p values for the null hypotheses “$F(x) \ge p$” and “$F(x) \le p$” are given by $G_{\varvec{N}_{\!n},p}(n \widehat{F}_n(x))$ and $1 - G_{\varvec{N}_{\!n},p}(n \widehat{F}_n(x) - 1)$, respectively. These imply two different $(1 - \alpha )$-confidence regions for F(x), namely

$$\begin{aligned} \bigl \{ p \in [0,1] : G_{\varvec{N}_{\!n},p}(n \widehat{F}_n(x)) \ge \alpha \bigr \}&= \ \bigl [ 0, b_\alpha (\varvec{N}_{\!n},n \widehat{F}_n(x)) \bigr ] , \\ \bigl \{ p \in [0,1] : G_{\varvec{N}_{\!n},p}(n \widehat{F}_n(x) - 1) \le 1 - \alpha \bigr \}&= \ \bigl [ a_\alpha (\varvec{N}_{\!n},n \widehat{F}_n(x)), 1 \bigr ]. \end{aligned}$$

Here $b_\alpha (\varvec{N}_{\!n},y)$ is the unique solution $p \in (0,1)$ of the equation $G_{\varvec{N}_{\!n},p}(y) = \alpha$ if $0 \le y \le n-1$, and $b_\alpha (\varvec{N}_{\!n},n) = 1$. Likewise, $a_\alpha (\varvec{N}_{\!n},y)$ is the unique solution $p \in (0,1)$ of the equation $G_{\varvec{N}_{\!n},p}(y-1) = 1 - \alpha$ if $1 \le y \le n$, and $a_\alpha (\varvec{N}_{\!n},0) = 0$. Obviously, one can combine lower and upper bounds and compute the Clopper and Pearson (1934) type $(1 - \alpha )$-confidence interval $\bigl [ a_{\alpha /2}(\varvec{N}_{\!n},n \widehat{F}_n(x)), b_{\alpha /2}(\varvec{N}_{\!n},n\widehat{F}_n(x)) \bigr ]$ for F(x).

Note that the computation of all these confidence bounds for F boils down to determining only finitely many values $a_\lambda (\varvec{N}_{\!n},y)$ and $b_\lambda (\varvec{N}_{\!n},y)$ for $\lambda = \alpha , \alpha /2$ and $y \in \{0,1,\ldots ,n\}$.

If we would ignore the ranks $R_i$ and just pretend that $X_1, X_2, \ldots , X_n$ are i.i.d. with distribution function F, then we would work with the distribution function $G_{n,p}$ of the binomial distribution $\mathrm {Bin}(n,p)$ instead of $G_{\varvec{N}_{\!n},p}$. This would lead to the traditional confidence bounds $a_{\alpha }^\mathrm{st}(n,n\widehat{F}_n(x))$, $b_{\alpha }^\mathrm{st}(n,n\widehat{F}_n(x))$ and the confidence interval of Clopper and Pearson (1934) with endpoints $a_{\alpha /2}^\mathrm{st}(n,n\widehat{F}_n(x))$, $b_{\alpha /2}^\mathrm{st}(n,n\widehat{F}_n(x))$ for F(x).

Confidence bands We may compute Kolmogorov–Smirnov-type confidence bands for the unknown distribution function F as follows: Let $\kappa _{}^\mathrm{Z}(\varvec{N}_{\!n},\alpha )$ be the $(1 - \alpha )$-quantile of the random variable $\Vert \widehat{B}_n^\mathrm{Z} - B\Vert _\infty = \sup _{t \in [0,1]} \bigl | \widehat{B}_n^\mathrm{Z}(t) - t \bigr |$. Then, we may conclude with confidence $1 - \alpha$ that

$$\begin{aligned} F(x) \ \in \ \bigl [ \widehat{F}_n^\mathrm{Z}(x) \pm \kappa _{}^\mathrm{Z}(\varvec{N}_{\!n},\alpha ) \bigr ] \quad \text {for all} \ x \in \mathbb {R}. \end{aligned}$$

The quantiles $\kappa _{}^\mathrm{Z}(\varvec{N}_{\!n},\alpha )$ may be estimated via Monte Carlo simulations. As explained before, this procedure is particularly convenient to implement for the moment-matching estimator $\widehat{F}_n^\mathrm{M}$, whereas for the likelihood estimator $\widehat{F}_n^\mathrm{L}$ it would be very computer-intensive.

Numerical example Figure 1 shows for $n = 210$ and $\varvec{N}_{\!n}= (70,70,70), (100,70,40)$ the estimator value $\widehat{F}_n^\mathrm{M}(X_{(y)})$ and the two-sided $95\%$-confidence bounds $a_{2.5\%}(\varvec{N}_{\!n},y)$, $b_{2.5\%}(\varvec{N}_{\!n},y)$, $a_{2.5\%}^\mathrm{st}(n,y)$ and $b_{2.5\%}^\mathrm{st}(n,y)$ as a function of $y \in \{0,1,\ldots ,n\}$. One sees that the additional rank information leads to more accurate confidence bounds in the balanced setting. In the unbalanced situation, ignoring the rank information and pretending the $X_i$ to be i.i.d. would induce a severe bias, and the coverage probabilities would be substantially smaller than $95\%$.

Fig. 1

Estimator $\widehat{F}_n^\mathrm{M}$ and pointwise $95\%$-confidence intervals for F: For $y \in \{0,1,\ldots ,n\}$ one sees the value $\widehat{F}_n^\mathrm{M}(X_{(y)})$ (dashed), the exact confidence bounds $a_{2.5\%}(\varvec{N}_{\!n},y)$ and $b_{2.5\%}(\varvec{N}_{\!n},y)$ (solid), and the classical bounds $a_{2.5\%}^\mathrm{st}(n,y)$ and $b_{2.5\%}^\mathrm{st}(n,y)$ (dotted)

For Kolmogorov–Smirnov-type confidence bands centered at $\widehat{F}_n^\mathrm{M}$, we estimated the quantiles $\kappa _{}^\mathrm{M}(\varvec{N}_{\!n},5\%)$ in $10^5$ Monte Carlo simulations and obtained

$$\begin{aligned} \widehat{\kappa }_{}^\mathrm{M}(\varvec{N}_{\!n},5\%) \ = \ {\left\{ \begin{array}{ll} 0.0790 &{} \text {for} \ \varvec{N}_{\!n}= (70,70,70), \\ 0.0812 &{} \text {for} \ \varvec{N}_{\!n}= (100,70,40). \end{array}\right. } \end{aligned}$$

For the usual Kolmogorov–Smirnov confidence band with $n = 210$ observations, the critical value would be $\kappa (n,5\%) = 0.0927$.

Unequal group sizes The point estimators $\widehat{F}_n^\mathrm{L}, \widehat{F}_n^\mathrm{M}$ and the confidence regions just described may be extended easily to a more general setting with independent observations $(X_i,R_i,k_i)$, $1 \le i \le n$, where $k_i \ge 1$ is a fixed integer, $R_i$ is a fixed or random rank in $\{1,2,\ldots ,k_i\}$, and

$$\begin{aligned} \mathop {\mathrm {I\!P}}\nolimits (X_i \le x \,|\, R_i = r) \ = \ B_{r,k_i+1-r}(F(x)) , \end{aligned}$$

see, for instance, Bhoj (2001) or Chen (2001). Here $B_{r,s}$ denotes the distribution function of the beta distribution with parameters r and s.

3 Asymptotic considerations

We consider the asymptotic behavior of the estimators $\widehat{B}_n^\mathrm{S}$, $\widehat{B}_n^\mathrm{M}$ and $\widehat{B}_n^\mathrm{L}$ for fixed k as $n \rightarrow \infty$ and

$$\begin{aligned} \pi _{nr} := \frac{N_{nr}}{n} \ \rightarrow \ \pi _r \quad \text {for} \ 1 \le r \le k. \end{aligned}$$

Recall that we condition on the rank vector $\varvec{R}_{n}$. The former condition is satisfied with $\pi _r = 1/k$ both in Huang’s (1997) setting and in the JPS setting almost surely. In general, we assume that

$$\begin{aligned} {\left\{ \begin{array}{ll} \pi _1, \ldots , \pi _k> 0 &{} \text {in connection with} \ \widehat{B}_n^\mathrm{S}, \\ \pi _1, \pi _k > 0 &{} \text {in connection with} \ \widehat{B}_n^\mathrm{M}, \widehat{B}_n^\mathrm{L}. \end{array}\right. } \end{aligned}$$

Linear expansions and limit theorems In what follows, let

$$\begin{aligned} \mathbb {V}_{nr} \ := \ \sqrt{N_{nr}} \Big (\widehat{B}_{nr} - B_r\Big ) \circ B_r^{-1} \end{aligned}$$

for $1 \le r \le k$. Each stochastic process $\mathbb {V}_{nr}$ has the same distribution as a standardized empirical distribution function of $N_{nr}$ independent random variables with uniform distribution on [0, 1], see also “Appendix.” Moreover, the processes $\mathbb {V}_{n1}, \ldots , \mathbb {V}_{nk}$ are stochastically independent. Our first result shows that the three estimators $\widehat{B}_n^\mathrm{S}$, $\widehat{B}_n^\mathrm{M}$ and $\widehat{B}_n^\mathrm{L}$ may be approximated by simpler processes involving $\mathbb {V}_{n1}, \ldots , \mathbb {V}_{nk}$.

Theorem 2

(Linear expansion). For $\mathrm{Z} = \mathrm{S}, \mathrm{M}, \mathrm{L}$ and any fixed $\delta \in [0,1/2)$,

$$\begin{aligned} \sup _{t \in (0,1)} \frac{ \bigl | \sqrt{n} (\widehat{B}_n^\mathrm{Z}(t) - t) - \mathbb {V}_n^\mathrm{Z}(t) \bigr |}{t^\delta (1-t)^\delta } \ \rightarrow _p \ 0 , \end{aligned}$$

where

$$\begin{aligned} \mathbb {V}_n^\mathrm{Z}(t) \ := \ \sum _{r=1}^k \gamma _{nr}^\mathrm{Z}(t) \, \mathbb {V}_{nr}(B_r(t)) \end{aligned}$$

with continuous functions $\gamma _{n1}^\mathrm{Z},\ldots ,\gamma _{nk}^\mathrm{Z} : [0,1] \rightarrow [0,\infty )$. Precisely, for $t \in (0,1)$,

$$\begin{aligned} \gamma _{nr}^\mathrm{S}(t)&:= \ \frac{1}{k \sqrt{\pi _{nr}}} , \\ \gamma _{nr}^\mathrm{M}(t)&:= \ \sqrt{\pi _{nr}} \bigr / \sum _{s=1}^k \pi _{ns} \beta _s(t) , \\ \gamma _{nr}^\mathrm{L}(t)&:= \sqrt{\pi _{nr}}\, w_r(t) \Big / \sum _{s=1}^k \pi _{ns} w_s(t) \beta _s(t) \end{aligned}$$

with $w_r = \beta _r/(B_r(1 - B_r))$. Moreover,

$$\begin{aligned} \sup _{t \in (0,c] \cup [1-c,1)} \, \frac{|\mathbb {V}_n^\mathrm{Z}(t)|}{t^\delta (1 - t)^\delta } \ \rightarrow _p \ 0 \quad \text {as} \ n \rightarrow \infty \ \text {and}\ c \downarrow 0. \end{aligned}$$

The next theorem shows that all estimators $\widehat{F}_n^\mathrm{S}, \widehat{F}_n^\mathrm{M}, \widehat{F}_n^\mathrm{L}$ are asymptotically equivalent in the tail regions. Moreover, the asymptotic behavior in the left and right tail is driven mainly by the processes $\mathbb {V}_{n1}$ and $\mathbb {V}_{nk}$, respectively.

Theorem 3

(Linear expansion in the tails). For $\mathrm{Z} = \mathrm{S}, \mathrm{M}, \mathrm{L}$ and any fixed $\kappa \in [1/2,1)$,

$$\begin{aligned} \sup _{t \in (0,c]} \frac{\bigl | \sqrt{n} (\widehat{B}_n^\mathrm{Z}(t) - t) - \mathbb {V}_{n}^{(\ell )}(t) \bigr |}{t^\kappa } \ \rightarrow _p \ 0 \end{aligned}$$

and

$$\begin{aligned} \sup _{t \in [1-c,1)} \frac{\bigl | \sqrt{n} (\widehat{B}_n^\mathrm{Z}(t) - t) - \mathbb {V}_{n}^{(r)}(t) \bigr |}{(1 - t)^\kappa } \ \rightarrow _p \ 0 \end{aligned}$$

as $n \rightarrow \infty$ and $c \downarrow 0$, where

$$\begin{aligned} \mathbb {V}_n^{(\ell )}(t) \ := \ \frac{\mathbb {V}_{n1}(B_1(t))}{k \sqrt{\pi _{n1}}} \quad \text {and}\quad \mathbb {V}_n^{(r)}(t) \ := \ \frac{\mathbb {V}_{nk}(B_k(t))}{k \sqrt{N_{nk}/n}}. \end{aligned}$$

It follows from Donsker’s theorem for the empirical process that $\mathbb {V}_{nr}$ behaves asymptotically like a standard Brownian bridge process $\mathbb {V}= (\mathbb {V}(u))_{u \in [0,1]}$. Together with Theorem 2, this leads to the following limit theorem:

Corollary 4

(Asymptotic distribution). For $\mathrm{Z} = \mathrm{S}, \mathrm{M}, \mathrm{L}$, the stochastic process $\mathbb {V}_n^\mathrm{Z}$ converges in distribution in the space $\ell _\infty ([0,1])$ to a centered Gaussian process $\mathbb {V}^\mathrm{Z}$ with continuous paths on [0, 1]. Precisely, for $t \in [0,1]$,

$$\begin{aligned} \mathbb {V}^\mathrm{Z}(t) \ = \ \sum _{r=1}^k \gamma _r^\mathrm{Z}(t) \mathbb {V}_r(B_r(t)) \end{aligned}$$

with independent standard Brownian bridges $\mathbb {V}_1, \ldots , \mathbb {V}_k$ and continuous functions $\gamma _1^\mathrm{Z}, \ldots , \gamma _k^\mathrm{Z} : [0,1] \rightarrow [0,\infty )$ given by

$$\begin{aligned} \gamma _r^\mathrm{S}(t)&:= \ \frac{1}{k \sqrt{\pi _r}} , \\ \gamma _r^\mathrm{M}(t)&:= \ \sqrt{\pi _r} \bigr / \sum _{s=1}^k \pi _s \beta _s(t) , \\ \gamma _r^\mathrm{L}(t)&:= \ {\left\{ \begin{array}{ll} \displaystyle \sqrt{\pi _r}\, w_r(t) \Big / \sum _{s=1}^k \pi _s w_s(t) \beta _s(t) &{} \mathrm{for} \ 0< t < 1 , \\ \sqrt{\pi _r} \, r / (\pi _1 k) &{} \mathrm{for} \ t = 0 , \\ \sqrt{\pi _r} (k+1-r) / (\pi _k k) &{} \mathrm{for} \ t = 1. \end{array}\right. } \end{aligned}$$

Theorem 2 and Corollary 4 show that all three estimators $\widehat{F}_n^\mathrm{S}, \widehat{F}_n^\mathrm{M}, \widehat{F}_n^\mathrm{L}$ are root-n-consistent. In the asymptotically balanced case with

$$\begin{aligned} \pi _1 = \pi _2 = \cdots = \pi _k = 1/k , \end{aligned}$$

(2)

one can easily deduce from $\sum _{s=1}^k \beta _s \equiv k$ that

$$\begin{aligned} \gamma _r^\mathrm{M} \ \equiv \ \gamma _r^\mathrm{S} \ = \ 1 / \sqrt{k} \quad \text {for} \ 1 \le r \le k. \end{aligned}$$

Hence, in this particular case the estimators $\widehat{F}_n^\mathrm{S}$ and $\widehat{F}_n^\mathrm{M}$ are asymptotically equivalent. But otherwise $\widehat{F}_n^\mathrm{S}$ may be substantially worse than $\widehat{F}_n^\mathrm{M}$, as shown later.

Relative asymptotic efficiencies Let K be the covariance function of a standard Brownian bridge $\mathbb {V}$, i.e., $K(s,t) = \min \{s,t\} - st$ for $s,t \in [0,1]$. Then the covariance function $K^\mathrm{Z}$ of the Gaussian process $\mathbb {V}^\mathrm{Z}$ in Corollary 4 is given by

$$\begin{aligned} K^\mathrm{Z}(s,t) \ = \ \sum _{r=1}^k \gamma _r^\mathrm{Z}(s) \gamma _r^\mathrm{Z}(t) K \bigl ( B_r(s), B_r(t) \bigr ). \end{aligned}$$

In particular, for $0< t < 1$ the asymptotic distribution of $\sqrt{n} \bigl ( \widehat{B}_n^\mathrm{Z}(t) - t \bigr )$ equals $\mathcal {N} \bigl ( 0, K^\mathrm{Z}(t) \bigr )$ with $K^\mathrm{Z}(t) := K^\mathrm{Z}(t,t)$ given by

$$\begin{aligned} K^\mathrm{S}(t)&= \ \sum _{r=1}^k \frac{B_r(t)(1 - B_r(t))}{k^2 \pi _r} , \\ K^\mathrm{M}(t)&= \ \sum _{r=1}^k \pi _r B_r(t)(1 - B_r(t)) \Big / \left( \sum _{s=1}^k \pi _s \beta _s(t) \right) ^2 , \\ K^\mathrm{L}(t)&= \ \sum _{r=1}^k \pi _r w_r(t)^2 B_r(t)(1 - B_r(t)) \Big / \left( \sum _{s=1}^k \pi _s \beta _s(t) w_s(t) \right) ^2 \\&= \ 1 \Big / \sum _{s=1}^k \pi _s \beta _s(t) w_s(t). \end{aligned}$$

The latter equation follows from $w_r = \beta _r/(B_r(1 - B_r))$. The next result provides a detailed comparison of these asymptotic variances.

Theorem 5

(Relative asymptotic efficiencies). For arbitrary $t \in (0,1)$,

$$\begin{aligned} K^\mathrm{L}(t) \ \le \ K^\mathrm{S}(t) \end{aligned}$$

with equality for at most one $t \in (0,1)$. Furthermore,

$$\begin{aligned} K^\mathrm{L}(t) \ \le \ K^\mathrm{M}(t) \end{aligned}$$

with equality if, and only if, $t = 1/2$ and $k = 2$. On the other hand,

$$\begin{aligned} \sup _{\pi } \frac{K^\mathrm{S}(t)}{K^\mathrm{L}(t)}&= \ \infty , \\ \sup _{\pi } \frac{K^\mathrm{M}(t)}{K^\mathrm{L}(t)}&= \ \frac{\rho (t) + \rho (t)^{-1} + 2}{4} \ \le \ \frac{k + k^{-1} + 2}{4} , \end{aligned}$$

where the suprema are over all tuples $(\pi _r)_{r=1}^k$ with strictly positive components summing to one, and

$$\begin{aligned} \rho (t) \ := \ \max _{r=1,\ldots ,k} w_r(t) \Big / \min _{r=1,\ldots ,k} w_r(t) \ \le \ k. \end{aligned}$$

Numerical examples In case of $k = 2$, the upper bound for $K^\mathrm{M}(t)/K^\mathrm{L}(t)$ equals $9/8 = 1.125$. More precisely,

$$\begin{aligned} \frac{\rho (t) + \rho (t)^{-1} + 2}{4} \ = \ 1 + \frac{u^2}{9 - u^2} \ \le \ 1.125 \end{aligned}$$

with $u := 2t - 1 \in [-1,1]$, see the supplement for more details.

Fig. 2

Asymptotic variances of $\widehat{B}_n^\mathrm{L}$, $\widehat{B}_n^\mathrm{S}\equiv \widehat{B}_n^\mathrm{M}$, $\widehat{B}_n$ (left panel) and relative efficiencies of $\widehat{B}_n^\mathrm{L}$ versus $\widehat{B}_n^\mathrm{Z}$ (right panel) in case of $\pi _1 = \pi _2 = \pi _3 = 1/3$

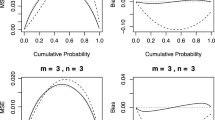
In case of $k = 3$, the upper bound for $K^\mathrm{M}(t)/K^\mathrm{L}(t)$ equals $4/3 \approx 1.333$. Figures 2 and 3 show the asymptotic variance functions $K(\cdot )$ of $\widehat{B}_n$ and $K^\mathrm{Z}(\cdot )$ of $\widehat{B}_n^\mathrm{Z}$ for $\mathrm{Z} = \mathrm{S}, \mathrm{M}, \mathrm{L}$ in the balanced and one unbalanced situation. Note that in the balanced setting, $\widehat{B}_n^\mathrm{S}\equiv \widehat{B}_n^\mathrm{M}$ and thus $K^\mathrm{S}(\cdot ) \equiv K^\mathrm{M}(\cdot )$. In addition, one sees the asymptotic relative efficiencies

$$\begin{aligned} E^\mathrm{Z}(t) \ := \ \frac{K^\mathrm{Z}(t)}{K^\mathrm{L}(t)} \end{aligned}$$

of $\widehat{B}_n^\mathrm{L}$ versus $\widehat{B}_n^\mathrm{Z}$ together with the upper bound

$$\begin{aligned} E_\mathrm{max}^\mathrm{M}(t) \ := \ \bigl ( \rho (t) + \rho (t)^{-1} + 2 \bigr ) / 4 \end{aligned}$$

for $E^\mathrm{M}(t)$. One sees clearly that the inefficiency of $\widehat{B}_n^\mathrm{M}$ versus $\widehat{B}_n^\mathrm{L}$ is moderate, whereas the inefficiency of $\widehat{B}_n^\mathrm{S}$ may become substantial in unbalanced settings. Note also that in case of $\pi _1> \pi _2 > \pi _3$ the accuracy in the left tail increases at the expense of larger errors in the right tail.

Fig. 3

Asymptotic variances of $\widehat{B}_n^\mathrm{S}$, $\widehat{B}_n^\mathrm{M}$, $\widehat{B}_n^\mathrm{L}$ (left panel) and relative efficiencies of $\widehat{B}_n^\mathrm{L}$ versus $\widehat{B}_n^\mathrm{Z}$ (right panel) in case of $(\pi _1,\pi _2,\pi _3) = (10/21,7/21,4/21)$

Implications for confidence intervals One can deduce from Corollary 4 that $n^{1/2} \kappa _{}^\mathrm{Z}(\varvec{N}_{\!n},\alpha )$ converges to the $(1 - \alpha )$-quantile of the random supremum norm $\Vert \mathbb {V}^\mathrm{Z}\Vert _\infty$. Moreover, for any $x \in \mathbb {R}$ with $0< F(x) < 1$, the pointwise confidence bounds satisfy

$$\begin{aligned} a_\alpha (\varvec{N}_{\!n},n \widehat{F}_n(x))&= \ \widehat{F}_n^\mathrm{M}(x) - \frac{\sqrt{K^\mathrm{M}(F(x))}}{\sqrt{n}} \, \Phi ^{-1}(1 - \alpha ) + o_p(n^{-1/2}) \end{aligned}$$

(3)

$$\begin{aligned} b_\alpha (\varvec{N}_{\!n},n \widehat{F}_n(x))&= \ \widehat{F}_n^\mathrm{M}(x) + \frac{\sqrt{K^\mathrm{M}(F(x))}}{\sqrt{n}} \, \Phi ^{-1}(1 - \alpha ) + o_p(n^{-1/2}) \end{aligned}$$

(4)

with $\Phi ^{-1}$ denoting the standard Gaussian quantile function, see the supplement.

4 A real data example and imperfect rankings

4.1 Population sizes of Swiss municipalities

Every 5 years, the Swiss Federal Office of Statistics releases data about all municipalities of Switzerland, including their population sizes. There are currently 2289 communities, and the two most recent data collections are from 2010 and 2015. Suppose we would have wanted to estimate the distribution function F of population sizes by the end of 2015 in early 2016. Back then only the data of 2010 would have been available, the data of 2015 having been released later in 2016 and corrected in 2017. In principle one could have approached each single municipality to obtain its population size by the end of 2015, but this would have been time-consuming of course. Hence, one could have applied RSS sampling as follows: One chooses randomly $n = 210$ disjoint sets of $k = 3$ communities. Within the i-th set, one determines the unit with rank $R_i$ according to population sizes in 2010 and obtains its precise population size $X_i$ by the end of 2015. The ranks $R_1,\ldots ,R_n \in \{1,2,3\}$ are prespecified. If one is particularly interested in smaller municipalities, one could choose $\varvec{R}_{n}$ such that, say, $\varvec{N}_{\!n}= (100,70,40)$.

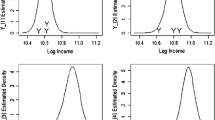
Having the complete data of 2010 and 2015, one can easily simulate this sampling scheme. Figure 4 shows for one such sample the estimated distribution function $\widehat{F}_n^\mathrm{M}$ together with pointwise and simultaneous $95\%$-confidence intervals as described in Sect. 2. Since the distribution of population sizes is heavily right-skewed, the horizontal axis shows the decimal logarithms of population sizes. In the lower panel, the point estimator $\widehat{F}_n^\mathrm{M}$ is replaced with the true distribution function F, i.e., the empirical distribution function of all 2289 population sizes in 2015.

Fig. 4

Inference about the distribution of population sizes (Sect. 4.1) with $\varvec{N}_{\!n}= (100,70,40)$. The smoother function is the true c.d.f. F. The inner and outer two step functions are the pointwise and simultaneous $95\%$-confidence band for F

We simulated this sampling scheme $10^5$ times and analyzed the performance of both $\widehat{F}_n^\mathrm{M}$ and the confidence intervals. The Monte Carlo estimator of

$$\begin{aligned} \mathrm {BIAS}(x) \ := \ \mathop {\mathrm {I\!E}}\nolimits \widehat{F}_n^\mathrm{M}(x) - F(x) \end{aligned}$$

was everywhere between $- 10^{-4}$ and $10^{-3}$, whereas the MC estimator of

$$\begin{aligned} \mathrm {RMSE}(x) \ := \ \Big ( \mathop {\mathrm {I\!E}}\nolimits \, (\widehat{F}_n^\mathrm{M}(x) - F(x))^2 \Big )^{1/2} \end{aligned}$$

was nowhere larger than 0.0263. The left panel of Fig. 5 depicts these two functions $\mathrm {BIAS}$ and $\mathrm {RMSE}$. For each sample and any $x \in \mathbb {R}$, we obtained a pointwise and simultaneous $95\%$-confidence interval, denoted by $C_\mathrm{pw}(x)$ and $C_\mathrm{sim}(x)$, respectively. The MC estimator of the error probability $\mathop {\mathrm {I\!P}}\nolimits \bigl ( F(x) \not \in C_\mathrm{pw}(x) \bigr )$ was nowhere larger than $4.22\%$, and the one of $\mathop {\mathrm {I\!P}}\nolimits \bigl ( F(x) \not \in C_\mathrm{sim}(x) \ \text {for some} \ x \in \mathbb {R}\bigr )$ turned out to be smaller than $2.8\%$. The confidence intervals being conservative are probably a consequence of sampling without replacement, which results in more accurate estimators than sampling with replacement. The right panel of Fig. 5 shows MC estimates of the average widths

$$\begin{aligned} \mathrm {AW}_\mathrm{pw}(x) \ := \ \mathop {\mathrm {I\!E}}\nolimits \mathrm {width}(C_\mathrm{pw}(x)). \end{aligned}$$

Here one sees clearly the effect of unbalanced sampling with $N_{n1}> N_{n2} > N_{n3}$, the benefit being shorter intervals in the left tail at the expense of longer intervals in the right tail.

Fig. 5

Inference about the distribution of population sizes (Sect. 4.1) with $\varvec{N}_{\!n}= (100,70,40)$. Left panel: bias and root mean squared error of $\widehat{F}_n^\mathrm{M}$. Right panel: Average width of pointwise $95\%$-confidence band for F

Note that the ranking of municipalities within the n groups of size $k = 3$ was based on the population sizes in 2010 and thus imperfect. Indeed, a reasonable model for the pairs of log-transformed population sizes in 2010 and 2015 seems to be a bivariate Gaussian distribution with correlation 0.9986. As a consequence, in our MC simulations the average proportion of imperfect ranks $R_i$ turned out to be $3.1\%$.

Analogous simulations for $k = 4,5$ and different choices of $\varvec{N}_{\!n}$ led to similar results. Enlarging k without changing n leads to larger coverage probabilities, presumably an effect of sampling without replacement, while the modulus of the bias of $\widehat{F}_n^\mathrm{M}$ and the proportion of imperfect ranks get larger.

4.2 Imperfect rankings

In case of sampling with replacement, the previous data example would fit the model of Dell and Clutter (1972) for ranked set sampling with imperfect rankings quite well. They consider 2nk independent random variables $X_{ij} \sim F$ and $\varepsilon _{ij} \sim \mathcal {N}(0,\tau ^2)$ with $1 \le i \le n$ and $1 \le j \le k$. Instead of the true rank of $X_{ij}$ among $X_{i1}, \ldots , X_{ik}$ one obtains the ranks

$$\begin{aligned} R_{ij} \ := \ \sum _{\ell =1}^k 1_{[Y_{i\ell } \le Y_{ij}]} \end{aligned}$$

of the concomitant variables $Y_{ij} := X_{ij} + \varepsilon _{ij}$. If $\sigma > 0$ denotes the standard deviation of the $X_{ij}$, the correlation between $X_{ij}$ and $Y_{ij}$ equals $\rho = (1 + \tau ^2/\sigma ^2)^{-1/2}$. Finally we obtain for $1 \le i \le n$ the observation $(X_i,R_i) = (X_{i1}, R_{i1})$ in JPS and $(X_{iJ(i)}, R_i)$ in RSS, where J(i) is the unique index in $\{1,\ldots ,k\}$ such that $R_{iJ(i)} = R_i$.

Fig. 6

Performance of $\widehat{F}_n^\mathrm{L}$ in balanced setting with $N_{n1} = N_{n2} = N_{n3} = 70$: Bias and root mean squared error (left panel) and relative efficiency versus $\widehat{F}_n^\mathrm{S}$ (right panel) for correlations $\rho = 1$ (dotted), $\rho = 0.95$ (dashed) and $\rho = 0.9$ (solid)

In this model, the stratified estimator $\widehat{F}_n^\mathrm{S}$ is still unbiased, see Presnell and Bohn (1999) for the RSS setting with $N_{n1},\ldots ,N_{nk} > 0$ and Dastbaravarde et al. (2016) for the JPS setting. For that reason, we considered $\widehat{F}_n^\mathrm{S}$ as a gold standard in our simulation study: We simulated $10^5$ RSS data sets from this model with standard Gaussian distribution function $F = \Phi$, sample size $n = 210$ and different options for $\varvec{N}_{\!n}$ and $\rho$. With these simulations, we estimated the bias and root mean squared error,

$$\begin{aligned} \mathrm {BIAS}^\mathrm{Z}(x) \ := \ \mathop {\mathrm {I\!E}}\nolimits \widehat{F}_n^\mathrm{Z}(x) - F(x) \quad \text {and}\quad \mathrm {RMSE}^\mathrm{Z}(x) \ := \ \bigl ( \mathop {\mathrm {I\!E}}\nolimits \, (\widehat{F}_n^\mathrm{Z}(x) - F(x))^2 \bigr )^{1/2} , \end{aligned}$$

for $\mathrm{Z} = \mathrm{S}, \mathrm{M}, \mathrm{L}$. In addition we estimated the relative efficiency

$$\begin{aligned} \mathrm {RE}^\mathrm{Z}(x) \ := \ \mathrm {RMSE}^\mathrm{S}(x)^2 / \mathrm {RMSE}^\mathrm{Z}(x)^2 \end{aligned}$$

of $\widehat{F}_n^\mathrm{Z}$ versus the stratified estimator $\widehat{F}_n^\mathrm{S}$.

Firstly we considered $N_{n1} = N_{n2} = N_{n3} = 70$. Here $\widehat{F}_n^\mathrm{S}\equiv \widehat{F}_n^\mathrm{M}\equiv \widehat{F}_n^{}$. In Fig. 6, one sees on the left-hand side the functions $\mathrm {BIAS}^\mathrm{L}$ and $\mathrm {RMSE}^\mathrm{L}$ for three different values of the correlation $\rho$. While $\widehat{F}_n^\mathrm{S}\equiv \widehat{F}_n^\mathrm{M}$ is unbiased, the bias of $\widehat{F}_n^\mathrm{L}$ gets worse as $\rho$ decreases. For all three estimators $\widehat{F}_n^\mathrm{Z}$, the root mean squared error increases as $\rho$ decreases. The right-hand side of Fig. 6 depicts the relative efficiency function $\mathrm {RE}^\mathrm{L}$. As predicted by asymptotic theory, $\mathrm {RE}^\mathrm{L} > 1$ in case of $\rho = 1$, but for smaller correlations the relative efficiency drops below 1 in the tails.

Secondly we considered the unbalanced situation with $\varvec{N}_{\!n}= (100, 70, 40)$. Now the three estimators $\widehat{F}_n^\mathrm{Z}$ are different, and only $\widehat{F}_n^\mathrm{S}$ is unbiased. In Fig. 7, we show bias and root mean squared errors of $\widehat{F}_n^\mathrm{M}$ and $\widehat{F}_n^\mathrm{L}$. Clearly, the bias of $\widehat{F}_n^\mathrm{M}$ and $\widehat{F}_n^\mathrm{L}$ gets worse as $\rho$ decreases, where $\widehat{F}_n^\mathrm{M}$ is a bit more robust than $\widehat{F}_n^\mathrm{L}$. Nevertheless, the plots of the relative efficiencies $\mathrm {RE}^\mathrm{M}$ and $\mathrm {RE}^\mathrm{L}$ show that for $\rho = 0.95$ the moment-matching estimator outperforms the stratified one everywhere, and also the likelihood estimator is better at most places. For $\rho = 0.9$, the likelihood estimator is less favorable than the other two.

Fig. 7

Performance of $\widehat{F}_n^\mathrm{M}$ and $\widehat{F}_n^\mathrm{L}$ in unbalanced setting with $\varvec{N}_{\!n}= (100,70,40)$: Biases and root mean squared errors (upper panels) and relative efficiencies versus $\widehat{F}_n^\mathrm{S}$ (lower panels) for correlations $\rho = 1$ (dotted), $\rho = 0.95$ (dashed) and $\rho = 0.9$ (solid)

5 Conclusions and future research

The present paper confirms and generalizes previous findings that the estimator $\widehat{F}_n^\mathrm{L}$ is the most efficient one in case of perfect ranking, both in balanced and unbalanced situations. In terms of computational efficiency, however, the estimator $\widehat{F}_n^\mathrm{M}$ has clear advantages and is particularly convenient as an ingredient for simultaneous confidence bands. Further, it is closely related to pointwise confidence bands for F. For now, we restricted ourselves to Kolmogorov–Smirnov-type bands, but other variants might be worthwhile to study.

The simulations in Sect. 4.2 indicate that even in case of imperfect rankings, both $\widehat{F}_n^\mathrm{M}$ and $\widehat{F}_n^\mathrm{L}$ perform well compared to $\widehat{F}_n^\mathrm{S}$, as long as the ranking precision is high. While $\widehat{F}_n^\mathrm{L}$ appears to be most sensitive to imperfect rankings, $\widehat{F}_n^\mathrm{M}$ seems to offer a good compromise in terms of efficiency (for perfect rankings) and robustness against ranking errors. Investigating and understanding these differences thoroughly would be an interesting topic for future research.

Appendix

We first recall two well-known facts about uniform empirical processes, see Shorack and Wellner (1986).

Proposition 6

Let $U_1, U_2, U_3, \ldots$ be independent random variables with uniform distribution on [0, 1]. For $N \in \mathbb {N}$ and $u \in [0,1]$ define

$$\begin{aligned} \mathbb {V}^{(N)}(u) \ := \ N^{-1/2} \sum _{i=1}^N \bigl ( 1 \{U_i \le u\} - u) . \end{aligned}$$

Then, as $N \rightarrow \infty$, $\mathbb {V}^{(N)}$ converges in distribution in $\ell _\infty ([0,1])$ to a standard Brownian bridge $\mathbb {V}$ on [0, 1]. Moreover, for any fixed $\delta \in [0,1/2)$ and $\epsilon > 0$,

$$\begin{aligned} \sup _{N \ge 1} \mathop {\mathrm {I\!P}}\nolimits \left( \sup _{u \in (0,1)} \frac{|\mathbb {V}^{(N)}(u)|}{u^\delta (1 - u)^\delta } \ge C \right)&\rightarrow \ 0 \quad \text {as} \ C \uparrow \infty , \\ \sup _{N \ge 1} \mathop {\mathrm {I\!P}}\nolimits \left( \sup _{u \in (0,c] \cup [1-c,1)} \frac{|\mathbb {V}^{(N)}(u)|}{u^\delta (1 - u)^\delta } \ge \epsilon \right)&\rightarrow \ 0 \quad \text {as} \ c \downarrow 0. \end{aligned}$$

For the estimators $\widehat{F}_n^\mathrm{M}$, $\widehat{F}_n^\mathrm{L}$ we need some basic facts and inequalities for the auxiliary functions $w_k$ and $B_k$ which are proved in the supplement:

Lemma 7

(a):

For $r = 1,2,\ldots ,k$, the function $w_r$ on (0, 1) may be written as $w_r(t) = \widetilde{w}_r(t) / (t(1-t))$ with $\widetilde{w}_r : [0,1] \rightarrow (0,\infty )$ continuously differentiable. Moreover, for $r = 1,2,\ldots ,k$ and $t \in (0,1)$,

$$\begin{aligned} 1 \ \le \ \widetilde{w}_r(t) \ \le \ \max (r,k+1-r). \end{aligned}$$

(b):

For any constant $c \in (0,1)$ there exists a number $c' = c'(k,c) > 0$ with the following property: If $t,p \in (0,1)$ such that

$$\begin{aligned} \frac{|p - t|}{t(1-t)} \ \le \ c , \end{aligned}$$

then for $r = 1,2,\ldots ,k$,

$$\begin{aligned} \max \left\{ \left| \frac{w_r(p)}{w_r(t)} - 1 \right| , \left| \frac{B_r(p) - B_r(t)}{\beta _r(t) (p - t)} - 1 \right| \right\} \ \le \ c' \frac{|p - t|}{t(1-t)}. \end{aligned}$$

Proof of Theorem 2

We start with the weight functions $\gamma _{nr}^\mathrm{Z}$: Note that by Lemma 7,

$$\begin{aligned} \gamma _{nr}^\mathrm{S}(t)&= \ \frac{1}{k \sqrt{\pi _{nr}}} , \\ \gamma _{nr}^\mathrm{M}(t)&= \ \sqrt{\pi _{nr}} \bigr / \sum _{s=1}^k \pi _{ns} \beta _s(t) , \\ \gamma _{nr}^\mathrm{L}(t)&= \sqrt{\pi _{nr}}\, \widetilde{w}_r(t) \Big / \sum _{s=1}^k \pi _{ns} \widetilde{w}_s(t) \beta _s(t) \end{aligned}$$

with the probability weights $\pi _{nr} := N_{nr}/n$ and continuous functions $\widetilde{w}_r : [0,1] \rightarrow [1,k]$. Since the beta densities $\beta _r$ are also continuous with $\beta _1(0) = \beta _k(1) = k$, this shows that $\gamma _{nr}^\mathrm{Z}$ is well-defined and continuous, provided that its denominator is strictly positive, i.e.,

$$\begin{aligned} {\left\{ \begin{array}{ll} \pi _{n1}, \ldots , \pi _{nk}> 0 &{} \text {if} \ \mathrm{Z} = \mathrm{S} , \\ \pi _{n1}, \pi _{nk} > 0 &{} \text {if} \ \mathrm{Z} = \mathrm{M}, \mathrm{L}. \end{array}\right. } \end{aligned}$$

For sufficiently large n this is the case, because $\lim _{n\rightarrow \infty } \pi _{nr} = \pi _r$ for all r. The functions $\gamma _r^\mathrm{Z}$ in Corollary 4 are continuous, too, and elementary considerations reveal that

$$\begin{aligned} \max _{t \in [0,1], \, 1 \le r \le k} \bigl | \gamma _{nr}^\mathrm{Z}(t) - \gamma _r^\mathrm{Z}(t) \bigr | \ \rightarrow \ 0 \end{aligned}$$

(5)

as $n \rightarrow \infty$. In particular, $\max _{t \in [0,1], 1 \le r \le k} \gamma _{nr}^\mathrm{Z}(t) = O(1)$.

Note that for $n \ge 1$ and $1 \le r \le k$, the empirical process $\mathbb {V}_{nr}$ is distributed as $\mathbb {V}^{(N_{nr})}$ in Proposition 6. Note also that the distribution functions $B_r$ satisfy $B_1 \ge B_2 \ge \cdots \ge B_k$, because for $1 \le r < k$ the density ratio $\beta _{r+1}/\beta _r$ is a positive multiple of $t/(1 - t)$ and thus strictly increasing. Consequently, for $1 \le r \le k$,

$$\begin{aligned} B_r(t) \ \le \ B_1(t) \ \le \ kt \quad \text {and}\quad 1 - B_r(t) \ \le \ 1 - B_k(t) \ \le \ k(1-t) , \end{aligned}$$

so

$$\begin{aligned} \frac{B_r(t)(1 - B_r(t))}{t(1-t)} \ \le \ k. \end{aligned}$$

Consequently,

$$\begin{aligned} \sup _{t \in (0,1)} \frac{|\mathbb {V}_{nr}(B_r(t))|}{t^\delta (1 - t)^\delta }&\le \ k^\delta \sup _{u \in (0,1)} \frac{|\mathbb {V}_{nr}(u)|}{u^\delta (1 - u)^\delta } \ = \ O_p(1) \quad \text {and} \\ \sup _{u \in (0,c] \cup [1-c,1)} \frac{|\mathbb {V}_{nr}(B_r(t))|}{t^\delta (1 - t)^\delta }&\le \ k^\delta \sup _{u \in (0,kc] \cup [1 - kc,1)} \frac{|\mathbb {V}_{nr}(u)|}{u^\delta (1 - u)^\delta } \ \rightarrow _p \ 0 \end{aligned}$$

as $n \rightarrow \infty$ and $c \downarrow 0$. All in all, we may conclude that

$$\begin{aligned} \sup _{t \in (0,1)} \, \frac{|\mathbb {V}_n^\mathrm{Z}(t)|}{t^\delta (1 - t)^\delta }&= \ O_p(1) , \end{aligned}$$

(6)

$$\begin{aligned} \sup _{t \in (0,c] \cup [1-c,1)} \, \frac{|\mathbb {V}_n^\mathrm{Z}(t)|}{t^\delta (1 - t)^\delta }&\rightarrow _p \ 0 \quad \text {as} \ n \rightarrow \infty \ \text {and}\ c \downarrow 0. \end{aligned}$$

(7)

It remains to be shown that the process $\sqrt{n} (\widehat{B}_n^\mathrm{Z} - B)$ may be approximated by $\mathbb {V}_n^\mathrm{Z}$. In case of $\mathrm{Z} = \mathrm{S}$ it follows from $\sum _{r=1}^k \beta _r \equiv k$ that $\sum _{r=1}^k B_r = k B$, and this implies that

$$\begin{aligned} \sqrt{n} (\widehat{B}_n^\mathrm{S}- B) \ = \ \sum _{r=1}^k \frac{\sqrt{n} (\widehat{B}_{nr} - B_r)}{k} \ = \ \sum _{r=1}^k \gamma _{nr}^\mathrm{S} \, \mathbb {V}_{nr} \circ B_r \ = \ \mathbb {V}_n^\mathrm{S}. \end{aligned}$$

For $\mathrm{Z} = \mathrm{M}, \mathrm{L}$ it suffices to show that for any fixed number $b \ne 0$ and

$$\begin{aligned} p_n^\mathrm{Z}(t) \ := \ t + \frac{\mathbb {V}_n^\mathrm{Z}(t) + b t^\delta (1-t)^\delta }{\sqrt{n}} \end{aligned}$$

the following statements are true: If $b < 0$, then with asymptotic probability one,

$$\begin{aligned} \left. \begin{array}{c} \displaystyle \inf _{t \in (0,1)} \left( n \widehat{B}_n(t) - \sum _{r=1}^k N_{nr} B_r(p_n^\mathrm{M}(t)) \right) \\ \displaystyle \inf _{t \in (0,1)} \, L_n'(t,p_n^\mathrm{L}(t)) \end{array}\right\} \ \ge \ 0. \end{aligned}$$

(8)

If $b > 0$, then with asymptotic probability one,

$$\begin{aligned} \left. \begin{array}{c} \displaystyle \sup _{t \in (0,1)} \left( n \widehat{B}_n(t) - \sum _{r=1}^k N_{nr} B_r(p_n^\mathrm{M}(t)) \right) \\ \displaystyle \sup _{t \in (0,1)} \, L_n'(t,p_n^\mathrm{L}(t)) \end{array}\right\} \ \le \ 0. \end{aligned}$$

(9)

Here we use the conventions that $L_n'(t,\cdot ) := \infty$ and $B_r := 0$ on $(-\infty ,0]$ while $L_n'(t,\cdot ) := -\infty$ and $B_r := 1$ on $[1,\infty )$.

To verify these claims, we split the interval (0, 1) into $(0,c_n]$, $[c_n,1-c_n]$ and $[1-c_n,1)$ with numbers $c_n \in (0,1/2)$ to be specified later, where $c_n \downarrow 0$.

On $[c_n,1-c_n]$ we utilize Lemma 7: For $t \in [c_n, 1 - t_n]$ and $p \in (0,1)$ such that $|p - t| \le t(1-t)/2$ we may write

$$\begin{aligned}&n \widehat{B}_n(t) \ - \sum _{r=1}^k N_{nr} B_r(p) \\&\quad = \ \sum _{r=1}^k \sqrt{N_{nr}} \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^k N_{nr}(B_r(p) - B_r(t)) \\&\quad = \ \sum _{r=1}^k \sqrt{N_{nr}} \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^m N_{nr} \beta _r(t) (p - t) + \rho _n^\mathrm{M}(t,p) \\&\quad = \ \sum _{r=1}^k N_{nr} \beta _r(t) \left( \frac{\mathbb {V}_n^\mathrm{M}(t)}{\sqrt{n}} - (p - t) \right) + \rho _n^\mathrm{M}(t,p) \end{aligned}$$

and

$$\begin{aligned} L_n'(t,p)&= \ \sum _{r=1}^k \sqrt{N_{nr}} w_r(p) \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^k N_{nr} w_r(p) (B_r(p) - B_r(t)) \\&= \ \sum _{r=1}^k \sqrt{N_{nr}} w_r(t) \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^k N_{nr} w_r(t) \beta _r(t) (p - t) + \rho _n^\mathrm{L}(t,p) \\&= \ \sum _{r=1}^k N_{nr} w_r(t) \beta _r(t) \left( \frac{\mathbb {V}_n^\mathrm{L}(t)}{\sqrt{n}} - (p - t) \right) + \rho _n^\mathrm{L}(t,p) , \end{aligned}$$

where

$$\begin{aligned} |\rho _n^\mathrm{M}(t,p)|&\le \ \frac{O(n) |p - t|^2}{t(1-t)} , \\ |\rho _n^\mathrm{L}(t,p)|&\le \ \frac{O_p(\sqrt{n}) t^{\delta } (1 - t)^{\delta } |p - t|}{t(1-t)} + \frac{O(n) |p - t|^2}{t^2(1-t)^2}. \end{aligned}$$

Note that for $t \in [c_n,1-c_n]$,

$$\begin{aligned} \frac{\bigl | p_n^\mathrm{Z}(t) - t \bigr |}{t(1-t)} \ \le \ \frac{O_p(1) t^\delta (1 - t)^{\delta }}{\sqrt{n} \, t(1-t)} \ \le \ \frac{O_p(1)}{\sqrt{n} \, c_n^{1-\delta }}. \end{aligned}$$

Hence we choose $c_n$ such that $c_n \downarrow 0$ but $n c_n^{2(1-\delta )} \rightarrow \infty$. With this choice, we may conclude that uniformly in $t \in [c_n,1-c_n]$,

$$\begin{aligned} \bigl | \rho _n^\mathrm{M}(t,p_n^\mathrm{M}(t)) \bigr |&\le \ O_p(c_n^{\delta -1}) t^\delta (1-t)^\delta , \\ \bigl | \rho _n^\mathrm{L}(t,p_n^\mathrm{L}(t)) \bigr |&\le \ O_p(c_n^{\delta -1}) t^{\delta -1}(1-t)^{\delta -1}. \end{aligned}$$

On the other hand, since $\beta _1(t) + \beta _k(t) \ge \beta _1(1/2) + \beta _k(1/2) = k 2^{2-k}$,

$$\begin{aligned} \sum _{r=1}^k N_{nr} \beta _r(t)&\ge \ k 2^{2 - k} \min \{N_{n1},N_{nk}\} , \\ \sum _{r=1}^k N_{nr} w_r(t) \beta _r(t)&\ge \ \frac{k 2^{2-k} c_w}{t(1-t)} \, \min \{N_{n1},N_{nk}\}. \end{aligned}$$

Consequently,

$$\begin{aligned}&n \widehat{B}_n(t) \ - \sum _{r=1}^k N_{nr} B_r(p_n^\mathrm{M}(t)) \\&\quad = \ \sum _{r=1}^k N_{nr} \beta _r(t) \frac{- b t^\delta (1-t)^\delta }{\sqrt{n}} + \rho _n^\mathrm{M}(t,p_n^\mathrm{M}(t)) \\&\quad = \ \sum _{r=1}^m N_{nr} \beta _r(t) \frac{t^\delta (1-t)^\delta }{\sqrt{n}} \left( - b + O_p(c_n^{\delta -1} n^{-1/2}) \kappa _n^\mathrm{M}(t) \right) \end{aligned}$$

and

$$\begin{aligned} L_n'(t,p_n^\mathrm{L}(t))&= \ \sum _{r=1}^k N_{nr} w_r(t) \beta _r(t) \frac{-b t^\delta (1-t)^\delta }{\sqrt{n}} + \rho _n^\mathrm{L}(t,p_n^\mathrm{L}(t)) \\&= \ \sum _{r=1}^k N_{nr} w_r(t) \beta _r(t) \frac{t^\delta (1-t)^\delta }{\sqrt{n}} \Bigg ( - b + O_p\left( c_n^{\delta -1} n^{-1/2}\right) \kappa _n^\mathrm{L}(t) \Bigg ) \end{aligned}$$

for some random functions $\kappa _n^\mathrm{M}, \kappa _n^\mathrm{L} : [c_n,1-c_n] \rightarrow [-1,1]$. These considerations show that (8) and (9) are satisfied with $[c_n,1-c_n]$ in place of (0, 1).

It remains to verify (8) and (9) with $(0,c_n]$ in place of (0, 1); the interval $[1-c_n,1)$ may be treated analogously. Note first that for $2 \le r \le k$,

$$\begin{aligned} B_r(t) \ \le \ B_2(t) \ \le \ k(k-1) t^2/2 \quad \text {and}\quad \beta _r(t) \ \le \ k 2^{k-1} t , \end{aligned}$$

so

$$\begin{aligned} \bigl | B_r(p) - B_r(t) \bigr | \ = \ \Bigl | \int _t^p \beta _r(u) \, \mathrm{d}u \Bigr | \ \le \ O(\max (p,t)) (p - t). \end{aligned}$$

Furthermore, since $B_1(t) = 1 - (1 - t)^k$,

$$\begin{aligned} B_1(p) - B_1(t) \ = \ k (p - t) + O(\max (t,p)) (p - t). \end{aligned}$$

Hence for $t \in (0,c_n]$ and $p \in (0,2c_n]$,

$$\begin{aligned}&n \widehat{B}_n(t) \ - \sum _{r=1}^k N_{nr} B_r(p) \\&\quad = \ \sum _{r=1}^k \sqrt{N_{nr}} \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^k N_{nr}(B_r(p) - B_r(t)) \\&\quad = \ - N_{n1} k (p - t) + \rho _n^\mathrm{M}(t,p) \end{aligned}$$

and

$$\begin{aligned} L_n'(t,p)&= \ \sum _{r=1}^k \sqrt{N_{nr}} w_r(p) \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^k N_{nr} w_r(p) (B_r(p) - B_r(t)) \\&= \ - N_{n1} w_1(p) k (p - t) + \rho _n^\mathrm{L}(t,p) , \end{aligned}$$

where

$$\begin{aligned} |\rho _n^\mathrm{M}(t,p)|&\le \ o_p(\sqrt{n}) t^\delta + O(n c_n) (p - t) , \\ |\rho _n^\mathrm{L}(t,p)|&\le \ o_p(\sqrt{n}) p^{-1} t^\delta + O(n c_n) p^{-1} (p - t). \end{aligned}$$

Note also that

$$\begin{aligned} \sup _{t \in (0,c_n]} \Bigl | \frac{\sqrt{n}(p_n^\mathrm{Z}(t) - t)}{t^\delta (1-t)^\delta } - b \Bigr | \ \rightarrow _p \ 0. \end{aligned}$$

In particular, $\sup _{t \in (0,c_n]} p_n^\mathrm{Z}(t) = c_n + o_p(n^{-1/2} c_n^\delta ) = c_n (1 + o_p(1))$, and in case of $b > 0$, $\mathop {\mathrm {I\!P}}\nolimits \bigl ( p_n^\mathrm{Z}(t) > 0 \ \text {for} \ 0 < t \le c_n \bigr ) \rightarrow 1$.

In case of $b > 0$, these considerations show that for $0 < t \le c_n$,

$$\begin{aligned}&n \widehat{B}_n(t) \ - \sum _{r=1}^k N_{nr} B_r(p_n^\mathrm{M}(t)) \\&\quad = \ - N_{n1} k (p_n^\mathrm{M}(t) - t) + \rho _n^\mathrm{M}(t,p_n^\mathrm{M}(t)) \\&\quad \le \ \frac{N_{n1} k t^\delta (1-t)^\delta }{\sqrt{n}} \bigl ( -b + o_p(1) \bigr ) + o_p(\sqrt{n}) t^\delta + O(\sqrt{n} c_n) t^\delta \\&\quad \le \ \frac{N_{n1} k t^\delta (1-t)^\delta }{\sqrt{n}} \bigl ( - b + o_p(1) \bigr ) \end{aligned}$$

and

$$\begin{aligned} L_n'(t,p_n^\mathrm{L}(t))&= \ - N_{n1} w_1(p) k (p_n^\mathrm{L}(t) - t) + \rho _n^\mathrm{L}(t,p_n^\mathrm{Z}(t)) \\&\le \ \frac{N_{n1} w_1(p) k t^\delta (1-t)^\delta }{\sqrt{n}} \bigl ( - b + o_p(1) \bigr ) + o_p(\sqrt{n}) p^{-1} t^\delta \\&\quad + O(\sqrt{n} c_n) p^{-1} t^\delta \\&\le \ \frac{N_{n1} w_1(p) k t^\delta (1-t)^\delta }{\sqrt{n}} \bigl ( - b + o_p(1) \bigr ). \end{aligned}$$

Analogously, in case of $b < 0$, for any $t \in (0,c_n]$ we obtain the inequalities

$$\begin{aligned} n \widehat{B}_n(t) \!-\! \sum _{r=1}^k N_{nr} B_r(p_n^\mathrm{M}(t))&\ge {\left\{ \begin{array}{ll} \displaystyle \frac{N_{n1} k t^\delta (1-t)^\delta }{\sqrt{n}} \bigl ( - b + o_p(1) \bigr ) &{} \text {if} \ p_n^\mathrm{M}(t)> 0 , \\ 0 &{} \text {if} \ p_n^\mathrm{M}(t) \le 0 , \end{array}\right. } \\ L_n'(t,p_n^\mathrm{L}(t))&\ge {\left\{ \begin{array}{ll} \displaystyle \frac{N_{n1} w_1(p) k t^\delta (1-t)^\delta }{\sqrt{n}} \bigl ( - b + o_p(1) \bigr ) &{} \text {if} \ p_n^\mathrm{L}(t) > 0 , \\ \infty &{} \text {if} \ p_n^\mathrm{L}(t) \le 0. \end{array}\right. } \end{aligned}$$

Hence, (8) and (9) are satisfied with $(0,c_n]$ in place of (0, 1). $\square$

Proof of Theorem 3

For symmetry reasons it suffices to prove the first part about the left tails. Let $(c_n)_n$ be a sequence of numbers in (0, 1 / 2] converging to zero. Then for $t \in (0,c_n]$ and $\delta := \kappa /2 \in (0,1/2)$,

$$\begin{aligned} \bigl | \sqrt{n} \bigl ( \widehat{B}_n^\mathrm{S}(t) - t \bigr ) - \mathbb {V}_n^{(\ell )}(t) \bigr | \ = \ \left| \sum _{r=2}^k \frac{\mathbb {V}_{nr}(B_r(t))}{k \sqrt{N_{nr}/n}} \right| \ \le \ t^{2 \delta } o_p(1) \ = \ t^\kappa o_p(1). \end{aligned}$$

Concerning $\widehat{B}_n^\mathrm{M}$ and $\widehat{B}_n^\mathrm{L}$, for any $t \in (0,c_n]$ and $p \in (0,1)$,

$$\begin{aligned}&n \widehat{B}_n(t) \ - \sum _{r=1}^k N_{nr} B_r(p) \\&\quad = \ \sum _{r=1}^k \sqrt{N_{nr}} \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^k N_{nr}(B_r(p) - B_r(t)) \\&\quad = \ \sqrt{N_{n1}} \mathbb {V}_{n1}(B_1(t)) - N_{n1} k(p - t) + \rho _n^\mathrm{M}(t,p) \\&\quad = \ N_{n1} k \Bigl ( \frac{\mathbb {V}_{n1}(B_1(t))}{k \sqrt{N_{n1}}} - (p - t) \Bigr ) + \rho _n^\mathrm{M}(t,p) \end{aligned}$$

and

$$\begin{aligned} L_n'(t,p)&= \ \sum _{r=1}^k \sqrt{N_{nr}} w_r(p) \mathbb {V}_{nr}(B_r(t)) - \sum _{r=1}^k N_{nr} w_r(p) (B_r(p) - B_r(t)) \\&= \ \sqrt{N_{n1}} w_1(p) \mathbb {V}_{n1}(B_1(t)) - N_{n1} w_1(p) k (p - t) + \rho _n^\mathrm{L}(t,p) \\&= \ N_{n1} k w_1(p) \left( \frac{\mathbb {V}_{n1}(B_1(t))}{k \sqrt{N_{n1}}} - (p - t) \right) + \rho _n^\mathrm{L}(t,p) , \end{aligned}$$

where

$$\begin{aligned} |\rho _n^\mathrm{M}(t,p)|&\le \ o_p(\sqrt{n}) t^{2\delta } + O(n) \max (t,p) (p - t) , \\ |\rho _n^\mathrm{L}(t,p)|&\le \ o_p(\sqrt{n}) p^{-1} t^{2\delta } + O(n) p^{-1} \max (t,p) (p - t). \end{aligned}$$

Now we proceed similarly as in the proof of Theorem 2, defining

$$\begin{aligned} p_n(t) \ := \ t + \frac{\mathbb {V}_n^{(\ell )}(t) + b t^\kappa }{\sqrt{n}} \end{aligned}$$

for some fixed $b \ne 0$. Note that for $t \in (0,c_n]$,

$$\begin{aligned} |p_n(t) - t| \ \le \ o_p(n^{-1/2}) t^\delta + O(n^{-1/2}) t^\kappa \ = \ o_p(n^{-1/2}) t^\delta , \end{aligned}$$

because $\kappa > \delta$. Note also that

$$\begin{aligned} t + \frac{\mathbb {V}_n^{(\ell )}(t)}{\sqrt{n}} \ = \ t + \frac{\mathbb {V}_{n1}(B_1(t))}{k \sqrt{N_{n1}}} \ = \ t - \frac{1 - (1-t)^k}{k} + \frac{\widehat{B}_{n1}(t)}{k} \ > \ 0 \quad \text {on} \ (0,1) , \end{aligned}$$

because $\widehat{B}_{n1} \ge 0$ and $t \mapsto t - (1 - (1-t)^k)/k$ is strictly convex on [0, 1] with derivative 0 at 0. Thus $p_n(t) > 0$ for all $t \in (0,c_n]$ in case of $b > 0$.

In case of $b > 0$, we may conclude that

$$\begin{aligned}&n \widehat{B}_n(t) \ - \sum _{r=1}^k N_{nr} B_r(p_n(t)) \\&\quad = \ N_{n1} k \frac{-b t^\kappa }{\sqrt{n}} + \rho _n^\mathrm{M}(t,p_n(t)) \\&\quad \le \ \frac{N_{n1} k}{\sqrt{n}} \bigl ( -b t^\kappa + o_p(1) t^{2\delta } + O(1) (t + o_p(n^{-1/2}) t^\delta ) t^\delta \bigr ) \\&\quad \le \ \frac{N_{n1} k t^\kappa }{\sqrt{n}} \bigl ( -b + o_p(1) \bigr ) , \end{aligned}$$

and

$$\begin{aligned} L_n'(t,p_n(t))&\le \ \frac{N_{n1} k w_1(p) t^\kappa }{\sqrt{n}} \bigl ( -b + o_p(1) \bigr ). \end{aligned}$$

Hence for any fixed $b > 0$,

$$\begin{aligned} \mathop {\mathrm {I\!P}}\nolimits \left( \sqrt{n} (\widehat{B}_n^\mathrm{Z}(t) - t) \le \mathbb {V}_n^{(\ell )}(t) + b t^\kappa \ \text {for} \ t \in (0,c_n] \right) \ \rightarrow \ 0. \end{aligned}$$

Similarly we can show that for any fixed $b < 0$, with asymptotic probability one, $\sqrt{n} (\widehat{B}_n^\mathrm{Z}(t) - t) \le \mathbb {V}_n^{(\ell )}(t) + b t^\kappa$ for all $t \in (0,c_n]$. $\square$

Proof of Corollary 4

It follows from Proposition 6 that

$$\begin{aligned} \sup _{1 \le r \le k, \, u \in [0,1]} |\mathbb {V}_{nr}(u)| \ = \ O_p(1). \end{aligned}$$

Together with (5) this entails that $\sup _{t \in [0,1]} \bigl | \mathbb {V}_n^\mathrm{Z}(t) - \widetilde{\mathbb {V}}_n^\mathrm{Z}(t) \bigr | \rightarrow _p 0$, where $\widetilde{\mathbb {V}}_n^\mathrm{Z} := \sum _{r=1}^k \gamma _r^\mathrm{Z} \, \mathbb {V}_{nr} \circ B_r$. But $\gamma _r^\mathrm{Z} \equiv 0$ whenever $\pi _r = 0$. In case of $\pi _r > 0$ it follows from Proposition 6 that $\mathbb {V}_{nr}$ converges in distribution to $\mathbb {V}_r$. Consequently, $\widetilde{\mathbb {V}}_n^\mathrm{Z}$ converges in distribution to the Gaussian process $\mathbb {V}^\mathrm{Z} = \sum _{r=1}^k \gamma _r^\mathrm{Z} \, \mathbb {V}_r \circ B_r$. $\square$

Proof of Theorem 5

The asserted inequalities follow from Jensen’s inequality. On the one hand, it follows from $w_r = \beta _r / (B_r(1 - B_r))$ and $\sum _{r=1}^k \beta _r \equiv k$ that

$$\begin{aligned} K^\mathrm{S}(t)&= \ \frac{1}{k} \sum _{r=1}^k \frac{\beta _r(t)}{k} \cdot (\pi _r w_r(t))^{-1} \\&\ge \ \frac{1}{k} \left( \sum _{r=1}^k \frac{\beta _r(t)}{k} \cdot \pi _r w_r(t) \right) ^{-1} \\&= \ \left( \sum _{r=1}^k \pi _r \beta _r(t) w_r(t) \right) ^{-1} \ = \ K^\mathrm{L}(t). \end{aligned}$$

Equality holds if, and only if,

$$\begin{aligned} \pi _1 w_1(t) = \pi _2 w_2(t) = \cdots = \pi _k w_k(t). \end{aligned}$$

But

$$\begin{aligned} w_1(t) \ = \ \frac{k}{(1-t)( 1 - (1 - t)^k)} \quad \text {and}\quad w_k(t) \ = \ \frac{k}{t(1 - t^k)} , \end{aligned}$$

so

$$\begin{aligned} \frac{w_k(t)}{w_1(t)} \ = \ \frac{(1-t)(1 - (1-t)^k)}{t(1-t^k)} \ = \ \frac{\sum _{j=0}^{k-1} (1-t)^j}{\sum _{j=0}^{k-1} t^j} \end{aligned}$$

is strictly decreasing in t. Hence there is at most one solution of the equation $\pi _1 w_1(t) = \pi _k w_k(t)$.

Similarly, with $a_r(t) := \pi _r \beta _r(t) \big / \sum _{s=1}^k \pi _s \beta _s(t)$,

$$\begin{aligned} K^\mathrm{M}(t)&= \ \sum _{r=1}^k \pi _r \beta _r(t) \cdot w_r(t)^{-1} \Big / \left( \sum _{s=1}^k \pi _s \beta _s(t) \right) ^2 \\&= \ \sum _{r=1}^k a_r(t) \cdot w_r(t)^{-1} \Big / \sum _{s=1}^k \pi _s \beta _s(t) \\&\ge \ \left( \sum _{r=1}^k a_r(t) w_r(t) \right) ^{-1} \Big / \sum _{s=1}^k \pi _s \beta _s(t) \\&= \ \left( \sum _{r=1}^k \pi _r \beta _r(t) w_r(t) \right) ^{-1} \ = \ K^\mathrm{L}(t). \end{aligned}$$

Here the inequality is strict unless

$$\begin{aligned} w_1(t) = w_2(t) = \cdots = w_k(t). \end{aligned}$$

But $w_1(t) = w_k(t)$ implies that $t = 1/2$. Moreover, $w_1(1/2) = 2k/(1 - 2^{-k})$ and

$$\begin{aligned} w_{k-1}(1/2) \ = \ \frac{2k(k-1)}{(k+1)(1 - (k+1)2^{-k})} \end{aligned}$$

are identical if, and only if, $k^2 + k + 2 = 2^{k+1}$. But $2^{k+1} = 2 \sum _{j=0}^k \left( {\begin{array}{c}k\\ j\end{array}}\right)$ is strictly larger than $2(1 + k + k(k-1)/2) = k^2 + k + 2$ if $k \ge 3$.

As to the ratios $E^\mathrm{Z}(t) := K^\mathrm{Z}(t)/K^\mathrm{L}(t)$, note first that

$$\begin{aligned} E^\mathrm{S}(t)&= \ \sum _{r=1}^k \frac{B_r(t)(1 - B_r(t))}{k^2 \pi _r} \sum _{s=1}^k \pi _s \beta _s(t) w_s(t) \\&\ge \ \min _{r,s=1,\ldots ,k} \frac{B_r(t)(1 - B_r(t)) \beta _s(t) w_s(t)}{k^2} \Big / \min _{r=1,\ldots ,k} \pi _r \\&\rightarrow \ \infty \quad \text {as} \ \min _{r=1,\ldots ,k} \pi _r \downarrow 0. \end{aligned}$$

On the other hand, with $a_r(t)$ as above,

$$\begin{aligned} E^\mathrm{M}(t) \ = \ \sum _{r=1}^k a_r(t) w_r(t)^{-1} \sum _{s=1}^k a_s(t) w_s(t) \ = \ \mathop {\mathrm {I\!E}}\nolimits (W) \mathop {\mathrm {I\!E}}\nolimits (W^{-1}) \end{aligned}$$

with a random variable W with distribution $\sum _{r=1}^k a_r(t) \delta _{w_r(t)}$. But with $\ell (t) := \min _r w_r(t)$ and $u(t) := \max _r w_r(t)$, convexity of $w \mapsto w^{-1}$ on $[\ell (t),u(t)]$ implies that

$$\begin{aligned} W^{-1} \ \le \ \frac{W - \ell (t)}{u(t) - \ell (t)} u(t)^{-1} + \frac{u(t) - W}{u(t) - \ell (t)} \ell (t)^{-1} , \end{aligned}$$

so

$$\begin{aligned} \mathop {\mathrm {I\!E}}\nolimits (W) \mathop {\mathrm {I\!E}}\nolimits (W^{-1})&\le \ \mathop {\mathrm {I\!E}}\nolimits (W) \left( \frac{\mathop {\mathrm {I\!E}}\nolimits (W) - \ell (t)}{u(t) - \ell (t)} u(t)^{-1} + \frac{u(t) - \mathop {\mathrm {I\!E}}\nolimits (W)}{u(t) - \ell (t)} \ell (t)^{-1} \right) \\&= \ \frac{\mathop {\mathrm {I\!E}}\nolimits (W) (\ell (t) + u(t) - \mathop {\mathrm {I\!E}}\nolimits (W))}{\ell (t) u(t)} \\&\le \ \frac{(\ell (t) + u(t))^2}{4 \ell (t)u(t)} \ = \ \frac{\rho (t) + \rho (t)^{-1} + 2}{4}. \end{aligned}$$

This upper bound for $E^\mathrm{M}(t)$ is attained approximately, if the distribution of W approaches the uniform distribution on $\{\ell (t),u(t)\}$. Hence we should choose $(\pi _r)_{r=1}^k$ as follows: Let r(1), r(2) be two different numbers in $\{1,\ldots ,k\}$ such that $w_{r(1)}(t) = \ell (t)$ and $w_{r(2)}(t) = u(t)$. Then let

$$\begin{aligned} \pi _r \ \approx \ {\left\{ \begin{array}{ll} \beta _{r}(t)^{-1}/(\beta _{r(1)}^{-1} + \beta _{r(2)}^{-1}) &{}\text {for} \ r \in \{r(1),r(2)\} , \\ 0 &{}\text {for} \ r \not \in \{r(1),r(2)\}. \end{array}\right. } \end{aligned}$$

The inequality $\rho (t) \le k$ follows from Lemma 7 and the fact that $\rho (t)$ remains unchanged if we replace $w_r(t)$ with $\widetilde{w}_r(t) = t(1-t) w_t(t) \in [1,k]$. $\square$