Spatially varying SAR models and Bayesian inference for high-resolution lattice data

Abstract

We discuss a new class of spatially varying, simultaneous autoregressive (SVSAR) models motivated by interests in flexible, non-stationary spatial modelling scalable to higher dimensions. SVSAR models are hierarchical Markov random fields extending traditional SAR models. We develop Bayesian analysis using Markov chain Monte Carlo methods of SVSAR models, with extensions to spatio-temporal contexts to address problems of data assimilation in computer models. A motivating application in atmospheric science concerns global CO emissions where prediction from computer models is assessed and refined based on high-resolution global satellite imagery data. Application to synthetic and real CO data sets demonstrates the potential of SVSAR models in flexibly representing inhomogeneous spatial processes on lattices, and their ability to improve estimation and prediction of spatial fields. The SVSAR approach is computationally attractive in even very large problems; computational efficiencies are enabled by exploiting sparsity of high-dimensional precision matrices.

1 Introduction

Applied studies in multiple areas involving spatial and spatio-temporal systems increasingly challenge our modelling and computational abilities as data volumes increase. Similarly, as spatial scales move to increasingly high resolution, there is an almost inevitable increase in complexity and diversity of dependency patterns. Traditional spatial models often fail to capture the complex dependence structure in the data, whereas more complicated spatially adaptive models are usually so computationally demanding that their application potential is limited.

Challenging motivating applications arise in inverse estimation and data assimilation in computer modelling. A specific applied context is in atmospheric chemistry, where spatially and temporally aggregated satellite sensor measurements of atmospheric carbon monoxide (CO) concentrations are to be used to evaluate and integrate with predictions from a computer model; one main goal is prediction of ground-level source fluxes of CO at regional scales around the globe. A chemical transport model—a deterministic, forward simulation computer model—determines responses of the atmospheric CO concentrations to the regional source fluxes, and data assimilation aims to combine these computer model predictions with actual satellite retrieval data representing globally varying CO levels in the atmosphere over time. There is an increasing interest in analyzing the satellite retrievals at finer spatial and temporal resolutions to better understand process-level drivers of emissions (Arellano et al. 2004, 2006; Chevallier et al. 2005a, b; Chevallier 2007; Chevallier et al. 2009a, b; Meirink et al. 2008; Kopacz et al. 2009, 2010). Global lattices have $10^5$–$10^6$ grid points and applications involve repeat observations over the year; as resolution increases, the interest in dealing with spatial inadequacies is increasing. Predictions from computer models of atmospheric chemistry have errors with spatial dependencies due to various reasons, including assumed forms of transport fields that are inputs to the models. Our modelling approach aims to address the need to incorporate such unstructured dependencies through spatially non-stationary fields on the lattice.

A traditional approach to lattice data uses continuously indexed geostatistical spatial process models after spatially aggregating over the areal units that define the lattice grid cells (or points). These approaches do not, however, scale well with lattice dimension. For example, deformation approaches (Sampson and Guttorp 1992), spatial moving-average models (Higdon et al. 1999) and other non-stationary covariance models incorporate spatial dependencies through the covariance structure of a Gaussian process. Bayesian posterior sampling algorithms for these models are prohibitively slow for large lattices as they require full (non-sparse) matrix inversions/Cholesky decompositions in every iteration. The computational cost is $\mathcal {O}(n^3)$ floating point operations (FLOPs) where $n$ is the number of point realizations from the continuous spatial process. Typically, $n$ is much larger than the lattice size since the regional aggregations use Monte Carlo integration with many points from each areal unit. Dimension reduction approximations (e.g., Higdon 1998; Gneiting 2002; Fuentes 2002) are rarely applicable here, due to the need to integrate the resulting continuous process over the region.

In contrast, Markov random field (MRF) models offer a more useful framework for high-resolution spatial lattice data. Gaussian MRF models involve sparse structure of defining precision matrices of Gaussian distributions. This yields reductions in computational complexity—typically, from $\mathcal {O}(n^3)$ to $\mathcal {O}(nb^2)$ where $b$ is the minimal bandwidth of the sparse matrices involved (Rue 2001; Rue and Held 2005; Golub and Loan 1996). Construction of meaningful sparse precision matrices for spatial lattices is, however, non-trivial. One general approach is conditional autoregressive (CAR) modelling (Besag 1974; Besag and Kooperberg 1995), where all conditional distributions are specified as regressions on the neighboring realizations. This approach exploits the connection between the Gaussian precision matrix and the conditional distributions to model spatial associations, since more concentrated conditional distributions imply higher spatial association in the neighborhoods, and vice-versa. Sparsity comes through local parametrization of the conditionals. However, symmetry and positive-definiteness of the CAR precision matrix remain a major concern for extensions beyond simple parametric forms. Two noteworthy adaptive extensions are due to Brewer and Nolan (2007) and Reich and Hodges (2008) who have developed non-stationary generalizations of the intrinsic CAR model. Another relevant development is in  Dobra et al. (2011), where priors for precision matrices of Gaussian graphical models (Jones et al. 2005; Jones and West 2005) use the CAR structure to adaptively incorporate spatial non-stationarities.

A more attractive and, for larger problems, computationally feasible approach is based on extensions of simultaneous autoregressive (SAR) models (Whittle 1954). SAR models are MRFs that are increasingly popular in spatial econometrics (Anselin 1988) and other areas, but have as yet been less well-explored and exploited in mainstream spatial statistics in environmental and natural science applications. Our interests in the SAR model stem from its naturally symmetric and positive-definite precision matrix, the corresponding sparsity structure, and the ability to embed the basic structure in more elaborate hierarchical non-stationary extensions. To enable this development, we introduce the class of spatially varying SAR (SVSAR) models. We do this by modelling observed spatial data on the lattice as arising from conditional SAR models, and then by modelling the spatial dependence parameter field of this data-level model as itself arising as a latent SAR model. This hierarchical Markov random field structure thus incorporates “locally stationary” features within a “globally non-stationary” framework. We develop Markov chain Monte Carlo (MCMC) methods for Bayesian model exploration, fitting and prediction, with extensions to spatio-temporal contexts.

Section 2 discusses theoretical aspects of SAR models and their sparse Markovian structure, then Sect. 3 introduces the new SVSAR models. Section 4 discusses prior specification and MCMC analysis for SVSAR models, with some supporting technical details in the Appendix. Section 5 explores analysis of a synthetic data set generated to resemble the CO data assimilation problem; analysis of simulated data yields insights into model fit and predictive performance, and shows substantial dominance of the SVSAR model over SAR approaches. Section 6 discusses SVSAR model analysis of the real CO satellite imagery data and assimilation with computer model predictions. Some summary comments appear in Sect. 7.

2 Simultaneous autoregressive models

Regions $V = \{A_1, \ldots , A_n\}$ are said to form a lattice of an area $D$ if $A_1 \cup \ldots \cup A_n = D$ and $A_i \cap A_j = \emptyset$ for all $i \ne j$. For each region $A_i,$ suppose that a scalar quantity $y_i$ is measured over that region. An SAR model on $y = (y_1, \ldots , y_n)'$ is defined via a system of autoregressive equations

$$\begin{aligned} y_i \; = \; \mu _i + \sum _{j: j \ne i} \phi \; \frac{w_{ij}}{w_{i+}} \; (y_j - \mu _j) + \epsilon _i, \;\; \epsilon _i \; \sim \; {N}(0,\tau ^2) , \quad i=1,\ldots ,n, \end{aligned}$$

(1)

where $w_{ii} = 0$ and $w_{i+} = \sum _j w_{ij}$. Here $\phi$ is often referred to as the spatial dependence parameter. The inherent sparse structure of SAR models is based on many of the $w_{ij}$ being zero, so that each $y_i$ is regressed on only a neighboring subset of $y_j$ values corresponding to those non-zero values. For example,

$$\begin{aligned} w_{ij} = \left\{ \begin{array}{l@{\quad }l} 1, &{} \text{ if } \; A_i \; \text{ shares } \text{ a } \text{ common } \text{ edge } \text{ or } \text{ border } \text{ with } \; A_j \; \text{ for } \quad i \ne j,\\ 0, &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(2)

In addition, non-zero $w_{ij}$ values may incorporate location-specific information, such as distance between centroids of neighboring regions. The matrix $W = (w_{ij})$ is called the proximity matrix. The simultaneous specification in (1) leads to the joint distribution $y \sim {N}( \mu , Q^{-1} )$ (Anselin 1988) where $\mu = (\mu _1, \ldots , \mu _n)'$ and the precision matrix is

$$\begin{aligned} Q = \tau ^{-2} (I_n - \phi \widetilde{W})' (I_n - \phi \widetilde{W}) \end{aligned}$$

(3)

with $\widetilde{W} = (w_{ij}/w_{i+})$ and $I_n$ the $n \times n$ identity matrix. The SAR precision matrix $Q$ is symmetric and positive semi-definite for any proximity matrix $W,$ any $\phi$ and $\tau ^2>0$; it is positive definite if $\phi \lambda \ne 1$ for each of the eigenvalues $\lambda$ of $\widetilde{W}$. Any continuous prior on $\phi$, therefore, defines $Q$ to be almost surely positive-definite.

Conditional dependence neighborhoods implied by the simultaneous autoregressive specification (1) are larger than the neighborhoods defined by the $w_{ij}$. Refer to the neighborhoods defined by the proximity matrix as W-neighborhoods. Two regions are conditionally dependent if they are W-neighbors or if they have least one common W-neighbor. Consequently, $Q$ is less sparse than $W$. To see this, note that the (complete) conditional distribution of $y_i$ given $y_{-i} = (y_1, \ldots , y_{i-1}, y_{i+1}, \ldots , y_n)'$ is normal with

$$\begin{aligned} E(y_i \mid y_{-i}) = \mu _i- Q_{ii}^{-1} \sum _{j: j \ne i} Q_{ij} \ (y_j-\mu _j) \quad \mathrm and \quad V(y_i \mid y_{-i}) = Q_{ii}^{-1}. \end{aligned}$$

(4)

For any $i\ne j,$ note that

$$\begin{aligned} \tau ^2 Q_{ij} = - \phi \ \left( \frac{w_{ij}}{w_{i+}} + \frac{w_{ji}}{w_{j+}} \right) + \phi ^2 \, \sum _k \frac{w_{ki} w_{kj}}{w_{k+}^2} \end{aligned}$$

(5)

while the diagonal elements are defined by

$$\begin{aligned} \tau ^2 Q_{ii} = 1+\phi ^2 \ \sum _k \frac{w^2_{ki}}{w_{k+}^2}. \end{aligned}$$

(6)

Now $y_i$ is conditionally independent of $y_j$ ($i \ne j$) if, and only if, $Q_{ij}=0.$ The non-zero values define the conditional dependence graph of the joint distribution (e.g., Jones et al. 2005; Jones and West 2005). Assuming the practically relevant cases of $\phi \ne 0,$ we see that $Q_{ij}\ne 0$ if $w_{ij}$ and $w_{ji}$ are non-zero (via first order $W$-terms in $Q_{ij}$), or if there exists a $k$ such that both $w_{ki}$ and $w_{kj}$ are non-zero (via second order product of $W$-terms in $Q_{ij}$). In other words, $y_i$ and $y_j$ ($i \ne j$) are conditionally dependent in the SAR model if $A_i$ and $A_j$ are W-neighbors, or if they have a common W-neighbor $A_k$. We refer to the neighborhoods in the SAR conditional dependence graph as the G-neighborhoods. If the W-neighborhoods are defined by centered $(2p+1)\times (2p+1)$ squares on a regular lattice, all interior G-neighborhoods are centered $(4p+1)\times (4p+1)$ squares; see Fig. 1 for an example with $p=1$.

Fig. 1

a Centered $(2p+1)\times (2p+1)$ W-neighborhood of a SAR model on a regular lattice with $p=1$. b Corresponding interior G-neighborhoods that are centered $(4p+1)\times (4p+1)$ squares

The SAR complete conditional distributions are important in generalizing the model for spatial non-stationarities. Without loss of generality here, suppose a zero mean process, setting $\mu _i = 0$ for all $i$. Defined by the expressions in (4), (5) and (6), note that the location and concentration of $p(y_i|y_{-i})$ are monotonic in $\phi \in (0,1)$. For $\phi$ close to zero, the conditional mean is close to zero and the conditional variance is close to $\tau ^2$. As $\phi$ increases to one, the conditional mean increases to a weighted average of the $y_j$ in the G-neighborhood of $A_i$, and the conditional variance decreases. The parameter $\tau$ scales conditional variability. All conditional distributions behave in the same way. That is, increasing $\phi$ and decreasing $\tau ^2$ shift the conditional means towards their neighborhood averages (under the assumption of zero $\mu _i$), while decreasing conditional variances. The resulting conditional distributions are more concentrated at each lattice point, which generates a smoother random field. Our generalized SVSAR model developed in the next section defines a parametrization that allows varying spatial smoothness in different parts of the lattice through varying conditional distributions.

Note that it is not essential to restrict to $0<\phi <1$ to define a valid model. An SAR model with $\phi$ larger than but close to $1$ represents a strongly spatially smooth random field, whereas a small negative value of $\phi$ gives rise to negligible spatial dependencies. In both cases, the conditional distributions behave as intended; in addition, the precision matrices are symmetric and positive-definite.

3 Spatially varying simultaneous autoregressive models

Our spatially varying generalization of the SAR model has region-specific defining parameters, allowing spatial dependencies and levels of smoothness to vary across the lattice. In region $A_i,$ region-specific parameters $\phi _i$ and $\tau ^2_i$ are introduced. The SVSAR system of simultaneous autoregressive equations is then

$$\begin{aligned} y_i \; = \; \mu _i + \sum _{j: j \ne i} \phi _i \; \frac{w_{ij}}{w_{i+}} \; (y_j - \mu _j) + \epsilon _i, \;\; \epsilon _i \; \sim \; {N} (0,\tau _i^2) , \;\; i=1,\ldots ,n. \end{aligned}$$

(7)

The new hierarchical model adopts an SAR prior on the $\phi$-field defined by the location-specific $\phi _i$ quantities; this allows the imposition of spatial smoothness on the field of $\phi _i$ coefficients. Specifically, we adopt the following system of simultaneous autoregressive equations:

$$\begin{aligned} \phi _i \; = \; m + \sum _{j: j \ne i} \rho \; \frac{w_{ij}}{w_{i+}} \; (\phi _j - m) + e_i, \;\; e_i \; \sim \; {N}(0,\sigma ^2) , \;\; i=1,\ldots ,n. \end{aligned}$$

(8)

With $\phi = (\phi _1, \ldots , \phi _n)'$, $\varDelta _{\phi } = \text {diag}(\phi )$, $\varGamma _{\phi } = \text{ diag }(\tau _1^2, \ldots , \tau ^2_n)$ and $1_n$ denoting the $n \times 1$ vector of ones, the full hierarchical model then has the form

$$\begin{aligned} y \mid \phi&\sim {N} ( \mu , \varOmega _\phi ^{-1} ), \qquad \varOmega _\phi = (I_n - \varDelta _{\phi } \widetilde{W})' \, \varGamma ^{-1}_{\phi } \, (I_n - \varDelta _{\phi } \ \widetilde{W}), \end{aligned}$$

(9)

$$\begin{aligned} \phi&\sim {N}( m 1_n, \varLambda ^{-1}), \qquad \varLambda = \sigma ^{-2} (I_n-\rho \widetilde{W})' (I_n-\rho \widetilde{W}). \end{aligned}$$

(10)

The parameters $\rho$ and $\sigma ^2$ determine the level of spatial smoothness in the $\phi$ field, while the scalar $m$ defines the mean. Setting $\sigma ^2 = 0$ is equivalent to using the spatially homogeneous SAR model from Sect. 2 where each $\phi _i = m$. In the data field model of Eq. (9), the precision matrix $\varOmega _{\phi }$ is symmetric, and almost surely positive-definite under the continuous prior on the $\phi$ field. The $\phi$ field precision matrix $\varLambda$ has the same sparsity structure as $\varOmega _{\phi }$. In both cases, the $G$-neighborhoods for a given $W$ are as discussed in Sect. 2.

One useful extension of the general model is to link the two parameters $(\phi _i,\tau _i)$ within region, setting $\tau ^2_i = \tau ^2_i(\phi _i)$ to be a decreasing function of $\phi _i.$ This reflects the fact that simultaneous increases in $\phi _i$ and decreases in $\tau ^2_i$ are necessary for increasing spatial smoothness. Our models introduce a specific form of dependence, namely $\tau ^2_i(\phi _i) = \tau ^2 \, \exp {(-\kappa \phi _i)}$ for some $\kappa >0$ to do this.

Adaptivity to locally varying spatial associations can be observed through the implied complete conditional distributions for the $(y_i|y_{-i})$ as for the SAR model. The SVSAR implies that the conditional dependence graphical structure has moments as in (4), but now the controlling elements of $Q$ are given for each $i$ and $j\ne i$ by

$$\begin{aligned} Q_{ij}&= - \left( \tau _i^{-2} \phi _i \frac{w_{ij}}{\, w_{i+}} + \tau _j^{-2}\phi _j \frac{w_{ji}}{ \, w_{j+}} \right) + \sum _k \tau _k^{-2} \phi _k^2 \, \frac{w_{ki} \, w_{kj}}{\, w_{k+}^2}, \\ Q_{ii}&= \tau _i^{-2} + \sum _k \tau _k^{-2} \phi _k^2 \, \frac{w_{ki}^2}{\ w_{k+}^2}. \end{aligned}$$

For given $\tau _i$ the conditional mean and variance of $y_i$ depend functionally on those $(\phi _j,\tau _j)$ values in its G-neighborhood. If (10) defines a spatially smooth $\phi$ field then all $\phi _j$ values in the G-neighborhood are similar; relationships between the conditional distributions with $\phi _j$ in the G-neighborhood are similar to the relationships between the SAR conditionals and $\phi$, as discussed in Sect. 2. In a neighborhood where the local $\phi _j$ values are small, the conditional mean of $y_i$ will be close to $\mu _i$ and the conditional variance close to $\tau _i^2$. The conditional distribution is relatively flat in this case; consequently, there is little local smoothing. If the $\phi _j$ values in a neighborhood are closer to one, the conditional mean is closer to a weighted average of the G-neighboring $y_j$ and the conditional variance is smaller than $\tau _i^2$. Here, the conditional distribution is concentrated around the neighboring realizations and, therefore, it causes strong local smoothing. In neighborhoods between these two extremes, as the $\phi$-values change from zero to one, the conditional distributions shift in location from the overall regional average $\mu _i$ to the neighborhood average realizations and become more concentrated. As a general matter, cases where the $\phi$ field lacks spatial smoothness are of far less practical importance.

4 Prior specification and posterior computation

In Sect. 3, we discussed how local smoothness and global adaptability in the SVSAR $\phi$ field effectively accommodates non-stationarities in the data. This is reflected in prior distributions on $\rho$ and $\sigma ^2$. We use a Beta prior for $\rho$ with density concentrated near one, and a conditionally conjugate inverse-Gamma prior for $\sigma ^2$ with density concentrated over small positive values. Our prior for $m$ reflects our belief on average spatial smoothness in the data field, either through a truncated normal distribution, or through a uniform distribution on $(0,1)$. In more elaborate models, $\mu$ could be specified via a regression model based on candidate predictor variables; such context specific extensions are deferred to future work. Finally, we use a conditionally conjugate inverse-Gamma prior for the global scaling $\tau ^2$ appearing in the region-specific $\tau ^2_i = \tau ^2_i(\phi _i)$ terms.

MCMC involves operations with matrices $\varOmega _{\phi }$ and $\varLambda$ whose sparsity is controlled by $W$. For example, band-Cholesky decompositions of these sparse matrices are much faster than complete Cholesky decompositions. On an $R \times C$ rectangular lattice with proximity matrix $W$ defined by centered $(2p+1)\times (2p+1)$ neighborhoods, computing band-Cholesky decomposition takes $\mathcal {O}(n_1^3 n_2 p^2)$ FLOPs where $n_1 = \min (R,C)$ and $n_2 = \max (R,C)$ (Rue 2001; Rue and Held 2005). Typically, $p$ is much smaller than $R$ and $C$ so this yields what can be a very substantial $\mathcal {O}(p^2/n_2^2)$ reduction in computing time.

Conditional updating of the $\phi$ field is the key and most challenging task. Consider first the case of small lattices. Given values of $( y,\mu ,\tau ^2,m,\rho ,\sigma ^2)$ together denoted simply by $-$, the density of the complete conditional posterior for $\phi$ is

$$\begin{aligned} p(\phi \mid - ) \; \propto \; |\varOmega _{\phi }|^{1/2} \; \exp { \left\{ -\frac{1}{2} \; \left( \phi ' Q_{\phi } \phi - 2 \phi ' b_{\phi } + c_{\phi } \right) \right\} } \end{aligned}$$

where $Q_{\phi } = (\varDelta _a \varGamma _{\phi }^{-1} \varDelta _a + \varLambda )$, $b_{\phi } = \{ \varDelta _a \varGamma _{\phi }^{-1} (y-\mu ) + \varLambda (m 1_n) \}$ and $c_{\phi } = (y-\mu )' \varGamma _{\phi }^{-1} (y-\mu )$, and in which $a = \widetilde{W} (y-\mu )$ and $\varDelta _a=\mathrm diag (a);$ see the Appendix for details of this derivation. A Metropolis–Hastings (MH), complete blocked updating step has been developed and works well in our examples. We need an MH proposal distribution to generate candidate fields $\phi ^*$ based on a current field $\phi .$ Based on the form of the conditional posterior above, a natural choice is $(\phi ^*|\phi ) \sim {N}(\phi ^* | Q_{\phi }^{-1} \, b_{\phi }, Q_{\phi }^{-1})$, resembling the exact conditional. A candidate $\phi ^*$ is sampled from the proposal and then accepted with probability

$$\begin{aligned} \alpha (\phi ) = \text{ min }\left\{ 1, \;\; \frac{p(\phi ^* \mid -) \; {N}(\phi \mid Q_{\phi ^*}^{-1} \, b_{\phi ^*},Q_{\phi ^*}^{-1})}{p(\phi \mid -) \;\,\ {N}(\phi ^* \mid Q_{\phi }^{-1} \, b_{\phi }, Q_{\phi }^{-1})} \right\} . \end{aligned}$$

Note that the matrix $Q_{\phi }$ has the same sparsity structure as $\varOmega _{\phi }$ and $\varLambda$, so our comment about sparse matrix computations applies directly to the sampling and density evaluations associated with this acceptance ratio.

Complete blocked updating of $\phi$ does not work well for large lattices. The Gaussian proposal tends to become increasingly dissimilar to the conditional distribution as lattice size increases, resulting in reduced Metropolis–Hastings acceptance probabilities. In this situation, we use blocked variants that update smaller blocks of $\phi$ conditional on the remaining values of the field; the version used here works well in yielding reasonable acceptance probabilities across our examples to date. Consider updating of $\phi _{S}$, a sub-vector of $\phi$. Now extending the conditioning values $-$ to also include current values of the remaining $\phi$ field, the conditional posterior has density $p(\phi _S | -)$ proportional to

$$\begin{aligned} |\varOmega _{\phi }|^{1/2} \ \exp { \left[ - \frac{1}{2} \left\{ \phi _{S}' \ Q_{\phi ,S,S} \ \phi _{S} - 2 \phi _{S}' \ \left( b_{\phi ,S} - Q_{\phi ,S,c[S]} \ \phi _{c[S]} \right) + c_{\phi ,S} \right\} \right] }. \end{aligned}$$

Here $c[S]$ represents the complement-set of $S$, while $u_{I}$ (or $u_{\phi ,I}$) denotes the sub-vector of the vector $u$ (or $u_{\phi }$) with elements in index set $I$. Similarly, $U_{\phi ,I,J}$ is the sub-matrix of the matrix $U_{\phi }$ with row indices in $I$ and column indices in $J$ and $c_{\phi ,I}$ denotes $c_{\phi ,I} = (y_I-\mu _I)' \ \varGamma _{\phi ,I,I}^{-1} \ (y_I-\mu _I)$. Following the ideas and strategy for complete block sampling, we propose candidate samples from a proposal distribution constructed to imitate the exponential part of this conditional for the block $S.$ That is, draw candidates $\phi _S^*$ from the normal proposal with mean $Q_{\phi ,S,S}^{-1} \ (b_{\phi ,S} - Q_{\phi ,S,c[S]} \ \phi _{c[S]})$ and precision matrix $Q_{\phi ,S,S}^{-1},$ with the resulting MH test for acceptance based on probability

$$\begin{aligned} \alpha (\phi _{S})= \text{ min } \left\{ 1,\; \frac{ p(\phi _{S}^* \mid -) \; {N} \left( \phi _{S} \mid Q_{\phi ^*,S,c[S]}^{-1} \ (b_{\phi ^*,S} - Q_{\phi ^*,S,c[S]} \ \phi _{c[S]}), Q_{\phi ^*,S,S}^{-1} \right) }{ p(\phi _{S} \mid -) \; {N} \left( \phi ^{*}_{S} \mid Q_{\phi ,S,S}^{-1} \ (b_{\phi ,S} - Q_{\phi ,S,c[S]} \ \phi _{c[S]}), Q_{\phi ,S,S}^{-1} \right) } \right\} . \end{aligned}$$

Sparsity in $Q_{\phi }$ reduces computational costs of the term $Q_{\phi ,S,c[S]} \ \phi _{c[S]}$ to $\mathcal {O}(|n[S]|^2)$ FLOPs, where $n[S]$ is the index set of G-neighbors of $S$ outside $S$. The proposal sampling costs only $\mathcal {O}(|S|^3)$ FLOPs, where $|S|$ is the sub-block size. Density evaluations in the acceptance probability calculation require band-Choleskey decomposition of the entire $\varOmega _{\phi }$ for each sub-block, which requires $\mathcal {O}(nb^2)$ FLOPs for matrix-bandwidth $b$. However, sequentially updating appropriately selected subsets of $\phi$ substantially reduces this cost, as illustrated below.

To illustrate the selection of the block $S$, consider an $R \times C$ regular rectangular lattice where the proximity matrix is defined with centered $(2p+1)\times (2p+1)$ neighborhoods. Rows and columns of $\phi$ are convenient blocks for updating the $\phi$ field in this case. We index the $\phi$ field in column-major format and update consecutive columns of $\phi$ from left to right. When the sub-block is the $c$th column of the $\phi$ field, $n[S]$ is only $2p$ columns from both sides, as shown in Fig. 2. Moreover, while updating the $c$th column, the left-Cholesky decomposition $L_{\phi }$ of $\varOmega _{\phi }$ can reuse $C(c-1)$ top rows of $L_{\phi }$ from the earlier decomposition; this induces huge reductions in computing time with even modest dimensional lattices. A row-major indexing and row-sweep updating of $\phi$ is equally efficient. We recommend alternating between row-sweep and column-sweep updating of $\phi$ in every alternative iteration with occasional random single-cell updating for better mixing of the chain.

Fig. 2

Blocking for computations on the $R \times C$ regular rectangular lattice with W-neighborhoods based on centered $(2p+1)\times (2p+1)$ squares. The column enclosed in the solid-line box has G-neighborhood of $2p$ columns in each side, marked by the dashed box

Conditionally updating $m,$ $\tau ^2$ and $\sigma ^2$ in the MCMC uses easy Gibbs steps to sample from their respective truncated normal and two inverse-Gamma complete conditional distributions. Updating $\rho$ is performed with a random-walk Metropolis–Hastings step, where the step-size is defined adaptively during the burn-in phase of the MCMC, and later kept fixed.

Before proceeding to examples and application, we note extensions of the MCMC analysis to address the potential for missing data. In our CO application, multiple lattice locations suffer missing data over time, so that this is a very real practical issue. The data field model of the SVSAR is a precision matrix model, which is convenient for handling missing observations. Let $M$ denote the index set of missing observations in a lattice and $H$ its complementary set. Assuming ignorable missingness, we can treat the missing observations $y_M$ as unknown parameters and then sample them at each of the MCMC iterations. The relevant conditional predictive distributions are simply

$$\begin{aligned} p(y_M \mid y_H, -) = {N} \left( \mu _M-\varOmega _{M,M}^{-1} \varOmega _{M,H} (y_H-\mu _H), \varOmega _{M,M}^{-1} \right) \end{aligned}$$

where $y_H$ is the observed data sub-vector, $\mu _M$ and $\mu _H$ are sub-vectors of $\mu$ for the missing and observed subsets, $\varOmega _{M,M}$ is the sub-matrix of $\varOmega$ with row and column indices in $M$ and $\varOmega _{M,H}$ is the sub-matrix with row indices in $M$ and column indices in $H$. Actual sampling from this distribution requires Cholesky decomposition of a $|M| \times |M|$ matrix $\varOmega _{M,M}$ and solving a linear system of dimension $|M|$ (Rue 2001; Rue and Held 2005), which does not add measurably to the computational complexity of the overall analysis in realistic problems with small degrees of missing data.

Another extension of general importance, as well as used in our application below, is to address multiple observations $y_1,\ldots ,y_T$ on the same underlying random $\phi$ field. The conditional posteriors for the $\phi$ field and $\tau$ parameter now include a product of $T$ terms of the same functional forms. The resulting conditional posteriors are then sampled using the same Metropolis–Hastings method for $\phi$ and direct sampler for $\tau$, with the obvious modifications. Conditional updating of $m,$ $\rho$ and $\sigma ^2$ in the MCMC remains unaffected.

5 Synthetic data analysis

We first illustrate the SVSAR model using a synthetic dataset. The lattice is borrowed from our real data example which consists of $4^{\circ }$ latitude $\times$ $5^{\circ }$ longitude grid-boxes spanning $50^{\circ }$N–$50^{\circ }$S of the Earth. The resulting lattice is a $26 \times 72$ regular rectangular grid with $n = 1872$ grid-cells, with its left and right edges wrapped around. We generated a smoothly varying $\phi$ field on this lattice from a known model with realistic characteristics; see Fig. 3a. Given this true $\phi$ field, we then simulated five replicate, independent data fields $\tilde{y}_1, \ldots , \tilde{y}_5$ using the SVSAR data-model with proximity matrix based on centered $3 \times 3$ W-neighborhoods. We use $\tau ^2 = 1$ and $\kappa = 6.75$ in (9) to specify $\varGamma _{\phi }$. Variations in the $\phi$ field give rise to varying degree of spatial smoothness in the synthetic data fields, which can be seen in the spatial plot of $\tilde{y}_1$ in Fig. 4. We flag a total of $79$ observations as missing spread across these $5$ data fields, mimicking the missing-data pattern in our real data application.

Fig. 3

a A $\phi$ field on the $26 \times 72$ lattice discussed in Sect. 5 that is used to simulate spatial random fields. b Posterior expectation of the SVSAR $\phi$ field based on MCMC samples from analysis of the synthetic data set $\{ \tilde{y}_i,\ i=1,\ldots ,4\}$ as discussed in Sect. 5. c A randomly selected MCMC sample of the SVSAR $\phi$ field in the same analysis

Fig. 4

One of the 5 simulated data fields, $\tilde{y}_1,$ based on the synthetic $\phi$ field of Fig. 3a. The deep blue grid-cells mark missing observations

One objective is to investigate the extent to which the SVSAR model can discover the “true” $\phi$ field from the data fields, and compare the SVSAR model with a simple SAR model in terms of goodness-of-fit to the synthetic data. Hence, we fit a zero-mean SVSAR model and a zero-mean SAR model, the latter with precision matrix parameterized as $\delta ^{-2} (I_n - \eta \widetilde{W})' (I_n - \eta \widetilde{W}).$ The models are defined using the same, true proximity matrix. We fit these two models to a data set defined by four repeat observational fields $\{ \tilde{y}_i,\ i=1,\ldots ,4\}.$ The data field $\tilde{y}_5$ is held back as “test data” for predictive evaluations. A uniform $(0,1)$ distribution is specified as prior for SVSAR parameter $m$ and SAR parameter $\eta$. An inverse-Gamma($6,5$) distribution (mean $1$, coefficient of variation $0.5$) is specified as prior distribution for the data variance parameters, namely $\tau ^2$ in SVSAR and $\delta ^2$ in the SAR model. Spatial smoothness in the SVSAR $\phi$ field is enforced with the $\text{ Beta }(5,1)$ prior for $\rho$ and an inverse-Gamma$(6,0.005)$ prior for $\sigma ^2$. In each analysis, the MCMC is initialized with all parameters at their respective prior means. The MCMC for the SVSAR model alternates between row-sweeps and column-sweeps for updating $\phi$, with occasional updating of random single-cells. Chains are run for 50000 iterations after burn-in of 10000 iterations; multiple subjective and quantitative assessments were evaluated and confirm satisfactory mixing and MCMC convergence for practicable purposes.

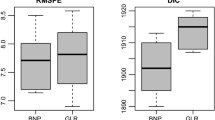
We use the following measures to compare our models: (i) the deviance information criterion (DIC) (Spiegelhalter et al. 2002), (ii) average in-sample log likelihood based on data $\{ \tilde{y}_i,\ i=1,\ldots ,4\},$ and (iii) the posterior-predictive log-likelihood of the test-sample $\tilde{y}_5$. The DIC is the mean posterior deviance of a model penalized by the effective number of parameters; a lower DIC score implies a better model. DIC is particularly suitable for comparing hierarchical models based on Markov chain Monte Carlo.

The posterior mean deviance is $\bar{D} = E_{\theta |x}\{D(\theta )\}$ where $D(\theta ) = -2 \log p(x|\theta ) + 2 \log h(x)$ is the “Bayesian deviance” of the model for data $x$ and with parameters $\theta$. Here $p(x|\theta )$ denotes the likelihood function and $h(x)$ is a fully specified standardizing term that is function of the data alone. The overall summary $\bar{D}$ is trivially estimated from the MCMC samples. The effective number of parameters of the model is computed as $p_D = \bar{D} - D(\bar{\theta })$, where $\bar{\theta }$ is the posterior mean of $\theta$ or some other measure of central tendency. Deviance is a model complexity measure that does not require specification of the total number of unknown parameters; the latter are typically meaningless—and hard to define—in complex hierarchical models where parameters often outnumber observations. DIC is defined as DIC = $\bar{D} + p_D$. We focus on the difference of DIC scores between the SVSAR and SAR models; the standardizing term $h(x)$ is simply set to zero as it is the same for both models, and the difference makes its value irrelevant.

From analysis of the synthetic training data set $\{ \tilde{y}_i,\ i=1,\ldots ,4\},$ Fig. 3 shows the posterior mean and a randomly selected posterior sample of the SVSAR $\phi$ field alongside the “true” field. Visual inspection of these fields reveals that the posterior successfully recovers the prominent highs and lows in the $\phi$ field on a correct scale. To illustrate the dominance of the SVSAR model, we show DIC comparison scores in Table 1. The DIC score and in-sample log likelihood both indicate very substantial support for the SVSAR model relative to the SAR. The effective number of parameters for the SAR model is a little less than the sum of total of the number of missing observations in the four data fields, which is $67$, and the total number of model parameters, which is $2$. This reduction in dimension can be attributed to the spatial smoothing in the missing observations induced by the SAR model. The corresponding number for the SVSAR model is much lower than the sum of the number of missing observations and the number of model parameters, $67+1876 = 1943$. This arises as the SVSAR $\phi$ field is parsimoniously smooth while capturing all essential non-stationarities in the data. Most critically, the posterior-predictive log-likelihood of $\tilde{y}_5$ provides really strong evidence in support of the SVSAR model.

Table 1 Model comparison scores for the synthetic data analysis in Sect. 5

6 Inverse estimation of CO source fluxes

Our application adaptively models spatial non-stationarities in an inverse estimation study of carbon monoxide (CO) source fluxes. The study uses the setup of Arellano et al. (2004) where satellite sensor measurements of atmospheric CO concentrations (Level 2 V3 MOPITT daytime column CO retrievals from the TERRA satellite) from April to December 2000 are used to estimate CO emissions from 15 source categories. The source categories consist of CO emissions from fossil fuel and biofuel combustion in 7 geographical regions, biomass burning in 7 geographical regions and oxidation of biogenic isoprene and monoterpenes on a global scale. Measurements from $50^{\circ }$N–$50^{\circ }$S of the Earth are gridded at $4^{\circ } \times 5^{\circ }$ resolution and averaged every month to yield monthly measurements on a $26 \times 72$ regular rectangular lattice, where left and right edges of the lattice are wrapped around. Our quality control criteria require at least 5 days of observations in the month for a grid-cell to be considered valid, marking a total of $139$ observations missing over 9 months.

The canonical model for this inverse problem is given by

$$\begin{aligned} y_t = K_t x + \epsilon _t, \;\; \epsilon _t \ \sim \ {N}(0,S_{\epsilon }), \;\;\; t=1,\ldots ,9, \end{aligned}$$

(11)

where $y_t$ is the $1872 \times 1$ vector of atmospheric CO concentration measurements in month $t$, $x$ is the $15 \times 1$ vector of source fluxes and $K_t$ is the Jacobian matrix of a computer driven atmospheric chemical transport model. In this study, the matrix $K_t$ is derived from the GEOS-Chem model, which is a global 3-D chemical transport model driven by meteorological information. The scale of the elements of the data in each $y_t$, and hence of elements in both $K_tx$ and $\epsilon _t,$ is parts per billion (ppb), that of the assessed atmospheric concentrations of CO. The scale of the CO from source elements in $x$ is teragrams per year, denoted by Tg/year$^{-1}.$ The random vector $\epsilon _t$ accounts for measurement errors and inaccuracies in the linear approximation of the chemical transport model, as well as representativeness errors arising from differences in resolution between the measurement and model-calculated concentration fields. Our focus is on modelling the error covariance matrix $S_{\epsilon }$. Many atmospheric chemistry inverse modelling applications have assumed $S_{\epsilon }$ to be a diagonal matrix for the sake of convenient closed-form posterior expressions for $x$. However, to fully exploit the information content in these high-dimensional, spatially dense satellite measurements, one must incorporate potential spatial dependencies among measurements through the error structure that are not predicted by the transport model. This impact can be substantial, as shown in Chevallier (2007) and Mukherjee et al. (2011). However, strength of residual spatial dependencies may vary over the lattice, and should be taken into consideration. Our SVSAR model provides a framework for systematically incorporating spatial non-stationarities in the high-resolution error fields.

To get a initial sense of the nature and scale of the data, and the relative scales of predictive and residual components, we display some of the data (that at $t=3$), together with some of the results from our analysis which are detailed and discussed further below. These provide insights into the spatial structures and quantitative scale; see Fig. 5.

Fig. 5

An example of the data (at $t=3$) together with corresponding posterior means of model and residual following SVSAR analysis. Upper frame Observed data field $y_3$. The deep blue grid-cells mark missing observations. Center frame $K_3 \hat{x}$ where $\hat{x}$ is the posterior estimate of $x$ from the SVSAR analysis. Lower frame $\hat{\epsilon }_3 = y_3-K_3\hat{x}.$ All are on the atmospheric concentration scale of parts per billion (ppb)

We model the error fields in (11) as independent realizations from a zero-mean SVSAR model with proximity matrix based on centered $3 \times 3$ W-neighborhoods. CO source fluxes are strictly non-negative. Prior distributions reflect this via independent, truncated normal priors on the elements of $x,$ namely ${N}(x_i|m_{a,i},v_{a,i}) {I}(x_i>0)$ for each $x_i$, where prior locations $m_{a,i}$ are based on traditional bottom-up flux estimates and the $v_{a,i}=m_{a,i}/2,$ consistent with prior studies. The global variance factor $\tau ^2$ is assumed to follow an inverse-Gamma prior with coefficient-of-variation $0.5$ and the variance of the prior-predicted error fields as its mean. The average spatial smoothness parameter $m$ of the error fields has a $U(0,1)$ prior. Finally, spatial smoothness in the SVSAR $\phi$ field is reflected by a $\text{ Beta }(5,1)$ prior for $\rho$ and an inverse-Gamma$(6,0.005)$ prior for $\sigma ^2$. As an alternative model for the error fields, an SAR model parametrized as $S_{\epsilon }^{-1} = \delta ^{-2} (I_n - \eta \widetilde{W})' (I_n - \eta \widetilde{W})$ is also fitted to compare and validate the need for the non-stationary SVSAR error structure. The spatial correlation parameter $\eta$ is specified to have a uniform prior distributions on $(0,1)$ and the error field variance $\delta ^2$ is assumed to follow the inverse-Gamma prior distribution specified for SVSAR parameter $\tau ^2$.

The CO model extends the basic SVSAR form to include the predictive regression component $K_tx$ in (11), replacing the earlier constant mean of the spatial field. A second extension is that we are now using the model with multiple observations on the same underlying random $\phi$ field. These practical model extensions require changes to the MCMC analysis in detail, but the basic ideas and overall computational strategy are unchanged. First, consider the changes related to incorporating information from the repeat data over $T=9$ months. At each iterate of the MCMC given a “current” source flux vector $x,$ we simply extract the implied realized residual fields $\epsilon _t = y_t-K_tx$ for each month $t=1:T.$ These represent conditionally independent draws from the spatial model; we have $T$ copies of the observation Eq. (9) obtained by just replacing $y$ and $\mu$ of those equations with $\epsilon _t$ and $0$, respectively, at each $t=1:T.$ Hence the conditional posteriors for each of the $\phi$ field and $\tau$ parameter are as discussed earlier. Further, we update $\phi$ with alternating row-sweep and column-sweep in alternative MCMC iterations, besides occasional random single-cells updating.

The extension to include the predictive regression $K_tx$ also, of course, adds conditional posterior simulations for the flux sources themselves. That is, at each MCMC iterate, we resample the source flux vector $x$ as follows. As a function of individual elements $x_i,$ the conditional likelihood function is the product of $T$ terms that define a normal form in $x_i.$ As a result, the conditional posterior density for each univariate $x_i$ has a form proportional to ${N}(x_i|m_{a,i}^*,v_{a,i}^*){I}(x_i>0)$ where the quantities $m_{a,i}^*,v_{a,i}^*$ are the usual normal prior: normal likelihood updates of the prior parameters $m_{a,i},v_{a,i}.$ This truncated normal is easily simulated directly. Sequencing through each element $x_i$ leads to resampling the full source vector $x$ in a Gibbs sampling format. The MCMC for the SAR model is similarly extended. As in the analysis of the synthetic data sets, MCMC chains are run for 50000 iterations after burn-in of 10000 iterations. A range of subjective and quantitative assessments were evaluated and confirmed satisfactory mixing and MCMC convergence for practicable purposes.

Table 2 Model comparison criteria for the CO data analysis in Sect. 6

We first look at the goodness-of-fit measures in Table 2. The average sample log-likelihood and the DIC scores provide strong evidence in favor of the SVSAR model; a reduction of $2387.63$ from the SAR model DIC score to the SVSAR model DIC score is substantial on the log-likelihood scale. The effective number of parameters for the SVSAR error model is much smaller than sum of total of the number of missing observations, number of source categories and number of error model parameters, which is $139+15+1876=2030$. This indicates that the SVSAR error model parsimoniously adapts to the spatial non-stationarities in the data fields. We observe evident spatial non-stationarities from posterior samples of the $\phi$ field; see Fig. 6. We observe smaller $\phi _i$ values over North America, China and moderately small $\phi _i$ values over many continental grid-cells in contrast to values in the oceanic grid-boxes that are closer to one. This finding is in agreement with the fact that anthropogenic activities in the continental regions cause active CO transport in the atmosphere, resulting in higher fluctuations in atmospheric CO concentrations. As a side note, the posterior mean from the basic SAR model analysis is approximately 0.994, and we see that the estimated $\phi$-field in the SVSAR model naturally ranges from values that are lower to higher than this.

Fig. 6

Top panel Posterior mean of the SVSAR $\phi$ field based on the MCMC samples from the CO inverse estimation study discussed in Sect. 6. Bottom panel A randomly selected MCMC sample of the SVSAR $\phi$ field in the same analysis. No measurement scale is noted since the $\phi$ elements are dimensionless quantities

Fig. 7

Plots of 95% prior and posterior credible intervals for the CO sources in the MOPITT data inversion analysis. The scale of the CO from source elements in $x$ is teragrams per year, denoted by Tg/year$^{-1}.$ Posterior means for both SVSAR and SAR models are marked with diamonds inside the corresponding intervals, while diamonds on the prior credible intervals represent the corresponding prior means. Source category numbers in the figure represent fossil-fuel (FFBF) or biomass burning (BIOM) CO source region, as follows: 1 FFBF North America, 2 FFBF Europe, 3 FFBF Russia, 4 FFBF East Asia, 5 FFBF South Asia, 6 FFBF Southeast Asia, 7 FFBF Rest of the World, 8 BIOM Other, 9 BIOM Northern Latin America, 10 BIOM Southern Latin America, 11 BIOM Northern Africa, 12 BIOM Southern Africa, 13 BIOM South and Southeast Asia, 14 BIOM Boreal. Source category 15 represents the global source of CO from biogenic hydrocarbon oxidation

Figure 7 plots summary posterior inference for all source flux categories $x$. This shows prior and posterior means together with $95\%$ prior and posterior credible intervals for each $x_i$ from each of the SAR and the SVSAR models. In addition, useful subjective insights into the nature of the inferred spatial field, and aspects of the uncertainty associated with the posterior for the field, can be generated by viewing sequences of images of posterior samples of $\phi$ as the MCMC progresses. Two such videos are available in the web-based supplementary material. The first shows the sampled $\phi$-field over the first 30 iterations of the MCMC beginning at a constant field, giving an indication of the rapid pick-up of relevant spatial patterns; the second sequences through another 30 MCMC samples beginning at MCMC iterate 3000, well after the chain has stabilized and appears to be sampling $\phi$-fields approximately from the posterior distribution.

We observe significant differences between the source flux estimates and corresponding uncertainties for several of the CO source categories. In view of the major dominance of the SVSAR model in terms of the tabulated measure of fit, and the fact that SAR structure is embedded within the SVSAR model framework and so would be identified if relevant, we simply cannot view the inferences based on the SAR model as worth attention. The fact that they can differ so substantially from the data-supported inferences under the SVSAR model indicates a critical need for this flexible, non-stationary spatial modelling approach.

7 Concluding remarks

Having introduced, explored and developed analysis of the new class of SVSAR models for spatial lattice data, our study in data assimilation and computer model assessment in atmospheric chemistry demonstrates their utility and potential. Defined via hierarchical extensions of SAR models, the SVSAR approach has the ability to flexibly represent globally non-stationary patterns in spatial dependence structure by building spatial priors over dependence parameters of traditional SAR models. Based on their inherent hierarchical Markov random field structure, SVSAR models are also amenable to computationally efficient model fitting for high-resolution spatial lattice data applications such as represented by the CO source flux inverse problem in our applied study.

Neatly extending traditional SAR models, the SVSAR approach represents a class of spatially varying coefficient models, using a second-stage class of SAR forms as spatial prior for the local dependence parameters at the data level. A spatial Markov random field model for the spatial distribution of parameters allows them to reflect smooth variation in structure of the local dependencies among spatial outcomes. In essence, this is a spatial analogue of the time-varying autoregressive (TVAR) extension of traditional AR models in time series (e.g., Kitagawa and Gersch 1996; West and Harrison 1997; Akaike and Kitagawa 1998; Prado and West 2010). TVAR models have been, and are, very widely applied and hugely successful in many areas of time series and signal processing, and we regard the new class of spatially varying SVSAR models to be of similar potential in increasingly complex and high-dimensional spatial problems. The study also demonstrates direct integration with time series structures to define novel spatio-temporal extensions of SVSAR models relevant for various applications including computer model inversion and data assimilation over time.

As something of an aside, but of potential interest to some readers, we note that an alternative formulation of spatially varying SAR models might consider so-called “source-dependent”, rather than “target-dependent” $\phi$ parameters, i.e., replacing $\phi _i$ with $\phi _j$ in the key defining model Eq. (7). We find this a much less natural conceptual approach. Having also explored it in detail, we find it to be less effective for imposing local smoothness as well as being dominated by our models in terms of model fit in analyses we have explored. Nevertheless, it is of interest to note the idea and some details are included in the Appendix.

Current and near-term interests in methodology and computation include a range of model extensions as well as questions of increasing computational efficiency of the MCMC analysis.

Modelling extensions of current interest include developments to embed SVSAR processes as latent components of larger models, and also to explore their use as alternative spatial factor loadings models in more structured dynamic spatial factor models (e.g., Lopes et al. 2008). Applications in the context of studies of CO source estimation using high-resolution satellite data are increasing the ability to generate finer spatial and temporal resolution data; models more directly reflecting temporal dynamics overlaying spatially varying spatial dependencies should aim to capitalize on the increasingly rich information such data will provide. Additional extensions that represent open research directions concern modelling time variation in the SVSAR fields, and potential dependence of the spatial residual fields on source fluxes, the latter being in part in connection with computer model calibration questions.

On computation, we have stressed the ability to define effective algorithms, and show the utility of “ Metropolis–Hastings within Gibbs” blocking strategies for updating components of the spatially varying parameter fields in these rectangular lattice models. These approaches are effective and our example concerns a relatively high-dimensional lattice. Nevertheless, faster and more efficient MCMC algorithms are of interest to enable swifter processing and substantial increases in dimension that will arise with increasingly fine-resolution lattice data. More refined blocking approaches, combined with our strategy of interlaced sweeps through horizontal and vertical blocks of the random parameter field, are of interest. Algorithmic extensions to enable partial parallelization for multi-core and/or more massive distributed computing via graphics processing unit (GPU) enabled systems (e.g., Suchard et al. 2010a, b) are a natural current area of investigation.

8 Appendix A

8.1 MCMC details: Complete conditional distribution of $\phi$

Let $d = y-\mu$. Then, the complete conditional distribution of $\phi$ has density

$$\begin{aligned}&p(\phi \mid y,\mu ,\tau ^2,m,\rho ,\sigma ^2) \;\; \propto \;\; p(y \mid \mu ,\phi ,\tau ^2) p(\phi \mid m,\rho ,\sigma ^2) \\&\quad \propto \;\; |\varOmega _{\phi }|^{1/2} \exp {\left\{ -\frac{1}{2} d' (I_n - \varDelta _{\phi } \widetilde{W})' \varGamma _{\phi }^{-1} (I_n-\varDelta _{\phi } \widetilde{W}) d \right\} }\\&\qquad \times \exp {\left\{ -\frac{1}{2} (\phi -m 1_n)' \varLambda (\phi -m 1_n)\right\} } \\&\quad \propto \;\; |\varOmega _{\phi }|^{1/2} \; \exp { \Bigg ( -\frac{1}{2} \bigg [ d' (\varGamma _{\phi }^{-1}-2\widetilde{W}' \varDelta _{\phi } \varGamma _{\phi }^{-1}+\widetilde{W}' \varDelta _{\phi } \varGamma _{\phi }^{-1} \varDelta _{\phi } \widetilde{W}) d }\\&\qquad + \{\phi ' \varLambda \phi - 2\phi ' \varLambda (m 1_n) \} \bigg ] \Bigg ) \\&\quad = \;\; |\varOmega _{\phi }|^{1/2} \; \exp { \Bigg ( -\frac{1}{2} \bigg [ (d' \varGamma _{\phi }^{-1} d - 2 d' \widetilde{W}' \varDelta _{\phi } \varGamma _{\phi }^{-1} d + d' \widetilde{W}' \varDelta _{\phi } \varGamma _{\phi }^{-1} \varDelta _{\phi } \widetilde{W} d) } \\&\qquad + \{\phi ' \varLambda \phi - 2\phi ' \varLambda (m 1_n) \} \bigg ] \Bigg ). \end{aligned}$$

Set $\varDelta _{\theta } = \mathrm diag (\theta )$ for any vector $\theta .$ Then, $\theta ' \varDelta _{\phi } = \phi ' \varDelta _{\theta }$ and $\varDelta _{\phi } \theta = \varDelta _{\theta } \phi$. Also, let $a = \widetilde{W} d$. Therefore, we have $d' \widetilde{W}' \varDelta _{\phi } \varGamma _{\phi }^{-1} d = a' \varDelta _{\phi } \varGamma _{\phi }^{-1} d = \phi ' \varDelta _{a} \varGamma _{\phi }^{-1} d$, and $d' \widetilde{W}' \varDelta _{\phi } \varGamma _{\phi }^{-1} \varDelta _{\phi } \widetilde{W} d = a' \varDelta _{\phi } \varGamma _{\phi }^{-1} \varDelta _{\phi } a = \phi ' \varDelta _{a} \varGamma _{\phi }^{-1} \varDelta _{a} \phi$. It follows that

$$\begin{aligned}&p(\phi \mid y,\mu ,\tau ^2,m,\rho ,\sigma ^2) \\&\quad \propto \;\; |\varOmega _{\phi }|^{1/2} \; \exp { \Bigg ( -\frac{1}{2} \bigg [ ( \phi ' \varDelta _{a} \varGamma _{\phi }^{-1} \varDelta _{a} \phi - 2 \phi ' \varDelta _{a} \varGamma _{\phi }^{-1} d + d' \varGamma _{\phi }^{-1} d ) }\\&\quad \quad + \{ \phi ' \varLambda \phi - 2\phi ' \varLambda (\mu 1_n) \} \bigg ] \Bigg ) \\&\quad = \;\; |\varOmega _{\phi }|^{1/2} \; \exp { \Bigg ( -\frac{1}{2} \bigg [ \phi ' ( \varDelta _{a} \varGamma _{\phi }^{-1} \varDelta _{a} + \varLambda ) \phi - 2 \phi ' \{ \varDelta _{a} \varGamma _{\phi }^{-1} d} \\&\qquad {+ \varLambda (m 1_n) \} + d' \varGamma _{\phi }^{-1} d \bigg ] \Bigg ) } \\&\quad = \;\; |\varOmega _{\phi }|^{1/2} \; \exp { \left\{ -\frac{1}{2} \; \left( \phi ' Q_{\phi } \phi - 2 \phi ' b_{\phi } + c_{\phi } \right) \right\} }, \end{aligned}$$

where $Q_{\phi } = (\varDelta _a \varGamma _{\phi }^{-1} \varDelta _a + \varLambda )$, $b_{\phi } = \{ \varDelta _a \varGamma _{\phi }^{-1} d + \varLambda (m 1_n) \}$ and $c_{\phi } = d' \varGamma _{\phi }^{-1} d$.

8.2 MCMC details: Complete conditional distribution of $\phi _S$

Notation: (i) $c[S]$: complement of the index set $S$, (ii) $u_{I}$ (or $u_{\phi ,I}$): sub-vector of vector $u$ (or $u_{\phi }$) with elements in the index set $I$, (iii) $U_{\phi ,I,J}$: sub-matrix of matrix $U_{\phi }$ with row indices in index set $I$ and column indices in index set $J$. Conditional distribution of $\phi _{S}$ is proportional to the complete conditional distribution of $\phi$ when $\phi _{c[S]}$ is remains constant. Then, with $c_{\phi ,S} = d_{S}' \varGamma _{\phi ,S,S}^{-1} d_{S},$ we have

$$\begin{aligned}&p(\phi _{S} \mid \; \phi _{c[S]},y,\mu ,\tau ^2,m,\rho ,\sigma ^2) \;\; \propto \;\; |\varOmega _{\phi }|^{1/2} \; \exp { \left\{ -\frac{1}{2} \; \left( \phi ' Q_{\phi } \phi - 2 \phi ' b_{\phi } + c_{\phi } \right) \right\} } \\&\quad \propto \, |\varOmega _{\phi }|^{1/2} \, \exp {\left[ - \frac{1}{2} \left\{ \phi _{S}' \ Q_{\phi ,S,S} \ \phi _{S} - 2 \phi _{S}' \ (b_{\phi ,S} - Q_{\phi ,S,c[S]} \ \phi _{S}) + c_{\phi ,S} \right\} \right] }. \end{aligned}$$

8.3 A note on an alternative SVSAR formulation

As noted in the concluding remarks of Sect. 7, a possible alternative formulation of spatially varying SAR models would involve replacing the $\phi _i$ with $\phi _j$ in our model of Eq. (7). This can be referred to as a “source-dependent” model compared to our “target-dependent” model. The precision matrix in this case takes the form

$$\begin{aligned} \varOmega _{\phi }&= (I_n - \tilde{W} \varDelta _{\phi })' \Gamma ^{-1}_{\phi } (I_n - \tilde{W} \varDelta _{\phi }) \\&= \Gamma ^{-1}_{\phi } - \varDelta _{\phi } \tilde{W}' \Gamma ^{-1}_{\phi } - \Gamma ^{-1}_{\phi } \tilde{W} \varDelta _{\phi } + \varDelta _{\phi } \tilde{W}' \Gamma ^{-1}_{\phi } \tilde{W} \varDelta _{\phi }, \end{aligned}$$

which leads to

$$\begin{aligned} Q_{ij}&= - \left( \tau _i^{-2} \phi _j \frac{w_{ij}}{\, w_{i+}} + \tau _j^{-2}\phi _i \frac{w_{ji}}{ \, w_{j+}} \right) + \sum _k \tau _k^{-2} \phi _i \phi _j \, \frac{w_{ki} \, w_{kj}}{\, w_{k+}^2}, \\ Q_{ii}&= \tau _i^{-2} + \sum _k \tau _k^{-2} \phi _i \phi _j \, \frac{w_{ki}^2}{\ w_{k+}^2}. \end{aligned}$$

However, this leads to a specification we regard as less natural while also being less conducive to imposing local smoothness; We can no longer, for example, easily link variability (the $\tau ^2_i$) with the local dependence parameters (the $\phi _i$ in our model). This fact is quantitatively supported by our experiments with synthetic data, where the DIC for the source-dependent SVSAR model is significantly larger than for our target-dependent SVSAR model. Hence, although both models fit the inhomogeneous spatial fields better than a basic SAR model, we have not taken this exploration further.