1 Introduction

Three dimensionally ordered mesoporous (3DOm) carbons were synthesized by Fan, Tsapatsis and coworkers as a template materials for the synthesis of zeolitic materials with order at both microporous and mesoporous length scales [1]. This was done with the goal of improving the mass transfer characteristics of the zeolitic materials for catalysis and separations. The synthesis starts with ordered colloidal crystals that are formed from silica nanoparticles [1, 2]. Polymerization of furfuryl alcohol in the presence of oxalic acid as a catalyst within the void space of the colloidal crystal, followed by carbonization and removal of the silica leaves a mesoporous carbon structure. The structure is an ordered array of spherical pores interconnected by windows created by sintering of the templating silica particles. Changing the primary particle size in the colloidal crystal template allows the creation of 3DOm carbons with a wide range of pore sizes. For carbon materials the degree of structural order in these systems is remarkably high as is immediately clear from SEM images [1]. This makes it very worthwhile to study the materials as carbon adsorbents and as model mesoporous materials with ordered, three dimensionally interconnected void spaces.

Experimental adsorption results on 3DOm carbon were presented by Gor et al. [3] and Cychosz et al. [4], including nitrogen (77.4 K) and argon (87.3 K) adsorption/desorption isotherms for 3DOm carbons using templates with 10, 20, 30, and 40 nm nanoparticles. The resulting isotherms showed hysteresis characteristic of the mesoporosity in the systems with the width and location of the hysteresis loops varying with the pore size. This study was accompanied by a theoretical study using the density functional theory (DFT) treating the system as a collection of independent spherical pores. The theory and experiment gave a picture of the pores sizes that was consistent with those predicted on the basis of the colloidal template primary particle size and SEM images.

In this paper we present a modeling study of adsorption and desorption of gases in these remarkable materials using a coarse grained approach that can address the full microstructure of the material without assuming a decomposition into independent pores. Our approach uses a lattice gas model treated in the context of mean field density functional theory (MFDFT) [5,6,7,8,9,10,11]. In addition we study the dynamics of adsorption and desorption using dynamic mean field theory (DMFT) [12, 13] for the same model. The construction of our model parallels the experimental synthesis. We model the silica nanoparticles as spheres in an fcc crystalline state. Next we coarse grain the spheres on to a simple cubic lattice. Finally we create the porous 3DOm structure by exchanging the occupancy on the lattice so that void sites become occupied and vice versa. Allowing the spheres to overlap to some degree models the effect of sintering among the silica nanospheres creates the windows between the pores. We consider the effects of allowing some degree of disorder by having a distribution of sphere sizes. We calculate the adsorption/desorption isotherms of density vs. relative pressure as well as the grand free energy. We find that the model is able to describe quite accurately the behavior seen experimentally. In particular the shape of the adsorption/desorption isotherms is given correctly. We see that the spherical geometry of the pores has an important effect on the hysteresis behavior in the system as discussed in earlier work [4]. We also calculate the scanning curves for the system and find good agreement with experiments presented by Cimino et al. [14] in the context of a study of a different approach to modeling the scanning behavior. Among the important features captured by our modeling are the changes of curvature exhibited by the desorption scans.

2 Models and methods

2.1 Lattice gas model

The coarse grained lattice model for this study has been constructed in a manner similar to the experimental method of synthesizing 3DOm carbons [1]. The silica nanospheres are modeled as spheres placed on the sites of an fcc lattice at a density near close packing. We used 108 (\(4n^3\) with \(n=3\)) spheres to build the model. (We did some calculations with 256 spheres but the results were not significantly different.) The system was then mapped on to a much finer simple cubic lattice to discretize the space for the lattice model. Lattice sites with locations inside each sphere labelled as occupied by solid, with the remaining sites as void. After that the occupancies are flipped to create our coarse grained model of the 3DOm carbon. The process is illustrated in Fig. 1.

Fig. 1
figure 1

Lattice model of a 3DOm carbon established from coarse graining of spheres in an fcc crystal

Full size image

The structure thus described actually produces a system of isolated spherical pores in an fcc arrangement. The actual 3DOm carbon has windows between the spherical pores that are created by sintering of the silica nanospheres during the colloid crystal synthesis. We mimic that effect in our model by growing the size of the spheres in the initial structure to create overlaps between them prior to the coarse graining. Another variation of the model is to consider the effect of polydispersity in the nanosphere diameters. This is done by choosing the sphere diameters from a gaussian distribution similar to pore size distribution estimated from experiments [1, 4]. We will examine the effects of these structural features upon the adsorption/desorption behavior in these materials.

Our base model was for the 3DOm carbon formed from 30nm silica nanospheres [1]. In the lattice model the coarse graining was done so that the sphere diameter was 18 lattice constants. For the system with windows, the width of the windows was 8 lattice constants. This defines the lattice constant for the base model as 1.67 nm.

2.2 MFDFT

The model for fluid behavior in the system is a single occupancy lattice gas, with nearest neighbor interactions in the presence of an external field describing the interaction of the confined fluid with the adsorbent solid. The grand free energy for the system in MFDFT is given by Kierlik et al. [5, 13]

$$\begin{aligned}&\varOmega =kT\sum _{{\mathbf {i}}}\left[ \rho _{{\mathbf {i}}} \ln (\rho _{{\mathbf {i}}}) + (1- \rho _{{\mathbf {i}}})\ln (1- \rho _{{\mathbf {i}}}) \right] \nonumber \\&\quad\quad - \frac{\varepsilon }{2}\sum _{{\mathbf {i}}, {\mathbf {j}}}{ }^{\prime } \rho _{{\mathbf {i}}}\rho _{{\mathbf {j}}} +\sum _{{\mathbf {i}}}\rho _{{\mathbf {i}}}\left( \phi _{{\mathbf {i}}}-\mu \right) \end{aligned}$$
(1)

where k is Boltzmann’s constant, T is absolute temperature, \(\rho _{{\mathbf {i}}}\) is the mean density at site \({\mathbf {i}}\) and \(\mu\) is the chemical potential. \({\mathbf {i}}\) (or \({\mathbf {j}}\)) denote a set of simple cubic lattice coordinates, and \(\varepsilon\) is the strength of the nearest neighbor attraction. The prime on the second summation denotes the restriction to nearest neighbors. \(\phi _{{\mathbf {i}}}\) is the field at site \({{\mathbf {i}}}\) and is given by a nearest-neighbor interaction with strength \(-\alpha \varepsilon\).

By minimizing \(\varOmega\) at fixed chemical potential, we can determine the grand free energy and density distribution in the system. The necessary condition for minimizing the grand free energy at fixed temperature and chemical potential is

$$\begin{aligned} \left( \frac{\partial \varOmega }{\partial \rho _{{\mathbf {i}}}}\right) _{\mu ,T,{\phi }} = 0 \;\; \forall \;\; {{\mathbf {i}}} \end{aligned}$$
(2)

Imposing the condition in Eq. (2) on Eq. (1) yields the following set of nonlinear equations

$$\begin{aligned} kT\ln \left[ \frac{\rho _{{\mathbf {i}}}}{1- \rho _{{\mathbf {i}}}}\right] -\varepsilon \sum _{{\mathbf {j}}}{ }^{\prime }\rho _{{\mathbf {j}}}+\phi _c-\mu =0 \;\; \forall \;\; {{\mathbf {i}}} \end{aligned}$$
(3)

where the primed summation denotes a restriction to nearest neighbors of site \({\mathbf {i}}\). In the grand ensemble these equations are solved iteratively for the density distribution, {\(\rho _{{\mathbf {i}}}\)} at fixed uniform {\(\mu _{{\mathbf {i}}}=\mu\)}, T and {\(\phi _{{\mathbf {i}}}\)}.

2.3 DMFT

DMFT [13] provides a description of the time evolution of the system after a change in chemical potential or bulk pressure and we use it here to study the dynamics of adsorption and desorption. The transport mechanism is stochastic hopping of molecules between nearest neighbor sites on the lattice a process known as Kawasaki dynamics.

The evolution of the density distribution is governed by

$$\begin{aligned} \frac{\partial \rho _{{\mathbf {i}}}(t)}{\partial t} = - \sum _{{\mathbf {j}}}{}^{\prime } \left\{ w_{{\mathbf {i}}\rightarrow {\mathbf {j}}} \rho _{{\mathbf {i}}}(t)[1-\rho _{{\mathbf {j}}}(t)] - w_{{\mathbf {j}}\rightarrow {\mathbf {i}}} \rho _{{\mathbf {j}}}(t)[1-\rho _{{\mathbf {i}}}(t)] \right\} \end{aligned}$$
(4)

where \(w_{{\mathbf {i}}\rightarrow {\mathbf {j}}}\) are transition probabilities for a molecule to hop between site \({\mathbf {i}}\) and site \({\mathbf {j}}\). Using the expressions for the transition probabilities, Eq. (4) can be solved to obtain {\(\rho _{{\mathbf {i}}}(t)\)}. The mean Kawasaki dynamics are given as follows [15]

$$\begin{aligned} w_{{\mathbf {i}}\rightarrow {\mathbf {j}}}(\{\rho \})=w_0\exp (-E_{{\mathbf {i}}{\mathbf {j}}}/kT) \end{aligned}$$
(5)

where

$$\begin{aligned} E_{{\mathbf {i}} {\mathbf {j}}} = \left\{ \begin{array}{ll} 0 &{} E_{{\mathbf {j}}}<E_{{\mathbf {i}}} \\ E_{{\mathbf {j}}}-E_{{\mathbf {i}}} &{} E_{{\mathbf {j}}}>E_{{\mathbf {i}}} \end{array} \right. \end{aligned}$$
(6)

with

$$\begin{aligned} E_{{\mathbf {i}}}=-\varepsilon \sum _{{\mathbf {j}}}\rho _{{\mathbf {j}}}+\phi _{{\mathbf {i}}} \end{aligned}$$
(7)

\(w_0\) is the jump rate in the absence of interactions in the system and is used to define a dimensionless time. Using Eqs. (4) and (5) we obtain

$$\begin{aligned} \frac{\partial \rho _{{\mathbf {i}}}(t)}{\partial t} = - \sum _{{\mathbf {j}}}w_{{\mathbf {i}}\rightarrow {\mathbf {j}}} \rho _{{\mathbf {i}}}(t)(1-\rho _{{\mathbf {j}}}(t))[1-exp\{(\mu _{\mathbf {i}}-\mu _{\mathbf {j}})/kT\}] \end{aligned}$$
(8)

For situations such as the dynamics of adsorption and desorption, this expression shows that in the long time limit of the DMFT equations, where flux approaches zero, is associated with uniform chemical potential throughout the system. The resulting state corresponds to a solution of the static mean field density functional equations, demonstrating that DMFT is consistent with the equilibrium thermodynamic picture of the system within density functional theory.

2.4 Implementation

To obtain adsorption/desorption isotherms the following procedure was followed. To study an adsorption isotherm the MDFT equations were solved for a sequence of states starting from a low value of the pressure relative to the bulk vapor pressure, \(p/p_0\), all the way to saturation. The initial guess for the density distribution at the lowest pressure was a uniform value at the bulk density. For subsequent states the density distribution from the previous state was used as the initial guess. Similar procedures were used for the study of scanning curves in the hysteresis region. Desorption scanning curves were initiated from states on the adsorption boundary curve and adsorption scanning curves were initiated from states on the desorption boundary curve. To mimic the bulk a layer 20 lattice sites deep is added on each side of the lattice structure. The temperature was set at \(T^*=kT/\varepsilon =1\) which is two thirds of the bulk critical temperature [11] in DMFT. All calculations in this work are for \(\alpha =3.0\).

DMFT was implemented as follows. For a given pore geometry the DFT equations were solved at an initial value of the chemical potential or relative pressure (\(p/p_0\)) to give the initial density distribution in the system. A layer of sites at the perimeter of the system was added at the periphery of the system where the density is fixed at the value associated with the relative pressure of the state to which the system has to be evolved. The fixed density layer acts as a source or sink of fluid during the dynamics. The state of the system is then evolved by numerically solving Eq. (8) via Euler’s method. For Euler’s method to be of acceptable accuracy time steps less than \(w_0\varDelta t= 0.1\) have been used.

Although our model is relatively simple and coarse grained the calculations presented here are still a significant computational undertaking. For instance, our base model of the 30 nm 3DOm carbon the dimension of the cubic lattice used was \(110^3\). This means that the application of MFDFT requires the solution of 1,331,000 coupled nonlinear equations with same number of differential equations for DMFT.

3 Results

3.1 Static behavior

3.1.1 3DOm carbon with uniform pore size

We begin by considering our model with full crystalline order and uniformly sized nanospheres in the templating. We look at two cases: (i) a system with no windows so that the spherical pores are isolated and (ii) a system where the pores are interconnected via windows. Isolated pores cannot adsorb in nature but the adsorption can be studied theoretically in the grand canonical ensemble. The results obtained from static MFDFT are shown in Fig. 2 which shows the adsorption/desorption isotherms and the free energy isotherms for the two geometries under study. The density plotted is averaged over a region that excludes sites close to the external surface of the porous structure to reduce finite size effects. Sites within 20 lattice constants of the external surface are so excluded.

Fig. 2
figure 2

Adsorption/desorption isotherms for density (upper curves) and grand free energy (lower curves) from MFDFT for a 3DOm pore structure with interconnected pores (full line) and for independent pores (dashed line)

Full size image

The density isotherms for the two systems are quite similar with both showing a fairly wide hysteresis region comparable in magnitude to that seen experimentally, with a slightly wider hysteresis for the isolated pore system. The curvature at low pressure is associated with monolayer formation. In common with the density isotherms, the grand free energy also shows two branches which cross within the hysteresis region but quite close to the adsorption branch. This indicates that the phase equilibrium state between the vapor-like and liquid-like states of the confined fluid lies close to the adsorption branch. This contrasts with the behavior seen for systems like slit pores and cylindrical pores in contact with the bulk where the desorption branch of the hysteresis coincides with phase equilibrium. We will return to this point shortly. Another feature to note is that the hysteresis region is wider for the isolated pore, where the desorption occurs via cavitation at the stability limit of the confined liquid. In the system with interconnected pores the desorption occurs via invasion percolation (pore blocking) mechanism. This is indicated by the two step desorption isotherm.

Fig. 3
figure 3

Visualizations of the density distributions for states along the isotherm for adsorption in the model 3DOm pore structure with isolated pores. The states on the left are for adsorption and those on the right for desorption. The values of \(p/p_0\) for each state are as follows: a 0.002, b 0.1, c 0.877, d 0.879, e 0.99, f 0.99, g 0.675, h 0.673, i 0.671, j 0.1 s

Full size image
Fig. 4
figure 4

Visualizations of the density distributions for states along the isotherm for adsorption in the model 3DOm pore structure with interconnected pores. The states on the left are for adsorption and those on the right for desorption. The values of \(p/p_0\) for each state are as follows: a 0.002, b 0.1, c 0.877, d 0.879, e 0.99, f 0.99, g 0.675, h 0.673, i 0.671, j 0.1

Full size image

We can see all this behavior more clearly by visualizing the density distribution for states on the isotherm as illustrated in Figs. 3 and 4. These figures visualize the density in a 100 plane of the fcc lattice that bisects the system. The white regions denote the porous solid. The remaining regions are the pore space and, at the periphery, the bulk region. These regions are shaded in grayscale with dark shades denoting high fluid density, and lighter shades denoting lower fluid density. For the independent pore system pore filling occurs first by film growth at the pore walls followed by condensation in the middle (see Fig. 3c,  d). The mechanism of the desorption process in the hysteresis region is cavitation. The density distribution shows that the liquid has a substantially lower density just before cavitation (see Fig. 3h). For interconnected pores pore filling proceeds by film formation accompanied by bridging of the pore windows and then condensation in the center of the pore (see Fig. 4b–d). The window bridging appears to be a continuous process. Once the windows are bridged the condensation process is similar to that for the isolated pore system. On desorption the pores that are closest to the bulk are the first to empty (Fig. 4g). This is followed by the emptying of the inner pores in a step wise manner (Fig. 4h, i). The inner pores cannot empty unless the fluid in the surrounding pores has been emptied. This confirms the invasion percolation (pore blocking) mechanism.

Fig. 5
figure 5

The relative pressures at condensation (filled diamonds), vapor-liquid equilibrium (filled square) and evaporation (filled circles) versus inverse pore size for a single spherical pore from MFDFT for the lattice gas model. The horizontal dashed line denotes the bulk liquid spinodal pressure

Full size image

To provide additional insight into the isolated spherical pore we applied MFDFT to study the fluid behavior in a single isolated lattice model sphere. The size of the sphere was varied from a width of \(D=10\) lattice sites to \(D=50\) lattice sites. Figure 5 shows the metastable condensation and desorption points for varying pore sizes, together with the phase equilibrium points and the bulk liquid spinodal line on a graph of \(p/p_0\). We note first that the desorption points lie close to the liquid spinodal line and converge to it for large pore size, reflecting that desorption is a cavitation process. The phase equilibrium points lie quite close to the metastable condensation points and the two appear to merge for large pore diameter approaching \(p/p_0=1\). These findings are in line with the work by Rasmussen et al. [16] and earlier work by Ravikovitch and Neimark [17]. Gor et al. [3] compared their results with the Derjaguin–Broekhoff–de Boer (DBdB) theory [18] and found qualitative agreement. Evidently the spherical pore geometry plays a central role in the adsorption/desorption behavior in 3DOm carbons.

3.1.2 3DOm carbon with variation in pore size

A degree of polydispersity among the silica nanospheres will lead to a distribution of porosity across the system. Experimental adsorption studies on a 3DOm carbon systems indicate a pore size distribution with a standard deviation of a few nanometers [4]. We have incorporated both these sources of disorder into our model. We modeled the pore size distribution with a Gaussian distribution of sphere sizes with the mean at the original value used in our base model and a standard deviation chosen so that the pore size distribution is similar to that estimated experimentally. The isotherms were calculated for 100 samples of the structure and averaged over those samples. The results are shown in Fig. 6. In contrast to the results for a single sample the isotherms are smooth curves and correspond to type IV(a) in the IUPAC classification of adsorption isotherms [19] with type H1 hysteresis. In Fig. 7 we compare these results with experimental results from Cychosz et al. [4] for carbon with mean pore sizes of 20 nm and 30 nm. We see that the agreement is qualitatively excellent with all features of the experimental isotherms captured by the theory. The agreement is closest with the experimental results for the 30nm system as expected, given that this was the system targeted in constructing the model.

Fig. 6
figure 6

Average adsorption/desorption isotherms from MFDFT for a model 3DOm pore network with a pore size distribution

Full size image
Fig. 7
figure 7

Normalized adsorption/desorption isotherms for model 3DOm materials from MFDFT (straight line) and nitrogen adsorption isotherms at 77 K for 20 nm 3DOm carbon (filled square) and for 30 nm 3DOm carbon (filled circle). The curves are scaled so that the density is unity at \(p/p_0=1\)

Full size image
Fig. 8
figure 8

Desorption scanning curves (a) and adsorption scanning curves (b) for the model 10 nm 3DOm carbon (left) and for the model 40 nm 3DOm carbon (right) from MFDFT

Full size image

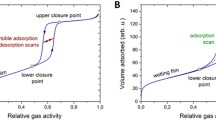
We also calculated adsorption and desorption scanning curves to compare with experiments [14] and these are shown in Fig. 8 for our model of the 10 nm and 40 nm 3DOm materials. The corresponding experimental results [14] are shown in Fig. 9. A desorption scanning curve starts on the adsorption boundary curve and proceeds along a path of decreasing pressure until it reconnects with the main isotherm at lower pressure. Similarly an adsorption scanning curve starts on the desorption boundary curve and proceeds along a path of increasing pressure until it reconnects with the main isotherm at higher pressure. Focusing first on the results in Fig. 8 there are two particular features that we find especially noteworthy. First of all the desorption scans especially for the 40nm system exhibit a change of curvature. At high pressure the desorption scans have the negative curvature in common with the adsorption boundary curve. At lower pressure the desorption scans have a positive curvature in common with the desorption boundary curve. This suggests a change in the pathway of desorption along the scanning curve from something like the reverse of the adsorption curve to something like the invasion percolation behavior on the desorption boundary. Because our calculation are done by averaging over 100 samples it is not possible to visualize the behavior directly. The second feature of the model results is that the adsorption scanning curves have very similar curvature to the adsorption boundary curve and rejoin it smoothly. This is consistent with the states on the desorption boundary being generated via invasion percolation. Initiating an adsorption scan from one of these states leads to filling of the evacuated states in the structure via a similar process to that on the adsorption boundary curve.

Fig. 9
figure 9

Desorption scanning curves (top) and adsorption scanning curves (bottom) for Ar adsorption in 10 nm 3DOm carbon (left) and in 40 nm 3DOm carbon (right) from experiment [14]

Full size image
Fig. 10
figure 10

a Density versus time for a model 3DOm carbon network during a change in the relative pressure from \(p/p_0\) = 0.00576 to \(p/p_0\) = 0.941 from DMFT. b Density versus time for a model 3DOm carbon network during a change in the relative pressure from \(p/p_0\) = 0.941 to \(p/p_0\) = 0.00576 from DMFT. In each case dashed line gives the average density throughout the pore network and the full line gives the average density in the middle of the pore network

Full size image
Fig. 11
figure 11

Visualizations of the density distribution for a model 3DOm carbon network from DMFT during a change of the relative pressure from \(p/p_0\) = 0.00576 to \(p/p_0\) = 0.941: a \(w_0t\) = 5000, b \(w_0t\) = 8000, c \(w_0t\) = 27,500, d \(w_0t\) = 42,500, e \(w_0t\) = 62,500, f \(w_0t\) = 75,000

Full size image

In general the experimental results [14] are consistent with those from the model (see Fig. 9). The one exception is that the experimental adsorption scans for the 40nm system seem to approach the adsorption boundary curve with finite slope. However, it is possible that the resolution of the pressure scale in the experiments was not sufficient to show that detail. We note in the model, the slope of the adsorption scans increases rapidly very close to the adsorption boundary curve.

3.2 Dynamic behavior from DMFT

Figure 10a shows the uptake dynamics as calculated from DMFT for the interconnected pore system during a change of bulk pressure at a dilute gas bulk state to one close to bulk saturation. Both the averaged density throughout the pore structure and the density averaged over an inner cube are plotted. The two curves show the evolution of the density at different regions in the porous structure during the dynamics. The pore averaged density shows different regimes of behavior as seen in the visualizations of the density distribution at various stages of the dynamics as shown in the visualizations Fig. 11, which were prepared in the same way as those shown for the static behavior earlier. The short time behavior is associated with the filling of the windows at the corners of the system (Fig. 11a). This liquid then propagates to fill the open pores at the sample surface (Fig. 11b, c). The windows at the corners are the first to fill as these regions have the highest fluid flux from the bulk phase. Figure 11c shows the asymmetric filling of pores with liquid as the fluid permeates in from the exterior. Each spherical pore fills by film growth at the pore walls leading to an asymmetric bubble which disappears as more fluid enters the pore. This process is repeated as the condensation progresses into the core of the sample (Fig. 11d, e).

The desorption dynamics during a change in pressure from a state close to bulk saturation to one in a dilute gas bulk state has also been considered. The plot of density versus time is shown in Fig. 10b, again averaged both over the entire pore structure and in the middle of the pore structure. Desorption dynamics does not require nucleation (the vapor-liquid interface already exists at the external surface) and is much fast than adsorption dynamics. The density distribution visualizations are shown in Fig. 12. Desorption proceeds through the evaporation of the liquid at the vapor liquid interface (Fig. 12a). The resulting vapor liquid menisci retract through the pore (Fig. 12b, c) with the pores in the center of the structure emptying the last (Fig. 12e). At each stage the liquid bridging the windows is the last to evaporate, seen especially clearly in Fig. 12f.

Fig. 12
figure 12

Visualizations of the density distribution for a model 3DOm carbon network from DMFT during a change of the relative pressure from \(p/p_0\)= 0.941 to \(p/p_0\)= 0.00576: a \(w_0t\) = 500, b \(w_0t\) = 1500, c \(w_0t\) = 2000, d \(w_0t\) = 3500, e \(w_0t\) = 5000, f \(w_0t\) = 6000

Full size image
Fig. 13
figure 13

Visualizations of the density distribution for a model 3DOm carbon network with variation in pore size from DMFT during a change of the relative pressure from \(p/p_0\) = 0.00576 to \(p/p_0\) = 0.941: a \(w_0t\) = 5000, b \(w_0t\) = 8000, c \(w_0t\) = 27,500, d \(w_0t\) = 42,500, e \(w_0t\) = 62,500, f \(w_0t\) = 75,000

Full size image
Fig. 14
figure 14

Visualizations of the density distribution for a model 3DOm carbon network with variation in pore size from DMFT during a change of the relative pressure from \(p/p_0\) = 0.941 to \(p/p_0\) = 0.00576: a \(w_0t\) = 500, b \(w_0t\) = 1800, c \(w_0t\) = 3000, d \(w_0t\) = 5000, e \(w_0t\) = 6500, f \(w_0t\) = 9000

Full size image

The density vs. time behavior for a single sample of the system with the pore size distribution is qualitatively similar to that shown in Fig. 10. Visualizations are shown in Figs. 13 and 14 . The mechanisms in play are the same as for the single pore size but the density distributions are modified by the spatial variations in the window sizes. During desorption it is possible that local cavitation may be occurring for cases where a spherical pore ends up with mostly narrower windows as suggested by Fig. 14e.

4 Summary and discussion

We have presented a coarse grained lattice gas model for the thermodynamics and dynamics of adsorption in 3DOm mesoporous carbons. The systems were modeled as an assembly of interconnected spherical pores in an fcc structure. These were then coarse grained on to a simple cubic lattice gas. The adsorption was modeled using MFDFT and the dynamics via DMFT. These are relative simple but realistic approaches that makes the study of these complex three dimensional systems much computationally accessible than would otherwise be possible.

We studied cases with both uniform pore size and pore size distributions. We calculated the adsorption/desorption isotherms of density vs. relative pressure as well as the grand free energy and fluid density distributions in the systems. We studied the relationship between hysteresis and underlying phase transitions in the systems. We find that the model is able to describe quite accurately the adsorption/desorption behavior seen experimentally [4]. In particular the shape of the adsorption/desorption isotherms is given correctly. During adsorption, the filling of the windows between pores starts the process of pore filling. The evaporation of liquid from the system on desorption is primarily an invasion percolation process. We observe that the spherical geometry of the pores has an important effect on the hysteresis behavior in the system as discussed in earlier work [4]. These distributions confirm that evaporation of fluid from the pore on desorption occurs via invasion percolation. We have also calculated both adsorption and desorption scanning curves for the system and find good agreement with those measured in experiments [14]. We especially note the desorption scans which exhibit a change of curvature.

Our DMFT calculations complement the MFDFT studies and showed the dynamic mechanisms associated with condensation and evaporation in the systems. Pore condensation proceeds by liquid bridging at the windows in a pore closest to the external surface. This is followed by film growth from the pore walls and the collapse of an asymmetric bubble in the pore. Desorption is seen as a dynamic invasion percolation of a vapor-liquid interface into the system starting from the external surface.

This work represents another example where the coarse grained lattice gas approach provides useful information about the adsorption/desorption behavior in three dimensional, interconnected, pore structures [5,6,7,8,9,10,11] which would not be accessible by other methods.