1 Introduction

Ceramic materials possess high strength and modulus at elevated temperature. But their use as structural components is severely limited because of their brittleness. Continuous fiber-reinforced ceramic-matrix composites, by incorporating fibers in ceramic matrices, however, not only exploit their attractive high-temperature strength but also reduce the propensity for catastrophic failure. Carbon fiber-reinforced silicon carbide ceramic-matrix composites (C/SiC CMCs) are one of the most promising candidates for many high temperature applications [1]. Many of the potential applications for CMC components are characterized by oxidized environments at elevated temperatures [2]. The non-oxide CMCs exhibit distinct behaviors at stresses above and below the matrix cracking stress, which is associated with the onset of matrix cracking and with the formation of hysteresis loops that result from matrix cracking and frictional sliding of the fibers bridging those matrix cracks. In the absence of environmentally-stable fibers and fiber coatings in oxidizing environments, the matrix cracking stress has long been considered the maximum allowable design stress for non-oxide CMCs in applications involving oxidizing environments. During the long-term applications at elevated temperatures, the matrix cracking stress would degrade, due to interphase oxidation through microcracking caused by thermal expansion coefficient mismatch between fibers and the matrix, which would affect the durability and reliability of CMCs [3].

Many researchers performed the experimental and theoretical investigations on matrix cracking of fiber-reinforced CMCs. For analytical modeling, the energy balance approach developed by Aveston, Cooper and Kelly (ACK) [4], and Budiansky, Hutchinson and Evans (BHE) [5], and the fracture mechanics approach proposed by Marshall, Cox and Evans (MCE) [6], and McCartney [7] have been used to investigate the matrix cracking stress. The analytical results show that the matrix cracking stress was closely related with the interface friction stress. Rajan and Zok [8] investigate the mechanics of a fully bridged steady-state matrix cracking in unidirectional CMCs under shear loading. However, the models mentioned above do not consider the effect of long-term oxidation on matrix cracking stress in CMCs. Lamouroux et al. [9] investigated the oxidation behavior of 2D woven C/SiC composite at different temperatures based on thermogravimetric analysis. It was found that the oxidation behavior of C/SiC exist three temperature domains, i.e., (1) at low temperature (<800 °C), the reaction mechanism between carbon and oxygen control the oxidation kinetics; (2) at intermediate temperatures, (between 800 °C and 1,100 °C), the oxidation kinetics are controlled by the gas-phase diffusion through matrix microcracks; and (3) at high temperature (>1,100 °C), the diffusion mechanisms are affected by matrix crack closure and sealing of cracks by silica. Halbig et al. [10] investigated the oxidation behavior of carbon fibers, C/SiC composite with and without stress. The applied load and temperature would affect the openings of the as-fabricated microcracks, which degrades the mechanical properties of C/SiC composite at elevated temperatures. Casas et al. [11] developed a creep-oxidation model for fiber-reinforced CMCs at elevated temperature, including the effects of interface and matrix oxidation, creep of fibers and degradation of fibers strength with time. The broken fibers fraction increases with time in an accelerated manner due to fibers strength degradation.

In this paper, the synergistic effects of temperature and oxidation on matrix cracking in CMCs has been investigated using energy balance approach. The shear-lag model cooperated with interface oxidation model, interface debonding model, fiber strength degradation model, and fiber failure model has been adopted to analyze the stress distribution in fibers and the matrix. The relationships between matrix cracking stress, interface debonding and slipping, fiber failure, oxidation temperatures and time have been established. The effects of fiber volume fraction, interface properties, fiber strength and oxidation temperatures on the evolution of matrix cracking stress versus oxidation time have been analyzed.

2 Stress Analysis

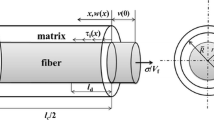
As the mismatch of the axial thermal expansion coefficient between the carbon fiber and silicon carbide matrix, i.e., −0.38 × 10−6/°C vs 4.6 × 10−6/°C, there are unavoidable microcracks existed within the SiC matrix when the composite was cooled down from high fabricated temperature to ambient temperature. These processing-induced microcracks mainly existed in the surface of the material, which do not propagate through the entire thickness of the composite. However, at elevated temperature, the microcracks would serve as avenues for the ingress of the environment atmosphere into the composite, as shown in Fig. 1. The oxygen reacts with carbon layer along the fiber length at a certain rate of dζ/dt, in which ζ is the length of carbon lost in each side of the crack [11].

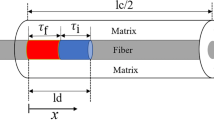
$$ \zeta ={\varphi}_1\left[1- \exp \left(-\frac{\varphi_2t}{b}\right)\right] $$
(1)

where φ 1 and φ 2 are parameters dependent on temperature and described using the Arrhenius type laws; and b is a delay factor considering the deceleration of reduced oxygen activity. In the interface oxidation region, i.e., z∈[0, ζ], the stress transfer between the fiber and the matrix is controlled by a sliding stress τi(x) = τf, different from the interface shear stress in the interface debonded region, i.e., z∈[ζ, l d], τi(x) = τi. This new interface shear stress τf is lower than τi.

Fig. 1
figure 1

The schematic of crack-tip, interface debonding and oxidation

Full size image

The oxidation of fiber is assumed to be controlled by diffusion of oxygen gas through matrix cracks. When the oxidizing gas ingresses into the composite, a sequence of events is triggered starting first with the oxidation of the fiber [12]. For simplicity, it is assumed that both the Weibull and elastic moduli of the fibers remain constant and that the only effect of oxidation is to decrease the strength of fibers. The time-dependent strength of fibers would be controlled by surface defects resulting from the oxidation, with the thickness of the oxidized layer representing the size of the average strength-controlling flaw [2]. According to linear elastic fracture mechanics, the relationship between strength and flaw size is determined by the Eq. (2) [13].

$$ {K}_{\mathrm{IC}}=Y{\sigma}_0\sqrt{a} $$
(2)

where K IC denotes the critical stress intensity factor; Y is a geometric parameter; σ 0 is the fiber strength; and a is the size of the strength-controlling flaw.

Considering that the oxidation of fibers is controlled by diffusion of oxygen through oxidized layer, the oxidized layer will grow on fiber’s surface according to [13]

$$ \alpha =\sqrt{kt} $$
(3)

where α is the thickness of the oxidized layer at time t; and k is the parabolic rate constant.

By assuming the fracture toughness of the fibers remains constant and that the fiber strength σ 0, is related to the mean oxidized layer thickness according to Eq. (2), i.e., a = α, then the time dependence of the fiber strength would be determined by the Eq. (4a, 4b) [13].

$$ {\sigma}_0(t)={\sigma}_0,t\le \frac{1}{k}{\left(\frac{K_{IC}}{Y{\sigma}_0}\right)}^4 $$
(4a)
$$ {\sigma}_0(t)=\frac{K_{IC}}{Y\sqrt[4]{kt}},t>\frac{1}{k}{\left(\frac{K_{IC}}{Y{\sigma}_0}\right)}^4 $$
(4b)

The two-parameter Weibull model is adopted to describe the fiber strength distribution, and the Global Load Sharing (GLS) assumption is used to determine the load carried by the intact and fracture fibers [14].

$$ \frac{\sigma }{V_{\mathrm{f}}}=T\left[1-P(T)\right]+\left\langle {T}_{\mathrm{b}}\right\rangle P(T) $$
(5)

where V f denotes the fiber volume fraction; T denotes the load carried by intact fibers; 〈T b〉 denotes the load carried by broken fibers; and P(T) denotes the fiber failure probability.

$$ P(T)=\eta {P}_a(T)+\left(1-\eta \right){P}_b(T)+{P}_c(T) $$
(6)

where η denotes the oxidation fibers fraction in the oxidation region; and P a (T), P b (T), P c (T), and P d(T) denote the fracture probability of oxidized fibers in the oxidation region, unoxidized fibers in the oxidation region, interface debonded region and interface bonded region, respectively.

$$ {P}_a(T)=1- \exp \left\{-\frac{1}{m+1}\frac{r_{\mathrm{f}}{T}^{m+1}}{\tau_{\mathrm{f}}{l}_0{\left[{\sigma}_0(t)\right]}^m}\left[1-{\left(1-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}T}\zeta \right)}^{m+1}\right]\right\} $$
(7)
$$ {P}_b(T)=1- \exp \left\{-\frac{1}{m+1}\frac{r_{\mathrm{f}}{T}^{m+1}}{\tau_{\mathrm{f}}{l}_0{\left({\sigma}_0\right)}^m}\left[1-{\left(1-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}T}\zeta \right)}^{m+1}\right]\right\} $$
(8)
$$ {P}_c(T)=1- \exp \left\{-\frac{1}{m+1}\frac{r_{\mathrm{f}}{T}^{m+1}}{l_0{\tau}_{\mathrm{i}}{\left({\sigma}_0\right)}^m}\left[{\left(1-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}T}\zeta \right)}^{m+1}-{\left(1-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}T}\zeta -\frac{2{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}T}\left({l}_{\mathrm{d}}-\zeta \right)\right)}^{m+1}\right]\right\} $$
(9)
$$ \begin{array}{l}{P}_d(T)=1- \exp \left\{-\frac{2{r}_{\mathrm{f}}{T}^m}{\rho {l}_0{\sigma}_0^m\left(m+1\right)\left(1-\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{i}}}\frac{\zeta }{l_{\mathrm{s}}}-\frac{l_{\mathrm{d}}-\zeta }{l_{\mathrm{s}}}-\frac{\sigma_{\mathrm{f}\mathrm{o}}}{T}\right)}\right.\hfill \\ {}\left.\kern4em \times {\left[\left(1-\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{i}}}\frac{\zeta }{l_{\mathrm{s}}}-\frac{l_{\mathrm{d}}-\zeta }{l_{\mathrm{s}}}-\frac{\sigma_{\mathrm{f}\mathrm{o}}}{T}\right)\left(\rho \frac{l_{\mathrm{s}}-{l}_{\mathrm{d}}}{r_{\mathrm{f}}}\right)-\left(1-\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{i}}}\frac{\zeta }{l_{\mathrm{s}}}-\frac{l_{\mathrm{d}}-\zeta }{l_{\mathrm{s}}}\right)\right]}^{m+1}\right\}\hfill \end{array} $$
(10)

where r f denotes the fiber radius; m denotes the fiber Weibull modulus; σ 0(t) denotes the oxidized fiber strength; t denotes the oxidation time; l d denotes the interface debonded length; and l s denotes the slip length over which the fiber stress would decay to zero if not interrupted by the far–field equilibrium stresses.

$$ {l}_{\mathrm{s}}=\frac{r_{\mathrm{f}}T}{2{\tau}_{\mathrm{i}}} $$
(11)

The stress carried by broken fibers is determined by the Eq. (12).

$$ \left\langle {T}_{\mathrm{b}}\right\rangle =T\left[{\left(\frac{\sigma_{\mathrm{c}}}{T}\right)}^{m+1}-\frac{1-P(T)}{P(T)}\right] $$
(12)

Substituting Eqs. (6) and (12) into Eq. (5), the stress T carried by intact fibers at the matrix cracking plane can be determined. Substituting the intact fiber stress T into the Eqs. (7)–(10), the relationship between fiber failure probability and applied stress can be determined.

2.1 Downstream Stresses

The composite with fiber volume fraction V f is loaded by a remote uniform stress σ normal to a long crack plane, as shown in Fig. 1. The unit cell in the downstream Region I contained a single fiber surrounded by a hollow cylinder of matrix is extracted from the ceramic composite system, as shown in Fig. 2. The fiber radius is r f, and the matrix radius is R (R = r f/V f 1/2). The length of the unit cell is half matrix crack spacing l c/2, and the interface oxidation length and interface debonded length are ζ and l d, respectively. In the oxidation region, the fiber/matrix interface is resisted by a constant frictional shear stress τf; and in the debonded region, the interface is resisted by τi, which is higher than τf. For the debonded region in Region I, the force equilibrium equation of the fiber is given by Eq. (13).

$$ \frac{d{\sigma}_{\mathrm{f}}(z)}{dz}=-\frac{2{\tau}_{\mathrm{i}}(z)}{r_{\mathrm{f}}} $$
(13)
Fig. 2
figure 2

The schematic of shear-lag model considering interface oxidation and debonding

Full size image

The boundary condition at the crack plane z = 0 is given by Eqs. (14) and (15).

$$ {\sigma}_{\mathrm{f}}\left(z=0\right)=T $$
(14)
$$ {\sigma}_{\mathrm{m}}\left(z=0\right)=0 $$
(15)

The total axial stresses in Region I satisfy the Eq. (16).

$$ {V}_{\mathrm{f}}{\sigma}_{\mathrm{f}}(z)+{V}_{\mathrm{m}}{\sigma}_{\mathrm{m}}(z)=\sigma $$
(16)

Solving Eqs. (13) and (16) with the boundary conditions given by Eqs. (14) and (15), and the interface shear stress in the oxidation and debonded region, the fiber and matrix axial stresses in the interface oxidation and debonded region, i.e., 0 < z < l d, can be determined by Eqs. (17) and (18).

$$ {\sigma}_{\mathrm{f}}^{\mathrm{D}}(z)=\left\{\begin{array}{l}T-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}}z,z\in \left(0,\zeta \right)\\ {}T-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}}\zeta -\frac{2{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}}\left(z-\zeta \right),z\in \left(\zeta, {l}_{\mathrm{d}}\right)\end{array}\right. $$
(17)
$$ {\sigma}_{\mathrm{m}}^{\mathrm{D}}(z)=\left\{\begin{array}{l}2\frac{V_{\mathrm{f}}}{V_{\mathrm{m}}}\frac{\tau_{\mathrm{f}}}{r_{\mathrm{f}}}z,z\in \left(0,\zeta \right)\\ {}2\frac{V_{\mathrm{f}}}{V_{\mathrm{m}}}\frac{\tau_{\mathrm{f}}}{r_{\mathrm{f}}}\zeta +2\frac{V_{\mathrm{f}}}{V_{\mathrm{m}}}\frac{\tau_{\mathrm{i}}}{r_{\mathrm{f}}}\left(z-\zeta \right),z\in \left(\zeta, {l}_{\mathrm{d}}\right)\end{array}\right. $$
(18)

For the bonded region (l d < z) in the downstream Region I, the fiber and matrix axial stresses and the interfacial shear stress can be determined using the composite-cylinder model adopted by BHE [5]. The free body diagram of the composite-cylinder model is illustrated in Fig. 2, where the fiber closure traction T that causes interfacial debonding between the fiber and the matrix over a distance l d and the crack opening displacement v(0). The radius of the matrix cylinder is given by the Eq. (19).

$$ R=\frac{r_f}{\sqrt{V_f}} $$
(19)

The model can be further simplified by defining an effective radius \( \overline{R} \) (\( {r}_{\mathrm{f}}<\overline{R}<R \)) such that the matrix axial load to be concentrated at \( \overline{R} \) and the region between r f and \( \overline{R} \) carries only the shear stress.

$$ \ln \left(\frac{\overline{R}}{r_{\mathrm{f}}}\right)=-\frac{2 \ln {V}_{\mathrm{f}}+{V}_{\mathrm{m}}\left(3-{V}_{\mathrm{f}}\right)}{4{V}_{\mathrm{m}}^2} $$
(20)

Considering the equilibrium of the radius force acting on the differential element dz(dr)(rdθ) in the domain \( {r}_{\mathrm{f}}<r<\overline{R} \) of the bonded matrix region (i.e., z ≥ l d), leads to the following differential equation.

$$ \frac{\partial {\tau}_{\mathrm{rz}}}{\partial r}+\frac{\tau_{\mathrm{rz}}}{r}=0 $$
(21)

The shear stress τrz is given by

$$ {\tau}_{\mathrm{rz}}\left(r,z\right)=\frac{r_{\mathrm{f}}{\tau}_{\mathrm{i}}(z)}{r} $$
(22)

The matrix in the region \( {r}_{\mathrm{f}}<r<\overline{R} \) only carries the shear stress, the stress–strain relation can be determined by the Eq. (23).

$$ {\tau}_{\mathrm{rz}}={G}_{\mathrm{m}}\frac{\partial w}{\partial r} $$
(23)

where G m is the matrix shear modulus; and w is the axial displacement.

Substituting the Eq. (22) into the Eq. (23), the interfacial shear stress τi(z), in the interface bonded region can be given by the Eq. (24).

$$ {\tau}_{\mathrm{i}}(z)=\frac{G_{\mathrm{m}}\left({w}_{\mathrm{m}}-{w}_{\mathrm{f}}\right)}{r_{\mathrm{f}} \ln \left(\overline{R}/{r}_{\mathrm{f}}\right)} $$
(24)

where w f = w(r f, z) and \( {w}_{\mathrm{m}}=w\left(\overline{R},z\right) \) denote the fiber and the matrix axial displacement, respectively.

$$ \frac{d{w}_{\mathrm{f}}}{dz}=\frac{\sigma_{\mathrm{f}}}{E_{\mathrm{f}}} $$
(25)
$$ \frac{d{w}_{\mathrm{m}}}{dz}=\frac{\sigma_{\mathrm{m}}}{E_{\mathrm{m}}} $$
(26)

where E f and E m denote the fiber and matrix elastic modulus.

Substituting Eqs. (24)–(26) into the Eq. (13), and applying the boundary condition of Eqs. (14) and (15), the fiber and matrix axial stresses in the bonded region (l d < z) become

$$ {\sigma}_{\mathrm{f}}^{\mathrm{D}}={\sigma}_{\mathrm{f}\mathrm{o}}+\left[T-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}}\zeta -\frac{2{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}}\left({l}_{\mathrm{d}}-\zeta \right)-{\sigma}_{\mathrm{f}\mathrm{o}}\right] \exp \left(-\rho \frac{z-{l}_{\mathrm{d}}}{r_{\mathrm{f}}}\right) $$
(27)
$$ {\sigma}_{\mathrm{m}}^{\mathrm{D}}={\sigma}_{\mathrm{m}\mathrm{o}}+\left[2\frac{V_{\mathrm{f}}}{V_{\mathrm{m}}}\frac{\tau_{\mathrm{f}}}{r_{\mathrm{f}}}\zeta +2\frac{V_{\mathrm{f}}}{V_{\mathrm{m}}}\frac{\tau_{\mathrm{i}}}{r_{\mathrm{f}}}\left({l}_{\mathrm{d}}-\zeta \right)-{\sigma}_{\mathrm{m}\mathrm{o}}\right] \exp \left(-\rho \frac{z-{l}_{\mathrm{d}}}{r_{\mathrm{f}}}\right) $$
(28)
$$ {\tau}_i^D(z)=\frac{\rho }{2}\left[T-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}}\zeta -\frac{2{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}}\left({l}_{\mathrm{d}}-\zeta \right)-{\sigma}_{\mathrm{f}\mathrm{o}}\right] \exp \left(-\rho \frac{z-{l}_{\mathrm{d}}}{r_{\mathrm{f}}}\right) $$
(29)

where ρ denotes the shear-lag model parameter, and

$$ {\sigma}_{\mathrm{f}\mathrm{o}}=\frac{E_{\mathrm{f}}}{E_{\mathrm{c}}}\sigma +{E}_{\mathrm{f}}\left({\alpha}_{\mathrm{c}}-{\alpha}_{\mathrm{f}}\right)\varDelta \mathrm{T} $$
(30)
$$ {\sigma}_{\mathrm{m}\mathrm{o}}=\frac{E_{\mathrm{m}}}{E_{\mathrm{c}}}\sigma +{E}_{\mathrm{m}}\left({\alpha}_{\mathrm{c}}-{\alpha}_{\mathrm{m}}\right)\varDelta \mathrm{T} $$
(31)

where E c denotes the composite elastic modulus; α f, α m and α c denote the fiber, matrix and composite thermal expansion coefficient, respectively; and ∆T denotes the temperature difference between the fabricated temperature T0 and testing temperature T1 (∆T = T1–T0).

2.2 Upstream Stresses

The upstream region III as shown in Fig. 1 is so far away from the crack tip that the stress and strain fields are also uniform. The fiber and matrix have the same displacements and the fiber and matrix stresses are given by Eqs. (32) and (33).

$$ {\sigma}_{\mathrm{f}}^{\mathrm{U}}={\sigma}_{\mathrm{f}\mathrm{o}} $$
(32)
$$ {\sigma}_{\mathrm{m}}^{\mathrm{U}}={\sigma}_{\mathrm{m}\mathrm{o}} $$
(33)

3 Interface Debonding

When matrix crack propagates to fiber/matrix interface, it deflects along the interface. The fracture mechanics approach is adopted in the present analysis. The interface debonding criterion is given by Eq. (34) [15].

$$ {\xi}_{\mathrm{d}}=-\frac{F}{4\pi {r}_{\mathrm{f}}}\frac{\partial {w}_{\mathrm{f}}(0)}{\partial {l}_{\mathrm{d}}}-\frac{1}{2}{\displaystyle {\int}_0^{l_{\mathrm{d}}}{\tau}_{\mathrm{i}}\frac{\partial v(z)}{\partial {l}_{\mathrm{d}}}dz} $$
(34)

where F(=πr f 2 σ/V f) denotes the fiber load at the matrix cracking plane; w f(0) denotes the fiber axial displacement on the matrix cracking plane; and v(z) denotes the relative displacement between the fiber and the matrix.

The axial displacements of the fiber and matrix, i.e., w f(z) and w m(z), are given by Eqs. (35) and (36).

$$ \begin{array}{c}\hfill {w}_{\mathrm{f}}(z)={\displaystyle {\int}_{\infty}^z\frac{\sigma_{\mathrm{f}}}{E_{\mathrm{f}}}dz}\hfill \\ {}\hfill ={\displaystyle {\int}_{\infty}^{l_{\mathrm{d}}}\frac{\sigma_{\mathrm{f}\mathrm{o}}}{E_{\mathrm{f}}}dz}-\frac{T}{E_{\mathrm{f}}}\left({l}_{\mathrm{d}}-z\right)-\frac{\tau_{\mathrm{f}}}{r_{\mathrm{f}}{E}_{\mathrm{f}}}\left({\zeta}^2-2\zeta {l}_{\mathrm{d}}+{z}^2\right)+\frac{\tau_{\mathrm{i}}}{r_{\mathrm{f}}{E}_{\mathrm{f}}}{\left({l}_{\mathrm{d}}-\zeta \right)}^2\hfill \\ {}\hfill -\frac{r_{\mathrm{f}}}{\rho {E}_{\mathrm{f}}}\left[T-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}}\zeta -\frac{2{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}}\left({l}_{\mathrm{d}}-\zeta \right)-{\sigma}_{\mathrm{f}\mathrm{o}}\right]\hfill \end{array} $$
(35)
$$ \begin{array}{c}\hfill {w}_{\mathrm{m}}(z)={\displaystyle {\int}_{\infty}^z\frac{\sigma_{\mathrm{m}}}{E_{\mathrm{m}}}dz}\hfill \\ {}\hfill ={\displaystyle {\int}_{\infty}^{l_{\mathrm{d}}}\frac{\sigma_{\mathrm{m}\mathrm{o}}}{E_{\mathrm{m}}}dz}-\frac{V_{\mathrm{f}}{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_m}{\left({l}_{\mathrm{d}}-\zeta \right)}^2+\frac{V_{\mathrm{f}}{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_m}\left({\zeta}^2-2\zeta {l}_{\mathrm{d}}+{z}^2\right)\hfill \\ {}\hfill -\frac{r_{\mathrm{f}}}{\rho {E}_{\mathrm{m}}}\left[2\frac{\tau_{\mathrm{f}}{V}_{\mathrm{f}}}{r_{\mathrm{f}}{V}_{\mathrm{m}}}\zeta +2\frac{V_{\mathrm{f}}{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}{V}_{\mathrm{m}}}\left({l}_{\mathrm{d}}-\zeta \right)-{\sigma}_{\mathrm{m}\mathrm{o}}\right]\hfill \end{array} $$
(36)

The relative displacement between the fiber and the matrix, i.e., v(z), is given by the Eq. (37).

$$ \begin{array}{c}\hfill v(z)=\left|{w}_{\mathrm{f}}(z)-{w}_{\mathrm{m}}(z)\right|\hfill \\ {}\hfill =\frac{T}{E_{\mathrm{f}}}\left({l}_{\mathrm{d}}-z\right)+\frac{E_{\mathrm{c}}{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}\left({\zeta}^2-2\zeta {l}_{\mathrm{d}}+{z}^2\right)-\frac{E_{\mathrm{c}}{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}{\left({l}_{\mathrm{d}}-\zeta \right)}^2\hfill \\ {}\hfill +\frac{r_{\mathrm{f}}{E}_{\mathrm{c}}}{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}\left[T-\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}}\zeta -\frac{2{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}}\left({l}_{\mathrm{d}}-\zeta \right)-{\sigma}_{\mathrm{f}\mathrm{o}}\right]\hfill \end{array} $$
(37)

Substituting w f(z = 0) and v(z) into the Eq. (34), it leads to the form of Eq. (38).

$$ \begin{array}{l}\frac{E_{\mathrm{c}}{\tau}_{\mathrm{i}}^2}{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{f}}{E}_{\mathrm{m}}}{\left({l}_{\mathrm{d}}-\zeta \right)}^2+\frac{2{E}_{\mathrm{c}}{\tau}_{\mathrm{f}}{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{f}}{E}_{\mathrm{m}}}\zeta \left({l}_{\mathrm{d}}-\zeta \right)-\frac{\tau_{\mathrm{i}}}{2{E}_{\mathrm{f}}}\left(\frac{\sigma }{V_{\mathrm{f}}}+T\right)\left({l}_{\mathrm{d}}-\zeta \right)\hfill \\ {}+\frac{E_{\mathrm{c}}{\tau}_{\mathrm{i}}^2}{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}\left({l}_{\mathrm{d}}-\zeta \right)+\frac{r_{\mathrm{f}}\sigma T}{4{V}_{\mathrm{f}}{E}_{\mathrm{f}}}-\frac{r_{\mathrm{f}}{\sigma}^2}{4{V}_{\mathrm{f}}{E}_{\mathrm{c}}}-\frac{\tau_{\mathrm{f}}\sigma \zeta }{2{V}_{\mathrm{f}}{E}_{\mathrm{f}}}-\frac{\tau_{\mathrm{f}}T}{2{E}_{\mathrm{f}}}\zeta +\frac{E_{\mathrm{c}}{\tau}_{\mathrm{f}}^2}{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{f}}{E}_{\mathrm{m}}}{\zeta}^2\hfill \\ {}-\frac{r_{\mathrm{f}}{\tau}_{\mathrm{i}}\sigma }{2\rho {V}_{\mathrm{f}}{E}_{\mathrm{f}}}+\frac{E_{\mathrm{c}}{\tau}_{\mathrm{f}}{\tau}_{\mathrm{i}}}{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}\zeta -{\xi}_{\mathrm{d}}=0\hfill \end{array} $$
(38)

Solving Eq. (26), the interface debonded length l d is determined by Eq. (39).

$$ \begin{array}{c}\hfill {l}_{\mathrm{d}}=\left(1-\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{i}}}\right)\zeta +\frac{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{m}}}{4{E}_{\mathrm{c}}{\tau}_{\mathrm{i}}}\left(\frac{\sigma }{V_{\mathrm{f}}}+T\right)-\frac{r_f}{2\rho }-\left\{\frac{r_{\mathrm{f}}^2{V}_{\mathrm{m}}{E}_{\mathrm{m}}{T}^2}{4{E}_{\mathrm{c}}{\tau}_{\mathrm{i}}^2}\left[\frac{V_{\mathrm{m}}{E}_{\mathrm{m}}}{4{E}_{\mathrm{c}}}{\left(\frac{\sigma }{V_{\mathrm{f}}T}+1\right)}^2\right.\right.\hfill \\ {}\hfill {\left.\left.+\frac{V_{\mathrm{f}}{E}_{\mathrm{f}}}{E_{\mathrm{c}}}{\left(\frac{\sigma }{V_{\mathrm{f}}T}\right)}^2-\frac{\sigma }{V_{\mathrm{f}}T}\right]+\frac{r_{\mathrm{f}}^2{V}_{\mathrm{m}}{E}_{\mathrm{m}}}{4\rho {E}_{\mathrm{c}}{\tau}_{\mathrm{i}}}\left(\frac{\sigma }{V_{\mathrm{f}}}-T\right)+{\left(\frac{r_{\mathrm{f}}}{2\rho}\right)}^2+\frac{r_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{f}}{E}_{\mathrm{m}}}{E_{\mathrm{c}}{\tau}_i^2}{\xi}_{\mathrm{d}}\right\}}^{\frac{1}{2}}\hfill \end{array} $$
(39)

4 Matrix Cracking Stress

The energy relationship to evaluate the steady-state matrix cracking stress is determined by the Eq. (40) [5].

$$ \begin{array}{l}\frac{1}{2}{\displaystyle {\int}_{-\infty}^{\infty}\left[\frac{V_{\mathrm{f}}}{E_{\mathrm{f}}}{\left({\sigma}_{\mathrm{f}}^{\mathrm{U}}-{\sigma}_{\mathrm{f}}^{\mathrm{D}}\right)}^2+\frac{V_{\mathrm{m}}}{E_{\mathrm{m}}}{\left({\sigma}_{\mathrm{m}}^{\mathrm{U}}-{\sigma}_{\mathrm{m}}^{\mathrm{D}}\right)}^2\right]dz}+\frac{1}{2\pi {R}^2{G}_{\mathrm{m}}}{\displaystyle {\int}_{-{l}_{\mathrm{d}}}^{l_{\mathrm{d}}}{\displaystyle {\int}_{r_{\mathrm{f}}}^R\left(\frac{r_{\mathrm{f}}{\tau}_{\mathrm{i}}(z)}{r}\right)2\pi rdrdz}}\hfill \\ {}={V}_{\mathrm{m}}{\xi}_{\mathrm{m}}+\left(\frac{4{V}_{\mathrm{f}}{l}_{\mathrm{d}}}{r_{\mathrm{f}}}\right){\xi}_{\mathrm{d}}\hfill \end{array} $$
(40)

where ξ m is the matrix fracture energy; and G m is the matrix shear modulus. The contribution of the shear energy term in Eq. (40) was neglected in the ACK model [4]. It was verified that this negligence is well accepted for the interface slip length larger than a few fiber radii. Following the ACK model, the contribution of shear energy is neglected in the present analysis. Substituting the fiber and matrix stresses of Eqs. (17), (18), (27)–(29) and the debonded length of Eq. (39) into Eq. (40), the energy balance equation leads to the form of

$$ {\eta}_1{\sigma}^2+{\eta}_2\sigma +{\eta}_3=0 $$
(41)

where

$$ {\eta}_1=\frac{l_{\mathrm{d}}}{E_{\mathrm{c}}}+\frac{r_{\mathrm{f}}{V}_{\mathrm{f}}{E}_{\mathrm{f}}}{2\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{c}}} $$
(42a)
$$ {\eta}_2=-\frac{2{V}_{\mathrm{f}}T{l}_{\mathrm{d}}}{E_{\mathrm{c}}}-\frac{r_{\mathrm{f}}{V}_{\mathrm{f}}T}{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}}+\frac{2{V}_{\mathrm{f}}{\tau}_{\mathrm{f}}\zeta }{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}}+\frac{2{V}_{\mathrm{f}}{\tau}_{\mathrm{i}}}{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}}\left({l}_{\mathrm{d}}-\zeta \right) $$
(42b)
$$ \begin{array}{c}\hfill {\eta}_3=\frac{V_{\mathrm{f}}{l}_{\mathrm{d}}{T}^2}{E_{\mathrm{f}}}-\frac{V_{\mathrm{f}}}{E_{\mathrm{f}}}\left(\frac{2{\tau}_{\mathrm{f}}}{r_{\mathrm{f}}}\right)\zeta \left(2{l}_{\mathrm{d}}-\zeta \right)T-\frac{V_{\mathrm{f}}}{E_{\mathrm{f}}}\left(\frac{2{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}}\right){\left({l}_{\mathrm{d}}-\zeta \right)}^2T\hfill \\ {}\hfill +\frac{4}{3}\left(\frac{V_{\mathrm{f}}{E}_{\mathrm{c}}}{V_{\mathrm{m}}{E}_{\mathrm{f}}{E}_{\mathrm{m}}}\right){\left(\frac{\tau_{\mathrm{i}}}{r_{\mathrm{f}}}\right)}^2\left[{\left({l}_{\mathrm{d}}-\zeta \right)}^3+{\left(\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{i}}}\right)}^2{\zeta}^3\right]\hfill \\ {}\hfill +\left(\frac{4{V}_{\mathrm{f}}{E}_{\mathrm{c}}}{V_{\mathrm{m}}{E}_{\mathrm{f}}{E}_{\mathrm{m}}}\right)\frac{\tau_{\mathrm{f}}{\tau}_{\mathrm{i}}}{r_{\mathrm{f}}^2}\zeta \left({l}_{\mathrm{d}}-\zeta \right)\left[{l}_{\mathrm{d}}-\left(1-\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{i}}}\right)\zeta \right]\hfill \\ {}\hfill +\frac{r_{\mathrm{f}}{V}_{\mathrm{f}}{E}_{\mathrm{c}}{T}^2}{2\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}+\frac{2{V}_{\mathrm{f}}{E}_{\mathrm{c}}{\tau}_{\mathrm{f}}^2}{\rho {r}_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}{\zeta}^2+\frac{2{V}_{\mathrm{f}}{E}_{\mathrm{c}}{\tau}_{\mathrm{i}}^2}{\rho {r}_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}{\left({l}_{\mathrm{d}}-\zeta \right)}^2\hfill \\ {}\hfill -\frac{2{V}_{\mathrm{f}}{E}_{\mathrm{c}}T{\tau}_{\mathrm{f}}}{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}\zeta -\frac{2{V}_{\mathrm{f}}{E}_{\mathrm{c}}{\tau}_{\mathrm{i}}T}{\rho {V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}\left({l}_{\mathrm{d}}-\zeta \right)\hfill \\ {}\hfill +\frac{4{V}_{\mathrm{f}}{E}_{\mathrm{c}}{\tau}_{\mathrm{f}}{\tau}_{\mathrm{i}}}{\rho {r}_{\mathrm{f}}{V}_{\mathrm{m}}{E}_{\mathrm{m}}{E}_{\mathrm{f}}}\zeta \left({l}_{\mathrm{d}}-\zeta \right)\hfill \\ {}\hfill -{V}_{\mathrm{m}}{\xi}_{\mathrm{m}}-\left(\frac{4{V}_{\mathrm{f}}{l}_{\mathrm{d}}}{r_{\mathrm{f}}}\right){\xi}_{\mathrm{d}}\hfill \end{array} $$
(42c)

5 Discussion

The ceramic composite system of C/SiC is used for the case study and its material properties are given by: V f = 30 %, E f = 230 GPa, E m = 350 GPa, r f = 3.5 μm, ξ m = 6 J/m2, ξ d = 0.6 J/m2, τ i = 15 MPa, and τ f = 5 MPa, α f = −0.38 × 10−6/°C, α m = 4.6 × 10−6/°C, ΔT = −1,000 °C, σ 0 = 2.6 GPa, and m f = 5.

5.1 Effect of Fiber Volume Fraction

The matrix cracking stress σ mc, interface debonded length l d/r f and interface oxidation length ζ/l d versus oxidation time curves corresponding to different fiber volume fractions of V f = 30 % and 40 % are illustrated in Fig. 3.

Fig. 3
figure 3

a The matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time corresponding to different fiber volume fractions of V f = 30 % and 40 %

Full size image

When V f = 30 %, the matrix cracking stress σ mc decreases from 83 MPa to 43 MPa after 10 h oxidation at 800 °C, as shown in Fig. 3(a); the interface debonded length l d/r f first decreases from 8.4 to 8.2 after 1.9 h oxidation at 800 °C, and then increases to 10.6 after 10 h oxidation at 800 °C, as shown in Fig. 3(b); and the interface oxidation length ζ/l d increases from zero to 0.8 after 10 h oxidation at 800 °C, as shown in Fig. 3(c).

When V f = 40 %, the matrix cracking stress σ mc decreases from 106 MPa to 57 MPa after 10 h oxidation at 800 °C, as shown in Fig. 3(a); the interface debonded length l d/r f first decreases from 6.5 to 6.4 after 1.3 h oxidation at 800 °C, and then increases to 9.4 after 10 h oxidation at 800 °C, as shown in Fig. 3(b); and the interface oxidation length ζ/l d increases from zero to 0.9 after 10 h oxidation at 800 °C, as shown in Fig. 3(c).

With increasing fiber volume fraction, the matrix cracking stress σ mc and the interface oxidation length ζ/l d increase, and the interface debonded length l d/r f decreases.

5.2 Effect of Interface Debonded Energy

The matrix cracking stress σ mc, interface debonded length l d/r f and interface oxidation length ζ/l d versus oxidation time curves corresponding to different interface debonded energy of ξ d/ξ m = 0.1 and 0.2 are illustrated in Fig. 4.

Fig. 4
figure 4

a The matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time corresponding to different interface debonded energy of ξd/ξm = 0.1 and 0.2

Full size image

When ξ d/ξ m = 0.1, the matrix cracking stress σ mc decreases from 94 MPa to 49 MPa after 10 h oxidation at 800 °C, as shown in Fig. 4(a); the interface debonded length l d/r f first decreases from 7.4 to 7.2 after 1.5 h oxidation at 800 °C, and then increases to 9.9 after 10 h oxidation at 800 °C, as shown in Fig. 4(b); and the interface oxidation length ζ/l d increases from zero to 0.85 after 10 h oxidation at 800 °C, as shown in Fig. 4(c).

When ξ d/ξ m = 0.2, the matrix cracking stress σ mc decreases from 152 MPa to 115 MPa after 10 h oxidation at 800 °C, as shown in Fig. 4(a); the interface debonded length l d/r f first decreases from 6.1 to 6.0 after 1 h oxidation at 800 °C, and then increases to 9.1 after 10 h oxidation at 800 °C, as shown in Fig. 4(b); and the interface oxidation length ζ/l d increases from zero to 0.93 after 10 h oxidation at 800 °C, as shown in Fig. 4(c).

With increasing interface debonded energy, the matrix cracking stress σ mc and the interface oxidation length ζ/l d increase, and the interface debonded length l d/r f decreases.

5.3 Effect of Interface Shear Stress

The matrix cracking stress σ mc, interface debonded length l d/r f and interface oxidation length ζ/l d versus oxidation time curves corresponding to different interface shear stress of τ i = 15 and 25 MPa are illustrated in Fig. 5.

Fig. 5
figure 5

a The matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time corresponding to different interface shear stress of τ i = 15 and 25 MPa

Full size image

When τ i = 15 MPa, the matrix cracking stress σ mc decreases from 94 MPa to 49 MPa after 10 h oxidation at 800 °C, as shown in Fig. 5(a); the interface debonded length l d/r f first decreases from 7.4 to 7.2 after 1.5 h oxidation at 800 °C, and then increases to 9.9 after 10 h oxidation at 800 °C, as shown in Fig. 5(b); and the interface oxidation length ζ/l d increases from zero to 0.85 after 10 h oxidation at 800 °C, as shown in Fig. 5(c).

When τ i = 25 MPa, the matrix cracking stress σ mc decreases from 125 MPa to 50 MPa after 10 h oxidation at 800 °C, as shown in Fig. 5(a); the interface debonded length l d/r f first decreases from 5.6 to 5.5 after 1.1 h oxidation at 800 °C, and then increases to 9.3 after 10 h oxidation at 800 °C, as shown in Fig. 5(b); and the interface oxidation length ζ/l d increases from zero to 0.91 after 10 h oxidation at 800 °C, as shown in Fig. 5(c).

The matrix cracking stress σ mc, interface debonded length l d/r f and interface oxidation length ζ/l d versus oxidation time curves corresponding to different interface shear stress of τ f = 1 and 5 MPa are illustrated in Fig. 6.

Fig. 6
figure 6

a The matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time corresponding to different interface shear stress of τ f = 1 and 5 MPa

Full size image

When τ f = 1 MPa, the matrix cracking stress σ mc decreases from 74 MPa to 28 MPa after 10 h oxidation at 800 °C, as shown in Fig. 6(a); the interface debonded length l d/r f first decreases from 9.1 to 9 after 1.5 h oxidation at 800 °C, and then increases to 11.9 after 10 h oxidation at 800 °C, as shown in Fig. 6(b); and the interface oxidation length ζ/l d increases from zero to 0.71 after 10 h oxidation at 800 °C, as shown in Fig. 6(c).

When τ f = 5 MPa, the matrix cracking stress σ mc decreases from 74 MPa to 48 MPa after 10 h oxidation at 800 °C, as shown in Fig. 6(a); the interface debonded length l d/r f first decreases from 9.1 to 8.9 after 2.2 h oxidation at 800 °C, and then increases to 10.6 after 10 h oxidation at 800 °C, as shown in Fig. 6(b); and the interface oxidation length ζ/l d increases from zero to 0.79 after 10 h oxidation at 800 °C, as shown in Fig. 6(c).

With increasing interface shear stress of τ i and τf, the matrix cracking stress σ mc and the interface oxidation length ζ/l d increase, and the interface debonded length l d/r f decreases.

5.4 Effect of Fiber Strength

The matrix cracking stress σ mc, interface debonded length l d/r f and interface oxidation length ζ/l d versus oxidation time curves corresponding to different interface shear stress of σ 0 = 1 and 2 GPa are illustrated in Fig. 7.

Fig. 7
figure 7

a The matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time corresponding to different fiber strength of σ 0 = 1 and 2 GPa

Full size image

When σ 0 = 1 GPa, the matrix cracking stress σ mc decreases from 68 MPa to 44 MPa after 10 h oxidation at 800 °C, as shown in Fig. 7(a); the interface debonded length l d/r f first decreases from 8.9 to 8.8 after 1.9 h oxidation at 800 °C, and then increases to 10.5 after 10 h oxidation at 800 °C, as shown in Fig. 7(b); and the interface oxidation length ζ/l d increases from zero to 0.8 after 10 h oxidation at 800 °C, as shown in Fig. 7(c).

When σ 0 = 2 GPa, the matrix cracking stress σ mc decreases from 72 MPa to 47 MPa after 10 h oxidation at 800 °C, as shown in Fig. 7(a); the interface debonded length l d/r f first decreases from 9.1 to 8.9 after 2.1 h oxidation at 800 °C, and then increases to 10.6 after 10 h oxidation at 800 °C, as shown in Fig. 7(b); and the interface oxidation length ζ/l d increases from zero to 0.79 after 10 h oxidation at 800 °C, as shown in Fig. 7(c).

With increasing fiber strength, the matrix cracking stress σ mc and the interface debonded length l d/r f increase, and the interface oxidation length ζ/l d decreases.

5.5 Effect of Oxidation Temperature

The matrix cracking stress σ mc, interface debonded length l d/r f and interface oxidation length ζ/l d versus oxidation time curves corresponding to different oxidation temperature of Tem = 600 °C and 700 °C are illustrated in Fig. 8.

Fig. 8
figure 8

a The matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time corresponding to different oxidation temperature of T = 600 °C and 700 °C

Full size image

When Tem = 600 °C, the matrix cracking stress σ mc decreases from 74.7 MPa to 66.9 MPa after 10 h oxidation, as shown in Fig. 8(a); the interface debonded length l d/r f decreases from 9.1 to 8.9 after 10 h oxidation, as shown in Fig. 8(b); and the interface oxidation length ζ/l d increases from zero to 0.14 after 10 h oxidation, as shown in Fig. 8(c).

When Tem = 700 °C, the matrix cracking stress σ mc decreases from 74.7 MPa to 57 MPa after 10 h oxidation at 800 °C, as shown in Fig. 8(a); the interface debonded length l d/r f first decreases from 9.1 to 8.9 after 5 h oxidation, and then increases to 9.1 after 10 h oxidation, as shown in Fig. 8(b); and the interface oxidation length ζ/l d increases from zero to 0.4 after 10 h oxidation, as shown in Fig. 8(c).

With increasing oxidation temperature, the matrix cracking stress σ mc decrease, and the interface oxidation length ζ/l d and the interface debonded length l d/r f increase.

6 Experimental Comparisons

Yang [16] investigated the mechanical behavior of C/SiC composite after unstressed oxidation at 700 °C in air. The composite was divided into two types based on the interface bonding, i.e., strong interface bonding and weak interface bonding. For C/SiC with strong interface bonding, the monotonic tensile stress–strain curves corresponding to the cases of without oxidation, 4 h and 6 h unstressed oxidation are illustrated in Figs. 9(a)–(c). The matrix cracking stresses of C/SiC corresponding to the proportional limit stresses in the tensile curves are 37, 30 and 20 MPa corresponding to the cases of without oxidation, 4 h oxidation and 6 h unstressed oxidation, respectively. For C/SiC with weak interface bonding, the monotonic tensile stress–strain curves corresponding to the cases of without oxidation, 2 h and 6 h unstressed oxidation are illustrated in Figs. 10(a)–(c). The matrix cracking stresses of C/SiC corresponding to the proportional limit stresses in the tensile curves are 27, 20 and 13 MPa corresponding to the cases of without oxidation, 2 h oxidation and 6 h unstressed oxidation, respectively. The material properties are given by: V f = 20 %, E f = 200 GPa, E m = 350 GPa, r f = 3.5 μm, ξ m = 6 J/m2, ξ d = 1.2 J/m2 (strong interface bonding), ξ d = 0.6 J/m2 (weak interface bonding), τ i = 6 MPa, and τ f = 1 MPa, α f = −0.38 × 10−6/°C, α m = 4.6 × 10−6/°C, ΔT = −1,000 °C, σ 0 = 2.6 GPa, and m f = 5. The experimental and theoretical predicted matrix cracking stresses of C/SiC composite with strong and weak interface bonding after unstressed oxidation at 700 °C in air are illustrated in Figs. 11 and 12, respectively.

Fig. 9
figure 9

The monotonic tensile stress–strain curves of C/SiC composite with strong interface bonding corresponding to (a) without oxidation; (b) unstressed oxidation of 4 h; and (c) unstressed oxidation of 6 h

Full size image
Fig. 10
figure 10

The monotonic tensile stress–strain curves of C/SiC composite with weak interface bonding corresponding to (a) without oxidation; (b) unstressed oxidation of 2 h; and (c) unstressed oxidation of 6 h

Full size image
Fig. 11
figure 11

a The experimental and theoretical predicted matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time of C/SiC composite after unstressed oxidation at 700 °C in air corresponding to strong interface bonding

Full size image
Fig. 12
figure 12

a The experimental and theoretical predicted matrix cracking stress versus oxidation time; (b) the interface debonded length l d/r f versus oxidation time; and (c) the interface oxidation length ζ/l d versus oxidation time of C/SiC composite after unstressed oxidation at 700 °C in air corresponding to weak interface bonding

Full size image

For C/SiC with strong bonding, the matrix cracking stress decreases 18.9 % after oxidation for 4 h, and 46 % after oxidation for 6 h, and the theoretical predicted results agreed with experimental data, as shown in Fig. 11(a); the interface debonded length l d/r f first decreases from 15 to 14.8 after 0.9 h oxidation, and then increases to 21.8 after 10 h oxidation, as shown in Fig. 11(b); and the interface oxidation length ζ/l d increases from zero to 0.83 after 10 h oxidation, as shown in Fig. 11(c).

For C/SiC with weak bonding, the matrix cracking stress decreases 25.9 % after oxidation for 1 h, and 51.8 % after oxidation for 6 h, and the theoretical predicted results agreed with experimental data, as shown in Fig. 12(a); the interface debonded length l d/r f first decreases from 18 to 17.7 after 1.5 h oxidation, and then increases to 23.7 after 10 h oxidation, as shown in Fig. 12(b); and the interface oxidation length ζ/l d increases from zero to 0.76 after 10 h oxidation, as shown in Fig. 12(c).

7 Conclusions

In this paper, the synergistic effects of temperature and oxidation on matrix cracking in CMCs has been investigated using energy balance approach. The shear-lag model cooperated with interface oxidation model, fiber strength degradation model, fiber failure model and interface debonding criteria has been adopted to analyze the stress distribution in CMCs. The relationships between matrix cracking stress, interface debonding and slipping, fiber failure, oxidation temperature and time have been established. The effects of fiber volume fraction, interface properties, fiber strength, and oxidation temperature on the evolution of matrix cracking stress versus oxidation time have been analyzed.

  1. (1)

    With increasing fiber volume fraction, interface debonded energy and interface shar stress, the matrix cracking stress σ mc and the interface oxidation length ζ/l d increase, and the interface debonded length l d/r f decreases.

  2. (2)

    With increasing fiber strength, the the matrix cracking stress σ mc and the interface debonded length l d/r f increase, and the interface oxidation length ζ/l d decreases.

  3. (3)

    With increasing oxidation temperature, the matrix cracking stress σ mc decrease, and the interface oxidation length ζ/l d and the interface debonded length l d/r f increase.