Simultaneous Wide-Field Planar Strain–Fiber Orientation Distribution Measurement Using Polarized Spatial Domain Imaging

Abstract

In the present study, we demonstrate that soft tissue fiber architectural maps captured using polarized spatial frequency domain imaging (pSFDI) can be utilized as an effective texture source for DIC-based planar surface strain analyses. Experimental planar biaxial mechanical studies were conducted using pericardium as the exemplar tissue, with simultaneous pSFDI measurements taken. From these measurements, the collagen fiber preferred direction $\theta _{\text {p}}$ was determined at the pixel level over the entire strain range using established methods (https://doi.org/10.1007/s10439-019-02233-0). We then utilized these pixel-level $\theta _{\text {p}}$ maps as a texture source to quantify the deformation gradient tensor ${\mathbf {F}}({\mathbf {X}},t)$ as a function of spatial position ${\mathbf {X}}$ within the specimen at time t. Results indicted that that the pSFDI approach produced accurate deformation maps, as validated using both physical markers and conventional particle based method derived from the DIC analysis of the same specimens. We then extended the pSFDI technique to extract the fiber orientation distribution $\Gamma (\theta ,{\mathbf {X}},t)$ as a function of ${\mathbf {F}}({\mathbf {X}},t)$ from the pSFDI intensity signal. This was accomplished by developing a calibration procedure to account for the optical behavior of the constituent fibers for the soft tissue being studied. We then demonstrated that the extracted $\Gamma (\theta ,{\mathbf {X}},t)$ was accurately computed in both the referential (i.e. unloaded) and deformed states. Moreover, we noted that the measured $\Gamma (\theta ,{\mathbf {X}},t)$ agreed well with affine kinematic deformation predictions. We also demonstrated this calibration approach could also be effectively used on electrospun biomaterials, underscoring the general utility of the approach. In a final step, using the ability to simultaneously quantify ${\mathbf {F}}({\mathbf {X}},t)$ and $\Gamma (\theta ,{\mathbf {X}},t)$, we examined the effect of deformation and collagen structural measurements on the measurement region size. For pericardial tissues, we determined a critical length of $\sim$ 8 mm wherein the regional variations sufficiently dissipated. This result has immediate potential in the identification of optimal length scales for meso-scale strain measurement in soft tissues and fibrous biomaterials.

Introduction

Occurring in multitudinous forms,³ collagen is the primary fibrous component of the extracellular matrix (ECM) in most soft-tissues,^60,64 thus determining the tissue’s macroscale mechanical response.^19,18 In addition to understanding normal physiological function, many widespread health problems involve degeneration of their collagenous components. Our understanding of these diseases and our ability to inform the rational development of treatment is often limited by an incomplete understanding of the underlying structure-function relations. This has led to the development and application of numerous imaging techniques to quantify collagen fiber structures^12,21,52,59 (the interested reader is referred to Reference [23] for a comprehensive review). However, there is often a trade-off between achieving data-collection times that are appropriate to capture a dynamic microstructure on a deforming tissue surface over a length scale that is functionally meaningful.^32,63 Moreover, extant methods available have a number of limitations, such as requiring optical clearin,⁶⁵ physical marking,^46,57,62 or are unsuitable for the examination of local effects.²⁴

Polarized Spatial Frequency Domain Imaging (pSFDI) is an optical based technique originally developed by Tunnell et al. ^23,22,66 that can rapidly characterize planar collagen and polymeric fiber architectures over a wide field at pixel-level resolutions. In pSFDI, linearly polarized light is projected incident to the specimen surface and the birefringent scattering response measured. pSFDI produces a spatial map of the reflected light intensity $I(\theta )$ as a function of the in-plane angle $\theta$ that is related to the the local fiber structure. From the analysis of $I(\theta )$, several structural quantities can be directly derived, including the preferred fiber direction $\theta _{\text {p}}$ a relative index of the local degree of structural anisotropy. pSFDI thus allows rapid, full-field characterization of the fibrous micro-structures with pixel level resolution. In addition, as it is a reflectance based technique it can be applied in a completely non-contacting, non-destructive manner. pSFDI has been extensively utilized in a variety of applications^32,22,30

Yet, quantification of soft-tissue microstructure is just the start. The full picture must also include the corresponding tissue deformation to understand how local fiber structure convects. There have been numerous studies along these lines for soft tissues, collagenous tissue constructs, and fibrous biomaterials.^{4,10,11,20,28,31,41,55,58,67} These studies have primarily focused on how to model the specific mechanisms of fiber kinematics under generalized loading conditions. A common approach assumes that the affine kinematic transformation is valid (e.g. Ref. 16), wherein the local fiber deformations can be predicted from the tensorial transformation of the local tissue macro-level strain tensor. The affine model is of particular interest in structural soft tissue models,^{36,38,39,40,50} and has been experimentally validated at the tissue scale for several soft tissues and fibrous biomaterials.^16,43,6 With respect to understanding its function, the presence of affine kinematics suggested that the constituent fibers are largely non-interacting and deform in accordance with the bulk tissue.

To acquire tissue level surface deformation information, a large number of experimental techniques exist. A particularly attractive, well established method is digital image correlation (DIC)^46,27 that has been utilized extensively to elucidate stress-strain behaviors of various soft tissues^33,34,35 and biomaterials.^29,47,13 DIC relies on a non-uniform surface texture source that deforms with the tissue surface. The texture source is typically a dark paint pattern or fine powder that is physically applied to the tissue surface, as the natural surface textures are generally insufficient. A set of sequential images of the tissue surface is then acquired as the tissue is deformed, and image correlation algorithms are applied to estimate the local surface displacement vector field. While quite robust, introduction of surface textures adds complexity to the study, and most importantly hinder simultaneous optical measurements of the underlying fibrous structure.

As mentioned above, pSFDI is a pixel level technique so that the resultant data is spatially dense and spans the entire tissue surface. In the present work, we explored the possibility of using the high density pSFDI data as a DIC texture source for tissue surface strain measurements and for simultaneous fibrous structural quantification. To acquire the requisite data, we integrated our pSFDI and biaxial mechanical testing systems to allow generation of the requisite data under highly controlled conditions. We first demonstrate that measured fiber preferred direction $\theta _{\text {p}}({\mathbf {X}})$ at each surface spatial position $\mathbf{X }$ generated by pSFDI can be utilized as a texture source for DIC-based surface strain measurements. Secondly, we demonstrate a method to extract the fiber orientation distribution function $\Gamma (\theta )$ from the pSFDI intensity data $I_{\text {pSFDI}}(\theta )$. This new approach was necessary as $\Gamma (\theta )$ cannot be directly extracted from $I(\theta )$, as the latter quantity is convolved with the single fiber intensity $I_{\text {fiber}}(\theta )$.⁶⁶ Finally, we note that strain measurements in the soft tissue mechanics literature are typically performed using ad-hoc approaches, without informed knowledge of the relevant length scales pertinent to the functional questions under consideration. Thus, in the final step, we utilized the novel combined deformation and structural data to investigate the role of measurement length scale on strain measurements, with an aim to inform soft tissue material modeling.

Methods

Experimental

Polarized Spatial Domain Imaging

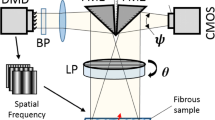
Polarized Spatial Domain Imaging (pSFDI) exploits the birefringent properties of the constituent fibers to obtain information about local structure over the full illumination field. It can thus be used in the study of collagenous and polymeric fibrous biomaterials.^32,24,22 Briefly, randomly polarized light illuminates a digital micro mirror device which produces a sinusoidal pattern with a known spatial frequency and is projected through a rotating linear polarizer producing a spatially sinusoidal pattern of linearly polarized light on the tissue surface (Fig. 1a). This spatial frequency pattern was shifted in phase twice by 120$^\circ$, and the sample imaged at each phase. The three images were then demodulated into what are commonly referred to as the $I_{DC}$ and $I_{AC}$ reflectance components, defined as

$$\begin{aligned} I_{DC}&= (I_{0}+ I_{120} + I_{240})/3 \end{aligned}$$

(1)

$$\begin{aligned} I_{AC}&= \frac{\sqrt{2}}{3} \sqrt{(I_{0}-I_{120}) +(I_{120} - I_{240}) + (I_{240} - I_{0})}, \end{aligned}$$

(2)

where $I_0$, $I_{120}$, and $I_{240}$ are the measured intensities recorded at the associated phase angle, $I_{DC}$ is equivalent to the total reflectance from the sample under planar illumination, and $I_{AC}$ is the spatially modulated reflectance recovered for a given spatial frequency.^9,45,14 Calibration of the system for polarization and reflection effects is carried out using data collected from a TiO₂ reflectance standard over the angular sweep used for specimen imaging. Typically, a spatial frequency is selected that has an associated mean free path that limits the penetration of the incident photons in to the tissue. The resulting intensity signal is then modulated by the tissue fibrous structure (Fig. 1a). Then the reflected beam passes through the polarizer a second time and is captured by a camera. The modification of the light emitted from the source by the system (polarizer and specimen) can be expressed mathematically by applying Mueller calculus. The measured intensity signal $I_{\text {fiber}}(\theta )$ can be described using

$$\begin{aligned} I_{\text {fiber}}(\theta )= & {} {\mathbf {S}}_{\text {out}} = \tau _{sys} {\mathbf {M}}_{\text {p}}{\mathbf {R}}_{\text {p}}(-\theta \pm \rho ) \nonumber \\&\cdot {\mathbf {M}}_{\text {s}} {\mathbf {R}}_{\text {p}}(\theta \pm \rho ) \cdot {\mathbf {M}}_{\text {p}} {\mathbf {S}}_{\text {in}}, \end{aligned}$$

(3)

where ${\mathbf {M}}_{\text {p}}$ and ${\mathbf {R}}_{\text {p}}$ are the Mueller matrix and rotational matrix for a linear polarizer, ${\mathbf {M}}_{\text {s}}$ is the sample Mueller matrix, and ${\mathbf {S}}_{\text {out}},{\mathbf {S}}_{\text {in}}$ are the input and output Stokes vectors, with ${\mathbf {I}}_{\text {fiber}}$ representing the experimentally measured intensity signal. An extended description of these Mueller matrices can be found in ²². Non-polarization dependent system efficiencies are captured with the $\tau _{sys}$ term, which we will omit from this point forward, as it only contributes to linear scaling of the final signal that is accounted for through calibration. $\theta$ is the orientation with respect to the $X_1$ axis (Fig. 1b) (as defined in the pSDFI system by the linear polarizer axis), and $\rho$ is the fiber axial direction (Fig. 1b). Solving this system gives

$$\begin{aligned} I_{\text {fiber}}(\theta )= & {} \frac{1}{4}[M_{11} + M_{11} \, \cos ^{2}[2(\theta \pm \rho )]\nonumber \\&+ 2M_{12} \, \cos [2(\theta \pm \rho )] + M_{33} \, \sin ^{2}[2(\theta \pm \rho )], \end{aligned}$$

(4)

where $M_{ij}$ are the Mueller matrix components. The resulting intensity response for a single fiber,$I_{\text {fiber}}(\theta )$, will have a characteristic double peak pattern (Fig. 2). The $I_{\text {fiber}}(\theta )$ signal pattern can be further simplified into a sum of cosines that are more suitable for fitting to ${\mathbf {I}}$ data.

$$\begin{aligned} I_{\text {fiber}}(\theta ) = a_0 + a_2 \, \cos [2(\theta - \rho )]+ a_4 \, \cos [4(\theta - \rho )], \end{aligned}$$

(5)

where $a_i$ are constants specific for a particular tissue’s optical properties. When these measurements are subsequently repeated over a range of polarizer angles, the total reflected light intensity as a function of $\theta$ for the entire tissue, $I_{\text {pSFDI}}(\theta )$, is obtained.

Figure 1

(a) Schematic of the pSFDI; a monochromator generates a beam of light with a known spatial frequency that is passed through a linear polarizer (that can be rotated to change the polarization of the incident beam incrementally between S- and P- polarization). The polarized light is modulated by the sample that is composed of birefringent fibers before passing through the linear polarizer a second time and imaged by a camera. (b) Schematic showing the coordinates of the polarizer relative to the specimen. The angle $\rho$ here represents the angle of the polarizer axis (green line).

In addition to describing the $I_{\text {fiber}}(\theta )$, Eq. (5) can be used to approximate $I_{\text {pSFDI}}(\theta )$ directly. This is possible because that in pSFDI, $I_{\text {pSFDI}}(\theta )$ is the convolution of $\Gamma (\theta )$ and $I_{\text {fiber}}$.^23,22 Thus the form of ${\mathbf {I}}_{\text {pSFDI}}(\theta )$ will generally follow ${\mathbf {I}}_{\text {fiber}}$. This allows direct estimation of $\theta _{\text {p}}$ from the measured $I_{\text {pSFDI}}(\theta )$ data at each pixel location using

$$\begin{aligned} I_{\text {pSFDI}}(\theta )\approx & {} a'_0 + a'_2 \, \cos [2(\theta _f - \theta _{\text {p}})]\nonumber \\&+ a'_4 \, \cos [4(\theta _f - \theta _{\text {p}})]. \end{aligned}$$

(6)

Here, $\theta _{\text {p}}$ represents the fiber population average preferred direction at each pixel location ${\mathbf {X}}$. Note that the in this application the constants $a'_0,a'_2,a'_4$ should be understood as products of the fitting procedure and should not be confused with the single-fiber values used in Eq. (5). The end result of this approach is a pixel-level map of $\theta _{\text {p}}({\mathbf {X}})$ over the tissue surface.

Figure 2

Qualitative schematic of the scattering intensity response from a single fiber, I($\uprho$) as the polarizer is rotated over a period of 180$^\circ$ at various relative orientations of the electric vector of the linearly polarized incident beam (red arrows) and the fiber axis. As shown, there are peaks in the scattering intensity when parallel and orthogonal configurations are formed by the beam polarization and fibers.

Specimen Preparation

In the present work, we chose cross-linked bovine pericardium as the representative soft tissue, due to its ease of use, dense collagen fiber composition, and its relevance as a biomaterial in medical devices. Large sections (approximately 50 mm $\times$ 75 mm $\times$ 0.5 mm thick) tissue specimens were prepared according to established methods⁴⁹ and pSFDI-generated $\theta _{\text {p}}$ maps of the entire tissue section were used to identify $\sim$ 20 mm x $\sim$ 20 mm regions with regular structures. From these regions a specimen with a preferred direction at 0$^\circ$ (specimen 1) and one with 45$^\circ$ (specimen 2) were obtained. Two ’calibration’ specimens were also prepared as above but taken from a region with greater structural variations to allow for a broader span of structures.

Next, we re-examined data from electrospun (ES) biomaterials utilized in Ref. 22 to demonstrate that the methods developed for collagenous tissues could be successfully applied. Three structural alignment levels (S1,S2, and S3) were studied in three separate specimens. Details of the specimen preparation have been provided in Ref. 22. Briefly, the specimens were fabricated using a custom-made electrospinning mandrel. A 10 % (weight/volume) solution of prolactone was dissolved in hexafluoroisopropanol and the solution was ejected from a charged needle onto the grounded aluminium mandrel. The degree of alignment of the specimens were increased by increasing the rotational velocity of the mandrel. The structural anisotropy of the six specimens used in the study were distinct and represented a diverse collection of fiber structures analogous to those found in soft-tissues. The specimens were cut to $\approx$ 1 cm² prior to being bathed in solutions of ethanol and distilled water in order to make them more hydrophilic. pSFDI images were recorded (see technique details below) with the ES specimens immersed in distilled water. After pSFDI imaging, the same specimens were dried and sputter-coated with 15 nm platinum/palladium nanoparticles. The specimens were each imaged at nine locations evenly spaced across the entire specimen surface at 1000X magnification with a scanning electron microscope (Super40-SEM, Zeiss, Oberkochen Germany). The distribution of fiber diameters was determined from the same image set, using the DiameterJ plugin for ImageJ.

Integrated Planar Biaxial Mechanical-pSFDI Measurements

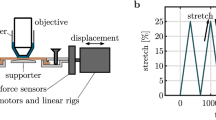
A complete description of the biaxial testing^25,26 and pSFDI systems^23,66 have been previously presented in-depth. For the present study, we integrated the pSFDI system over the biaxial testing system by mounting on a metal frame support (Fig. 1). This setup also allowed for the physical markers on the bottom surface of the specimen to be tracked optically during the loading, in parallel with pSFDI imaging of the top surface. The following experimental studies were conducted for both tissue specimens. First, each test specimen was mounted, then subjected to 10 preconditioning cycles using an equi-biaxial stress protocol to a maximum stress of 225 kPa. Next, each specimen was then tested to the same equi-biaxial stress level, but with the biaxial stress applied over 30 discrete steps. During each step, the current stress level was held to facilitate the pSFDI imaging of the unmarked top surface.

Next, as particle based textures typically utilized in conventional DIC studies,⁴⁶ we performed a second experiment on the same specimens to verify the DIC experimental methodology. This was performed after the above pSFDI protocol was completed by unloading each specimen and draining the water tank temporally. An acrylic paint texture was then applied to the top-surface of the specimen (Fig. 3a), and the water tank refilled, then the stepped loading protocol repeated. This approach allowed validation the surface strain approach by allowing the comparison of pSFDI with both the conventional physical markers (which give a regional average) and texture source for a more detailed comparison.

DIC-Based Surface Strain Analysis

Image Pre-processing

Application of DIC to the pSFDI images requires the $\theta _{\text {p}}({\mathbf {X}})$ data to be represented as a texture. As in our previous studies, we first represented the maps as 8-bit RGB images²² for inspection (Fig. 3b). In the present study, we then represented the maps in grayscale with specific upper and lower limits of $\theta _{\text {p}}$ to optimize $\theta _{\text {p}}({\mathbf {X}})$ as a DIC texture (Fig. 3c) using

$$\begin{aligned} \bar{\theta _{\text {p}}}({\mathbf {X}}) = \theta _{\text {p}}({\mathbf {X}}) \cdot (\theta _{\text {p}} - \theta _{\text {p}}^{\text {lower}})/(\theta _{\text {p}}^{\text {upper}} -\theta _{\text {p}}^{\text {lower}}) \cdot 255, \end{aligned}$$

(7)

where $\theta _{\text {p}}^{\text {upper}}$ and $\theta _{\text {p}}^{\text {lower}}$ are the upper and lower limits of $\theta _{\text {p}}$, respectively. $\theta _{\text {p}}^{\text {upper}}$ and $\theta _{\text {p}}^{\text {lower}}$ were chosen to optimize for the DIC analysis, as discussed in the following section. Note that if $\theta _{\text {p}} > \theta _{\text {p}}^{\text {upper}}, \bar{\theta _{\text {p}}} = 255$ and if $\theta _{\text {p}} < \theta _{\text {p}}^{\text {lower}}, \bar{\theta _{\text {p}}} = 0$.

Figure 3

A mounted pericardial specimen showing (a) particle texture, (b) pSFDI texture expressed as an RGB image, and (c) pSFDI texture as a grayscale for optimal DIC analysis.

DIC Analyses

From the post-processed imaging data, DIC analysis was carried out using the open-source software $\mu$DIC.⁴⁶ In brief, $\mu$DIC takes pixel-level measurements of the gray-scale intensities of a reference image and registers their positions to a finite element surface. For a variety of synthetically generated rigid body motion and actual deformation modes, excellent agreement (within $\pm 0.1\%$) was established between the applied and measured F using DIC analysis. This level of accuracy was achieved for both texture sources, lending support that the pSFDI $\theta _{\text {p}}$ field can be an effective DIC texture source. We then focused our results on the a central region of interest (ROI) approximately 10 mm $\times$ 10 mm. Strain analysis were tracked while an equi-biaxial stress up to 225 kPa was applied specimens 1 and 2 n over approximately sixteen steps. Complete details of the DIC methodology, analysis pipeline, and synthetic validation studies that verify our approach are presented in Appendix (§5)

Extraction of $\Gamma (\theta )$ from $I_{\text {pSFDI}}(\theta )$

General Characteristics of $\Gamma (\theta )$

As we are dealing with planar tissues we define ${\mathbf {n}}(\theta )$ as the normal vector parallel to the local fiber direction $\theta \in [-\pi ,\pi ]$. We treat pericardium as a single, homogeneous fibrous structure. It should be noted that the following can be utilized for either single or multiple layered tissue models, such as that developed for the mitral valve.⁶⁹ As with any probability distribution, normalization requires

$$\begin{aligned} \int _{-\pi }^{\pi }\Gamma [\mathbf{n }(\theta )]d\theta = 1. \end{aligned}$$

(8)

Due to the inherent symmetries of any fiber orientation distribution, $\Gamma$ will be a symmetric function of ${\mathbf {n}}(\theta )$

$$\begin{aligned} \Gamma [\mathbf{n }(\theta )]=\Gamma [-\mathbf{n }(\theta )], \end{aligned}$$

(9)

Based on these observations and our previous pericardial studies,⁵⁰ we used the following wrapped Von Mises distribution with an explicit isotropic component to represent $\Gamma (\theta )$

$$\begin{aligned} \Gamma \left( \theta ,\mu ,\kappa ,d\right) =\frac{d}{2}\left( \frac{\exp \left( \kappa \cos \left( \theta -\mu \right) \right) +\exp \left( \kappa \cos \left( \theta -\mu -\pi \right) \right) }{2\pi I_0\left( \kappa \right) }\right) +\frac{1-d}{2\pi }, \end{aligned}$$

(10)

where $\mu$,$\kappa$, and d are the distribution mean, shape factor, and isotropic component fraction, respectively, and $I_0(\kappa )$ is the modified Bessel function of the first kind, order 0. $\kappa$ can be best understood as a measure of concentration; a reciprocal measure of dispersion, so that $1/\kappa$ is analogous to square of the standard deviation, $\sigma ^2$. Note that $\mu$ was set to $\theta _{\text {p}}$ derived from Eq. (6), so that only $\kappa$ and d need to be fit.

Extraction of $\Gamma (\theta )$ from $I_{\text {pSFDI}}(\theta )$

Closed form version of the convolution integral As mentioned in ‘Polarized Spatial Domain Imaging’, in the pSFDI measurement approach $\Gamma (\theta )$ cannot be extracted directly. Rather, $I_{\text {pSFDI}}$ is a weighted sum of the ${\mathbf {I}}_{\text {fiber}}$ contributions from each of the individual fibers for all orientations. $I_{\text {pSFDI}}(\theta )$ can thus be presented by a convolution integral^23,22,66

$$\begin{aligned}&I_{\text {pSFDI}}(\theta ) = \int ^{\pi }_{-\pi } \Gamma (\theta ;\mu ,\kappa ,d) \, \nonumber \\&\quad I_{\text {fiber}}(\theta ;\theta _{\text {p}},a_0,a_2,a_4) \, d\theta _{\text {p}}, \end{aligned}$$

(11)

where $I_{fiber}$ is given by Eq. (5). However, evaluation of Eq. (11) involves evaluating this integral at millions of pixels, which can add significant computational time for both calibration and routine pSFDI image processing. To avoid this, we took advantage of certain mathematical identities available for the Von Mises distribution¹ to derive the following closed form solution of Eq. (11)

$$\begin{aligned}&I_{\text {pSFDI}}(\theta ) = a_0+\frac{a_2 d}{2} \cos \left( 2\left( \theta -\mu \right) \right) \nonumber \\&\quad +\frac{a_4 d \left( 24+\kappa ^2\right) \cos \left( 4\left( \theta -\mu \right) \right) }{2\kappa ^2}\nonumber \\&\quad -\frac{d I_1\left( \kappa \right) \left( a_2\kappa ^2\cos \left( 2\left( \theta -\mu \right) \right) +2a_4\left( 6+\kappa ^2\right) \cos \left( 4\left( \theta -\mu \right) \right) \right) }{\kappa ^3I_0\left( \kappa \right) }\nonumber \\&\quad +\frac{a_2 d}{2} \cos \left( 2\left( \theta -\mu -\pi \right) \right) \nonumber \\&\quad +\frac{a_4 d \left( 24+\kappa ^2\right) \cos \left( 4\left( \theta -\mu -\pi \right) \right) }{2\kappa ^2}\nonumber \\&\quad -\frac{d I_1\left( \kappa \right) \left( a_2\kappa ^2\cos \left( 2\left( \theta -\mu -\pi \right) \right) +2a_4\left( 6+\kappa ^2\right) \cos \left( 4\left( \theta -\mu -\pi \right) \right) \right) }{\kappa ^3I_0\left( \kappa \right) }. \end{aligned}$$

(12)

where $I_1(\kappa )$ is the modified Bessel function of the first kind, order 1. To further simplify, we take advantage of the $2\pi$ periodicity of cosine function, which reduces to the final result

$$\begin{aligned}&I_{\text {pSFDI}}(\theta ) = a_0+a_2 d \cos \left( 2\left( \theta -\mu \right) \right) \nonumber \\&\qquad\qquad +\frac{a_4 d \left( 24+\kappa ^2\right) \cos \left( 4\left( \theta -\mu \right) \right) }{\kappa ^2}\nonumber \\&\qquad\qquad -\frac{2d I_1\left( \kappa \right) \left( a_2\kappa ^2\cos \left( 2\left( \theta -\mu \right) \right) +4a_4\left( 6+\kappa ^2\right) \cos \left( 4\left( \theta -\mu \right) \right) \right) }{\kappa ^3I_0\left( \kappa \right) }. \end{aligned}$$

(13)

Normalization and calibration parameter estimation In previous work, we have applied pSFDI to fibrous electrospun biomaterials and utilized SEM images to estimate $\Gamma (\theta )$, so that $I_{fiber}(\theta ;\theta _{\text {p}},a_0,a_2,a_4)$ could be directly estimated.^24,22 These studies have demonstrated the ability to extract $\Gamma (\theta )$ from $I_{\text {pSFDI}}(\theta )$ for these relatively simple materials when a reference standard specimen is available. However, because the optical properties of the individual tissue components (e.g. collagen fibers) are difficult to determine both as isolated structures and integrated in intact tissues, direct determination of the $a_i$ is practically difficult. We circumvented this problem by exploiting the ability to directly obtain $\Gamma (\theta ))$ using the SALS method.⁵³ This was done by using the third ’calibration’ specimen, which was first imaged using pSFDI. Next, this specimen was optically cleared with an aqueous glycerol solution and the $\Gamma (\theta )$ mapped using SALS at a resolution of 0.25 mm. The resulting ${\mathbf {I}}_{\text {pSFDI}}(\theta ,{\mathbf {X}})$ and $\Gamma _{SALS}(\theta ,{\mathbf {X}})$ data were co-registered to the same coordinate system $\mathbf{X }$.

In principal, this combined dataset can be used to obtain a single representative values for $a_i$ for a given tissue type. However, this method can be affected by natural variations tissue optical properties, which while not large can nevertheless result in less accurate predictions of $\Gamma (\theta )$. This issue was accounted for using the following normalization process. First, we note that for any form of $\Gamma (\theta )$ the mean value of $I_{\text {pSFDI}}(\theta )$, $I_{mean} = a_0$. Thus, variations in the optical properties of the non-aligned tissue components will mainly affect the value of $a_0$ in different tissue regions, while the $a_2$ and $a_4$ still account for the local fiber optical anisotropic properties. We thus first normalized $I_{\text {pSFDI}}(\theta )$ using ${\bar{I}}_{\text {pSFDI}}(\theta ) = I_{\text {pSFDI}}(\theta )/I_{mean}$, so that $a_0 = {\bar{a}}_0$, where the bar indicates the normalized parameter value. While the choice of ${\bar{a}}_0$ value is arbitrary, we choose ${\bar{a}}_0=3$ so that $I_{\text {pSFDI}}(\theta )>0 \ \forall \theta$. The resulting calibration problem thus reduces to determining the calibration parameters ${\bar{a}}_2$ and ${\bar{a}}_4$ for the tissue or biomaterial in question.

This method was implemented using the two “calibration” pericardial tissue specimens as follows. First, the resulting SALS-derived orientation data was fit $\Gamma (\theta )$ using Eq. (10) to extract the local values for $\sigma$ and $\mu$ at each SALS measurement point at over the entire specimen Fig. 4. Next, the local ${\bar{I}}_{[\text {SFDI}}(\theta )$ was determined at each pixel, from which the optimal values for ${\bar{a}}_2$ and ${\bar{a}}_4$ for the specimen by fitting Eq. (13). This method was applied to both specimen 1 and 2 in the referential and deformed states to extract $\Gamma (\theta ,{\mathbf {X}})$ and $\Gamma (\theta ,{\mathbf {x}})$, respectively.

Figure 4

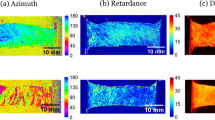
(a) Example of $\Gamma (\theta )$ derived from SALS showing the fit of the wrapped normal distribution (red) to the raw data (cyan), showing an excellent fit. (b) The resultant SALS-derived data for one of the pericardial reference specimens showing the preferred collagen fiber direction (black lines) and fiber splay standard deviation (color). Note here that while the preferred direction demonstrated an overall horizontal trend, the fiber splay spatially varied substantially, which was beneficial to establish a wide range for calibration with the pSFDI method.

An Affine Deformation Evaluation

An advantage of the present approach that we can also investigate if the measured $\Gamma (\theta ,{\mathbf {X}};\mu ,\sigma )$ follow certain mathematical rules. Specifically, we took advantage of the fact that (1) ${\mathbf {F}}$ is known at each pixel throughout the loading path, and (2) utilized the fact that for many soft tissues fiber kinematics closely follow an affine rule (e.g. References [41, 16]). The following affine mathematical transformation rule was used to predict $\Gamma (\theta ,{\mathbf {X}};\mu ,\sigma )$ in the deformed state¹⁶

$$\begin{aligned} \begin{aligned} \Gamma (\beta )&= \Gamma (\theta ;\theta _{\text {p}},\mu ,\sigma ) \, \frac{{\mathbf {n}}(\theta )({\mathbf {C}}{\mathbf {n}}(\theta ))}{J_{2D}} \\ \beta&= tan^{-1} \left[ \frac{F_{21}cos(\theta ) + F_{22}\sin (\theta )}{F_{11}cos(\theta ) + F_{12}\sin (\theta )} \right] , \end{aligned} \end{aligned}$$

(14)

where $\Gamma (\beta ,{\mathbf {x}})$ is the collagen fiber orientation distribution in the deformed state at the new position ${\mathbf {x}}$, ${\mathbf {C}} = {\mathbf {F}}^T{\mathbf {F}}$, $J_{2D} = \parallel {\mathbf {C}}\parallel$, and $\beta$ is the $\theta$ fiber orientation in the deformed state. We then applied this approach to the extracted $\Gamma (\theta )$ biaxial deformed specimen and compared predictions. This was done by taking the extracted $\Gamma (\theta )$ in the referential state, then using the ${\mathbf {F}}$ measured at the same location to compute the predicted $\Gamma (\beta )$. To facilitate a direct comparison, we fit the predicted $\Gamma (\beta )$ to Eq. (10) to determine the equivalent $\sigma$ value.

On the Inter-relationship Between Region Size and Tissue Strain and Structural Variation

One natural outcome of the present integrated methodology is the ability to explore the relation between a characteristic length scale on the underlying strain–structure relations. This was done by considering the deformation gradient tensor component fields for a fully loaded specimen’s central region, where the stress and strain tensors are considered the most uniform. Starting at five smaller sub-regions, the local ${\mathbf {F}}$ was determined from the displacements of the sub-region corners. In addition, the mean $\mu ,\sigma$ for each sub-region was computed. Each sub-region was then gradually expanded to the extent of the full ROI and results compared.

Results

Surface Strain Analyses

Soft Tissue Responses

The deformation field of the central ROI were tracked successfully using DIC analysis to an accuracy of a single pixel ($\sim 40\mu$m). This was confirmed via the comparison of F components derived from the trajectory of physical markers with those derived from ’virtual’ markers. The resulting spatial maps of ${\mathbf {F}}({\mathbf {X}})$ were predictably complex. This can be best seen in the fully loaded state, where ${\mathbf {F}}({\mathbf {X}})$ demonstrated complex, spatially varying behaviors (Fig. 5). The resulting principal stretches $\Lambda _i$ and directions ${\mathbf {e}}_i$ better illustrate the actual trends, which were consistent with the $X_1$ collagen fiber preferred direction in this specimen, so that $\Lambda _I$ was demonstrated to be the largest component aligned to the $X_2$ direction. Additionally, there was minimal shearing observed, as well as an overall heterogeneity in the deformation field (Fig. 6).

Figure 5

(a–d) DIC results for the central ROI of specimen 1 in the fully loaded state showing the spatial distribution of the four components of ${\mathbf {F}}$. Note the spatial heterogeneity.

Figure 6

Principal stretches of the deformation results shown in Fig. 5, which more clearly demonstrate the nature of the deformation field in the ROI.

As mentioned in ‘DIC-Based Surface Strain Analysis’, we compared ${\mathbf {F}}({\mathbf {X}})$ derived from physical markers (Fig. 1) and the ’virtual’ ${\mathbf {F}}$ from the tracked ROI region corners to confirm equivalence. This was done for both the pSFDI and physical particle texture sources. An excellent agreement was observed for both the pSFDI and physical textures with the conventional physical markering technique (Fig. 7). It is important to note that although the physical and pSFDI texture data were recorded from the same specimen, the data was acquired during different experimental tests and therefore exhibits slightly different results due small inelastic effects that are unrelated to the accuracy of the strain measurements used. The Pearson correlation coefficient was calculated to evaluate the extent of agreement for F components calculated using physical and virtual markers, with excellent results (Table 1). Similar results were obtained on a second specimen with a preferred direction of 45$^\circ$, with correlations $\ge 0.99$ (Table 1). The shear angles calculated using both marker types were within $\pm 1^o$, as were the rigid body rotation angles (physical markers = 0.67$^\circ$ and virtual markers = 0.36$^\circ$).

Figure 7

For both the pSFDI and particle based texture sources, a comparison with the physical marker data of the evolution of F₁₁ (green) and F₂₂ (red) as equi-biaxial stress is applied to the specimen 1, showing excellent agreement for both textures. Collectively, these results indicate that the pSFDI and particle based textures produce equivalent results.

Table 1 Deformation Data for the Soft-Tissue Specimens.

Extracted Fiber Structures

We fit Eq. (13) to pSFDI data from calibration specimen 1, which fit the data quite well, with a mean value of $a_4^{\text {cal}} = 20.8094$ determined. We then applied this method to calibration specimen 2, which indicated that the preferred directions were accurately obtained to within $\pm 1^{\circ}$ of the actual value. Similarly, the estimated standard deviation from the pSFDI data was $\sigma _{\text {pSFDI}} = 39.917^{\circ}$, which compared very closely with the actual measured value of $\sigma _{SALS} = 39.792^{\circ}$. This approach thus allowed us to reliably extract $\Gamma (\theta )$ and account for small variations to local tissue properties. Note that this information is generated at the pixel level, and is thus at a very high density.

We then applied this same technique to specimen 1 (preferential fiber alignment was 0 degrees). The normalized ${\bar{I}}_{\text {pSFDI}}(\theta )$ from the referential and deformed states, for specimen 2, demonstrated both dual peaks and rotation (Fig. 8a). An excellent fit to Eq. (13) was consistently obtained ($r^2 \ge 0.97$) (Fig. 8a) for all data-points for both specimens. The resulting maps of the referential fiber structure demonstrated noticeable local variation in tissue structure, primarily in $\sigma$ (Fig. 8b). Next, the results $\sigma$ were computed and mapped . The improvement in alignment with deformation was clearly evidenced by the reduced values of $\sigma$, as observed (Fig. 8c).

Next, we took the mapped $\Gamma (\theta )$ results (Figs. 8a and 8b) and evaluated how well the affine model (Eq. (14)) agreed with the experimental results. As stated above, we utilized the $\sigma$ parameter as the best overall metric of collagen fiber realignment under the measured deformation. Results indicated an average drop in mean $\sigma$ of approximated five degrees, which was statistically significant (Fig. 9a). This result agreed quite well with the predicted affine model predictions (Fig. 9a).

When applied to the three sets of ES biomaterials, the measured and computed values of $\sigma$ for the three ES biomaterials studied with varying alignment, showing excellent agreement.

Figure 8

(a) An example of the fit to Eq. (13) to the $I_{\text {pSFDI}}$ data showing excellent results. Mapped $\sigma$ from the ROI in the (b) referential and (b) deformed states for specimen 1 (0 degree aligned). Here, both regional heterogeneity as well as a predictable reduction $\sigma$ with increased deformation were observed.

Figure 9

(a) Average $\sigma$ from the computed $\Gamma (\theta )$ in the referential (black) and deformed (red) states, which indicated a measured drop of approximately five degrees in $\sigma$. Next, we compared the affine model predicted values of $\sigma$ (green) agreed well with the experimental predictions. In (b) are shown the measured and computed values of $\sigma$ for the three ES biomaterials studied with varying alignment, showing excellent agreement.

Strain–Structure–Length Scale Relations

In Fig. 10a is shown the actual starting regions used for this analysis. We first observed substantial regional variations the smallest size of $\sim$ 2 mm for ${\mathbf {F}}$. These mean values then converged to a common value as the distinct sub-regions were increased in size (Fig. 10b). Similar trends were observed in the $\sigma$, but with less overall initial variation (Fig. 10c). Collectively, these results indicated that there is a critical length (conservatively $\sim$8 mm) at which the strain measurements become more representative of the bulk (i.e. homogenized) tissue.

Figure 10

(a) The five distinct sub-regions selected within the $\sim$10 mm per side ROI (red box) for specimen 1. (b) The F₁₁ and F₂₂ values determined by expanding each sub-region within the ROI, along with the standard error. (c) Fiber splay results for the same five expanding sub-regions and the mean. The vertical black line in each plot indicates the approximate length scale at local variations become negligible.

Discussion

Summary of Findings

In the present study, we first demonstrated that fiber architectural maps captured using pSFDI can be used as a texture source for DIC-based surface strain analyses. This facilitated the simultaneous measurement of the tissue level deformation and fiber structure behavior. The technique was confirmed via the agreement of F derived from physical markers and non-contact pSFDI ’virtual’ ROI corner markers derived from the DIC analysis. The resulting close correlation lent support to our findings. Agreement with the conventional particle based methods were also confirmed the accuracy and robustness of our DIC-based strain measurement pipeline.

Extraction of $\Gamma (\theta )$ from the $I_{\text {pSFDI}}$ measurements was also a novel aspect of the present study. The basic idea for this has been attempted before on a single homogeneous biomaterial.⁶⁶ That is, if $I_{\text {fiber}}(\theta )$ can be determined, extraction of $\Gamma (\theta )$ is a simple deconvolution operation. However, achieving this for soft tissues is complicated by the need for a reference standard specimen approach to determine $I_{\text {fiber}}(\theta )$ for the tissue under study. Moreover, unlike previous attempts using simpler fibrous materials, $I_{\text {fiber}}(\theta )$ will be in general be heterogeneous for most soft tissue applications, given the natural variations in composition and density. In the present study, we circumvented these problems using an identically prepared tissue as a reference standard specimen and a secondary method for $\Gamma (\theta )$ determination. Normalization of $I_{\text {fiber}}(\theta )$ also helped to both simplify and account for natural variations. In future applications, additional optical theoretical work is needed to look deeper theoretical and experimental means to further extend this approach.

Broader Relevance of the Structure–Function Relationship of Soft Tissues

The structure–function relationship in soft tissues is determined by the structure and organization of the local collagen fiber network. For example, local collagen fiber architecture is known to dictate mechanical performance of heart valve leaflets in heath and disease.^42,44,56,70 Thus, our ability to understand and simulate the underlying function of soft tissues in health and disease is largely based on our ability to both quantify structure and integrate such information into simulations.^{15,17,42,44,56,70} A critical barrier this work addressed is the functional behavior of collagen fiber-rich tissues using non-destructive, non-contacting technologies that simultaneously quantify fiber architectures and local deformations over wide, organ-level fields-of-view (1–10 cm$^2$). We have shown that pSFDI can be non-destructively applied to native tissues and biomaterials in a sterile environment in a rapid, completely non-contacting manner. We then show that pSFDI-derived structural information as a texture source for digital image correlation (DIC) surface deformation estimates, allowing direct integration between local fiber kinematics and tissue strain. Future improvements include higher speed pSFDI image acquisition for increased dynamic measurement speed and real-time DIC processing.

Lengths Scales in Strain Measurements

Strain measurement in soft tissues and biomaterials has a long history. Optical techniques have generally been preferred, due to their high spatial resolution and non-contacting nature. However, their actual application is typically performed on an ad-hoc manner; spatial length scales are usually determined by limits of the measurement technique and local anatomy. In reality, ’strain’ is quite relative; it is highly dependent on the length scale used, its relation to the underlying structure, and the referential state chosen. Determining optimal methods is often beyond the study scope or not possible. In the present study, we demonstrated a step towards addressing this problem using a non-contacting, non-destructive approach to minimize measurement artifact. When the deformation behavior of distinct subregions within the ROI were examined, it was found that at the critical length of $\sim$ 8 mm (Fig. 10). This result suggests that the scale for tissue structurally similar to pericardium tends to behave more homogeneously at a scale $\sim$ 1 cm under the planar modes studied herein. Future studies will have to (1) establish similar length scales for other tissues, and (2) the underlying basis for these findings.

Fiber Kinematics

In the present study, we tested whether affine fiber kinematics, a well-established model of collagen fiber kinematics, was an acceptable kinematic model. It should be noted that when discussing collagen fiber kinematics, a distinction should be made between so-called ’long-fiber’ and ’short-fiber’ native and synthetic tissue responses. In natural soft tissues, collagen fibers are very long (often extending the entire length of the tissue) and mechanically behave in a largely kinematically independent manner from other fibers. In contrast, highly interconnected fibrous networks that occur in collagen gels^10,2,68 and polymeric scaffolds^6,61 behave in a more complex manner due to the presence of local interconnections. Even so, simulations of such systems have demonstrated affine-like behaviors at larger scales (> 1 mm).^8,7 In either case it is evident that changes tissue fibrous structure during function are both determined and driven by the local tissue deformation, so that simultaneous tissue deformation behaviour is required for a complete picture of the phenomenon. Moreover, such information is typically local, and can vary considerably within a single tissue structure (e.g. Refs. 48, 54), so that that such studies require high spatial measurement densities.

Limitations

A potential issue with the use of pSFDI as a texture source is that $\Gamma (\theta )$ will in general change with applied loads due to fiber rotations in addition to deformations, unlike a standard DIC texture source. Therefore, a large step in strain that results in a significant modification in microstructure can cause changes in local pixel intensities. This can produce artifacts where features in the pSFDI texture that are caused by fiber orientation rather than the displacement of points on the surface. As DIC relies on the conservation of the intensity within the ROI between steps, such artifacts can potentially confound DIC analysis. In the the present study, we demonstrated equivalent, high accuracy of the DIC method (Fig. 7). This was made possible in-part through the use of small loading steps. It is therefore important that small strain steps are employed in such investigations.

Both simulation⁵ and experiment^14,37 have shown that with sufficiently high spatial frequencies, the majority of detected light originates from sub-millimeter scattering events within tissue. The polarization coherence gating of co-polarized imaging further confines the photons to superficial layers, as has been previously described.²³ In some circumstances, where it is desirable to isolate superficial components of multi-layered tissue, high spatial frequency pSFDI measurements can be used. In this study, our goal was to match SALS data for thin samples, and therefore only the DC component was used. Due to the thinness of the samples (0.5mm and below), DC pSFDI measurements (essentially, polarized light imaging measurements) were directly comparable to the through-thickness transmission measurements of SALS. Although outside of the primary scope of this study, only very small changes in structural information were observed for these samples at moderate spatial frequencies.

Finally, we note that while the use of affine fiber kinematics is broadly applicable to determine $\Gamma (\theta )$ in the deformed state, it should be verified for each tissue studied. We have done this is similar studies (e.g. Refs. 4,16,43). We underscore this as tissue structures in both health and disease can vary quite considerably regionally and in different disease states (e.g. Refs. 54,51), increasing the potential complexity of the local fiber deformation patterns.

Conclusions

The aim of the present study was to demonstrate that the spatial variations of polarized spatial frequency domain imaging (pSFDI) measurements of microstructural collagen fiber architecture can be used as a texture source for digital image correlation in a manner equivalent to the physically applied speckle patterns that are typically employed. This facilitated the simultaneous measurement of the tissue level deformation and collagen structure behavior. In addition to the separated analysis, the integration of both information pipelines allowed the study of some important aspects of tissue deformation analysis, such as the representative length scale. Finally, in future work there is the potential for hardware improvements to facilitate the study of real-time of biological systems.

Appendix

Appendix 1: Surface Strain Analysis

From the post-processed imaging data, DIC analysis was carried out using the open-source software $\mu$DIC.⁴⁶ In brief, $\mu$DIC takes pixel-level measurements of the gray-scale intensities of a reference image and registers their positions to a finite element surface (Fig. 11). B-splines are used to discretize the deformation field into a bi-directional grid of ${\mathbf {m}} \times {\mathbf {n}}$ control points. The control points are used to manipulate the spline field and the coordinates ${\mathbf {x}}(u,v)$ on the B-spline surface are

$$\begin{aligned} \mathbf{x }(u,v) = \sum _{i=0}^{m}\sum _{j=0}^{n} \, N_{i,p}(u) N_{j,q}(v) \, \mathbf{m }_{ij} \end{aligned}$$

(15)

where $N_{i,p}$ and $N_{j,q}$ are the B-spline basis functions, $u,v \in [0, 1]$ are the spline coordinates, p, q denote the polynomial order, ${\mathbf {m}}_{ij}$ are the control points’ coordinates. The resulting 2D B-spline surface convects (deforms) and the mapped $I_{\text {pSFDI}}({\mathbf {X}})$ is compared with the deformed image. A modified Newton scheme was then used to minimize the sum of squared differences between the reference and current images.

This method produced pixel-level resolution spatial maps of ${\mathbf {F}}({\mathbf {X}})$ for each applied deformation step. To allow direct comparison to the physical marker (Fig. 1) ${\mathbf {F}}$ results, the positions of each of the four ROI corners for each loading step (Fig. 11) were extracted and used to compute an equivalent ’virtual’ ${\mathbf {F}}$. Finally, to thoroughly validate pSFDI as a texture source for DIC-based strain measurement, we conducted extensive synthetic deformation validation studies. Reference images of both the pSFDI and particle textures were synthetically deformed in relevant modes. Details of the synthetic testing methods and results can be found in the Appendix.

Figure 11

Schematic of the finite element surface of µDIC in the (a) reference and (b) deformed states showing the displacement of the measurement points (red dots) within elements (black squares) as the control points (line intersections) are moved.

Appendix 2: Synthetic Deformation Validation

Overview

This section covers the synthetic image testing that was used to confirm that the pSFDI texture source could be utilized to carry-out DIC analysis. Reference images of soft-tissue specimens, one with a physically applied particle texture and another imaged with pSFDI were synthetically deformed in modes that were relevant to the tissue testing performed on the specimens. The synthetic deformations were administered by applying a known F and the effectiveness of the texture for the application of DIC analysis was verified by the successful extraction of synthetic F. The synthetic deformations were both homogeneous (uniaxial stretch, biaxial stretch, simple shear, pure shear, subsimple shear) and heterogeneous(uniaxial and biaxial sinusoidal displacement fields). Rigid body transformations were also applied (translation and rotation).

Software Pipeline

An in-house code was used to generate the synthetic image sets that operates as follows; The type of synthetic deformation is selected, then the number of deformation steps and their individual extent is chosen. Once the synthetic images have been generated, they are passed to the µDIC solver where an ROI and interpolation degree are applied by the user before finally, after DIC analysis, the individual deformation gradient component tensor fields are outputted (for each synthetic deformation step) as a spatial contour map, the displacement field is outputted as a vector plot and the average deformation gradient tensor components at each step are outputted (Fig. 12).

Figure 12

Software pipeline for synthetic image validation.

Rigid Body Motion

Rigid body displacement and rotation (Fig. 13) synthetic image sequences were generated and their direction and magnitudes were successfully ascertained by the DIC analysis. Moreover, both textures produce identical results, which is consistent as the same translation was applied in each case.

Figure 13

Displacement fields (black arrows) measured from (a) particle textured and (b) pSFDI($\uptheta$_p) textured image sets with a 10 pixel rigid body displacement in the $X_1$ direction synthetically applied. Measured rigid body rotation data for (c) particle and (d) pSFDI($\uptheta$_p).

Stretch and Shear

Next, synthetic stretch and synthetic simple shear images were produced from both the particle texture (Fig. 14) and the pSFDI($\uptheta$_p) reference images (Fig. 15). For the homogeneously deformed synthetic images, it can be seen that the measured deformation was well within 0.5 % of the the applied deformation.

Figure 14

Synthetically applied (a) F₁₁ unidirectional stretch, (b) F₁₂ simple shear, (c) F₂₁ simple shear and (d) F₂₂ unidirectional stretch simple shear generated from an image of the particle textured surface. The measured deformation gradient field is appended to the image and show an excellent agreement between the applied deformation and the measured deformation.

Figure 15

Synthetically applied (a) F₁₁ unidirectional stretch, (b) F₁₂ simple shear and (c) F₂₁ simple shear and (d) F₂₂ unidirectional stretch simple shear generated from an image of the pSFDI textured surface. The measured deformation gradient field is appended to the image and show an excellent agreement between the applied and the measured deformations.

Heterogeneous Deformation Modes

Finally, sinusoidal deformation fields were applied to the reference images to test the ability of the DIC software’s tracking of heterogeneity. These were applied in a single direction (Figs. 16 and 17) and bidirectionally (Figs. 18 and 19). It can be seen that in each case, the undulating deformation is followed effectively by µDIC, using both textures.

Figure 16

(a) A plot of the measured F₁₁ deformation gradient component (red dots) co-plotted with the equivalent synthetic data (black line). (b) Measured deformation gradient component fields for a synthetically applied strip-biaxial deformation of the particle textured reference image.

Figure 17

(a) A plot of the measured F₁₁ deformation gradient component (red dots) co-plotted with the equivalent synthetic data (black line). (b) Measured deformation gradient component fields for a synthetically applied strip-biaxial deformation of the pSFDI($\uptheta$_p) textured reference image.

Figure 18

(a) Measured deformation gradient component fields for a synthetically applied bidirectional sinusoidal deformation of the particle textured reference image. (b) A plot of the measured F₁₁ deformation gradient component (red dots) co-plotted with the equivalent synthetic data (black line).

Figure 19

(a) A plot of the measured F₁₁ deformation gradient component (red dots) co-plotted with the equivalent synthetic data (black line). (b) Measured deformation gradient component fields for a synthetically applied bidirectional sinusoidal deformation of the pSFDI($\uptheta$_p) textured reference image.