Introduction

Contemporary clinical practices designed for the risk assessment of proximal femur fracture are based on either radiographic21,28,31 or bone mineral density (BMD) measurements obtained by applying two-dimensional or three-dimensional imaging techniques, such as dual-energy X-ray absorptiometry (DXA) or quantitative computer tomography (QCT).21,28,31 These techniques have been successful for the risk assessment of femur fracture because the decline in BMD manifests directly in the variation of bone material, such as loss of calcium, which can eventually lead to fragility of the bone tissue. However, BMD measurements alone have shown limited correlations (r 2 = 0.49–0.69) with the experimentally determined femur bone strength. As a result, many clinicians have to consider additional factors like geometry,2,24 aging,23 anatomic site,15 increasing or persistent pain1,2,26 and activity level,29 to increase the reliability of these traditional imaging techniques for the estimation of femur fracture risk. Therefore, objective criteria for identification of the region that is at risk of fracture should be established for a more efficient and less costly measurement of an impending fracture or the effects of therapeutic treatments.

The fractures in the proximal femur due to aging or pathological changes depend on the strength of the bone and the applied loads.6,18,27 The increased fragility associated with the presence of lytic defects or osteoporosis suggests that either the strength of the tissue comprising the defect and surrounding bone decreases, or the stress within the bone under applied loads increases as a result of alterations in its geometry. Hence, any method that predicts fracture risk must be able to measure both the changes in bone material behavior (by monitoring apparent bone density or BMD) and its structural geometry (by monitoring cross-sectional area and cross-sectional moment of inertia). In clinical scenarios such as osteoporosis and skeletal metastasis, the prediction of fractures depends on the objective criteria of evaluating changes in the bone mechanical properties which reflect the combined effect of bone material properties and bone cross-sectional geometry.

Numerical studies using finite element (FE) modeling have been performed by taking into account various mechanical factors such as size and shape of bones and tumor cells, and the three-dimensional variation of bone density.5,7,20 These parameters were usually ignored in simple radiographic assessments. Recently, Keyak et al. showed that FE modeling can predict fracture loads of proximal femurs with or without metastatic disease.16 However, FE modeling itself raised new challenges because the relationships between the mechanical properties and the density used to generate the models differ for cortical bone with and without metastases.13 Also, the clinical incidence of fractures in the proximal femur is much higher than fractures in the shaft region i.e. pathologic fractures in the proximal femur occur twice as often as those in the shaft region.9

In our previous work, we successfully tested proximal femurs with simulated defects using QCT-image derived algorithm and a custom-made mechanical jig.17 This article’s intention is to show the viability of the proposed technique to monitor the risk of femoral fracture in intact femurs. Also, fracture sites of femurs with and without machined defects are identified to demonstrate that this QCT-based structure analysis can provide a more objective criteria for patients who have imminent bone fractures due to either aging or pathologic reasons.

Materials and Methods

Preparation of Specimens

A series of 12 frozen human cadaver femora (age range 39–77, 8 male, 4 female, Table 1) from donors were obtained. After removing the surrounding soft tissues, two orthopedic surgeons examined each of the specimens radiographically to confirm the absence of pathological or traumatic defects. All specimens were stored in a −32 °C walk-in freezer (Kolpak, Model P7-1010-FS/FT, Marshfield, MA) to avoid dehydration. Prior to the QCT scan, they were thawed at room temperature (21 ± 1 °C). Freezing appears to have little effect on the mechanical properties of bone.10 The earlier results obtained from the defective femurs17 are analyzed together with the results obtained from the intact femurs in the current study.

Table 1 Results of image and mechanical analysis of intact and defective femurs
Full size table

Quantitative Computer Tomography (QCT) Scanning

The geometry of the contiguous femur transverse cross-sections that were 3 mm thick and 3 mm apart was captured by utilizing the high-speed helical CT scanner (Signa-5, General Electric Medical System, Milwaukee, WI). The X-ray tube current was 200 mA and the pixel spacing was 0.586 mm. Two femur specimens were enclosed in each cylindrical acrylic tube (diameter: 20 cm, height: 100 cm) that was filled with saline solution during the CT scan. The first step required in evaluating the elastic modulus on the basis of the empirical density-to-modulus relationships available in the literature,25,27 is the estimation of apparent bone density. In order to determine the apparent bone density, a calcium hydroxyapatite phantom (CIRS, Norfolk, VA) comprising of five chambers of known densities (0.003, 0.078, 0.178, 1.048, 1.597 g/cc) was positioned in the same image view (Fig. 1). Subsequently, this phantom was utilized to transform the image gray data to apparent bone density (ρapp), which was in turn used in the computation of elastic modulus.

Figure 1
figure 1

QCT images showing the transverse scanning of two femurs with 5-rod hydroxyapatite phantom

Full size image

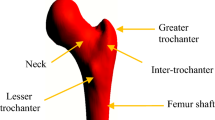
Derivation of the hip cross-section in proximal femur

The contiguous transverse cross-sectional QCT data was stored in DICOMFootnote 1 medical image format and analyzed using a public domain image processing program called “NIH Image” (Research Service Branch, National Institutes of Health, MD). Subsequently, the CT-slices were cropped to 256 × 256 pixels from 512 × 512 pixels for the data analysis of each femur. The compilation of all the corresponding images (90–110 slices from head of the femur to mid-diaphysis) of a femur into a stack enables the frontal (coronal) section visualization, as observed in Fig. 2. The slices, in which the cortical bones of the femoral neck and shaft appear distinctly clear, were chosen as the frontal sections in each femur. Linear axes were used to represent the shaft and the neck, as the centroid that corresponds to each of these cross-sections appear to lie on straight lines. The two centerlines that represent the longitudinal axes of the femoral neck and mid-shaft are sketched in Fig. 3 (white line illustrated as ‘G’). A hyperbolic axis system with axes asymptotic to the centerlines of the femoral neck and shaft was chosen to represent the intertrochanteric region where the femoral neck and the shaft intersect (yellow line illustrated as ‘N’). The cross-sections corresponding to the lines drawn at 2 mm interval, perpendicular to the axes representing various entities of frontal section were chosen to compute the structural rigidity properties of the femur.

Figure 2
figure 2

The frontal section of a femur (a) with an anterior-medial (AM) side defect in the inter-trochanteric region and (b) an intact femur

Full size image
Figure 3
figure 3

Predicting failure load for tensile and compressive failure strains for transaxial cross-sections perpendicular to the trajectory of geometric centroid (white). Modulus weighted centroid is illustrated in yellow. Fracture occurred at the cross-section of the minimum predicted compressive failure load (red)

Full size image

Calculation of Cross-Sectional Rigidities of Proximal Femur

The equivalent density of each pixel was calculated to compute the elastic modulus (E) in the region of interest by using a public domain Java image processing program called ‘Image J.’ After extracting the equivalent densities, the corresponding elastic modulus of each pixel representing the trabecular (E ρ = 0.82*ρ2 + 0.07)25 and cortical bone (E ρ = 21.91*ρ − 23.5)27 was computed using the linear empirical relationships. The axial (EA) and bending (EI) rigidities at each transaxial cross-section of interest was computed by the summation of the density-weighted areas of each pixel on the basis of their relative positions with respect to the corresponding density weighted centroid. The following equations were utilized in the computation of axial (EA, N) and bending (EI, Nm2) rigidities,

$$ {\text{Axial}}\,{\text{rigidity,}}\,EA = \sum\limits_{A} {E_{i} (\rho_{i} )da} $$
(1)
$$ {\text{Bending\,rigidity}},\;EI_{y} = \sum\limits_{A} {\lfloor {E_{i} \left( {\rho_{i} } \right) \cdot x_{i}^{2} } \rfloor da} $$
(2)

where da denotes the area of a pixel obtained from the CT-images, E i (ρ i ) represents the elastic modulus as a function of the apparent density, EA represents the axial rigidity as computed in Eq. (1), and x i indicates the coordinate of each pixel with respect to the axis of centroid corresponding to each elastic modulus-weighted cross-section (Fig. 4). The computed rigidity values using these equations were utilized to evaluate fracture loads of femurs at a later stage.

Figure 4
figure 4

Axial (EI) and bending (EA) rigidities calculated as sum of the product of modulus weighted area of each pixel, da, by its position (x i , y i ) relative to the centroid (x′, y′)

Full size image

Experimental Evaluation of the Fracture Loads of Various Femurs

A custom-made hydraulic mechanical testing system was employed to test the specimens to failure under the combination of loads resulting from axial compression and flexural bending in the medial-lateral direction as illustrated in Fig. 5a. The mechanical design of the apparatus is such that the load case in the whole femur can be simplified to one that corresponds to a 2D plane (y–z direction in Fig. 5a) that neglects the x-component. This implies that the loads were assumed to be applied only in the plane containing the femoral neck. Two aluminum plates (10 cm × 25 cm) were connected to the biaxial wedge to constrain the frontal plane motion in a manner such that the femur was restricted to move only in the Y–Z plane.

Figure 5
figure 5

(a) Schematic diagram of the hydraulic femur testing system.17 (b) Picture the testing femur with simulated defect in anterior-medial (AM) region

Full size image

The femur’s distal end was embedded in an aluminum chamber (dimensions: 10 cm × 10 cm × 10 cm) filled with PMMA. Due to the difference in size between the medial and lateral condyles,8 an offset of approximately 3° was applied between the horizontal line and the line joining the two condyles as the femur specimen was positioned vertically. In order to mimic the varus-valgus stiffness of a cadaver knee, which is approximately 8 Nm,19 two custom-made moment-relief springs were attached to the bottom of the aluminum chamber. The mechanical simulation of the single-legged stance mode6 was achieved by attaching a bi-axial wedge (21.6° in the medial-lateral direction and 8.1° in the anterior–posterior direction) below the springs. The torsional moment relief of a typical knee was realized by inserting a stainless steel ball bearing (ABEC-7, McMaster-Carr, New Brunswick, NJ) inside the mechanical jig. Subsequently, in order to measure the loads and moments along three mutually perpendicular axes, a six degree-of-freedom (DOF) load-cell (MC5 Force-Torque load cell, AMTI, MA) was positioned under the mechanical jig. A custom-made I-beam plate was placed under the whole experimental setup in order to shift it in the y-direction. This was done in order to obtain the necessary axial force from the actuator located at the bottom of the setup. A closer view of a femur with simulated defect in the y–z plane on the anterior-medial side can be seen in Fig. 5b.

Parametric Failure Analysis of Femurs

The failure load of a structure depends on its weakest link instead of its average mechanical properties. It is well established that the load bearing capacity of a bone is determined by the lowest structural rigidity12,30 obtained from various cross-sections along the bone. This is because the trabecular bone fails at a constant strain independent of the apparent density.14

Both the material properties and the overall geometry of the structure were taken into consideration in the analytical engineering beam theory. Hence, the structural rigidities computed from the QCT images (Fig. 3) were integrated with the engineering beam theory (Eq. 3) to compute the fracture load corresponding to each selected cross-section in the scans. The cross-section with the least predicted load was assumed to be the location of fracture initiation and the corresponding load was considered as the failure load. The cross-sectional geometry and the material properties were utilized to compute the yield load under the combined axial compression and bending as follows:

$$ \varepsilon = \frac{{F_{z} }}{EA} \pm \frac{{M_{y} c}}{EI} $$
(3)

where ε represents the failure strain and F z represents the axial yield load. Subsequently, in order to accurately estimate the predicted failure load,14 both the compressive and tensile failure strains of 1 and 0.8% respectively were used. EA, the axial rigidity, is the summation of the products between the area of each pixel and the associated elastic modulus (Eq. 1). EI, the bending rigidity about the y-axis that passes through the centroid of each cross-section, is the summation of the multiple products between the area of each pixel, the corresponding elastic modulus and the square of its distance from the y-axis (Eq. 2). M y represents the bending moment about a principle axis (y-axis as shown in Fig. 4) and c denotes the distance of the outer edge from the neutral bending axis. For the accurate calculation of the bending moment, the anterior–posterior direction was aligned to coincide with the y-axis by rotating the cross-sectional images. The positive and negative signs in Eq. (3) can be explained by the fact that the lateral side of the femur in this study is under tension due to the bending moment, while the medial side is under compression.

The bending moment (M) is calculated by obtaining the product of the force normal to the transaxial cross-section and the corresponding lever arm (d) with respect to the neutral axis, i.e., M = F n d. θ denotes the angle between each slice of a femur model and the vertical line, while the force normal to the cross-section (F n ) is computed by multiplying the axial force (F z ) and sinθ. By substituting these relations into Eq. (3) and manipulating it slightly, we obtain Eq. (4).

$$ F_{z} = \frac{\varepsilon }{{\frac{1}{EA} + \frac{{d \cdot c \cdot ({ \sin }\,\theta )}}{EI}}} $$
(4)

The coefficient of determination (R 2) was computed for the various structural and geometrical configurations with respect to the measured failure load by the application of linear regression analysis. The correlation between the dependent and the independent variables was evaluated by measuring the coefficient of determination (R 2). In this study, the coefficient of regression shows the extent of variation in the measured failure loads as the result of the changes affected in the structural and geometrical properties of the femur. After conducting extensive coefficient of determination analysis, it was observed that the QCT image-derived beam theory predicts the failure load to a reasonably good extent. The Bland–Altman analysis was performed for both intact and defective femur groups to show the agreement between the calculations of measured and predicted fracture loads. The analysis was performed by using SPSS v.16 (SPSS Inc. Chicago, IL).3

Results

The QCT predicted load for the intact femur bone at various slices has been plotted with respect to the relevant slice numbers in Fig. 6. The lowest predicted load occurs at a slice in the femoral neck region. This implies that a defect free femur is most likely to fracture in the neck region. The slice with the lowest predicted failure load represents the most probable structural failure site and the corresponding load, the failure load of the entire femur structure. It can be observed that the QCT predicted loads are the highest for the slices in the shaft region, indicating that a failure in this region for the given loading is least likely for an intact femur. The predicted failure loads in the intertrochanter appear to lie between that of the femoral neck and the shaft regions. The slices in the intertrochanter region which are closer to the femoral neck exhibit predicted failure loads that are closer to that of the femoral neck, whereas the slices closer to the shaft exhibit predicted failure loads closer to that of the shaft.

Figure 6
figure 6

Predicted fracture loads according to the slice number of an intact femur

Full size image

Figure 7 depicts the QCT predicted failure loads for various slices of defective femur bone samples. It can be observed from this figure that the failure pattern has changed. The predicted failure loads have decreased in the slices with the defective regions of the femoral neck and the intertrochanter region, as compared to the respective slices of the intact femur. The values of the predicted failure loads in the defective region for most of the slices in the intertrochanteric region that are closer to the femoral neck have decreased to less than or equal to 5 kN, which is lower than the least predicted failure load in the femoral neck of the intact femur. The comparative analysis of Figs. 6 and 7 indicates that the failure location and load would most probably correspond to the slice close to the defect, irrespective of whether the defect is present in the femoral neck region or the intertrochanteric region.

Figure 7
figure 7

Predicted fracture loads according to the slice number of a defective femur

Full size image

Linear regression analysis of intact and defective femur groups (Figs. 8 and 9 respectively) was performed by choosing the independent variable as the predicted fracture load (lowest of all slices) and the measured fracture load as the dependent variable for each intact femur. It can be observed from Fig. 8 that the slope of the regression line was found to be 1.44, while the y-intercept worked out to be 0.79. These values indicate the deviation of results as compared to the ideal correlation straight line with slope of one that passes through the origin. In order to obtain a lucid picture of the correlation that exists between the QCT-predicted failure loads and the experimental loads, the coefficient of determination (R 2) was computed and was found to be 0.80. This implies that 80% of the variability in the experimental loads for the intact femurs can be explained by the QCT predicted failure loads. The Bland–Altman analysis for assessing agreement between two methods was performed for both intact (Fig. 10) and defective (Fig. 11) femur groups. The mean differences between predicted and measured fracture loads were −0.45 and −0.25 for intact and defective femur groups, respectively. The standard deviation of the intact and defective femur groups were 1.01 and 0.48, respectively.

Figure 8
figure 8

Measured fracture load vs. QCT-predicted fracture load of 12 intact femurs. The overall regression was R 2 = 0.80

Full size image
Figure 9
figure 9

Measured fracture load vs. QCT-predicted fracture load of 20 femurs with machined defect. The overall regression was R 2 = 0.87.17

Full size image
Figure 10
figure 10

Bland–Altman analysis of agreement in intact femur group

Full size image
Figure 11
figure 11

Bland–Altman analysis of agreement in defective femur group

Full size image

Discussion

This study illustrates that the fracture load of a proximal femur can be predicted by the application of a composite beam theory to the femur model reconstructed from the QCT images. The femoral failure load was computed by using the QCT-derived structural rigidities that were obtained from the sequentially selected cross-sectional slices. It was assumed in this study that the femur failure load would primarily depend on cumulative structural properties rather than individual parameters like the cross-sectional geometry, material properties and size of the defect. In other words, the structural rigidities corresponding to the cross-section associated with the least computed failure load were assumed to be the key factors that influence the prediction of proximal femoral failure.

The composite beam theory was applied to predict the failure load in this analysis due to the relative ease of its application to patient-specific cases, as compared to more complex, labor intensive and computationally expensive methods like the non-linear finite element analysis. In general, the QCT structural analysis used in this study takes less than 2 h to complete by a non-specialist, as compared to the non-linear finite element analysis which typically takes between 4 to 10 h to complete, depending on the size of the model.11,22,30 Since the QCT analysis is essentially a two dimensional computation, it yields results faster than the three dimensional finite element analysis, which needs to include a larger number of elements to improve its accuracy. As time is of essence in a clinical situation, it would be inconvenient for the patients to wait for up to 10 h to obtain the status of their fracture risk.

The coefficients of determination obtained from the intact femurs (Fig. 8, R 2 = 0.80), as well as the ones with machined defects (Fig. 9, R 2 = 0.87),11,22,30 strongly support our hypothesis that the composite beam theory can be used to predict the proximal femoral failure. Despite the simplifications made in our QCT-analysis, the high correlation between the predicted load and the experimental load is noteworthy. On the other hand, the coefficient of determination (R 2) obtained from the computationally expensive non-linear finite element analysis is 0.96.11,22,30 Although a preliminary comparison of the R 2 value shows that finite element analysis seems to be a better predictor of fracture loads, a slight compromise in predictive capability leads to a much larger reduction in the time taken for patient-specific fracture risk assessment.

Another statistical approach, the Bland–Altman analysis for assessing agreement between two measurements, was performed since a high correlation does not necessarily imply that the two methods agree. In the Bland–Altman analysis, most of the mean differences were expected to lie between ±2SD (standard deviation) to be considered as good agreement. All of the data from both defective and intact groups were within the mean ± 2SD region, which is often considered as the limit of agreement. Therefore, we conclude that the predicted fracture load using the composite beam theory agrees with the measured fracture loads. However, in terms of percentage change, the maximum deviation for defective femurs is 10% and that of the intact femurs is 61% (calculated from the raw data). The higher deviation in the intact group may be attributed to the comparatively smaller sample size.

An apparently counter-intuitive observation in our results is the increase in the value of coefficient of determination for the femur samples with machined defects as opposed to the value corresponding to the intact femurs. A statistical test revealed that the predictive capabilities of this QCT-analysis for femurs with machined defects were marginally better than intact femurs (p = 0.086). This increase in the coefficient of determination, despite the introduction of a stress riser factor as a result of the induced defects, could be due to the fact that the plane of fracture need not exactly coincide with the planes chosen for the QCT rigidity analysis or the range of the failure loads utilized in the linear regression analysis. In addition to these factors, there is a need to take into account that the composite beam theory was applied to an irregular bone structure made up of heterogeneous material. The predicted failure loads provide the load at which the structure yields, whereas the experimental fracture loads that were measured correspond to the catastrophic failure that occurs following the elastic yield and post-yield plastic deformation. Furthermore, by analyzing the results in Table 1, it can be seen that the range of the predicted loads (1–7.1 kN) and the measured loads (1.6–8.2 kN) is different for the failure tests performed on the intact femur, as compared to the range of the predicted loads (5.6–10.7 kN) and the measured loads (5.3–9.8 kN) corresponding to the defective femurs. This difference can have a slight impact on the comparison of statistical parameters and may also be a reason for the unexpected increase in the coefficient of determination from intact to defective femurs. A more objective comparison between the coefficients of determination can only be performed when the ranges of the independent and dependent variables are comparable. The fact that the structural analysis used in this study was only employed in the 2D plane (i.e. frontal plane containing the femoral neck) contributes partially to the error of this study. Simultaneous scanning of two femurs in a chamber may introduce the beam-hardening effect when reconstructing the CT images.4 The effect would be considered when carrying out quantitative measurements, especially for high attenuating tissues like the bone.

In comparison to the earlier studies, the experimental setup used in this work for the measurement of femur fracture loads mimicked the physiological loading scenario of the femur more closely, as the entire femur was taken into account for the purpose of experimentation. This was done in addition to mimicking realistic boundary conditions at the knee joint by the use of a varus-valgus moment relief spring, a turn table that allowed free rotation and the biaxial wedge which constrained the frontal plane motion of the femur bottom to the Y–Z plane. The study can be concluded by inferring that the non-invasively derived rigidities from the QCT scans can be reliably utilized to predict the proximal femoral failure loads, as much of the load bearing capacity variance can be explained by the coefficient of variance.