The Transport of Nanoparticles in Blood Vessels: The Effect of Vessel Permeability and Blood Rheology

Abstract

The longitudinal transport of nanoparticles in blood vessels has been analyzed with blood described as a Casson fluid. Starting from the celebrated Taylor and Aris theory, an explicit expression has been derived for the effective longitudinal diffusion (D _eff) depending non-linearly on the rheological parameter ξ_c, the ratio between the plug and the vessel radii; and on the permeability parameters $\Uppi$ and $\Upomega ,$ related to the hydraulic conductivity and pressure drop across the vessel wall, respectively. An increase of ξ_c or $\Uppi$ has the effect of reducing D _eff, and thus both the rheology of blood and the permeability of the vessels may constitute a physiological barrier to the intravascular delivery of nanoparticles.

Introduction

The transport of a passive solute in small channels is of great importance in several fields from chemical, to environmental and biomedical engineering. Many natural and industrial processes involve the injection, mixing, and dispersion of a bolus of a passive solute into a fluid. The solute dispersion is regulated by the classical transport equation which reads as

$$ \frac{\partial C}{\partial t}+{\mathbf{u}}\cdot \nabla C=D_{\rm m} \nabla^{2}C $$

(1)

where C is the local solute concentration, u is the fluid velocity field, and D _m is the solute Brownian diffusion coefficient in a quiescent fluid. The transport equation emphasizes that the solute dispersion is governed by pure convection $({\mathbf{u}}\cdot \nabla C)$ and pure diffusion (D _m ∇² C).

Numerical approaches can always be adopted to solve Eq. (1) (see, among others, Ananthakrishnan et al.1; Phillips and Kaye13; Siegel et al.16; Latini and Bernoff11). However, approximate analytical solutions, when sufficiently accurate, can give more insights on the behavior of the whole system. Taylor17 and Aris2 introduced the idea of an effective longitudinal diffusion coefficient D _eff, accounting for both the diffusive and convective contributions, by solving (1) averaged over the cross section of a straight channel with radius R _e and mean fluid velocity U. They derived an effective diffusion coefficient having the form $D_{\rm eff} = D_{\rm m} [1+P_{\rm e}^2 /48],$ with P _e the Peclet number (P _e = R _e U/D _m). The non-dimensional parameter D _eff/D _m gives a measure of the relative contribution of longitudinal convection compared to molecular diffusion: P _e < 1 is for diffusion-dominated flows, whereas P _e > 1 is for convection-dominated flows. The celebrated analysis of Taylor and Aris is valid in the limit of large times or long channels, that is to say in the steady state limit. Gill9 in 1967, and successively Gill and Sankarasubramanian10 in 1970, extended this study to comprise also the short-term evolution of C and derived a transient expression for D _eff, showing how this transient effective diffusion grows steadily with time tending in the long term to the Taylor and Aris limit.

In biomedical applications, macromolecules and nanoparticles are systemically administered and transported within capillaries with different radii, lengths, and properties. Depending on the organ, the capillary walls can be impermeable, as for the blood–brain endothelium, or can be highly permeable, as for the capillary of the kidney or those of developing tumor masses. In addition to this, the velocity profile in capillaries can be significantly different from parabolic (Poiseuille flow), because of the presence of red blood cells (RBCs), which tend to accumulate in a central ‘core’ region of the capillary leaving a marginal ‘cell-free layer.’ Even if blood flow should be considered as a multi-phase flow (plasma and blood cells) and consequently it could not be defined, strictly speaking, a local velocity field, on the average the velocity profile over the vessel cross section can be decently approximated through the well-known Casson law with a central plug region (zero radial velocity gradient) of radius r _c (plug radius) and an outer region with a parabolic velocity profile. Generally the plug radius is assumed to be equal to the radius of the core region where RBCs accumulate, so that the ‘cell-free layer’ thickness is given by the difference between the vessel radius R _e and r _c.

The velocity profile as well as the wall permeability have a significant effect on the convective transport of a solute. In 1993, Sharp15 derived explicit expressions for D _eff considering non-Newtonian fluids with different rheological laws, namely for a Casson, Bingham plastic, and power-law fluid. In particular, for a Casson fluid, it was determined

$$ D_{\rm eff} =D_{\rm m} \left[1+\frac{P_{\rm e_0}^2}{48}\frac{E(\xi_{\rm c})}{A^{2}(\xi_{\rm c})} \right] $$

(2)

with A(ξ_c) and E(ξ_c) depending on the rheological parameter ξ_c = r _c/R _e, the ratio between the plug radius r _c and the capillary radius R _e, as shown explicitly in the following Eqs. (6) and (24), respectively. In 2006, Decuzzi and collaborators4 revisited the Taylor and Aris solution to derive D _eff for a Newtonian fluid in a permeable capillary obtaining

$$ D_{\rm eff} =D_{\rm m} \left[1+\frac{P_{\rm e_0}^2}{48}f(\Upomega, \Uppi, \tilde{z})\right], $$

(3)

where ${P}_{{{\rm e}_0}}$ is the Peclet number at the entrance of the capillary, and f is a function of the permeability and pressure parameters $\Uppi$ and $\Upomega,$ given explicitly in the following Eqs. (10) and (11), respectively, and of the longitudinal non-dimensional coordinate $\tilde{z}$ along the capillary.

In this work, the longitudinal transport of molecules and nanoparticles injected into the blood stream is analyzed in terms of effective diffusivity with an emphasis on the permeability of the capillary and the rheology of blood.

Formulation

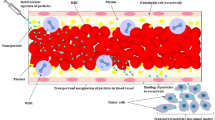
A straight circular capillary with radius R _e and length l is considered, where the blood flow is described by a Casson fluid-law (Fig. 1). The capillary walls may be permeable or impermeable to the fluid, but are impermeable and not adsorbent for the solute.

Figure 1

Longitudinal transport of molecules or nanoparticles in a blood capillary with a Casson velocity profile

In the following paragraphs, for the sake of completeness, the velocity profile and the mean velocity for a Casson fluid are briefly recalled and expressed in terms of the longitudinal pressure gradient dp/dz. Finally, the steady-state effective diffusion coefficient D _eff is derived explicitly as a function of the rheological parameter ξ_c and of the permeability and pressure parameters $\Uppi$ and $\Upomega ,$ respectively.

Mean Fluid Velocity in a Casson Fluid

It is assumed that the permeability of the capillary is sufficiently small not to modify the one-dimensional Casson velocity distribution, that is to say that the lateral fluid flow across the permeable walls affects only the flow rate. Due to mass conservation, a reduction in mean velocity U along the capillary is then expected.

In a Casson fluid, the velocity profile is described by the piecewise relation (Fung,6 §3)

$$ u(r)=-\frac{R_{\rm e}^2}{4\eta}\frac{dp}{dz}\times \left\{\begin{array}{ll} 1-8/3\xi_{\rm c}^{1/2} +2\xi_{\rm c} -1/3\xi_{\rm c}^2 &\quad \hbox{for } r < r_{\rm c}\\ 1-\left(r/R_{\rm e}\right)^{2}-\frac{3}{8}\left(1-\left(r/R_{\rm e}\right)^{3/2}\right) \xi_{\rm c}^{1/2} +2\left(1-\left(r/R_{\rm e}\right)\right) \xi_{\rm c} &\quad \hbox{for } r > r_{\rm c} \end{array}\right. $$

(4)

with r the radial coordinate. The volume flow rate $\dot{Q}$ is derived by integrating the velocity field (4) along the cross section of the capillary leading to

$$ \dot{Q}=2\pi \int_0^{R_{\rm e}} u(r)rdr =-\frac{\pi}{8\eta}\frac{dp}{dz}R_{\rm e}^4 A(\xi_{\rm c}), $$

(5)

where

$$ A(\xi_{\rm c})=1-\frac{16}{7}\sqrt{\xi_{\rm c}}+\frac{4}{3}\xi_{\rm c} -\frac{1}{21}\xi_{\rm c}^4. $$

(6)

From (5), the mean velocity U is readily derived as

$$ U=\frac{\dot{Q}}{\pi R_{\rm e}^2}=-\frac{1}{8\eta}\frac{dp}{dz}R_{\rm e}^2 A(\xi_{\rm c}). $$

(7)

As the rheological parameter ξ_c goes to zero, the term A(ξ_c) tends to unity recovering the classical Poiseuille relations for $\dot{Q}$ and u(r). On the other hand, as ξ_c grows the mean velocity U reduces being zero for ξ_c = 1. Notice that in such a case the pressure drop along the capillary is not enough to overcome the fluid yield stress so no deformation or flow would occur.

The Pressure Gradient in Permeable Capillaries

In capillaries with permeable walls, the fluid flows laterally depending on the hydraulic conductivity L _p, the interstitial fluid pressure π _i , the inlet and outlet vascular pressures p ₀ and p ₁. Following Decuzzi et al.,4 the differential equation relating these parameters to the pressure drop ∂p/∂z along the channel can be written as

$$ -\frac{\pi R_{\rm e}^4}{8\eta}\frac{\partial^{2}p}{\partial z^{2}}-L_{\rm p} \left(\pi_i -p\right)\lambda_p =0, $$

(8)

and the vascular pressure p straightly derived as

$$ \tilde{p}(\xi_{\rm c}, \Upgamma, \tilde{z},\Upomega)=(\tilde{p}_1 -1) \Upomega \,\hbox{cosh} \left(\Upgamma (\xi_{\rm c} ) \tilde{z}\right)+\frac{\left(\tilde{p}_1 -1\right)\left(1-\Upomega \,\hbox{cosh} (\Upgamma (\xi_{\rm c} ))\right)}{\hbox{sinh} (\Upgamma (\xi_{\rm c}))}\hbox{sinh} (\Upgamma (\xi_{\rm c} ) \tilde{z})+1, $$

(9)

with the dimensionless parameters $\tilde{z}, \ \tilde{p},$ and $\Upomega$ defined as

$$ \tilde{z}=z/l;\quad \tilde{p}=p/\pi_i;\quad \Upomega =\frac{\tilde{p}_0 -1}{\tilde{p}_1 -1}; $$

(10)

and the permeability parameter $\Upgamma (\xi_{\rm c})$ given by

$$ \Upgamma (\xi_{\rm c} )=\frac{4l}{R_{\rm e}}\sqrt{\frac{\eta}{R_{\rm e}}L_{\rm p}} \frac{1}{\sqrt{A(\xi_{\rm c} )}}=\frac{\Uppi}{\sqrt{A(\xi_{\rm c} )}}, $$

(11)

which differs from the simpler $\Uppi$ because of the additional term A(ξ_c) accounting for the rheology of blood. Notice that at the entrance of the channel, that is when z = 0, Eq. (9) reduces to $\tilde{p}(\xi_{\rm c}, \Upgamma, 0,\Upomega)=(\tilde{p}_1 -1) \Upomega\,+\,1=\tilde{p}_0,$ the pressure at the inlet being always $\tilde{p}_0$ whatever the values for $\Uppi,\, \Upomega ,$ and ξ_c.

Combining Eqs. (7) with (9), the mean velocity for the Casson flow in a permeable capillary can be derived as

$$ U(\xi_{\rm c}, \Upgamma, \Upomega, \tilde{z})=\frac{\hbox{cosh} (\tilde{z}\Upgamma (\xi_{\rm c} ))-\Upomega \hbox{cosh} (\Upgamma (\xi_{\rm c} )-\tilde{z}\Upgamma (\xi_{\rm c} ))}{1-\Upomega \hbox{cosh} (\Upgamma (\xi_{\rm c} ))}U_0 $$

(12)

where

$$ U_0 =\frac{\left[(\tilde{p}_1 -1)-(\Upomega (\tilde{p}_1 -1))\hbox{cosh} (\Upgamma (\xi_{\rm c} )) \right]\hbox{cosh} (\Upgamma (\xi_{\rm c} ))\pi_i R_{\rm e}^2}{8\eta l}\Upgamma (\xi_{\rm c} )A(\xi_{\rm c}) $$

(13)

is the mean velocity at the capillary inlet $(\tilde{z}=0).$

The Effective Longitudinal Diffusion

Following Sharp,15 the transport equation along the capillary with respect to a frame of reference moving with mean velocity U can be written as

$$ \frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial C}{\partial r}\right)=\frac{\hat{u}}{D_{\rm m}}\frac{\partial C}{\partial \tilde{z}} $$

(14)

where $\hat{u}=u-U$ and $\tilde{z}=z-Ut.$ Within the capillary core $(r < r_{\rm c}),\ \hat{u}=\hat{u}_{\rm c},$ upon integrating Eq. (14) twice with respect to r with the boundary conditions

$$ C=0\quad \hbox{ at } r=0 $$

(15a)

$$ \frac{\partial C}{\partial r}=0 \quad \hbox{ at } r=0 $$

(15b)

it results

$$ C_1 (r)=-\frac{dp}{d\tilde{z}}\frac{R_{\rm e}^2}{8\eta}\frac{r^{2}}{4D_{\rm m}} B (\xi_{\rm c} )\frac{\partial C}{\partial \tilde{z}}=U\frac{r^{2}}{4D_{\rm m}}\frac{B(\xi_{\rm c} )}{A(\xi_{\rm c} )}\frac{\partial C}{\partial \tilde{z}};\quad \hbox{for }r < {r}_{\rm c} $$

(16)

where

$$ B(\xi_{\rm c} )=1-\frac{64}{21}\xi_{\rm c}^{1/2} +\frac{8}{3}\xi_{\rm c} -\frac{2}{3}\xi_{\rm c}^2 +\frac{1}{21}\xi_{\rm c}^4. $$

(17)

Whilst the homogeneous boundary condition in (15a) is arbitrarily imposed, the condition of the first derivative in (15b) has a precise physical meaning following from the axial symmetry of the problem. As regarding (15a), it is clear from the definition for the effective diffusion coefficient given in Eq. (22), that D _eff is not affected by the value of C at r = 0, so that the homogenous condition can be conveniently enforced.

Similarly in the cell-free layer, considering the condition of impermeability of the solute at the walls

$$ \frac{\partial C}{\partial r}=0\quad \hbox{at } r=R_{\rm e} $$

(18a)

and imposing the condition of continuity of concentration at the interface (r = r _c) between the central plug region and outer region with a parabolic velocity profile

$$ C=C_1 (r)\quad \hbox{at }r=r_{\rm c} $$

(18b)

it results

$$ C_2 (r)=-\frac{dp}{dz}\frac{R_{\rm e}^2}{8\eta}\frac{R_{\rm e}^2}{D_{\rm m}} \frac{\partial C}{\partial \tilde{z}}F (\xi_{\rm c}, r)=\frac{U}{A(\xi_{\rm c} )}\frac{R_{\rm e}^2}{D_{\rm m}} \frac{\partial C}{\partial \tilde{z}}F (\xi_{\rm c}, r);\quad \hbox{for } r\geq r_{\rm c} $$

(19)

where

$$ \begin{aligned} F(\xi_{\rm c}, r)=& -\frac{\xi_{\rm c}^4}{8}+\frac{64}{147}\left(\frac{r}{R_{\rm e}}\right)^{7/2} \xi_{\rm c}^{1/2} -\frac{4}{9}\left(\frac{r}{R_{\rm e}}\right)^{3}\xi_{\rm c} +\left(\frac{r}{R_{\rm e}}\right)^{2}\times \left(\frac{1}{4}-\frac{16}{21}\xi_{\rm c}^{1/2} +\frac{2}{3}\xi_{\rm c} +\frac{\xi_{\rm c}^4}{84}\right)\\ & -\frac{\xi_{\rm c}^4}{42}\hbox{ln } \left(\frac{\left(r/R_{\rm e} \right)}{\xi_{\rm c}}\right) -\frac{115}{3528}\xi_{\rm c}^4. \end{aligned} $$

(20)

The flux J of solute across a section at fixed $\hat{z}$ is given as

$$ J=\frac{1}{\pi R_{\rm e}^2}\left[\int_0^{r_{\rm c}}\left(\hat{u}_{\rm c} C_1 -D_{\rm m} \frac{\partial C}{\partial \tilde{z}}\right)2\pi r dr +\int_{r_{\rm c}}^{R_{\rm e}} \left(\hat{u} C_2 -D_{\rm m} \frac{\partial C}{\partial \tilde{z}}\right)2\pi rdr\right] $$

(21)

from which the effective diffusion coefficient is derived as

$$ D_{\rm eff} =-J\left/\frac{\partial C}{\partial \tilde{z}}\right. =D_{\rm m} \left[1+\frac{1}{48}\left(\frac{U\times R_{\rm e}}{D}\right)^{2}G (\xi_{\rm c})\right]. $$

(22)

Substituting Eq. (12) in (22), it follows

$$ D_{\rm eff} =D_{\rm m} \left[1+\frac{P_{{\rm e}_0}^2}{48}\left(\frac{\hbox{cosh} (\tilde{z}\Upgamma (\xi_{\rm c}))-\Upomega \hbox{cosh} (\Upgamma (\xi_{\rm c} )-\tilde{z}\Upgamma (\xi_{\rm c} ))}{1-\Upomega \hbox{cosh} (\Upgamma (\xi_{\rm c} ))}\right)^{2}G(\xi_{\rm c} ) \right] $$

(23)

where $P_{{{\rm e}_{0}}}$ is the Peclet number at the inlet, and

$$ \begin{aligned} G(\xi_{\rm c} )A^{2}(\xi_{\rm c} ) = 1 & -\frac{5888}{1555}\xi_{\rm c}^{1/2}+\frac{558368}{56595}\xi_{\rm c} -\frac{6144}{715}\xi_{\rm c}^{3/2}+\frac{128}{45}\xi_{\rm c}^{2}+ \frac{244}{21}\xi_{\rm c}^{4}\\ &-\frac{272128}{3773}\xi_{\rm c}^{9/2}+\frac{385312}{2205}\xi_{\rm c}^{5} -\frac{4096}{21}\xi_{\rm c}^{11/2}+\frac{11464}{165}\xi_{\rm c}^{6}\\ &+\frac{55808}{1555}\xi_{\rm c}^{13/2}-\frac{6976}{165}\xi_{\rm c}^{7} +\frac{430331}{66885}\xi_{\rm c}^{8}-\frac{512}{147}\xi_{\rm c}^{17/2} +\frac{64}{21}\xi_{\rm c}^{9}\\ &-\frac{872}{1555}\xi_{\rm c}^{10}+\frac{4}{147}\xi_{\rm c}^{1/2} -\frac{8}{147}\xi_{\rm c}^{8}\hbox{ ln} (\xi_{\rm c}). \end{aligned} $$

(24)

For ξ_c tending to zero (Poiseuille flow), Eq. (22) coincides with D _eff derived in Decuzzi et al.;4 whereas for $\Uppi = 0$ (impermeable capillaries) Eq. (23) coincides with the result given for D _eff by Sharp.¹

Results

The expression derived for the effective longitudinal diffusion D _eff (Eq. 23) comprises two terms: a molecular diffusion term D _m and a convective term which is proportional to $P_{{\rm e}_0}^2.$ This second term depends on the permeability of the vessel, expressed through $\Uppi$ and $\Upomega ;$ and on the rheology of blood, expressed through ξ_c. In Decuzzi et al.,4 it was shown that the permeability of the vessel causes a reduction of the effective diffusivity. This behavior was associated with the variation of the mean fluid velocity U along the permeable vessel $({D}_{\rm eff}\propto U^{2}).$ A similar result was derived by Sharp15 who showed a steady decrease in D _eff with a growing ξ_c.

In this study, it is assumed the dynamic viscosity η to be 1.8 × 10⁻³ P·s; the temperature T to be 300 K, the molecular diffusion D _m (= k _B T/(6π ηa)) to be about 6.1 × 10⁻¹³ m² s⁻¹, corresponding to a nanoparticle with a radius a = 200 nm (k _B = 1.38065 × 10⁻²³ J/K).

The influence of ξ_c on the effective longitudinal transport is shown in Fig. 2 where the ratio D _eff/D _m is plotted for different values of the Peclet number and in the case of impermeable vessel walls $(\Uppi =0, \ \Upgamma (\xi_{\rm c})=0).$ An increase in ξ_c leads to a reduction of the term G(ξ_c), and thus of D _eff. This is explained observing that as ξ_c increases, the core region of the capillary with a flat velocity profile grows reducing the thickness of the lateral cell free layer. Since longitudinal transport is enhanced by radial velocity gradients (shear diffusion), the larger is ξ_c the smaller is the difference between the longitudinal effective diffusion D _eff and the molecular diffusion D _m. Also, at fixed ξ_c, an increase of P _e, as expected, leads to an increase of the convective contribution to the effective diffusion, and thus of the ratio D _eff/D _m. For ξ_c tending to unity, the effective diffusion goes to D _m.

Figure 2

The dimensionless effective diffusion (D _eff/D _m) as a function of the rheological parameter ξ_c = r _c/R _e, for different values of P _e, in impermeable capillaries $(\Uppi=0, \Upgamma (\xi_{\rm c})=0)$

Figures 3 and 4 show the variation of D _eff/D _m along a permeable vessel $(\Uppi =2, 4; \ \Upomega =-2)$ for different values of the rheological parameter ξ_c ranging between 0 and 1. The permeability of the vessel and a blunt velocity profile have the same influence on D _eff/D _m: the effective diffusion reduces and becomes equal to D _m as $\Uppi$ and ξ_c increase. More importantly, it is also shown that the portion of the capillary where D _eff = D _m becomes wider as $\Uppi$ and ξ_c increase. The effect of $\Upomega$ is presented in Figs. 5 and 6: the D _eff profile along the vessel changes and the portion of the vessel with D _eff = D _m moves downwards, as the absolute value of $\Upomega$ increases.

Figure 3

The dimensionless effective diffusion (D _eff/D _m) as a function of the rheological parameter ξ_c = r _c/R _e in permeable capillaries $(\Uppi =2; \, \Upomega =-2; \, P_{{{\rm e}_0}}\simeq 16)$

Figure 4

The dimensionless effective diffusion (D _eff/D _m) as a function of the rheological parameter ξ_c = r _c/R _e in permeable capillaries $(\Uppi =4; \, \Upomega =-2; \, P_{{{\rm e}_0}}\simeq 16)$

Figure 5

The dimensionless effective diffusion (D _eff/D _m) as a function of the rheological parameter ξ_c = r _c/R _e in permeable capillaries $(\Uppi =2; \, \Upomega =-4; \, P_{{{\rm e}_0}}\simeq 16)$

Figure 6

The dimensionless effective diffusion (D _eff/D _m) as a function of the rheological parameter ξ_c = r _c/R _e $(\Uppi =2; \, \Upomega=-8; \, P_{{{\rm e}_0}}\simeq 16)$

A critical value for ξ_c can be also defined as the value below which D _eff would be larger than D _m everywhere along the capillary. Obviously, (ξ_c)_cr depends on $\Uppi$ and $\Upomega,$ as shown in Fig. 7, and decreases as $\Uppi$ increases, whereas the effect of $\Upomega$ is much less important.

Figure 7

The critical value (ξ_c = r _c/R _e of the rheological parameter as a function of $\Uppi$ and for different values of $\Upomega (=−2;\,−6;\,−8),$

Discussions

Systemically administered macromolecules or nanoparticles are transported by the blood stream within the circulatory system, where three different patterns of flow occur: high Reynolds number flow, in large vessels as the aorta and human larger arteries; laminar flow, in arterioles, capillary, and venules; and single-file flow in small capillaries, where the Red Blood Cells (RBCs) are compelled to deform into a folded or parachute-like configuration. Whilst in large vessels blood can be treated as a Newtonian fluid; in arterioles, capillaries, and venules (the microcirculation), the multiphasic nature of blood (plasma and cells), can not be disregarded. This has a number of important consequences, usually summarized in the well-known Fahraeus and Lindquist effect,5,12 as: (i) blood viscosity reduces with the vessel diameter being almost that of water in small capillaries; (ii) existence of a cell-free layer at the vessel walls; (iii) decrease in hematocrit with the vessel diameter; and (iv) blunted velocity profile, well approximated by a Casson rheological law.

The parameter ξ_c is not constant in the circulatory system. In fact, if in the macro circulation the percentage by volume of RBCs in blood (hematocrit H) lies in the range 40–50%; in arterioles and venules, where the RBCs are packed in a narrow central area of the vessel and have almost twice the velocity of plasma, the hematocrit can be as small as 20–25%. In small capillaries, H can fall down to zero if no RBCs are observed to pass through. As a consequence, the thickness of the cell free layer, that is generally assumed to be the difference between the radius of the vessel wall R _e and the plug radius r _c, would depend on the vessel diameter and on the hematocrit. An approximate expression for ξ_c as a function of R _e and for a local hematocrit of 25% (microcirculation) can be derived by interpolating the data given by Sharan and Popel14 to obtain

$$ \xi_{\rm c} =1-3R_{\rm e}^{-0.8}\quad \hbox{for } 10\,\mu\hbox{m} \leq R_{\rm e} \leq 70\, \mu\hbox{m} $$

(25)

in good agreement with in vitro and in vivo experimental results. Based on the above relation, the relative thickness of the plug region increases with R _e being ξ_c = 0.5 for R _e  = 10 μm and ξ_c = 0.9 for R _e = 70 μm. Moving from capillaries, characterized by R _e = O(10 μm) and U = O(100 μm/s), to arterioles and venules, characterized by R _e = O(100 μm) and U = O(1 mm/s), leads to an increase of P _e and a decrease of G(ξ_c). As a consequence, the effective longitudinal diffusion of a 200 nm particle would be in arterioles and venules 10⁴–10⁵ times larger than in capillaries (Table 1).

Table 1 Average dimensions and velocities of blood vessels7

Normal capillaries are of three types: continuous, fenestrated, and discontinuous, in order of increasing permeability to water. Continuous capillaries are found in muscle, skin, lung, fat, connective tissue, and nervous system; fenestrated capillaries (≤100 nm openings) occur in tissues specialized for fluid exchange, as the kidney, exocrine glands, intestinal mucosa, and synovial lining of joints; discontinuous capillaries possess intercellular gaps larger than 100 nm and occur in the bone marrow, spleen, and liver. Typical values for the hydraulic conductivity of capillaries L _p in various organs are listed in Table 2 together with the corresponding values of the permeability parameter $\Uppi.$ The permeability of the vessel walls causes a reduction of D _eff which is not uniform along the vessel. Depending on $\Uppi$ and $\Upomega,$ a longitudinal portion of the vessel can see an effective diffusion coefficient equal to D _m. For $\Uppi =2$ (Fig. 3), with a ξ_c = 0.4, nearly 30% of the blood vessel length would be characterized by a D _eff = D _m. The percentage grows as permeable arterioles or venules are considered (ξ_c > 0.5). Therefore, using physiologically relevant values for ξ_c and $\Uppi ,$ D _eff can be significantly reduced as the particle moves from larger to smaller vessels, and from impermeable to permeable vessels, or along impermeable vessels.

Table 2 The hydraulic conductivity of capillaries L _p for various organs (from Ganong7) and the corresponding values of the permeability parameter $\Uppi,$ for R _e = 10 μm and l = 100 μm

And, since in a network of capillaries, a transported solute would follow in a larger quantity the path with the largest effective diffusion,4 both vessel permeability and the biphasic nature of blood would constitute a physiological barrier to the delivery of nanoparticles, and macromolecules, from the macro to the microcirculation. And the smaller is D _m, that is the larger is the nanoparticle $(\propto D_{\rm m}^{-1}),$ the higher is the barrier. Evidently, this is not the case of small and rapidly diffusing species as albumin (D _m = 6.5 × 10⁻¹¹ m²/s and ∼69 kDa with a theoretical hydraulic radius smaller than 5 nm) or oxygen (D _m = 2 × 10⁻⁹ m²/s, ∼32 kDa) whose transport is mainly governed by molecular diffusion. On the other hand, particles and macromolecules have much larger sizes (≥10 nm) and low molecular diffusivity (≤10⁻¹³ m²/s), and then are more susceptible to be convected.

Since particles are expected to follow paths with large effective diffusivities (large P _e), it is likely that a large number of particles injected at the systemic level would be transported along the macrocirculation and a smaller amount would leave the larger vessels for the smaller arterioles and capillaries, where the effective diffusion is smaller than in larger vessels. A way to increase the percentage of particles delivered to the microcirculation from larger vessels might be that of designing spontaneously ‘marginating particles.’ In other words, particles designed to accumulate within the ‘cell-free layer’ so to leave more easily the larger vessels in favor of the smaller capillaries. Notice that, such a behavior is just the opposite of what RBCs do, as described by the well-known ‘plasma skimming effect.’ An effective way to control the dynamic of nanovectors and thus their margination properties would be controlling their size, shape, and density. Whereas spherical particles in a capillary flow have been shown to marginate only under the effects of external force fields (gravitational and electromagnetic),3 non-spherical particles exhibit a fairly complex dynamic, in that they experience rotations, revolutions, and spins which finally result in much more complex margination dynamics.8

Conclusions

Taylor and Aris’ coefficient of diffusion has been revised to account for the permeability of the vessels and the rheology of blood. Three governing parameters have been introduced, namely ξ_c the ratio between the plug and the vessel radii; $\Uppi$ and $\Upomega,$ which are permeability parameters related to the hydraulic conductivity and pressure drop across the vessel wall, respectively. It has been shown that both ξ_c and $\Uppi$ have the effect of reducing D _eff as they increase.

For physiologically relevant values of the hematocrit, and in the case of impermeable vessels, it has been shown that the ratio D _eff/D _m lies in the range 10⁴–10⁵ for particles with a characteristic size of 200 nm and moving within the microcirculation. It has been confirmed that the permeability of the vessel walls causes a dramatic decrease of D _eff, especially in arterioles and venules, where the effect of $\Uppi$ and ξ_c combines.

Finally, a strategy to increase the number of systemically injected nanoparticles delivered to the local microcirculation could be that of designing spontaneously ‘marginating particles.’