1 Introduction

Particle separation in microfluidic is a process by which particles of different sizes and shapes can be separated using microfluidic devices. This process is used in many applications, such as biomedical (Stroncek and Rebulla 2007; Suresh 2007; Alshareef et al. 2013) and pharmaceutical research (Jia et al. 2022; Cui and Wang 2019), drug delivery (Maeki et al. 2018; Mancera-Andrade et al. 2018), and environmental monitoring (Chon et al. 2007; Jokerst et al. 2012). The particles are typically sorted using a combination of physical and chemical methods, such as dielectrophoresis, magnetophoresis (Alnaimat et al. 2018; Sophia Lee et al. 2011; Kadivar 2014), hydrodynamic focusing (Kadivar et al. 2013; Daniele et al. 2015; Olfati Chaghagolani and Kadivar 2023), and fluorescence-activated cell sorting (Raddatz et al. 2008; Chen et al. 2010). The advantages of particle sorting in microfluidics include high accuracy, high throughput, and low cost (Sajeesh and Sen 2014). Among the several sorting techniques, dielectrophoresis is popular method. Dielectrophoresis (DEP) is a phenomenon in which a force is exerted on a particle when it is subjected to a non-uniform electric field. The force experienced by the particle is dependent on the particle size, particle shape, applied electric field, and dielectric properties of particle and carrier phase. DEP can be used to manipulate, separate, and analyze particles in a variety of applications, including microfluidics and bioprocessing (Chan et al. 2018).

Two types of current can be used in the particle sorting by applying the electric filed: direct current and alternating current. Direct current dielectrophoresis (DC-DEP) (Kang et al. 2008) is a phenomenon in which particles suspended in a fluid are subjected to the non-uniform electric field, resulting in a force that can be used to manipulate the particles. It is a type of dielectrophoresis that utilizes the direct current electric field, as opposed to an alternating current (AC) field (Lewpiriyawong and Yang 2012). DC-DEP is used in a variety of applications, including the separation of particles, the manipulation of cells (Srivastava et al. 2008), and the assembly of nanostructures (Ali and Park 2016; Nguyen et al. 2022).

Size-based multiple particle separation using dielectrophoresis is a process used to separate particles of different sizes. It is commonly used in industrial processes such as filtration (Suehiro et al. 2003), centrifugation (Zhang et al. 2019; Yeo et al. 2018), and sedimentation (Luo et al. 2018). In these processes, particles are separated based on their size, relative permittivity and electrode shape. The dynamics of particle trajectory in the microfluidic channel using COMSOL Multiphysics under different electrode shapes have been investigated by Zhang and Chen (2020). They have investigated the response of three bioparticle to dielectrophoresis force for three electrode shapes (Zhang and Chen 2020). Zackria Ansar et al. developed a bioparticle separation for five particle sizes and different electrode shape (Ansar et al. 2020). A new separation strategy for biocell separation using the frequency coupled dielectrophoresis force has been proposed by Wang et al. (2009). Using a large-scale floating electrodes array, Jiang et al. numerically demonstrated dielectrophoresis separation of binary colloid mixture in the microfluidic channel (Jiang et al. 2018).

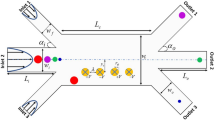
A boundary element method is an interesting numerical method to investigate the dynamics of particle motion in the microfluidic channel (Kadivar 2018; Erfan Kadivar and Zarneh 2022). The advantage of boundary element method is that only the boundary of the problem is necessary to be discretized into elements (Pozrikidis 1992). To our knowledge, most studies on the boundary element method are restricted to the straight microchannel (House and Luo 2010; Çetin et al. 2017). In this work, we study the particle sorting using the dielectrophoresis phenomenon produced by triangular-shape electrodes. In this way, boundary element method (BEM) and point-particle approach (PPA) are applied to study the separation dynamics. In this study, the effect of particle size, electric potential, electrode spacing, tip angle of triangular electrodes, and relative permittivity on the dynamics of particle trajectory are investigated. Figure 1 illustrates the schematic geometry of our work. The microchannel consists a straight mother channel and two inlets and outlets. The straight channel also consists of up and down triangular electrodes.

This paper is structured as follows: in Sect. 2, we will formulate the Laplace equation for electric potential, Stokes equation and boundary conditions for the electric potential and velocity field at the particle interface as well as at the channel walls. In Sect. 2, the numerical implementation to solve the boundary integral representation equation for the electric potential and velocity of particle are included. In Sect. 3, we introduce the dielectrophoresis and drag forces to solve the dynamics of particle motion. Finally, the numerical results obtained from both models are reported in Sect. 5.

Fig. 1
figure 1

A top view of our proposed microchannel geometry in the x–y plane. \(L_i\), \(L_c\), and \(L_o\) are the inlet, straight, and outlet channel lengths, respectively. \(W_c\) is the width of straight channel

Full size image

2 Boundary element method

In this study, the trajectory of solid particle in the presence of electric field in the microfluidic channel is studied using boundary element method and point-particle approach. In this section, we explain how the boundary element method can be used to investigate the particle separation. Consider a small solid particle suspended in a dielectric fluid under the influence of the electric field. Figure 1 illustrates the top view of our studied microfluidic channel in the x–y plane. The considered microfluidic device consists of two inlets (for sample flow and buffer flow), two outlets and a separate region, wherein the non-uniform electric field generated by a pair of side wall electrodes arrangements. The rest channel walls are insulated. As shown in Fig. 1, the triangular-shape electrodes are located on up and down walls in the straight channel. Electric potentials of 0 and \(\phi _1\) are applied adjacently to down electrodes and 0 and \(\phi _2\) are applied to up electrodes. The horizontal distance of electrodes is labeled by \(\lambda\). The height of down and up electrodes are called by \(h_1\) and \(h_2\), respectively. \(w_c\) and \(w_o\) are the channel width of the straight and outlet channels, respectively. Our considered problem is two-dimensional where the particle travels in the x–y plane while rotating about the z-axis.

In the boundary element formulation, the flow and electric field are calculated together in the presence of solid particle. The electric field is calculated on the wall domain as well as on the particle domain. The conductivity and permittivity of liquid phase and particles are labeled by \(\sigma\) and \(\epsilon\). The electric potential, \(\phi\), presents varying function of the in-plane coordinates x and y and is governed by the two-dimensional Laplace equation:

$$\begin{aligned} \nabla ^2\phi =0, \end{aligned}$$
(1)

together with Dirichlet boundary condition on the channel walls as well as on electrodes.

At the low Reynolds numbers limit, the flow liquid phase in the present of solid particle is described by the Stokes equation and continuity equation Batchelor and Batchelor (2000):

$$\begin{aligned}{} & {} \varvec{\nabla }P= \mu \varvec{\nabla }^2{\textbf{V}}~, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \varvec{\nabla }.{\textbf{V}}=0~, \end{aligned}$$
(3)

where P(x, y) is the pressure, \(\mathbf {V(x,y)}\) is the velocity, and \(\mu\) is the dynamic viscosity of continuous phase. In electrokinetic regime, a non-neutral diffuse layer is formed on the charged particle or wall surface which is called electrical double layer (EDL). Under thin-electric double layer (EDL) assumption, the slip velocity of fluid at the channel walls and particle surface read

$$\begin{aligned}{} & {} V_s=-\frac{\epsilon _m\zeta _w E_{t}}{\mu } \qquad \textrm{on} \quad \textrm{walls} \nonumber \\{} & {} V_s=-\frac{\epsilon _m\zeta _p E_{t}}{\mu } \qquad \textrm{on} \quad \textrm{particle} \end{aligned}$$
(4)

where \(E_t\) is tangential component of electric field, \(\zeta _w\), and \(\zeta _p\) are the zeta potential at channel wall and particle surface, respectively. \(\epsilon _m\) is permittivity of carrier phase. In the laboratory coordinate systems, the velocity at each point on the particle contour is the combination of the slip velocity and rigid particle motion,

$$\begin{aligned} \mathbf {V({\textbf{r}}})={\textbf{V}}_s+{\textbf{V}}_b={\textbf{V}}_s+{\textbf{V}}_c+\mathbf {\omega }{\textbf{k}}\times \left( {\textbf{r}}-{\textbf{r}}_c\right) , \end{aligned}$$
(5)

where \(\mathbf {\omega }\) is angular velocity of the particle, \({\textbf{k}}\) is the unit vector along the z-axis, \({\textbf{r}}_c\) is the position of the center of particle, and \({\textbf{V}}_c\) is the velocity at the selected center of the particle. At the low Reynolds numbers, we assume that the particle is buoyant and particle inertia is negligible. Hence, the total traction and total torque exerted on particle are zero:

$$\begin{aligned}{} & {} \int _{\Gamma _{p}}{\textbf{f}}\textrm{d}l=0, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \int _{\Gamma _{p}}({\textbf{r}}-{\textbf{r}}_c)\times {\textbf{f}}\textrm{d}l=0, \end{aligned}$$
(7)

where \(\Gamma _{p}\) is particle contour, \({\textbf{f}}\) is local fraction and \({\textbf{r}}_c\) is position of particle center.

2.1 Integral representation

In order to investigate the dynamics of particle motion in the presence of electric field, Eq. 1 is numerically solved together with Eq. 2. It is important to mention that the solution of equation 1 is independent of Eq. 2. However, by applying the boundary conditions 4, the solution of Stokes equation depends on the solution of Laplace equation for the electric potential on particle and walls. Hence, using the boundary element method, we numerically solve them sequentially.

Following the formulation of boundary integral equations (Pozrikidis 2002), the electric potential at point (\({\textbf{r}}_0)\) that lies in the continuous fluid satisfies a self-consistent integral equation of the following form:

$$\begin{aligned} \phi \left( {\textbf{r}}_0\right) =-\int _{\Gamma _p,\Gamma _w} G\left( {\textbf{r}},{\textbf{r}}_0\right) \left[ {\textbf{n}}\cdot \nabla \phi \right] \textrm{d}\ell +\int _{\Gamma _p,\Gamma _w} \phi \left[ {\textbf{n}}\cdot \nabla G\left( {\textbf{r}},{\textbf{r}}_0\right) \right] \textrm{d}\ell , \end{aligned}$$
(8)

where \({\textbf{r}}=(x,y)\), \({\textbf{r}}_0=(x_0,y_0)\) are the field and the singular points, respectively. When integration point \({\textbf{r}}\) approaches the evaluation point \(\mathbf {r_0}\), the integrands exhibit a singularity. Therefore, when the point \({\textbf{r}}_0\) lies exactly on the channel contour or on the particle contour, we read

$$\begin{aligned} \phi \left( {\textbf{r}}_0\right) =-2\int _{\Gamma _p,\Gamma _w} G\left( {\textbf{r}},{\textbf{r}}_0\right) \left[ {\textbf{n}}\cdot \nabla \phi \right] \textrm{d}\ell +2\int _{\Gamma _p,\Gamma _w} ^{PV} \phi \left[ {\textbf{n}}\cdot \nabla G\left( {\textbf{r}},{\textbf{r}}_0\right) \right] \textrm{d}\ell . \end{aligned}$$
(9)

where and PV denotes the principal value. The normal vector \({\textbf{n}}\) points from the particle contour or wall into the continuous phase. \(\Gamma _p\) and \(\Gamma _w\) are particle contour and the contour of wall, respectively. The function

$$\begin{aligned} G\left( {\textbf{r}},{\textbf{r}}_0\right) =\frac{-1}{2\pi }\ln \left| {\textbf{r}}-{\textbf{r}}_0\right| , \end{aligned}$$
(10)

indicates the free Green’s function of the two-dimensional Laplace equation 1.

The boundary conditions of electric potential read as follows:

  • On the channel walls: the normal component of electric field is zero, \({\textbf{n}}\cdot \nabla \phi =0\).

  • On the particle-carrier phase interface: the normal component of electric field is continuous.

  • On the surface electrode: applied electric potential.

The fluid velocity, \({\textbf{V}}\), is decomposed into the combination of the background velocity, \({\textbf{V}}_{\infty }\), and the disturbance velocity due to the presence of the particle, \({\textbf{V}}_D\). One way to obtain the disturbance velocity field is to numerically compute a self-consistent integral equation for velocity field on the particle boundary as well as on the channel walls. Following the formulation of boundary integral equations (Pozrikidis 1992, 2002; Zeb et al. 1998), the jth component (x, y) of the particle velocity at point (\({\textbf{r}}_0)\) that lies inside the continuous fluid satisfies a self-consistent integral equation

$$\begin{aligned} V_{D,j} ({\textbf{r}}_0)=\frac{-1}{4\pi \mu } \oint _{\Gamma _{p},\Gamma _{w}}f_i ({\textbf{r}})G_{ij} ({\textbf{r}},{\textbf{r}}_0) \textrm{d}\ell +\frac{1}{4\pi }\oint _{\Gamma _{p},\Gamma _{w}} V_{D,i} ({\textbf{r}}) T_{ijk} ({\textbf{r}},{\textbf{r}}_0)n_k \textrm{d}\ell , \end{aligned}$$
(11)

where \({\textbf{f}}\) is the traction vector and unknown variable. \(G_{ij}\) and \(T_{ijk}\) are velocity and stress tensor Green’s functions of Stokes equation, respectively. Free-space Green’s functions of Stokes equation are given by Pozrikidis (1992, 2002)

$$\begin{aligned}{} & {} G_{ij}({\textbf{r}},\mathbf {r_0})=-\delta _{ij}\ln |\rho |+\frac{{\hat{\rho }}_i{\hat{\rho }}_j}{\rho ^2}, \end{aligned}$$
(12)
$$\begin{aligned}{} & {} T_{ijk}=-4\frac{{\hat{\rho }}_i{\hat{\rho }}_j{\hat{\rho }}_k}{\rho ^4}. \end{aligned}$$
(13)

where \(\varvec{{\hat{\rho }}}={\textbf{r}}-\mathbf {r_0}\), and \(\rho =|\varvec{{\hat{\rho }}}|\). The domain integral on the right-hand side of Eq. ( 11) is directly computed by domain discretization followed by numerical integration.

The first step in the implementation of the boundary element method is to discretize the boundary into finite numbers of elements which are defined boundary elements. We discretize the channel walls, inlets and outlets into a collection of straight segments defined by the element end-points. The particle contour is discretized by applying the circular arc elements. The grid independence study was performed by calculation of particle trajectory function of node numbers. We have found that 80 points for particle contour and 440 straight elements for fixed boundaries are satisfactory and any increase beyond this mesh size would lead to insignificant changes in results. The boundary integrals of Laplace and Stokes equations are discretized over contours with sums of integrals over the boundary elements. The unknown variables, such as \({\textbf{n}}\cdot \nabla \phi\) on walls, \(\phi\) on particle, \({\textbf{f}}\) on walls and particle are replaced with constant functions over the individual boundary elements (Pozrikidis 2002). First, we solve the integral equation of the electric potential, Eq. 9, over the particle contour and channel walls. Then, using the Eq. 4, the slip velocities at the particle surface and channel walls are computed. Now, we calculate the disturbance velocity, \({\textbf{V}}_D\) by subtracting the slip velocity from the background velocity. In order to match the number of equations with the number of unknown variables, the addition equations from 6 and 7 are added to the linear algebraic equations. Figure 2a indicates the schematic representation of channel and particle domains. Boundary integration is computed counter-clockwise around a domain. The integrals over each boundary element should be computed accurately by the Gauss–Legendre quadrature with 12 nodes. The system of linear algebraic equations was solved by Gaussian elimination method.

Fig. 2
figure 2

Top view of the computational mesh used in the point-particle approach. a Discretization of channel and particle in the boundary element method. b Schematic representation of triangular meshes of the considered microchannel in the point-particle approach method

Full size image

3 Point-particle approach

In this section, the dynamics of particle separation in the present of electric field using point-particle approach is presented. In the point-particle approach, a particle is assumed to be a point mass, with no volume or internal structure. This approach is useful for studying the behavior of individual small particle, as well as for studying the behavior of many small particles in a system. In this approach, the particle is described by its position, momentum, and other properties, such as mass and charge. The motion of the particle is determined by Newton’s laws of motion, and the forces acting on it, such as gravity, drag force, and electromagnetic forces. At the low Reynolds numbers and normal temperature, the inertial force and force caused by Brownian motion are negligible. Furthermore, in the Hele–Shaw limit, where a channel height being much smaller than any in-plane length scale, sedimentation force is very small. Therefore, the dynamics of particle motion is affected by drag force, \({\textbf{F}}_{d}\) and dielectrophoretic force, \({\textbf{F}}_\textrm{DEP}\):

$$\begin{aligned} m_p\frac{\textrm{d}{\textbf{V}}_c}{\textrm{d}t}={\textbf{F}}_d+{\textbf{F}}_\textrm{DEP}, \end{aligned}$$
(14)

where \(m_p\) is the mass of particle and \({\textbf{V}}_c\) is the central mass velocity of particle. The drag force acting on a spherical particle reads by

$$\begin{aligned} {\textbf{F}}_d=6\pi \mu R \left( {\textbf{V}}-{\textbf{V}}_c\right) , \end{aligned}$$
(15)

where R is the particle radius, \(\mu\) is dynamic viscosity, and \({\textbf{V}}\) is the velocity of carrier fluid. The dielectrophoretic force is exerted on a particle when it is subjected to a non-uniform electric field. This force is dependent on the dielectric properties of the particle, the frequency and strength of the applied electric field, and the shape of the particle. The time averaged DEP force acting on the particle is given by Pohl (1978)

$$\begin{aligned} {\textbf{F}}_\textrm{DEP}=2\pi R^3\epsilon _m \text {Re}\left[ K^*(\omega )\right] \nabla |{\textbf{E}}^2|, \end{aligned}$$
(16)

where \(\epsilon _m\) is the permittivity of the medium, and \(\text {Re}[K^*(\omega )]\) refers to the real part of the complex Clausius–Mossotti (CM) factor. CM factor reads by

$$\begin{aligned} K(\omega )=\frac{\epsilon ^* _p - \epsilon ^* _m}{\epsilon ^* _p+2\epsilon ^* _m}, \end{aligned}$$
(17)

where \(\epsilon ^*=\epsilon +\sigma /(i\omega )\), and \(\sigma\) is the electric conductivity. The subscripts p and m refer to the particle and the medium, respectively. The sign of CM factor indicates the polarizability between the particle and carrier liquid. When \(\epsilon _p>\epsilon _m\), CM factor is positive, while, when \(\epsilon _p<\epsilon _m\), CM factor becomes negative. Totally, \(\textit{Re}[K^*(\omega )]\) has a value between \(-0.5\) and 1.0 Pohl (1978). In the electrostatics state, the electric potential distribution in the microfluidic channel is obtained from the Laplace equation 1 and the electric field distribution can be calculated from the gradient of the electric potential, \({\textbf{E}}=-\nabla \phi\).

In the microfluidic systems, particles have a size in the micrometer scale. At the low Reynolds number, the time scale of variation in the electric field is much higher than the time scale of particle acceleration. Therefore, one can neglect the particle acceleration in the Eq. 14. Therefore, the particle velocity reads

$$\begin{aligned} {\textbf{V}}_c= {\textbf{V}}-\frac{ R^2\epsilon _m}{3\mu } \text {Re}[K^*(\omega )]\nabla \left| {\textbf{E}}^2\right| \end{aligned}$$
(18)

At the low Reynolds number, the carrier velocity, \({\textbf{V}}\), (in the absence of any particle) is calculated from the Stokes and continuity equations 3 together with boundary condition of slip velocity at the channel walls, equation 4.

Therefore, unknown variables (carrier velocity, electric potential, and electric field) can be obtained by solving a set of equations including Stokes equation, continuity equation, and Laplace equation together with appropriate boundary conditions. These set of equations were solved using COMSOL Multiphysics 6.0. In this way, we considered two-dimensional simulation model to investigate the device performance and efficiency. The laminar flow has been selected for initial velocity of the inlet fluids. The electroosmotic velocity, Eq. 4, has been selected for the boundary condition at the channel walls. In order to simulate the electric field in the presence of triangular electrodes, the electric current interface model has been applied. The applied electric potentials are governed by Laplace’s equation. Therefore, the electric field inside of microchannel is calculated from the electric potential. Finally, particle trajectory was determined using particle tracing module.

The simulations are performed in a two-dimensional computational domain. In the point-particle approach, the channel domain are discretized into a collection of 32215 triangular segments. Figure 2b shows a schematic mesh representation of channel domain.

In order to report our numerical results in dimensionless numbers, the width of straight channel (separate region), \(w_c\), and the zeta potential of the channel wall, \(\zeta _w\), are used as the characteristic length and electric potential scale. In this way, the particle velocity and traveling time become dimensionless by \(V_\infty =\epsilon _m\zeta _w ^2/(\mu w_c)\), and \(T_0=w_c/V_\infty\), respectively.

4 Validation of the model

In order to validate our model, the numerical results obtained from the boundary element method and point-particle approach were compared to the experimental data of Piacentini et al. (2011). Comparing two numerical methods of the current study with the experimental results reported by Piacentini et al. (2011) are presented in the Fig. 3. As one can see, result of the boundary element method is in good agreement with the experimental results as well as point-particle approach simulations.

Fig. 3
figure 3

Particle trajectory in the microfluidic channel, computed with the boundary element method (green line), point-particle approach (blue line), and compared to experiment, Piacentini et al. (2011), (red line)

Full size image

5 Results

In this paper, we mainly focus on the effect of particle size, electric potential, and physical characterizes of particle on the particle separation in the microfluidic channel. Figure 1 shows the schematic of the channel geometry. The considered microchannel consists of two inlets, main straight channel, and two outlets. The different voltages are applied to up and down triangular electrodes. The particles are injected into the inlet 1 with flow velocity \(V_1\) and carrier flow (buffer flow) is flown through the inlet 2 with flow velocity \(V_2\). For each simulation run, particles are flown through the inlet 1. When particles arrive in the vicinity of electrode, the particles experience the DEP force. The trajectory of particle depends on the strength of DEP force. As we have mentioned before, DEP force strongly depends on the gradient of the electric potential generated by triangular electrodes. Figure 4 shows the electric potential distribution map in the straight channel and as well as around the electrodes. It is easy to find that the electrodes are at the different voltages and a non-uniform electric field is produced by them. Therefore, particle experiences the dielectrophoretic force.

Fig. 4
figure 4

Electric potential distribution map in the microfluidic channel

Full size image

The particle dynamics has a strong dependence on the electric field generated by electrodes. The final destination of the particle is determined by trade-off between the dielectrophoretic force, drag force, and driving force. Figure 5 illustrates the particle trajectory for three different values of applied electric potential. The results have been extracted from the boundary element method. As one can see, the different trajectories are mapped to different electric potential. The electric field and particle size play a significant role in the particle trajectory. According to Eqs. 16 and 15, the dielectrophoresis force is proportional to the gradient of the second power of the electric field and the third power of the particle radius. On the other hand, the drag force has a linear relationship with the particle radius

As one can see in the Fig. 5, there are three different scenarios of particle trajectories. The particle either is trapped at the straight channel or travels into up/down outlets. Figure 6 illustrates subsequent snapshots in time of the three different scenarios of particle trajectories. When the particles flow through the up or down channel outlets, it is called the up-outlet regime (UR) or down-outlet regime (DR), respectively (see videos in Supplementary materials). However, when the particles are trapped in the vicinity of electrodes, calls trapped regime (TR) (see video in Supplementary materials). Therefore, we should find two critical values which correspond to transition between up regime and down regime, C1, as well as the transition between down regime and trap regime, C2. The videos of numerical simulation should be found in the Supplementary materials. The snapshot pictures and supplementary movies have been extracted from the boundary element method.

Fig. 5
figure 5

Particle trajectories for three different particle sorting regimes. When the particles flow into the up- or down-outlet channel, it is label the upper regime (UR) or down regime (DR), respectively. However, when the particle is trapped in the vicinity of electrodes, it calls the trapped regime (TR)

Full size image
Fig. 6
figure 6

Subsequent snapshots of particle trajectories for three different values of electric potential: a up-outlet regime (UR), b down-outlet regime (DR), and c trapped regime (TR)

Full size image

5.1 Effect of electrode potential

Figure 7 shows the particle velocity as a function of particle position for two different values of applied electric potential. The color bar indicates the absolute value of particle velocity at each coordinate (x, y). As we one can see, the particle velocity increases when the electric potential ratio of up to down electrodes increases. In addition, by increasing the applied electric potential ratio, the particle trajectory shifts towards the down electrodes of the straight channel. Therefore, the final destination of the large radius particle, is quite different from the smaller radius. However, the critical radius of particle depends on the applied electric potential ratio. The numerical results obtained from the boundary element method and point-particle approach are presented in the Fig. 8. Figure 8 shows the critical radius of particle as a function of applied voltage ratio of up electrodes to down electrodes. Concerning the Fig. 8, it is easy to find that the boundary element method can predict the dynamics of particle trajectory in the presence of applied electric potential. We have found a good agreement between two numerical methods. As shown in Fig. 8, results indicate that by increasing the applied electric potential ratio, critical particle radius decreases. The physical reason is that the particle velocity increases with the increase of the applied electric potential ratio. It means that the transition between different sorting regimes occurs at small particle when the applied electric potential ratio increases.

Let us express our results in terms of dimensional quantities. According to Fig. 8, we can predicts that the final destination of three particles PLT, RBC, and WBC. For potential ratio less than 1.3, it leads to separate the WBC which has particle diameter about 7 \(\upmu\)m. In this case, the WBCs travel to down-outlet (outlet 2) and PLTs and RBCs and flow through the up outlet (outlet 1). For electrode potential ratio between 1.3 and 1.9, RBCs and WBCs flow through the down-outlet and PLTs travel into the up-outlet. For \(1.9\le \Phi _u/\Phi _d\le 2.5\), one can see the three different regimes, PLTs (\(R_\textrm{PLT}=1.60\) \(\upmu \textrm{m})\) and RBCs (\(R_\textrm{RBC}=3.50\) \(\upmu \textrm{m})\) travel to up and down outlets, respectively. While the white blood cells are trapped in the vicinity of the electrodes. By increasing the potential ratio, the PLTs also travel into the down-outlet.

Fig. 7
figure 7

Particle velocity as a function of its location for two different values of applied electric potential. The color bar indicates the particle velocity

Full size image
Fig. 8
figure 8

Critical radius as a function of applied electric potential for two different numerical methods. The different separation regimes are labeled by UR, DR, and TR

Full size image

5.2 Effect of inlet flow rate

The inlet velocity ratio is another important parameter which plays a significant role in the separation dynamics. Now, we study the influence of inlet velocity ratio, \(V_2/V_1\), on the particle trajectory. In this way, the inflow velocity of upper inlet, \(V_1\), is kept fixed and we vary the lower inflow velocity, \(V_2\). Figure 9 illustrates the effect of inlet velocity ratio on the particles sorting dynamics. The simulation results obtained from BEM and PPA were reported in the Fig. 9. Depending on the particle radius, the different sorting regimes can be seen in the Fig. 9. In terms of dimensional parameters, for example, numerical results obtained from BEM and PPA are able to predict the final destination of PLT, RBC, and WBC particles. Concerning the Fig. 9, for \(V_2/V_1\) smaller than 1, the PLT and RBC particles travel into the down-outlet, WBCs are trapped in the straight channel. However, for \(1\le V_2/V_1\le 2\), PLTs travel into the up-outlet channel (UR), RBCs flow through the down-outlet (outlet 2), and WBCs are trapped in the vicinity of electrodes in the straight channel.

Fig. 9
figure 9

Particle critical radius as a function of inflow velocity ratio of lower inlet to upper inlet. The different sorting regimes are labeled by UR, DR, and TR

Full size image

5.3 Effect of electrode angle

The electrode shape has important role on the non-uniform produced electric field. Indeed, the non-uniform electric field is generated by the electrical electrodes. The various triangular electrodes with the different angles are considered in the straight channel. Figure 10 illustrates the electric potential in the microfluidic channel for two different values of tip angle. One can see that the distribution the electric potential strongly depends on the tip angle of triangular electrode. Figure 11 shows the different separation regimes as a function of tip angle of triangular electrode for two different numerical methods. As one can see, by increasing the tip angle of triangular electrode, the non-uniform electric field distribution region around the electrodes reduces. Therefore, the DEP force acting on the particle decreases. In this case, the transition between different separation regimes occur at the large particle when the tip angle of electrode increases. We also find a good agreement between boundary element method and point-particle approach method.

Fig. 10
figure 10

Electric potential distribution map for two different tip angles of triangular electrode

Full size image
Fig. 11
figure 11

Separation diagram of particle as a function of tip angle of triangular electrode. The different sorting regimes are labeled by UR, DR, and TR

Full size image

5.4 Effect of electrode shift

It is clear that DEP force strongly depends on the distribution of electric potential in the microchannel. The electric field is generated by the gradient of the electric potential. Therefore, the electric field depends on the position of electrodes. As we have indicated in Fig. 1, the electrode tip to tip distance is labeled by \(\lambda\). In order to investigate the effect of electrode position on the particle sorting, we have kept fixed the up electrodes and down electrodes were shifted with respect to the up electrodes from 0 to \(6\lambda /8\) at an increment of \(\lambda /8\). For example, these shifts were 0 (no shift) and \(\lambda /2\) (the down electrodes are leading the up electrodes by \(\lambda /2\) spacing). Figure 12 indicates the different regimes of particle separation on the down electrode displacement at a given value of applied electric potential for boundary element method and point-particle approach method. As one can find in Fig. 12, the transition between up-outlet sorting regime and down-outlet sorting regime occurs at higher radius when the electrode shift increases. However, the transition between the down sorting regime (DR) and trapped particle regime occurs at the lower radius when the electrodes shift increases. For example, when the down electrodes were displaced by \(5\lambda /8\) from the symmetry position (no shift), the RBCs are trapped in the straight channel instead of flowing towards the down outlet.

Fig. 12
figure 12

Sorting diagram of particle critical radius as a function of down electrodes displacement. The different sorting regimes are labeled by UR, DR, and TR

Full size image

5.5 Effect of electrode height ratio

Up to now, we considered the same height for the up and down electrodes. However, changing the height ratio of the up and down electric electrodes changes the non-uniform electric field distribution in the channel. Therefore, the particles experience the different dielectrophoresis force with respect to symmetric electrode. Here, we investigate the influence of height ratio of the up electrode (\(h_2\)) to down electrode (\(h_1\)) on the particle sorting in a given value of electric potential ratio. In this way, the electric potential ratio, \(\Phi _u/\Phi _d=2.5\), and velocity ratio, \(V_2/V_1=1.32\) were kept constant and the height ratio varies from 1 to 4. Figure  13, illustrates the sorting diagram of particle radius as a function of height ratio of up and down electrodes, \(h_2/h_1\). We have found a good agreement between two numerical methods. Numerical results indicate that the critical radius increases by increasing the height ratio of electrodes. The insets of Fig. 13 illustrate when the height ratio increases, the non-uniform electric field distribution area decreases. It means that the dielectrophoresis force decreases with increasing the height ratio.

Fig. 13
figure 13

Sorting diagram of particle critical radius as a function of height ratio of up and down electric electrodes. The different sorting regimes are labeled by UR, DR, and TR. The insets show the electric potential distribution map for two different values of height ratio

Full size image

5.6 Effect of permittivity ratio

Now, we investigate the effect of permittivity ratio on the particle separation regimes at a given value of the applied electric potential ratio. According to Eq. (16), the DEP force strongly depends on the electric permittivity. Therefore, the particles with different permittivities, experiences the different values of DEP force. Figure 14 illustrates the different sorting regime as a function of particle permittivity. The results indicate that the transition between the up-outlet regime to down-outlet regime occurs at lower radius when the relative permittivity increases. On other hands, the by increasing the relative permittivity the critical particle radius for down-outlet regime to particle trapped regime decreases. As one can see in Fig. 14, the results obtained from the boundary element method are close to those obtained from the point-particle approach.

Fig. 14
figure 14

Sorting diagram of particle critical radius as a function of relative particle permittivity. The different sorting regimes are labeled by UR, DR, and TR

Full size image

6 Conclusion

In this study, active sorting of solid particles inside of microfluidic channel using the electric field was numerically studied. The boundary element method to solve for Laplace equation of electric potential and Stokes equation was adopted. We also numerically investigated dielectrophoresis particle motion using the point-particle approach. The channel geometry consists a straight channel (separation region), two inlets, and two outlets. It was found that the BEM results are able to predict the particle trajectory on basis of particle size, electric potential, and electrodes arrangement. The effect of the particle radius, electric potential, relative permittivity, and electrodes arrangement on the particle separation has been numerically studied. The numerically results obtained from both numerical models are compared with each other. We have found a good agreement between results obtained from boundary element method and point-particle approach. Numerical results indicate that depending on the control parameters, three different sorting regimes can be observed for the particles injected from the upper inlet of the microchannel.