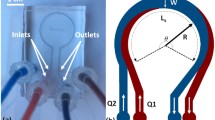
Abstract
Lateral flow in microfluidic channels are of utmost importance. They are the main mechanism and/or challenge in many microfluidic applications. Despite this, there is a dearth of design rule of thumbs or mathematical models to predict the characteristics of the lateral flow. The lateral flow can be either caused by channel geometry or flowing fluid inhomogeneity. The aim of the present study is to provide a much-needed model for fluid inhomogeneity-induced lateral flow in the form of an empirical dimensionless model. The model is based on a numerical model which is in turn validated by experiments. The experiments are carried out by fabricating a microfluidic chip and observing the 3D structure of the flow under fluorescent confocal microscope. Based on the results, it is found that a single model, based on Grashof and Reynolds numbers, is capable of modeling the lateral flow due to fluid inhomogeneity regardless of the inhomogeneous property. The empirical model is capable of predicting the rotation caused by the lateral flow within 10% and is valid in lateral flows caused by either, diffusion or density inhomogeneity in the supplied liquid. The results provided here can be used with ease to improve the design of microfluidic devices dealing with lateral flow, density disparity, mixing, and chemical reaction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Microfluidics is the name of an emerging area in science and engineering that is concerned with predicting the behavior, precise control, and manipulation of fluids and particles at the scale of tens to hundreds of cubic micrometers. These devices hold the potential for world-changing innovations. They can be small and hence portable, easy to use; they can function with small sample volumes and have a potential of using micro-fabrication techniques to decrease costs and for production in large volumes. The range of applications is enormous, from biomedical applications such as detection of single cancer cells circulating in blood to synthesis of complicated materials or production of electricity from bacteria and enzymes. Many of these applications promise a revolutionary improvement over conventional methods, but many challenges remain before most microfluidic devices, apart from a few exceptions, are competitive with conventional methods.
One such challenge presents itself in the form of controlling and predicting the flow characteristics when two fluids come into contact. While the behavior of two-phase flows at large scales is well known, those at microscale are not yet adequately investigated. The two-phase fluid dynamics at microscales differ greatly from those on a larger scale. The main difference comes from the fact that phenomena such as surface tension, buoyancy or diffusion have varied scaling with size. For example, on a large scale, surface tension is typically negligible but it plays a large role in many microfluidics.
One result of these various behaviors is that the formation of new two-phase flow patterns is not possible on a larger scale. One common and notable example is the flow side by side of two aqueous solutions (Atencia and Beebe 2005), also known as horizontally stratified flow. Figure 1 shows a schematic of this flow pattern. In ideal conditions, the resulting flow regime produces a quasi-stable interface (the interface dissipates as the solutes diffuse into the other solution) between the two fluids at which diffusion is the only mode of species transport between the two solutions (Tarn et al. 2014; Hossain and Kim 2017). This flow regime enables the core functions of many microfluidic devices (Petersson et al. 2005; Prabhakarpandian et al. 2013; Vicari et al. 2021; Darros-Barbosa et al. 2003; González Fernández et al. 2020); subsequently any divergence from a perfectly vertical interface can disrupt these functions (Xuan et al. 2012; Gómez-Pastora et al. 2018a, b).
Schematic of a horizontally stratified flow. Left—top view. Top right—side view. The two liquids enter the junction and interact at middle of the channel. A number of phenomena may occur at the interface depending on the liquids. If the liquids are solutions with different concentrations, there will be diffusion at the interface, which will show up as a triangle in the top view
Preceding work on this flow regime focused on characterizing the diffusion patterns. Ismagilov et al. (2000) presented equations, based on confocal microscopic images, to quantify the diffusion at the interface of this flow pattern as it relates to chemical patterning. They found that, once the flow reaches a steady state, the width of the reaction–diffusion zone adjacent to the channel wall and transverse to the flow direction scales with power one-third of both the axial distance down the channel from the initial contact line and the average velocity of the flow, rather than the more familiar one-half power scaling.
Yoon et al. (2005) were the first to report experimental evidence of a rotation of the interface between the two liquids, in the case of unequal solution densities. Their analysis showed that the reorientation of the streams depended only on the gravitational and viscous forces, and not on inertia. Yamaguchi et al. (2007) experimentally and numerically investigated the flow pattern when there is a density mismatch between the two solutions; they found that, in this case, the interface begins to rotate such that the heavier fluid sinks and the lighter fluid rises to the top, effectively altering the flow regime to a more stable pattern of vertical stratification. In this case, the difference between the buoyancy forces reinforces the separation of the two phases and the flow pattern. These authors also discussed how the shape of an interface varies depending on whether either diffusion or hydrodynamics of the flow is dominant, with the interface becoming more and more “S” shaped like as diffusion becomes more dominant.
The hydrodynamics of these flow regimes are recently reported to be complicated by a lateral flow dominated by the diffusion disparity between the two liquids. According to Heravi et al. (2021), once the two solutions come into contact with each other, the solution with the greater diffusion coefficient diffuses more rapidly than the opposing solution, immediately disrupting the delicate density homogeneity required to maintain a vertical interface. The solution with greater diffusivity hence becomes lighter and subsequently shifts toward the top through buoyancy forces, while the other solution sinks to the bottom. Another behavioral fact revealed in the previous investigation was that the rotation begins at the interface and is initially negligible far from it, but it slowly propagates to encompass the entire channel on traveling downstream. The combined effects of diffusion, dependence of density on concentration, and buoyancy forces hence lead to secondary flow of a new type, which rotates and deforms the interface, which in most cases would introduce undesirable inefficiency into the system.
Regarding the behavior and the characteristics of inhomogeneity-induced lateral flow (IILF), it is known that the axis of the rotation is the cross product of the direction of a vector pointing from the light to the heavy solution and gravity. As mentioned previously, two possible causes for IILF observed so far are diffusivity and/or density disparity. As mentioned before, lateral flow is central to many microfluidic applications, such as being the main method for passive particle separation, enhanced mixing, chemical reaction. Despite this, to best knowledge of the authors, no empirical or analytical model is available at this moment.
To predict the IILF effects, one must transcend the current understanding that is limited to the mechanisms leading to their formation and be able to predict its propagation throughout the channel and how it interacts and behaves in response to geometrical and operational changes. In the present work, it is hence attempted to provide insight into the hydrodynamics of the IILF through numerical and experimental investigations. The investigation encompasses vortices that might be generated in IILF and studies the effects of various geometric parameters and material properties.
First a base case, where the two solutes have equal density and are flowing in a straight channel of square cross section, is defined. In these conditions, the only cause for lateral flow must be diffusion. The diffusion across the centerline in the channel is unequal due to the difference between the diffusivity of the two solutes. Once an appropriate model is obtained for this aspect of the flow, it will be shown that lateral flow due to density difference between the solutions/pure liquids can also be explained by the same model. In fact, the lateral flow due to density difference is perfectly described by a reduced form of the basic model.
2 Methods and materials
2.1 Microfluidic device fabrication
The experiments were performed using microfluidics devices of polydimethylsiloxane (PDMS) on glass, with rectangular cross sections 100 μm × 100 μm at the inlets and 100 μm × 200 μm at the main flow channel at which the liquids meet. (The width in the main channel is twice the width of the inlets so as to focus the flow in the junction). The devices were molded using SU-8 molds fabricated with lithography on silicon wafers (100 mm). The type of SU-8 was 3050; the height of the channel dimensions was confirmed with a profilometer (and later revalidated from microscope images). The mask for the fabrication was designed in CAD and printed on a transparent film. The PDMS was made with a mixture (10:1) of Sylgard 184 types A:B.
2.2 Experimental setup
The liquid flow was created with a single syringe pump (KDS 200P Dual Syringe Infusion Pump, Kd Scientific) and two syringes (5 mL luer, Terumo). Safety-winged infusion tubings with luer connections (internal diameter 1.6 mm) served for the fluid connections. A spinning-disk fluorescent confocal microscope (AndorDragonfly 200, Oxford Instruments) and a sCMOS CCD camera (Andor Zyla5.5, Oxford Instruments) were used to capture digital images from the flow; the images were then formatted, sorted, and enhanced with Fusion® software from Andor and ImageJ.
2.3 Materials and chemicals
Two types of solutions were used. One consisted of doubly distilled water, urea (Scharlau) at varied concentration and green fluorescent particles (Fluoro-MaxG200B, ThermoFischer Scientific) of diameter 0.2 μm and emitting light at the 508 nm. The other consisted of doubly distilled water, sucrose (Scharlau) at varied concentration and red fluorescent particles (Fluoro-Max R200B, ThermoFischer Scientific) also of diameter 0.2 μ but emitting light at 612 nm. The fluorescent dyes were added at volumetric ratio 0.0025:1 to the solution. As reported (Yao et al. 2021), most nanoparticles diffuse into the PDMS walls and increase the background noise. For the purposes of this study, however, it was necessary to accept that fault as using small particles, such as commonly used fluorescent salts (Hejazian et al. 2020) presented their own set of challenges. Smaller particles would have diffused into both fluid phases and would show a less sharp interface between the fluids. Choosing large particles at 200 nm ensured that the diffusion coefficient would be multiples of magnitude less than the other solutes and eliminate error due to the diffusion of the fluorescent particles.
2.4 Governing equations
Considering all probable contributions to the two-phase dynamics, a numerical model was built, consisting of equations for mass transport, continuity, and momentum (including gravity) while accounting for variations in density, diffusivity, and viscosity due to changes in concentration. As the heat generation in relevant devices was negligible, the energy equation was mostly irrelevant and is routinely neglected in numerical investigations regarding relevant devices (Zhou and Papautsky 2020; Ren and Leung 2016; Chen 2018; Uspal et al. 2013). The conservation of mass is expressed with
in which ρ (kg m−3) and v (m s−1) represent density and velocity field, respectively.
Momentum was solved using the Navier–Stokes equation,
in which P (Pa) is static pressure, μ (Pa s) denotes viscosity, and g (m s−2) is the gravitational acceleration. The momentum equation was solved assuming weak compressibility conditions in COMSOL Multiphysics, which accounted for buoyancy forces but otherwise assumed incompressible conditions. The general form of mass transport equation is
in which c (mol m−3) represents concentration, D (m2 s−1) is diffusivity of the substances, and R is the source term for concentration. For the simulations in this part of the study, it was assumed no generation or consumption of species. The values corresponding to one of the two liquids are subscripted as either S or U representing sucrose and urea, respectively.
2.5 Material properties
The material properties and operational conditions are summarized in Table 1. The values of density, viscosity, and diffusivity were calculated for 20 °C and atmospheric pressure. In the present model, the dependence of these properties on concentration of solutes is of utmost importance, meaning that their values are not constant throughout the flow and depend on the partial concentration of both solutes. For this reason, it was important to choose substances that are thoroughly studied; otherwise it would be necessary to perform experiments to measure all properties for all relevant concentrations. Urea and sucrose are among the most commonly used materials; there are studies that provide values for their diffusivity, density, and viscosity for varied concentrations, temperatures, and pressures (Darros-Barbosa et al. 2003; Telis et al. 2007; Makarov and Egorov 2018; Sorell and Myerson 1982).
The values of diffusivity for various concentrations of both substances were taken from Sorell and Myerson (1982). In their results, the value of diffusivity decreased with concentration for both solutions. For urea, the decrease began linearly until near saturation at which point there is a sharp decrease. For sucrose, the initial slope was sharper; however, unlike urea, the slope softened as concentration increased.
3 Results
The baseline case has aqueous solutions of equal density 1.145 kg/cm3. The reason to choose this density as the base case is that, as it will be shown subsequently, the greater the concentration, the stronger the IILF. Hence, a density corresponding to just below the saturation level of solutes was chosen as the base case. This basic model was previously validated by the same team (Heravi et al. 2021). All other cases were studied relative to this base model, by varying one parameter at a time to isolate the intended effects.
3.1 Validation of numerical model
Before studying the flow, it is required to validate the model, which is achieved through Fig. 2. The figure shows orientation of the interface as measured in experiment versus the predictions made by numerical simulations of various mesh density. From the figure, it can be deduced that the model starts to become independent of mesh density above 300 k, after which point there are negligible changes observed in the results. Note, to improve accuracy and convergence, all variables were discretized on a quadratic basis with the exception of pressure which was based on linear discretization. Therefore, the total degrees of freedom modeled was close to one million. In addition, it can be seen that the model follows the trend of the experimental results fairly well, though it is typically slightly lower than the experiments. The maximum error is 20 percent while the average error is approximately 7 percent. The figure further demonstrates that the rotation is not linear with respect to time or location but rather follows a sigmoid shape. The shape of the curves follows the same pattern: they always begin at 0, corresponding to the initial horizontal stratification conditions; the rate of change then increases until 45° at which point the rate of change decreases; eventually the angle of the interface reaches 90°, corresponding to a vertical stratification pattern that is the stable form of this flow regime. 45° is always the inflection point for the rate of change. This pattern is seen in all cases, as will be shown in the next sections.
Validation of the numerical model. The figure shows the results for the orientation of the interface as obtained by experiment and numerical models of various mesh density. As can be seen, the model gets more accurate and more precise with increased mesh density until it reaches mesh independence threshold
3.2 Streamlines and vortices in IILF
Figure 3 shows the formation and evolution of the secondary flows in the channel. The secondary flow began to form directly after the two solutions came into contact. The diffusion-induced secondary flow as expected was such that the fluid with a smaller diffusion coefficient was pushed upwards whereas the fluid with a smaller diffusion coefficient sank to the bottom. The reason for this phenomenon was previously explained to be due to a distribution of density caused by this diffusion difference (Heravi et al. 2021). Figure 4 demonstrates the projected lateral flow streamlines at multiple distances from the inlet. These streamlines make evident that the IILF is always in the form of three vortices, with the middle vortex rotating counter to the other two vortices. Both at the beginning and near the end of the rotation, the middle vortex is stronger; however, than the other two, only this velocity vortex corresponds to the main concentration gradient (Fig. 3). These facts indicate that the main driving vortex is the vortex in the middle that causes the other two vortices and drives the lateral flow.
3.3 Deformation of the interface
An effective initial point is the formation of the secondary flow and the evolution of the shape of the interface and IILF streamlines as the fluids travel down the channel. In Fig. 5, notice the shape of the interface and projected streamlines at two hydraulic diameters (\(D_{h} \, = \,\frac{{area\,of\,cross - section}}{{Preimeter\,of\,Cross - section}}\)) from the inlet. The rotation begins directly upon contact of the two liquids and there is no noticeable delay between the solutions entering the channel and the onset of formation of secondary flow. Also, the interface is not always a straight line, and alters into a “S” pattern as soon as the rotation begins. The reason for the shape originates in the density distribution in the cross section. As reported by Ismagilov et al. (2000), because of wall effects, the diffusion zone broadens, with increased distance from the center of the channel. This effect subsequently results in disruption of density in the same pattern with more density mixing occurring near the walls; the strength of the IILF flow is hence stronger away from the center.
As mentioned above, the interface is not a straight line; in many applications what is important, however, is the position of the three-point lines, at which the wall and the two phases come into contact. Thus, for practicality, the interface is simplified as a straight line connecting the two three-point lines at any cross section normal to the flow direction. The angle of rotation is the angle between this line and the vertical axis (Fig. 5).
3.4 Empirical model for evolution of the interface
As this work is the first to attempt an analytical model, the first step is to find how various parameters affect the IILF hydrodynamics. To this end, experimental results for the effects of some parameters that affect the rotation of the flow are plotted against \({L}_{\pi /2}\) (the distance from initial contact at which the flow attains a horizontal condition (\(\theta =\frac{\pi }{2}\))) in Fig. 6. It can be seen that \({L}_{\pi /2}\) is proportional to velocity and the inverse of the square root of hydraulic diameter. While the relationship between velocity and distance being linear was expected, it could not be assumed to be trivial. After all, it is already demonstrated in Sect. 3.1 that the relationship between interface orientation and \(x\) is not linear.
Other parameters previously shown to be important in the flow regime are interdependent (e.g., density, concentration, and viscosity); it would be impracticable to isolate their effects and to find similar relations for them experimentally. This information was still suitable, however, as the basis to find a combination of dimensionless number group that correctly predicts the behavior of the angle of rotation.
Having tested multiple equation forms, it was found that the following sinusoidal form is an effective approximation for the results,
in which \(x\) is the distance from initial contact. Regarding this equation, only one parameter, \({L}_{\pi /2}\), is needed to plot the curves and to find the angle of rotation for any and all distance from the initial contact point. This model combined with the results from Fig. 6, regarding the relationship between velocity and \({L}_{\pi /2}\), provide a good reference point for an empirical model as it essentially allows separation of the model into two parts. One part governing the relationship between \(\theta\), \(x\), and \({L}_{\pi /2}\), describing the evolution of the model along the channel. While the other part provides a model for \({L}_{\pi /2}\) for various liquid–liquid systems, so that it can be used for other concentrations or solute systems.
For the aforementioned second part of the empirical model, after some trial and error, it was found that the following dimensionless group shows a remarkable proportionality to the results,
in which g is the gravitational acceleration, \(\beta\) is the coefficient of expansion \(-\frac{1}{\rho }\left(\frac{\partial \rho }{\partial {C}}\right)\), \({C}_{1}\) is the maximum concentration of the solution, \({C}_{0}\) is the minimum concentration of the solution (zero if each solute enters the channel from only one inlet), \({D}_{h}\) is the hydraulic diameter of the channel, \(\vartheta\) is the kinematic viscosity, \(\mu\) is dynamic viscosity, and \({L}_{\theta }\) is the distance from initial contact at which the flow rotates by \(\theta\). Here the dimensionless numbers \(Gr\) and \(Re\) are Grashof (mass transfer formulation) and Reynolds numbers which are defined as
To alter the proportional sign in Eq. (5) into an equal sign, it is required to multiply the right side with a constant, but it should also be noted in this particular case that there are two solutes in the solutions. It can be intuitively inferred from the flow pattern that the two solutes work in opposite directions (as also experimentally shown in the authors’ previous investigation Heravi et al. 2021), each diffusing into the other and creating IILF in opposite directions; any proposed model must consider their comparative differences. Rewriting Eq. (5) as an equality equation:
Here, subscripts a and b correspond to the separate inlet solutions; \(\alpha\) is the constant relating the dimensionless group to distance to rotate \(\theta\) degrees.
The observations on the relation between the left and right sides of Eq. (8) are presented in Fig. 7. The slope of the lines equals the value of \(\alpha\). For any given angle, the two sides show a linear relation as expected. Based on the obtained results, the best fit for \(\alpha\) at \(\pi /2\) is found to be 1.24. This value can be linearly scaled to generate \(\alpha\) for any other interface orientation; for example, \(\alpha\) for \(\pi /4\) and \(\pi /8\) are 6.2 and 3.1, respectively.
It is now possible to model the flow on finding the value for \({L}_{\theta }\) for any experimental setup from Eq. (8) and then inserting that value into Eq. (4). Figure 8 shows the results (interface angle \(\theta\) vs distance from initial contact line \(x\)) of such a model for baseline case. The results show an effective match between experiment and the proposed model for various operating conditions.
While the model was obtained based on a multicomponent system of equal supply-side density, Eq. (8) indicates that there is nothing in the model that prevents it from being used for a single component or equal-density system. In the case of only a single solute component, Eq. (8) is simplified to:
The model was tested on a system of aqueous sucrose solution–doubly distilled water and aqueous sucrose–urea solutions of unequal initial densities (Fig. 9); the model also fits tightly these experimental results, despite being originally obtained for diffusion-induced lateral flow in multicomponent systems. This implies that the model is valid for inhomogeneity-induced lateral flow in stratified flows, and is without limit on liquids flowing in a microchannel, or for an initial interface angle. This greatly increases the potential uses of the model without adding complicated extensions on top of the model.
4 Conclusion
Maintaining a stable interface in horizontally stratified flows on a microscale is a fundamental problem in microfluidics. This quasi-stable condition becomes easily disturbed from inhomogeneity in density or diffusion. The results of experimental flow visualization and numerical simulations of a liquid–liquid (aqueous urea and sucrose solutions) multiphase flow system in a horizontal stratification flow regime were presented. A fluorescent confocal microscope captured the hydrodynamics of the flow; the numerical simulation counterpart was undertaken with COMSOL Multiphysics.
The results revealed the dependence of the shape and strength of the IILF in square microchannels on Grashof and Reynolds numbers. It was shown that the distance required for full rotation (\({L}_{\pi /2}\)) is proportional to the Grashof number divided by the Reynolds number. Value \({L}_{\pi /2}\) was used to derive an empirical model for the angle of interface and any point along the channel. This model was shown to be capable of predicting the orientation of the interface for various conditions, such as when the liquids lack density equilibrium, or when one or both sides are pure substances.
The proposed model also opens the possibility to control or to stabilize the interface completely, through balancing the dimensionless number group of one side by the other. This aspect of the model can be of significant interest to the microfluidics engineering community, allowing an improved efficiency through extending a vertical interface or a possibility of new designs that take advantage of the ability to predict the interface orientation.
References
Atencia J, Beebe DJ (2005) Controlled microfluidic interfaces. Nature 437:648–655
Chen H (2018) A triplet parallelizing spiral microfluidic chip for continuous separation of tumor cells. Sci Rep 8:4042
Darros-Barbosa R, Balaban MO, Teixeira AA (2003) Temperature and concentration dependence of density of model liquid foods. Int J Food Prop 6:195–214
Gómez-Pastora J, González-Fernández C, Fallanza M, Bringas E, Ortiz I (2018a) Flow patterns and mass transfer performance of miscible liquid-liquid flows in various microchannels: Numerical and experimental studies. Chem Eng J 344:487–497
Gómez-Pastora J et al (2018b) Computational modeling and fluorescence microscopy characterization of a two-phase magnetophoretic microsystem for continuous-flow blood detoxification. Lab Chip 18:1593–1606
González Fernández C et al (2020) Continuous-flow separation of magnetic particles from biofluids: how does the microdevice geometry determine the separation performance? Sensors 20:3030
Hejazian M, Darmanin C, Balaur E, Abbey B (2020) Mixing and jetting analysis using continuous flow microfluidic sample delivery devices. RSC Adv 10:15694–15701
Heravi P, Chu L, Yao D-J (2021) Observation of a rotating interface in side-by-side flow of two aqueous solutions of equal density inside microchannels. Proc MicroTAS 2:2
Hossain S, Kim K-Y (2017) Optimization of a micromixer with two-layer serpentine crossing channels at multiple reynolds numbers. Chem Eng Technol 40:2212–2220
Ismagilov RF, Stroock AD, Kenis PJA, Whitesides G, Stone HA (2000) Experimental and theoretical scaling laws for transverse diffusive broadening in two-phase laminar flows in microchannels. Appl Phys Lett 76:2376–2378
Makarov DM, Egorov GI (2018) Density and volumetric properties of the aqueous solutions of urea at temperatures from T=(278 to 333) K and pressures up to 100 MPa. J Chem Thermodyn 120:164–173
Petersson F, Nilsson A, Holm C, Jönsson H, Laurell T (2005) Continuous separation of lipid particles from erythrocytes by means of laminar flow and acoustic standing wave forces. Lab Chip 5:20–22
Prabhakarpandian B et al (2013) SyM-BBB: a microfluidic blood brain barrier model. Lab Chip 13:1093–1101
Ren Y, Leung WWF (2016) Numerical investigation of cell encapsulation for multiplexing diagnostic assays using novel centrifugal microfluidic emulsification and separation platform. Micromachines 7:17
Sorell LS, Myerson AS (1982) Diffusivity of urea in concentrated, saturated and supersaturated solutions. AIChE J 28:772–779
Tarn MD, Lopez-Martinez MJ, Pamme N (2014) On-chip processing of particles and cells via multilaminar flow streams. Anal Bioanal Chem 406:139–161
Telis VRN, Telis-Romero J, Mazzotti HB, Gabas AL (2007) Viscosity of aqueous carbohydrate solutions at different temperatures and concentrations. Int J Food Prop 10:185–195
Uspal WE, Burak Eral H, Doyle PS (2013) Engineering particle trajectories in microfluidic flows using particle shape. Nat Commun 4:2666
Vicari F, Galia A, Scialdone O (2021) Development of a membrane-less microfluidic thermally regenerative ammonia battery. Energy 120:221
Xuan J, Leung MKH, Leung DYC, Wang H (2012) Towards orientation-independent performance of membraneless microfluidic fuel cell: Understanding the gravity effects. Appl Energy 90:80–86
Yamaguchi Y et al (2007) Influence of gravity on two-layer laminar flow in a microchannel. Chem Eng Technol 30:379–382
Yao J et al (2021) Optimization of PTFE coating on PDMS surfaces for inhibition of hydrophobic molecule absorption for increased optical detection sensitivity. Sensors 21:1754
Yoon SK, Mitchell M, Choban ER, Kenis PJA (2005) Gravity-induced reorientation of the interface between two liquids of different densities flowing laminarly through a microchannel. Lab Chip 5:1259–1263
Zhou J, Papautsky I (2020) Viscoelastic microfluidics: progress and challanges. Microsyst Nanoeng 6:113
Acknowledgements
The authors would like to thank Navid Aminnia and Keivan Faghih Niresi for their insightful comments and discussions.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Heravi, P., Chu, LA. & Yao, DJ. An empirical model for lateral flow in horizontally stratified flows. Microfluid Nanofluid 27, 4 (2023). https://doi.org/10.1007/s10404-022-02612-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10404-022-02612-5