Numerical investigation of heat transfer and mixing process phenomena inside a channel containing a triangular bluff body and elastic micro-beam: gap spacing and geometric characteristic effects

Abstract

In this paper, heat transfer and mixing quality enhancement is an original concept that has been studied using Vortex-Induced Vibration (VIV) as a passive method inside a straight two-dimensional channel. Effect of an elastic micro-beam oscillation that is located at different distances from a triangular bluff body is investigated on mixing process and heat transfer. Governing equations for fluid and solid domains with related initial and boundary conditions have been solved using the finite element method. Drag coefficient, Nusselt number, Strouhal number and beam tip displacement have been validated against published data with good agreement. The numerical results have been extracted for Re = 200 at dimensionless time t = 300. At the Re = 200, the vortex shedding behind the triangular cylinder is seen, and when the elastic beam is added to the channel at certain distances from the triangle, the oscillating vortices hit the beam and cause it to oscillate. Obtained results clarify that gap spacing mainly influences the vortex generation as well as mixing performance and heat transfer inside the channel. Using the flexible beam at G = 4b and 5b improves the mixing quality of the basic design by 7.7%, 12.4% and enhances the average Nusselt number by 2.87%, 6.14%, respectively. Finally, it has been concluded that while the beam oscillates freely without external force other than that exerted by the flow itself, using the current method illustrates a great potential for the performance enhancement of multifunctional heat exchangers/reactors.

1 Introduction

The fluid flow over bluff bodies with various cross-section shapes, such as rectangle, triangle, square, circle, and elliptic has been investigated for a long period due to its wide range of applications in real life, natural, and engineering systems. These systems include buildings, automobiles, pipelines, bridges, cooling towers, heat exchangers, gas turbine blades, marine risers, cooling systems in electronic components, space heating, probes and sensors, and so on (Bourguet et al. 2011; Jaiman et al. 2015; Tham et al. 2015; Gurugubelli and Jaiman 2015, 2019). The flow regime mainly depends on the geometry of the bluff body and the incoming Reynolds number. Generally, above a certain Reynolds number, the flow regime starts to be periodic and the Von-Karman vortex street in the flow downstream is created (Dash et al. 2019). This periodic regime produces a pressure drop and fluctuates unsteady forces such as lift and drag which are exerted on the bluff body. Therefore, understanding the boundary layer, shear layer, or the near wake region in the vortex shedding process is necessary (Lee et al. 2019).

Modeling of the flow structures over the bluff bodies helps to provide insight into the physical mechanism of flow pattern and fundamental concepts. As said before, locating of bluff bodies with different geometries in flow field plays an important role in mixing quality and heat transfer enhancement. There are two general ways to affect the flow pattern. Active and passive methods were proposed to control the unsteady wake region of a bluff body. Active methods rely on exerting external energy fields, whereas passive methods are associated with geometrical manipulations. Active control methods mainly include a heated cylinder (Lecordier et al. 1991), a vibrating cylinder (Koopmann 1967), and suction near the leading edge of the bluff body (Atik et al. 2005). On the other hand, splitter beam (Serson et al. 2014; Bearman 1965; Gu et al. 2012; Kwon and Choi 1996; Bao and Tao 2013), slits parallel to the incoming flow (Baek and Karniadakis 2009), fairings (Xie et al. 2015; Yu et al. 2015; Baarholm et al. 2015), moving boundary layer control (Korkischko and Meneghini 2012), helical strakes (Trim et al. 2005; Allen and Henning 2003), suction-based flow control (Chen et al. 2013; Dong et al. 2008), streamlining of the structural geometry (Corson et al. 2014; Pontaza and Menon 2008), and several other add-on devices (Bearman and Branković 2004; Owen et al. 2001) are examples of passive control methods. Using the splitter beam can be an effective passive method.

In the last decades, a large number of research projects have focused on vortex shedding suppression with a rigid splitter beam located behind a bluff body (Chauhan et al. 2018; Nakamura 1996) both experimentally and numerically. Rigid vortex generators are frequently used for mixing and heat transfer enhancement due to their ability in disrupting the boundary layers and generating complex coherent vortices that destabilize the flow. Various applications of this technique can be found in flow jets, chemical reactors, static mixers, heat exchangers and systems in which continuous process is needed. Some researchers widely considered the vortex shedding controlling using a flexible beam(s) instead of a rigid one due to its better aerodynamic performance (Shen et al. 2019; Sharma and Dutta 2020). The splitter beam delays the separation process. It can place in downstream or upstream of the bluff body. Also, it can be either detached or attached to the bluff body. In the attached case, the beam length plays a significant factor to control the flow. On the other hand, for the detached case both the beam length and the gap between the bluff body and splitter beam are important (Chauhan et al. 2017).

Recently, numerical and experimental researches have been carried out to study the effect of the flexible beams on the flow structures. Wang et al. (2018) numerically investigated the flow-induced vibration (FIV) of a flexible beam placed at the rear of a circular cylinder. They found two mechanisms producing the needed power of the beam to vibrate in both first and second bending modes. Shi et al. (2013, 2014) analyzed an aspect-ratio of 1.67 flexible polyethylene terephthalate membrane placed within the wake region of a square cylinder to find the influences of Re upon its energy distribution and consequence flapping behavior. Ryu et al. (2019) numerically studied the hydrodynamic characteristics of the flexible beam. They showed that the flow turbulence level depends on fluctuations of the stream-wise component of the velocity around the tip of the beam. Jin et al. (2018) experimentally used particle image velocimetry (PIV) technique for the flow characterization and particle tracking velocimetry (PTV) technique for tracking the tip of the wall-mounted flexible beam. Their results reveal that the natural frequency of the beam across various degrees of flexibility mainly influences the beam’s oscillations. Shukla et al. (2013) experimentally examined the response of a flexible splitter beam placed behind a circular cylinder. They concluded that parameters of the flow speed, splitter beam length, and beam rigidity (EI) are very important in the vortex shedding controlling process.

Usefian et al. (2019) studied the electro‑osmotic micro‑mixing of Newtonian and non‑Newtonian fluids numerically inside the micro channel and investigated the electric field effect on the mixing quality. Mixing of fluids has important and wide applications ranging from everyday used home appliances to high-tech industries such as cooling of the electronic devices, air conditioning, and refrigeration, aerospace, automotive, nuclear reactors, biology, etc. (Usefian et al. 2019; Jalili et al. 2020; MortezaBayareh and Ashani 2020; Soltanipour 2020; Bayareh 2020; Razeghi et al. 2016). Moreover, many researchers have paid remarkable attention to develop different methods in enhancing mass transfer in fluids. Among the proposed methods, vortex generators are deemed the most successful (Razeghi et al. 2016).

In this paper, numerical coupled fluid–structure interaction (FSI) simulations are used to investigate freely oscillating elastic beam in a two-dimensional (2D) channel flow and evaluate its ability in increasing mixing and heat transfer. Based upon the above discussion, it can be concluded that the fluid flow problem over a bluff body is one of the most important concepts in the fluid mechanics field. Also, the effect of elastic beam size and location inserted inside the flow field and near the triangular cylinder has rarely been studied, so in the present work, as a novelty, the heat and mass transfer enhancement has been investigated. The gap size between triangle and flexible beam, the length and thickness of the beam effects on the flow structure, heat and mass transfer have been simulated numerically using an FSI solver. Moreover, to validate the extracted results, the published data have been used.

2 Mathematical formulation

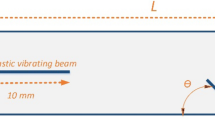
In the present work, a 2D laminar and incompressible flow is passing through a horizontal channel of height H and length ${X}_{u}+{X}_{d}$. The channel includes a triangular cylinder with a side size of b and a, flexible splitter beam with length l and thickness $\delta$ placed horizontally at the wake region with a gap distance of G from the cylinder. The tip of the splitter beam has been fileted. The triangular cylinder is positioned on the centerline of the channel at a distance ${X}_{u}$= 9b from inlet and ${X}_{d}$= 23b from the outlet. A schematic illustration of the physical model along with the corresponding nomenclature is given in Fig. 1a and b.

Fig. 1

a Schematic illustration of the elastic beam placed in the wake region of triangular cylinder (b) fluid and solid computational domains

2.1 Governing equations

2.1.1 Flow field

The incompressible fluid flow governs by the continuity equation and the Navier–Stokes (NS) equations.

Continuity equation:

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$

(1)

x-Momentum equation:

$$\frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = - \frac{\partial P}{{\partial x}} + \frac{1}{Re}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)$$

(2)

y-Momentum equation:

$$\frac{\partial v}{{\partial t}} + u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} = - \frac{\partial P}{{\partial y}} + \frac{1}{Re}\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)$$

(3)

2.1.2 Concentration field

The concentration field is governed by the convection–diffusion equation, which can be written as:

Mass equation:

$$\frac{\partial \emptyset }{{\partial t}} + u\frac{\partial \emptyset }{{\partial x}} + v\frac{\partial \emptyset }{{\partial y}} = \frac{1}{Re \cdot Sc}\left( {\frac{{\partial^{2} \emptyset }}{{\partial x^{2} }} + \frac{{\partial^{2} \emptyset }}{{\partial y^{2} }}} \right)$$

(4)

2.1.3 Temperature field

The temperature field is solved by the energy transfer equation, which is as follows:

$$\frac{\partial \theta }{{\partial t}} + u\frac{\partial \theta }{{\partial x}} + v\frac{\partial \theta }{{\partial y}} = \frac{1}{{{\text{Re}} \cdot Pre}}\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right)$$

(5)

In the above equations, the non-dimensional parameters, such as, longitudinal and transverse components of coordinates system (x, y), time ($t$), flow velocity (u, v), pressure (P), the mass fraction ($\mathrm{\varnothing }$), temperature ($\theta$), Reynolds number (Re), Prandtl number (Pr) and Schmidt number (Sc) are defined as:

$$x = \frac{x*}{b},\;y = \frac{y*}{b},\;t = \frac{{x*u_{\max } }}{b},\;u = \frac{u*}{{u_{\max } }},\;v = \frac{v*}{{v_{\max } }},\;p = \frac{p*}{{\rho u_{\max }^{2} }},\;\emptyset = \frac{{C - C_{0} }}{{C_{0} }},\;\theta = \frac{{T* - T_{\infty } }}{{T_{w} - T_{\infty } }},$$

$$Re = \frac{{bu_{\max } \rho }}{\mu },Sc = \frac{\mu }{\rho D},\;Pr = \frac{\mu Cp}{K}$$

where superscript * indicates the dimensional variables such as Cartesian coordinates (x*, y*), time (t*), velocity components (u*, v*), temperature (T*) and pressure (p*). The triangle width is b, ρ is density, μ indicates dynamic viscosity, and D refers to the diffusion coefficient. In this study, the values of Reynolds number and time is selected at which the flow regime over the triangular cylinder is fully periodic (Re = 200 and t = 300). In addition, diffusion of the momentum, heat, and mass are considered at the same rate (Pr = Sc = 1). The dimensionless physical properties of the elastic beam are assumed as $\frac{{\rho_{s} }}{{\rho_{f} }} = 1$ (density of the elastic beam), the $\frac{E}{{\rho_{s} *u_{{{\text{mean}}}}^{2} }} = 1400$ (Young’s modulus), and $v = 0.4$ (Poisson’s ratio).

2.1.4 Solid domain

To obtain the variables related to the solid domain, the structural dynamic equation is defined as follows:

$$\rho_{s} \frac{{\partial^{2} u_{s} }}{{\partial^{2} t}} = \nabla \cdot FS$$

(6)

In the above equation, u_s shows the displacement of the solid body, F is the deformation gradient tensor, and S is the second Piola–Kirchhoff stress tensor. F and S can be written as:

$$F = I + \nabla u_{s}$$

(7)

$$S = 2\frac{\partial W}{{\partial {\mathcal{C}}}}$$

(8)

where I is the unit tensor, W of the strain energy density and C indicate the Cauchy-Green deformation tensor, which is given as:

$${\mathcal{C}} = F^{T} F$$

(9)

There are different ways for modeling the elastic materials based on different strain energy densities (W). The present study uses the Neo-Hookean model, in which the density of strain energy is expressed as:

$$W = \frac{1}{2}\mu \left( {I_{1}^{{\mathcal{C}}} - 3} \right) - \mu Lnj + \frac{1}{2}\lambda (Lnj)^{2}$$

(10)

Here ${I}_{1}^{\mathcal{C}}$ is the first invariant of the C tensor, $\mu$ and λ are the Lam constants which are related to the modulus of elasticity and the Poisson’s ratio according to the following relations:

$$\mu = \frac{E}{2(1 + \upsilon )}$$

(11)

$$\lambda = \frac{\upsilon E}{{(1 + \upsilon )(1 - 2\upsilon )}}$$

(12)

In Eq. (10) j is the ratio of the beam volume at deformed state (V) to the beam volume at rest state (V₀), which is defined as the determinant of deformation gradient tensor (F):

$$j = \frac{V}{{V_{0} }} = Det\left[ F \right]$$

(13)

$$\left\{ {\begin{array}{*{20}c} {j > 1;} & {{\text{expansion}}} \\ {j = 1;} & {{\text{isochoric}}} \\ {j < 1;} & {{\text{contraction}}} \\ \end{array} } \right.$$

(14)

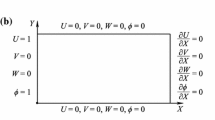
2.2 Initial and boundary conditions

2.2.1 Initial conditions

The following expressions are the initial conditions which are applied in present simulation:

$$u\left( {x,y,0} \right) = 0,v\left( {x,y,0} \right) = 0,P\left( {x,y,0} \right) = 0,\theta \left( {x,y,0} \right)\;{\text{and}}\;\emptyset \left( {x,y,0} \right) = 0.$$

(15)

Moreover, initial and maximum time steps are taken equal to 0.06 and 0.12, respectively.

2.2.2 Hydrodynamic boundary conditions

At the channel inlet, the fully developed laminar flow with the normal velocity of u is prescribed:

$$u=1-{\left(\left|1-2\times \left(\frac{y}{H}\right)\right|\right)}^{2}$$

(16)

Also, at channel outlet: “Neumann boundary condition” is applied:

$$\frac{{\partial u}}{{\partial x}} = 0{\mkern 1mu} {\text{ and }}{\mkern 1mu} \frac{{\partial v}}{{\partial x}} = 0$$

(17)

On the surface of cylinder and channel walls, “No-slip boundary condition” is enforced:

$$u = 0{\text{ and }}v = 0$$

(18)

2.2.3 Mass transfer boundary conditions

At the inlet, two fluids with different spices concentrations but the same properties enter the channel. Briefly:

From the upper half of the inlet channel:

$$C = 1\left( {{\text{mol}}.{\text{m}}^{ - 3} } \right)$$

(19)

From the lower half of the inlet channel:

$$C = 0\left( {{\text{mol}}.{\text{m}}^{ - 3} } \right)$$

(20)

At channel outlet:

$$\frac{\partial C}{\partial n}=0$$

(21)

On channel walls:

$$n \cdot \nabla C = 0$$

(22)

2.2.4 Heat transfer boundary conditions

The fluid with uniform temperature enters the channel and there is 5 K temperature difference between the channel walls (with constant temperature) and inlet fluid:

$${\theta }_{w}=1$$

(23)

$${\theta }_{\infty }=0$$

(24)

$$\Delta T={T}_{w}-{T}_{\infty }=5K$$

(25)

The thermal insulation boundary condition is imposed on the rigid barrier and the elastic beam:

$$\frac{\partial \theta }{\partial n}=0$$

(26)

At the channel outlet, the Neumann boundary condition for temperature is also selected:

$$\frac{\partial \theta }{\partial n}=0$$

(27)

2.2.5 Boundary conditions for the solid domain

On the flexible beam-fluid interface, the normal stress and the velocity fields are continuous:

$$u_{f} = u_{s} \;{\text{and}}\;v_{f} = v_{s}$$

(28)

$$\sigma_{f} \cdot n = \sigma_{s} \cdot n$$

(29)

where n is the normal unit vector to the interface. Furthermore, base of the beam (left side of the beam) is fixed (${u}_{s}={v}_{s}=0$).

3 Numerical method

The governing equations and related initial and boundary conditions that are specified mathematically by Eqs. (1) to (27) are solved numerically by the finite element method. To study the mesh independency in current work, four different finite element meshes, i.e. G1 (coarse), G2 (normal), G3 (fine), and G4 (finer) are employed. Computed results of the average drag coefficient, average Nusselt number and mixing quality for used elements numbers are summarized in Table 1. Figure 2. illustrated the vorticity contours for different grid resolutions to ensure that there is no artificial errors.It is found that the variations in parameters between G3 and G4 are negligible. Thus, the grid G3 is selected based on a detailed grid independence study to reduce the memory requirement and computational time. This mesh size has been used for both validations where the flexible beam is situated inside the horizontal channel. The dynamic mesh method has been employed in the current study which utilizes an unstructured mesh. Figure 3 illustrates the triangular unstructured mesh (grid G3) used to discretize the fluid and solid domains. Close-up views of the channel wall and the obstacles are also demonstrated in Fig. 3. To enhance the computational fluid dynamics (CFD) resolution, mesh concentration is arranged near the bluff body, flexible beam, and channel walls.

Table 1 Average drag coefficient, average Nusselt number and mixing quality versus the different number of elements

Fig. 2

Vortex contours for different grid

Fig. 3

Used mesh in current study

4 Validation

To verify the used simulation method in the current study, the obtained numerical results for the fluid flow passes over a cylinder has been extensively validated by Srikanth et al. (De and Dalal 2007) and De and Dalal (Srikanth et al. 2010). Furthermore, additional quantitative validation is performed for the flow passes over the circular cylinder with a flexible beam by Turek and Hron (Turek and Hron 2006). The average drag coefficient (${\overline{C} }_{D}$), Strouhal number ($St$) and average Nusselt number ($\overline{Nu }$) obtained in this work are compared with the results in De and Dalal (2007); Srikanth et al. 2010) that are listed in Table 2. The maximum computational error between the results in the values of the average Nusselt number is found to be about 3% for Re = 80. The beam displacement in x and y directions is illustrated in Fig. 4. According to results of Table 2 and Fig. 4, there is an acceptably good agreement between current results and those in references (De and Dalal 2007; Srikanth et al. 2010; Turek and Hron 2006).

Table 2 Comparison of the present results with those of references (De and Dalal 2007) and (Srikanth et al. 2010); drag coefficient, Strouhal number, and mean Nusselt number for Re = 80, 100 and 150

Fig. 4

Time histories of the displacements of the splitter beam tip in (a) x and (b) y-direction

5 Global quantities: mixing quality, local and average Nusselt number, mass and heat performance index

To investigate the mixing quality ($MQ$), the concentration distribution of fluid at the channel exit is needed. Equation 4 indicates the mixing quality of the channel at the exit section (Fallah et al. 2020),

$$MQ=1-CV$$

(30)

$$CV=\frac{1}{{C}_{\mathrm{mean}}}{\left[\frac{\sum_{i=1}^{m}{({C}_{i}-{C}_{\mathrm{mean}})}^{2}}{m}\right]}^\frac{1}{2}$$

(31)

Here, ${C}_{i}$ is the concentration of mixed fluid at the $i$th grid element and $m$ denotes the number of data points in the lateral direction of the channel, and ${C}_{\mathrm{mean}}$ is the fully mixed concentration of fluid which is 0.5. The value of zero for $MQ$ indicates no mixing, whereas the value of 100% means complete mixing. The value of $MQ\ge 95\mathrm{\%}$ is usually acceptable for most applications (Karimi et al. 2021; Bahrami et al. 2020).

For evaluation of the heat transfer between the heated walls of the channel and working fluid, the Nusselt number has been formulated as:

$$Nu=\frac{hH}{k}=-\frac{\partial \theta }{\partial n}$$

(32)

where $h$ is the local heat transfer coefficient, $k$ is the thermal conductivity of the fluid, and $n$ is the direction normal to the channel walls. The average Nusselt number is governed by integrating the local Nusselt number along the channel walls:

$$\overline{Nu} = \frac{{\overline{h}H}}{k} = \frac{1}{S}\int_{S} Nu \cdot dS$$

(33)

$$\overline{h }=\frac{Q}{S({T}_{w}-{T}_{\infty })}$$

(34)

where, $\overline{h }$ is the average heat transfer coefficient over the channel surface, $S$ is the heat transfer surface area of the channel per unit length, $Q$ is the total heat transfer rate on the whole surface of the channel.

Mass performance index (γ) and thermal performance index ($\alpha$) are important factors for the overall assessment of the effect of inserting a flexible beam behind the triangular cylinder on the simulation results. These parameters can be used for comparing and selecting the best cases in terms of mass and thermal performance between different studied cases. The following equations are used to obtain the mass and thermal performance index:

$$\gamma = \frac{{MQ_{j} /MQ_{0} }}{{\left( {\Delta P_{j} /\Delta P_{0} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}$$

(35)

$$\alpha = \frac{{\overline{Nu}_{j} /\overline{Nu}_{0} }}{{\left( {\Delta P_{j} /\Delta P_{0} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}$$

(36)

where subscript of $j$ corresponds to cases with flexible beam and subscript of 0 to the case without the flexible beam. Understanding the value of the dimensionless pressure drop is important. The dimensionless pressure drop is defined as:

$$\Delta P=\frac{\Delta {P}^{*}}{{\rho }_{f}{u}_{\mathrm{max}}^{2}}$$

(37)

In the above equation, ΔP^* denotes the pressure drop (Pa), ${\rho }_{f}$ refers to fluid density (Kg/m³) and ${u}_{\mathrm{max}}$ is the maximum fluid velocity at the inlet (m/s). To calculate ΔP^*, the pressure difference between the inlet and outlet of the channel is obtained.

6 Results and discussions

In this section, the influence of gap spacing between triangular cylinder and elastic beam on flow behavior, mixing quality and heat transfer will be presented. Moreover, the effect of geometrical characteristics of the elastic beam on mass and heat transfer will be discussed. Once the best gap spacing range is obtained, the effect of thickness and length of the elastic beam variation on the flow parameters, mixing quality and heat transfer will be studied.

6.1 Effect of gap spacing varying

According to previous discussions, the gap spacing between bluff body and splitter beam as well as the Reynolds number have significant effects on the flow pattern. Thus, supplementary simulations have been performed within the wide spacing range G = 0, b, 2b, 3b, 4b, and 5b for Re = 200 and dimensionless time t = 300 in this study. Figure 4 shows the vorticity contours and streamlines for different gaps between cylinder and beam. As shown in Fig. 5, for the case without beam, the flow that passes the rigid triangular body is periodic and the Von-Karman vortices are created in the wake region. By inserting the elastic beam and placing it at different distances from the triangular cylinder, it can be seen that the flow pattern changes significantly. For G = 0, 4b and 5b cases, the flow field after the triangular cylinder includes vortices which leads the flexible beam to vibrate. But for G = b, 2b and 3b it is observed that the separated vortices from the triangular body envelop the elastic beam, however, no vortex shedding appears and flow regime inside the channel remains steady state.

Fig. 5

Streamline and vorticity contours of fluid flow over the triangular cylinder and flexible beam at various gap spacings for Re = 200

To better understanding, the maximum tip displacement of the elastic beam in the vertical direction and the frequency of the oscillating beam associated with the gap spacing are given. As shown in Fig. 6, maximum tip displacement and a maximum frequency of oscillating elastic beam occur when G = 0, 4b and 5b. The orbital trajectories of the beam tip at the various gap spacings of the elastic beam from the rigid body are plotted in Fig. 7.

Fig. 6

a Vibration amplitudes and b vibration frequencies of the flexible beam tip

Fig. 7

Trajectories of the beam tip at different gap spacings

Figure 8 illustrates the variations of the average and maximum Von-Mises stress (on the cylinder surface) versus dimensionless time for different gap spacings. The minimum pressure on the beam appears when G = 0. Although the maximum Von-Mises stress exerted on the elastic beam for G = 4b and 5b is almost the same, the average Von-Mises stress for G = 4b is higher than the others. The maximum stress is about 0.28 MPa which is much less than the yield stress of 2.4 MPa. Thus, it can be anticipated that employed elastic beam in current work is in the safe design zone and it would not experience failure.

Fig. 8

a Average and b maximum Von-Mises stress variation versus dimensionless time

To study the mixing performance, the inlet of the channel is divided into two equal parts and the fluid enters the channel with two different concentrations. Concentration contours for gap spacing range of 0 ≤ G ≤ 5b are shown in Fig. 9. Since the flow regime changes from periodic to laminar in G = b, 2b and 3b cases, the mixing is not performed in these cases.

Fig. 9

Concentration contours for various gap spacings at Re = 200 and t = 300

Figure 10 shows the lateral distribution of concentration at the channel outlet. It is observed that the concentration distribution varies significantly between the two walls of the channel from 0 to 1 (these magnitudes refer to no mixing). If the mixing quality tends to 0.5, it means that fluids are being mixed better. However, to have a more rigorous decision on the most efficient design, a mixing efficiency coefficient needs to be defined. In the gap spacings of G = 4b and 5b, the dimensionless concentration is about 0.4–0.6, which shows that the mixing is greatly enhanced. This improvement is because of the oscillation of the flexible beam associated with the vorticity generation as shown in Fig. 5. As expected, the concentration distribution at the channel outlet is more uniform where the flexible beam is situated at the gap spacings of 4b and 5b.

Fig. 10

Concentration distribution at a lateral distance of channel outlet for various gap spacings

The mixing quality (MQ) and the dimensionless pressure drop are given for the channel containing the triangular cylinder with and without elastic splitter beam in Table 3. As can be seen, by adding the elastic beam at the gap spacings of 0, b, 2b, and 3b, the pressure drop decreases significantly compared to the case without the elastic beam. For the other two cases (G = 4b and 5b), the pressure drop slightly increases, and also the mixing has been improved compared to the case with no splitter beam.

Table 3 Mixing quality and dimensionless pressure drop for different gap spacings

Generally, the efficient structures (G = 4b and 5b) provide the best mixing quality of 90.8 and 95.5, respectively while the typical channel (with no splitter beam) has mixing quality of 83.1%. This is attributed to the vorticity generation and also perturbation in the interfacial area of the fluids.

According to the definition of the mass performance index and the values of mixing quality and pressure drop presented in Table 3, the values of the mass performance index for all gap spacing ranges are given in Table 4. Obtained results show that G = 4b and 5b cases have a better mass performance index. Therefore, these cases can be proposed as the best cases in terms of better mixing performance. From the above discussions, it is observed that G = 5b is the best case in terms of the mass performance index. For this purpose, the effect of increasing and decreasing the thickness and length of the elastic beam will be performed for the case of G = 5b in the rest of this study.

Table 4 The mass performance index for various gap spacing ranges

Figure 11 is a schematic illustration of the thermal boundary conditions. It should be said that the Nusselt number is calculated from X = 8b to the channel outlet.

Fig. 11

Thermal boundary conditions in current study

The local Nusselt number distribution for the upper wall of the channel is illustrated in Fig. 12. The corresponding vorticity and temperature contours are also demonstrated in the figure at dimensionless time t = 300. According to the local Nusselt number variations, the maximum Nusselt values occur where the vortex cores is being produced in the weak region which is arising from the reduction of the thermal boundary layer thickness. On the other hand, the minimum local Nusselt number points coincide with stream-wise situations of walls shear layers which leads to the thicker thermal boundary layer. By placing the elastic beam behind the cylinder (G = 0), we see a decrease in the fluctuations of the local Nusselt diagram, which is due to the reduction of the vortex power formed behind the cylinder. For the states G = b, 2b and 3b due to the non-oscillation of the flow, there will be only one peak on the local Nusselt variation due to the proximity of the flow lines around the cylinder. By vibrating the elastic beam in cases with G = 4b and 5b, the vortices created behind the triangular bluff body move toward the channel walls and cause significant oscillations in the Nusselt number plot.

Fig. 12

Stream-wise fractionation of the immediate local Nusselt number on the upper channel wall at the specified time of t = 300, along with temperature and vorticity contours

To investigate the effect of the elastic beam location on the heat transfer through the channel more precisely, the average Nusselt number is given in Table 5. The cases with G = 4b and G = 5b improve the average Nusselt number compared with case without an elastic beam (about 2.87% and 6.14% respectively). Table 6 show that the best thermal performance is related to the state G = 5b.

Table 5 Average Nusselt number and dimensionless pressure drop for different gap spacings

Table 6 The thermal performance index for various gap spacing ranges

6.2 Effect of the geometric characteristics of the elastic beam

The investigated elastic beam has the geometric characteristics of l/b = 2.5 and δ/b = 0.125 namely model 2. Table 7 shows the various cases with different geometric characteristics (when G = 5b). Figures 13 illustrates the vorticity contours and streamlines for different beam thicknesses and lengths for Re = 200 and t = 300. At first, it can be seen that the thickness and length of the elastic beam variation do not affect the flow regime around the cylinder and the flow remains periodic. Also, the numerical results indicate that for all models, the oscillation frequency of the elastic beam did not change much and for all models is almost equal to 4.733 (1/s).

Table 7 Geometrical characteristics of the elastic beam (thickness and length)

Fig. 13

Vorticity and streamline contours for different beam thicknesses and lengths when Re = 200 and t = 300

Figure 14 shows the maximum displacement of the elastic beam tip for different thicknesses and lengths. As shown in Fig. 14, the maximum amplitude of the lateral oscillations of the elastic beam tip at constant length occurs when δ/b = 0.1. On the other hand, at constant beam thickness, the maximum displacement occurs when l/b = 2.25.

Fig. 14

Maximum displacement of the elastic beam tip versus beam (a) thickness and b length

The orbital trajectories of the beam tip at the constant length and variable thickness of the beam are plotted in Fig. 15. According to Fig. 15, the maximum lateral oscillations of the elastic beam tip are related to the lowest value examined for thickness ($\delta$ = 0.1b). Also, due to the direction of movement of the beam tip in the x and y directions, as the thickness of the beam increases, the oscillations of the beam tip in both directions become more limited. Also, the orbital trajectories of the beam tip at the constant thickness and variable length of the beam are plotted in Fig. 16. It shows the maximum lateral oscillations and the path of the elastic beam tip in the x and y directions for the different lengths of the beam. By keeping the beam thickness constant and changing its length, results show that the maximum amplitude of the lateral oscillations in model l = 2.25b is greater than the other models.

Fig. 15

Trajectories of the beam tip for various beam thicknesses

Fig. 16

Trajectories of the beam tip for various beam lengths

Figure 17 indicates the variation of the maximum Von-Mises stress (on the surface of the beam) versus time. The extracted results are related to the case in which the distance of the beam from the cylinder is constant but the beam thickness varies. It is clear that by increasing the beam thickness, the value of Von-Mises stress grows up. Also, Fig. 18 shows the variations in the maximum Von-Mises stress (on the surface of the beam) while the beam thickness is constant and the beam length is variable. Results reveal that the value of the maximum stress on the beam surface is related to the minimum length of the elastic beam.

Fig. 17

Maximum Von-Mises stress variation versus time for different beam thickness

Fig. 18

Maximum Von-Mises stress variation versus time for different beam length

Tables 8 and 9 give us a quick look to see the effect of the thickness ($\delta /b$ = 0.1, 0.125, 0.15 and 0.175) and length (l/b = 2, 2.25, 2.75 and 3) of the flexible beam on the concentration field and the mixing quality at the channel outlet, respectively. As observed from the mixing quality at the outlet cross-section of all cases in Table 8, decreasing the thickness of the flexible beam significantly improves the mixing performance. The mixing quality increases from 91.59% to 95.95% as the beam thickness decreases from 0.175b to 0.1b. Moreover, the smooth concentration profile at the channel outlet can be seen in Fig. 19a for 0.175b. Furthermore, for different l/b ratios, the lowest mixing quality value is related to the maximum beam length.

Table 8 Concentration contours and mixing quality values for various beam thickness

Table 9 Concentration contours and mixing quality values for various beam length

Fig. 19

Concentration distribution graph at the channel outlet for various beam (a) thickness and b length

Figure 19 shows the variations of dimensionless concentration at the channel outlet for various beam thicknesses and lengths. The concentration varies around the value of 0.5 at the channel outlet for all models. But for the cases with δ = 0.1b and l = 2b the concentration distribution is smoother and closer to the value of 0.5 which confirms the good mixing in these cases.

Figure 20 demonstrates the local Nusselt number variation on the upper wall of the channel for different thicknesses and lengths of the elastic beam along with the temperature and vorticity contours at t = 300 and G = 5b. The results of Fig. 20 reveal that the created vortices behind the triangular bluff body are divided into the two separated vortices when they collide with the elastic beam. As discussed before, these vortices move toward the upper and/or lower walls and destroy the boundary layer at those regions. This process causes oscillations in the Nusselt number plot. The effect of thickness and length of the beam variation on heat transfer has been presented in terms of the average Nusselt values in Table 10. As the length of the elastic beam increases, the value of the average Nusselt number also enhanced due to oscillations of the beam tip, as shown in Fig. 16. Model 7 has the highest average Nusselt number value and improved the heat transfer by about 7.46% compared to the model with no elastic beam.

Fig. 20

Stream-wise fractionation of the immediate local Nusselt number on the upper channel wall for different length and thickness of elastic beam at t = 300 and G = 5b, along with temperature and vorticity contours

Table 10 Average Nusselt number for different length and thickness of elastic beam when G = 5b

Figure 21 illustrates the variation of dimensionless pressure drop versus beam thickness and length. It reveals that by increasing the beam length, the dimensionless pressure drop increases but the pressure drop shows a chaotic trend for the beam thickness. Figure 22 depicts the variation of mass and thermal performance indices versus beam thickness and length. By increasing the beam thickness and/or length, the mass performance index decreases. The optimized model based on the mass performance index is related to the model 1 with geometrical characteristics of δ = 0.1b and l = 2.5b. On the other hand, the thermal performance index shows a chaotic trend for the elastic beam length. The best model in terms of thermal performance index is model 7 with geometrical characteristics of δ = 0.125b and l = 2.75b.

Fig. 21

Dimensionless pressure drop along the channel for various beam thickness and length

Fig. 22

a Mass performance index and b thermal performance index for various beam thickness and length

7 Conclusions

In this research, the Vortex-Induced Vibration (VIV) method is proposed to increase the heat and mass transfer inside a 2D channel. First, the effects of elastic beam placement at six different distances from the triangular bluff body on the fluid flow and solid fields, local and average Nusselt number, mixing quality, pressure drop along the channel length, and finally thermal and mass performance indices are investigated. The results show that the location of the elastic beam remarkably affects the flow regime inside the channel. At distances G = b, 2b and 3b the fluid flow at the Reynolds number 200 does not become periodic. By placing the elastic beam at intervals of G = 4b and 5b, the heat transfer and mixing quality improves. In the following, it was shown that in the optimal distance, by changing the thickness and length of the elastic beam, the thermal and mass parameters change and amidst the different thicknesses and lengths of the elastic beam, the best models in terms of mass and thermal performance are given. For future work, the effects of changes in the physical properties of the structure, the three-dimensional consideration of the problem and the investigation of the problem in different Reynolds numbers are going to be studied.