Multiple interactions between microfluidic droplets and on-chip pneumatic valves

Abstract

Microfluidic droplet arrays potentially allow to carry out assays involving complex workflows at the single-cell level. In recent developments [e.g. (Jeong et al. in Lab Chip 16:1698, 2016)], each droplet of the array can be addressed individually thanks to on-chip pneumatic valves. In this experimental and theoretical work, we investigate the multiple interaction regimes between one or several droplets and a pneumatic valve. In particular, two main trapping modes are characterized, with very distinct flow features. We quantify the potentially huge increase of hydrodynamic resistance induced by the droplet/valve interaction. Finally, we rationalize the main transitions between trapped and non-trapped regimes through a generic theoretical model of the balance between capillary, hydrodynamic and elastic forces.

1 Introduction

Droplet microfluidics has emerged two decades ago as a miniaturised and potentially reusable alternative to microtiter plates for life science assays. The biological samples (e.g. cells, analytes, barcodes) are loaded in aqueous solutions that are then partitioned into sub-nanoliter droplets immersed within an immiscible oil phase (Shang et al. 2017). As long as the affinity of the samples for the oil is marginal (Mary et al. 2008), each droplet behaves as an individual microreactor that can host an independent assay without significant risk of cross-contamination. Droplets can be transported and screened sequentially, sorted (Ahn et al. 2006; Agresti et al. 2010; Mazutis et al. 2013), merged (Niu et al. 2008) and split (Link et al. 2004) almost at will through the channel networks of microfluidic chips.

Most of these operations can be performed individually with throughputs that reach a few thousand droplets per second (Baret et al. 2009). However, many assays require incubating the biological material for minutes to hours in between operations. When the number of droplets is of the order of thousands or more, on-chip incubation is only possible for a few minutes through delay lines (Frenz et al. 2009). Longer incubation on larger droplet populations must be performed off-chip and the droplets have then to be re-injected in another chip for further processing (Agresti et al. 2010; Brouzes et al. 2009). In either case, the order of the droplets cannot be preserved, the emulsion may be subjected to stability issues, and the addition of reagents to each droplet after incubation requires non-trivial synchronisation (Kaminski and Garstecki 2017). By contrast, when the assay can be limited to a few hundreds of droplets, the latter can be trapped and incubated on-chip in droplet arrays, which alleviates much of the aforementioned challenges (Amselem et al. 2016; Sart et al. 2017; Zhang et al. 2018b). Droplet arrays have been successfully used to assemble cells in spheroids (Sart et al. 2017). Moreover, each trap may welcome several droplets and possibly pair droplets from different populations (Jin et al. 2015; Chung et al. 2017; Tomasi et al. 2020). The droplets of each trap are then prompted to merge, which allows to perform cell assays (Tomasi et al. 2020; Saint-Sardos et al. 2020), to screen cell communities (Kehe et al. 2019) or to investigate cell–cell interactions (Jin et al. 2017). Cell culture over several days is possible by transforming the droplet into an hydrogel bead and subsequently substituting the carrier oil with culture medium (Sart et al. 2017). Several lipid phases can also be flushed around the trapped droplets to form synthetic cell membranes (Matosevic and Paegel 2013).

There are several ways to trap droplets at dedicated locations on-chip, e.g. thanks to buoyancy (Labanieh et al. 2015; Segaliny et al. 2018), valve-induced flow stopping (Leung et al. 2012; Babahosseini et al. 2019; Rho and Gardeniers 2020) or capillary forces. The latter are induced by a change of confinement. In most droplet-based microfluidic chips, droplets are squeezed in between microchannel walls: their volume is too large to allow them to take a spherical shape. Consequently, any modification of this squeezing results in a change of interfacial energy, and thus in a capillary force on the droplet. A repulsive force can prevent droplets from entering narrow channels where they would have to squeeze more (Huebner et al. 2009; Zhang et al. 2018a). Conversely, an attractive force can retain droplets in wider cavities where they would be squeezed less (Schmitz et al. 2009; Abbyad et al. 2010). After incubation, droplets may be released altogether from a capillary trap by either reversing the flow direction (Boukellal et al. 2009; Huebner et al. 2009; Xu et al. 2012) or by increasing the flow speed of the continuous phase and subsequent hydrodynamic force on the droplets (Abbyad et al. 2010; Dangla et al. 2011; Nagel et al. 2014). One incoming droplet can sometimes push another one out of the trap, which then behaves as a buffer for the droplets (Abbyad et al. 2010; Korczyk et al. 2013; Schmitz et al. 2009). By contrast, the release of specific droplets (e.g. those in which an assay would optically be detected as positive) requires some addressing of each individual trap. For example, the selected droplets may be released one at a time, thanks to the thermocapillary flows induced by the local heating of a focused laser beam (Fradet et al. 2011).

Pneumatic valves are thin membranes that locally replace channel walls (Unger et al. 2000; Abate et al. 2010). Depending on the applied transmembrane pressure, the membrane deflection narrows or enlarges the local channel cross section. Therefore, pneumatic valves can change the geometry and resulting capillary force of each individual trap (Brouzes et al. 2014; Jin et al. 2015; Padmanabhan et al. 2017; Jeong et al. 2019), thereby controlling droplet capture and release. In addition, pneumatic valves can be used to tune droplet formation (Abate et al. 2009; Lee et al. 2009) or even to form droplets on demand (Lin and Su 2008). Other on-chip valves, e.g. thermoactuated (Miralles et al. 2015) may have the same abilities. The modification of hydrodynamic resistance induced by a closed valve allows to control droplet trajectories at bifurcations (Abate et al. 2010; Chen et al. 2016; Han et al. 2009; Hamidovic et al. 2019). Large droplets encountering a partially closed valve may be split into several parts (Choi et al. 2010; Yoon et al. 2013; Raveshi et al. 2019; Sun et al. 2019). Valves can also promote the merging of successive droplets (Lin and Su 2008; Jamshaid et al. 2013; Yoon et al. 2014) without the need to synchronising them (Mazutis 2012). In comparison with off-chip valves, on-chip valves have much smaller dead-volumes (Kaminski and Garstecki 2017) and they can be integrated in much larger numbers [e.g. a hundred valves in Jeong et al. (2019)]. Individual valve addressing allows fine control on droplet operations and reprogrammability of workflows (Jeong et al. 2016, 2019; Rho and Gardeniers 2020), in a similar way to EWOD (electro-wetting on dielectric) systems. By comparison with the latter, droplet traps may deal faster with a larger number of smaller droplets while avoiding fouling issues (Kaminski and Garstecki 2017), but special care must be taken to prevent unwanted droplet pervaporation through the thin PDMS membrane (Huebner et al. 2009; Salmon and Leng 2010).

Despite this promising early work on droplet microfluidic systems controlled with pneumatic valves, the myriad of possible interactions between droplets and valves remains poorly described. These interactions involve a complex interplay of capillary, hydrodynamic and elastic forces. The corresponding physical models, required for the design of such systems, are still lacking. This experimental and theoretical work aims at providing a physical description of the different interaction regimes, and localising their boundaries in the parameter space. The experimental setup is described in Sect. 2. The main experimental results are presented in Sect. 3. Finally, the theoretical model that rationalises these results is developed in Sect. 4. This model may serve as a tool for the early design of microfluidic chips involving droplets and pneumatic valves. Indeed, it approximately predicts the regime of interaction between droplet and the membrane as a function of the relevant physical parameters and dimensions, without any need for calibration.

2 Experimental setup

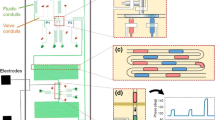
The design of the microfluidic chip is represented in Fig. 1. It consists of two patterned PDMS layers (one for the droplet channels and one for the pneumatic channels) separated by a thin PDMS membrane. The PDMS layers are fabricated by conventional soft-lithography from a negative SU8-2050 master (van Loo et al. 2016). The PDMS channels of the droplet layer are initially coated with Aquapel to prevent the contact between the water droplets and the PDMS channel walls. The thickness of the microchannels $H \simeq 30 \pm 2$ $\upmu$m corresponds to the thickness of spin-coated SU8. The membrane of thickness $h = 8 \pm 1$ $\upmu$m is obtained by directly spin-coating 2.5 g of PDMS on a 4$''$ silicon wafer. The nominal channel width is $W \simeq 0.1$ mm.

The chip comprises two liquid inlets (water and oil) and two liquid outlets (selection and waste). Both inlets feed an emulsification junction (flow focusing), from which the produced droplets flow down to a bifurcation that leads to either the waste outlet or the selection outlet. The length of the channels from the emulsification junction to the bifurcation, from the bifurcation to the selection outlet, and from the bifurcation to the waste outlet, are respectively $L_{\mathrm{u}} = 31.8$ mm, $L_{\mathrm{s}} = 70.6$ mm, and $L_{\mathrm{w}} = 12.2$ mm. At the bifurcation, the droplets are guided in either selection or waste branch in response to the activation of pneumatic valves. A by-pass (Cristobal et al. 2006) immediately downstream of the bifurcation allows the valve activation to significantly modify the local flow rate and direct the droplets accordingly, independently of the hydrodynamic resistance of channels further downstream. The by-pass comprises micro-pillars separated by channels of width 30 $\upmu$m that prevent droplets from switching branch in normal operating conditions. Downstream of the by-pass, the selection branch comprises another pneumatic valve referred as the valve of interest, since this paper focuses on the interaction of droplets with that specific valve. The pneumatic layer comprises three pneumatic channels that do not overlap the droplet channels, except at their dead-end where each of them forms a pneumatic valve of length $L_{\mathrm{v}}$.

The chip is positioned horizontally and observed from the top with a high-speed camera (Photron Fastcam Mini UX100) mounted on a stereo-microscope (Zeiss Discovery v12), providing a field of view of about 4 mm by 3 mm (Fig. 1b) and a resolution of about 3 $\upmu$m per pixel. Movies are recorded at either 125 of 250 frames per second. The position x and length $L_{\mathrm{d}}$ of each droplet in the longitudinal direction are measured on each frame thanks to custom-built image processing in Matlab. As the resolution is critical to the measurement of distances, it is determined on each recording with an accuracy of 0.3%.

Both liquid inlets are connected from above to reservoirs pressurised independently by pressure controllers (Fluigent MFCS-EZ) of accuracy 1 mbar and observed response time of the order of one second. The reservoirs are placed at approximately the same height as the chip ($\pm 1$ cm) so the error induced by the hydrostatic pressure is also of the order of 1 mbar. The water reservoir contains DI water while the oil reservoir is filled with a mixture of fluorinated oil HFE-7500 (3M Novec) and 0.5% (w/w) Fluosurf surfactant (Emulseo). The dynamic viscosity is $\mu _{\mathrm{w}} \simeq 10^{-5}$ mbar s for water and $\mu _{\mathrm{o}} \simeq 1.3 \times 10^{-5}$ mbar s for oil. The measured interfacial tension is $\sigma \simeq 0.17$ mbar mm.

The pneumatic valves are also pressurised with a separate line of the pressure controller. This pressure $p_{\mathrm{v}}$ can be switched on/off independently in each pneumatic line thanks to a solenoid valve (FESTO MH1, normally closed). The solenoid valves are actuated with a digital controller (WAGO 750-881 and 750-530) interfaced with Labview. The observed response time of the pneumatic valves is of the order of 10 ms (closing) to 20 ms (opening) and it is mostly due to the hydrodynamic capacitance of both PDMS layers and tubings.

Fig. 1

a CAD design of the microfluidic chip. The first layer (black) contains the channels that transport the liquids (oil, water and subsequent emulsion). The second layer (magenta) contains the pneumatic channels. b Microscope view on the zone in the dotted red box in a. The thick arrows indicate the direction of the flow. The dotted black box corresponds to the zone shown in the snapshots of the subsequent figures (colour figure online)

Many parameters may influence the droplet/valve interaction: the fluid properties $\mu _{\mathrm{o}}$, $\mu _{\mathrm{w}}$, $\sigma$, the membrane thickness h, length $L_{\mathrm{v}}$ and elastic parameters, the channel dimensions W and H, the droplet length $L_{\mathrm{d}}$ and speed v, and the pneumatic pressure $p_{\mathrm{v}}$. Among them, we chose to vary four parameter that are key to the interaction: the valve length $L_{\mathrm{v}} \in \{300, 600\}~{\upmu }{\mathrm{m}} = \{3W, 6W \}$, the valve pressure $p_{\mathrm{v}} \in [0, 1000]$ mbar, the droplet length $L_{\mathrm{d}} \in [59, 280]~\mathrm{\mu m} = [0.59 W, 2.8W]$, and the droplet speed $v \in [0.06, 3.2]$ mm/s. The range of these parameters has been chosen in order to browse different regimes. It could be extended in future experimental investigations. The last two parameters are measured a posteriori; they vary together with controlled variations of inlet water pressure $p_{\mathrm{w}} \in [77, 236]$ mbar and inlet oil pressure $p_{\mathrm{o}} \in [70, 217]$ mbar. All the pressures are expressed relatively to the atmospheric pressure. The droplet speed v refers to the speed of all the droplets that are in the selection channel but sufficiently far from the valve (either upstream or downstream). It is assumed to be close to the average flow speed in the channel (Jakiela et al. 2011). The Capillary number ${\mathrm{Ca}} = \mu _{\mathrm{o}} v / \sigma \in [4.6, 245] \times 10^{-6}$ is introduced as a common dimensionless version of the droplet speed.

3 Experimental results

3.1 Four regimes

Our experiments evidence four main regimes of interaction between a microfluidic droplet and a pneumatic valve. They are denoted as P (passing), TF (trapped in front), TB (trapped below) and S (splitting), respectively, and described hereafter. Figures 2, 3, 4 and 5 are representative examples of these regimes for specific parameter values, though the four regimes have been observed in the much wider range of parameter values given in Sect. 2.

Fig. 2

Example of regime P (the droplet passes below the membrane without being stopped), here for a droplet of length $L_{\mathrm{d}} \simeq 2.27 W$ and ${\mathrm{Ca}} = 7.9 \times 10^{-5}$ at $L_{\mathrm{v}} = 3W$ and $p_{\mathrm{v}} = 150$ mbar. The four horizontal strips on top correspond to snapshots of the selection channel (ROI in Fig. 1b) at times separated by 0.2 s. The picture at the bottom is a spatio-temporal diagram (horizontal dimension along channel length, vertical dimension along time) of the pixels on the dotted line. The dashed lines on this diagram indicate the time of the four snapshots. Regime P is indicated with in subsequent graphs. The corresponding video (S1) is available in ESI (colour figure online)

In regime P (Fig. 2), the valve is either open or not completely closed, so the droplet can pass below without being stopped. However, it slows down when passing the valve, then it accelerates right beyond the valve. Overall the valve may not necessarily cause any significant delay, as revealed by the spatio-temporal diagram of Fig. 2.

Fig. 3

Example of regime TB (the droplet is trapped below the membrane), here for a droplet of length $L_{\mathrm{d}} \simeq 1.04W$ and ${\mathrm{Ca}} = 8.2 \times 10^{-5}$ at $L_{\mathrm{v}} = 6W$ and $p_{\mathrm{v}} = 0$ mbar. The three horizontal strips on top correspond to snapshots of the selection channel (ROI in Fig. 1b) at times separated by 0.4 s. The picture at the bottom is a spatio-temporal diagram (horizontal dimension along channel length, vertical dimension along time) of the pixels on the dotted line. The dashed lines on this diagram indicate the time of the three snapshots. Regime TB is indicated with in subsequent graphs. The corresponding video (S2) is available in ESI (colour figure online)

In regime TB, the membrane is slightly deflected towards the pneumatic layer, so the droplet channel is locally enlarged (Fig. 3). Droplets therein may adopt a shape of lower surface energy (i.e. closer to a sphere) compared to the confined shape imposed by the channel walls downstream. In some conditions to be detailed hereafter, the droplets can be trapped in this well of potential energy (similarly to Jin et al. (2015)), while the oil may still flow on its sides.

Fig. 4

Example of regime TF (the droplet is trapped in front of the membrane), here for a droplet of length $L_{\mathrm{d}} \simeq 1.9W$ and ${\mathrm{Ca}} = 8.7 \times 10^{-6}$ at $L_{\mathrm{v}} = 3W$ and $p_{\mathrm{v}} = 500$ mbar. The three horizontal strips on top correspond to snapshots of the selection channel (ROI in Fig. 1b) at times separated by 0.4 s. The picture at the bottom is a spatio-temporal diagram (horizontal dimension along channel length, vertical dimension along time) of the pixels on the dotted line. The dashed lines on this diagram indicate the time of the three snapshots. Regime TF is indicated with in subsequent graphs. The corresponding video (S3) is available in ESI (colour figure online)

In regime TF, the membrane is sufficiently deflected to obstruct the channel. Then the droplet remains indefinitely trapped in front of the valve (Fig. 4), while the oil keeps flowing around (similarly to Miralles et al. (2015), or Korczyk et al. (2013), in which oil can flow in a dedicated side channel). The droplet may experience some significant elongation of its sides and partially penetrate below the membrane (about $W/2 = 50~\upmu$m from the membrane edge in Fig. 4) in response to the hydrodynamic force exerted by the oil flow.

Fig. 5

Example of regime S (the droplet is split by the valve), here at $L_{\mathrm{v}} = 3W$ and $p_{\mathrm{v}} = 300$ mbar. The four horizontal strips on top correspond to snapshots of the selection channel (ROI in Fig. 1b) at times separated by 0.8 s. The picture at the bottom is a spatio-temporal diagram (horizontal dimension along channel length, vertical dimension along time) of the pixels on the dotted line. The dashed lines on this diagram indicate the time of the four snapshots. Regime S is indicated with in subsequent graphs. The initial droplet, of length $L_{\mathrm{d}} \simeq 2.12W$ and ${\mathrm{Ca}} = 9.0 \times 10^{-6}$, is split by the valve in two droplets, of length $L_{\mathrm{d}} \simeq 0.95W$ (flushed downstream) and $L_{\mathrm{d}} \simeq 1.57W$ (trapped upstream, at ${\mathrm{Ca}} = 1.8 \times 10^{-5}$), respectively. The latter is then split into droplets of length $L_{\mathrm{d}} \simeq 0.88W$ (flushed downstream) and $L_{\mathrm{d}} \simeq 1.12W$ (trapped upstream, at ${\mathrm{Ca}} = 3.4 \times 10^{-5}$). No more splitting happens in these conditions. The corresponding video (S4) is available in ESI (colour figure online)

Finally in regime S, the valve is closed, but not sufficiently to trap the droplet (Fig. 5). Consequently, one of the droplet sides squeezes below the membrane to the point where the droplet splits in two parts [similarly to Choi et al. (2010)]. The spatio-temporal diagram of Fig. 5 reveals that the droplet side elongation does not increase monotonically, so the droplet makes several attempts before it finally crosses the splitting threshold. The daughter droplet at the front finally escapes downstream of the valve. Depending on conditions, the daughter droplet at the back may remain trapped upstream of the valve, it may pass below the membrane and escape, or it may even split again, as in Fig. 5. The split of trapped droplets may be induced by transient events such as the opening of the valve of interest, or the closure of other valves. However, in the explored range of parameters, splitting was never observed when the droplet was trapped below the membrane of an open valve. The length of the escaping daughter droplet is reported in ESI (S0-Section 1).

3.2 Modification of resistance induced by droplet/valve interactions

When a droplet interacts with a valve, the speed v of other droplets is modified, which indicates that the total flow rate in the selection channel changes in response to a modification of its total resistance. Recirculation patterns inside and in the vicinity of a microfluidic droplet usually induce some additional resistance. This resistance was measured in the simplest case of single droplets moving at constant speed in a straight channel of constant cross section (e.g. Adzima and Velankar 2006; Labrot et al. 2009; Vanapalli et al. 2009; Jakiela 2016). A theoretical model was recently proposed for the particular case of long droplets (Rao and Wong 2018). Nevertheless, a comprehensive rationale of the variation of this droplet-induced resistance with channel, fluid and flow parameters is still far from achieved, even in this simple configuration. As described in ESI (S0—section 2 and corresponding videos S7, S8), we have observed recirculation patterns inside the trapped droplets. In regime TF, these patterns suggest some significant viscous dissipation and consequently a strong increase in resistance. This increase was already evidenced in several previous works in which a droplet would be stopped by a channel constriction (Boukellal et al. 2009; Lee and Yoo 2011; Bithi et al. 2017; Chen and Ren 2017) or a pneumatic valve (Jin et al. 2015; Jeong et al. 2019), and subsequent droplets would choose an alternative, less-resistive pathway. However, the induced resistance increase has only been quantified in the case of an axisymmetric channel constriction (Bithi et al. 2017). Some bistability was observed, owing to the coexistence of two different droplet positions relative to the constriction. For each position, the increase of resistance with increasing Ca was fairly weak.

The estimation of the resistance involves several modelling assumptions that will be detailed in the next section. Here, we simply report the modifications of flow rate induced by the interactions between a droplet and a valve. We distinguish three configurations in which the speed v of droplets far from the valve is measured: $v_{\mathrm{o}}$ when the valve is open with no droplet in its immediate neighbourhood, $v_{\mathrm{c}}$ when the valve is closed with no droplet in its immediate neighbourhood, and $v_{\mathrm{d}}$ when a droplet is interacting with the valve (either open or closed). The ratios $v_{\mathrm{c}}/v_{\mathrm{o}}$ and $v_{\mathrm{d}}/v_{\mathrm{o}}$ are reported in Fig. 6. When there is no droplet nearby, closing a valve of length $L_{\mathrm{v}} = 6W$ significantly decreases the speed compared to an open valve ($v_{\mathrm{c}} / v_{\mathrm{o}} \simeq 0.6$ for $L_{\mathrm{v}} = 6W$ and $p_{\mathrm{v}} = 800$ mbar). So closing such valve may significantly modify the resistance of the whole selection channel, even though the valve length is more than 100 times smaller than the channel length. The speed decrease is much less severe when the shorter valve of length $L_{\mathrm{v}} = 3W$ is closed ($v_{\mathrm{c}} / v_{\mathrm{o}} \simeq 0.9$), and it depends on the pressure $p_{\mathrm{v}}$ applied to the valve. When a droplet is trapped in front of a closed valve (regime TF), the resulting speed $v_{\mathrm{d}}$ of other droplets is always smaller than $v_{\mathrm{c}}$, and it can be as small as 10% of $v_{\mathrm{o}}$. It suggests that droplets in regime TF may generate a very high contribution to the resistance. By contrast, when a droplet is trapped below an open valve (regime TB), $v_{\mathrm{d}}$ is almost unchanged, so the corresponding modification of resistance is marginal.

Fig. 6

Ratios $v_{\mathrm{d}}/v_{\mathrm{o}}$ and $v_{\mathrm{c}}/v_{\mathrm{o}}$, where $v_{\mathrm{o}}$, $v_{\mathrm{c}}$ and $v_{\mathrm{d}}$ represent the speed of droplets in the selection channel far from the valve in different configurations: $v_{\mathrm{o}}$ when the valve is open and not interacting with a droplet, $v_{\mathrm{c}}$ when the valve is closed and not interacting with a droplet, and $v_{\mathrm{d}}$ when the valve (either open or closed) interacts with a droplet. Filled red squares () correspond to regime TF at $L_{\mathrm{v}}=6W$ and $p_{\mathrm{v}} = 800$ mbar. Empty red squares () correspond to regime TF at $L_{\mathrm{v}}=3W$ and $p_{\mathrm{v}} = 500$ mbar (thin line) or $p_{\mathrm{v}}=800$ mbar (thick line). Filled purple bullets () correspond to regime TB at $L_{\mathrm{v}} = 6W$ and $p_{\mathrm{v}} = 0$. The black solid lines correspond to $v_{\mathrm{d}} = v_{\mathrm{c}}$, $v_{\mathrm{c}}=v_{\mathrm{o}}$ and ${v_{\mathrm{d}}}={v_{\mathrm{o}}}$ (colour figure online)

3.3 Transition between regimes

Owing to the four independent parameters varied in this study ($L_{\mathrm{v}}$, $p_{\mathrm{v}}$, $L_{\mathrm{d}}$ and Ca), we expect that the transition between each of the four regimes is a hypersurface in a phase space of dimension 4, which is difficult to represent graphically and characterise thoroughly. Therefore, we here consider representative two-dimensional cross sections of this phase space.

First, we focus on a $(p_{\mathrm{v}}, {\mathrm{Ca}})$ cross section, for droplets of length $L_{\mathrm{d}} > 1.5 W$ (Fig. 7) and for a valve of length $L_{\mathrm{v}} = 3 W$. Regime P (passing droplets) was observed as long as the valve was sufficiently open (i.e. at $p_{\mathrm{v}} < 200$ mbar), and regime S (splitting droplets) was systematically observed in the range $p_{\mathrm{v}} \in [200, 400]$ mbar, for all considered Ca. For $p_{\mathrm{v}} > 400$ mbar, regime S was only observed for ${\mathrm{Ca}} > 2 \times 10^{-5}$ while regime TF (droplet trapped in front of the valve) was observed otherwise. Regime TB was never observed for such long droplets in the explored range of Ca and $p_{\mathrm{v}}$. Most importantly, the regimes P, S and TF appear well-separated in Fig. 7, though droplets of very different length ($L_{\mathrm{d}} / W \in [1.5, 2.8]$) are considered together. It suggests that setting $p_{\mathrm{v}}$ and Ca only is sufficient to control the interaction regime of long droplets.

Fig. 7

Transition between regimes P (passing droplets, ), S (split droplets, ) and TF (droplets trapped in front of a closed valve, ), for $L_{\mathrm{v}} =3W$ and for sufficiently long droplets only ($L_{\mathrm{d}} > 1.5 W)$, as a function of the valve pressure $p_{\mathrm{v}}$ and the capillary number Ca (colour figure online)

The second analysed cross section is $L_{\mathrm{d}}/W$ vs. Ca plane, at $L_{\mathrm{v}} = 3 W$ and $p_{\mathrm{v}} = 500$ mbar or $p_{\mathrm{v}} = 800$ mbar (Fig. 8). In such conditions, the valve is closed so the droplet has to squeeze to attempt a passage in the unobstructed gutters on the membrane sides. Regime TF (droplet trapped in front of the valve) is observed for small $L_{\mathrm{d}}$ and low Ca. There, the hydrodynamic force that pushes the droplet below the membrane is dominated by the capillary force resulting from the droplet deformation. By contrast, regime S (splitting) is observed for large $L_{\mathrm{d}}$ and high Ca, where the hydrodynamic force can overcome the capillary force. The boundary between these regimes is a curve of decreasing Ca for increasing $L_{\mathrm{d}}$. In other words, $L_{\mathrm{d}}$ is not the only parameter that governs the trap-to-split transition, and droplets as long as 1.9W may still be trapped without splitting provided that the average flow speed in the channel is sufficiently small. The position of the boundary is shifted to higher $L_{\mathrm{d}}$ and Ca when the valve pressure $p_{\mathrm{v}}$ is increased.

Fig. 8

Transition between regime TF (droplets trapped in front of the valve, ) and regime S (droplets split by the valve, ), for $L_{\mathrm{v}} =3W$, as a function of the droplet length $L_{\mathrm{d}}$ and the capillary number Ca. The black lines represent Eq. (36). Thin symbols and dashed line correspond to $p_{\mathrm{v}} =500$ mbar, while thick symbols and solid line correspond to $p_{\mathrm{v}} =800$ mbar (colour figure online)

The third analysed cross section is also a $L_{\mathrm{d}}/W$ vs. Ca plane, although now at $p_{\mathrm{v}} = 0$ for both $L_{\mathrm{v}}=3W$ and $L_{\mathrm{v}}=6W$ (Fig. 9). In such conditions, the valve is open, and the droplet channel below the membrane is slightly inflated owing to the higher pressure on the liquid side of the membrane. Regime P (passing droplet) is observed for large $L_{\mathrm{d}}$ and high Ca, which again corresponds to a hydrodynamic force dominating the capillary force required to deform the droplet. By contrast, regime TB (droplets trapped below the membrane) is observed for small $L_{\mathrm{d}}$ (of the order of W or less) and low Ca, when the capillary force dominates. Again, the boundary is a curve of decreasing Ca for increasing $L_{\mathrm{d}}$, which is shifted to lower $L_{\mathrm{d}}$ and Ca when the valve length $L_{\mathrm{v}}$ is decreased.

Fig. 9

Transition between regime P (passing droplets, ) and regime TB (droplets trapped below the membrane, ), at $p_{\mathrm{v}} =0$ mbar (valve open) as a function of the normalised droplet length $L_{\mathrm{d}}/W$ and the capillary number Ca. Empty symbols correspond to $L_{\mathrm{v}} =3W$ while full symbols correspond to $L_{\mathrm{v}}=6W$. The black line corresponds to Eq. (41) (colour figure online)

3.4 Several incoming droplets: buffer and multiple-drop storage

We now consider scenarios where several droplets interact simultaneously with the valve, either in regime TF or in regime TB. An example with three droplets is given in Fig. 10. The valve is initially closed and the first droplet is trapped in regime TF. When the second and third droplets join, they are stored behind the first. When the valve opens, the first two droplets pass beyond the membrane while the last droplet remains trapped in the TB regime. We observe that there is a storage capacity for each trap, namely a maximum number of droplets that can be stored. In the conditions of Fig. 10, the storage capacity is one droplets for the TB trap, while it is larger than three droplets for the TF trap. Droplets in excess are evacuated in a first-in first-out manner. The existence of a storage capacity can be justified as follows. The capillary force that traps the droplets is mostly prescribed by the deformation of the first droplet in the row, so it is likely independent of the number of droplets. By contrast, the hydrodynamic force likely increases with the number of stored droplets. Therefore, there must be a critical number of droplets beyond which the hydrodynamic force overcomes the capillary force, which pushes at least one droplet out of the trap.

Fig. 10

Storage with closed valve, observed for droplets of length $L_{\mathrm{d}} \simeq 0.97 W$ and initial $Ca = 3.4 \times 10^{-5}$ at $L_{\mathrm{v}} = 6W$ and $p_{\mathrm{v}} = 800$ mbar or 0 mbar. The seven horizontal strips on top correspond to snapshots of the channel at times 0 s, 0.4 s, 1.6 s, 2.4 s, 2.8 s, 3.2 s and 4.0 s. The picture at the bottom is a spatio-temporal diagram (horizontal dimension along channel length, vertical dimension along time) of the pixels on the dotted line. The dashed lines on this diagram indicate the time of the seven snapshots. The corresponding video (S5) is available in ESI

4 Modelling of the transitions

The transitions from regimes TF to S and from regimes TB to P both involve a competition between capillary forces that tend to trap the droplet, and hydrodynamic forces that tend to push the droplet downstream. In this section, we aim at providing an algebraic model of both forces as a function of the main system parameters (geometry, fluid properties, etc.) from which each transition can be fairly captured. The hydrodynamic force is determined from the resistance that needs to be estimated in the different valve configurations (open or closed, with or without trapped droplet). To this aim, we first develop an algebraic model of the membrane deformation, from which we estimate the increase of hydrodynamic resistance induced by closing the valve. Then, we identify a way to calculate the resistance induced by the droplet/valve interaction, starting from the measured speed v of other droplets, and we infer an empirical equation to estimate this additional resistance from the main parameters. Finally, the determination of the capillary force requires a model of the droplet deformation (and associated surface energy) induced by its interaction with the valve, which we develop for each interaction regime.

4.1 Membrane deformation

We first propose an analytical model of a membrane stretched in response to transmembrane pressure and confined by the walls of a microfluidic channel. The model is adapted from Srivastava and Hui (2013). We consider a membrane that, in its undeformed state, is planar and horizontal, of length $L_{\mathrm{v}}$ in the x-direction, width W in the y-direction and thickness h. It is pinned to the channel walls in $x = \pm L_{\mathrm{v}}/2$ and in $y = \pm W/2$. The vertical direction z is normal to the undeformed membrane, which is in $z=0$. The model assumes the membrane to be much longer than wide ($L_{\mathrm{v}} \gg W$); so in first approximation, the deflection is considered in the (y, z)-plane only (and constant along x). As long as the membrane deflection significantly exceeds its thickness, the bending stress can be neglected in front of the stretching stress.

We assume that PDMS behaves as a linear elastic material, so the tension (per unit length) in the membrane is given by $K_{\mathrm{s}} \varepsilon$, where $\varepsilon$ is the membrane strain and $K_{\mathrm{s}}$ is the stretching modulus. The latter is given by $K_{\mathrm{s}} = E h / (1-\nu ^2)$, where E and $\nu$ are the Young’s modulus and the Poisson ratio of the membrane, respectively. The Young’s modulus E of PDMS is of the order of $10^4$ mbar, but its exact value depends on the fabrication recipe (Johnston et al. 2014). It also seems to increase with decreasing thickness when the latter is less than a few hundred micrometers (Liu et al. 2009). We here assume that $E \simeq 7500$ mbar and $\nu \simeq 0.5$, so $K_{\mathrm{s}} \simeq 80$ mbar mm.

The transmembrane pressure is given by $P_{\mathrm{v}} = p_{\mathrm{v}} - p_{\mathrm{h}}$, where $p_{\mathrm{v}}$ is the pneumatic pressure above the membrane and $p_{\mathrm{h}}$ is the hydrodynamic pressure below the membrane. The latter depends on the variable resistance in the selection channel, so its exact value is unknown. However, a lower bound can be estimated from the resistance of the selection channel without droplets (Bruus 2005):

$$\begin{aligned} p_{\mathrm{h}} \gtrsim \frac{12 \mu _{\mathrm{o}} v L_{\mathrm{s}}}{H^2 \left( 1 - 0.63 \frac{H}{W} \right) }, \end{aligned}$$

(1)

which is 48 mbar for the highest Ca considered in these experiments. An upper bound may also be found as an intermediate between the pressure at the emulsification junction and the atmospheric pressure at the waste outlet:

$$\begin{aligned} p_{\mathrm{h}} \lesssim \frac{L_{\mathrm{w}}}{L_{\mathrm{u}} + L_{\mathrm{w}}} p_{\mathrm{o}} \simeq 0.28 p_{\mathrm{o}}. \end{aligned}$$

(2)

To obtain this upper bound, both the resistance of oil and water inlet channels and the flow in the selection channel have been neglected. Since $p_{\mathrm{o}} \le 217$ mbar, then $p_{\mathrm{h}} < 60$ mbar. This is fairly consistent with the lower bound approximation, and it is an order of magnitude smaller than $p_{\mathrm{v}}$ as long as the valve is closed ($p_{\mathrm{v}} \gtrsim 300$ mbar).

According to the Laplace law, the transmembrane pressure $P_{\mathrm{v}}$ is equal to the membrane curvature 1/R multiplied by the membrane tension, so

$$\begin{aligned} P_{\mathrm{v}} =K_{\mathrm{s}} \frac{\varepsilon }{R}. \end{aligned}$$

(3)

We assume that the tension in the membrane is constant in space, even if the membrane is locally tangent to the the channel walls. Indeed, it is still separated from the walls by a thin liquid layer so there should not be any significant shear load applied by the channel walls on the membrane. Wherever the membrane is suspended, $P_{\mathrm{v}}$ applies uniformly so R should be constant and the membrane should describe a circular arc of central angle $\theta$. Wherever the membrane is tangent to the straight walls over a finite distance, $R \rightarrow \infty$ so $P_{\mathrm{v}}$ should be counterbalanced by reaction forces from the walls.

As $P_{\mathrm{v}}$ is increased, the deformed membrane is progressively pressed against the channel walls. We consider three different deformation regimes depicted in the schematics of Fig. 11. In the first regime, the membrane does not touch the bottom of the channel so it is entirely suspended. In the second regime, the membrane touches the bottom of the channel but not yet the side walls of the channel. In the third regime, the membrane touches both the bottom and the side walls of the channel. We denote $\delta _1$ the vertical deflection of the membrane in $y=0$ and $\delta _2$ the distance over which the membrane is tangent to the bottom channel wall.

Fig. 11

Three regimes of membrane deformation expected successively for increasing $P_{\mathrm{v}}$. Geometrical variables are defined for each regime. The shaded yellow regions below the membrane are accessible to the liquid (colour figure online)

In regime 1, the membrane is a circular arc of radius R entirely suspended from $(y,z) = (\pm W/2,0)$, so $\delta _1 < H$. This geometrical configuration yields

$$\begin{aligned} \delta _1 = R (1-\cos \theta ), \quad \frac{W}{2} = R \sin \theta , \end{aligned}$$

(4)

so the stretching strain is $\varepsilon = (2 \theta R - W)/W$, and Laplace law yields

$$\begin{aligned} \frac{W P_{\mathrm{v}}}{2K_{\mathrm{s}}}= \theta - \sin \theta , \quad \tan \left( \frac{\theta }{2} \right) = \frac{2 \delta _1}{W}. \end{aligned}$$

(5)

Regime 1 is valid as long as $\delta _1 < H$, so here for $P_{\mathrm{v}} < 317$mbar.

For larger $P_{\mathrm{v}}$, the membrane becomes tangent to the bottom channel wall over a finite distance $\delta _2$. If $\delta _2 < W - 2H$, the suspended parts of the membrane describe two circular arcs of radius R pinned in $(y,z)=(\pm W/2,0)$ and coming tangentially to the bottom in $(y,z) = (\pm \delta _2/2, H)$. This geometrical configuration yields

$$\begin{aligned} H = R (1-\cos \theta ), \quad \frac{W - \delta _2}{2} = R \sin \theta , \end{aligned}$$

(6)

so the stretching strain is $\varepsilon = (2 \theta R + \delta _2 - W)/W$, and Laplace law yields

$$\begin{aligned} \frac{W P_{\mathrm{v}}}{2K_{\mathrm{s}}}= \theta - \sin \theta , \quad \tan \left( \frac{\theta }{2} \right) = \frac{2 H}{W - \delta _2}. \end{aligned}$$

(7)

When $\delta _2 > W - 2H$ (i.e. here when $P_{\mathrm{v}} > 913$ mbar), the membrane also becomes tangent to the side walls in $y = \pm W/2$ so the circular arcs are now quarter circles that extend from $(y,z) = (\pm W/2, H - W/2 + \delta _2/2)$ to $(\pm \delta _2/2, H)$. This geometrical configuration yields:

$$\begin{aligned} \frac{W-\delta _2}{2} = R, \end{aligned}$$

(8)

so the stretching strain is $\varepsilon = [\pi R + \delta _2 + 2 (H-R) - W]/W$, and Laplace law yields

$$\begin{aligned} \frac{W P_{\mathrm{v}}}{2K_{\mathrm{s}}}= \frac{\pi }{2} + 2 \frac{H - W + \delta _2}{W- \delta _2}. \end{aligned}$$

(9)

The space left for the liquids (both oil and water droplets) to flow below the membrane can be characterised by the radius r of the corresponding incircle. We denote $\varphi$ the angle between the vertical and the line joining the centres of the membrane arc of circle and the incircle. Variables r and $\varphi$ can be geometrically obtained as functions of the membrane deflection parameters. In regime 1,

$$\begin{aligned} \left\{ \begin{array}{ll} (R+r) \cos \varphi + r &{}= H + R \cos \theta \\ (R+r) \sin \varphi + r &{}= \frac{W}{2}, \end{array} \right. \end{aligned}$$

(10)

so

$$\begin{aligned} \left\{ \begin{array}{ll} \tan \frac{\varphi }{2} &{}= -1 + \sqrt{\frac{W+2R}{H+R(1+\cos \theta )}} \\ r &{}= \frac{W/2 - R \sin \varphi }{1 + \sin \varphi }. \end{array} \right. \end{aligned}$$

(11)

In regime 2,

$$\begin{aligned} \left\{ \begin{array}{ll} (R+r) \cos \varphi + r &{}= H + R \cos \theta \\ (R+r) \sin \varphi + r &{}= \frac{W}{2} - \frac{\delta _2}{2}, \end{array} \right. \end{aligned}$$

(12)

so

$$\begin{aligned} \left\{ \begin{array}{ll} \tan \frac{\varphi }{2} &{}= -1 + \sqrt{\frac{W+2R - \delta _2}{H+R(1+\cos \theta )}} \\ r &{}= \frac{(W-\delta _2)/2 - R \sin \varphi }{1 + \sin \varphi }. \end{array} \right. \end{aligned}$$

(13)

In regime 3, $\varphi = \pi /4$ and

$$\begin{aligned} r = \frac{\sqrt{2}-1}{\sqrt{2}+1} \frac{W-\delta _2}{2}. \end{aligned}$$

(14)

Both the membrane deflections ($\delta _1$ and $\delta _2$) and the incircle radius r are represented in Fig. 12 as a function of the transmembrane pressure $P_{\mathrm{v}}$.

Fig. 12

Membrane deformation variables $\delta _1$ (solid blue line) and $\delta _2$ (dash-dot blue line), and characteristic radius r of the spacing below the membrane (dashed red line) as a function of the transmembrane pressure $P_{\mathrm{v}}$. The membrane of stretching modulus $K_{\mathrm{s}} = 80$ mbar$\cdot$mm covers a channel of width $W=0.1$ mm and height $H=0.03$ mm. The horizontal dotted black line is in $\delta _1 = H$, while the vertical dotted black lines represent the boundaries between regimes 1 and 2, and regimes 2 and 3, respectively (colour figure online)

4.2 Resistance of the oil flow below a closed valve

We now model the additional resistance induced by the oil flow below the deformed membrane (without the droplets). By definition, the resistance $\mathcal {R} = \Delta p / Q$ of a channel segment is the ratio between the pressure drop $\Delta p$ along the segment and the corresponding flow rate Q. For a channel segment of length L and rectangular cross section $W \times H$ entirely filled with the oil phase, the resistance is approximated by $\mathcal {R} \simeq 12 \mu _{\mathrm{o}} L / H^3 (W - 0.63 H)$ (Bruus 2005). We define the dimensionless resistance coefficient $\beta$ as

$$\begin{aligned} \beta = \frac{H^4}{\mu _{\mathrm{o}} L} \mathcal {R}, \end{aligned}$$

(15)

so $\beta \simeq 12 H / (W - 0.63 H)$ for the rectangular channel cross section. When the channel is obstructed by the membrane over a longitudinal distance $L_{\mathrm{v}}$, $\beta$ is expected to be significantly higher. In the limit where $L_{\mathrm{v}} \gg W$, an approximation of $\beta$ can be obtained by solving the 2D Stokes equations for the variations of the unidirectional fluid velocity u (along the channel) as a function of the position (y, z) in the cross section:

$$\begin{aligned} \frac{\partial ^2 u}{\partial y^2} + \frac{\partial ^2 u}{\partial z^2} = \frac{\Delta p}{\mu _{\mathrm{o}} L_{\mathrm{v}}} = \frac{\beta }{H^4} \int _{\mathrm{s}} u \mathrm{d}y \mathrm{d}z. \end{aligned}$$

(16)

This equation is solved for u(y, z) with a custom finite element method implemented in Matlab (Larson and Bengzon 2010), for various membrane deflections. No-slip boundary conditions are applied at the channel walls and on the membrane. The characteristic mesh size is set to r/20. An example of velocity profile in membrane regime 2 is shown in Fig. 13. The resistance coefficient $\beta$ is then inferred from the velocity field. As seen in Fig. 14, it increases with decreasing incircle radius r, according to the power law

$$\begin{aligned} \beta \simeq 0.56 \frac{H^4}{r^4}, \end{aligned}$$

(17)

in membrane regimes 2 and 3. In regime 1, the calculated $\beta$ is smaller than the prediction from Eq. (17). It matches with the theoretical prediction $\beta = 12 H / (W - 0.63 H)$ for a rectangular channel when the membrane deflection $\delta _1$ tends to zero and r tends to H/2.

Fig. 13

Finite element simulation of the single phase flow below the deformed membrane of a closed valve ($\delta _1 = H$, $\delta _2 = 0.57 H$). The local velocity u (colour, in arbitrary units) is represented as a function of the position (y, z) in the channel cross section (colour figure online)

Fig. 14

Resistance coefficient $\beta$ as a function of the radius r characteristic of the space left below the membrane, normalised by the channel height H. The thick solid line corresponds to Eq. (17). The dash-dotted vertical lines separate regimes 3 (left), 2 (middle) and 1 (right). The black square corresponds to the rectangular channel cross section of an open valve, namely $\beta = 12 H / (W - 0.63 H)$

4.3 Additional resistance induced by a trapped droplet

The increase of resistance induced by a droplet interacting with a pneumatic valve is hard to estimate from theoretical arguments. Therefore, it is here determined experimentally. We denote $\mathcal {R}_{\mathrm{o}}$ the resistance of the whole selection channel in the case of an open valve, when the speed of droplets is $v_{\mathrm{o}}$. We denote $\mathcal {R}_{\mathrm{c}}$ the additional resistance induced by the closure of the valve (without droplet) when the speed of the droplets is $v_{\mathrm{c}}$. It is determined from Eq. (17), as

$$\begin{aligned} \mathcal {R}_{\mathrm{c}} = 0.56 \frac{\mu _{\mathrm{o}} L_{\mathrm{v}}}{r^4}. \end{aligned}$$

(18)

Finally, we denote $\mathcal {R}_{\mathrm{d}}$ the additional resistance induced by the presence of a trapped droplet (in front of a closed valve as in regime TF, or below an open valve as in regime TB), when the speed of other droplets is $v_{\mathrm{d}}$.

The ratio of resistances $\mathcal {R}_{\mathrm{d}}/\mathcal {R}_{\mathrm{c}}$ can be calculated from the measured droplet speeds as follows. The pressure $p_1$ at the entrance of the selection channel is given by

$$\begin{aligned} p_1 = N p_{\mathrm{d}} + \mathcal {R} Q, \end{aligned}$$

(19)

where N is the number of droplets in the selection channel, $p_{\mathrm{d}}$ is the pressure jump associated to the droplet interfaces (Vanapalli et al. 2009), $\mathcal {R}$ is the resistance of the selection channel and Q is the flow rate therein. In a linear network, the pressure at each point is an affine function of the other pressures and flow rates. In general for any network comprising resistive elements only, there must be a relation

$$\begin{aligned} p_1 = A - B Q, \end{aligned}$$

(20)

that is independent of Eq. (19), where constants A and B can be functions of the number of droplets in each channel, as well as the resistance of each other channel (i.e. other than the selection channel) and the pressure at every other inlet/outlet. Importantly, A and B do not vary if only the resistance $\mathcal {R}$ of the selection channel is modified.

In regime TF, we assume that the valve state modifies the resistance of the selection channel while it has no immediate influence on the total number of droplets in each channel or on the resistance of other channels. Therefore,

$$\begin{aligned} (\mathcal {R}_{\mathrm{o}} + B) v_{\mathrm{o}}= & {} (\mathcal {R}_{\mathrm{o}}+\mathcal {R}_{\mathrm{c}} + B) v_{\mathrm{c}} \nonumber \\= & {} (\mathcal {R}_{\mathrm{o}}+\mathcal {R}_{\mathrm{c}}+\mathcal {R}_{\mathrm{d}} + B) v_{\mathrm{d}} \nonumber \\= & {} \frac{A - N p_{\mathrm{d}}}{WH}, \end{aligned}$$

(21)

from which we deduce a way to calculate $\mathcal {R}_{\mathrm{d}}/\mathcal {R}_{\mathrm{c}}$ from the measurement of droplet speeds only:

$$\begin{aligned} \frac{\mathcal {R}_{\mathrm{d}}}{ \mathcal {R}_{\mathrm{c}}} = \frac{v_{\mathrm{o}} (v_{\mathrm{c}} - v_{\mathrm{d}})}{v_{\mathrm{d}} (v_{\mathrm{o}} - v_{\mathrm{c}})}. \end{aligned}$$

(22)

Similarly in regime TB,

$$\begin{aligned} (\mathcal {R}_{\mathrm{o}} + B) v_{\mathrm{o}}= & {} (\mathcal {R}_{\mathrm{o}}+\mathcal {R}_{\mathrm{c}} + B) v_{\mathrm{c}} = (\mathcal {R}_{\mathrm{o}}+\mathcal {R}_{\mathrm{d}} + B) v_{\mathrm{d}} \nonumber \\= & {} \frac{A - N p_{\mathrm{d}}}{WH}, \end{aligned}$$

(23)

from which we deduce

$$\begin{aligned} \frac{\mathcal {R}_{\mathrm{d}}}{\mathcal {R}_{\mathrm{c}}} = \frac{v_{\mathrm{c}} (v_{\mathrm{o}} - v_{\mathrm{d}})}{v_{\mathrm{d}} (v_{\mathrm{o}} - v_{\mathrm{c}})}. \end{aligned}$$

(24)

The resistance $\mathcal {R}_{\mathrm{d}}$ can therefore be calculated from droplet speed measurements in the three valve configurations ($v_{\mathrm{o}}$, $v_{\mathrm{c}}$ and $v_{\mathrm{d}}$) and from $\mathcal {R}_{\mathrm{c}}$, which is obtained from the membrane deflection and corresponding incircle radius r (Eq. 18). In Fig. 15, $\mathcal {R}_{\mathrm{d}}$ is represented as a function of the droplet length-to-width ratio $L_{\mathrm{d}}/W$, for various inlet pressures (and corresponding number of droplets and subsequent resistance in each other channel), as well as for both valve lengths and different pneumatic pressures. Data indicate that in regime TF, the additional resistance induced by the droplet increases linearly with the droplet length:

$$\begin{aligned} \mathcal {R}_{\mathrm{d}} \simeq 2 \times 10^5 \left( \frac{L_{\mathrm{d}}}{W} - 1 \right) \frac{\mu _{\mathrm{o}}}{H^3}. \end{aligned}$$

(25)

The increase of $\mathcal {R}_{\mathrm{d}}$ with $L_{\mathrm{d}}$ suggests that the additional resistance is not only due to the sealing of the gaps below the membrane induced by the deformation of the droplet trapped in front of it. In addition, there must be some significant viscous dissipation in the oil gutters along the droplet as their length also varies linearly with $L_{\mathrm{d}}$. The offset between data and Eq. (25) in Fig. 15 for $L_{\mathrm{d}} \simeq W$ might result from $\mathcal {R}_{\mathrm{d}}$ being comparable to $\mathcal {R}_{\mathrm{c}}$ in that regime. By contrast, the ratio $\mathcal {R}_{\mathrm{d}}/\mathcal {R}_{\mathrm{c}}$ can be of the order of 20 for $L_{\mathrm{d}} \sim 2W$, which indicates that the increase of resistance induced by trapping long droplets is an order of magnitude larger than the increase of resistance induced by simply closing the valve. In regime TB, the resistance induced by the trapped droplet is an order of magnitude smaller than in regime TF, as already inferred from Fig. 6. It is possibly because of the significantly smaller velocity gradients observed in regime TB (Fig. 3 vs. Fig. 5 in ESI).

Fig. 15

Resistance $\mathcal {R}_{\mathrm{d}}$ induced by the droplet, normalised by $\mu _{\mathrm{o}}/H^3$, as a function of the normalised droplet length $L_{\mathrm{d}}/W - 1$. Filled symbols correspond to $p_{\mathrm{v}} = 800$ mbar and $L_{\mathrm{v}}=6W$, empty symbols with thin lines correspond to $p_{\mathrm{v}} =500$ mbar and $L_{\mathrm{v}}=3W$, and empty symbols with thick lines correspond to $p_{\mathrm{v}}=800$ mbar and $L_{\mathrm{v}}=3W$. () corresponds to regime TF while () corresponds to regime TB. The solid line corresponds to Eq. (25) (colour figure online)

4.4 Transition between regimes TF and S

The transition from regime TF (trapped in front) to regime S (splitting) occurs when the capillary force $F_{\sigma }$ that maintains the droplet in front of the valve is not sufficient anymore to counterbalance the hydrodynamic force $F_{\mu }$ that drives the droplet in the gap below the membrane. The capillary force $F_{\sigma }$ can be estimated from the increase of surface energy needed by the droplet to virtually squeeze in one of the gaps below the membrane, as schematically represented in Fig. 16. We assume that both the front and the back of the trapped droplet comprise a finite region of constant cross section, referred as f and b, respectively. This is valid as long as the droplet is sufficiently long and $L_{\mathrm{v}}/W$ is sufficiently large for the 1D membrane model to apply. The virtual squeezing implies that the back interface of the droplet moves a distance $\mathrm{d}l_{\mathrm{b}}$ downstream towards the valve, thereby reducing the length of region b by the same amount, while the front interface moves a distance $\mathrm{d}l_{\mathrm{f}}$ downstream below the membrane, thereby increasing the length of region f by the same amount. Conservation of volume yields

$$\begin{aligned} S_{\mathrm{f}} \mathrm{d}l_{\mathrm{f}} = S_{\mathrm{b}} \mathrm{d}l_{\mathrm{b}}, \end{aligned}$$

(26)

where $S_{\mathrm{f}}$ and $S_{\mathrm{b}}$ are the areas of the droplet cross section in regions f and b, respectively. The increase of surface energy associated to the virtual move is

$$\begin{aligned} \Delta E_{\sigma } = \sigma \left( C_{\mathrm{f}} \mathrm{d}l_{\mathrm{f}} - C_{\mathrm{b}} \mathrm{d}l_{\mathrm{b}} \right) , \end{aligned}$$

(27)

where $C_{\mathrm{f}}$ and $C_{\mathrm{b}}$ are the respective cross-sectional perimeters. The capillary force is deduced from the energy gradient:

$$\begin{aligned} F_{\sigma } = \frac{\mathrm{d} \Delta E_{\sigma }}{\mathrm{d}l_{\mathrm{b}}} = \sigma S_{\mathrm{b}} \left( \frac{C_{\mathrm{f}}}{S_{\mathrm{f}}} - \frac{C_{\mathrm{b}}}{S_{\mathrm{b}}} \right) . \end{aligned}$$

(28)

Fig. 16

Schematic top view of a microfluidic droplet (blue) trapped in front of a closed valve (black) and attempting to squeeze in one of the gaps below the membrane. The solid line delimits the droplet in its initial state, while the dashed line delimits the droplet after its virtual progression downstream. The dash-dotted vertical lines correspond to the cross sections f and b in which the cross-sectional perimeter C and area S of the droplet are calculated (colour figure online)

In order to estimate C and S in each section, an approximation of the section shape is needed. The droplet interface satisfies the same Laplace law as the membrane, so similar assumptions can be made about its shape: it is considered as tangent to the channel walls wherever it is constrained and it forms circular arcs of radius $\xi$ wherever it is not constrained. The thickness of the Bretherton film between the droplet and the channel walls is here neglected since it is less than 1% of the channel height for ${\mathrm{Ca}} < 10^{-3}$. At the back of a droplet in regime TF, the cross section is simply confined by the undeformed channel walls away from the membrane, as represented in Fig. 17. Therefore, the cross-sectional perimeter and area are, respectively, given by:

$$\begin{aligned} C_{\mathrm{b}} = 2 H + 2 W + (2 \pi - 8) \xi _{\mathrm{b}}, \quad S_{\mathrm{b}} = W H + (\pi - 4) \xi _{\mathrm{b}}^2. \end{aligned}$$

(29)

The radius $\xi _{\mathrm{b}}$ is obtained by minimising the corresponding ratio $C_{\mathrm{b}}/S_{\mathrm{b}}$ (Musterd et al. 2015):

$$\begin{aligned} \xi _{\mathrm{b}}= & {} \frac{ H+W - \sqrt{(H+W)^2-(4-\pi )HW}}{4-\pi } \simeq 12~{\upmu }\mathrm{m}, \nonumber \\ \frac{C_{\mathrm{b}}}{S_{\mathrm{b}}}= & {} \frac{1}{\xi _{\mathrm{b}}}. \end{aligned}$$

(30)

Fig. 17

Cross section of a droplet confined to a height H and a width W by the four walls of a microchannel. The radius $\xi$ of the droplet interface in the channel corners is obtained through minimising the corresponding ratio of cross-sectional perimeter and area

At the front, the droplet in regime TF or S is squeezed below the membrane, which is itself in deformation regime 2. The droplet shape to be optimised is, therefore, represented in Fig. 18. It comprises a circular arc tangent to the membrane of curvature radius R (between angular positions $\psi$ and $\phi$), two straight segments tangent to the channel bottom and side walls respectively, and circular arcs of radius $\xi$ in between, i.e. wherever the droplet is not tangent to solid boundaries. In addition to Eq. (6) that relates the central angle $\theta$ of the membrane arc to its radius R, there are two geometrical constraints originating from the match of the different droplet segments and that prescribe $\psi$ and $\phi$ as functions of $\xi$:

$$\begin{aligned} \cos \psi = \frac{R-\xi }{R+\xi }, \qquad \sin \phi = \frac{R \sin \theta - \xi }{R + \xi }. \end{aligned}$$

(31)

The perimeter and area are given by:

$$\begin{aligned} C_{\mathrm{f}}= & {} R \left( \phi - \psi + 1 - \cos \phi - \sin \psi + \sin \theta \right) \nonumber \\&+ \xi \left( \frac{7 \pi }{4} + \phi - \psi - 2 - \cos \phi - \sin \psi \right) , \end{aligned}$$

(32)

and

$$\begin{aligned} S_{\mathrm{f}}= & {} \frac{R^2}{2} \left( 2 \sin \theta - \sin \psi - \sin \theta \cos \phi + \psi - \phi \right) \nonumber \\&- \frac{\xi R}{2} \left( 2 \sin \psi + \cos \phi + \cos \phi \sin \theta \right) \nonumber \\&+ \frac{\xi ^2}{2} \left( \frac{7 \pi }{4} - 2 +\phi - \psi - \sin \psi - \cos \phi \right) . \end{aligned}$$

(33)

The radius $\xi _{\mathrm{f}}$ is again chosen to minimise the perimeter-to-area ratio $C_{\mathrm{f}} / S_{\mathrm{f}}$ of the droplet cross section. This minimum is very well approximated in the whole range of membrane deformation (in regime 2) by

$$\begin{aligned} \xi _{\mathrm{f}} \simeq 3r/5, \quad \frac{C_{\mathrm{f}}}{S_{\mathrm{f}}} = \frac{1}{\xi _{\mathrm{f}}} \simeq \frac{5}{3r}. \end{aligned}$$

(34)

The capillary force $F_{\sigma }$ is finally obtained by substituting Eqs. (30) and (34) in Eq. (28).

It can be checked a posteriori that the membrane shape is marginally affected by the presence of the squeezed droplet. Indeed, the capillary pressure exerted by the droplet on the membrane is $\sigma /\xi _{\mathrm{f}} \simeq 51$ mbar for a membrane deformation corresponding to $p_{\mathrm{v}} = 800$ mbar.

Fig. 18

Cross section of a droplet squeezed below the membrane of a closed valve. The thick black lines are the channel bottom and side walls. The thick red line represents the membrane in regime 2. It comprises a straight segment tangent to the channel bottom wall, and a circular arc of radius R and central angle $\theta$. The thick blue line represents the droplet. It comprises straight segments tangent to the channel bottom and side walls, a circular arc tangent to the membrane in the range of angular position $[\psi , \phi ]$ from the vertical, and circular arcs of radius $\xi$ to join the other segments. The dashed blue line is the incircle of radius r from Fig. 11 (colour figure online)

The hydrodynamic force $F_{\mu }$ may comprise contributions from the pressure difference between the front and the back of the droplet, and from the shear along the droplet sides. If the gap between the droplet and the channel walls is of the order of $\xi$, the pressure contribution scales as $\mu _{\mathrm{o}} L_{\mathrm{d}} Q S / \xi ^4$ while the shear contribution scales as $\mu _{\mathrm{o}} Q L_{\mathrm{d}} / \xi$. Therefore, the latter can be neglected in comparison with the former since $\xi ^2 \ll S$. We can then infer the hydrodynamic force $F_{\mu }$ induced by the pressure drop along the trapped droplet, thanks to the resistance measurement of Eq. (25):

$$\begin{aligned} F_{\mu } = S_{\mathrm{b}} \mathcal {R}_{\mathrm{d}} W H v = 2 \times 10^5 \left( \frac{L_{\mathrm{d}}}{W} - 1 \right) \frac{\mu _{\mathrm{o}} v S_{\mathrm{b}} W}{H^2}. \end{aligned}$$

(35)

The transition between regimes TF and S should be in $F_{\sigma } \simeq F_{\mu }$, which yields:

$$\begin{aligned} {\mathrm{Ca}} = \frac{\left( \frac{1}{\xi _{\mathrm{f}}}- \frac{1}{\xi _{\mathrm{b}}}\right) \frac{H^2}{W}}{2 \times 10^5 \left( \frac{L_{\mathrm{d}}}{W}- 1\right) }. \end{aligned}$$

(36)

This equation is represented in Fig. 8 for the valve pressure values $p_{\mathrm{v}}$ (and subsequent r, $\xi _{\mathrm{b}}$ and $\xi _{\mathrm{f}}$) corresponding to the data. It approximates the observed transition reasonably well, given that it does not involve any fitting parameter once $\mathcal {R}_{\mathrm{d}}$ is determined. However, Eq. (36) predicts a vertical asymptote in $L_{\mathrm{d}} = W$ which the data do not corroborate. The absence of such asymptote certainly results from both the hydrodynamic force remaining finite (and not zero) for droplets that are laterally unconfined ($L_{\mathrm{d}}<W$) and the capillary force being less than predicted since the curvature at the back of the droplet is higher than the $1/\xi _{\mathrm{b}}$ in Eq. (36).

4.5 Transition between regimes TB and P

The model developed for the transition between regimes TF and S can be adapted to capture the transition between regimes TB and P, which is also expected to result from a balance of hydrodynamic and capillary forces. In this configuration, the droplet back is below the membrane, while the droplet front penetrates the channel downstream. The membrane is slightly deflected upwards since $p_{\mathrm{v}} = 0$ and $p_{\mathrm{h}} > 0$. Moreover, the capillary pressure inside the droplet should be taken into account as it is also transmitted to the membrane. It is of the order of $\sigma /\xi _{\mathrm{b}} \sim 14$ mbar, which cannot be neglected as the absence of pressure in the pneumatic layer makes any other contribution significant. Therefore, the transmembrane pressure is

$$\begin{aligned} P_{\mathrm{v}}=-p_{\mathrm{h}} - \frac{\sigma }{\xi _{\mathrm{b}}} < 0, \end{aligned}$$

(37)

where $\xi _{\mathrm{b}}$ is the radius of curvature at the droplet back. It is estimated by adapting Fig. 17 and Eq. (30) to a channel of height $H - \delta _1$, where $\delta _1 < 0$ (upward membrane deflection):

$$\begin{aligned} \xi _{\mathrm{b}} = \frac{ H-\delta _1+W - \sqrt{(H-\delta _1+W)^2-(4-\pi )(H-\delta _1)W}}{4-\pi }. \end{aligned}$$

(38)

The droplet front is constrained by the undeformed channel, so its radius of curvature $\xi _{\mathrm{f}}$ exactly corresponds to Eq. (30). The capillary force is again calculated as $F_{\sigma } = \sigma S_{\mathrm{b}} \left( \frac{1}{\xi _{\mathrm{f}}} - \frac{1}{\xi _{\mathrm{b}}} \right)$. The hydrodynamic force is estimated from the oil flow in the gutters around the trapped droplet. Since $|\delta _1| \ll H$, the incircle radius of these gutters is approximately $r_{\mathrm{g}}=(\sqrt{2}-1)\xi _{\mathrm{f}} /(\sqrt{2}+1)$. The corresponding resistance can be estimated from Eq. (17), where a factor 1/2 should be added as there are four gutters in parallel around the droplet while there were only two below the membrane:

$$\begin{aligned} \beta = \frac{1}{2} \left( 0.56 \frac{H^4}{r_{\mathrm{g}}^4} \right) \sim 12560. \end{aligned}$$

(39)

This equation is only valid for a null velocity on the gutter boundaries, which is certainly not the case at the gutter/droplet interface. Therefore, the estimation should be considered as an upper bound on the resistance and on the subsequent hydrodynamic force:

$$\begin{aligned} F_{\mu } = \beta \frac{\mu _{\mathrm{o}} (L_{\mathrm{d}}-W)}{H^3} v W H S_{\mathrm{b}}. \end{aligned}$$

(40)

At the transition from regime TB to regime P, the capillary and hydrodynamic forces should balance, and therefore

$$\begin{aligned} {\mathrm{Ca}} = \frac{ \left( \frac{1}{\xi _{\mathrm{f}}} - \frac{1}{\xi _{\mathrm{b}}}\right) H^3}{\beta W^2 \left( \frac{L_{\mathrm{d}}}{W} - 1 \right) }. \end{aligned}$$

(41)

This equation is represented in Fig. 9. It captures very well the transition in the case of the long valve $L_{\mathrm{v}} = 6W$. However, it should be shifted towards slightly lower $L_{\mathrm{d}}$ in order to capture the observed transition at $L_{\mathrm{v}} = 3W$. Although it does not involve any fitting parameter, it also makes crude assumptions about both hydrodynamic and capillary forces that can hardly be satisfied when $L_{\mathrm{d}} \lesssim W$ as at this transition.

5 Conclusions

In this work, a systematic experimental exploration on the interactions between a microfluidic droplet and a pneumatic valve has been conducted, for various droplet length, capillary number, valve pressure and valve length. It revealed four main regimes: the droplet may pass below the membrane, it may remain trapped either below the membrane or in front of it, or it may split. The simultaneous interaction of several droplets with the valve has also been described. The transitions between these regimes have been identified as a function of the four aforementioned parameters. A first-order model made of algebraic equations only has been proposed to rationalise these transitions. It includes an estimation of the deflection of the membrane, the induced resistance and subsequent hydrodynamic force, and the droplet shape and subsequent capillary force. This model is implemented in a Matlab script provided in ESI (S6), which may be used in the early design of droplet microfluidic chips involving on-chip pneumatic valves. The model predicts the interaction regime corresponding to each set of physical parameters prescribed by the user.

The interactions between microfluidic droplets and pneumatic valves are rich, and nevertheless controllable in real time through an adjustment of both inlet and pneumatic pressures. A single microfluidic element (i.e. the valve) can simultaneously implement a myriad of elementary microfluidic operations, such as trapping, splitting or buffering. In both trapping modes evidenced here, the droplet content is permanently stirred and the risk of fouling is minimised thanks to the sustained lubrication film that separates the droplet from the channel walls (Kaminski and Garstecki 2017). With appropriate surfactants, the valve may also command the merging of successive droplets (Chen et al. 2017; Niu et al. 2008; Lin and Su 2008; Jeong et al. 2019). Finally, the huge increase of resistance associated to the trapping of a droplet in front of a valve may potentially trigger global flow reconfigurations inside the chip, which may serve for the implementation of event-driven microfluidic operations. This experimental description and subsequent model of the elementary interactions between a droplet and a valve should be helpful for the early design of complex droplet-based microfluidic systems such as addressable droplet arrays.