1 Introduction

Droplet-based microfluidics is an advanced liquid handling technique with advantages such as low contamination, high sensitivity, accuracy and reliability (Schneider et al. 2013; Whitesides 2006). Devices for droplet-based microfluidics are generally of low cost and small. The common configurations for droplet formation are the T-junction (Tan and Nguyen 2011; Xi et al. 2016) and the flow-focusing (Ma et al. 2016; Teo et al. 2017) geometry. Active control methods have been used in these devices to manipulate the formation of droplets. One of the most successful methods (Link et al. 2006; Yoon et al. 2014) uses an AC electric field to induce change in the droplet size (Chaudhuri et al. 2017; Malloggi et al. 2007; Yeo et al. 2004). The application of this form of external energy has also been previously utilised for droplet sorting (Baret et al. 2009), merging (Thiam et al. 2009), deformation (Xi et al. 2016), injection (Abate et al. 2013), and generation (Huang et al. 2017). Placing the electric field at the location of droplet formation induces an external force to the fluid interface, affecting the formation of the emerging droplet.

Without an applied electric field, the size of the droplet formed at a T-junction depends on the properties of the fluids and the channel geometries (Li et al. 2012). Common parameters affecting the droplet formation process are the capillary number \({\text{Ca}} = \mu_{\text{C}} Q_{\text{C}} /\sigma A\), the flow rate ratio \(Q_{\text{D}} /Q_{\text{C}}\), viscosity ratio \(\mu_{\text{D}} /\mu_{\text{C}}\), aspect ratio \(h/w_{\text{C}}\), and the channel width ratio \(w_{\text{D}} /w_{\text{C}}\), where \(\mu_{\text{C,D}}\), \(Q_{\text{C,D}}\) and \(w_{\text{C,D}}\) are the dynamic viscosity, flow rate and channel width of the corresponding phases. Subscripts \({\text{C}}\) and \({\text{D}}\) refer to the continuous and dispersed phases, respectively. Furthermore, \(\sigma\) is the interfacial tension, \(A\) is the cross-sectional area of the fluidic channel and \(h\) is the height of the channel. The two major droplet formation regimes are the dripping regime (shear-dominated) and squeezing regime (pressure-dominated) separated by the critical capillary number \({\text{Ca}}\sim 0.01\) (Garstecki et al. 2006). Upon the introduction of an alternate-current (AC) electric field, further extension of these regimes such as dripping, unstable and axisymmetric jetting was observed in flow-focusing configurations (Castro-Hernández et al. 2015). In these cases, the electric field induces a Maxwell stress at the fluid interface which has a pressure component normal to the interface, opposing the Laplace pressure of the interfacial tension (Castro-Hernández et al. 2015). Unfortunately, there is little mention of the effects of an AC electric field on droplet generation in devices employing T-junction designs, leading to our interest in the current work.

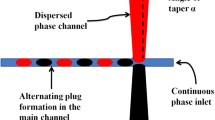
This paper experimentally investigates the change of droplet size by varying the AC electric field and the electrical conductivity of the dispersed phase, Fig. 1. The applied AC electric field induces a voltage \(V_{\text{TIP}}\) at the fluid interface between the continuous and dispersed phases as reported previously (Tan et al. 2014a, b). Following this approach, we vary the applied voltage \(V_{\text{APP}}\), the frequency \(f\), and the conductivity of the dispersed phase \(k\) to vary the size of the formed droplets. We introduce the normalised dimensionless variable \(G\) to represent the change in droplet size. We also establish a dimensionless response time of the system \(\tau^{*}\) to represent the response time of the fluid system relative to the change of the applied AC voltage. We also develop an electric circuit model to estimate the relationship between G and the relative response time \(\tau^{*}\).

Fig. 1
figure 1

Experimental setup showing the schematic diagram of the T-junction and the electrode configuration for the generation of a uniform AC electric field across the junction

Full size image

Following the establishment of the relationship between droplet size and the applied AC electric field, non-Newtonian fluids as dispersed phase were used to demonstrate that their behaviour also follows that of Newtonian fluids. We used dilute xanthan gum solutions with concentrations of 0.5 g/L and 1 g/L as shear-thinning non-Newtonian fluids. The results demonstrate the robustness of the control method that is independent of the viscoelasticity of the dispersed phase. Keeping the flow rates constant eliminates the effect of shear thinning phenomenon across all experiments, leaving the control to the AC voltage only. Lastly, we also demonstrate on-demand single droplet generation using 0.5 g/L xanthan gum solution. On-demand droplet generation using AC electric fields has been previously demonstrated by others (Gu et al. 2008; Malloggi et al. 2007). However, the method demonstrated here does not require direct fluid–electrode contact, and does not charge up the dispersed phase, making it suitable for a wide range of applications.

2 Experimental method

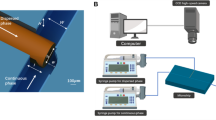
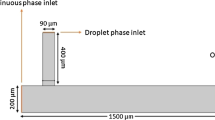
A PDMS T-junction device was fabricated using standard soft lithography and bonding to a glass slide coated with indium tin oxide (ITO). The channel dimensions are given in the Supplementary Figure A. The device was placed on an inverted microscope (Eclipse Ti, Nikon Instruments) for observation and image recording with a high-speed camera (Phantom Miro3, Vision Research), Fig. 1. The camera was linked to a computer, allowing real-time image acquisition and control of flow rates using a set of syringe pumps (neMESYS, Centoni GmbH).

Sunflower oil (Sigma Aldrich) was used in our experiments for the continuous phase with a viscosity of 53.5 mPa.s (Shojaeian and Hardt 2018). Initial experiments were conducted using deionised (DI) water with a viscosity of 1 mPa.s (Teo et al. 2017) and average interfacial tensions of 23.5 N/m (Shojaeian and Hardt 2018). Sodium chloride (NaCl, Chem-Supply Pty Ltd) was used to provide a series of different conductivities \(k\) up to 3200 µS/cm. The viscosities of these solutions have previously been well studied, and reported to be constant at room temperatures (Aleksandrov et al. 2012). For the demonstration with non-Newtonian fluids, DI water and xanthan gum powder (Sigma Aldrich) were mixed at two different concentrations, 0.5 g/L and 1 g/L, respectively. The polymer solutions were stirred at 40 °C using a magnetic stirrer for 30 min until no visible powder was observed and left to stand for another 30 min to remove bubbles before carrying out experiments. The polymer solutions have low shear viscosities of 205 mPa s for 0.5 g/L and 460 mPa s for 1 g/L as previously reported by Tam and Tiu (Tam and Tiu 1989), and an average interfacial tension of 23.5 mN/m (Shojaeian and Hardt 2018). Likewise, the conductivities are measured before each experiment. The viscosity of xanthan gum solutions is insensitive to salt concentration up to a high concentration levels (Rochefort and Middleman 1987); therefore, no other properties of the fluid apart from the conductivity are affected through this step.

Throughout the experiments, the size of the droplets generated at the junction was tuned only by the electric field. Electrodes were fabricated beside the junction where indium was filled into the electrode channels to accurately generate a localised electric field at the junction (Gañán-Calvo et al. 2018; Guo et al. 2018; Ma et al. 2016). The black electrodes in Fig. 1 were connected to the ground, and the two red electrodes next to the dispersed phase channel delivered the AC electric field to the junction. These electrodes are connected to an external setup comprising of a function generator (33210A, Keysight Technologies) and a voltage amplifier (Model 623B, Trek Inc). An oscilloscope (TBS1102B, Tektronix) was used to observe and record the output voltage of the amplifier which is directly fed to the device. The readings obtained from the oscilloscope are, therefore, the voltage \(V_{\text{APP}}\) used in our analysis.

The flow rates of the continuous and dispersed phases were, respectively, \(Q_{\text{Continuous}} =\) 150 μL/h and \(Q_{\text{Dispersed}} =\) 30 μL/h with a corresponding capillary number of \({\text{Ca}} = 0.016\), implying that the system is in the dripping regime where the droplet generation is dominated by the force balance between the shear force and interfacial force at the junction (Xu et al. 2008). Generated droplets posed a good monodispersity within 3%. Videos of droplet generation were captured at 500 frames/s with more than 60 droplets were generated per recording. Accordingly, we process each video using the Automated Droplet Measurement software (ADM) (Chong et al. 2016) to obtain the droplet areas from each video. Due to the relatively shallow microchannel, the droplets formed have a flat cylindrical shape which allows us to approximate the volume using the droplet area measured.

3 Results and discussion

We first systematically observed the influence of the applied voltage \(V_{\text{APP}}\) on droplet area for DI water, Fig. 2a. Making use of DI water with a low conductivity of approximately 0.65 µS/cm, the size of the droplet was observed with \(V_{\text{APP}}\) increasing from 0 to 400 VRMS while the AC frequency was maintained at 30 kHz. Initial observations reveal that the droplet size was relatively independent of the increase in \(V_{\text{APP}}\). The same experiment was repeated using water at a higher conductivity of 162 µS/cm, where a surprisingly different trend was observed. As \(V_{\text{APP}}\) increases, the droplet area decreases significantly by almost 40% of its original size, indicating that the applied electric field is the main player in the formation process. Increasing \(V_{\text{APP}}\) further reduced the droplet size of droplet with 162 µS/cm solution. The frequency of droplet generation at each point was also observed to be in good agreement with the equation \(f_{\text{Generation}} = Q_{\text{Dispersed}} /\left( {{\text{Area}}\; \times \;{\text{Height}}} \right)\) with up to 8% variation. We attribute these variations to slight inaccuracies in the droplet size measurement software (ADM), and fluidic instabilities during experimentation. With these initial results, we hypothesised that the conductivity of the dispersed phase plays an important role in controlling the size of the generated droplets.

Fig. 2
figure 2

Experimental results of droplet size versus the magnitude of the applied voltage: a droplet area against voltage VAPP for 0.65 µS/cm and 162 µS/cm DI water at AC frequency of 30 kHz; b images of droplet generation for both fluids from 0 to 400 VRMS. Scale bar denotes 100 µm

Full size image

Observation of the videos recorded for the 162 µS/cm solution also revealed a visible effect of the electric field on the droplet formation process, Fig. 2b. With the electric field turned on, the liquid finger was observed to be pulled out towards the ground electrode on the opposite side of the channel for the dispersed phase. The applied voltage \(V_{\text{APP}}\) induces a voltage at the liquid–liquid interface \(V_{\text{TIP}}\), resulting in a force perpendicular to the flow direction of the continuous phase. Tan et al. demonstrated that this force is similar to that induced by the Maxwell stress developed by the electric field on the fluid interface (Tan et al. 2014b). The force accordingly pulls the dispersed phase liquid finger further across the main channel, resulting in an increase in upstream pressure on the exposed liquid finger. This process leads to a greater hydrodynamic force pushing the liquid finger downstream, inducing a greater shear. The larger the magnitude of the applied voltage \(V_{\text{APP}}\), the larger is the pushing force, and the faster is the breakup process, leading to a smaller droplet.

Next, we investigated the effects of adjusting the AC frequency \(f\) for the electric field applied with five different conductivities of the dispersed phase. The five conductivity values were 0.63 µS/cm, 9.7 µS/cm, 32 µS/cm, 218 µS/cm and 3,200 µS/cm, with \(V_{\text{APP}}\) remaining constant at 273 VRMS and AC frequency ranging from 10 to 50 kHz. Figure 3a shows that different conductivities lead to different trends of droplet size as function of frequency. Corresponding microscope images for each conductivity and frequency are given in Fig. 3b. Fluids with a lower conductivity of 0.63 µS/cm and 9.7 µS/cm showed a decreasing effect of the electric field; whereas, the solution with a higher conductivity of 218 µS/cm shows an increasing effect. The effect of the electric field on the 32 µS/cm solution on the other hand shows a drastic drop toward 10 kHz and then increases slightly with increasing frequency \(f\). The solution with a high conductivity of 3,200 µS/cm showed a minimum change in droplet size compared to the case without the electric field. This behaviour can be explained by introducing the relative response time \(\tau^{*}\):

$$\tau^{*} = \frac{{\tau_{\text{RC}} \left( k \right)}}{{\tau_{\text{AC}} \left( f \right)}} = \frac{f}{k}\left( {\varepsilon_{\text{o}} \varepsilon_{\text{rDI}} } \right);$$
(1)
Fig. 3
figure 3

Experimental results showing the influence of varying AC frequency and conductivity of the dispersed phase: a Effect of conductivity k of the dispersed phase and frequency f on droplet area; b microscope images of droplet generation junction for fluids at various conductivities at different AC frequencies. The applied voltage \(V_{\text{APP}}\) remains constant at 273 VRMS. Scale bar denotes 100 µm

Full size image

\(\tau^{*}\) is defined as a ratio of the relaxation time or the RC response time of the dispersed phase with \(\tau_{\text{RC}} = \varepsilon_{o} \varepsilon_{\text{r}} /k\) against the periodic characteristic time of the applied AC electric field \(\tau_{\text{AC}} = 1/f\), where \(\varepsilon_{o}\) refers to the vacuum permittivity of 8.85 × 10−12 F/m, \(\varepsilon_{\text{r}}\) is the relative permittivity of 80 for deionised water. Thus, the response time related to the properties of “the fluidic system” is represented by \(\tau_{\text{RC}}\), while the characteristic excitation time of the AC source termed “the electric system” is determined by \(\tau_{\text{AC}}\). In this analysis, we only observe the order of magnitude due to the large range of \(\tau^{*}\). Experimental results indicate that the droplet size is affected by the electric field, and an optimal \(\tau^{*}\) exists for the maximum effect of the electric field.

To generalise the results across all sets of experiments, we introduce a dimensionless normalised variable \(G\) that is obtained using experimental droplet areas. This variable determines the measure of influence of the electric field on the droplet area:

$$G = \frac{{\Delta A_{\text{N}} }}{{\Delta A_{\text{MAX}} }} \propto \frac{{V_{\text{TIP}} }}{{V_{\text{APP}} }},$$
(2)

where \(G = 1\) shows that the droplet generated is experiencing the maximum influence of the electric field, \(\Delta A_{\text{N}}\) is the decrease in the droplet area upon activation of the electric field at each frequency and conductivity. \(\Delta A_{\text{MAX}}\) is the maximum change in droplet area obtained based on all the droplet areas tabulated from the different conductivity values. In this case, \(\Delta A_{\text{MAX}} =\) 4100 µm2 observed at \(f = 20\) kHz and \(k = 37\) µS/cm. These data were plotted against the relative response time \(\tau^{*}\) as given by the blue markers in Fig. 4a. At low values of \(\tau^{*}\) (base), \(G\) is observed to have an average value of 0.4, which climbs to a plateau of 1 when \(\tau^{*} \sim 3 \times 10^{ - 3}\) and subsequently drops.

Fig. 4
figure 4

Effect of relative response time on the droplet area: a Normalised change of droplet area G showing effect of electric field on droplet area for both Newtonian (blue markers) and non-Newtonian (red markers) fluids versus \(\tau^{*}\). Blue line shows \(V_{\text{TIP}} /V_{\text{APP}}\) against \(\tau^{*}\) obtained from the electric circuit. The applied voltage \(V_{\text{APP}}\) was kept constant at 273 \(V_{\text{RMS}}\); b Electric circuit of the system

Full size image

With the above experimental data, we hypothesise that the behaviour of the droplet formation is determined by the electric circuit of the system. The circuit depicted in Fig. 4b is derived based on the various elements within the device comprising of the positive and ground electrodes, PDMS walls, dispersed phase fluid column, glass layer and ITO layer which is another ground electrode. Details of this model are provided in Supplementary Figure A. The applied voltage \(V_{\text{APP}}\) was introduced via the positive electrode (red). The grounded electrodes (black) were placed on the opposite side of the main fluidic channel. Due to this arrangement of the electrodes, the electric field is perpendicular to the main microchannel (orange). The applied voltage \(V_{\text{APP}}\) here induces a voltage at the tip of the dispersed phase \(V_{\text{TIP}}\). This voltage depends directly on the resultant impedance of the dispersed phase segment that is within the positive electrodes and represented as \(Z_{\text{F1}}\) in Supplementary Figure A. For the dispersed phase segments that are outside of the positive electrodes, the corresponding impedances are given as \(Z_{\text{F2}}\) and \(Z_{\text{F3}}\). Each of these impedances is determined by the conductivity of the dispersed phase \(k,\) the characteristic length \(L_{\text{N}}\) and the cross-sectional area \(A_{\text{N}}\) of the segment: \(Z_{\text{N}} = \frac{{L_{\text{N}} }}{{kA_{\text{N}} }}\).

Apart from the resistive elements in the circuit, there are capacitive elements formed by the PDMS walls and glass layers. Schematic diagrams for these elements are provided in the insets of Supplementary Figure A. The capacitance due to the PDMS wall between the electrode and fluidic channel can be estimated using a parallel plate approximation, where \(C_{\text{P}} = 2\varepsilon_{o} \varepsilon_{\text{rPDMS}} \left( {\frac{{L_{\text{F1}} H}}{{W_{\text{PDMS}} }}} \right)\). Here, \(\varepsilon_{\text{rPDMS}}\) the relative permittivity of 2.5 for PDMS, \(L_{F1}\) the length of the electrode for dispersed phase section F1, \(H\) the height of the channel at 28 µm, and \(W_{\text{PDMS}}\) the width of the PDMS wall. The capacitance of the glass is expressed as two independent terms due to the high dependency on the conductivity of the dispersed phase fluid. For the case of a highly conductive dispersed phase fluid, the impedances of \(Z_{\text{F1}}\), \(Z_{\text{F2}}\) and \(Z_{\text{F3}}\) decrease significantly. This causes the capacitive effect of the area of glass directly below the dispersed phase within the electrodes to be more prominent. We represent this capacitance as \(C_{\text{G1}} = \varepsilon_{o} \varepsilon_{\text{rGLASS}} \left( {\frac{{L_{\text{F1}} W_{\text{D}} }}{{T_{\text{GLASS}} }}} \right),\) where \(\varepsilon_{\text{rGLASS}}\) is 7.75, \(W_{\text{D}}\) is the width of the dispersed phase channel and \(T_{\text{GLASS}}\) is the thickness of glass. Correspondingly, when a low-conductivity fluid is used, the impedances increase across the dispersed phase column, enhancing the effects of the capacitance of the glass below the column within the circuit. This capacitance is referred to as \(C_{\text{G2}} = \varepsilon_{o} \varepsilon_{\text{rGLASS}} \left( {\frac{{S_{\text{D}} }}{{T_{\text{GLASS}} }}} \right),\) where \(S_{\text{D}}\) is the surface area of the dispersed phase outside the electric field. \(C_{\text{G2}}\) in this scenario only takes into consideration the dispersed phase column outside the electrodes as the effect of the column within the electrodes is already accounted for by \(C_{\text{G1}}\). The total impedance of the circuit is:

$$Z_{\text{TOTAL}} \left( {f,k} \right) = Z_{\text{P}} \left( f \right) + Z_{\text{F1}} \left( k \right) + Z_{\text{F2,F3,G1,G2}} \left( {f,k} \right),$$
(3)

where \(Z_{\text{P}}\) is a function of frequency \(f\) that is due to the capacitance of the PDMS wall \(C_{\text{P}}\), \(Z_{\text{F1}}\) the impedance from \(F1\) and \(Z_{\text{F2,F3,G1,G2}}\) the impedance from the parallel segment of the circuit

$$Z_{\text{F2,F3,G1, G2}} \left( {f,k} \right) = \frac{1}{{2\pi jC_{\text{G1}} }}\left( {\frac{{\frac{{L_{2} }}{{kA_{2} }} + \frac{{L_{3} }}{{kA_{3} }} + \frac{1}{{2\pi jfC_{\text{G2}} }}}}{{\frac{1}{{2\pi jC_{\text{G1}} }} + \frac{1}{{2\pi jC_{\text{G2}} }} + \frac{f}{k}\left( {\frac{{L_{2} }}{{A_{2} }} + \frac{{L_{3} }}{{A_{3} }}} \right)}}} \right),$$
(4)

with \(j^{2} = - 1\).

Based on this circuit model, the overall relationship between the induced voltage and the applied voltage across the fluidic system is:

$$\frac{{V_{\text{TIP}} }}{{V_{\text{APP}} }} = \frac{{Z_{\text{F2,F3,G1,G2}} \left( {f,k} \right)}}{{Z_{\text{P}} \left( f \right) + Z_{\text{F1}} \left( k \right) + Z_{\text{F2,F3,G1,G2}} \left( {f,k} \right)}}.$$
(5)

The results from this equation are then plotted in Fig. 4a as given by the blue line. The line shows a base value of \(V_{\text{TIP}} /V_{\text{APP}} = 0.13\) that slowly climbs to a plateau of 0.8 when \(\tau^{*} \sim 3 \times 10^{ - 1}\) followed by a drop.

We observed a similar trend by comparing both the experimental data of the droplet size (blue marker) and the results obtained from Eq. 5 (blue line). First, the amplitude of both \(G\) and \(V_{\text{TIP}} /V_{\text{APP}}\) increases when \(\tau^{*} < 3 \times 10^{ - 3}\). After the peak, there was, however, a steady decline for the experimental data; whereas, the theoretical line continues to increase and peaks at \(\tau^{*} = 3 \times 10^{ - 1}\). Further evaluation of this phenomenon leads to a few observations. Firstly, the derived electric circuit is based on the electrode configuration used in the device and the fluidic properties of the dispersed phase fluid. This analysis is similar to the one introduced by Tan et al. (2014b). In the present work, we adopted the same electrode configuration and developed a similar electric circuit diagram. The analysis of the previous circuit diagram revealed a high-pass filter effect within the range of \(10^{4} < f/k < 10^{9}\), which translates to a range of \(10^{ - 6} < \tau^{*} < 10^{ - 1}\) with \(\varepsilon_{o} = 8.85 \times 10^{ - 12}\) and \(\varepsilon_{\text{rDI}} = 80\). This is similar to our current results given in Fig. 4.

Tan et al. experimentally ascertained that the influence of the electric field on droplet size agreed well with the analysis of the electric circuit. However, the team employed a flow-focusing configuration. This meant that the flow direction of the generated droplets was aligned along the electric field. Droplets were formed at the junction through squeezing the dispersed phase by the continuous phase flowing on either side of the column (Teo et al. 2017). This causes the column to eventually break and form a droplet (Christopher and Anna 2007). Activating the electric field induced a Maxwell stress that is normal to the interface and speeds up the droplet breakup. This process correspondingly generated smaller droplets (Saville 1997; Tan et al. 2014b). In the case of a T-junction configuration, the direction of the forces described is evidently different from the case of the flow-focusing configuration. Although the electrically induced Maxwell stress component is still in the same direction, the participating continuous phase exerts shearing instead squeezing of the liquid column (Xu et al. 2008). Furthermore, in contrast to the previous work with flow-focusing configuration, the direction of the droplet flow is also perpendicular from the electric field.

Considering that the main difference between the two works is in the junction design, we hypothesise that droplet size is affected by the junction geometry. The experimental data in Fig. 4 indicate that the effects on the droplet size are dominated by the electric field when \(\tau^{*} < 3 \times 10^{ - 3}\), shown by the increasing trends of both curves. After the peak, this dominance is lost as \(G\) declines rapidly even though the theoretical curve still increases. This behaviour is similar to the trend of the theoretical curve when \(\tau^{*} > 10^{1}\).

The values of \(\tau^{*}\) of the peaks of the two curves are two orders of magnitude apart, Fig. 4a. As the model is purely based on the electrical system and neglects the fluidic system, we expected this discrepancy. Optimisation of the channel dimensions may narrow the gap of discrepancy between \(V_{\text{TIP}} /V_{\text{APP}}\) and \(G\), but is currently out of the scope of this manuscript. The overall trend of the influence on the electric field is still effectively represented by both experimental data of droplet size change G and the electrical gain \(V_{\text{TIP}} /V_{\text{APP}}\). To further validate the electric circuit model, we tested the robustness of the electrical circuit by examining the breakdown voltage of the device.

Hypothetically, the device would fail when the 50-µm PDMS wall at the electrode breaks down, causing the indium used for the electrode to leak out into the main fluidic channel. This happens when the breakdown voltage of the PDMS material is reached and can be calculated based on the electric circuit model. According to manufacturer specifications, the dielectric strength of PDMS is given to be 19.7 MV/m. This means a 50-µm PDMS wall would break down if experiencing a voltage of 945 VRMS across it, corresponding to the predicted value of \(V_{\text{APP}} = 1041\)VRMS at 10 kHz for DI water at \(k = 263\) mS/cm. Using the salt solution at this \(k\) value, we experimentally increased \(V_{\text{APP}}\) until visually observed the breakdown of the PDMS wall. We observed a breakdown voltage at approximately \(V_{\text{APP}} =\) 1180 VRMS, close to the predicted value from Eq. 5. The slight deviation may be caused by fabrication imperfections whereby the wall thickness between the electrode and fluidic channel may have slight variations. Furthermore, the composition of the PDMS used for the fabrication may differ from that tested by the manufacturer. Nevertheless, this finding provides further evidence that the circuit developed is accurate and reliable.

As mentioned earlier, the electric circuit diagram neglects the flow field, and is, therefore, independent of the flow rates. The flow rates only determine the initial droplet size without the AC electric field. With the introduction of the electric field, the effects on the droplet size are assumed to be determined by the \(V_{\text{TIP}} /V_{\text{APP}}\) purely based on the electric circuit diagram. The effect on the droplet size at a different flow rate is also represented by the normalised dimensionless \(G\) variable, which already accounts for the initial drop size. Thus, we expect that the results would be the same for different flow rates given a condition that the flow rates remain in the dripping regime with \(0.1 < {\text{Ca}} < 0.3\) (Xu et al. 2008).

Proceeding with the above insights, experiments were conducted with non-Newtonian fluids, 0.5 g/L and 1 g/L xanthan gum solutions for the dispersed phase and compared against pure DI water. For this set of experiments, we keep the frequency constant at \(f = 30\) kHz, while increasing \(V_{\text{APP}}\) from 0 to 400 VRMS, Fig. 5a. By increasing \(V_{\text{APP}}\) and comparing the droplet areas, we observed that all three fluids show different trends where the one with the most drastic decrease was the 0.5 g/L xanthan gum solution with a conductivity of 67 µS/cm. For this fluid, the decrease in area was 59%, whereas 48.5% for the 1 g/L xanthan gum solution and 20% for the DI water. According to Eq. 5, increasing \(V_{\text{APP}}\), increases \(V_{\text{TIP}}\) correspondingly and, therefore, results in a decrease in droplet area. However, due to the different \(k\) values, the influence was not contingent. Thus, the experiment was repeated with the same conductivity value \(k\) of all three fluids, Fig. 5b. The results reveal that all fluids experience the same decreasing trend with all the droplet areas dropping by 40%. This is in good agreement with the evaluation of Eq. 5 for the particular relative response time \(\tau^{*}\), the droplet area decreases with increasing \(V_{\text{APP}}\) as predicted.

Fig. 5
figure 5

Effect of the AC electric field on Newtonian and non-Newtonian fluids with different concentrations of xanthan gum: a different conductivities lead to different voltage dependencies; b The same conductivity leads to the same voltage dependency. A constant AC frequency of 30 kHz was used in the experiments. Scale bars represent 100 µm

Full size image

This set of results also reveals another interesting phenomenon that the droplet area generated was the same for both Newtonian and non-Newtonian fluids. The typical shear-thinning behaviour that is characteristic of the pseudoplastic non-Newtonian fluid was not observed in our experiments due to the low shear rate in the experiment (Katzbauer 1998), and only the shear rate of the continuous phase affects the formation process. There was also no consequential difference on the droplet size when using 0.5 g/L or 1 g/L xanthan gum solution. This set of results further accentuates our hypothesis that the trends observed in Fig. 5a are different due to the different conductivities of the various fluids used and not due to the viscoelastic properties of each fluid.

Accordingly, we proceed to study the influence of the \(k\) and \(f\) for the 0.5 g/L xanthan gum solution and the results are plotted as the red markers in Fig. 4a. The \(k\) values used in this case are 67 µS/cm, 218 µS/cm and 3,200 µS/cm, respectively. \(\Delta A_{\text{MAX}}\) used for this case is 4,400 µm2 that was observed with \(f = 40\) kHz and 0.5 g/L xanthan gum solution at \(k = 218\) µS/cm. These conductivity values are the same for the Newtonian fluid. Plotting these results in the same figure as the DI water further proves the similarity of the Newtonian and non-Newtonian fluids. Observations from the red markers also show a base \(G = 0.68\) when below \(\tau^{*} = 2 \times 10^{ - 4}\), followed by a climb to 0.81 when \(\tau^{*} =\)\(2 \times 10^{ - 3}\). As the xanthan gum solution could not attain lower conductivity levels due to the presence of the polymer particles, relative response time of \(\tau^{*} > 10^{ - 2}\) could not be achieved. Based on both sets of results, we observe that both fluids behave in as similar manner against change in relative response time \(\tau^{*}\).

Finally, we demonstrate on-demand droplet generation using the 0.5 g/L xanthan gum solution. We employed a pressure controller (OB1, Elveflow) to achieve a stable interface, where no droplet was generated at first as previously reported (Teo et al. 2017). The pressures used for the continuous phase and dispersed phase was 300 mBar and 196 mBar, respectively, for two different conductivities of the dispersed phase. Conductivities of 67 µS/cm and 3200 µS/cm were chosen for this experiment as they represent both the peak and constant base of the trendline shown in Fig. 4a. For each of these fluids, we first achieve a stable liquid–liquid interface at the orifice before introducing the AC electric field. Upon the electric signal, the induced force pulls the liquid column out of the orifice where the pressure from the continuous phase accordingly generates a shearing force to slice off a portion of the extended finger, forming the droplet. After each signal is turned off, the liquid finger moves back into the orifice to form a stable interface due to the pressure balance between the two fluids. Each experiment was run by manually by introducing square electric signals at 300 VRMS, from 10 kHz to 60 kHz. A minimum of 10 droplets was obtained for each set of experiment and videos was recorded and processed accordingly to obtain the droplet areas.

Figure 6 shows the droplet area as function of the applied frequency. The 67 µS/cm line (red triangles) shows a decreasing trend with increasing frequency, indicating that raising the frequency leads in the formation of smaller droplets. This is similar to the trend observed for the same fluid in Fig. 4a, where increasing the frequency affects the change of droplet size as depicted by \(G\). In contrast, xanthan gum solution with 3200 µS/cm shows negligible change in droplet area over a range of frequency. The droplet area was also approximately 50% smaller than the one of 67 µS/cm xanthan gum solution. This result further verifies that our hypothesis can be applied in droplet on-demand on a T-junction for non-Newtonian fluids.

Fig. 6
figure 6

Droplet on demand demonstrated using pressure control for non-Newtonian fluid. Droplet area trends observed here fit well with the fluidic system trend observed in Fig. 3. Scale bars represent 100 µm

Full size image

4 Conclusion

We demonstrated the successful control of droplet generation in a T-junction device using Newtonian fluids using an AC electric field. We first experimentally examined the influence of the conductivity \(k\) of the dispersed phase on droplet area through initial experiments with a Newtonian fluid, while adjusting the magnitude \(V_{\text{APP}}\) and the frequency \(f\). The effects of the AC electric field on droplet area were observed with the use of a normalised droplet area G. The influence of the AC electric field can be determined with the help of an electric circuit model. The model provides an equation describing the relationship between key parameters such as the applied voltage \(V_{\text{APP}}\), the frequency \(f\), the conductivity of dispersed phase \(k\) and the voltage at tip of dispersed phase \(V_{\text{TIP}}\). Comparing experimental droplet size data and the gain of the electric circuit shows the same trend, indicating that the established correlation is sound. However, further investigation would be needed for the difference in absolute values for the frequency. The same electrical circuit also successfully predicts the breakdown voltage of the device, which was experimentally observed at approximately 1180 VRMS. Subsequently, non-Newtonian fluids, 0.5 g/L and 1 g/L xanthan gum solutions, were used as dispersed phase. The results indicate that the viscoelastic property of the dispersed phase does not affect the size of the droplet in this control scheme. The influence of the AC electric field on the 0.5 g/L xanthan gum solution also shows similar results as the Newtonian fluid where maximum \(G\) was observed with a conductivity of 67 µS/cm. We also successfully demonstrated on-demand droplet generation of non-Newtonian fluid using AC electric field on a pressure controller. Results obtained were consistent with earlier trends where the 67 µS/cm 0.5 g/L xanthan gum solution generated a larger droplet than the 3200 µS/cm counterpart. We conclude that our hypothesis is suitable for the prediction of the size of both Newtonian and non-Newtonian droplets.