An analytical model for void-free priming of microcavities

Abstract

The present work deals with the microfluidic evolution of capillary surfaces that are formed during the priming of microcavity structures with a non-wetting liquid. Due to the large contact angle of the priming liquid, a trapping of air within the microcavities poses a major impediment to a complete filling. We tackle this issue by developing a two-dimensional analytical model describing the geometrical shape of capillary surfaces formed in microcavity structures. In particular, the model is employed to derive two quantitative conditions for a void-free priming of a microcavity structure in terms of its aspect ratio, rounding parameters and the channel width. Microfluidic experiments are performed to verify the analytical results. Finally, we make use of the model to demonstrate a pressure-driven aliquoting of a non-wetting sample liquid in a flow chamber with an array of 55 microcavities by introducing a second immiscible liquid acting as a sealant. In this way, our work constitutes a basis for the design of microcavity-based liquid aliquoting structures that are used in various fields of application like PCR arrays, cell culture chips or digital reaction arrays.

1 Introduction

Microfluidic lab-on-chip systems promise a fully automated and rapid point-of-care analysis of patient samples using molecular diagnostics. By interconnecting various fluidic unit operations, the implementation of complex assay workflows into a microfluidic environment can be accomplished (Haeberle and Zengerle 2007; Strohmeier et al. 2015). However, to become a disruptive technology, a low-cost high-throughput fabrication technique is indispensable for mass production of disposable lab-on-chip cartridges. This requirement limits the range of materials suitable for cost-efficient lab-on-chip solutions. One material class is given by microstructured polymer substrates that can be cheaply produced by injection molding or thermoforming. However, polymeric substrates often feature hydrophobic or only slightly hydrophilic surface properties. The large contact angle of aqueous liquids on hydrophobic surfaces increases the risk of air trapping at channel corners, in cavities and dead-end structures, as well as geometries featuring large aspect ratios in general. Although surface modifications like a plasma treatment or the attachment of hydrophilizing molecules to the surface can improve the wettability of polymers (Jang et al. 2014), their formation requires an additional process step, they may affect chemical reactions, and their long-term stability under certain environmental conditions have to be secured. Therefore, we see an urgent need for the development of strategies dealing with bubble-free priming of microfluidic structures that exhibit a hydrophobic or only slightly hydrophilic surface. Known filling strategies are based on the solubility of priming gases in the fluid like carbon dioxide in aqueous solutions (Zengerle et al. 1995), capillary effects like pinning at phaseguides (Goldschmidtboeing et al. 2006; Vulto et al. 2011), centrifugation (Mark et al. 2011; Hoffmann et al. 2012), evacuation (Takulapalli et al. 2012), or the dissolution of monosaccharides attached to the surface (Wang et al. 2012).

Such strategies are particularly important for void-free priming of microfluidic structures with large aspect ratios. An outstanding example for such structures is given by microcavity arrays that can be employed for microfluidic aliquoting of liquids into sub-microliter amounts (Liu et al. 2009; Poritz et al. 2011). Compartment-based aliquoting devices enable a plurality of applications ranging from quantitative multiplex polymerase chain reaction (PCR) (Liu et al. 2009; Poritz et al. 2011; Matsubara et al. 2004; van Doorn et al. 2007) or digital PCR (Shen et al. 2010; Heyries 2011; Schuler et al. 2016) and enzyme-linked immunosorbent assay (ELISA) (Rissin 2010) to single molecule analysis (Zhang et al. 2012), cell culture (Lindstrom et al. 2009) and sequencing (Margulies 2005). Furthermore, microcavity array structures may be combined with enhanced array-based (optical) detection techniques like supercritical angle fluoresence (Hung et al. 2015) or systems like whispering-gallery mode micro-goblet lasers (Wondimu et al. 2017) in order to realize novel powerful lab-on-chip devices for multiplex sample analysis. However, in contrast to the large variety of developed filling strategies and cases of application, fewer work (Wang et al. 2012; Sposito and DeVoe 2017) was done regarding the appropriate layout of microcavities so far.

Here, we address this problem by taking a look at the evolution of capillary surfaces formed in microcavity structures. In particular, we focus on the priming of microcavities with non-wetting liquids, where a trapping of air inside the microcavities is likely to occur. We develop a two-dimensional geometrical model to elucidate the relationship between the layout of a microcavity and its microfluidic priming behavior. The predictions of the model are compared with experimental results and comprehensively discussed. Finally, we apply our findings to show that an aliquoting of a liquid can be accomplished in a microfluidic flow chamber comprising an array of nanoliter volume cavities by the introduction of a second immiscible liquid acting as a sealant. The aliquoting approach used here may be easily implementable in polymer-based lab-on-chip devices.

Fig. 1

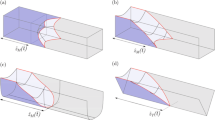
a Geometrical construction of a two-dimensional capillary surface that is confined between a flat and an arbitrarily shaped boundary described by the function f(x). The angle $\alpha =\arctan (f'(x))$ represents the slope of the lower boundary. b Cavity structure corresponding to the geometry parameters $s = r_1 = d = r_2 = w/3$. The shown capillary surfaces were calculated for a contact angle $\theta =120{^{\circ }}$. The rectangle indicated by the gray dashed line marks the area that is considered for the deviation of the filling conditions in panel c. c Sketch of the capillary surface with maximum meniscus tilt that is formed around the critical point C

2 Analytical model for two-dimensional capillary surfaces formed in microcavity structures

When dealing with small volumes of liquids, interfacial forces often exceed inertial and gravitational forces. This fact is expressed by the so-called capillary length, which amounts for water $l_{\mathrm{cap}}= \sqrt{\gamma /(\rho g)} =2.7 \,\mathrm {mm}$ at $20\,^\circ$C with $\gamma =0.073 \,\mathrm {J}/\,\mathrm {m}^2$, $\rho =10^3 \,\mathrm {kg}/\,\mathrm {m}^{3}$, $g=9.81 \,\mathrm {kg}/\,\mathrm {m}\,\mathrm {s}^2$ (Jensen et al. 2004). A minimization of the surface energy results in a spherical shape of small droplets and more general in a certain pressure that is related to the principal curvatures of a capillary surface, as stated by the Young–Laplace equation. Furthermore, for liquid interfaces that are in contact with solid surfaces, the interplay of the present surface forces at the three-phase lines corresponds to the formation of a characteristic contact angle comprised by the liquid surface and the solid surface. Based on these fundamentals, we derived a simple geometrical model (see Fig. 1) for artificial two-dimensional capillary surfaces that are formed in microfluidic structures by making the following two assumptions.

Firstly, we assumed that at the two three-phase points (labeled A and B in Fig. 1a) the tangent to the boundary of the liquid-confining solid and the tangent to the capillary surface of the liquid comprise a certain fixed angle $\theta$. This assumption reflects the formation of a contact angle due to the present interfacial forces. We disregard contact angle hysteresis and consider the idealized case of a “quasi-static” process (Jensen et al. 2004), where variations of the contact angle due to the dynamics of the microfluidic process are neglected. Later on, we will demonstrate that such a behavior can be achieved experimentally by slow down the filling process appropriately that only slight variations in the contact angle occur.

Secondly, we assumed that the two-dimensional capillary surface has the shape of a circular arc, which can be characterized entirely by its radius of curvature r. The circular shape of a two-dimensional capillary surface follows directly from the Young-Laplace equation under the absence of gravity.

Figure 1a illustrates the geometrical construction of a two-dimensional capillary surface that is situated between an upper flat boundary ($y=0$) and a lower arbitrarily shaped boundary given by $y=f(x)$ based on the two assumptions made above. For this particular situation, the radius of curvature r of the capillary surface can be expressed in terms of the contact angle $\theta$, the slope of the lower boundary represented by the angle $\alpha =\arctan (f'(x))$ with $f'(x)={\mathrm{d}}/{\mathrm{d}}x \, f(x)$, and the vertical dimension y of the channel. By exploiting trigonometric relations (see Fig. 1a) and making use of the symmetry $\cos (x) = \cos (-x)$ and $\sec (x)=1/\cos (x)$, we arrive at the following analytical expression for the radius of curvature r in dependence on $\theta$, $\alpha$, and y:

$$\begin{aligned} r(\theta ,\alpha ,y) = y/2 \, \sec (-\alpha /2) \, \sec (\alpha /2-\theta +\pi ) \end{aligned}$$

(1)

Fig. 2

a Contour plot of the absolute value of the radius of curvature r in dependence on the angle $\theta$ and the slope of the lower boundary $\alpha$ in a logarithmic false color scale representation for a fixed vertical dimension y of the confinement. b Contour plot of the radius of curvature r in dependence on $\alpha$ and the vertical dimension $y/y_{\mathrm{max}}$ of the confinement for a fixed contact angle $\theta =112.5{^{\circ }}$. c Contour plot of the meniscus tilt t in dependence on $\alpha$ and $y/y_{\mathrm{max}}$. The shown trajectory illustrates the evolution of the meniscus tilt in a cavity structure parameterized by s, $r_1$, d, and $r_2$. The insets in panels a–c exhibit specific cases as described in the text

Equation 1 allows us to calculate two-dimensional capillary surfaces formed in various geometrical confinements. However, here we will focus on a microfluidic channel with a dead-end microcavity structure as depicted in Fig. 1b. This specific geometry may be parameterized by the channel size s, the width w and depth d of the cavity, and the rounding parameters $r_1$ and $r_2$. The cavity illustrated in Fig. 1b corresponds to the parameter choice $s=r_1=d=r_2=w/3$. Figure 1b also shows a sequence of two-dimensional capillary surfaces that has been calculated with Eq. 1 for a contact angle $\theta =120{^{\circ }}$. The sequence may be interpreted as the quasi-static evolution of a two-dimensional liquid meniscus during the propagation through the specific cavity structure. The radius of curvature r and tilt t of the capillary surface (see Fig. 1a) vary significantly during the various stages of the filling process. The variation of these parameters will be discussed in the following within the context of Fig. 2. Furthermore, Fig. 1c will also be discussed within the context of Fig. 2.

Figure 2 comprises three contour plots with insets that illustrate the dependence of the radius of curvature r and tilt t of the capillary surface on the contact angle $\theta$, the slope of the lower boundary $\alpha$, and the local vertical dimension y of the microfluidic structure. The insets provide visualizations of some specific cases. Figure 2a shows a contour plot of the radius of curvature r in dependence on the contact angle $\theta$ and the slope of the lower boundary $\alpha$ for a fixed vertical dimension y of the structure. The false color scale is chosen logarithmically and indicates the absolute value of the radius of curvature, i.e., the sign of curvature is neglected in the plot. Hence, the plot is symmetric around the point $(\alpha ,\theta )=(0^\circ ,90^\circ )$. For a flat confinement ($\alpha =0^\circ$, vertical dashed line in Fig. 2a), the absolute value of the radius of curvature r is minimal for the extremal contact angles $\theta =0^\circ$ and $\theta =180^\circ$, namely half the channel width y/2 (see Eq. 1 and inset in the bottom left corner). For contact angles in between these extremal values $0^\circ \le \theta \le 180^\circ$ (see inset in the bottom right corner), the absolute value of the radius of curvature increases toward $\theta =90^\circ$, where the meniscus is stretched out and the radius of curvature becomes infinite. In general, that means for arbitrary values of $\alpha$, the radius of curvature diverges if the (Concus-Finn) condition $\alpha = 2 \theta - \pi$ is fulfilled (see inset in the top right corner). The condition defines a divergence line in Fig. 2a, which splits the shown parameter space of $\alpha$ and $\theta$ into two areas of opposite sign of the radius of curvature (not visible in Fig. 2a since the absolute value of the radius of curvature is plotted). The plot illustrates that for contact angles $45^\circ \le \theta \le 135^\circ$ there always exists an $\alpha = 2 \theta - \pi$ where the meniscus is stretched out (see inset in the top right corner and corresponding capillary surfaces in Fig. 1b or Fig. 3a and i).

Figure 2b shows a corresponding contour plot of the absolute value of the radius of curvature r in dependence on the slope of the lower boundary $\alpha$ and the normalized vertical dimension of the confinement $y/y_{\mathrm{max}}$ (where $y_{\mathrm{max}}$ is the maximum vertical dimension of the structure, see inset) for a fixed contact angle $\theta =112.5^\circ$. In this case, the divergence line is located at $\alpha =2\theta -\pi =2\cdot 112.5^\circ -180^\circ =45^\circ$. For any other value of $\alpha$, the radius of curvature r is proportional to the vertical dimension y of the confinement (see Eq. 1).

Figure 2c shows a contour plot of the meniscus tilt $t=y \tan (-\alpha /2)$ which amounts to the horizontal distance of the both three-phase points A and B, that is the distance between the orthogonal projection $A'$ of A on the line $y=0$ and the point B (see Fig. 1a). The meniscus tilt t becomes maximal for an angle $\vert \alpha \vert = 90^\circ$ and is proportional to the vertical dimension y of the confinement. Hence, during the propagation through a microcavity structure like the one shown in Fig. 1b, the meniscus tilt t becomes maximal when the three-phase point B reaches the lower end of the cavity side wall. This finding is illustrated by the trajectory (white line) and the insets shown in Fig. 2c, which indicate the evolution of the meniscus tilt t during the propagation of the capillary surface through a cavity structure parameterized by s, $r_1$, d, and $r_2$ (see Fig. 1b or inset in Fig. 2b also).

The maximum tilt, that is the maximum horizontal expansion which is spanned by the capillary surface, plays an important role in the filling process of the considered dead-end cavity structure: If the maximum horizontal expansion of the capillary surface exceeds the width of the cavity, the capillary surface comes into contact with both side walls of the cavity before the cavities’ ground is entirely wetted by the liquid. This will cause a trapping of air at the cavities’ ground. Based on this criterion, we will now derive conditions from our model that allow us to predict the filling behavior of a particular cavity structure. Furthermore, the conditions serve as guidelines for an appropriate design of microcavity structures providing a void-free priming (VFP) with a given sample liquid.

For the sake of simplicity, we approximate the cavity structure by a rectangle of side lengths $2\, r_2+w$ (total width) and $s+r_1+d+r_2$ (total height) as indicated by the dashed gray line in Fig. 1b, and consider the tilt of the capillary surface at the critical point C where $\alpha =-90^\circ$ and $t=y \tan (-\alpha /2)=y=s+r_1+d$. The situation at the critical point C is sketched in more detail in Fig. 1c for contact angles $90^\circ \le \theta \le 180^\circ$. Figure 1c indicates two areas (I) and (II) (dark gray colored regions) where a trapping of air may take place at the cavities’ ground. Based on the above formulated criterion, we are now able to derive two conditions for a void-free priming of a microcavity structure: (I) $2\, r_2+w>c+r$ and (II) $r_2>c+r-a$. With the geometrical relations $c=r \sin (\theta -\pi /2)$,  $r=a/\sqrt{2}/ \sin (\theta -\pi /4)$, and $a=s+r_1+d$ (see Fig. 1c) we obtain for $\theta \ge 90^\circ$ the two VFP conditions in the following form:

$$\begin{aligned} {\mathrm{AR}}_1 \equiv (2 \cdot r_2+w)/(s+r_1+d) > g(\theta ) \end{aligned}$$

(2)

and

$$\begin{aligned} {\mathrm{AR}}_2 \equiv r_2/(s+r_1+d) > g(\theta )-1 \end{aligned}$$

(3)

where

$$\begin{aligned} g(\theta ) = \frac{\cos (\theta )-1}{\cos (\theta )-\sin (\theta )} \end{aligned}$$

(4)

is a dimensionless parameter, that only depends on the (contact) angle $\theta$. The both conditions given in Eqs. 2 and 3 relate the aspect ratios ${\mathrm{AR}}_1$ and ${\mathrm{AR}}_2$ with the void-free priming geometry parameter $g(\theta )$. The parameter $g(\theta )$ increases strictly monotonically in the interval $90^\circ \le \theta \le 180^\circ$ with the extremal values $g(90^\circ )=1$ and $g(180^\circ )=2$.

For $\theta =90^\circ$, the first VFP condition yields $2 r_2 + w > s + r_1 + d$, that is the width of the cavity have to be larger than its height to allow for a void-free priming (see Fig. 1b, c). The second VFP condition (Eq. 3) is always fulfilled for $\theta \le 90^\circ$, since no air trapping can occur at the left corner of the cavities’ ground when a wetting sample liquid is used. For contact angles $\theta >90^\circ$, both conditions limit the aspect ratio of a microcavity as well as the minimum rounding $r_2$ at the ground of the cavity that are necessary to enable a void-free priming. In the following, we will compare our analytical results with findings from microfluidic experiments.

Fig. 3

a Model-based calculation of the evolution of a two-dimensional capillary surface that is formed during the filling of a cavity structure. The assumed contact angle is $\theta = 110^\circ$ and the design parameters are $3\, s = 6\, r_1 = 6\, r_2 = 4\, w = 1200 \,\upmu \mathrm {m}$ and $d = 0 \,\upmu \mathrm {m}$. b–i Microscopic snapshots taken during the filling process of a microcavity structure corresponding to the simulation results shown in panel a. All images are equally scaled; the scalebar in panel b corresponds to $200\,\upmu \mathrm {m}$. j Schematic drawing of a microfluidic flow chamber with an array of 55 cavities. The cross section of each of the cavities has got the same proportions as the cavity structure investigated in panels a–i. k–n Micrographs showing the filling of the cavity array structure sketched in panel j. All images are equally scaled; the scalebar in panel k corresponds to $500\,\upmu \mathrm {m}$. The field of view is indicated by the black frame in panel j

3 Comparison of the analytical model with experimental results

For the microfluidic experiments, test structures were fabricated from injection molded polycarbonate substrates (Makrolon, Bayer MaterialScience) by ultra short pulse laser ablation with a frequency-tripled neodymium yttrium-aluminum-garnet (Nd:YAG) laser light source ($355\,\mathrm {nm}$ wavelength, $2\,\mathrm {W}$ average power, 3–5$\,\mathrm {ps}$ pulse duration, $500\,\mathrm {kHz}$ repetition rate, Lumera GmbH). After laser micromachining, the structured polycarbonate substrates were sealed with a pressure sensitive sealing film (HJ Bioanalytik GmbH).

During the microfluidic experiments, the liquids were introduced into the microfluidic test structures via on-chip meandering channels, which served as a microfluidic resistance in order to throttle the flow rate appropriately. For an assumed Hagen-Poiseuille flow profile inside the meandering channels with a quadratic cross section of width $w=100\,\upmu \mathrm {m}$ and a total length of about $l=30\,\mathrm {mm}$, one obtains for an applied pressure $\varDelta p=5\,\mathrm {hPa}$ and a viscosity $\eta =1\,\mathrm {mPa}\,\mathrm {s}$ a volume flow rate of ${\mathrm{d}}V/{\mathrm{d}}t = K\, w^4/(12\, \eta l) \, \varDelta p \approx 60 \,\mathrm {nl}/\,\mathrm {s}$ (with $K=0.4218$). To trigger the microfluidic flow in the experiments, a pressure controller (DPI 515, Druck Ltd.) was used to apply a small underpressure on the outlets of the microfluidic structures. In this way, average flow rates as low as a few $\mathrm {nl}/\mathrm {s}$ were experimentally achieved. An optical microscope (BX61, Olympus K.K.) was used to image the temporal evolution of the capillary surfaces that were formed in the test structures during the filling process.

Figure 3a shows a drawing of the microcavity structure which corresponds to the parameter choice $s=400\,\upmu \mathrm {m}$, $r_1=200\,\upmu \mathrm {m}$, $d=0\,\upmu \mathrm {m}$, $r_2=200\,\upmu \mathrm {m}$, and $w=300\,\upmu \mathrm {m}$. The sketched two-dimensional capillary surfaces were calculated with Eq. 1 for a contact angle $\theta =110^\circ$. Again, they feature a significant variation in both the radius of curvature r and the meniscus tilt t.

Panels (b) to (i) of Fig. 3 show a series of microscopic snapshots that was taken during the priming of a polycarbonate test structure with blue-dyed deionized water (with 0.1% Tween 80). The scalebar in panel (b) of Fig. 3 corresponds to $200 \,\upmu \mathrm {m}$. The test structure has got a constant height of $200 \,\upmu \mathrm {m}$ and the in-plane dimensions given above and in panel (a) of Fig. 3 (cavity volume about $56\,\mathrm {nl}$). The microscopic snapshots depict the microfluidic evolution of the capillary surface during the priming of the microcavity structure and reveal characteristic features of the filling process: From panel (e) to (h), the upper three-phase point of the capillary surface remains nearly at the same position, whereas the lower three-phase point propagates along the cavities’ ground. This stopping of the upper three-phase point is reproduced by the filling model as visible in panel (a) of Fig. 3. The snapshot in panel (i) of Fig. 3 depicts the situation where the liquid meniscus is stretched out entirely and the radius of curvature of the capillary surface becomes infinite. This characteristic feature is also predicted by the analytical model (see panel (a) of Fig. 3). All in all, a complete filling of the cavity structure is achieved, which is consistent with the deviated void-free priming conditions given by Eqs. 2 and 3 that are fulfilled for the chosen geometry and contact angle: ${\mathrm{AR}}_1=1.167>1.074=g(110^\circ )$ and ${\mathrm{AR}}_2=0.333>0.047=g(110^\circ )-1$. However, despite the overall good agreement between model and experiment, dynamic effects and contact angle hysteresis, which are not included in the model, may also play a role in the real filling process. This becomes evident in the snapshot depicted in panel (g), where the liquid surface slightly deviates from an exact spherical shape. Later on, we will discuss the limitations and short-comings of the model in more detail.

Next, a microfluidic flow chamber with 55 circular cavities in a hexagonal arrangement was investigated (see top view sketch in panel (j) of Fig. 3). The arrangement of the cavities has been chosen hexagonally in order to achieve both a maximum areal density of cavities and a constant inter-cavity distance. Each of the circular cavities has got the same (out-of-plane) cross section which resembles the geometric proportions of the cavity structure investigated in panels (a)–(i) of Fig. 3. Panels (k)–(n) of Fig. 3 show four micrographs that were taken during the filling process of the cavity array chamber with blue-dyed deionized water (with 0.1% Tween 80). The field of view of the micrographs is indicated by the black frame in Fig. 3j. The micrographs illustrate that the cavities are filled one after another and column by column. This ordered column by column priming behavior can be explained by a phase-guiding (Vulto et al. 2011) that is caused by the individual cavity columns. In this way, a wetting of the whole flow chamber can be assured. Furthermore, each of the cavities is entirely filled without any trapping of air inside. Although this observation might be expected on the basis of the previous analytical and experimental results from the cavity structure (panels (a)–(i) of Fig. 3), we will discuss the role of the third dimension later on within the context of Fig. 4.

Fig. 4

a Sketch of a cavity structure representing the design parameters $s = d = 2\, r_1 = 2\, r_2 = 2\, w =200\,\upmu \mathrm {m}$. The shown capillary surfaces have been calculated based on the filling model for an assumed contact angle $\theta = 110^\circ$. b–f Micrographs revealing the evolution of the capillary surface during the propagation through the cavity structure. All images are equally scaled; the scalebar in panel b corresponds to $200\,\upmu \mathrm {m}$. g Micrograph showing an arrangement of five cavities. Due to the large aspect ratio of the cavities, a trapping of air takes place inside. The scalebar corresponds to $500\,\upmu \mathrm {m}$. h Schematic drawing of a microfluidic flow chamber with an array of 55 cavities. The cross section of each of the cavities has got the same proportions as the cavity structure investigated in panels a–g. i–l Micrographs taken during the filling of the cavity array chamber sketched in panel h. The white dashed circles indicate two cavities showing a differing filling behavior. All images are equally scaled; the scalebar in panel i corresponds to $500\,\upmu \mathrm {m}$. The field of view is indicated by the black frame in panel h

Figure 4 shows the results for another cavity geometry given by the parameter set $s=200\,\upmu \mathrm {m}$, $r_1=100\,\upmu \mathrm {m}$, $d=200\,\upmu \mathrm {m}$, $r_2=100\,\upmu \mathrm {m}$, and $w=100\,\upmu \mathrm {m}$. Again, the model was employed to calculate the two-dimensional capillary surfaces depicted in panel (a) of Fig. 4. The corresponding experimental results are shown in Fig. 4b–g. The first three micrographs in panels (b) to (d) of Fig. 4 demonstrate that a circular water-air meniscus is formed, which is consistent with the filling model. However, then the water-air meniscus stabilized by the surface tension touches the opposite side wall of the cavity before the cavities’ ground is entirely wetted by the liquid. As a consequence, air is trapped at the lower part of the cavity and the cavity is not entirely filled with the liquid (see panels (e) to (g) of Fig. 4). This experimental finding is also predicted by the filling model in terms of the void-free priming conditions given by Eqs. 2 and 3 that are not fulfilled for the chosen geometry and the present contact angle: ${\mathrm{AR}}_1=0.6<1.074=g(110^\circ )$ and ${\mathrm{AR}}_2=0.2>0.047=g(110^\circ )-1$.

Again, the filling of a flow chamber with an array of 55 cavities of a corresponding (out-of-plane) cross section was investigated (see sketch in panel (h) of Fig. 4). Like before, the liquid front propagates column by column through the cavity array chamber so that the whole chamber is wetted by the liquid (see panels (i)–(l) of Fig. 4). However, the majority of the cavities (29 of 44, that is 66% of the cavities visible in panel (l) of Fig. 4) is nearly entirely filled with the liquid in such a way that the amount of trapped air inside these cavities is much lower than the amount of trapped air inside the nearly two-dimensional cavity structure of same cross section (see panel (g) of Fig. 4 and the corresponding analytical result from the model in panel (a) of Fig. 4).

In order to understand this difference one should keep in mind that the model given in Sect. 2 describes artificial two-dimensional (2d) capillary surfaces. These 2d capillary surfaces only coincide with planar cross sections of 3d capillary surfaces for the case that the planes of principal curvatures of a 3d capillary surface are fixed during the propagation through the whole microfluidic structure. This is approximately the case for the (nearly two-dimensional) cavity structures investigated in Fig. 3b–i and 4b–g, where the height of the structures is fixed and significantly smaller than the other two dimensions of the structures. For this particular case, one plane of principal curvature approximately coincides with the image plane of the micrographs. Accordingly, we found overall good agreement between model and experiment in Fig. 3a–i and 4a–g. However, for arbitrary three-dimensional microfluidic structures, the model will only provide an approximative description of capillary surface cross sections: In general, a spatial variation of the confinement in all three dimensions will result in the formation of three-dimensional capillary surfaces with varying planes of principal curvature. Hence, planar cross sections of these capillary surfaces will differ from the two-dimensional capillary surfaces given by the model. In our case, the three-dimensional cavities of circular shape have a varying third dimension, which affects the capillary surface formation and thus the filling behavior. This can explain why a more complete filling of the three-dimensional cavities is experimentally achieved compared to the nearly two-dimensional cavity structures of same cross section.

Fig. 5

Aliquoting of a sample liquid in a cavity array structure by introducing a second immiscible liquid acting as a sealant. a Sketch of the aliquoting approach. Due to the large contact angle of the second immiscible liquid (shown in yellow), aliquots of the sample liquid (shown in blue) are enclosed inside the cavities. b and c Snapshots of the filling process of a cavity array chamber with 55 circular cavities. The scalebar in panel b corresponds to $1000\,\upmu \mathrm {m}$. The average flow rate of the filling process was about $0.5\,\upmu \mathrm {l}/\,\mathrm {s}$. An entire filling of all cavities is achieved. d and e Sealing of the filled cavities with mineral oil. The average flow rate was about $0.1\,\upmu \mathrm {l}/\,\mathrm {s}$. After sealing, each cavity contains an aliquot of the sample liquid (color figure online)

However, in addition to the fundamental difference between the investigated microfluidic structures and the limited applicability of the model to arbitrary three-dimensional situations, it is evident that the amount of trapped air inside the individual cavities varies significantly in the flow chamber filling experiment (in contrast to the experimental results shown in Fig. 2g). The white dashed circular lines in panels (i)–(l) of Fig. 4 highlight two cavities showing a differing filling behavior. Panels (i) and (k) of Fig. 4 demonstrate that the two cavities are reached by the liquid meniscus in a similar manner. Nevertheless, the cavity highlighted in panel (l) of Fig. 4 is nearly entirely filled, whereas air is trapped inside the cavity highlighted in panel (j). This finding illustrates that the experimental filling behavior may be also influenced by pinning effects at surface inhomogeneities or the process dynamics. Hence, both the sample quality as well as the fundamental limitations of the two-dimensional model must be taken into account when the model is applied to experimental situations. For substrates with a homogeneous surface quality and nearly two-dimensional microfluidic structures, an overall good agreement between model and experiment can be expected from the results given in Figs. 3 and 4.

4 Sample liquid aliquoting by oil sealing

After having elucidated the relationship between the layout of a cavity and its microfluidic priming behavior, we are finally going to address the aliquoting of a sample liquid inside a flow chamber comprising an array of microcavities by introducing a second immiscible liquid into the flow chamber after filling it with sample liquid. It appears likely that such microcavity array structures can be used for an aliquoting of a sample liquid if the contact angle $\theta _2$ of the second liquid $L_2$ with respect to the primed surface is sufficiently larger than the contact angle $\theta _1$ of the priming liquid $L_1$ with respect to the unprimed surface as illustrated in Fig. 5a.

In order to investigate this aliquoting approach experimentally, we used a flow chamber comprising an array of 55 circular microcavities as before. Panels (b)–(e) of Fig. 5 show four snapshots that were taken during the filling (panel b,c) and oil sealing (panel d, e), respectively. First, a blue-dyed PCR master mix was introduced into the flow chamber with an average flow rate of about $0.5\,\upmu \mathrm {l}/\,\mathrm {s}$. Due to the specific cavity layout, a complete priming of all 55 cavities is achieved as depicted in panels (b) and (c) of Fig. 5. After the filling, mineral oil was introduced into the flow chamber through the inlet channel with an average flow rate of about $0.1\,\upmu \mathrm {l}/\,\mathrm {s}$. A stable interface is formed between the aqueous phase and the oil phase due to the immiscibility of the two phases. As a consequence, the blue-dyed aqueous phase is pushed out of the flow chamber by the oil phase while it remains within the cavities (see panels (d) and (e) of Fig. 5). This finding can be explained by a large contact angle $\theta _2$ that is comprised by the oil phase and the wetted polymeric surface (see panel (a) of Fig. 5): If the contact angle $\theta _2$ is large enough, a trapping of the aqueous phase within the cavities takes place (just like a trapping of air inside the cavities may take place during priming). A close inspection of Fig. 5d and e reveals that some blue-dyed aqueous phase remains at the outer edges of the flow chamber also. Evidently, the aqueous phase present here is not displaced by the oil phase. This behavior can be as well ascribed to the large contact angle comprised by the oil phase and the wetted polymer surface and the present capillary forces: It can be considered as the counterpart of spontaneous capillary wetting of edges when the Concus–Finn condition is fulfilled.

5 Discussion and conclusions

Although two-dimensional capillary surfaces are artificial, they can be described analytically. Furthermore, they coincide with cross sections of three-dimensional capillary surfaces within their planes of principal curvature. The nearly two-dimensional cavity structures investigated in Fig. 3a–i and 4a–g thus demonstrated a good agreement between model and experiment. For arbitrary geometries with varying planes of principal curvature, the calculated two-dimensional capillary surfaces may serve as approximative solutions. This was the case for the three-dimensional microfluidic structure investigated in Fig. 4h–l where a more complete filling of the cavities could be achieved in comparison to its two-dimensional counterpart in Fig. 4a–g. Apart from this limitation, the simple, textbook-like model allows a rapid analytical calculation of two-dimensional capillary surface cross sections formed in various microfluidic geometries. As such it can be applied in accordance with numerical simulation methods based on computational fluid dynamics, lattice-Boltzmann equation or molecular dynamics (Chibbaro et al. 2009) in order to design microfluidic structures appropriately for a void-free priming.

However, an accurate flow rate control was required experimentally in order to minimize dynamical effects and to generate low flow rates ensuring quasi-static filling conditions. From a practical point of view, the need for a precise flow control may pose an impediment. In order to overcome this limitation, further work will address the development of more hydrophilic microcavities for capillary-assisted nanoliter-scale aliquoting of liquids. For instance, we found that microcavity arrays made from a hydrophilic float glass substrate allow for a highly reliable filling of the microcavity structures without any trapping of air inside due to the formation of capillary microchannels at the substrates’ rough surface. Depending on the application case the use of (non-polymeric) components with tailored wetting properties might be advantageous and also acceptable from a cost perspective.

In conclusion, we theoretically and experimentally investigated the microfluidic evolution of capillary surfaces formed in nanoliter-scale microcavity structures. We proposed a two-dimensional analytical model for capillary surfaces and compared it with the results from microfluidic experiments performed in polymeric test structures. Despite the short-comings of the two-dimensional model, like the neglect of contact angle hysteresis, pinning effects, dynamic phenomena, and the limited applicability to three-dimensional situations, it was in overall good agreement with the experimental results. Both model and experiments demonstrated that the observed filling behavior is closely related to the layout of a microfluidic cavity due to the shape of the formed capillary surfaces. From the model we derived quantitative conditions that indicate a void-free priming of a microcavity structure. Accordingly, the results presented here may serve as a basis for the design of compartment-based aliquoting devices that will find application in PCR analysis, cell culture or digital reaction arrays.