1 Introduction

Ultrasensitive, label-free, cost-effective, compact and deployable sensing systems are critical for medical diagnostics, environmental monitoring and homeland security applications. Chip-scale optical sensing systems integrating photonic, electrical and fluidic functions are especially intriguing for label-free sensing applications due to the high sensitivity of optical sensors, the compactness of chip scale systems and the low-cost fabrication techniques that are amenable to well-developed mass production.

Optical whispering gallery modes (WGMs) are morphology-dependent resonances occurring in a microcavity (or microresonator) and can be used for ultrasensitive optical detection (Righini et al. 2011; Soria et al. 2011; Ward et al. 2018; Vollmer et al. 2002; Avino et al. 2014; He et al. 2011; Tanyeri and Kennedy 2008; Zhi et al. 2017; Zhang and Wu 2017; Baaske and Vollmer 2012; Zhu et al. 2007, 2010). The utilization of high-quality (high Q factor) resonances in biosensing offers specific advantages such as a small sample volume, low concentration of analytes and high sensitivity. Generally, an optical microcavity is simply composed of a solid dielectric medium and can take various morphologies such as spheres, disks, toroids and capillary tubes (Soria et al. 2011; Baaske and Vollmer 2012). As a result of their compact mode volume in micron scale and ultrahigh Q factor, WGM microcavities enable significant (Raman or fluorescent) signal amplification due to the strong light–analyte interactions thereon. Detection of single viruses and other biomolecules has been demonstrated by monitoring the frequency shift of a WGM upon even trace amount of target analytes anchoring on the resonator surface (Baaske and Vollmer 2012). Since the refractive index of the optical cavity should be higher than the surrounding medium to confine the light inside by total internal reflection, silicon or glass is commonly used in case the surrounding medium is water or just ambient air. The vast majority of previous WGM works were performed on solid resonators such as glass beads and silica disks/toroids. Despite the high Q factor of solid WGM resonators, most of the light is confined inside their dielectric bulk and only the evanescent field can interact with the analytes adhered on the external surface of resonators, thereby limiting the further enhancement of Q factor. Hitherto, demonstration of feasibility of high-performance WGMs sensing in a fluidic environment was achieved only in rare cases, in which the cavity tube was filled with analyte solution or a bead-like resonator was immersed in the sample liquid and WGMs were monitored by a wavelength-swept laser. However, when the microresonator is surrounded by an aqueous solution, its Q factor is further decreased due to the reduced refractive index contrast resulting in more radiation loss. Moreover, these solid resonators are not readily amenable to biosensing in fluidic carriers, e.g., red cells in serum. Therefore, it is desirable to use liquid medium containing analytes itself as the optical cavity that enables more intimate and more intense interactions between the target analytes and the stimulated WGMs.

A liquid microdroplet with its characteristic size shorter than its capillary length (Newton et al. 2006), i.e., ~ 2.7 mm for water, can naturally form nearly perfect spherical shape with exceptionally smooth surface due to the dominant surface tension effect of liquid. This intriguing trait endows the microdroplet an ideal microcavity candidate of an impressive quality factor. Owing to their biocompatibility, structural flexibility and electrical tunability, liquid microdroplet resonators have attracted increasing interests in the optical sensing field (Ward et al. 2018; Avino et al. 2014; Bar-David et al. 2018; Zheng et al. 2018; Giorgini et al. 2017; Lin et al. 1992; Tzeng et al. 1984; Tanyeri et al. 2007; Kiraz et al. 2007a; Jonáš et al. 2012; Anand et al. 2016; Zullo et al. 2016; Dahan et al. 2016; Ashkin and Dziedzic 1977). For a microdroplet-based resonator, apart from the desired high Q factor of the microcavity, an efficient and facile coupling scheme is still necessary especially for chip-level implementations. So far, either tapered fiber coupling or free-space beam coupling are the most commonly utilized coupling methods in nearly all the WGMs-related work (Vollmer et al. 2002; Giorgini et al. 2017; Kiraz et al. 2007a; Jonáš et al. 2012; Gregor et al. 2010). In either coupling method, precise alignment of the tapered fiber or free-space beam adjacent to the equatorial surface of a resonator is required. Hence, they are not very facile to implement in a complex sample matrix. Although it has been more than 40 years since the first suggestion of droplet resonator sensors, the practical applications of this potentially powerful technique are still quite limited (Ashkin and Dziedzic 1977). Therefore, unlike their solid counterparts, to realize a feasible microdroplet-based high-performance sensing system, a robust, stable and facile optical coupling method must be developed.

Ease in light coupling, stableness in mechanics, convenience in implementation and preserving a high optical performance are key factors required for the high Q factor optical sensing. The WGMs along the meridian rim of a liquid microdroplet resting on a superhydrophobic surface meet most of those requirements. In particular, such meridian WGMs can be dexterously stimulated by a strip waveguide embedded in the substrate surface. Even though a superhydrophobic surface that can sustain a droplet with the contact angle as high as nearly 180° has been demonstrated (Tian et al. 2014), the meridian plane of a sessile microdroplet resting on a surface is still inevitably deformed. Besides maintaining the microdroplet within tens of microns in diameter, the deformation in the meridian plane can be controlled by tailoring the surface roughness of the substrate and hence the microdroplet’s wettability.

In this paper, we show that WGMs can be agilely excited and adaptively sustained along the meridian circumference of a liquid microdroplet sitting on a nanostructured superhydrophobic surface. To study the influence of nanoscale roughness on the microdroplet morphology including contact angle and local interface curvature and its impact on WGMs sensitivity, we conducted wetting characterization on the superhydrophobic surface by Surface Evolver (SE) and the finite-difference time-domain (FDTD) simulation of WGMs performance in this configuration. It is also shown that an embedded strip waveguide underneath the sessile droplet can efficiently stimulate such modes in a facile manner, offering a novel and robust optofluidic platform for ultrahigh Q factor sensing of trace chemicals and biomolecules.

2 Microdroplet resonator morphology modeling

For sensitive bioassay applications, a perfectly round liquid droplet is the ideal optical cavity in favor of the generation of high Q factor WGMs. In the presence of gravity, however, a sessile water droplet on a hydrophobic surface takes the shape of a spherical dome, as its contact angle cannot reach beyond 120° (Nishino et al. 1999). In particular, the morphology of the sessile droplet, whose degree of deformation can be reflected by the droplet’s contact angle and the ratio of droplet’s vertical height to lateral width, has a significant impact on the meridian WGMs generation. To alleviate gravity-induced flattening, the characteristic size of a sessile droplet should be much shorter than the capillary length, i.e., a small Bond number (Shin et al. 2009), so that surface tension becomes dominant to determine the droplet morphology, which makes the droplet close to a spherical shape with a higher value of the WGM quality factor. Moreover, for the purpose of reducing the optical radiation loss and saving the computational cost, a liquid droplet of 20 μm in diameter is selected by us for the optical meridian WGM study.

On the other hand, micro/nanoscale roughness decorated on a smooth surface has considerable influence on a fluid’s wettability thereon. Therefore, introducing nano/microstructures onto a smooth hydrophobic surface can enhance its hydrophobicity to ultrahydrophobicity or even to superhydrophobicity (Ma and Hill 2006; De Gennes 1985; Cheng et al. 2012; Zhao and Cheng 2018), which can sustain a water microdroplet with a contact angle exceeding 150°. In this regard, the wettability of a liquid microdroplet on a solid surface is determined collectively by the interfacial energies between the solid, liquid and air phases and the solid surface roughness. Figure 1 is the schematic of a liquid microdroplet sitting on a rough substrate with an array of nanopillars. Actually, the effects of surface roughness on contact angle were first reported in the seminal work of Wenzel (1936) regarding a sessile droplet penetrating the surface roughness and the work of Cassie and Baxter (1944) regarding a droplet sitting atop surface roughness, respectively. Both works introduced an apparent contact angle θA on a rough surface, which is related to the intrinsic contact angle θY on a flat surface, as shown in Fig. 1.

Fig. 1
figure 1

Schematic of droplet morphology and interfacial tensions on a micro/nanostructured surface, where a is the width of square pillars, s is the gap between pillars, h is the pillar height, hsag stands for the sagging of droplet base in to the roughness interstices, hgap is the space between the droplet curvature and the base surface of roughness interstices, θY is the intrinsic contact angle on a flat surface, and θA is the apparent contact angle on a rough surface. \( \gamma_{\text{ls}} \), \( \gamma_{\text{sv}} \), and \( \gamma_{\text{lv}} \) are the interfacial tensions of the liquid–solid interface, the solid–air interface, and the liquid–air interface, respectively

Full size image

While θY is determined by the interfacial tensions, i.e., Young’s equation, θA is dependent on the liquid’s interfacial tensions and the surface roughness in a combined manner. In this study, we assumed the liquid microdroplet cavities sit in the Cassie state with ultrahigh mobility. Based on the energy minimization principle, the Cassie–Baxter relation can be derived as (Banerjee 2008):

$$ \cos \theta_{\text{A}} = - 1 + f(1 + \cos \theta_{\text{Y}} ), $$
(1)

where \( f = a^{2} /(a + s)^{2} \) is the fraction of solid–liquid contact.

Besides the optofluidic properties of the microresonator itself, understanding and developing such a microdroplet-based cavity system necessitates detailed information of the microdroplet morphology such as local interface curvature, local variation in the contact angle and their evolutions with the changes of the geometrical shape or wettability of surface roughness. Therefore, the three-dimensional morphologies of sessile microdroplets resting on top of nanopillared surfaces are modeled by SE in this work. SE is a finite element method (FEM)-based liquid morphology analyzing software (Brakke 1992). After defining the initial droplet profile, SE evolves the surface toward the state with minimal surface energy by a gradient descent method.

The morphology of a sessile droplet in the Cassie–Baxter state depends on both the solid–liquid contact fraction \( f \) (Banerjee 2008) and the micro/nanopillar arrangement or configuration (Kashaninejad et al. 2012, 2013). For simplifying the modeling of droplet morphology and quantitatively analyzing the droplet contact angle, the apparent contact angle θA is modulated by adjusting the structural parameters of the nanopillar array based on Eq. (1). In this study, the textured surface is conformably coated by a thin layer of fluoropolymer (PFC1601V, Cytonix), so the intrinsic contact angle θY is constrained at 112° (Banerjee 2008), the water–air interfacial tension \( \gamma_{\text{lv}} \) is 0.072 N/m and the gravity acceleration g is 9.81 m/s2 in the simulation. SE distinguishes the inner and outer surface directions of a droplet surface by the surface normal, and the outer droplet surface is subject to the interfacial tension, including the liquid–solid tension and the liquid–air tension. Thus, a microdroplet in the Cassie–Baxter state would require assigning energy boundary conditions to the wetted portion of the nanopillars plus the free microdroplet–air interface. Accordingly, the difference between the liquid–solid interfacial tension and the solid–air interfacial tension \( \gamma_{\text{ls}} - \gamma_{\text{sv}} \) defines the energy boundary condition of the wetted nanopillar surface, and the liquid–air interfacial tension \( \gamma_{\text{lv}} \) defines the microdroplet-free facets. In practice, the energy of a nanopillar facet is implemented as a line integral applied to the edges of all nanopillar facets as suggested by Brakke (1992). The area of each facet is sequentially modified by the local surface energy and the global energy. The propagation of constraints during refinement is handled internally by SE. Every energy minimization step conducts a sequence of iteration, mesh refinement and vertex averaging. Finally, the Newton–Raphson method (Ishimoto and Morishita 2014) of energy minimization is executed for computation convergence. The convergence is regarded as achieved when the surface energy decrement is less than 10−19 units. In this SE model, a microdroplet of 20 µm in diameter in the final equilibrium state consists of ~ 30,000 individual nodes and the node number varies with the nanopillar geometries.

By adjusting the geometric parameters of the nanopillars, six different morphologies of water microdroplets in the Cassie–Baxter state with apparent contact angle θA ranging from 140° to 170° are achieved (see the morphology column in Fig. 5). Those microdroplet-based cavity models were adopted as the microcavities for the meridian WGMs simulation in this study. For the comparison purpose, all the microdroplet cavities were simulated with their lateral spreading radius r ~ 10 μm. The related geometrical information of the microdroplets and the nanopillar patterns are listed in Table 1.

Table 1 SE simulation results of sessile microdroplet morphologies on rough surfaces
Full size table

As shown in Fig. 2, the average difference between the theoretical contact angles predicted by Cassie–Baxter equation (Eq. 1) and the SE simulation results is only 1.35°, indicating all the six simulated models are in the Cassie state. We are also interested in the microdroplet local curvature within pillar intervals where sagging might exist. In our simulation, the smallest sagging depth hsag is ~ 3.7 nm for the case with θA = 141.7°; the biggest sagging depth is ~ 19.8 nm for the case with θA = 170.9°. The extent of sagging is governed by the balance of the internal Laplace pressure force and the capillary force (Bartolo et al. 2006). The Laplace pressure pushes the liquid interface into the surface interstices, whereas the capillary force functions as the counteracting force. The sagging extent is related to the intrinsic contact angle θY of the microdroplet and the geometry of surface textures (Deng et al. 2009; Extrand 2002; Jung and Bhushan 2007, 2008; Kusumaatmaja et al. 2008; Reyssat et al. 2006, 2007). For a microdroplet sitting on a relatively sparsely pillared surface, the microdroplet–pillar contact line length is shorter compared to a microdroplet on the densely textured surface. As a result, the capillary force as an antiwetting force (Fabbri et al. 2006) becomes relatively small so that the sagging depth tends to increase, which is consistent with our SE results as shown in Table 1. With the detailed morphology obtained, we studied the optical sensitivity of the microdroplet-based cavity.

Fig. 2
figure 2

Comparison of theoretical contact angles with simulated contact angles by Surface Evolver

Full size image

3 WGMs along the meridian plane of a microdroplet

Firstly, as a reference to the deformed cases, an ideal spherical water microdroplet with a radius of 10 μm was considered as the optical microcavity in the FDTD simulation. Our FDTD simulation approach is validated by comparing with the theoretical and experimental WGM results in the literature (Jampani et al. 2013), which shows an excellent agreement with each other. The wavelength of ~ 750 nm was chosen in the FDTD simulation due to its low water absorption. In this undeformed spherical cavity, q stands for the number of field maxima in the radial direction (Righini et al. 2011; Soria et al. 2011). The field distributions of its modes with q = 1, 2, 3 and 4 are illustrated in Fig. 3 and exhibit a perfect spherical symmetry. For the deformed microdroplet cavities with different contact angles, the modes stimulated in their meridian planes are mainly the deformed WGMs (see their resonant mode field distributions in Figs. 4 and 5). These deformed meridian WGMs show the following features: (1) Although the deformation of microdroplets affects the mode field distribution losing spherical symmetry, each mode in the deformed cavity could be easily traced back to the undeformed mode with the same q by scrutinizing the modes’ appearance similarity in Figs. 3 and 4. (2) Similar to an undeformed microdroplet, the deformed microdroplet cavity can also support many meridian WGMs with different q values. The allowed modes in a deformed microdroplet do not always start from q = 1 and heavily depend on the degree of droplet deformation. As shown in Fig. 4, the least q for the allowed modes in the deformed microdroplet with a large θA of 170.9° starts from 1 while it is from 2 in the deformed microdroplet with θA = 161.5°. This phenomenon can also be verified by their normalized intensity spectrum as illustrated in Fig. 5. For example, the narrow peaks corresponding to the least q = 1, 2, 3, and 4 for the cases with θA = 170.9°, 161.5°, 151.2° and 146.5°, respectively, are observed. (3) In each deformed microdroplet, the mode with the least q dominates the whole field distribution because its mode quality factor Q is much higher than the Q values of other modes with larger q values. Therefore, we only consider the mode with the least q in the following discussion. This feature is shown by the normalized intensity spectrums of the deformed microdroplets as illustrated in Fig. 5. For instance, even though the modes with q = 3, 4 also exist in the microdroplet of θA = 170.9° as shown in Fig. 4a, only the peaks corresponding to the modes of q = 1 and 2 are observed in Fig. 5, in which the mode with the least q = 1 exhibits the narrowest and highest peak implying the largest Q factor.

Fig. 3
figure 3

The mode field distributions of the undeformed water microdroplet cavity of 10 µm in radius with different q values. q is the number of field maxima in the radial direction. d is the distance from the cavity centroid to the principle maxima of the undeformed WGMs with different q values

Full size image
Fig. 4
figure 4

The resonant mode field distribution inside the deformed microdroplets: a the deformed q = 1, 2 and 3 meridian WGMs in the microdroplet with θA = 170.9°; b the microdroplet cavity morphology and the deformed q = 2 and 3 meridian WGMs in the microdroplet of θA = 161.5°

Full size image
Fig. 5
figure 5

The microdroplet cavity morphology, the intensity spectrum, and the least q meridian WGM field distribution for each microdroplet

Full size image

The feature (2) mentioned above for the deformed microdroplets can be further understood by analyzing the distance d from the cavity centroid to the principle maxima of the undeformed WGMs with different q values and the distance d′ from the centroid to the baseline of the deformed microdroplet with different contact angles. Quantitatively, the distances d are calculated to be 9.642 μm, 9.009 μm, 8.556 μm and 8.152 μm for the undeformed modes with q = 1, 2, 3 and 4, respectively (see the blue dashed lines in Fig. 6b, c). However, the distance d′ are 9.43 μm, 9.1 μm, and 8.148 μm for microdroplets with θA = 170.9°, 161.5°, and 151.2°, respectively. For the microdroplet cavity of θA = 170.9°, its d′ value of 9.43 μm is less than but close to the undeformed distance d of 9.642 μm for q = 1. Phenomenologically, this shorter distance d′ would lead to a deformed meridian WGM of q = 1 deviating from the undeformed counterpart. This depressed distance, on the other hand, indicates that other deformed modes with higher q can still be generated, as evidenced by the existence of the higher order modes in Fig. 4a. Moreover, with further decreasing d′, it would block the generation of deformed meridian WGM of q = 1. Thus, the microdroplet of θA = 161.5° cannot form the mode of q = 1 due to the short distance d′ = 9.1 μm. Similar to the microdroplet of θA = 161.5°, which cannot achieve meridian WGM of q = 1, the microcavities with a relatively smaller θA are constrained to generate deformed meridian WGMs with larger q values.

Fig. 6
figure 6

a The contours of sessile microdroplet profiles. b The variations of the baseline length l and the centroid-to-baseline distance d′ of the deformed water microdroplets with r = 10 µm. The blue dashed lines indicate the distances d from the principle maxima of the modes to the cavity centroid for undeformed modes of q = 1, 2, 3 and 4, respectively. c The cross sections of the deformed microdroplet cavities with different θA. The blue dashed lines are the positions of the principle maxima for the undeformed modes of q = 1, 2, 3 and 4, respectively

Full size image

The performance of an optical resonator is evaluated by the quality factor Q that is related to the dissipation rate of photons confined in the cavity. Generally, Q factor is associated with the spectrum of the resonator cavity through the formula Q = λres/ΔλFWHM, where λres and ΔλFWHM are the resonant wavelength and the full width at the half-maximum of individual resonant peaks in the spectrum, respectively. With regard to the WGMs along the meridian periphery of a microdroplet resonator resting on a superhydrophobic surface, the total quality factor Qtotal can be physically formulated by

$$ 1/Q_{\text{total}} = 1/Q_{\text{intrinsic}} + 1/Q_{\text{coupling}} , $$
(2)
$$ {\text{and}}\,1/Q_{\text{intrinsic}} = 1/Q_{\text{ab}} + 1/Q_{\text{rad}} + 1/Q_{\text{ss}} + 1/Q_{\text{def}} , $$
(3)

where Qintrinsic is the intrinsic quality factor of the deformed cavity, Qab due to the liquid absorption-related loss, Qrad due to the curvature radiation-related loss, Qss due to the surface roughness scattering-related loss, Qdef due to the deformation-related loss and Qcoupling due to the tunneling loss when using a waveguide to inject energy into the microcavity’s near field.

Theoretically, the curvature radiation-related loss factor Qrad is > 1011 and the scattering-related loss is safely negligible for the undeformed fundamental WGM with q = 1 (Giorgini et al. 2017; Jonáš et al. 2012). The material absorption loss dominates the upper limit of the intrinsic quality factor and this contribution can be expressed as \( Q_{\text{ab}} = 2\pi n/\alpha_{\text{ab}} \) (Giorgini et al. 2017; Jonáš et al. 2012), where water refractive index n = 1.33 and water absorption coefficient \( \alpha_{\text{ab}} \) ≈ 2.6 m−1 at the working wavelength. The resulting Qab ≈ 4.3 × 106 sets the upper limit of Qintrinsic, which is in the order of 106 for the undeformed spherical microdroplet cavity. Therefore, the intrinsic Qintrinsic of a sessile microdroplet cavity cannot reach beyond this upper bond due to the inevitable deformation along its meridian rim as shown in Fig. 7. For example, regarding deformed meridian WGM with the least q = 2 in the cavity of θA = 161.5°, Qintrinsic = 1.1 × 104; with regard to the deformed meridian WGM of q = 3, Qintrinsic = 1.2 × 103 for the case of θA = 151.2°. Besides, in the undeformed cavity, a large q mode is associated with a relatively low Qintrinsic value due to the large radiation loss. Its Qintrinsic values are estimated to be 4 × 105, 1 × 104, 2 × 103 for the high order modes of q = 2, 3, 4, respectively. Similarly, a microcavity with a smaller contact angle may lead to deformed meridian WGMs with large q values and consequently a relatively lower Qintrinsic. Therefore, the field energy loss increases as the contact angle of the deformed microdroplet cavity decreases. Moreover, Qintrinsic of the deformed meridian WGM is smaller than that of the undeformed cavity in the same mode, which shows this deformed meridian WGM has more energy loss compared to the same order undeformed mode. Obviously, such loss mainly results from the microdroplet deformation. The deformation-related loss dominates the intrinsic quality factor of the deformed microdroplets and this deformation-related loss is mainly caused by two factors: (1) the WGMs have a mismatch at the junction between the microdroplet base and the microdroplet above the pillar section, and (2) the distance d′ resulted from the cavity deformation generates a large radiation-related loss. In Figs. 5 and 6, as the contact angle θA decreases, the baseline length l increases and the distance d′ decreases, indicating a stronger mode mismatch (i.e., the deviated distribution of field maxima in the radial direction of the meridian plane), a larger radiation-related loss and consequently a smaller Qintrinsic factor. To better describe how the contact angle related-deformation influences Qintrinsic, we define two aspect ratios in the meridian plane as η1 = (r − d′)/r and η2 = l/2r, where r is the lateral radius of the deformed droplet and l is the baseline length as shown in Fig. 5. Compared to a perfectly spherical cavity, smaller values of η1 and η2 indicate the mitigated deformation of a microdroplet cavity; whereas η1 = 0 and η2 = 0 are associated with a perfectly circular rim of the meridian cross section of the microdroplet. For example, a sessile microdroplet with θA = 170.9° has the aspect ratios of η1 = 5.7% and η2 = 28.5%, indicative of a relatively small deformation. If the contact angle further decreases, the aspect ratio will increase, resulting in a larger deformation and a lower Qintrinsic. As shown in Fig. 7, when θA varies from 161.5° to 151.2°, η1 changes from 9.0 to 18.5%, and η2 increases from 36.3 to 50.9%, demonstrating a remarkable increase in the cavity deformation. Thus, it is not surprising to observe that Qintrinsic falls from 1.1 × 104 to 1.2 × 103 as θA decreases from 161.5° to 151.2°.

Fig. 7
figure 7

Q factor and the aspect ratio of the deformed microdroplet cavities

Full size image

4 Lab-on-a-chip coupling scheme to the microdroplet cavity

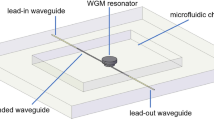
Due to the intriguing existence of the high Q-factor WGMs along the meridian plane of a sessile microdroplet, such modes could be excited in a more facile way, which is very different from the current schemes based on tapered fiber coupling or free-space beam coupling along the equatorial periphery. In this respect, a strip waveguide (Sun et al. 2013, 2014; An et al. 2009) embedded in a chip underneath the microdroplet can be utilized for coupling light into the meridian plane of the microdroplet cavity. This on-chip stationary coupling scheme without mechanical moving parts, e.g., motor-driven nanostage, would be realized by designing the strip waveguide on a nanoroughness-decorated chip surface, making it highly favorable for lab-on-a-chip applications. As shown in Fig. 8, the sessile microdroplet rests on top of a superhydrophobic chip surface with an embedded strip optical waveguide. The nanopillar array, fabricated by deep reactive ion etching or thermally dewetting platinum film on a solid substrate, functions as the superhydrophobic chip surface. This planar chip plays dual roles in this configuration: one is to mechanically support the deformed microdroplet on the surface without additional complex position-stabilizing equipment and the other is to accommodate the built-in waveguide for adaptive optical coupling.

Fig. 8
figure 8

Schematic and operation principles of the sessile microdroplet cavity system on a chip. We put forward to use meridian WGMs sensing of trace analytes contained in a liquid microdroplet. Coupling light or radiation into the microdroplet is accomplished by placing it on a chip surface that incorporates a planar optical waveguide, along with electrodes that can tune the morphology of the microdroplet cavity via electrowetting to optimize the coupling

Full size image

There are two basic requirements for an efficient light-coupling scheme: one is through the phase (or the effective refractive index neff) matching, and the other is by the sufficient spatial overlap of the evanescent electromagnetic fields between the mode of the sessile microdroplet cavity and that of the strip waveguide. Therefore, it is necessary to firstly investigate the effective refractive index neff of the deformed microdroplet and then the strip waveguide is designed accordingly. However, the neff of the deformed microdroplet cannot be directly calculated due to its loss of spherical symmetry. Instead, the neff of an undeformed spherically symmetric microdroplet cavity can be readily calculated by FEM. Moreover, as discussed in Sect. 3, the deformed meridian WGM with different q values can be traced back to the undeformed mode with the same q. Therefore, the neff of the deformed meridian WGM should be close to that of the undeformed counterpart. It is reasonable that the strip waveguide is firstly designed to match the neff of the undeformed microdroplet and is then adjusted to match the deformed microdroplet. For a microdroplet with radius of 10 µm, the neff of the undeformed modes with q = 1, 2 and 3 are calculated to be 1.2806, 1.2790 and 1.2743, respectively. Therefore, the neff of the waveguide was initially estimated around 1.28, based on which we can find the optimum waveguide geometry for matching the deformed microcavity. Besides, based on the refractive index of water, SiO2 and porous silicon dioxide (p-SiO2) were selected as the component materials for the strip waveguide and the substrate, respectively (Jeong et al. 2014; Wan et al. 2017). The variation of the neff of the strip waveguide with height H and width W is plotted in Fig. 9, from which the values of H = 0.525 μm and W = 0.8 μm, for example, are matching neff = 1.28.

Fig. 9
figure 9

The dependence of the calculated effective refractive index neff of the proposed strip waveguide on geometrical parameters of the waveguide and undeformed microdroplet cavity size. The black lateral dash line indicates neff ~ 1.28 of the underformed microdroplet with a radius of 10 µm

Full size image

The coupling between the strip waveguide and the microdroplet cavity can be analyzed by the coupled-mode theory. The amplitude of the input power in the waveguide and the amplitude of the output power in the waveguide are \( E_{\text{i}} \) and \( E_{\text{o}} \), respectively. Thus, the field transmission coefficient, which is the ratio of \( E_{\text{o}} \) to \( E_{\text{i}} \), can be described by (Grover et al. 2003):

$$ T = \frac{{E_{\text{o}} }}{{E_{\text{i}} }} = \frac{{\sqrt {1 - k^{2} } - \exp [ - (\alpha /2 + j\beta )L]}}{{1 - \sqrt {1 - k^{2} } \exp [ - (\alpha /2 + j\beta )L]}}, $$
(4)

where \( \alpha \) is the amplitude loss coefficient of the electric field in the microdroplet, and \( k \) is the coupling power loss factor between the waveguide and the microdroplet. The effective propagation constant \( \beta \) in the microdroplet is defined by \( \beta = (2\pi /\lambda )n_{\text{eff}} \), where \( n_{\text{eff}} \) is the effective refractive index of the microdroplet, and \( L \) is the circumference along the meridian plane of the microdroplet. On resonance, \( \beta L = 2m\pi \), where m is an integer. In case \( 1 - k^{2} = \exp ( - \alpha L/2) \), the numerator becomes zero and therefore the transmitted optical power at the output of the waveguide goes to zero on resonance, i.e., the critical coupling.

The transmitted optical power at the output of the waveguide relies heavily on the microdroplet-waveguide interface geometry, often termed as the gap with a height hgap between the base of the deformed microdroplet and the waveguide. The influence of hgap on the optical performance of the system with θA = 161.5°, W = 0.7 μm, H = 0.6 μm, and with θA = 161.5°, W = 1.0 μm, H = 0.6 μm, respectively, are investigated by the FDTD method. It can be seen in Fig. 10a that the critical coupling condition is achieved at W = 0.7 μm, H = 0.6 μm, hgap ~ 100 nm, in which less than 4% of the input power succeeds in transmission. The waveguide with W = 1.0 μm, H = 0.6 μm is not an ideal configuration because more than 11% of the input power evolves to the waveguide transmission. However, Qtotal of the system with W = 1.0 μm, H = 0.6 μm is larger than that of the system with W = 0.7 μm, H = 0.6 μm at any given hgap. Moreover, after Qtotal increases to a certain level with increasing hgap, it does not change significantly with hgap > 150 nm. It is also noteworthy that further increasing hgap is unfavorable to storing energy in the microdroplet because more power goes to the waveguide transmission at a larger gap. Therefore, a trade-off between the stored energy in the microdroplet and the quality factor Qtotal is necessary. For this microdroplet–waveguide system, the combination of W = 1.0 μm, H = 0.6 μm, and hgap = 100 nm allows for a relatively high Qtotal in conjunction with a large amount of energy stored in the microdroplet. It is worth noting that in the above analysis of the relationship between hgap and the optical WGM performance, the variation of hgap has no direct effect on the droplet morphology since all the microdroplets under consideration are in the Cassie–Baxter state and the pillar height h is larger than the droplet sagging depth hsag. Nevertheless, the optimal waveguide parameters of W, H, and hgap can be a guidance for designing the nanopillar height and the strip waveguide. In practice, even the pillar height is fixed, hgap can be adjusted by adaptively tuning hsag via electrowetting on dielectric (EWOD) (Cheng and Chen 2010a, b).

Fig. 10
figure 10

a Normalized transmission power and Qtotal against hgap with W = 0.7 μm, H = 0.6 μm and W = 1.0 μm, H = 0.6 μm for the microdroplet with θA = 161.5°. b Normalized transmission power, c Qtotal, d resonant wavelength versus height H and width W while θA = 161.5°, hgap = 100 nm. e The morphology, the resonant mode field distribution, transmission spectra of the deformed microdroplet with θA = 161.5°

Full size image

Besides, to understand how the system coupling is affected by the waveguide geometry, the simulated transmission power and the total quality factor Qtotal as well as the resonant wavelength for the system with eight waveguide widths at three different waveguide heights (H = 0.55, 0.60, 0.70 μm) are plotted in Fig. 10. Here, the microdroplet apparent contact angle θA and the gap thickness hgap are fixed at 161.5° and 100 nm, respectively. With the waveguide width W increasing from 0.6 μm to 1 μm, the normalized transmission power in the waveguide and the quality factor Qtotal increase. This is because the mode confinement factor in the waveguide becomes larger with increasing W, leading more power to waveguide transmission; whereas the electric field in the waveguide extends less into the microdroplet, leading to a smaller coupling strength and thus a higher Qtotal. With further increase of W, Qtotal increases only slightly for the system with height H = 0.55 or 0.60 μm. This is due to the fact that further increasing in W cannot lead to a smaller coupling strength. For the system with H = 0.70 μm, the quality factor Qtotal decreases with further increase of the waveguide width W. On the other hand, W = 1.0 μm with H = 0.60 μm is the better waveguide combination for achieving a relatively high Qtotal with mitigated transmission as shown in Fig. 10b, c. Moreover, for W = 1.0 μm and H = 0.60 μm, the transmission spectrum and the mode field distribution are plotted in Fig. 10e. As expected, the mode type stimulated by the waveguide is the deformed q = 2 meridian WGM.

Furthermore, Qtotal of the deformed microdroplet cavity systems with θA = 170.9°, 161.5°, 151.2°, and 146.5° are plotted in Fig. 7, respectively. The results show that Qtotal of the deformed microdroplet cavities is smaller than their Qintrinsic due to the coupling loss incurred by waveguide coupling. The Qtotal of the deformed microdroplet cavities with θA > 151.2° exceeds 103, which can fulfill the basic requirements of a variety of sensing applications. Moreover, the Qtotal of this microdroplet-based cavity system with θA = 161.5° and 170.9° can reach an impressive value of above 104, which can meet the requirements for advanced biosensing.

5 Refractive index sensing performance of the deformed microdroplet resonators

According to this study, a liquid microdroplet dwelling on a well-structured substrate can sustain resonant WGMs of high Q factors along its deformed meridian periphery, which are stimulated by a strip waveguide underneath. Therefore, this optofluidic system can provide a robust and stable platform of refractive index sensor. Moreover, in contrary to solid microresonators using evanescent-tail field for sensing, this optofluidic system directly exploits the enhancement of the energy contained in the microdroplet cavity. In other words, this microdroplet serves simultaneously as the analyte container and the optical cavity, endowing not only a stronger interaction between light and the analytes but also a larger interaction space compared to the solid counterparts. Based on these potential benefits, we estimated the performance of this optofluidic system for sensing applications.

A key parameter characterizing such a refractive index optical sensor is the sensitivity S, which is defined as the shift rate of the resonant wavelength λ with the refractive index n (Vollmer et al. 2002):

$$ S = {\text{d}}\lambda /{\text{d}}n, $$
(5)

where the shift of the resonant wavelength λ of the microdroplet cavity is attributed to the change of the refractive index n of the microdroplet due to the addition of even trace amount of analytes. Figure 11 shows a linear dependence of the resonance wavelength on n of the θA = 161.5° microdroplet. A high sensitivity S ~ 531.8 nm/RIU can consequently be achieved. Nevertheless, the resonance mode with a sensitivity below 100 nm/RIU [e.g., 30 nm/RIU in silica microsphere-based sensor and 22.8 nm/RIU in a sensor based on Si3N4 microdisk (Machavariani et al. 2002)] is due to the typical evanescent wave interaction with the surrounding medium and analytes. Compared to the solid counterparts, the remarkable sensitivity S of the water-based microdroplet cavity results in larger shift in the resonant wavelength for a given index change. The Qtotal, which is inversely proportional to ΔλFWHM, is another key parameter of optical sensors. A narrow line width ΔλFWHM, namely a high Q factor, will result in enhanced detection resolution. The Qtotal of this microdroplet cavity with θA = 161.5° and 170.9° can reach above 104, which is superior to that of some conventional optical sensors for biosensing applications [e.g., Q ~ 6000 in a slotted photonic crystal cavity with S ~ 500 nm/RIU (Scullion et al. 2011)]. That is, this microdroplet-based system has potential applications in high-resolution detection of single biomolecules.

Fig. 11
figure 11

Simulated resonance wavelength shifts for the deformed microdroplet-based sensor with θA = 161.5°

Full size image

Compared to the Qtotal of the solid WGM system or the droplet-based WGM system but coupled from the equatorial plane, the Qtotal of the meridian WGM system is relatively small. Nevertheless, this Qtotal value has less sensitivity to the ambient environment changes such as thermal disturbance. Furthermore, this meridian sensing system based on strip waveguide-droplet coupling is more stable and feasible for practical implementation. Intriguingly, this WGM sensing system can be easily integrated with the EWOD platform (Cheng and Chen 2010a, b) so that the microdroplet can be adaptively manipulated to pick up the target analytes, such as biological species or chemical reagents, thereby digital and precise biosensing can be achieved on this lab-on-a-chip system.

6 Conclusion

WGM sensing in water-based microcavities is highly desired in practice because they are more closely analogous to the biological environment. In this work, we analyzed a fluidic and deformed microdroplet system as an optical cavity, in which WGMs are stimulated by an embedded strip waveguide on a micro/nanostructured superhydrophobic surface. The embedded strip waveguide beneath the nanopillared surface can not only stabilize the microdroplet at the Cassie state, but also enable the WGMs to be generated in the meridian direction, which makes the coupling process more facile and more stable compared to the WGMs coupling along the equatorial plane. As a compromise, the unavoidable deformation in the microdroplet meridian plane weakens the quality factor Q. Nonetheless, the nanopillar patterned superhydrophobic surface above the waveguide can mitigate such deformation and have the potential to achieve a high quality Q factor. In this regard, the microdroplet with θA = 151.2° and 156.3° has total Q factor > 103; and the microdroplet with θA = 161.5° and 170.9° has total Q factor > 104. Besides, in terms of sensing application, making the microdroplet itself serves simultaneously as the trace analyte container and the optical cavity, a high sensitivity S > 530 nm/RIU can be achieved, which is more sensitive than the solid counterparts.

On the other hand, a water microdroplet may evaporate very fast when it is directly exposed to the ambient, causing the WGMs to drift during measurement. A prior study (Kiraz et al. 2007b) reported that the size stabilization of microdroplets containing no salt can be obtained via an electrically controlled mini humidity and demonstrated that the diameter variation of a 12 μm water droplet was only ~ 1 nm during 82.8 s. Even though water evaporation can be effectively mitigated by controlling the humidity inside a chamber, the WGM sensing system can be more easily applied without the enclosure. Currently, to slow down the evaporation process of a water droplet, a proper amount of glycerol was added in to water to form glycerol–water mixture in some WGM studies. In our meridian WGM configuration, owing to the high contact angle (θA > 160°) of the glycerol–water mixture on a superhydrophobic surface, fluidic microcavities with the geometry of a truncated sphere minimally distorted by gravity and contact line pinning effects could be generated. For future applications, the stable and feasible waveguide coupling microdroplet system can be integrated with EWOD platform leading to a digital lab-on-a-chip sensor with high throughput and high sensitivity even in a complex sample matrix.