1 Introduction

The dynamics of drop interaction in flow has been extensively studied both experimentally (Orme 1997; Couder et al. 2005; Willis and Orme 2003) and theoretically (Eggers et al. 1999; Janssen and Anderson 2011) due to their vital importance in a diverse spectrum of multiphase systems. In some cases, for example in food and pharmaceutical industries, it is desired that the emulsion is stable for extended periods of time; i.e., the size distribution of drops should not change over time due to flow (Kogan and Garti 2006). However, in other applications, for instance in oil extraction, an unstable emulsion is preferred since it makes it easier to separate the drop phase from the suspending medium.

Active and passive manipulation of non-Brownian particles in fluids has been a topic of interest in microfluidics for several years now. The recent review by Lu et al. discusses particle manipulations in non-Newtonian microfluidics for various passive manipulations, including focusing, separation, washing and stretching of particles (Lu et al. 2017). Despite practical advantages of passive manipulation of particles (Kang et al. 2009), for several applications more control is required and an active manipulation is desired. Researchers have used different actuation mechanisms to displace and transport rigid and deformable particles like electrostatics (den Toonder et al. 2008; Khatavkar et al. 2007), magnetics (Zhang et al. 2019; Wang et al. 2013, 2015, 2016) and light (van Oosten et al. 2009).

Similar to industrial processes, also microfluidic multiphase systems have complex fluids as their components (Utracki 1989). The collision of drops is a delicate process which can be influenced by many different factors, such as the flow field type, the position and shape of the drops, the interfacial and viscoelastic properties of the phases. Despite all the previous work done, both experimentally and theoretically, the coalescence of drops in viscoelastic materials is still not very well understood.

Investigating the head-on collision of two drops can provide information, such as the drainage time, which is the basis of coalescence. Changes in the microstructure of blends, induced by coalescence and breakup, influence the size distribution of the drops and hence determine the final properties (Tucker and Moldenaers 2002). Information obtained from the evolution of the microstructure can be used to derive models which characterize the droplet size and distribution macroscopically (Ferkl et al. 2016).

In this article, we investigate the effect of the viscoelasticity on the drainage time using numerical simulations in a regime relevant for microfluidics. A cylindrical coordinate system is used with imposed axisymmetry. For the modeling of the viscoelastic matrix material, the Giesekus model is used (Giesekus 1982). The Newtonian drops are suspended in the viscoelastic matrix and perform a head-on collision under a macroscopically applied biaxial extensional flow. The problem is discretized using the finite element method.

The structure of the article is as follows. In Sect. 2, we define the problem and present the mathematical model that will be used for the balance and constitutive equations. In Sect. 3, the employed finite element method is presented. In Sect. 4, we show the validation of our method together with the obtained results. Finally, in Sect. 5, our main conclusions are summarized.

2 Problem definition

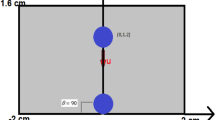
For the purpose of this work, two isolated drops having the same radius perform a head-on collision under biaxial extensional flow. The drops consist of a Newtonian fluid, whereas the matrix fluid is viscoelastic. To compute the viscoelastic stress, the Giesekus model is used. To reduce the computational cost, axisymmetry of the problem is assumed. The initial geometry of the colliding spherical drops is depicted in Fig. 1.

Fig. 1
figure 1

A 3D representation of the initial geometry of two spherical drops suspended in a fluid in biaxial extensional flow. The dash-dotted line represents the axis of rotational symmetry

Full size image

2.1 Governing equations

Since we are considering drops in a microfluidic environment, we assume that inertia can be neglected and that the fluid is incompressible. As a result, the momentum and the mass balance for both the drop and the matrix reduce to

$$\begin{aligned} -\varvec{\nabla } \cdot \varvec{\sigma } = {\varvec{0}}, \end{aligned}$$
(1)
$$\begin{aligned} \varvec{\nabla } \cdot {\varvec{u}} = 0, \end{aligned}$$
(2)

where \(\varvec{u}\) is the velocity vector and \(\varvec{\sigma }\) the stress tensor. The stress tensor \(\varvec{\sigma }\) is written as:

$$\begin{aligned} \varvec{\sigma }= -p \varvec{I} + \varvec{\tau }, \end{aligned}$$
(3)

where p is the pressure, \(\varvec{I}\) is the identity tensor and \(\varvec{\tau }\) is the extra stress tensor. For the Newtonian drop, the extra stress tensor is given by

$$\begin{aligned} \varvec{\tau }= 2 \eta _{\text {d}} \varvec{D}, \end{aligned}$$
(4)

with \(\eta _{\text {d}}\) the viscosity of the fluid in the drops and \(\varvec{D}=(\varvec{\nabla }\varvec{u}+(\varvec{\nabla }\varvec{u})^T)/2\) the symmetric part of the velocity gradient tensor. For the viscoelastic matrix fluid, there is a contribution from the Newtonian (solvent) part and a viscoelastic contribution \(\varvec{\tau }_\text {p}\) to the extra stress tensor:

$$\begin{aligned} \varvec{\tau }= 2 \eta _{\text {s}} \varvec{D} + \varvec{\tau }_\text {p}, \end{aligned}$$
(5)

where \(\eta _{\text {s}}\) is the solvent viscosity. The viscoelastic extra stress \(\varvec{\tau }_\text {p}\) is governed by the Giesekus constitutive model, given by

$$\begin{aligned} \lambda {\mathop {\varvec{c}}\limits ^{\scriptscriptstyle \bigtriangledown }} + \varvec{c} - \varvec{I} + \alpha (\varvec{c} - \varvec{I})^2 = \varvec{0}. \end{aligned}$$
(6)

where \(\varvec{c}\) is the conformation tensor, \(\lambda \) is the relaxation time, \(\alpha \) is the mobility and \({\mathop {()}\limits ^{\scriptscriptstyle \bigtriangledown }}\) is the upper convected derivative:

$$\begin{aligned} {\mathop {()}\limits ^{\scriptscriptstyle \bigtriangledown }} = \frac{\mathrm {D}()}{\mathrm {D}t}-(\nabla \varvec{u})^T \cdot () - () \cdot \nabla \varvec{u}, \end{aligned}$$
(7)

with \(\mathrm {D}()/\mathrm {D}t\) the material derivative. The polymer stress is given by

$$\begin{aligned} \varvec{\tau }_\text {p} = G(\varvec{c} - \varvec{I}), \end{aligned}$$
(8)

herein the polymer modulus is \(G=\eta _\text {p}/\lambda \), where \(\eta _\text {p}\) is the polymeric viscosity. The zero-shear-rate viscosity of the matrix fluid is \(\eta _0=\eta _{\text {s}} + \eta _\text {p}\).

2.2 Boundary and initial conditions

In this section, we define the boundary and initial conditions. It is assumed that the drop interface can be described by a sharp interface. This leads to a jump of the stress tensor at the boundary between the drops and the matrix, which can be expressed as:

$$\begin{aligned} \varvec{\sigma }\cdot \varvec{n}|_\text {m} - \varvec{\sigma }\cdot \varvec{n}|_\text {d} = \varGamma \kappa \varvec{n}, \end{aligned}$$
(9)

where the subscripts m and d indicate that the term is evaluated on the matrix and drop side, respectively, \(\varGamma \) is the surface tension coefficient, \(\varvec{n}\) is the outwardly directed unit normal vector and \(\kappa \) is the curvature defined as:

$$\begin{aligned} \kappa = \varvec{\nabla }_\text {s} \cdot \varvec{n}, \end{aligned}$$
(10)

with \(\varvec{\nabla }_\text {s}=(\varvec{I} - \varvec{n} \varvec{n})\cdot \varvec{\nabla }\) the surface gradient operator. Furthermore, there is no slip between the matrix and the drop fluids:

$$\begin{aligned} \varvec{u}|_\text {m} = \varvec{u}|_\text {d}. \end{aligned}$$
(11)

On the outer boundaries \(\partial {\Omega }_1,\partial {\Omega }_2\) and \(\partial {\Omega }_3\) (see Fig. 2), a macroscopic biaxial extensional velocity field is imposed, which in the axisymmetric case is given by

$$\begin{aligned} \varvec{u}(\varvec{x}) = {\dot{\epsilon }}\left( -z,\frac{r}{2}\right) , \end{aligned}$$
(12)

where \(\varvec{x}\) is the position vector with (z, r) coordinates and \({\dot{\epsilon }}\) is the extensional rate.

Due to axisymmetry, symmetry conditions on the z-axis at \(r=0\) are needed. This yields the following equation:

$$\begin{aligned} u_r(z,r=0) = 0. \end{aligned}$$
(13)

Boundary conditions at the inflow, i.e., boundaries \(\partial {\Omega }_1\) and \(\partial {\Omega }_3\), for the conformation are needed. Assuming that the boundaries are sufficiently far away from the stagnation point and the drops, we compute the conformation tensor for a purely biaxial extensional flow without the presence of any drops and prescribe it as follows:

$$\begin{aligned} \varvec{c}_{\partial {\Omega }_1}(t{\dot{\epsilon }}) = \varvec{c}_\text {e}(t{\dot{\epsilon }}), \quad \varvec{c}_{\partial {\Omega }_3}(t{\dot{\epsilon }}) = \varvec{c}_\text {e}(t{\dot{\epsilon }}), \end{aligned}$$
(14)

where \(\varvec{c}_\text {e}(t{\dot{\epsilon }})\) is the value of the conformation tensor for biaxial extensional flow without drops at time \(t{\dot{\epsilon }}\). Initial conditions for the conformation tensor are needed also, for which a stress-free state will be assumed:

$$\begin{aligned} \varvec{c}(t{\dot{\epsilon }}=0)=\varvec{I}. \end{aligned}$$
(15)
Fig. 2
figure 2

Initial geometry of spherical drops using a cylindrical coordinate system with axisymmetry. The dash-dotted line indicates the symmetry axis

Full size image

2.3 Interface tracking

Since we are dealing with sharp interfaces, it is needed to formulate appropriate equations that can track the motion of the interface. An interface can be described by a moving curvilinear coordinate system given by

$$\begin{aligned} \varvec{x} = \bar{\varvec{x}}(\xi ,t), \end{aligned}$$
(16)

where \(\xi \) represents the curvilinear coordinate and \(\bar{\varvec{x}}\) is the mapping function that converts the curvilinear coordinates to spatial coordinates \(\varvec{x}\). The velocity of the interface is given by

$$\begin{aligned} \dot{\varvec{x}} = \dfrac{\partial \bar{\varvec{x}}}{\partial t}\bigg |_\xi \end{aligned}$$
(17)

and follows the material velocity \(\varvec{u}\)

$$\begin{aligned} \dot{\varvec{x}} = \varvec{u}, \end{aligned}$$
(18)

i.e., the interface moves in a Lagrangian way.

3 Numerical description

To solve the mathematical model described in Sect. 2, the finite element method is used. The equations are solved on moving boundary-fitted meshes, where the movement of the nodes is coupled with the flow problem.

3.1 Weak form

The weak form can be obtained by multiplying Eqs. (1) and (2) with test functions \(\varvec{v}, q\): Find \(\varvec{u},p\) such that

$$\begin{aligned} (\varvec{v},-\varvec{\nabla }\cdot \varvec{\sigma })&=0 \quad \text {for all }\varvec{v}, \end{aligned}$$
(19)
$$\begin{aligned} (q,\varvec{\nabla }\cdot \varvec{u})&=0 \quad \text {for all }q. \end{aligned}$$
(20)

in both the Newtonian drops and the matrix fluid. Using partial integration, Gauss’ theorem, the interface condition Eq. (9) and the continuity of velocity Eq. (11), we obtain the following weak form: Find \(\varvec{u}\) and p such that

$$\begin{aligned} ((\varvec{\nabla }\varvec{v})^T,\varvec{\tau }) -(\varvec{\nabla }\cdot \varvec{v},p)&= -(\varvec{v},\varGamma \kappa \varvec{n})_{S}&\quad \text {for all }\varvec{v}, \end{aligned}$$
(21)
$$\begin{aligned} \,(q,\varvec{\nabla }\cdot \varvec{u})&=0&\quad \text {for all }q, \end{aligned}$$
(22)

using appropriate spaces for \(\varvec{u}\), p, \(\varvec{v}\) and q, where \(S = S_1 \cup S_2\). Now valid in the whole domain where in the Newtonian drops \(\varvec{\tau }\) is given by Eq. (4) and in the matrix fluid by Eq. (5). During a single time step, the momentum and mass balance equations are solved first, where the polymer stress \(\varvec{\tau }_\text {p}\) is obtained by using a semi-implicit scheme as proposed in D’Avino and Hulsen (2010). With the updated velocity, the evolution equation for the conformation tensor is then solved. The mesh consists of both constant and moving boundaries. That means that the fluid is described on a mobile grid, which moves in a non-Lagrangian way. Hence, it is essential to use the arbitrary Lagrange–Euler (ALE) formulation, where the material derivative is rewritten as

$$\begin{aligned} \frac{\mathrm {D}()}{\mathrm {D}t} = \frac{\partial ()}{\partial t}\bigg |_{\varvec{x}_\text {m}} + (\varvec{u} - \varvec{u}_\text {m}) \cdot (), \end{aligned}$$
(23)

where the partial derivative with respect to time t is calculated at constant mesh coordinate \(\varvec{x}_\text {m}\) and \(\varvec{u}_\text {m}\) is the mesh velocity. For stabilization, we use the SUPG technique (Brooks and Hughes 1982), and together with the log-conformation approach (Hulsen et al. 2005; Fattal and Kupferman 2004), the equation for the evolution of the conformation tensor Eq. (6) in its weak form with test function \(\varvec{d}\) becomes: Find \(\varvec{s}\) such that

$$\begin{aligned} \left( \varvec{d} + \tau (\varvec{u}-\varvec{u}_\text {m}) \cdot \varvec{\nabla }\varvec{d}, \frac{\mathrm {D}\varvec{s}}{\mathrm {D} t} - \varvec{g} ((\varvec{\nabla }\varvec{u} )^T, \varvec{s}) \right)&\quad \text {for all }\varvec{d}, \end{aligned}$$
(24)

where \(\varvec{s} = \log \varvec{c}\), \(\tau \) is the SUPG parameter and \(\varvec{u}_\text {m}\) is the mesh velocity. Further information about the log-conformation formulation and the expression for the function \(\varvec{g}\) can be found in Hulsen et al. (2005).

3.2 Discretization

The weak form is discretized using the finite element method employing a mesh of quadratic triangles. Quadratic interpolation \((P_2)\) for the velocity and position and linear interpolation \((P_1)\) for pressure and conformation are used. An additional Poisson equation is used for the movement of the mesh nodes which in its weak form using test function \(\varvec{w}\) reads: Find \(\varvec{x}\) such that

$$\begin{aligned} ((\varvec{\nabla }_n \varvec{w})^T, \varvec{\nabla }_n \varvec{x})&=0&\text {for all }\varvec{w}, \end{aligned}$$
(25)

where \(\varvec{\nabla }_n\) is the gradient using the position at the beginning of each time step as a reference. The tracking of the interface can be done by solving two separate problems, usually by first predicting the position of the interface in the new time step and then solving the momentum and mass balance problem (Villone et al. 2014). In a decoupled approach, the time step would be limited by the mesh capillary time (Courant et al. 1967). That is why we choose to solve Eqs. (21), (22), (25), coupled with the Poisson problem which has the interface tracking Eq. (18) as a boundary condition. The implementation is similar as in Mitrias et al. (2017), but now the whole domain is perturbed. In this way, our scheme is not limited by the characteristic mesh size time limit.

Regarding the time discretization, a semi-implicit stress formulation is implemented. That is not necessary for the case that will be studied in this work since a nonzero solvent viscosity is present, but the model has been derived such that \(\eta _s=0\) could be chosen. Thus, Eq. (6) using an explicit Euler scheme similar to D’Avino and Hulsen (2010) reads

$$\begin{aligned}\frac{\varvec{c}^{n+1}}{\varDelta t} + (\varvec{u}^{n} - \varvec{u}_\text {m}^{n})\cdot \varvec{\nabla }\varvec{c}^{n} & = \frac{\varvec{c}^n}{\varDelta t} + (\varvec{\nabla }\varvec{u})^{n,T} \cdot \varvec{c}^{n} \nonumber \\ & \quad + \varvec{c}^{n} \cdot \varvec{\nabla }\varvec{u}^{n} + \varvec{f}(\varvec{c}^{n}), \end{aligned}$$
(26)

where \(\varvec{f}(\varvec{c})\) for the Giesekus model (Giesekus 1982) is given by

$$\begin{aligned} \varvec{f}(\varvec{c}) = - \frac{\varvec{c} - \varvec{I}}{\lambda } - \frac{\alpha (\varvec{c} - \varvec{I})^2 }{\lambda }. \end{aligned}$$
(27)

With Eq. (26), we can compute the viscoelastic stress tensor at the new time as

$$\begin{aligned}\hat{ \varvec{\tau }}_\text {p}^{n+1} & = G \varDelta t ( -(\varvec{u}^{n+1} - \varvec{u}_\text {m}^{n+1})\cdot \varvec{\nabla }\varvec{c}^{n}\nonumber \\ & \quad + (\varvec{\nabla }\varvec{u})^{n+1,T} \cdot \varvec{c}^{n} + \varvec{c}^{n} \cdot \varvec{\nabla }\varvec{u}^{n+1} ) \nonumber \\ & \quad + G(\varvec{c}^n + \varDelta t \varvec{f}(\varvec{c}^{n}) - \varvec{I}) \end{aligned}$$
(28)

where \(\hat{ \varvec{\tau }}_\text {p}^{n+1}\) is a prediction of the viscoelastic stress tensor and it is substituted in Eq. (21). This leads to the final system of equations

$$\begin{aligned} ((\varvec{\nabla }\varvec{v})^T,2\eta _\text {s}\varvec{D} )+ ((\varvec{\nabla }_n \varvec{v})^T, G \varDelta t ( -(\varvec{u} - \varvec{u}_\text {m})\cdot \varvec{\nabla }_n & \varvec{c}^{n} \nonumber \\ + (\varvec{\nabla }_n \varvec{u})^{T} \cdot \varvec{c}^{n} + \varvec{c}^{n} \cdot (\varvec{\nabla }_n \varvec{u}) ) - (\varvec{\nabla }\cdot \varvec{v},p) & = - (\varvec{v},\varGamma \kappa \varvec{n})_{S} \nonumber \\ - ((\varvec{\nabla }_n \varvec{v})^T, G(\varvec{c}^n + \varDelta t \varvec{f}(\varvec{c}^{n}) & - \varvec{I}) )\, \text {for all }\varvec{v}, \end{aligned}$$
(29)
$$\begin{aligned} (q,\varvec{\nabla }\cdot \varvec{u})&=0 \qquad \text {for all }q, \end{aligned}$$
(30)
$$\begin{aligned} ((\varvec{\nabla }_n \varvec{w})^T, \varvec{\nabla }_n \varvec{x} )&=0 \qquad \text {for all }\varvec{w}, \end{aligned}$$
(31)
$$\begin{aligned} \left( \varvec{r}, \frac{3 \varvec{x} - 4 \varvec{x}^{n} + \varvec{x}^{n-1}}{2\varDelta t}- \varvec{u} \right)&= 0 \qquad \text {for all }\varvec{r}. \end{aligned}$$
(32)

where all superscripts \(()^{n+1}\) have been dropped to increase readability. Noticeably, Eqs. (29)–(32) form a nonlinear system of equations. For that reason, the system is linearized with \(\varvec{c}^n\) known and solved with the Newton–Raphson method. For the time discretization of the interface tracking, a second-order time integration (BDF2) is used (Ascher and Petzold 1998). Furthermore, the mesh velocity \(\varvec{u}_\text {m}\) is computed by a BDF2 formula and updated during iterations. Although a first-order scheme is used for the viscoelastic stress tensor in the momentum balance, the actual error is still \(\mathcal {O}(\varDelta t^2)\). After \(\varvec{u}^{n+1}, p^{n+1}, \varvec{x}^{n+1}\) have been obtained, \(\varvec{s}^{n+1}\) is computed from the discretized Eq. (24) using BDF2 and thus we can calculate \(\varvec{\tau }_{\text{p}}^{n+1}=G(\exp \varvec{s}^{n+1}-\varvec{I})\).

When the moving mesh becomes distorted, remeshing is performed. All the variables that need time integration, i.e., the position of the interfaces and conformation field at previous time steps, are projected onto the new mesh (Hu et al. 2001). To be able to compute the mesh velocity, the mesh coordinates at previous time steps are projected as well (Jaensson et al. 2015). The mesh is generated using Gmsh (Geuzaine and Remacle 2009).

The components of the conformation tensor form multiple systems of equations with the same matrix but a varying right-hand side. We choose to solve these systems using a direct solver provided by the HSL library (HSL 2013), which allows for the reuse of the LU-decomposition (Lay and Stade 2005). The system of equations formed by the momentum balance, mass balance and Poisson equations can grow fast due to the refinement of the approaching drop interfaces. This system is solved using a GMRES iterative solver from the Sparskit library (Saad 2001), with a modified preconditioner as explained in Jaensson et al. (2018). While the mesh is moving, the connectivity of the nodes does not change until remeshing is needed and the structure of the system matrix remains the same. Thus, it is possible to reuse the same preconditioner for multiple time steps, which significantly reduces the computational time. To reduce the size of the preconditioner, the graph that represents the system matrix is renumbered using MeTiS (Karypis and Kumar 1998).

4 Results

In the following sections, all the results will be presented in dimensionless form. There are several dimensionless groups that characterize different aspects of our problem, which are

$$\begin{aligned}&\mathrm {Wi} =\lambda {\dot{\epsilon }}, \quad \mathrm {Ca}=\frac{\eta _0{\dot{\epsilon }}R}{\varGamma }, \quad D=\frac{d_0}{2R}, \nonumber \\&\delta =\frac{\eta _\text {d}}{\eta _0}, \quad \beta =\frac{\eta _\text {s}}{\eta _0}, \quad \alpha , \end{aligned}$$
(33)

where Wi is the Weissenberg number, Ca is the capillary number, D is the normalized initial drop interface distance \(d_0\) with the drop diameter 2R, \(\delta \) is the ratio of the drop viscosity and the zero-shear viscosity of the viscoelastic fluid, \(\beta \) is the ratio of the solvent viscosity and zero-shear viscosity of the viscoelastic fluid and \(\alpha \) is the mobility parameter of the Giesekus model. For all the simulations that consist of a viscoelastic matrix fluid, the viscosity ratio \(\beta =0.5\), the mobility parameter \(\alpha =0.2\) and the viscosity ratio \(\delta =1\) will be fixed. The initial distance of the drop interfaces D = 3 is chosen such that there is enough time to build up viscoelastic stresses in the layer of fluid in between the drops. Note that these stresses require a scaled time of at least \(t {\dot{\epsilon }}={\text{Wi}}\) to develop. If the drops are initially placed close to each other, the role of viscoelastic effects would be insignificant. The size of the domain is 20 times the radius R both in axial and radial directions, so that the imposed boundary conditions for the conformation tensor do not affect the dynamics close to the drops. The schematic in Fig. 3 shows the interface distance at the center \(h_\text {cent}\) and the minimum interface distance \(h_\text {min}\) of the drops. When studying the film drainage, these are the important parameters that govern the drainage dynamics.

Fig. 3
figure 3

Three-dimensional representation of the two drops at the later stages of the collision process. The insert shows a schematic representation of the dimple shape of the drop interfaces, with the symmetry axis represented by the dash-dotted line

Full size image

4.1 Convergence test

In order to verify our numerical model, spatial and time convergence is investigated. For the constant parameters, we choose \(\mathrm {Ca}=0.1\), \(\mathrm {Wi}=0.1\) and D = 3. Five different meshes are used with a varying number of elements on the drop equator, \(n_\text {e}=40,45,60,75\) and 500. The corresponding number of nodes for the different meshes can be found in Table 1. The relative error is defined as

$$\begin{aligned} e_\text {r} = \bigg |\bigg |\frac{h_\text {cent}(t{\dot{\epsilon }})-h^\text {ref}_\text {cent}(t{\dot{\epsilon }})}{h^\text {ref}_\text {cent}(t{\dot{\epsilon }})}\bigg |\bigg |, \end{aligned}$$
(34)

where \(h^\text {ref}_\text {cent}(t{\dot{\epsilon }})\) is the reference interface distance at time \(t{\dot{\epsilon }}\) and \(h_\text {cent}(t{\dot{\epsilon }})\) the interface distance for the corresponding \(n_\text {e}\) at time \(t{\dot{\epsilon }}\). In Fig. 4, the error \(e_\text {r}\) at \(t{\dot{\epsilon }}=0.01\) of the interface distance at the center of the drops for the cases of \(n_\text {e}=40,45,60\) and 75 which is relative to the one with \(n_\text {e}=500\) is plotted. It can be seen that the error converges giving a maximum relative error of \(10^{-7}\). We now chose the number of elements on the drop equator to be \(n_\text {e}=60\), and we perform simulations with a varying time step. In Fig. 5, the relative error at \(t{\dot{\epsilon }}=0.1\) of time steps \(\varDelta t {\dot{\epsilon }}=10^{-3}, 5 \times 10^{-4}, 2.5 \times 10^{-4}\) and \(10^{-4}\) relative to the case of a time step \(\varDelta t {\dot{\epsilon }}=10^{-6}\) is plotted. The numerical method shows convergence, and in the remainder of this article, we are going to use \(n_\text {e}=60\) and \(\varDelta t {\dot{\epsilon }} = 10^{-3}\), which is a compromise between accuracy and numerical efficiency.

Table 1 Number of nodes \(N_\text {nodes}\) for meshes with different number of elements on the sphere equator \(n_{\text{e}}\)
Full size table
Fig. 4
figure 4

Relative error \(e_{\text {r}}\) of the \(h_\text {cent}\) using different meshes with the number of elements on the equator of the drops being \(n_\text {e}=40,45,60,75\) at \(t{\dot{\epsilon }}=0.01\). The dimensionless parameters are \(\mathrm {Ca}=0.1\), \(\mathrm {Wi}=0.1\), and D = 3. As a reference value, we use the result obtained from the case of \(n_\text {e}=500\)

Full size image
Fig. 5
figure 5

Relative error \(e_{\text {r}}\) of the \(h_\text {cent}\) using different time steps at \(t{\dot{\epsilon }}=0.1\). The error is plotted for the cases of \(\varDelta t {\dot{\epsilon }}=10^{-3},5\times 10^{-4},2.5\times 10^{-4},10^{-4}\) relative to the one obtained with \(\varDelta t {\dot{\epsilon }}=10^{-6}\). The dimensionless parameters are \(\mathrm {Ca}=0.1\), \(\mathrm {Wi}=0.1\), and D = 3

Full size image

To be able to correctly capture the flow in the thin layer that forms between the drop interfaces, the drop interfaces are refined so that there are enough elements in the fluid layer. In Figs. 6, 7, 8, the dimensionless first-normal stress difference of the polymer stress, \(N_1/{\tilde{\sigma }}\), where \(N_1=\tau _{\text {p},{11}}-\tau _{\text {p},{22}}\), is shown using 4, 8 and 16 elements between the drops. Here, \({\tilde{\sigma }}=\eta ({\dot{\gamma }}_\text {eff}){\dot{\gamma }}_\text {eff}\) is the total shear stress, where \(\eta ({\dot{\gamma }}_\text {eff})\) is the steady-state viscosity function of the viscoelastic model. Furthermore, the effective strain rate may be expressed as the magnitude of the rate of deformation tensor \({\dot{\gamma }}_\text {eff}=\sqrt{2 \varvec{D} : \varvec{D}}\). Eight elements are shown to be enough to accurately describe the polymer stress in the thin fluid layer.

Fig. 6
figure 6

Plotting the ratio of \(N_1 / {\tilde{\sigma }}\) while using four elements between the drop interfaces at time \(t{\dot{\epsilon }}=0.3\). The dimensionless parameters are \(\mathrm {Ca}=0.1\), \(\mathrm {Wi}=0.1\), and D = 3

Full size image
Fig. 7
figure 7

Plotting the ratio of \(N_1/{\tilde{\sigma }}\) while using eight elements between the drop interfaces at time \(t{\dot{\epsilon }}=0.3\). The dimensionless parameters are \(\mathrm {Ca}=0.1\), \(\mathrm {Wi}=0.1\), and D = 3

Full size image
Fig. 8
figure 8

Plotting the ratio of \(N_1/{\tilde{\sigma }}\) while using 16 elements between the drop interfaces at time \(t{\dot{\epsilon }}=0.3\). The dimensionless parameters are \(\mathrm {Ca}=0.1\), \(\mathrm {Wi}=0.1\), and D = 3

Full size image

4.2 Validation

We commence by validating our code by comparing to results obtained using the boundary integral method (BIM) of Janssen et al. (2006, 2008, 2011), where both the matrix and the drop consist of a Newtonian fluid. The parameters in this case are \(\mathrm {Ca}=0.05\), \(\delta =1\) and D = 0.5. In Fig. 9, it can be seen that there is a good agreement between our model and that of Janssen et al. (2006). The dimple shape as depicted in Fig. 3 is observed only at the later stages of the process. From this comparison, we can also conclude that our computational domain is sufficiently large, because of the good agreement with the boundary integral method which assumes a velocity field imposed at infinity.

Fig. 9
figure 9

Comparison of the \(h_\text {cent}\) and \(h_\text {min}\) with results obtained using the boundary integral method (Janssen et al. 2006). The dimensionless parameters are \(\mathrm {Ca}=0.05\) and D = 0.5

Full size image

4.3 Effect of viscoelasticity on the film drainage

Although there is limited literature regarding the film drainage during head-on collision of drops suspended in a viscoelastic matrix, it has been reported that the viscoelasticity promotes coalescence; i.e., it speeds up the film drainage (Yue et al. 2005). Yue et al. used a two-dimensional implementation of the diffuse-interface formulation to study the effect of viscoelasticity on the film drainage. As they mentioned, the observed speedup is a result of two stages with different effects. Initially, the viscoelastic stresses are negligible and thus the drops are allowed to move faster than the Newtonian case. In the second stage, the viscoelastic stresses are fully developed and the movement of the drops slows down. The first stage dominates the dynamics, and it is the one that is responsible for the speedup.

In our simulations, apart from the first stage that contributes to the speedup, we also observed that the complex nature of the flow between the two drops can lead to faster drainage depending on the \(\mathrm {Ca}\) number. Noticeably, a third stage that contributes to the speedup can be identified, when the drop interfaces are close to each other. At that moment, the local strain rates are minor and thus the viscoelastic stresses of the fluid inside the film layer are small. To better understand the dynamics during this process, in Fig. 10 we plot the viscoelastic stress magnitude \(\sqrt{\varvec{\tau }_\text {p}:\varvec{\tau }_\text {p}}\) for the case of \({\text{Ca}} = 0.05\) and \({\text{Wi}} = 0.2\) at different times. Initially, in Fig. 10a, it can be seen that at time \(t{\dot{\epsilon }}=0.3\) the stresses are low, since we start from a stress-free condition. When the drops approach each other, the stresses start to build up as it can be seen in Fig. 10b at time \(t{\dot{\epsilon }}=1.5\). Finally, in the last stage where the drops start to slow down, the viscoelastic stresses in the thin layer between the drop interfaces relax as shown in Fig. 10c.

Fig. 10
figure 10

Viscoelastic stress magnitude for \(\mathrm {Ca}=0.05\) and \(\mathrm {Wi}=0.2\) at a \(t{\dot{\epsilon }}=0.3\), b \(t{\dot{\epsilon }}=1.5\) and c \(t{\dot{\epsilon }}=3.0\) with the insert showing the region inside the red rectangle

Full size image

Thus, the dynamics between the drops are governed not only by the global Weissenberg number which is defined by the macroscopic imposed strain rates, but also by the local strain rates that the moving interfaces enforce. We therefore define a local Weissenberg number as:

$$\begin{aligned} \mathrm {Wi}_\text {cent}=\lambda {\dot{\epsilon }}_\text {cent}, \end{aligned}$$
(35)

herein \({\dot{\epsilon }}_\text {cent}\) is the local strain rate imposed by the drop interfaces given by

$$\begin{aligned} {\dot{\epsilon }}_\text {cent} = \frac{u_\text {cent}}{h_\text {cent}}, \end{aligned}$$
(36)

where \(u_\text {cent}\) is the magnitude of the velocity of the approaching interfaces at the centerline. In Fig. 11, the increase in the \(\mathrm {Wi}_\text {cent}\) is plotted over time, for the case of \(\mathrm {Wi}=0.4\) and a range of \(\mathrm {Ca}\). It can be seen that the local Weissenberg number \(\mathrm {Wi}_\text {cent}\) is increasing, as the drops are approaching each other. A maximum value is found for each \(\mathrm {Ca}\) which increases with decreasing \(\mathrm {Ca}\). This is expected since stiffer drops, i.e., small \(\mathrm {Ca}\), deform less and thus impose higher strains on the matrix fluid. For the case of the smallest \(\mathrm {Ca}=0.005\) that we studied, the maximum value of \(\mathrm {Wi}_\text {cent}\) is more than ten times larger than the macroscopically applied strain rate. Finally, at the last stage where the drops slow down, the value of \(\mathrm {Wi}_\text {cent}\) significantly decreases.

Fig. 11
figure 11

Local \(\mathrm {Wi}_\text {cent}\) as a function of time for a range of \(\mathrm {Ca}\) and \(\mathrm {Wi}=0.4\). Insert shows a zoomed-in section for \(1<t{{\dot{\epsilon }}}<10\)

Full size image

The speedup of the film drainage can be also identified by looking at the local \(\mathrm {Wi}_\text {cent}\) that the drop interfaces impose for different \(\mathrm {Wi}\) numbers and a constant \(\mathrm {Ca}\). As shown in Fig. 12, for \(\mathrm {Ca}=0.1\) the scaled \(\mathrm {Wi}_\text {cent}\) with the global \(\mathrm {Wi}\) increases with increasing \(\mathrm {Wi}\), meaning that the drop interfaces move faster toward each other and thus enforcing higher local strains. The small bump that is observed after \(t{\dot{\epsilon }}=3.75\) is related to the drop interfaces stop moving toward each other locally and start to divert, forming the dimple shape as shown in Fig. 3. Looking at the velocity profiles in the thin film between the drops, it can be seen that higher \(\mathrm {Wi}\) leads to larger velocities as expected (Fig. 13).

Fig. 12
figure 12

Scaled local \(\mathrm {Wi}_\text {cent}\) with the global \(\mathrm {Wi}\) as a function of time for a range of \(\mathrm {Wi}\) and \(\mathrm {Ca}=0.1\)

Full size image
Fig. 13
figure 13

Velocity profiles for the draining flow on the line \(y=0.015\) at \(t{\dot{\epsilon }}=2.5\) for a range of \(\mathrm {Wi}\) and \(\mathrm {Ca}=0.05\)

Full size image

The effect that viscoelasticity has on the drainage time is summarized in Figs. 14, 15, 16, 17, 18. For drops with a large \(\mathrm {Ca}\), this effect is significant, as it can be seen in Fig. 14 for the case of \(\mathrm {Ca}=0.2\), but diminishes with decreasing \(\mathrm {Ca}\). For values of \(\mathrm {Ca}<0.05\), we could not observe any considerable differences as shown in Figs. 17 and 18. It is worth noting that for the cases where \(\mathrm {Ca}<0.05\), due to the increasing computational costs, we could not reach the point where the dimple shape of the interface starts to form and the interface distances might start to differ. One of the reasons why the viscoelastic effect gets smaller with decreasing \(\mathrm {Ca}\) is the drastic increase in terms of \(\mathrm {Wi}_\text {cent}\) as shown in Fig. 11. This increase would also lead to increased viscoelastic stresses and thus contribute to the aforementioned slowdown of the film drainage for higher \(\mathrm {Wi}\). Similar effects have been reported in the literature by Dreher et al. (1999) where they presented experimental results for different sizes of droplets showing that larger drops reduce drainage time, whereas smaller drops had a slower film drainage than the Newtonian case.

Fig. 14
figure 14

Scaled interface distance \(h/d_0\) as a function of time for a range of \(\mathrm {Wi}\) and \(\mathrm {Ca}=0.2\)

Full size image
Fig. 15
figure 15

Scaled interface distance \(h/d_0\) as a function of time for a range of \(\mathrm {Wi}\) and \(\mathrm {Ca}=0.1\)

Full size image
Fig. 16
figure 16

Scaled interface distance \(h/d_0\) as a function of time for a range of \(\mathrm {Wi}\) and \(\mathrm {Ca}=0.05\)

Full size image
Fig. 17
figure 17

Scaled interface distance \(h/d_0\) as a function of time for a range of \(\mathrm {Wi}\) and \(\mathrm {Ca}=0.01\)

Full size image
Fig. 18
figure 18

Scaled interface distance \(h/d_0\) as a function of time for a range of \(\mathrm {Wi}\) and \(\mathrm {Ca}=0.005\)

Full size image

5 Conclusions

We have presented direct numerical simulation of Newtonian drops in viscoelastic matrices under biaxial extensional flow using the Giesekus model and imposed axisymmetry. The model was validated for the case of a Newtonian matrix with the implementation of Janssen et al. (2006). The influence of viscoelasticity on the drainage time was investigated for a range of Wi numbers to study the effect of viscoelasticity. It was shown that viscoelasticity reduces the drainage time, which is a result of three different stages. In the first stage, the viscoelastic stresses are negligible and thus the drops are moving faster than the Newtonian case. During the second stage, the stresses start to build up, but for Ca numbers above 0.01 they were not sufficient in order to slow down the drops. On the contrary, the drops move faster with increasing Wi number. For small Ca, there was no significant effect of viscoelasticity up to the interface distances that we were able to study. Finally, in the third stage, when the drop interfaces are close to each other, the local strain rates are small and thus the viscoelastic stresses of the fluid inside the film layer are negligible. It is worth noting that for smaller Ca numbers and interface distances than the ones presented in this work, different effects might be present.