1 Introduction

As the pretreatment for target cells or particles analyzing, particle manipulation is studied deeply and supposed to be performed more precisely, efficiently and conveniently (Sajeesh and Sen 2014). The inertial microfluidics, which can focus and separate different size particles only by hydrodynamic force with extremely high throughput, has emancipated particle manipulation from the expensive and complicated external field generators, such as acoustic (Ren et al. 2015), optical (Wang et al. 2005), magnetic (Nam et al. 2013) and dielectrophoresis (Song et al. 2015) devices. A variety of channel patterns have be applied to improve the precision and efficiency of the inertial microfluidic chip. Different size particles can be separated by inertial lift force FL in straight microchannels (Hur et al. 2011), and the particle separation results can be optimized by the equilibrium of inertial lift force FL and Dean flow force FD in spiral (Huang et al. 2016; Xiang and Ni 2015) or serpentine (Jiang et al. 2016; Zhang et al. 2014) microchannels. The contraction–expansion microchannel is another attractive flow pattern for continuous particle focusing (Park et al. 2009), sorting (Bhagat et al. 2011; Kwak et al. 2018; Wang et al. 2013) and trapping (Mach et al. 2011; Sollier et al. 2014) using inertial lift force and the vortex formed in the expansion chamber, and this kind of channel can be easily paralleled to multiply the throughput. The microvortices in the microchambers could also provide the environment for the origin of natural homochirality research (Sun et al. 2018), which broadens the applications of this microchannel. The multifunction of the contraction–expansion channel makes it a versatile device for particle manipulation and the corresponding mechanism analysis is indispensable for the channel structure design.

The particle focusing in contraction–expansion microchannels has been explained by the equilibrium of the shear-gradient inertial lift force FL towards the sidewalls and the wall-effect-induced lift force FW towards the centerline, and the momentum-change-induced inertial force at the entrance of the contraction section drives the different size particles apart (Kwak et al. 2018; Park and Jung 2009). However, maybe this is not the whole picture of the particle-focusing mechanism in the contraction–expansion microchannels. To obtain the mechanism of the migration rule of the particles, more details of the particle behavior and fluid field around have to be observed.

To learn more about the particle-focusing and separation mechanism of the contraction–expansion microchannel, we conducted numeral simulation of particle behaviors using lattice-Boltzmann method (LBM) coupled with immersed boundary method (IBM) (Feng and Michaelides 2004) and corresponding experimental validations in this paper. The LBM–IBM method is suitable for particle behavior simulation considering the volume effects of particles. Details of particle migration trajectories and the secondary flow in the microchannel can be obtained through the simulation, which are hard to be observed in the experiments. What’s more, the numerical and experimental researches of the particle-focusing mechanism were performed with different contraction–expansion ratios, flow rates and particle sizes, trying to found out the major factors that influence the focusing pattern of particles in the contraction–expansion microchannels.

2 Simulation and experimental methods

2.1 Microchannel design and fabrication

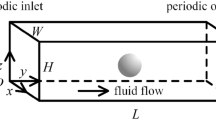
Periodic contraction–expansion microchannels employed to study the particle-focusing mechanism are sketched in Fig. 1. The dimensions of the focusing microchannel are 12 mm long, 80 µm wide and 40 µm high. The radius R0 of contraction section is fixed as 40 µm and the expansion section radii are chosen as R1 = 40 µm and R2 = 80 µm, which set the contraction–expansion ratio γ as 1.0 and 2.0, respectively. One cycle of the periodic structure is extracted as the calculation region for fluid field distribution computation. Periodic boundary condition was employed for the inlet and outlet of the calculation region to simulate a continuous contraction–expansion microchannel. The prototype microchannels were fabricated using polyvinyl chloride (PVC) hard film ablation technique with UV laser system (Zhang et al. 2016), which can dramatically shorten the microchannel fabrication time compared with the standard soft lithography chip fabrication method which is widely applied.

Fig. 1
figure 1

Sketch of the contraction–expansion microchannels with different contraction–expansion ratios γ

Full size image

2.2 Particle preparation and observation

150 µL 6 µm diameter and 300 µL 12 µm diameter fluorescent polystyrene microspheres suspensions (GFM06C, GFM12C, B.S%: 1%, Huge) were added into 20 mL deionized (DI) water, respectively, to prepare particle samples. 0.5 wt% Tween20 (Sigma-Aldrich) was also mixed into the suspension to prevent the particles from aggregation. The particle suspension samples were injected into the contraction–expansion microchannels through a syringe pump (KDS270, KD Scientific Inc.) with different flow rates from 80 µL/min to 640 µL/min, and the particle trajectories were observed under a fluorescence inverse microscope (IX71, Olympus) in the dark field. With 250 ms exposure time and 30 s shooting time, 50 image frames were captured using a 14-bit charge coupled device CCD camera (Exi Blue, Qimaging) and stacked by “Sum Slices” mode through ImageJ software (version 1.5i, NIH) to obtain the statistical particle trajectory distribution.

2.3 Numerical simulation method

The flow field distribution in the contraction–expansion microchannel is calculated through D3Q19 single relaxation time LBGK model (Qian et al. 1992) and the fluid is driven by external force term (Guo et al. 2002), which are often written as

$${f_i}({\varvec{x}}+{{\varvec{c}}_i}\Delta t,t+\Delta t)={f_i}({\varvec{x}},t)+\frac{1}{\tau }[f_{i}^{{eq}}(\rho ,{\varvec{u}}) - {f_i}({\varvec{x}},t)]+\Delta t{F_i}({\varvec{x}},t).$$
(1)

In this lattice-Boltzmann fluid field revolution equation, fi(x, t) represents the velocity distribution function at node x in the regular hexahedral meshed flow field at time t. τ is relaxation time and i denotes the 19 discrete directions from one note to its adjacent nodes in the D3Q19 model. ci is the lattice velocity moving with the 19 velocity directions, defined as

$${\varvec{c}}=c\left[ {\begin{array}{*{20}{r}} 0&1&{ - 1}&0&0&0&0&1&{ - 1}&1&{ - 1}&1&{ - 1}&1&{ - 1}&0&0&0&0 \\ 0&0&0&1&{ - 1}&0&0&1&{ - 1}&{ - 1}&1&0&0&0&0&1&{ - 1}&1&{ - 1} \\ 0&0&0&0&0&1&{ - 1}&0&0&0&0&1&{ - 1}&{ - 1}&1&1&{ - 1}&{ - 1}&1 \end{array}} \right],$$
(2)

where c = Δx/Δt, Δx is the lattice spacing and Δt is the time step. Equilibrium distribution function \(f_{i}^{{eq}}(\rho ,{\varvec{u}})\) can be calculated from the macroscopic fluid density ρ and velocity u of flow as

$$f_{i}^{{{\text{eq}}}}(\rho ,{\varvec{u}})={w_i}\rho \left[ {1+3\frac{{{{\varvec{c}}_i} \cdot {\varvec{u}}}}{{{c^2}}}+4.5\frac{{{{({{\varvec{c}}_i} \cdot {\varvec{u}})}^2}}}{{{c^4}}} - 1.5\frac{{{u^2}}}{{{c^2}}}} \right],$$
(3)

where weight coefficients ω0 = 1/3, ω1–6 = 1/18, and ω7–18 = 1/36.

The external force term Fi(x, t) can be expressed as

$${F_i}({\varvec{x}},t)=\left( {{\text{1}} - \frac{1}{{2\tau }}} \right){\omega _i}\left[ {{\text{3}}\frac{{{{\varvec{c}}_i} - {\varvec{u}}}}{{{c^{\text{2}}}}}+9\frac{{{{\varvec{c}}_i} \cdot {\varvec{u}}}}{{{c^{\text{4}}}}}{{\varvec{c}}_i}} \right] \cdot {\varvec{F}},$$
(4)

where F is the force on the fluid, including driving force and interaction force between particles and fluid in this case.

The macroscopic fluid density ρ, velocity u and the kinematic viscosity υ of the flow can be given as

$$\rho =\sum\limits_{i} {{f_i}} ,\;\rho {\varvec{u}}=\sum\limits_{i} {{{\varvec{c}}_i}{f_i}} {\text{+}}\frac{1}{2}{\varvec{F}}\Delta t,\;\upsilon =\frac{1}{3}\frac{{\Delta {x^2}}}{{\Delta t}}\left( {\tau - \frac{1}{2}} \right).$$
(5)

The interaction between particles and flow can be calculated through immersed boundary method (Krüger 2012). The force information can be exchanged between nodes of particle membrane surface and the fluid field. The particle membrane is usually meshed into N triangular surface elements using original icosahedron mesh generation method which can guarantee the isotropy of the sphere structure. The total energy of the elastic particle membrane contains four parts as \(E={E_{\textit{S}}}+{E_{\textit{B}}}+{E_{\textit{A}}}+{E_{\textit{V}}}\) (Krüger et al. 2011), where ES denotes strain energy, EB denotes bending energy, EA denotes area energy and EV denotes volume energy. For each triangular surface element, its strain energy has the form of

$${E_{{\textit{ST}}}}=\frac{{{\kappa _{\textit{S}}}}}{{12}}\left( {I_{1}^{2}+2{I_1} - 2{I_2}} \right)+\frac{{{\kappa _\alpha }}}{{12}}I_{2}^{2},$$
(6)

where strain invariants \({I_{\text{1}}}\,=\lambda _{1}^{2}{\text{ }}\,+\,\lambda _{2}^{2} - {\text{2}},{I_{\text{2}}}\,=\,\lambda _{1}^{2}\lambda _{2}^{2} - {\text{1}}\). λ1 and λ2 are principal stretch ratios. κS and κα are the surface elastic shear modulus and the area dilation modulus, respectively, which define the deformation magnitude. Through summing up the EST of every triangular face element, we can obtain

$${E_{\textit{S}}}=\sum\limits_{{n=1}}^{N} {{E_{{\textit{STn}}}}} .$$
(7)

Similarly, EB can be described through bending deformation between each triangular face element and its neighbor as

$${E_{\textit{B}}}=\frac{{{\kappa _{\textit{B}}}}}{2}\sum\limits_{{n=1}}^{{\frac{{3N}}{2}}} {{{({\phi _n} - {\phi _{n,0}})}^2}} ,$$
(8)

where ϕn,0 and ϕn denote the angle between normals of neighbor triangular face elements before and after deformation. κB denotes bending modulus.

E A and EV are usually calculated through the surface area and volume change of particles (Krüger 2012; Tsubota and Wada 2010) as the form of

$${E_{\textit{A}}}=\frac{{{\kappa _{\textit{A}}}}}{2}\frac{{{{(A - {A_0})}^2}}}{{{A_0}}},$$
(9)
$${E_{\textit{V}}}=\frac{{{\kappa _{\textit{V}}}}}{2}\frac{{{{(V - {V_0})}^2}}}{{{V_0}}}.$$
(10)

A0, A, V0, V denote surface area and volume before and after particle membrane deformation. κA and κV denote particle surface area modulus and volume modulus, respectively. To increase the elasticity moduli large enough, immersed boundary method can simulate rigid particles. And as this “penalty method”, if the particle deformation is small, different values of moduli have no significant effect on simulation results (Feng and Michaelides 2004). The node coordinates of elastic particle membrane and LBM-described fluid are represented as xn and xf, respectively, and the force exerted on particle membrane because of the particle deformation can be given as

$${\varvec{f}}{\text{(}}{{\varvec{x}}_n}{\text{)=}} - {{\partial E} \mathord{\left/ {\vphantom {{\partial E} {\partial {{\varvec{x}}_n}}}} \right. \kern-0pt} {\partial {{\varvec{x}}_n}}}.$$
(11)

According to the IBM, the particle and flow interaction force on the fluid can be calculated through transferring f(xn) to its nearby fluid node xf by

$${\mathbf{F}_{\textit{f}}}({{\varvec{x}}_{\textit{f}}}){\text{=}}\sum\nolimits_{\textit{p}} {{\varvec{f}}({{\varvec{x}}_n})} D{\text{(}}{{\varvec{x}}_n} - {{\varvec{x}}_{\textit{f}}}{\text{).}}$$
(12)

Dirac delta function \(D{\text{(}}{{\varvec{x}}_n} - {{\varvec{x}}_{\textit{f}}}{\text{)=}}\delta {\text{(}}{x_n} - {x_{\textit{f}}}{\text{)}}\delta {\text{(}}{y_n} - {y_{\textit{f}}}{\text{)}}\delta {\text{(}}{z_n} - {z_{\textit{f}}}{\text{)}}\) defines influence area and strength of the particle membrane node on fluid nodes nearby and

$$\delta {\text{(}}r{\text{)}}=\left\{ {\begin{array}{*{20}{c}} {\frac{1}{4}\left( {1+\cos \left( {\frac{{\pi r}}{2}} \right)} \right)}&{\left| r \right| \leq 2} \\ 0&{\left| r \right|>2} \end{array}} \right..$$
(13)

The interaction force on fluid node can be added to the external force term of the flow field evolution equation and then the flow field velocity distribution \({{\varvec{u}}_{\textit{f}}}{\text{(}}{{\varvec{x}}_{\textit{f}}}{\text{)}}\) can be recalculated. With the no slip boundary condition, particle membrane nodes velocity can be given as \({{\varvec{u}}_{\textit{p}}}{\text{(}}{{\varvec{x}}_n}{\text{)=}}\sum\nolimits_{{\textit{f}}} {{{\varvec{u}}_{\textit{f}}}{\text{(}}{{\varvec{x}}_{\textit{f}}}{\text{)}}} D({{\varvec{x}}_{\textit{f}}} - {{\varvec{x}}_n})\), which is an opposite procedure of the force information transferring. Finally, the position of particle membrane nodes can be updated and the next time step deformation of particles can be obtained again.

3 Results and discussion

For analyzing particle-focusing mechanics in contraction–expansion microfluidic channels, numerical simulation was performed by LBM–IBM model mentioned above. Parameters of simulation were assigned as lattice spacing Δx = 1.0 × 10−6 m, time step Δt = 2.0 × 10−8 s, kinematic viscosity υ = 1.0 × 10− 6 m2/s, particle membrane modulus κS = 3.2 × 10−1 N/m, κα = 3.2 × 10− 1 N/m, κB = 3.2 × 10−13 Nm, κA = 3.2 × 10− 2 N/m and κV = 3.2 × 104 N/m2. The flow field was actuated by external force to simulate specific flow rate and the periodic boundary was applied to the inlet and outlet of the calculation region in Fig. 1 to simulate a continuous contraction–expansion microfluidic channel. Several 12 µm and 6 µm diameter particles (ten 12-µm, six 6-µm-diameter particles for γ = 1.0 channel and ten 12-µm, ten 6-µm-diameter particles for γ = 2.0 channel because of space limitation) were released at the beginning of the simulation, and after 1,800,000 time steps the particle trajectories were obtained and the particles reached their equilibrium position already. With the acceleration a, which defines the driving force actuating the flow field, simulation parameter value of Reynolds number Re (Re = UDh/υ, where U denotes mean velocity of the channel, Dh denotes the hydraulic diameter) can be set as 10, 20, 30, 40 and 80 for γ = 1.0 and γ = 2.0 channel, respectively, to simulate the focusing behavior of the large and small particles in the contraction–expansion microchannels. However, as a = 32υ2Re/Dh3 is deduced from Poiseuille flow in a straight tube, after the simulation, we recalculated the actual Re in the simulation with the inlet flow rate and modified the Re numbers as 15, 30, 45, 60, 120. We draw the particle trajectories in the main stream of the contraction–expansion microchannels at the end of simulation time in Fig. 2 and more details about particle-focusing characters can be observed.

Fig. 2
figure 2

Simulation results of 6-µm and 12-µm-diameter particle trajectories in the contraction–expansion microchannels with γ = 1.0 (a) and γ = 2.0 (b)

Full size image

In Fig. 2, large particles are more easily focused at the contraction–expansion microchannel center when the Re is large enough. Most of small particles usually flow aside close to the sidewalls when the flow intensity is relatively low; however, there are still one or two of ten released small particles focusing at the flow center. When Re is larger than 60 in γ = 1.0 channel and reaches 120 in γ = 2.0 channel, most of the small particles begin to focus near the main flow center. For a larger γ contraction–expansion microchannel, a higher Re will be needed to focus different size particles as the same focusing pattern in a lower γ channel. What’s more, in the γ = 2.0 microchannel, a larger Re range can be obtained for small particles focusing along the sidewalls in the contraction channel. Flow intensity is much slower in the expansion section of the γ = 2.0 channel, which weakens the inertial lift force to focus particles at the main flow center and pushes the small particles further to the expansion chambers of channels. To sum up, a reasonably larger γ contraction–expansion microchannel helps to carry out a better performance for particle focusing or probably different size particle separation with relatively higher throughput.

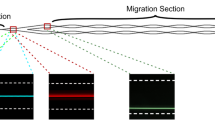
The particle-focusing trajectories in the contraction–expansion microchannels were also captured under microscope to validate the results in the simulation. As the microchannel fabrication, particle preparation and observation method mentioned above, 6-µm and 12-µm-diameter fluorescent particle stacked distributions of contraction–expansion ratio γ = 1.0 and γ = 2.0 microchannels are demonstrated in Fig. 3 with different false colors.

Fig. 3
figure 3

Stacked particle-focusing trajectories in the microfluidic channels with contraction–expansion ratio γ = 1.0 (a) and γ = 2.0 (b)

Full size image

Similarly to other scholars’ research results (Bhagat et al. 2011; Kwak et al. 2018), 12 µm particles are more likely to focus at the main flow center of the microchannel and the 6 µm particles are easier to focus close to the sidewalls with relatively lower flow intensity. With the increasing flow rate, small particles flow along the sidewalls at first and gradually focus at the center when the flow intensity is high enough. Large particles are easier to be focused at the channel center when the small ones are still flowing close to the sidewalls. The experimental results can also verify that a lower γ is helpful to focus large size particles at main flow center or align small particles near the sidewalls at a relatively low flow rate. However, a higher γ channel will help to align small particles aside with a better performance and focus different size particles into a narrower band at the channel center when the flow rate is high and thus the throughput is extremely raised. Because of the less accuracy of UV laser ablation manufacture technique, the contraction–expansion microchannels in the experiment are 1.3–1.4 times wider than we design, and the actual Re numbers are lower than the Re numbers labeled in Fig. 3. Distribution patterns of particles in this experiment are in qualitative agreement with the particles trajectories in the simulation.

Owing to the numerical simulation method, particle-focusing behaviors which are not easily observed in experiments can be obtained conveniently. To understand the particle-focusing mechanism further, the vertical focusing positions of different size particles in γ = 1.0 and γ = 2.0 microchannels are also recorded in Fig. 4. For Re ranging from 30 to 120, only vertical trajectories of 12-µm-diameter particles flowing at main flow center and 6-µm-diameter particles focusing aside are demonstrated to perform different size particles focusing trajectories more clearly.

Fig. 4
figure 4

Simulation results of 6-µm and 12-µm-diameter particle vertical trajectories in the contraction–expansion microchannels with γ = 1.0 (a) and γ = 2.0 (b)

Full size image

12-µm-diameter particles in the simulation results are basically always focusing at the vertical symmetric positions changelessly. Few large particles can flow at the channel symmetry center with little transverse diffusion when Re = 120 in γ = 1.0 channel (Chun and Ladd 2006). However, when Re = 30 in γ = 1.0 channel or Re = 30–60 in γ = 2.0 channel, 6-µm-diameter particles can be observed obviously that they migrate closer to the vertical center when they enter expansion section of the channel and flow towards top and bottom of the channel when they enter the contraction section of the microchannel. The flow intensity has a considerable influence on the inertial lift force acting on the small particles, which points to the cross-section corners in a rectangular microchannel. As 6-µm-diameter particles focus near the main flow center, their vertical trajectories are also basically flat as large particles no matter in contraction or expansion section of the microchannel, which means that the inertial lift force acting on the particles flowing at the main flow center changes little.

Actually, similar with the spiral or serpentine microchannel, the secondary flow also plays an important role in the contraction–expansion microchannel. The simulation results of secondary flow in the Re = 30, γ = 1.0 microchannel are shown in Fig. 5a for instance. The secondary flows in the cross section follow the channel pattern expanding and going backward periodically. Particularly, in the narrowest contraction section, the secondary flow becomes four small vortices flowing towards the channel center. The secondary flow force FS acting on the small particles, which points to the center of the channel, can balance the inertial lift force FL when the small particles flowing through the contraction section of the microchannel. Large particles basically focus at the flow center under the inertial lift force as they are in the low aspect ratio straight microchannel (Liu et al. 2015). However, small particles are more easily influenced by the secondary flow (Di Carlo et al. 2007), and through the pulling and pushing of the secondary flow, most small particles can separate from the large ones and flow close to the sidewalls. The equilibrium of FS and FL in the contraction section can strengthen the focusing effects of small particles. What’s more, the competition of FS and FL is also related to Re number and contraction–expansion ratio γ. Larger Re may strengthen the FL effect on the particles and focus the particle at the channel center. A higher contraction–expansion ratio γ may strengthen the secondary flow relatively in the contraction section and align the particles close to the sidewalls. Particle diameter, Re number and contraction–expansion ratio γ have comprehensive influence on the inertial and secondary flow force acting on the particles and decide the particle trajectory pattern.

Fig. 5
figure 5

The simulation results of secondary flow and sketch of the forces on particles in Re = 30, γ = 1.0 contraction–expansion microchannel (a). The rotations of particles are represented by vector P from particle center to a fixed node on the surface membrane (b). Angles between vector P and the coordinate axis are defined as θx, θy and θz (c)

Full size image

Large particles focusing at the main flow center usually rotate in the x–z plane driven by the FL. But for small particles, it is more complicated to learn the rotation state. In Fig. 5b, the particle rotation is described by the vector P which points from particle center to a fixed node on the membrane surface. Under the secondary flows sketched by purple arrows, large particles focusing at the symmetric center of the channel are confirmed to rotate in the x–z plane. Meanwhile, the rotation of the small particles is influenced by the secondary flow, but the shear effects of secondary flow cannot cause every small particle to rotate with it in the corresponding direction.

To analyze particle rotation more deeply, the time history of vector P coordinates of typical large particles focusing at the main flow center and small particles flowing aside before the end of the simulation time is demonstrated in Fig. 6.

Fig. 6
figure 6

Time history of vector P coordinates of typical large particles focusing at the main flow center and small particles flowing aside before the end of the simulation time in the contraction–expansion microchannels with γ = 1.0 (a) and γ = 2.0 (b)

Full size image

The motion of the large particles focusing at the channel center is clear. y-coordinates of the vector P of large particles remain unchanged when passing through the contraction and the expansion sections of the channels, and x-coordinates and z-coordinates basically change as the sine curve, which confirms that the rotations of the large particles are in x–z plane. The rotation of the small particles is more complicated. However, the coordinates of vector P of small particles also fluctuate periodically and the period is longer than that of larger particles. The influence of FL on small particles is weaker.

To describe the rotation of small particles in more detail, the angles between vector P of small particle and the coordinate axis are defined as θx, θy and θz in Fig. 5c and demonstrated with time history in Fig. 7.

Fig. 7
figure 7

Time history of angles between vector P of 6-µm-diameter particles and the coordinate axis in the contraction–expansion microchannels γ = 1.0 (a) and γ = 2.0 (b)

Full size image

For the γ = 1.0 contraction–expansion microchannel, with the increasing Re, the small particles flow closer to the main flow center quickly and then rotate in the x–z plane more steadily with invariable rotation rate. However, for the small particles focusing aside near the sidewalls in γ = 1.0 and γ = 2.0 microchannel, the rotation in y–z plane or x–y plane is more obvious. Actually, the rotation in y–z plane is the probably main reason to make the θy fluctuate because of the considerable secondary flow in the cross section. We extract angle curves in one period of contraction–expansion microchannel in Fig. 8. In Fig. 8, for the small particles focusing aside, the change of θy is faster when the small particle is passing through the contraction section and entering the expansion section of the microchannel, which means that the small particles are indeed influenced by the secondary flows in the contraction section.

Fig. 8
figure 8

Angles between vector P of 6-µm-diameter particles and the coordinate axis in the contraction–expansion microchannels γ = 1.0 (a) and γ = 2.0 (b)

Full size image

When the flow intensity of the contraction–expansion microchannel is relatively lower, the small particles are more easily influenced by the secondary flow than the large particles and isolated close to the sidewalls. During passing through the contraction section of the channel, the rotations of small particles are greatly controlled by the secondary flow with the vortices pattern and the focusing positions of small particles are decided by the equilibrium of FS and FL as discussed above. With the increasing of the flow intensity, the inertial lift force FL begins to play the dominant role and the small particles can also focus at the main flow center as the large particles.

4 Conclusions

The simple and classic contraction–expansion structure can be employed to the modern particle manipulation microfluidic channel. Here, we systematically explored the particle-focusing mechanics in different contraction–expansion ratio channels with the numerical simulation and experiment validation and found that the larger contraction–expansion ratio channels need higher flow rate to focus different size particles at their own equilibrium position. What’s more, the larger contraction–expansion ratio channels also have potentials to focus small particles near the sidewalls with a wider Re range when flow rate is relatively low and focus different size particles in a narrower band at the channel center with a better performance when the flow intensity is high enough. Basically, the flow intensity difference between contraction and expansion sections in large contraction–expansion ratio channel helps small particles to be easily driven by the secondary flow in the expansion away from the main flow center, and the focusing positions of the small particles isolated near the sidewalls are also determined by the secondary flow in the cross section, especially the vortices of secondary flow in the contraction section. We hope the results of this research will be helpful for the future extreme high-throughput particle/cell pretreatment structure design.