Time resolution effect on the apparent particle dynamics confined in a nanochannel evaluated by the single particle tracking subject to Brownian motion

Abstract

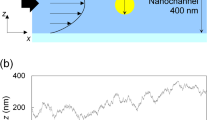
Experimental observation of fluid dynamics including the diffusion due to the Brownian motion in confined nanospace, e.g., nanochannels and biological cells, and at the interface between the fluid and solid wall in general relies on the tracking of nanoparticles. Combination of finite time resolution with force field between the particle and the wall can cause significant deviation of apparent position distribution and diffusion coefficient from the actual ones. In this article, we show that the exposure time and the frame interval affect the apparent particle dynamics in a nanochannel in different manners. Sufficiently short exposure time enables precise evaluation of the force field with a long frame interval, whereas sufficiently short frame interval is also required in the precise evaluation of the diffusion coefficient. The dependences of the apparent diffusion coefficient and force field on the frame interval with a fixed force field for different particle sizes collapse into a single curve with appropriate nondimensional characterization. These findings are ubiquitously important in the fields of fluid dynamics, chemistry, biology, and their related engineering, where single particle or molecule tracking in the vicinity of solid–fluid interface is the subject of study.

1 Introduction

Microfluidics has rapidly developed to manipulate small volumes of fluid for integration of various chemical operations in analysis and chemical synthesis, and enhancement of the efficiency of energy devices such as heat pipes and fuel cells (Mawatari et al. 2011). Recently, the research field has further down-scaled to nanofluidics exploiting 10–100 nm spaces for developments of novel devices such as single molecule analysis (Mawatari et al. 2014). Therefore, dynamics of colloidal nanoparticle suspended in a fluid near walls or in a confined channel, which is a classical and general issue in fluid mechanics, becomes more important for understanding of fluid flows, molecular transport, and chemical reactions in micro- and nanochannels with increased surface-to-volume ratio. Therefore, particle tracking methods for small spaces have been developed to determine the position and displacement of nanoparticles for studies on the flow profile, mass diffusion, and particle distribution. Micron-resolution particle image velocimetry ($\upmu$-PIV) using 100-nm particles and far-field optics is a wide-spread method for microchannels with dimensions in the order of 10–100 $\upmu$m (Santiago et al. 1998). To focus on the near-wall region within 100 nm with dominant surface effects, particle tracking methods based on the evanescent wave, which is the light exponentially decaying from the wall, have been developed. The position and displacement of individual nanoparticles can be determined at a space resolution in the order of 10 nm. Previous studies on fluid flows near the wall in the microchannel suggested slip lengths within nano-meters in pressure-driven flows (Jin et al. 2004; Li and Yoda 2010; Li et al. 2015) , flow profiles of electroosmotic flows under external electric fields with the electric double layers (Bouzigues et al. 2008), and near-wall behaviors of 100-nm particles suggested depletion of negatively-charged particles near a negatively-charged wall within distances in the order of nano-meters by surface interactions due to the electrostatic force and van der Waals forces (Li and Yoda 2008; Kazoe and Yoda 2011; Wu and Bevan 2005). They also revealed hindered Brownian motion of particles near the wall (Carbajal-Tinoco et al. 2007; Huang and Breuer 2007; Kazoe and Yoda 2011), which corresponds to the hydrodynamic viscous effects reported by classical studies (Brenner 1961; Goldman et al. 1967). Most recently, the particle tracking method using the evanescent wave has been applied to the nanochannel to investigate unique characteristics of fluid flows and dynamics of 10-nm particles in confined nanospaces (Kazoe et al. 2013, 2015). The results suggested larger slip length of pressure-driven flow, broader region of near-wall particle depletion, and more hindered Brownian diffusion, compared to those in the microchannel.

However, accuracy of these particle tracking methods for near-wall region and nanochannels has not been sufficiently addressed although it is significantly restricted by the finite time resolution. In general, the position of particle obtained from the measurement is not an exact position, but the average during the exposure time of the camera. More specifically, the finite time resolution caused by the exposure time and the frame interval in the imaging can make the apparently observed phenomena different from the original phenomena. In the measurements of nanoparticles near the wall and in the confined nanospaces, the difference between them can be even larger. The Brownian diffusion of nanoparticles near the wall and in the confined spaces becomes anisotropic owing to the hindered diffusion and restriction of the displacement by the wall, which makes contrast with the bulk situation. In addition, when the nanoparticle approaches the wall within the order of 100 nm, the force field caused by the particle–wall interactions usually affects the particle motion in the asymmetric manner in the wall normal direction. These factors can lead to a significant bias of the measured position and hence errors of the slip length of pressure-driven flow, the free energy (or potential) profile of particle interacting with the wall, and the diffusion coefficient near the wall. Indeed, previous studies pointed out that the apparent potential profile is shallower because of the Brownian diffusion with the finite time resolutions (Eichmann and Bevan 2010) and a bias error exists in the evanescent wave-based particle velocimetry by the near wall hindered diffusion (Sadr et al. 2007; Huang et al. 2009). Recently, Pouya et al. evaluated influences of the finite time resolution on the estimated near-wall velocities and diffusion coefficient parallel to the wall under uniform particle distribution, based on the numerical simulation using the Langevin equation (Pouya et al. 2015). Despite these studies, influences of the finite time resolution on the results including the particle depletion and the diffusion coefficients are not fully understood.

Therefore, it is important to clarify the influence of the finite time resolution in combination with the force field from transferable point of view. Using the smaller nanoparticles leads to more significant bias error of the particle tracking owing to larger displacement of the Brownian motion: for tracking 10-nm particle at a time resolution of 1 ms, the displacement of the Brownian diffusion becomes 100 nm, which is ten times larger than the particle size. In addition, there is no report on the influence of the finite time resolution on the particle tracking in the confined nanospace. Therefore, we employ the system configuration of the recent experimental work of nanoparticles inside nanochannel (Kazoe et al. 2015). We consider the influence of force field condition based on this previous study, but we try to make our discussion as universal as possible by reasonable simplification. Thereby the present study will play the pivotal role as a reference for the future studies by many researchers with more specific interest with respect to the force field. Our focus in this study is the influence on the existence of the (soft) excluded volume effect on the finite-time resolution. The finite time resolution itself mainly consists of two aspects: the exposure time $\tau _\mathrm{xp}$ and the frame interval $\tau _\mathrm{fr}$. The finite $\tau _\mathrm{xp}$ causes time-averaging of detected positions while $\tau _\mathrm{fr}$ does not, but $\tau _\mathrm{fr}$ can cause the different appearance in the dynamics based on the displacements. This implies the differences in the effect of $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$ on the position and displacements. The position distribution alone can directly affect the appearance of free energy profiles and the displacement distribution can further affect the appearance of diffusion coefficients. This is likely to be most manifested in the dynamics in the direction normal to the channel walls. We, therefore, focus on the position and displacement in the wall normal direction, which makes contrast with the existing reports on the flow velocity measurements. We show that the exposure time and the frame interval affect the apparent dynamics in different manners.

2 Model and methods

We simulate the Brownian dynamics of a nanoparticle suspended in a nanochannel as schematically shown in Fig. 1. We consider the dynamics in the z direction corresponding to the plane normal of the top and bottom walls of the nanochannel. The governing equation of motion is the over-damped linear Langevin equation taking into account the non-uniformity of the diffusion coefficient due to hydrodynamic effect (Ermak and McCammon 1978):

$$\begin{aligned} \varDelta z (t) \equiv z (t+\varDelta t) - z (t) = \frac{f _\mathrm{c}(z)D}{k_\mathrm{B}T}\varDelta t + \frac{\partial D}{\partial z}\varDelta t + \sqrt{2D\varDelta t}\psi (t), \end{aligned}$$

(1)

where $\varDelta z(t)$ is the displacement in the z direction at time t, D is the diffusion coefficient, $f_\mathrm{c}(z)$ is the conservative force, $k_\mathrm{B}$ is the Boltzmann’s constant, T is the absolute temperature, $\varDelta t$ is the time step of the dynamics, and $\psi$ is the normal random number. The model definition as a confined space like a nanochannel rather than a one-sided solid–fluid interface is advantageous for the simplicity of characteristic length scale and for the force field definition by a single parameter as mentioned below. We focus on the dependence of apparent position and displacement distribution on the exposure time and frame interval. The sensitivity of such dependencies may be affected not only by the particle size through the intensity of Brownian motion but also by the force field. Then, it is very important to describe the force field by minimum number of parameters to avoid the unnecessary complexity of the discussion. Our choice of functional form enables the discussion of force field with a single parameter. The hydrodynamic non-uniformity of the diffusion coefficient is described by

$$\begin{aligned} \alpha _\mathrm{wall}(z) = \frac{D}{D_\mathrm{bulk}}=\frac{6h^2+2ah}{6h^2+9ah+2a^2}, \end{aligned}$$

(2)

where h(z) is the distance of the particle surface from the wall that depends on the particle position z, $a=d/2$ is the particle radius (Brenner 1961; Happel and Brenner 1983), and $D_\mathrm{bulk}$ is the diffusion coefficient in the bulk, respectively. It should be noted that we discuss only the dynamics in the z direction in this article. The diffusion coefficient of a spherical particle suspended dilutely in the bulk is derived from the Stokes–Einstein relation:

$$\begin{aligned} D_\mathrm{bulk} = \frac{k_\mathrm{B}T}{6\pi \eta a}, \end{aligned}$$

(3)

where $\eta$ is the viscosity of the suspension fluid (i.e., water). For those who are interested in the validity of Stokesian drag at molecular scale, please see Hanasaki et al. (2015, 2016). In order to take into account both of the top and bottom walls of the nanochannel, the effect of Eq. (2) is superimposed as follows:

$$\begin{aligned} \alpha (z) = \alpha _\mathrm{top}(z)+\alpha _\mathrm{bottom}(z)-1, \end{aligned}$$

(4)

where $\alpha _\mathrm{top}$ and $\alpha _\mathrm{bottom}$ is the effect of Eq. (2) defined for each of the top and bottom wall, respectively. The plane walls are located at $z=\pm\, H/2$ and the distance of the particle from side walls are assumed to be sufficiently large. Based on the experimental report (Kazoe et al. 2015), the typical particle diameter d condition is $d=64$ nm and the channel height $H=410$ nm. The viscosity $\eta =0.89\times 10^{-3}$ P of the working fluid is based on the water at room temperature.

Fig. 1

Schematic diagram of the model configuration. The focus of this study is the particle dynamics in the z direction ranging from $-H/2$ to H / 2

Fig. 2

The relations between the actual, and apparent quantities under the conditions of $d=64$ nm, $\tau _\mathrm{xp}=200~\upmu$s and $\tau _\mathrm{fr}=260~\upmu$s corresponding to the previous experimental report (Kazoe et al. 2015): a dependence of the actual position distribution $\sigma _\mathrm{o}$ on the force field parameter $\sigma _\mathrm{n}$, b dependence of the apparent position distribution $\sigma _\mathrm{a}$ on the actual position distribution, c dependence of the apparent position distribution $\sigma _\mathrm{a}$ on the force field parameter $\sigma _\mathrm{n}$, and d dependence of the apparent diffusion coefficient $D_\mathrm{a}$ (compared to the actual value $D_\mathrm{o}$) on the actual position distribution $\sigma _\mathrm{o}$

Fig. 3

Comparison of the computational results of the present model and a previous experimental report (Kazoe et al. 2015) with respect to the influence of particle–wall interactions on the a displacement and b position distributions. It should be noted that the force field is simplified in the present model, and no experimental errors except for $\tau _\mathrm{xp}=200~\upmu$s and $\tau _\mathrm{fr}=260~\upmu$s are taken into account

Fig. 4

Comparison of the computational results of the present model and a previous experimental report of Kazoe et al. (2015) with respect to the influence of the exposure time $\tau _\mathrm{xp}$ on the a displacement and b position distributions. It should be noted that the force field is simplified in the present model, and no experimental errors except for $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$ are taken into account. The numerical model is based on $\tau _\mathrm{fr}=260~\upmu$s in common with the experimental condition. The experimental condition of the exposure time is $\tau _\mathrm{xp}=200~\upmu$s

Fig. 5

Exposure time dependence of apparent a diffusion coefficient and b position distribution when the actual force field parameter $\sigma _\mathrm{n}$ is varied while keeping particle diameter $d=64$ nm. Diffusive time scale $\tau _\mathrm{o}\approx 2.2\times 10^{-2}$ s. The frame interval is $\tau _\mathrm{fr}=260~\upmu$s

Fig. 6

Exposure time dependence of apparent a diffusion coefficient and b position distribution when the particle diameter d is varied while keeping $\sigma _\mathrm{n}/H=0.15$. Diffusive time scale $\tau _\mathrm{o}\approx 1.7\times 10^{-3},\,3.4\times 10^{-3},\,1.7\times 10^{-2},\,2.2\times 10^{-2},\,\mathrm{and}\,3.4\times 10^{-2}$ s for $d/H=1.2\times 10^{-2},\,2.4\times 10^{-2},\,1.2\times 10^{-1},\,1.6\times 10^{-1},\,\mathrm{and}\,2.4\times 10^{-1}$, respectively. The frame interval is $\tau _\mathrm{fr}=260\,\upmu$s

Fig. 7

Exposure time dependence of apparent a diffusion coefficient and b position distribution when the particle diameter d is varied while keeping $\sigma _\mathrm{n}/H=1$. Diffusive time scale $\tau _\mathrm{o}\approx 1.7\times 10^{-3},\,3.4\times 10^{-3},\,1.7\times 10^{-2},\,2.2\times 10^{-2},\,\mathrm{and}\,3.4\times 10^{-2}$ s for $d/H=1.2\times 10^{-2},\,2.4\times 10^{-2},\,1.2\times 10^{-1},\,1.6\times 10^{-1},\,\mathrm{and}\,2.4\times 10^{-1}$, respectively. The frame interval is $\tau _\mathrm{fr}=260\,\upmu$s

Fig. 8

Frame interval dependence of apparent a diffusion coefficient and b position distribution when the actual force field parameter $\sigma _\mathrm{n}$ is varied while keeping particle diameter $d=64$ nm. Diffusive time scale $\tau _\mathrm{o}\approx 2.2\times 10^{-2}$ s. The exposure time is $\tau _\mathrm{xp}=2$ ns

Fig. 9

Frame interval dependence of apparent a diffusion coefficient and b position distribution when the particle diameter d is varied while keeping $\sigma _\mathrm{n}/H=0.15$. Diffusive time scale $\tau _\mathrm{o}\approx 1.7\times 10^{-3},\,3.4\times 10^{-3},\,1.7\times 10^{-2},\,2.2\times 10^{-2},\,\mathrm{and}\,3.4\times 10^{-2}$ s for $d/H=1.2\times 10^{-2},\,2.4\times 10^{-2},\,1.2\times 10^{-1},\,1.6\times 10^{-1},\,\mathrm{and}\,2.4\times 10^{-1}$, respectively. The exposure time is $\tau _\mathrm{xp}=2$ ns

Fig. 10

Frame interval dependence of apparent a diffusion coefficient and b position distribution when the particle diameter d is varied while keeping $\sigma _\mathrm{n}/H=1$. Diffusive time scale $\tau _\mathrm{o}\approx 1.7\times 10^{-3},\,3.4\times 10^{-3},\,1.7\times 10^{-2},\,2.2\times 10^{-2},\,\mathrm{and}\,3.4\times 10^{-2}$ s for $d/H=1.2\times 10^{-2},~2.4\times 10^{-2},~1.2\times 10^{-1},~1.6\times 10^{-1},~\mathrm{and}~2.4\times 10^{-1}$, respectively. The exposure time is $\tau _\mathrm{xp}=2$ ns

The particle of interest is subject to the possible force field from the channel wall. The force field has been described by the combination of electrostatic and van der Waals potentials, but there are multiple parameters and the functional form is highly nonlinear. The apparently larger excluded volume thickness may be caused by originally different combination of van der Waals and electrostatic force fields. Therefore, the multiple parameters of the overall force field are not easily uniquely determined due to the highly nonlinear nature of the force field, especially when we consider the limited accuracy of the measurement even without the finite time resolution effect. We need to focus on the dependence of the essential or minimal feature of the soft excluded volume on the effect of finite time resolution. We aim to discuss more simple and universal aspects on the relation between the force field and the finite time resolution, which will contribute to the transferable discussion on the specific different system configurations leading to different components of force fields with similar feature. We expect that our work will be the reference of diverse future studies where the more specific characteristics of force field are focused on. To attain the well-focused discussion on the influence of time resolution, we consider one of the simplest forms of the force field. More specifically, based on the experimental observation (Kazoe et al. 2015), the free energy profile from the two walls of the nanochannel appears to be approximately represented by the harmonic functional form:

$$\begin{aligned} \phi (z)= \frac{k_\mathrm{B}T}{2\sigma _\mathrm{n}^2}z^2. \end{aligned}$$

(5)

Namely, the experimentally observed position distribution appears approximately Gaussian function and the free energy function corresponding to the Gaussian distribution is the harmonic form. This functional form requires only one parameter $\sigma _\mathrm{n}$, which is shared with the Gaussian distribution p(z) of the position z as follows:

$$\begin{aligned} p(z)= \frac{1}{\sqrt{2\pi \sigma _\mathrm{n}^2}} \exp \left[ -\frac{z^2}{2\sigma _\mathrm{n}^2}\right] , \end{aligned}$$

(6)

where Eq. (5) is derived from Eq. (6) through the following relation:

$$\begin{aligned} \phi (z)=-\,k_\mathrm{B}T\ln p(z). \end{aligned}$$

(7)

The conservative force in Eq. (1) is derived from

$$\begin{aligned} f_\mathrm{c}=-\frac{\partial \phi (z)}{\partial z}. \end{aligned}$$

(8)

The consequent free energy profile is validated by the agreement with the previous work Kazoe et al. (2015). The specific details of the force fields can vary diversely, depending on the surface conditions of both particles and channel walls, and the ionic strength and pH of the working fluid. However, it should be noted that our focus in this study is not in the origin of force field but its influence on the measurements with finite-time resolution. This drastic simplification also enables comprehensible discussion with multiple factors (exposure time, frame interval, particle size, and force field) affecting the results. We explore the parameter space of d and $\sigma _\mathrm{n}$ for the object of measurement while keeping other parameters such as H constant. The small $\sigma _\mathrm{n}$ indicates the large thickness of the excluded volume effect from the walls (or the longer Debye length in the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory) with a soft repulsive interaction.

We focus on the effect of time resolution on the apparent dynamics that can be different from the actual ones. More specifically, we examine the influence of the exposure time $\tau _\mathrm{xp}$ and frame interval $\tau _\mathrm{fr}$ of the camera in the measurement system. Equation (1) is numerically solved with a time step $\varDelta t=2$ ns. This is determined by the condition that it is sufficiently small to satisfy the approximately constant diffusion coefficient in the single displacement during a time step, but it is not too smaller than the inertial time scale $m/(6\pi \eta a)$, where m is the mass of a particle. For example, $\tau _\mathrm{o}=m/(6\pi \eta a)\approx 2$ ns for a polystyrene particle with $a=32$ nm in water. Numerical integration is exactly Eq. (1) using a random number generator based on the Box–Muller method. When a tentative particle displacement generated by the random number $\psi (t)$ crosses the top or bottom wall of the channel, the displacement is simply reflected at the wall position, i.e., the trajectory is folded, to avoid the crossing. This is a simplification of a random displacement to a linear one in a single frame interval, but this is reasonable in practice as far as the single displacement per $\varDelta t$ is sufficiently small compared to H. We find a posteriori that the fraction of the number of steps that required the reflection from the walls was less than 0.01% for the case with the largest diffusion coefficient (i.e., $d=5$ nm) without significant excluded volume effect by the force field (i.e., $\sigma _\mathrm{n}/H=1$). The sampling of the dynamics is conducted at the specified frame interval $\tau _\mathrm{fr}$ and the finite exposure time $\tau _\mathrm{xp}$ is simulated by averaging the positions during the multiple time steps of $\varDelta t$ in a $\tau _\mathrm{xp}$. As far as the one-to-one mapping between the fluorescent spot size and the z position is sufficiently precise under a sufficiently short exposure time condition, $\tau _\mathrm{xp}$ dependence of evaluated z position in the experiment is regarded as the time-averaging effect. A particle starts from $z=0$ and travels the channel height direction until the number of sampling steps per frame interval of $\tau _\mathrm{fr}$ reaches $10^6$ or the total number of time steps of the dynamics reaches $10^{11}$.

3 Results and discussion

Figure 2 shows how force field affects the apparent diffusion coefficient by paying attention to the force field parameter $\sigma _\mathrm{n}$. (The subscript “n” stands for a “nominal” quantity.) Sufficiently smaller $\sigma _\mathrm{n}$ corresponds to the larger thickness of the excluded volume effect from the channel walls. On the other hand, sufficiently large $\sigma _\mathrm{n}$ is effectively equivalent to no excluded volume effect from the walls except for the reflection on the crossing since $\sigma _\mathrm{n}$ is the standard deviation of the position distribution regardless of the wall position. Figure 2a shows that the actual standard deviation $\sigma _\mathrm{o}$ of the position distribution has monotonically positive correlation with the force field parameter $\sigma _\mathrm{n}$. $\sigma _\mathrm{o}$ is defined by the actual position distribution generated by the dynamics that is independent of the observation condition. (The subscript “o” stands for an “original” (i.e., actual) quantity.) However, the range of $\sigma _\mathrm{o}$ is inevitably small due to the confinement by the channel walls although wide range of $\sigma _\mathrm{n}$ is tested. The apparent standard deviation $\sigma _\mathrm{a}$ of the position distribution, which can be affected by the finite exposure time $\tau _\mathrm{xp}$ and/or the finite frame interval $\tau _\mathrm{fr}$, is close to the actual one $\sigma _\mathrm{o}$ on condition that d, $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$ are the same as the previous work of Kazoe et al. (2015) , i.e., $d=64$ nm besides $\tau _\mathrm{xp}=200~\upmu$s and $\tau _\mathrm{fr}=260~\upmu$s. (The subscript “a” stands for an “apparent” quantity.) Consequently, the relation between $\sigma _\mathrm{a}$ and $\sigma _\mathrm{n}$ shown in Fig. 2c is similar to Fig. 2a. Nevertheless, the apparent diffusion coefficients $D_\mathrm{a}$ evaluated from the mean squares of the apparent displacements are different from the actual diffusion coefficient $D_\mathrm{o}$ evaluated from the actual displacements at the time resolution of $\varDelta t$ in general. The time resolution of the apparent displacements used for the evaluation of $D_\mathrm{a}$ is $\tau _\mathrm{fr}$ and each of the two positions that consist each displacement is affected by the averaging in the finite exposure time $\tau _\mathrm{xp}$ as well. As shown in Fig. 2d, the dependence of $D_\mathrm{a}/D_\mathrm{o}$ on the actual position distribution $\sigma _\mathrm{o}$ is significantly nonlinear. In particular, $D_\mathrm{a}/D_\mathrm{o}$ becomes substantially smaller than unity when $\sigma _\mathrm{o}/H$ is smaller than ca. $5\times 10^{-2}$. This also corresponds to the condition of $\sigma _\mathrm{a}/H$ (cf. Fig. 2b). The previous experimental report (Kazoe et al. 2015) argues that the diffusion coefficient in the channel height direction is even substantially smaller than the value predicted by Eq. (2). The numerical result shown in Fig. 2d indicates that this is possible as an apparent decrease due to the finite time resolution of the measurement.

Figure 3 shows the comparison between the numerical model with minimal settings of the force field and the previous experimental report (Kazoe et al. 2015) with more data. The experimental condition corresponds to the case of buffer solution at 300 kPa (Kazoe et al. 2015). The influence of this force field parameter is not crucial in the displacement distribution on condition that d, $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$ are the same as the previous work of Kazoe et al. (2015). Nevertheless, the clearly single-peaked distribution of the position is obtained when the excluded volume effect is taken into account as shown in Fig. 3b, whereas the negligible force field results in a uniform distribution. With the same conditions of time resolutions $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$, the position distribution obtained by simple force field with $\sigma _\mathrm{n}/H=0.15$ roughly agrees with the experimental result. Figure 4 shows the comparison between the experimental and numerical results based on the harmonic model of the force field with $\sigma _\mathrm{n}/H=0.15$ that roughly agrees with the experimental result. There is a significant while small influence of finite $\tau _\mathrm{xp}$ on the displacement distribution as shown in Fig. 4a when the exposure time $\tau _\mathrm{xp}/\tau _\mathrm{o}=10^{-2}$ (i.e., $\tau _\mathrm{xp}=200~\upmu$s) is taken into account in the frame interval $\tau _\mathrm{fr}=260~\upmu$s, where $\tau _\mathrm{o}=H^2/D_\mathrm{o}$ and $D_\mathrm{o}$ employs bulk value for this nondimensionalization. The displacement distribution appears to be more biased with $\tau _\mathrm{xp}/\tau _\mathrm{o}=10^{-2}$ toward smaller displacements compared to the case of $\tau _\mathrm{xp}/\tau _\mathrm{o}=10^{-7}$ (i.e., $\tau _\mathrm{xp}=2$ ns). This is the time-averaging effect of the positions within an exposure time. The position distribution with $\tau _\mathrm{xp}/\tau _\mathrm{o}=10^{-2}$ also shows slightly narrower distribution compared to the case of negligibly small $\tau _\mathrm{xp}$ as shown in Fig. 4b. Basically, the averaging of position or accumulation of displacements during $\tau _\mathrm{xp}$ biases the apparent position closer to the expectation value, i.e., the middle of the channel where the particle is located in the lower free energy. Thus, there is a inter-related dependences of position and displacement on the measurement time resolution and force field.

Hereafter, we show how the displacement and position distributions are affected by the time resolutions $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$ of the measurement. We also examine how the sensitivity of them is affected by the force field $\sigma _\mathrm{n}$ and particle diameter d. Both can affect the actual dynamics and the characteristics of the dynamics affect how sensitively the apparent dynamics depends on the time resolution of the measurement. Based on the exhaustive parameter study, we first show the influence of the exposure time $\tau _\mathrm{xp}$ by Figs. 5, 6, and 7 with the constant $\tau _\mathrm{fr}=260~\upmu$s. Then, we show the influence of the frame interval $\tau _\mathrm{fr}$ by Figs. 8, 9, and 10 with the constant $\tau _\mathrm{xp}=2$ ns, i.e., when the exposure time is negligibly small.

Figure 5a shows the $\tau _\mathrm{xp}$ dependence of displacement distribution represented by the ratio of apparent diffusion coefficient $D_\mathrm{a}$ to the actual diffusion coefficient $D_\mathrm{o}$. The diffusion coefficients are based on the mean squared displacements for the time span of $\tau _\mathrm{fr}$ and $\varDelta t$ for $D_\mathrm{a}$ and $D_\mathrm{o}$, respectively. Each of the plotted points corresponds to a single case of simulation that yields displacement and position distributions such as those shown in Figs. 3 and 4. The apparent diffusion coefficient $D_\mathrm{a}$ can deviate substantially from the actual one $D_\mathrm{o}$ when there exists a significant excluded volume effect. Effectively narrower channel height due to this force field enhances this deviation. Furthermore, $D_\mathrm{a}$ decreases with increasing $\tau _\mathrm{xp}/\tau _\mathrm{o}$. There is a qualitatively similar trend also for the position distribution as shown in Fig. 5b. Sufficiently large effective channel height leads to the apparent position distributions close to the actual ones, but the small channel height due to the excluded volume effect causes apparently larger excluded volume thickness with increasing $\tau _\mathrm{xp}$. On the other hand, there is a difference in the trend of displacement and position distributions. In contrast to the apparent position distribution converging to the actual value for sufficiently short $\tau _\mathrm{xp}$, the asymptotic value of $D_\mathrm{a}/D_\mathrm{o}$ is not necessarily 1 but it can be smaller than 1. This is attributed to the dependence on the frame interval $\tau _\mathrm{fr}$ besides the exposure time $\tau _\mathrm{xp}$ as we will address this point in the later discussion.

The possible deviation of the apparent dynamics from the actual one depends not only on the force field but also on the actual diffusion coefficient of the particle of interest. Figure 6a shows that the dependence of $D_\mathrm{a}/D_\mathrm{o}$ on $\tau _\mathrm{xp}$ is more prominent when the particle diameter d is smaller. It should be noted here that $\tau _\mathrm{o}$ is defined to depend on d as $D_\mathrm{o}$ in $\tau _\mathrm{o}\equiv H^2/D_\mathrm{o}$ depends on d by the Stokes–Einstein relation. The variation of d also causes the difference of asymptotic values of $D_\mathrm{a}/D_\mathrm{o}$ for sufficiently small $\tau _\mathrm{xp}$. On the other hand, the asymptotic values of $\sigma _\mathrm{a}/\sigma _\mathrm{o}$ are 1 for the same regime as shown in Fig. 6b. The relations between the apparent and actual position distributions as a function of $\tau _\mathrm{xp}/\tau _\mathrm{o}$ with different particle diameters collapse into a single curve. It should be noted here that the parameter d affects only the excluded volume and the diffusion coefficient in this model definition. In reality, the particle size variation can change the charge density per particle, which leads to the variation of the force field. Our purpose of this study is to examine the role of Brownian motion independently. To understand how force field $\sigma _\mathrm{n}$ affects the sensitivity of $\tau _\mathrm{xp}$ dependence to particle diameter d, the cases with effectively no excluded volume effect (except for d itself) are shown in Fig. 7. The sensitivity of $\tau _\mathrm{xp}$ dependence of $D_\mathrm{a}/D_\mathrm{o}$ to d is less prominent compared to the case of significant excluded volume effect (Fig. 6). This also applies to the $\tau _\mathrm{xp}$ dependence of $\sigma _\mathrm{a}/\sigma _\mathrm{o}$.

The asymptotic values of $\sigma _\mathrm{a}/\sigma _\mathrm{o}$ for small $\tau _\mathrm{xp}/\tau _\mathrm{o}$ are always 1 regardless of force field $\sigma _\mathrm{n}$ or particle diameter d within the range investigated here as shown in Figs. 5b, 6b, and 7b. On the other hand, the asymptotic values of $D_\mathrm{a}/D_\mathrm{o}$ can remain significantly smaller than 1. The independence on $\tau _\mathrm{xp}$ implies the possible dependence on the frame rate $\tau _\mathrm{fr}$. Therefore, we have examined it as shown in Figs. 8, 9, and 10. First, it is clearly confirmed from Figs. 8b, 9b, and 10b that the position distribution $\sigma _\mathrm{a}/\sigma _\mathrm{o}$ does not depend on the frame interval $\tau _\mathrm{fr}$ regardless of the force field $\sigma _\mathrm{n}$ and particle diameter d. The apparent position distributions are the same as the actual ones. In contrast, $D_\mathrm{a}/D_\mathrm{o}$ can depend on the frame interval $\tau _\mathrm{fr}$. When the excluded volume effect is negligible (i.e., $\sigma _\mathrm{n}/H=1$), the apparent diffusion coefficient is the same as the actual one regardless of $\tau _\mathrm{fr}$ as shown in Fig. 8a. On the other hand, the significant thickness of excluded volume effect from the channel walls causes the decrease in the apparent diffusion coefficient with increasing $\tau _\mathrm{fr}$. This trend is more prominent with decreasing $\sigma _\mathrm{n}$.

Whereas there are differences of asymptotic values of $D_\mathrm{a}/D_\mathrm{o}$ with decreasing $\tau _\mathrm{xp}/\tau _\mathrm{o}$ for different d, the dependences of $D_\mathrm{a}/D_\mathrm{o}$ on $\tau _\mathrm{fr}/\tau _\mathrm{o}$ for different d collapse into a single curve as shown in Fig. 9a. Since the numerical values of $\tau _\mathrm{o}$ depend on d, this nondimensionalization of time scale reveals the universal property compared to the discussion of the $\tau _\mathrm{xp}$ dependence of $D_\mathrm{a}/D_\mathrm{o}$. This also applies to the dependence of $D_\mathrm{a}/D_\mathrm{o}$ on $\tau _\mathrm{fr}$ when the soft repulsive force field is negligible as shown in Fig. 10a. It can be confirmed that the existence of excluded volume effect leads to even smaller $D_\mathrm{a}/D_\mathrm{o}$, which corresponds to Fig. 8a. The diffusion coefficient, i.e., the distribution of displacement per time step or one of the dynamical characteristics, is more sensitive to the time resolution of the measurement, compared to the structural characteristic of position distribution. It is counter-intuitive when considering that the position distribution is generated from the trajectory that consists of displacements. However, this feature of higher sensitivity to the dynamic characteristics than the structural ones is found in the previous theoretical reports on the Brownian motion (Hanasaki et al. 2015, 2016).

The recent study of the time-resolution effect on the quantities defined in the direction parallel to the channel wall (Pouya et al. 2015) discusses the time resolution with a single parameter $\tau _\mathrm{xp}/\tau _\mathrm{fr}$. Our study rather revealed the different nature of $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$. This is reasonable when considering that the dynamics and, hence, the time scale are characterized by the Brownian motion whereas $\tau _\mathrm{xp}$ and $\tau _\mathrm{fr}$ are fundamentally independent of each other. It should also be noted that our discussion can be applied to the Brownian particles at solid–fluid interface in general without double-sided confinement. Although the quantitative detail changes, the mechanism of deviation between the apparent and actual dynamics is the same. Therefore, the part of the possible inconsistency between the observations and existing theories at the solid–fluid interface may be explained by the phenomena that we have clarified in this article. The point is that the pursuit of space resolution by miniaturization of the tracer or probe particles does not straightforwardly results in it. The smaller particles exhibits more intensive Brownian motion. In other words, the effect of finite time resolution is not likely to be significant in the cases where Brownian motion is negligible due to the large size of particles or higher viscosity of the fluid or simply the required space resolution is not demanding.

4 Concluding remarks

We have shown by numerical analysis that the finite time resolution of the observation can affect the apparent diffusion and force field. There is a difference between the exposure time $\tau _\mathrm{xp}$ and the frame interval $\tau _\mathrm{fr}$ in the manner that affects the apparent displacement and position distributions, which are directly related to the diffusion coefficient and free energy profile, respectively. The longer $\tau _\mathrm{xp}$ causes apparently smaller diffusion coefficient $D_\mathrm{a}$, expressed as the ratio $D_\mathrm{a}/D_\mathrm{o}$ to the actual value $D_\mathrm{o}$, and apparently larger excluded volume thickness, i.e., smaller $\sigma _\mathrm{a}$, in the nanochannel. The nominally (or actually) larger excluded volume thickness, i.e., smaller $\sigma _\mathrm{n}$ (or $\sigma _\mathrm{o}$), makes these effects more prominent. The smaller particle diameter d leads to smaller $D_\mathrm{a}/D_\mathrm{o}$, but $\sigma _\mathrm{a}$ is independent of d if $\tau _\mathrm{xp}$ is nondimensionalized by the characteristic time scale $\tau _\mathrm{o}=H^2/D_\mathrm{o}$ defined by the channel height H and original diffusion coefficient $D_\mathrm{o}$ (for the bulk in this evaluation). This trend of $\sigma _\mathrm{a}$ makes contrast with the that of $D_\mathrm{a}/D_\mathrm{o}$. The asymptotic values of $D_\mathrm{a}/D_\mathrm{o}$ with decreasing $\tau _\mathrm{xp}$ can remain smaller than unity. This remaining deviations are caused by the finite $\tau _\mathrm{fr}$. The larger $\tau _\mathrm{fr}$ leads to smaller $D_\mathrm{a}/D_\mathrm{o}$, and the smaller $\sigma _\mathrm{n}$ causes more prominent dependence on $\tau _\mathrm{fr}$. In contrast to the dependence on $\tau _\mathrm{xp}/\tau _\mathrm{o}$, the dependences of $D_\mathrm{a}/D_\mathrm{o}$ on d and $\tau _\mathrm{fr}/\tau _\mathrm{o}$ collapse into a single curve for fixed $\sigma _\mathrm{n}$. Therefore, the use of smaller d becomes advantageous for the precise measurement of $D_\mathrm{o}$ on condition that $\tau _\mathrm{xp}$ is sufficiently short. On the one hand, the finiteness of $\tau _\mathrm{fr}$ does not affect $\sigma _\mathrm{a}$ regardless of $\sigma _\mathrm{n}$ and d, which is rather clear by definition. Thus, $\sigma _\mathrm{o}$ can be evaluated precisely with a long $\tau _\mathrm{fr}$ as far as $\tau _\mathrm{xp}$ is sufficiently short. On the other hand, precise evaluation of $D_\mathrm{o}$ requires both the sufficiently short $\tau _\mathrm{fr}$ and $\tau _\mathrm{xp}$.