1 Introduction

Electrokinetic effects in a micro- and nanoscale channel have received a considerable amount of attention in many fields of applications, including biochemical processing (Li and Harrison 1997; Jacobson et al. 1999), electric power generation (Davidson and Xuan 2008; van der Heyden et al. 2007; Zhang et al. 2015; Haldrup et al. 2016; Cheng et al. 2017), filtration (Chun et al. 2002) and environmental engineering (Acar et al. 1995). To support the feasibility or to improve the performance of nanofluidic devices, recent studies have attempted to understand fundamental phenomena and explain physical mechanisms on the nanoscale level. Various experimental techniques have been explored regarding the observation of electrokinetic effects at the nanoscale, and state-of-the-art measuring equipment such as nanoelectrodes for electrochemical sensing, the atomic force microscope, and the high-resolution transmission electron microscope have been developed. Nevertheless, experimental observations (Brown et al. 2016; Hatsuki et al. 2013; Paul et al. 1998; Schoch and Renaud 2005; Saini et al. 2014) on the nanoscale are very limited, and it is nearly impossible to observe electrochemical reactions in a confined nanochannel. Theoretical models (Choi and Kim 2009; Taghipoor et al. 2015; Baldessari and Santiago 2009; Huang and Yang 2007) which are able to predict electric potential distributions and ionic concentrations in detail and analyze electrokinetic effects by various parameters are an essential step toward true comprehension. Therefore, it is necessary to establish the appropriate theoretical models with which to investigate the electrokinetic effects in nanochannels. Theoretical models are composed of governing equations for the electric potential, the spatial distribution of ions, the velocity field for pressure-driven flows, and the proper boundary conditions. While governing equations which are always applicable have been established, the boundary conditions for ionic concentrations remain unclear in channels with overlapped electric double layers (EDLs).

Previous theoretical models (Choi and Kim 2009; Taghipoor et al. 2015; Baldessari and Santiago 2009; Huang and Yang 2007) of the electrokinetic effects have employed different boundary conditions depending on the degree of EDL overlap in the channels. When the thickness of the EDL (λ D ) is much less than the channel height (H), electrokinetic channel flows can be analyzed using the linear Poisson–Boltzmann (PB) equation based on Debye–Hückel approximation (Vainshtein and Gutfinger 2002; Cetin et al. 2008) or on a nonlinear PB equation (Behrens and Borkovec 1999; Stein et al. 2004; Chang and Yang 2009) (λ D  < H). Either the nonlinear PB equation (Behrens and Borkovec 1999; Stein et al. 2004; Chang and Yang 2009) or the Poisson–Nernst–Planck (PNP) equation (Choi and Kim 2009; Mansouri et al. 2005; Mirbozorgi et al. 2007) can describe the electrokinetic effects of channel flows with overlapped EDLs (λ D  ~ H). When the thickness of the EDL is much greater than the channel height (λ D  ≫ H), the nonlinear PB equation cannot accurately predict the electrokinetic behavior (Baldessari and Santiago 2009; Qu and Li 2000; Mei et al. 2017; Ma et al. 2017), and predictions based on the Boltzmann equation show significant deviation from experimental data (Kwak and Hasselbrink 2005). To overcome the limitations of theoretical approaches based on the PB equation in overlapped EDLs, Qu and Li (2000) noted that the electric potential and ionic concentration distributions may not be predicted by the Boltzmann equation when the EDLs overlap because the Boltzmann equation fundamentally assumes that a single plate is in contact with an infinitely large electrolyte solution. Hence, they suggested new distributions of the electric potential and ionic concentrations by adopting boundary conditions considering overlapped EDLs. However, these outcomes are still not applicable in cases with highly overlapped EDLs (λ D  ≫ H) or with high zeta potential values because a site-dissociation model assuming a Boltzmann distribution of hydroxide ions is used to predict the surface charge density and because the Debye-Hückel approximation is employed. Since then, many researchers have focused on identifying the boundary conditions for nanochannels with highly overlapped EDLs (Baldessari and Santiago 2009; Huang and Yang 2007; Chang et al. 2012; Wang et al. 2010; Das et al. 2013; Conlisk et al. 2002). To investigate the effects on electro-osmotic flows in micro- and nanochannels with overlapped EDLs, Zheng et al. (2003) proposed a model employing boundary conditions for ionic concentrations determined by the equilibrium between the channel and the reservoir. However, as Baldessari and Santiago (2009) pointed out, Zheng et al. (2003) did not apply the global electroneutrality constraint to both the nanochannel and the reservoirs. Baldessari and Santiago (2009) proposed a new model employing global net electroneutrality to impose channel-to-reservoir equilibrium and introduced a boundary condition for ionic concentrations via equilibrium between the ionic concentrations in the channel and in the reservoirs for electro-osmotic flows. Chang et al. (2012) used an expression for the ion distribution with an ionic concentration in the reservoir identical to that of Baldessari and Santiago (2009) and applied the global net electroneutrality condition and the conservation of the ion number in the nanochannel to study pressure-driven flows. If the reservoir is very large compared to the channel, the ionic concentrations for counterions and co-ions flowing into a channel presented by Chang et al. (2012) become identical regardless of the degree of overlap, which is not physically realistic. Therefore, the ionic concentrations in the reservoir according to Chang et al. (2012) are not appropriate for predicting the ion distribution in a nanochannel with highly overlapped EDLs. For a better understanding of the electric potential distribution and the ionic concentrations in highly overlapped EDLs, it is necessary to propose a model that employs new boundary conditions for ionic concentrations at the wall.

The goal of the present study is to propose a new analytical model that accurately describes the electric potential distribution and the ionic concentrations in a confined nanochannel with highly overlapped EDLs using the effective ionic concentrations suitable for determining boundary conditions for ionic concentrations at the wall. The model is validated by comparing the outcome with the experimental data (van der Heyden et al. 2005) and results from existing numerical (Choi and Kim 2009; Wang et al. 2010) and analytical (Choi and Kim 2009; Yeh et al. 2014) models. In terms of the electroviscous effects, the objectives of this study are (a) to investigate the electroviscous effects in the channel according to variations of the pH, ionic concentration, and channel height and (b) to propose a new dimensionless parameter characterizing the electroviscous effect.

2 Mathematical approach

2.1 Theoretical model of pressure-driven flow in a parallel plate channel

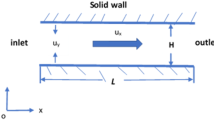
Electrostatic charges on a non-conducting solid surface will attract counterions, and an ionic concentration gradient layer known as an electric double layer (EDL) therefore appears in an electrolyte solution. In the electric double layer, the net electric charge density has a non-zero value. Flow-induced streaming potential arises in a direction opposite to that of pressure-driven flow due to the non-zero net charge density in EDLs when the pH value of the electrolyte solution exceeds the point of zero charge (PZC). As shown in Fig. 1, a nanochannel with reservoirs at both ends has a length of L and height of H. The channel walls in contact with an electrolyte solution are negatively charged, and the reservoir walls are assumed to be free of any charge. The electrolyte solution in the nanochannel is driven by the applied pressure difference at both ends of the nanochannel. An incompressible flow at a low Reynolds number can be predicted using the Stokes equation, including a body force term of the flow-induced electric potential. A momentum equation that combines a pressure term and an electro-osmosis term is as shown below.

$$ \mu \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} - \frac{{{\text{d}}p}}{{{\text{d}}x}} + \rho_{e} E_{x} = 0 $$
(1)

where u is the axial velocity of the liquid (m/s), μ denotes the viscosity of the liquid (N s/m2), dp/dx is the pressure gradient in the axial direction (Pa/m), ρ e (=∑ i z i en i ) represents the local net electric charge density per unit volume (C/m3), and E x is the flow-induced electric potential field (V/m). The electric potential can be expressed through the Poisson’s equation, representing the relationship with the electric charge density.

$$ \frac{{{\text{d}}^{2} \phi }}{{{\text{d}}y^{2} }} = - \frac{1}{{\varepsilon_{r} \varepsilon_{0} }}\rho_{e} $$
(2)

where ϕ is the electric potential normal to the solid surface (V), ε r is the dielectric constant of the electrolyte, and ε 0 denotes the permittivity of free space, i.e., 8.854 × 10−12 (C/V m). The dielectric constant of the electrolyte in the direction normal to the nanochannel wall may vary depending on the refractive index of the solvent and potential gradient due to solvent polarization. Das et al. (2012) reported that the change in the dielectric constant of the electrolyte is apparent within 10 nm from the charged channel wall based on their studies. Because the height of the nanochannel presented in our study is much larger than 10 nm, we assume that the dielectric constant of the electrolyte is constant. Ion transport can be formulated by the Nernst–Planck equation consisting of the summation of the diffusion term due to ionic concentration gradient, the conduction term by electrophoretic effect and the convection term of the liquid. If a fully developed laminar flow is in a steady state and the system is in an electrochemical equilibrium state, the Nernst–Planck equation can be simply expressed as the Nernst equation. In this case, the electric potential depends only on the y-coordinate (Plecis et al. 2005),

$$ \frac{1}{{n_{i} }}\frac{{{\text{d}}n_{i} }}{{{\text{d}}y}} = - \frac{{ez_{i} }}{{k_{B} T}}\frac{{{\text{d}}\phi }}{{{\text{d}}y}} , $$
(3)

where n i is the local ionic number concentration of ion i (1/m3), e is the elementary charge, 1.60218 × 10−19 (C), z i represents the valance number of ion i (z = z += z −), k B denotes the Boltzmann constant [1.38065 × 10−23 (J/K)], and T is the absolute temperature (K). The electric potential is zero, and the ionic concentration is equal to the bulk ionic concentration in the middle of an infinitely long channel when the electric double layers do not overlap. Given non-overlapped EDLs, the spatial distribution of ions may follow the Boltzmann equation. When the electric double layers are overlapped, the symmetry boundary conditions (d/dy = 0) in the middle of the channel and the boundary conditions at the wall may be used to determine the solution of the governing equations [Eqs. (1), (2), (3)]. The selection of appropriate boundary conditions is one of the most critical issues of the electroviscous effects in nanochannels with overlapped EDLs. Many researchers (Baldessari and Santiago 2009; Huang and Yang 2007; Chang et al. 2012; Wang et al. 2010; Das et al. 2013; Revil and Glover 1997; Qu and Li 2000) have proposed boundary conditions by theoretical studies. However, despite numerous studies of the electroviscous effects in micro- and nanochannels with overlapped electric double layers, the boundary conditions for ionic concentrations still remain controversial. To obtain the solution of the governing equations, Qu and Li (2000) have introduced the values in the middle of the nanochannel instead of the boundary conditions at the wall because it is convenient to handle the overlapped electric double layer field.

Fig. 1
figure 1

Schematic of a channel with reservoirs at both ends, and the boundary conditions for the system

Full size image

Baldessari and Santiago (2009) used the ionic concentrations and the electric potential in the middle of the nanochannel in order to obtain the ionic concentration distribution, and Eq. (3) can be solved as follows:

$$ n_{i} = n_{i}^{c} \exp \left[ { - \frac{{ez_{i} }}{{k_{\text{B}} T}}\left( {\phi - \phi^{c} } \right)} \right] $$
(4)

where n c i and ϕ c are the ionic number concentration and electric potential in the middle of the channel, respectively. Baldessari and Santiago (2009) utilized the volume-averaged ionic concentration in the reservoirs to determine the ionic concentration in the middle of the channel. In addition, Chang et al. (2012) used the same model as Baldessari and Santiago (2009) for a pressure-driven flow. Assuming electrochemical equilibrium of the system, the ionic concentration difference between the reservoirs and the channel must satisfy \( \nabla \overline{\mu }_{i} = 0 \) because the electrochemical potential μ i can be considered to be constant everywhere.

$$ n_{i}^{c} = n_{i}^{\text{int}} \exp \left[ { - \frac{{ez_{i} }}{{k_{\text{B}} T}}\left( {\phi^{c} - \phi^{\text{int}} } \right)} \right] $$
(5)

where n int i and ϕ int i are the ionic number concentration and the electric potential at the interface between the channel and the reservoir, respectively. The effective ionic concentration n int i in Eq. (5) refers to the surface-averaged value immediately before flowing into the channel, whereas Baldessari and Santiago (2009) used the volume-averaged ionic concentration in the reservoir. The electric potential in the vicinity of the inlet of the nanochannel, ϕ int is significantly lower than the electric potential in the middle of the nanochannel, ϕ c (ϕ int ≪ ϕ c). Substituting Eqs. (5) into (4) yields

$$ n_{i} = n_{i}^{\text{int}} \exp \left( { - \frac{{ez_{i} }}{{k_{\text{B}} T}}\phi } \right) $$
(6)

In a steady state, ion flow rate through the cross section of the reservoirs and the channel should be identical at any position in the channel. Hence,

$$ \int_{\text{reservoir}}^{{}} {n_{i} u{\text{d}}A} = \int_{\text{nanochannel}}^{{}} {n_{i} u_{i} {\text{d}}A} , $$
(7)

In this study, the ionic concentration n i and the liquid velocity u on the left side of Eq. (7) are considered to be values at the reservoir inlet for convenience. Equations (1)–(6) are similar to the theoretical model of previous studies (Baldessari and Santiago 2009; Chang et al. 2012), but Eq. (7) is different from that of Baldessari and Santiago (2009) and Chang et al. (2012). Equation (7) can be rearranged using the ionic number concentrations and the ion velocities of counterions and co-ions at the inlet of the reservoir.

$$ n_{i,0} u_{0} A_{\text{reservoir}} = 2w\int_{o}^{H} {n_{i} u_{i} {\text{d}}y} $$
(8)

where n i,0 and u 0 are the ionic number concentration and the liquid velocity at the inlet of the reservoir, respectively, and w is the width of the channel. The size of the reservoirs is assumed to be sufficiently large so as not to be affected by the charged channel. In Eq. (8), n i,0 is a measurable value and u 0 is equal to the liquid velocity because the reservoir walls are not charged. The velocity profile can be derived using Eqs. (1) and (2) with the boundary conditions in the middle of the channel (du/dy = 0, dϕ/dy = 0) and on the channel walls (u = 0, ϕ = ζ).

$$ u = u_{p} + u_{{E_{x} }} = \frac{{H^{2} }}{2\mu }\left( { - \frac{{{\text{d}}p}}{{{\text{d}}x}}} \right)\left[ {1 - \left( {\frac{y}{H}} \right)^{2} } \right] - \frac{{\varepsilon_{r} \varepsilon_{0} E_{x} \zeta }}{\mu }\left( {1 - \frac{\phi }{\zeta }} \right) $$
(9)

As shown in Eq. (9), the velocity of a liquid is expressed by a combination of the pressure-driven velocity and the streaming potential-driven velocity. The second term on the right-hand side of Eq. (9) represents the flow resistance caused by the streaming potential.

The excess charges in the vicinity of the channel walls are carried by the pressure-driven flow, forming a streaming current flowing downstream. The uneven charge distribution at both ends of the channel can generate the flow-induced electric potential field, E x (Hunter 1981; Lyklema 1991). The electric field gives rise to a conduction current in a direction opposite to that of the streaming current. The steaming electric field can be determined by the balance between the streaming current and the conduction current under a steady state.

$$ i = 2wez\int_{0}^{H} {\left( {n_{ + } u_{ + } - n_{ - } u_{ - } } \right){\text{d}}y} $$
(10)

The net ionic current passing through the cross section of the channel is expressed as Eq. (10) for symmetric electrolytes. The conduction current may be composed of the surface conduction and bulk conduction, which are divided into the Stern layer and the diffuse layer (Lyklema 2001; Delgado et al. 2007). In this study, it is assumed that the conduction effect of the Stern layer is of little importance. Equation (10) can be expressed as follows:

$$ i = 2wez\int_{0}^{H} {\left( {n_{ + } - n_{ - } } \right)u{\text{d}}y} + 2wezE_{x} \int_{0}^{H} {\left( {\mu_{ + } n_{ + } + \mu_{ - } n_{ - } } \right){\text{d}}y} $$
(11)

where μ i is the ion mobility. The first and second terms on the right-hand side of Eq. (11) refer to the streaming current and the conduction current, respectively. Persat et al. (2009) introduced a variety of useful ways to determine the ion mobility, but we use the ion mobility levels based on the ratio of the ionic concentration of each ion,

$$ \mu_{{{\text{K}}^{ + } }} = \frac{{n_{{{\text{K}}^{ + } ,0}} }}{{n_{{ + ,{\text{total}}}} }}\mu_{{{\text{K}}^{ + } ,\infty }} $$
(12a)
$$ \mu_{{{\text{H}}^{ + } }} = \frac{{n_{{{\text{H}}^{ + } ,0}} }}{{n_{{ + ,{\text{total}}}} }}\mu_{{{\text{H}}^{ + } ,\infty }} $$
(12b)
$$ \mu_{{{\text{Cl}}^{ - } }} = \frac{{n_{{{\text{Cl}}^{ - } ,0}} }}{{n_{{ - ,{\text{total}}}} }}\mu_{{{\text{Cl}}^{ - } ,\infty }} $$
(12c)
$$ \mu_{{{\text{OH}}^{ - } }} = \frac{{n_{{{\text{OH}}^{ - } ,0}} }}{{n_{{ - ,{\text{total}}}} }}\mu_{{{\text{OH}}^{ - } ,\infty }} $$
(12d)

where n +,total (or n −,total) is the sum of the ionic number concentration of all cations (or all anions) in an electrolyte solution and μ ∞ denotes the mobility at an infinite dilution level. If an electric field is not externally applied, the net ionic current is zero in a steady state and the electric field is represented by Eqs. (9) and (11).

$$ E_{x} = \frac{{\frac{{H^{2} }}{2\mu }\left( { - \frac{{{\text{d}}p}}{{{\text{d}}x}}} \right)\int_{0}^{H} {\left( {n_{ + } - n_{ - } } \right)\left[ {1 - \left( {\frac{y}{H}} \right)^{2} } \right]{\text{d}}y} }}{{\frac{{\varepsilon_{r} \varepsilon_{0} \zeta }}{\mu }\int_{0}^{H} {\left( {n_{ + } - n_{ - } } \right)\left( {1 - \frac{\phi }{\zeta }} \right){\text{d}}y} - \int_{0}^{H} {\left( {\mu_{ + } n_{ + } + \mu_{ - } n_{ - } } \right){\text{d}}y} }} $$
(13)

The ionic number concentrations at the interface between the channel and the inlet side reservoir can be obtained from Eq. (6), Eq. (8) and ion velocity equations (u ±=u ± E x μ ±).

$$ n_{ + }^{\text{int}} = \frac{{n_{ + ,0} u_{0} A_{\text{reservoir}} }}{{2w\int_{0}^{H} {\exp \left( { - \frac{ez}{{k_{B} T}}\phi } \right)\left[ {u + E_{x} \mu_{ + } } \right]{\text{d}}y} }} $$
(14a)
$$ n_{ - }^{\text{int}} = \frac{{n_{ - ,0} u_{0} A_{\text{reservoir}} }}{{2w\int_{0}^{H} {\exp \left( {\frac{ez}{{k_{B} T}}\phi } \right)\left[ {u - E_{x} \mu_{ - } } \right]{\text{d}}y} }} $$
(14b)

where A reservoir is the cross-sectional area of the reservoir inlet. Flow retardation of an electrolyte solution due to negatively charged channel walls alters the velocity profile and the mass flow rate based on traditional fluid dynamics. A change in the apparent viscosity that corresponds to an alteration of the electroviscosity-induced flow is referred to as an electroviscous effect (Huang and Yang 2007; Hunter 1981; Persat et al. 2009; Rice and Whitehead 1965; Ren and Li 2005; Yang and Li 1998; Schoch et al. 2008). In nanofluidics devices, the electroviscous effect is one of the most important issues that distinguish electrokinetic behavior from traditional fluid mechanics. In particular, the electroviscosity (or apparent viscosity) increases when the channel walls are negatively charged. The ratio of the apparent viscosity (μ a) to the actual viscosity (μ) can be used to indicate the degree of change in viscosity caused by the electroviscous effect (Huang and Yang 2007; Cetin et al. 2008; Chakraborty and Das 2008; Burgreen and Nakache 1964).

$$ \frac{{\mu_{\text{a}} }}{\mu } = \frac{{\frac{{H^{2} }}{2}\left( { - \frac{{{\text{d}}p}}{{{\text{d}}x}}} \right)\int_{0}^{H} {\left( {n_{ + } - n_{ - } } \right)\left[ {1 - \left( {\frac{y}{H}} \right)^{2} } \right]{\text{d}}y} }}{{\frac{{H^{2} }}{2}\left( { - \frac{{{\text{d}}p}}{{{\text{d}}x}}} \right)\int_{0}^{H} {\left( {n_{ + } - n_{ - } } \right)\left[ {1 - \left( {\frac{y}{H}} \right)^{2} } \right]{\text{d}}y} - \varepsilon_{r} \varepsilon_{0} E_{x} \zeta \int_{0}^{H} {\left( {n_{ + } - n_{ - } } \right)\left( {1 - \frac{\phi }{\zeta }} \right){\text{d}}y} }} $$
(15)

2.2 Surface charge density

Many of the significant properties of electrokinetic phenomena are affected directly or indirectly by the surface charge density defined as the total amount of charge per unit area or the zeta (ζ) potential in the vicinity of the outer Helmholtz plane (OHP) (Hunter 1981). For this reason, it is important to estimate the surface charge density or ζ-potential correctly. The relationship between the surface charge density and the ζ-potential is demonstrated in two ways, through a surface regulation model reflecting the chemical properties of the solid–liquid interface and by the Grahame equation that was derived from the Gouy-Chapman theory by presuming an electroneutrality condition. Behrens and Grier (2001) contended that self-consistent values are calculated by combining the two equations. In order to assess the surface charge density and ζ-potential, we used the surface regulation model suggested by Behrens and Grier (2001) in the diffuse layer,

$$ \zeta = \frac{{k_{\text{B}} T}}{ez}\left( {{\text{pK}}_{a} - {\text{pH}}} \right)\ln 10 - \frac{\sigma }{C} + \frac{{k_{\text{B}} T}}{ez}\ln \left( { - \frac{\sigma }{{e\varGamma_{\text{tot}} + \sigma }}} \right) , $$
(16)

where pK a is the logarithmic dissociation constant (= − log10 K a ), pH is a numeric scale used to specify the hydrogen ion concentration, σ denotes the surface charge density, C is the capacitance of the Stern layer, and Γ tot represents the fraction of all chargeable sites, respectively. Equation (16) accounts for chemical characteristics at the solid–water interfaces according to the pH and is based on the assumption that the deprotonation reaction is SiOH ↔ H++SiO− and that the potential drop is linear according to a basic Stern layer capacitance model (Baldessari and Santiago 2009; Hunter 1981). Behrens and Grier (2001) noted that self-consistent values of the surface charge density and ζ-potential can be calculated by combining Eq. (16) and the Grahame equation. Depending on whether the EDLs are overlapped or not, the EDL potential distribution for a symmetric electrolyte solution is represented by different equations (Chang and Yang 2009).

$$ \begin{aligned} & \phi \left( y \right) = \phi^{c} + \frac{{k_{\text{B}} T}}{ez}\ln cd^{2} \left( {\theta |m} \right) \\ & \theta = \frac{{y\sqrt {\frac{{2e^{2} z^{2} n_{ + }^{\text{int}} }}{{\varepsilon_{r} \varepsilon_{0} k_{\text{B}} T}}} }}{{2\exp \left( {\frac{ez}{{2k_{\text{B}} T}}\phi^{c} } \right)}} \\ & m = \frac{{n_{ - }^{\text{int}} }}{{n_{ + }^{\text{int}} }}\exp \left( {\frac{2ez}{{k_{\text{B}} T}}\phi^{c} } \right) \\ \end{aligned} $$
(17)
$$ \phi \left( y \right) = \frac{{2k_{\text{B}} T}}{ez}\ln \left[ {\frac{{1 + \tanh \left( {\frac{ez}{{4k_{\text{B}} T}}\zeta } \right)\exp \left( { - \frac{H - y}{{\lambda_{D} }}} \right)}}{{1 - \tanh \left( {\frac{ez}{{4k_{\text{B}} T}}\zeta } \right)\exp \left( { - \frac{H - y}{{\lambda_{D} }}} \right)}}} \right] $$
(18)

where cd(θ|m) is the Jacobi elliptical function with arguments θ and m and λ D (= κ −1) is the Debye screening length. When the EDLs are overlapped (ϕ c ≠ 0), the EDL potential distribution is given by Eq. (17). Equation (18) is used to describe the EDL potential distribution when the EDLs do not overlap (ϕ c ~ 0).

$$ \sigma = \varepsilon_{r} \varepsilon_{0} \frac{{{\text{d}}\phi }}{{{\text{d}}y}} = - \varepsilon_{r} \varepsilon_{0} \frac{{k_{\text{B}} T}}{ez}\frac{{\sqrt {\frac{{2e^{2} z^{2} n_{ + }^{\text{int}} }}{{\varepsilon_{r} \varepsilon_{0} k_{\text{B}} T}}} }}{{\exp \left( {\frac{ez}{{2k_{\text{B}} T}}\phi^{c} } \right)}}\left( {1 - m} \right)\left| {\frac{{sn\left( {v|m} \right)}}{{cn\left( {v|m} \right)dn\left( {v|m} \right)}}} \right| $$
(19)
$$ v = \frac{{H\sqrt {\frac{{2e^{2} z^{2} n_{ + }^{\text{int}} }}{{\varepsilon_{r} \varepsilon_{0} k_{\text{B}} T}}} }}{{2\exp \left( {\frac{ez}{{2k_{\text{B}} T}}\phi^{c} } \right)}} $$
$$ \sigma = \varepsilon_{r} \varepsilon_{0} \frac{{4k_{\text{B}} T}}{{\lambda_{D} ez}}\frac{{\tanh \left( {\frac{ez}{{4k_{\text{B}} T}}\zeta } \right)}}{{1 - \tanh^{2} \left( {\frac{ez}{{4k_{\text{B}} T}}\zeta } \right)}} $$
(20)

In our study, Eqs. (19) or (20) are used to predict the surface charge density and ζ-potential in place of the Grahame equation. Unlike previous studies (Qu and Li 2000; Baldessari and Santiago 2009) that define the Debye length using bulk ionic concentration, the Debye length in our study is defined using the effective ionic concentrations as

$$ \lambda_{D} = \sqrt {\frac{{\varepsilon_{r} \varepsilon_{0} k_{\text{B}} T}}{{e^{2} z^{2} \left( {n_{ + }^{\text{int}} + n_{ - }^{\text{int}} } \right)}}} $$
(21)

2.3 Calculation procedure and validation

We assume that an electrolyte solution contains four ionic species, i.e., K+, Cl−, H+ and OH−, with c i,0, i = 1, 2, 3 and 4 being their bulk molar concentrations, respectively (Yeh et al. 2014; Ma et al. 2015). Based on electroneutrality in the bulk solution, c 1,0 = c KCl, c 2,0 = c KCl + 10−pH–10pH-14, c 3,0 = 10−pH and c 4,0 = 10pH-14 for pH ≤ 7; and c 1,0 = c KCl-10−pH + 10pH-14, c 2,0 = c KCl, c 3,0 = 10−pH and c 4,0 = 10pH-14 for pH > 7 are given (Yeh et al. 2014). The theoretical models assume that (1) the system is in electrochemical equilibrium including the flow direction; (2) the internal flow is laminar and fully developed in a steady state; (3) only potential-determining ions are adsorbed on the solid surface (Healy and White 1978; Chan et al. 2006); (4) the liquid is incompressible; (5) the electric potential in the reservoirs is zero (Baldessari and Santiago 2009; Chang et al. 2012); (6) the pressure drop across the reservoir is neglected (Mirbozorgi et al. 2007; Daiguji et al. 2004); and (7) the ion concentration polarization is neglected (Zhou et al. 2016).

The calculation procedure to predict the electroviscosity is shown in Fig. 2. First, the dimensions of the channel and the reservoir, the bulk ionic concentration, the pressure difference at both ends of the channel and the pH are needed. Second, based on electroneutrality condition, the ionic concentrations (\( c_{{{\text{K}}^{ + } }} ,c_{{{\text{Cl}}^{ - } }} ,c_{{{\text{H}}^{ + } }} \) and \( c_{{{\text{OH}}^{ - } }} \)) are initialized by the pH. The surface charge density is then determined by Eqs. (16) and (19) or (20). Subsequently, the ion mobility levels of \( \mu_{{{\text{K}}^{ + } }} ,\mu_{{{\text{H}}^{ + } }} ,\mu_{{{\text{Cl}}^{ - } }} \) and \( \mu_{{{\text{OH}}^{ - } }} \) are calculated by Eqs. (12a)–(12d), after which the flow-induced electric potential field (E x ) and the effective ionic concentrations (n int i ) of the reservoir adjacent to the channel are calculated using Eqs. (13) and (14a) and (14b). If the concentration difference between the present (t) and previous (t − 1) time step reaches a certain standard, the calculation procedure is halted. Otherwise, the calculation is repeated and the modified Debye screening length is updated by the effective ionic concentrations. Finally, the ratio of the apparent viscosity to the actual viscosity is calculated by Eq. (15). The calculated values oscillate and converge on a solution through an iterative calculation procedure. As shown in Fig. 2, the zeta potential [Eq. (16)] and the surface charge density [Eqs. (19) or (20)] are calculated through the modified Debye screening length, which is updated by the effective ionic concentrations. Even though this process is iteratively repeated until convergence, the computing time is very short; it takes only a few seconds to a few tens of seconds.

Fig. 2
figure 2

Logical flow for calculating the electroviscosity

Full size image

Figure 3 shows the streaming conductance as a function of the KCl concentration in a channel 140 nm high which is also 50 μm wide and 4.5 mm long at a pH of 8. The reservoirs are assumed to be sufficiently large compared to the channel height. The pressure difference at both ends of the channel is 4 bar. The proposed models are compared with the numerical results from existing studies (Choi and Kim 2009; Yeh et al. 2014) and the experimental data from van der Heyden et al. (2005), as noted above. The electric potential difference between the electrodes is zero because the electrodes at two reservoirs are both grounded in the experiment of van der Heyden et al. Based on the fact that the electrodes are grounded, someone presumed that the electric potential difference across the nanochannel is also zero and there is no reversed electro-osmotic flow. Even if the both electrodes are grounded, however, the gradient of electric potential inside the nanochannel is not zero because there exists the ionic concentration difference caused by the pressure-driven flow across the nanochannel. In fact, the change in the electric potential due to the grounded electrodes occurs only at a very short distance (within a few micrometers) from the electrode surface. In conclusion, there is the reversed electro-osmotic flow in the nanochannel. The parameters (pK a , C, Γ tot) used in this study are not fixed values but in a range. We used parameter values corresponding to the silica channel walls reported in Yeh et al. (2014).

Fig. 3
figure 3

Streaming conductance as a function of the KCl concentration for the channel. The proposed model is compared with a number of existing models (Choi and Kim 2009; Yeh et al. 2014) and the experimental data from van der Heyden et al. (2005) [pKa = 6.6, C = 0.15 (F/m2), Γ tot = 8.0 × 1018 (sites/m2), and T = 298.15 (K)]

Full size image

The mean error between the results from the proposed model and the experimental data (van der Heyden et al. 2005) is 4.58%, and the standard deviation of the errors is 2.02. The mean error between the numerical results from the self-consistent NP model (Choi and Kim 2009) and the experimental data (van der Heyden et al. 2005) is 3.66%, and the standard deviation of the errors is 1.81. The mean error of the results of Yeh et al. (2014) is 12.83%. The numerical results from the self-consistent NP model (Choi and Kim 2009) show the closest approximation to the experimental data (van der Heyden et al. 2005). However, the applicable ranges for their proposed correlations are limited to 10−4 M < c 0 < 10−1 M. The proposed model is not only highly accurate compared with the analytical model (Yeh et al. 2014), but also applicable to a wider range than the numerical model (Choi and Kim 2009).

The effect of the different boundary conditions for the ionic concentrations in the middle of the channel inlet on the ζ-potentials is shown in Table 1. In this table, ζ A denotes the ζ-potential calculated by using the bulk ionic concentration, while ζ B the ζ-potential calculated by using the effective ionic concentration. When the initial ionic concentration is large, there is not much difference between the two ζ-potentials. However, as the initial ionic concentration decreases (or as the degree of EDL overlap increases), the difference between the two ζ-potentials increases.

Table 1 Comparison of the ζ-potential according to different ionic concentrations in the middle of the channel inlet for a 40 nm high channel at pH = 8
Full size table

3 Results and discussion

3.1 Ionic concentration

Figure 4 shows the concentrations of counterions and co-ions in the middle of the channel as a function of the bulk ionic concentration. The counterion concentrations according to the bulk ionic concentration are compared with the numerical results of Wang et al. (2010), solving the governing equations using the lattice Poisson–Boltzmann method. The co-ion concentrations follow the dashed line of symmetry, and the crosshair symbols represent the effective ionic concentrations between the channel inlet and the reservoir. Clearly, the effective ionic concentrations c int± should be distinguished from c well i in Baldessari and Santiago (2009) and Chang et al. (2012) considering volume-averaged ionic concentration in the wells. c well i is determined by global net neutrality and depends on the size of the reservoir (Baldessari and Santiago 2009; Chang et al. 2012). However, the reservoir size influencing c well i has certain limits because it is not possible to increase the reservoir size indefinitely. If the reservoir size is large enough to cover the intermediate zone, which is a small region near the channel inlet due to the axial gradients of the electric potential, the reservoir size is no longer an important parameter that affects the electroviscous effects in the nanochannel. In other words, the reservoir size should not affect the values of c int i or c well i if the reservoir size is large enough.

Fig. 4
figure 4

Concentrations of counterions and co-ions in the middle of the channel as a function of the bulk ionic concentration. The solid line represents the numerical results of Wang et al. (2010) using the lattice Poisson–Boltzmann method, and the symbols are the results of the proposed model

Full size image

3.2 Electroviscosity

Electroviscosity can be affected by several parameters, such as the initial bulk ionic concentration, the pH and the dimensionless Debye-Hückel parameter, κ 0 H. In addition, these parameters can influence the ζ-potential and the surface charge density. Figure 5 shows the ratio of the apparent viscosity to the actual viscosity as a function of the pH. The apparent viscosity is also increased as pH increases at low ionic concentrations, whereas if the ionic concentration increases, there is no significant change in the apparent viscosity. When the pH is increased from 6 to 8, the rate of increase in the apparent viscosity is approximately 1.22 times for a channel 140 nm high with c 0 = 1.518 × 10−4.

Fig. 5
figure 5

The ratio of the apparent viscosity to the actual viscosity as a function of the pH. Identical channel heights use the same symbol color

Full size image

In Fig. 6, the ratio of the apparent viscosity to the actual viscosity is presented as a function of (a) the background salt concentration and (b) dimensionless Debye–Hückel parameter. If the background salt concentration increases, the apparent viscosity becomes similar to the actual viscosity regardless of the channel height. Conversely, if the background salt concentration decreases, the apparent viscosity increases, but the growth rate is reduced when the pH is low. The apparent viscosity is affected by the channel height and κ 0 H, as shown in Fig. 6. The largest value of the ratio of the apparent viscosity to the actual viscosity is 1.894 for a channel which is 563 nm high at pH = 8 and with κ 0 H = 4.371. The dimensionless Debye-Hückel parameter κ 0 H is commonly used to quantify the effect of electroviscosity in previous works (Bowen and Jenner 1995; Mortensen and Kristensen 2008; Davidson and Harvie 2007). However, as κ 0 H becomes smaller (< 6 × 101), the dimensionless Debye–Hückel parameters show a scattered the ratio of the apparent viscosity to the actual viscosity, as shown in Fig. 6b. Therefore, it appears to be difficult for the dimensionless Debye–Hückel parameter to be a governing parameter to quantify the effect of electroviscosity. In this study, a new dimensionless parameter is introduced to quantify the effect of electroviscosity.

Fig. 6
figure 6

The ratio of the apparent viscosity to the actual viscosity as a a function of the background salt concentration and b dimensionless Debye–Hückel parameter, κ 0 H

Full size image

We propose a new dimensionless parameter (ζ/ζ 0)/(κH)a to quantify the effect of electroviscosity. The electroviscosity can be expressed as a function of (ζ/ζ 0)/(κH)a only, as shown in Fig. 7. The dimensionless parameter employs the zeta potential in addition to the dimensionless Debye–Hückel parameter (ζ 0 is the reference potential for nondimensionalization, − 1). The zeta potential is inversely proportional to the ionic concentration, and the overlapped EDL region increases as the ionic concentration decreases. In our study, an exponent of the parameter is 1/4 for fused silica and electrolytes with potassium. As shown in Fig. 7, the parameter (ζ/ζ 0)/(κH)1/4 creates a good curve fitting with a solid line created by least-squares regression, which is one way to draw a proper curve while minimizing the difference between the data and the curve. The quantification of the error in regression can be expressed using the correlation coefficient r (r = 1 signifies a perfect fit between the data and the line) (Chapra and Canale 2010).

$$ r = \frac{{n\sum {x{}_{i}y_{i} } - \left( {\sum {x_{i} } } \right)\left( {\sum {y_{i} } } \right)}}{{\sqrt {n\sum {x_{i}^{2} } - \left( {\sum {x_{i} } } \right)^{2} } \sqrt {n\sum {y_{i}^{2} } - \left( {\sum {y_{i} } } \right)^{2} } }} $$
(22)

where n represents the number of data instances and x i and y i denote the x-coordinate data and y-coordinate data. The result from Eq. (22) is 0.9913, and the coefficient of determination r 2 is 0.9827. The result indicates 98.27 percent of the original uncertainty. Significantly, the solid line has a third-degree polynomial. We propose a criterion by which one can tell whether the electroviscous effects are prominent or not, which can be safely neglected when (ζ/ζ 0)/(κH)1/4 is less than 20 in silica nanofluidic channels.

Fig. 7
figure 7

The ratio of the apparent viscosity to the actual viscosity as a function of (ζ/ζ 0)/(κH)a

Full size image

The effect of the different boundary conditions for the ionic concentrations in the middle of the channel inlet on the electroviscosity is shown in Table 2. In this table, μ a,A denotes the electroviscosity calculated by using the bulk ionic concentration, while μ a,B the electroviscosity calculated by using the effective ionic concentration. When the initial ionic concentration is large (or when the EDLs are not overlapped), there is not much difference between μ a,A and μ a,B . However, as the initial ionic concentration decreases, the difference between the electroviscosity increases.

Table 2 Comparison of the electroviscosity according to different ionic concentrations in the middle of the channel inlet for a 40 nm high channel at pH = 8
Full size table

4 Conclusions

In this paper, the electroviscous effects in an electrically charged nanochannel with reservoirs at both ends were examined. To do this, a new model employing the effective ionic concentration, defined as the concentration at the interface between the channel and the reservoir, is proposed. The theoretical framework of the proposed model has three features which distinguish it from existing models. First, the effective ionic concentrations for ionic concentrations were derived from the continuity equation for ions in place of either the global net neutrality condition or the conservation equation of the ion number in the nanochannel and reservoirs, or both. Second, the electric potential equation in the EDLs is based on the effective ionic concentration instead of the bulk ionic concentration. Third, the existing Debye screening length was modified using the effective ionic concentration. The introduction of the effective ionic concentration was validated using the numerical results of the lattice Poisson–Boltzmann method. Moreover, the numerical results obtained from the proposed model for streaming conductance as a function of the KCl concentration are in good agreement with the experimental data. Compared with the self-consistent NP model, the proposed model not only has comparable accuracy but also has a wider applicable range for salt concentration. The variation of the ratio of the apparent viscosity to the actual viscosity (μ a /μ) was presented with respect to the pH, the bulk ionic concentration, and the dimensionless Debye–Hückel parameter. A new dimensionless parameter (ζ/ζ 0)/(κH)a for electroviscosity was introduced to quantify the effect of the electroviscosity, which to the best of our knowledge is the first parameter to combine several governing parameters affecting the electroviscosity into one in such an electrically confined geometry. The electroviscosity can thus be expressed as a function of (ζ/ζ 0)/(κH)a only, and we proposed a criterion by which on can tell whether the electroviscous effects are prominent or not.