Complete study of a millifluidic flow battery using iodide and ferricyanide ions: modeling, effect of the flow and kinetics

Abstract

In this work, we present a comprehensive study dealing with the modeling of the conversion process occurring in a redox flow cell. Experiments are carried out on an original millifluidic flow battery with ferrocyanide and iodide as electrolytes. A simulation model supports the experimental data. In flow, intensity recovery is limited by the mass transfer. Thanks to diffusion, at low Peclet, the conversion is complete. On the contrary, at high Peclet, the convection prevents the diffusion of species and induces a conversion drop. A quantitative agreement is found between theoretic model and experiment both on current and on power curves. The originality of our work is to take into account the kinetics of the redox reaction at the electrodes. We evidence a new regime where the current intensity is constant as a function of the Peclet number. The maximal recovered power is obtained at a given flow rate and not at very high flow rate. This work paves the road for the optimization of the conversion process and for the measurements of the thermodynamic parameters involved in the redox process such as kinetic parameters at the electrodes.

1 Introduction

Since the emergence of intermittent renewable sources of energy as solar and wind technologies, energy storage has become a crucial point to increase the efficiency of electric grid. Lithium-based battery technology is a well-developed field, but is restricted to energy storage in portable devices (electrical vehicles, electronic devices...) as the cyclability and the capacity storage are limited. In the 1960s, in the prospects of mass energy storage, redox flow batteries have proved to be much more attractive for stationary storage as they combine reliability, large cyclability (more than 10,000 cycles), flexibility of the design and rapid response to external current fluctuation (Alotto et al. 2014; Leung et al. 2012; Wang et al. 2013). In this technology, the electrolytes (named catholyte and anolyte) contain the redox species (vanadium ions, bromium $\hbox {Br}_{2}/\hbox {Br}^{-}$, chromium $\hbox {Cr}^{3+}/\hbox {Cr}^{2+}$, cerium $\hbox {Ce}^{4+}/\hbox {Ce}^{3+}$, ...) solubilized in. They are flowed through a current extracting stack. The main advantage of this technology is the decoupling between power, linked to the stack design and the capacity, based on the total amount of active material stored in the tanks. Currently, vanadium redox flow batteries is around 800$/kWh, about eight times more than lithium technologies. A major challenge is to increase the capacity which is still quite low (around 50 Wh/L for 2 M of vanadium in sulfuric acid electrolyte), with limited cost increase. For this purpose, several strategies can be adopted. The most common idea is to improve the solubility of redox molecules. This idea was widely studied for vanadium with the use of specific ligands acetylacetonate (Liu et al. 2010), glycoxal (Wen et al. 2008) or other compounds such as bromine (Skyllas-Kazacos et al. 2010; Vafiadis and Skyllas-Kazacos 2006) or polyhalide (Skyllas-Kazacos 2003, 2008). Other projects deal with the modifications of the geometry of the cell (use of porous electrodes, of flow recirculations), or with the use of carbon particle solutions.

In this work, we aim to model the flow in a redox flow cell and to predict quantitatively the conversion. This study is motivated by three main reasons: the requirement to optimize the conversion process in redox flow cells and thus to find the best functioning point, the requirement to have a framework to compare the various experiments performed in the literature and last but not the least the possibility to measure thermodynamic parameters involved in the redox process such as kinetic parameters at the electrodes.

The basics of electrochemistry in flow have been studied since the 1970s with Newmann (1973) who studied the theory of an electrochemical conversion of a redox solution in laminar flow on a planar electrode. In particular, he found a scaling law $I \propto Pe^{1/3}$ which relates the intensity I and the Peclet number Pe at high flow rates. This work was followed by many studies on microelectrodes (Zhang et al. 1996) and rotating electrodes (Booth et al. 1995; Gabe 1995). A very detailed work can be found by Squires et al. (2008) wherein a Comsol simulation is realized with calculations at low and high Peclet numbers. The study mainly focuses on the caption on molecules for biosensors and not on electrochemistry.

In the field of flow batteries, although many works were done on electroconversion (Bazylak et al. 2005; Chang et al. 2006; Kjeang et al. 2008; Choban et al. 2005) with a laminar flow, very few articles compare modeling with experiment in a complete and quantitative way. One article of Kjeang et al. (2007) compares a Comsol modelization with experiments on the conversion of ruthenium. The comparison is, however, limited to the scaling law of the intensity with the flow at high Peclet number in the situation where the electrochemical reaction is a faster process than the mass transfer.

In our study, a particular attention is paid to the hydrodynamics of a millifluidic flow battery. The originality of our work is to develop a comprehensive numerical modeling that takes into account the kinetics of the electrochemical reaction. This allows us to predict the intensity in all the regimes. We can calculate the power and intensity curve. Note that previous models were not able to predict these curves as they were limited to high overpotentials.

We evidence a new regime at high Peclet where the current intensity is limited by the kinetics of the reaction and is constant as a function of the flow rate. The maximal recovered power is obtained at a given flow rate and not at very high flow rate. The knowledge of this regime and of its characteristics is fundamental in the situation where mass transfer is fast and kinetics is slow. It is likely to occur when porous electrodes Kjeang et al. (2007) or thin cells are used. This modeling is quantitatively compared to experiments. For this purpose, an original design of millifluidic battery is created and very simple redox couples are used: ferricyanide $\hbox {Fe}_\mathrm{III}(\hbox {CN})_{6}^{3-}/\hbox {Fe}_\mathrm{II}(\hbox {CN})_{6}^{4-}$ and iodide $\hbox {I}_{3}^{-}/\hbox {I}^{-}$. Although the final voltage of the redox reaction is 0.18 V, which is not suitable for battery applications, these compounds are cheap, safe, water soluble which make them particularly suitable for fundamental hydrodynamic studies. The first part of the article deals with the modeling. The second part describes the experimental setup. The third part is devoted to the analysis of the data and to the comparison between experiments and measurements. The last part deals with conclusion and outlooks.

2 Theory and modeling

To refine the comprehension on redox conversion in flow, a numerical simulation is realized to visualize the conversion of redox species flowing along a millifluidic channel with a Poiseuille profile (laminar flow). A current collector parallel to the stream, at which a voltage is applied, recovers or gives electrons coming from the redox reaction. A current value and a concentration profile can be determined in the channel when the flow is steady. This situation corresponds to a typical flow cell where a Nafion membrane separates the catholyte and anolyte flow. In our simulation, we only focus on one half of the cell (anolyte), but the situation is exactly the same at the catholyte side except the sign of the current and the type of redox species. We consider the anolyte reaction involving the formation of n electrons to have a positive current I:

$$ \hbox {Red} \Longrightarrow Ox + ne^{-} $$

(1)

The following schema (Fig. 1) describes the notations. The initial concentration of reductant is called $C_{0}$, and the reaction takes place in a rectangular-shaped channel with a length $Z_{0}$, a height $X_{0}$ and a width $Y_{0}$ with $Z_{0}>> Y_{0 }>> X_{0}$. The electrode is located on the plan (y O z) at the height $x=0$.

Fig. 1

Geometry of the channel and notations for the simulation

The goal of this simulation is to have a complete and adaptable model to foresee quantitatively the conversion regardless the dimension of the geometry and the redox couple. The problem remains quite complex, so we proceed with approximations. We neglect inertial effects (i.e., as the Reynolds number is small in most of our experiments), we assume that the fluid is Newtonian and that no slip occurs at the wall. We use lubrication theory (i.e., we formally assume that the flow has two dimensions) which has been shown to be remarkably insightful in somewhat related situations, i.e, when the aspect ratio is 1:10 between the height and the width and between the width and the length (Kjeang et al. 2007). We suppose that electro-osmosis is negligible. The diffusion law of the reactant writes:

$$\begin{aligned} D\frac{\partial ^{2} c}{\partial x^{2}}=-\,\frac{6V_{m}}{X_{0}^{2}}(x^{2}-X_{0}x)\frac{\partial c}{\partial z} \end{aligned}$$

(2)

c is the concentration of the reactant (oxidant or reductant) that is injected in the channel. To solve this equation, boundary conditions are required. At the entrance of the channel, the concentration c is taken as the bulk concentration $C_{0}$: $c(z=0,x)= C_{0}$ (Dirichlet condition). The Nafion membrane prevents the reductant to diffuse inside the other compartiment. This condition writes: $\frac{\partial c}{\partial x}(x=X_{0},z)=0$ (Neumann condition). The boundary condition at the surface of the current collector is more complex to write since it has to take into account the kinetics of the chemical reaction. In most of the studies (Kjeang et al. 2007), the concentration is taken as zero in $x=0$ along the z-axis as the reaction is considered as total. This situation is exact when the overpotential applied at the electrode is high enough with respect to the Nernst potential of the redox couple. However, this hypothesis narrowed the possibility of the simulation. In particular, we cannot model comprehensive power curves nor the voltage of the battery nor study reactions limited by kinetics. Our goal is to use microfluidics to characterize the redox processes, to measure the kinetic constants, to probe the yields in a redox flow cell. For this purpose, it is required to use a more realist boundary condition. For this purpose, the boundary condition at the surface of the current collector has to take into consideration the Butler Volmer equation which links the current density j(0, z) to the concentration c(0, z) of reductant and the potential E we apply at the electrode. Considering the general equation $\text{Red} \Longrightarrow Ox +ne^{-}$ these currents write:

$$ j(x=0,z)=nFk_{1} [C_\mathrm{Red} e^{\frac{\alpha nF \Delta E}{RT}} - \frac{k_{-1}}{k_{1}} C_{Ox} e^{\frac{-(1-\alpha ) nF \Delta E}{RT}}] $$

(3)

where $k_{1}=k_{o}e^{\frac{\alpha nF E_\mathrm{ref}}{RT}}$ , $\frac{k_{-1}}{k_{1}} =e^{\frac{- nF( E_\mathrm{ref}-E_0)}{RT}}$, $\Delta E=E-E_\mathrm{ref}$.

$C_{Ox}$ and $C_\mathrm{Red}$ are the respective concentrations of oxidant and reductant at $x=0$ (at the electrode), $k_{0}$ is the kinetic constant of the reaction, $E_0$ is the standard potential of the redox couple and $E_\mathrm{ref}$ is the potential of the reference. Assuming equal diffusive coefficient (similar-sized molecules) and in the absence of physical absorption, $C_{Ox}$ and $C_\mathrm{Red}$ can be linked to c(0, z). In the situation where the oxydant is injected, $C_{Ox}=c(0,z)$ and $C_\mathrm{Red}=C_{0}-c(0,z)$. In the situation where the reductant is injected, $C_\mathrm{Red}=c(0,z)$ and $C_{Ox}=C_{0}-c(0,z)$.

$k_{0}$ is the standard rate constant for the direct reaction (oxidation in this case). Usual values range between 1 and 10 cm/s for rapid conversion of species. This value depends on the kinetic of the reaction at the surface of the current collector. $\alpha$ is the transfer coefficient. It is very close to 0.5, meaning that the energy profiles for the forward ($Ox + ne^{-}$) and backward (red) processes of the reaction are symmetric. F is the Faraday constant. T is the room temperature and R, the universal gas constant. The density of faradaic current is also linked to flow of charge at the surface. In our situation, the mass transfer to the electrode is only made by diffusion: There is no perpendicular convection, and the migration can be considered as neglected. Indeed, the addition of a supporting electrolyte ($\hbox {Na}_2\hbox {SO}_{4}$) screens the surface charge of the electrode. Thus, the current of charges writes:

$$\begin{aligned} j\,(x=0,z)=nFD \frac{\hbox {d}C_\mathrm{Red}}{\hbox {d}x}(x=0,z) \end{aligned}$$

(4)

D is the diffusive coefficient of the injected species. Butler Volmer equation and (4) give a relation for the concentration c at $x=0$: In the situation where a reductant is injected, we get

$$\begin{aligned} D\frac{\hbox {d}c}{\hbox {d}x}(x=0,z)=k_{1}\left[c(x=0,z) e^{\frac{\alpha nF \Delta E}{RT}} - \frac{k_{-1}}{k_{1}}(C_{0}-c(x=0,z))e^{\frac{-(1-\alpha ) nF \Delta E}{RT}}\right] \end{aligned}$$

(5)

Equation 5 is modified in the situation where an oxidant is injected and writes:

$$ -\,D\frac{\hbox {d}c}{\hbox {d}x}(x=0,z)=k_{1}[(C_{0}-c(x=0,z))e^{\frac{\alpha nF \Delta E}{RT}} - \frac{k_{-1}}{k_{1}}c(x=0,z)e^{\frac{-(1-\alpha ) nF \Delta E}{RT}}] $$

(6)

The interest of the study lies in the simulation of every flow battery for every geometry using laminar flows. Consequently, the non-dimensionalization of Eq. (2) and the boundary condition (6) are necessary. The system of equations becomes, for dimensionless variables $\widetilde{x}=\frac{x}{X_{0}}$, $\widetilde{y}=\frac{y}{Y_{0}}$, $\widetilde{z}=\frac{z}{Z_{0}}$ and $\widetilde{c}=\frac{c}{C_{0}}$: In the situation where the reductant is injected:

$$\begin{aligned} \begin{cases}\frac{\partial ^{2} \widetilde{c}}{\delta \widetilde{x}^{2}}(\widetilde{x},\widetilde{z})&=-6P_{1}(\widetilde{x}^{2}-\widetilde{x})\frac{\partial \widetilde{c}}{\partial \widetilde{z}}(\widetilde{x},\widetilde{z}) \\ \frac{\partial \widetilde{c}}{\partial \widetilde{x}}(0,\widetilde{z})&=P_{3}[\widetilde{c}(0,\widetilde{z})e^{\alpha P_{2}}-P_{4}(1-\widetilde{c}(0,\widetilde{z}))e^{-(1-\alpha ) P_{2}}]\\ \widetilde{c}(\widetilde{x},0)&=1\\ \frac{\partial \widetilde{c}}{\partial \widetilde{x}}(1,\widetilde{z})&=0\end{cases}\end{aligned}$$

(7)

In the situation where the oxidant is injected:

$$\begin{aligned} \begin{cases}\frac{\partial ^{2} \widetilde{c}}{\delta \widetilde{x}^{2}}(\widetilde{x},\widetilde{z})&=-6P_{1}(\widetilde{x}^{2}-\widetilde{x})\frac{\partial \widetilde{c}}{\partial \widetilde{z}}(\widetilde{x},\widetilde{z})\nonumber \\ \frac{\partial \widetilde{c}}{\partial \widetilde{x}}(0,\widetilde{z})&=-P_{3}[ (1-\widetilde{c}(0,\widetilde{z}))e^{\alpha P_{2}}-P_{4}\widetilde{c}(0,\widetilde{z})e^{-(1-\alpha ) P_{2}}] \\ \widetilde{c}(\widetilde{x},0)&=1 \\ \frac{\partial \widetilde{c}}{\partial \widetilde{x}}(1,\widetilde{z})&=0\end{cases} \end{aligned}$$

(8)

Four parameters are in charge of the process.

• $P_{1}=Pe=\frac{V_{m}X_{0}^{2}}{D_\mathrm{red}Z_{0}}$ is the Peclet number Pe and represents the competition between convection and diffusion. Pe number is proportional to the flow rate and is the most important parameter to quantify the hydrodynamics. If $Pe<< 1$, the diffusion dominates.

• $P_{2}=\frac{nF\Delta E}{RT}$ is the ratio between the overpotential $\Delta E$ and the thermal motion. This parameter allows the plot of the power curves (I vs $\Delta E$).

• $P_{3}=\frac{k_{1}X_{0}}{D}$ represents the competition between the kinetic of the reaction and the diffusion toward the electrode. If $P_{3}<< 1$, the conversion is limited by the slow kinetics of the reaction.

• $P_{4}= \frac{k_{-1}}{k_{1}}$ depends upon the value of the reference.

The effect of all the parameters will be discussed in the result part, but a particular attention is paid to the Peclet number Pe which gives direct information on the effect of the flow rate.

The discretization in finite elements of the equations is realized with Euler approach with MATLAB software. The number of meshes along the x and z direction is carefully defined by Newmann criteria to ensure the convergence of the solution.

After the simulation, we can have access to the concentration profile in the channel. With these results, the yield of conversion of the reductant is obtained by integrating the area under the last curve, at the exit of the channel. The density of current at each point z is equal to $\widetilde{j}(z)=\frac{\hbox {d}\widetilde{c}}{\hbox {d}\widetilde{x}}(\widetilde{x}=0,\widetilde{z})$. An integration along the z-axis gives us the normalized current $\widetilde{I}=\int {\widetilde{j}(\widetilde{z})\hbox {d}\widetilde{z}}$. The following expression gives the relationship between the normalized current $\widetilde{I}$ and the real current I in Amperes:

$$\begin{aligned} I=\frac{nFD_\mathrm{red}Y_{0}Z_{0}C_{0}}{X_{0}}\int \frac{\hbox {d}\widetilde{c}}{\hbox {d}\widetilde{x}}(\widetilde{x}=0)\hbox {d}\widetilde{z}=\frac{nFD_\mathrm{red}Y_{0}Z_{0}C_{0}}{X_{0}} \widetilde{I} \end{aligned}$$

(9)

3 Experimental

3.1 Preparation of the “classical electrolytes” and “liquid electrodes”

The classical electrolytes used in the experimental part are aqueous solutions of iodide ion $\hbox {I}^{-}$ (catholyte) and ferricyanure $\hbox {K}_{3}\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}$ (anolyte). These electrolytes are prepared as following: aqueous solutions with a given amount of potassium iodide KI (Prolabo, RP Normapur, analytical reagent 99.8%) or potassium ferricyanide $\hbox {K}_{3}\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}$ (Potassium hexacyanoferrate(III), ReagentPlus 99% Sigma-Aldrich) are prepared in graduated flasks. One mole of salt $\hbox {Na}_{2}\hbox {SO}_{4}$ (ACS reagent > 99% anhydrous, granular, Sigma-Aldrich) is added for ionic conduction. These electrolytes are involved in the redox reaction: $2\hbox {Fe}^{3+} + 3\hbox {I}^{-} {\mathop {\leftarrow }\limits ^{\hbox {discharge}}} \quad {\mathop {\rightarrow }\limits ^{\hbox {charge}}} 2\hbox {Fe}^{2+} + \hbox {I}_{3}^{-}$. The opposite electrolytes are also formulated to study the discharge. For this purpose, solutions with triiodide $\hbox {I}_{3}^{-}$ (catholyte) (Fluka analytical, 0.5 M iodine solution) and ferrocyanide $\hbox {K}_{4}\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}$ (anolyte) (Acros organics, potassium ferrocyanide trihydrate 99+%) are prepared in 1 M of $\hbox {Na}_{2}\hbox {SO}_{4}$. Generally, the concentration of redox species ranges between 0.1 and 0.002 M. The sodium salt ensures a good ionic conductivity since the ratio of salt over redox species is much larger than 10. These solutions (anolyte and catholyte), prepared as such, are called in the following “classical electrolytes” as they do not contain any carbon particles. This preparation with dissolution of the redox species in solution (water or acid...) is the conventional preparation for redox flow electrolytes with vanadium, bromine, cerium..., and the redox reaction between the anolyte and the catholyte is the same: it involves iron and iodine species whose Nernst potentials are respectively $E^{0}(\hbox {Fe}_\mathrm{III}(\hbox {CN})_{6}^{3-}/\hbox {Fe}_\mathrm{II}(\hbox {CN})_{6}^{4-})=0.36\,\hbox {V}$ and $E^{0}(\hbox {I}_{3}^{-}/\hbox {I}^{-})=0.54\,\hbox {V}$ (vs SHE). Therefore, the standard potential of the flow battery is 0.18 V with the following reaction:

$$\begin{aligned} 2\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-} + 3\hbox {I}^{-} {\mathop {\leftarrow }\limits ^{\hbox {discharge}}}\quad {\mathop {\rightarrow }\limits ^{\hbox {charge}}} 2\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-} + \hbox {I}_{3}^{-} \end{aligned}$$

(10)

We chose these redox species for the sake of simplicity. They are only for demonstration since the voltage is not enough for any battery application. However, the formulation of electrolytes is convenient, cheap and harmless. The diffusion coefficients are mentioned in the literature for an infinite dilution regime in water, at room temperature: $D(\hbox {I}^{-})= 1.04 \times 10^{-9}\,\hbox {m}^{2}/\hbox {s}$ (Wang and Kennedy 1950), $D(\hbox {Fe}_\mathrm{III}(\hbox {CN})_{6}^{3-})= 8.9 \times 10^{-10}\, \hbox {m}^{2}/\hbox {s}$ Lide (2003), $D(\hbox {Fe}_\mathrm{II}(\hbox {CN})_{6}^{4-})= 7.8 \times 10^{-10}\,\hbox {m}^{2}/\hbox {s}$ Lide (2003) and $D(\hbox {I}_{3}^{-})= 1.07 \times 10^{-9}\,\hbox {m}^{2}/\hbox {s}$ (Ruff et al. 1972). As 1 M of salt is present in the electrolyte, the hypothesis of a diluted regime may be discussed. Therefore, the real diffusion coefficients are slightly lower than these values.

The ferricyanide/ferrocyanide couple is a rapid redox couple well studied in the literature. In addition, the green color of the species is convenient to study in visible spectrometry. The catholyte couple with iodine is also well known in the literature but has less advantages: The brown color of triiodide is light sensitive, and the conversion triiodide into iodide has a slow kinetic. Except in the kinetic part, the iodine species are introduced in excess in the catholyte and the limiting current will be given by the couple ferrocyanide/ferricyanide in the following.

3.2 Millifluidic setup for flow battery

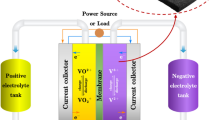
To test our different electrolytes, an experimental home-made device is used as a flow battery (Fig. 2). Two channels in poly(methyl methacrylate) PMMA (cathode and anode chamber) face each other with a Nafion membrane in between as the ionic separator. The ionic separator is a Nafion 117 membrane of 183 $\upmu \hbox {m}$ thick (FuelCell). The Nafion membrane is activated to improve the ionic conductivity: It is boiled during 1 h in 1 M of sulfuric acid and then boiled in 3% of $\hbox {H}_{2}\hbox {O}_{2}$ during 2 h. The membrane is stored at room temperature in distilled water. Each channel is 5 cm long with a width of 1 cm. The depth is 1 mm. The two extremities of the channel are connected to a 1/16” tubing with nanopores to allow the circulation of the electrolyte. To collect the current, a carbon paper electrode (Toray Paper 120, FuelCell, 320 $\upmu\text{m}$ thick) lines the channel and is connected to the external circuit thanks to a copper wire stuck with conductive epoxy glue (Radio Spare). The dimension of the carbon paper electrode is $10\,\hbox {mm}\times 3\,\hbox {cm}$. As the carbon paper is thick, the space under the current collector corresponds to a volume $V=X_{0}*Y_{0}*Z_{0}=0.680\,\hbox {mm} \times 10\,\hbox {mm} \times 3\, \hbox {cm}$. These values will be used in our simulation. The two channels are maintained together thanks to inox screw and circular gaskets seal the setup. The electrolytes are injected simultaneously in the two channels with a syringe pump (Harvard PHD 4400 Hpsi). The electric wires are connected on a potentiostat (CH instrument 600E) in a two-electrode configuration. The Reynolds number $Re=\frac{\rho Q}{Y_{0}\eta }$ associated with this geometry is between 1.8 and $1.8\times 10^{-4}$ and for flow rate Q from to 10,000 to 1 μL/min. Thus, this geometry respects the hypothesis of the simulation namely a laminar regime. As the electrolytes used here are aqueous solutions of salt, their viscosity is close to that of water. The hypothesis of a Poiseuille flow inside the channel is verified. The Poiseuille flow is, as in the simulation, only in the z direction with a speed dependence in x. Indeed, the hypothesis $X_{0}<<Y_{0}$ is respected in our geometry.

Fig. 2

Experimental setup for millifluidic flow battery. a Separated parts, b assembled cell, c Functioning the ferricyanide/iodide electrochemical cell

3.3 Intensity and power curves

As mentioned before, the half reaction $\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-} + e^{-} {\mathop {\leftarrow }\limits ^{\hbox {discharge}}} \quad {\mathop {\rightarrow }\limits ^{\hbox {charge}}} \hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}$ is the limiting reaction in our experiments (except in the kinetic part). The reaction is studied in charge or in discharge and the current is recorded with a potentiostat CH Instrument 600E in the current range 1 mA. Intensity curves and power curves are plotted for several flow rates of electrolytes.

To plot intensity curves, a fixed voltage is applied between the anode and the cathode to force the charge reaction. This situation differs from the ideal situation where a reference electrode is used to study only one couple as in Kjeang et al. (2007). However, it is a more realistic situation, closer to redox flow batteries situation, involving an anolyte and a catholyte. While applying the voltage between the electrode, the current is recorded for several flow rates imposed by the syringe pump. For high flow rates (higher than 1000 $\upmu$L/min), few minutes are enough to have a current stabilization, whereas for the lowest flow rates (less than 20 $\upmu$L/min), several hours of stabilization are necessary to measure the stationary current. Theoretically, the transient time corresponds to one passage by the electrode: $\tau = \frac{Z_{0}}{V_{m}}$. For flow rates around 10,000 $\upmu$L/min, $\tau=2$ s, whereas for 1 $\upmu$L/min, $\tau =5$ h. Example of curve obtained in this case is presented on the following Fig. 3. To compare with theory, the flow rate Q is converted into the Peclet number $Pe=\frac{V_{m}X_{0}^{2}}{D_\mathrm{red}Z_{0}}=\frac{QX_{0}}{D_\mathrm{red}Y_{0}Z_{0}}$ and the plateau current I into the normalized current $\widetilde{I}$ given by the relation (9): $I=\frac{nFD_\mathrm{red}Y_{0}Z_{0}C_{0}}{X_{0}} \widetilde{I}$ (9). $X_{0}$, $Y_{0}$ and $Z_{0}$ are the dimensions of the channel (Fig. 1), D and $C_{0}$ are respectively the diffusion coefficient and the initial concentration of redox species (ferricyanide or ferrocyanide). F is the Faraday constant, and n the number of electron exchanged ($n=1$ in our case). $V_{m}$ is the average speed of the flow and can be related to the flow rate Q with the relation $Q=V_{m}Y_{0}X_{0}$. The notations are detailed in the theoretic part 2. To follow the yield of conversion according to the Peclet number, samples of electrolytes are studied with spectrometer UV–visible UNICAM with Plexiglas Kartell tank of 1 cm width. The intensity of the peak corresponding to $\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-}$ is followed at 420 nm. An appearance of the peak means a redox conversion into $\hbox {Fe}^{3+}$. The electrolyte is directly analyzed by spectrometer without dilution to avoid any error in the concentration. For this purpose, a low concentration of 0.002 M $\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-}$ is used to prevent any saturation of spectrometer.

Fig. 3

Example of data obtained for several flow rates for an applied voltage of 0.3 V (charge reaction). Flow rates are indicated on each plateau in $\upmu$L/min. Concentration of $\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-}$ is 0.066 M

Power curves are also plotted for the discharge reaction $\hbox {Fe}_{\rm II}CN_{6}^{4-} {\mathop {\rightarrow }\limits ^{discharge}} e^{-} + \hbox {Fe}_{\rm III}CN_{6}^{3-}$ at a given flow rate. To record power curves, a flow rate is fixed, while the voltage is changed between the anode and the cathode. The intensity is measured at each voltage change. The time of current stabilization for each measure depends on the flow rate and ranges from 20 s for 5000 $\upmu L/\text{min}$ to 500 s for 20 $\upmu L/\text{min}$.

4 Results and discussion

4.1 Classical electrolytes: intensity studies in flow

In Fig. 4, we study the charge reaction of ferricyanide: $[\hbox {Fe}_{\rm III}CN_{6}^{3-} + e^{-}{\mathop {\rightarrow }\limits ^{\rm charge}} \hbox {Fe}_{\rm II}CN_{6}^{4-}$ and we compare with simulated curves. Several flow rates are applied. The associated Peclet number is calculated and the intensity is measured in flow after stabilization and normalized according to equation (9). The initial reactant is the oxydant: the ferricyanide. In our experimental conditions, iron species are the limiting reactants in the anolyte and iodide $\hbox {I}^{-}$ is in excess in the catholyte. Thus, we assume that the potential of the catholyte remains constant, at its standard potential. We take it as the reference $E_\mathrm{ref}=E^{0}(\hbox {I}^{3-}/\hbox {I}^{-})=0.54$ V. This potential is involved in the calculation of $P_{4}$: $P_{4}=e^{\frac{- nF( E_\mathrm{ref}-E_0)}{RT}}$ with $E_\mathrm{ref}-E^{0}=0.18$ V. $E^{0}$ is the standard potential of the studied redox couple ($\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}]^{3-}/\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}]^{4-}$) and is equal too 0.36 V. A voltage of 0.3 V is applied between the anode and the cathode to force the reaction. Thus, $\Delta E=E-E_\mathrm{ref}=E(\hbox {Fe}_\mathrm{III}(\hbox {CN})_{6}^{3-}-E(\hbox {I}^{-})=-0.3$ V. To model the reaction, we use Eq. 8. $X_{0}$, $Y_{0}$, $Z_{0}$ are respectively $680\,\upmu\text{m}$, 1 and 3 cm, the dimension of the channel under the electrode. $C_{0}=0.066\,\hbox {M}$ is the initial concentration of ferricyanide, $n=1$ is the number of electron for the half reaction. $k_{0}$ is taken equal to 0.01 m/s. The reaction is fast, but we do not have access to the exact value of $k_{0}$. However, we will see, in the kinetic part, that, for a rapid kinetics, whatever the value of $k_{0}$ greater than $10^{-5}$ m/s allows us to describe the behavior of the system. The only fitting parameter is the diffusion coefficient $D(\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}]^{3-})=6 \times 10^{-10} \hbox {m}^{2}/\hbox {s}$. We calculate a normalized standard deviation as std(Imod,Iexp) = $\sqrt{\frac{\Sigma _{i=1}^{i=n} (I\text{mod}(i)-I\exp(i))^2}{N}}/\frac{\Sigma _{i=1}^{i=n} (I\exp(i))}{N}$ where n is the number of experimental point, Imod is the intensity predicted by the modeling and Iexp, the experimental intensity. We obtain for the charge process for the data displayed in Fig. 4 std = 0.19.

Fig. 4

a Simulated curves for the normalized intensity $\widetilde{I}$ (cf eq (9)) versus Peclet number and comparison with the experiment figure c). b Simulated curves for the yield of conversion versus Peclet number. Experimental points are for the charge reaction of ferrocyanide $\hbox {Fe}^{3+}(\hbox {CN})_{6}^{3-} + e^{-} {\mathop {\rightarrow }\limits ^{\rm charge}} \hbox {Fe}^{2+}(\hbox {CN})_{6}^{4-}$ with $[\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}]=0.066$ and $[\hbox {I}^{-}]=0.5M$. $\Delta E=-0.3\,\hbox {V}$. Fitting value: $D(\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-})=6 \times 10^{-10}$ $\hbox {m}^{2}/\hbox {s}$. std(Imod, Iexp) = 0.19. d Simulated concentration profiles for the two hydrodynamic regimes: (1) when $Pe<1$ and (2) $Pe>1$ (example of profiles for $Pe=0.1$ and 100)

In Fig. 4c), a good accordance is noticed between the simulation and the experimental curve of intensity. For the sake of clarity, the absolute value of the intensity is presented since the sign of the current depends on the electrical connections. Two hydrodynamic regimes are observed at low and high Peclet number and will be carefully detailed in the further paragraph with the help of the simulation curves in Fig. 4a, b. The limit between the two regimes is around Pe = 1 where a change in slope is noticed: This value represents the transition between the diffusion-limited and the convection-limited domains. This change is also marked by a drop of conversion.

More theoretic curves are obtained with the MATLAB simulation to complete the analysis of the experimental curves. Results of the simulation are presented in Fig. 4a, b. Hydrodynamics is not straightforward since exhibition of two regimes is demonstrated. With the help of simulation and with scaling laws, the two hydrodynamic regimes can be described and explained.

For the first regime ($Pe<1$), diffusion is dominating and allows all the ferricyanides to reach the electrodes by diffusion. The conversion is complete and is maintained at a plateau value which only depends on the overpotentials applied at the electrode. The intensity $I=\frac{nFD_\mathrm{red}Y_{0}Z_{0}C_{0}}{X_{0}} \widetilde{I}$ is exactly equal to the amount of charge entering the channel per unit of time: $QnFC_{0}$. Q is the flow rate and can be related to the average speed $V_{m}$ multiplied by the section of the channel $X_{0} \times Y_{0}$. After simplification, we obtain: $\widetilde{I}=\frac{V_{m}X_{0}^{2}}{DZ_{0}}$ which is the Peclet number. This relation $I=Pe$ is exact when the overpotential is large meaning a conversion around 100%. When the flow rate is increasing and the Peclet number is higher than 1, convection dominates over diffusion. A depletion layer of reactant is forming at the surface of the electrode (Fig. 4d), and the conversion is incomplete at the end of the channel. In Fig. 4a, I varies roughly as $I=r\times Pe^{1/3}$ in accordance with classical analysis proposed earlier by Zhang (1996) and Newmann. Concerning the yield of conversion in Fig. 4b, the figure demonstrates a sharp drop for $1<Pe<10$. For Pe higher than 100, the percentage of conversion reaches hardly 10% . The effect of overpotential on the conversion is less visible than at low Peclet, but the conversion is always more efficient when |$\Delta E$| is large.

Several curves of intensity in charge are presented on the following graph (Fig. 5). To verify the robustness of the simulation with the experiments, concentrations in electrolytes as well as the thickness of the channel have been changed. The following graph (Fig. 5) presents the real intensity or the normalized intensity measured for the reaction of charge:$\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-} + e^{-} {\mathop {\rightarrow }\limits ^{\text{charge}}} \hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}$. Three concentrations of ferricyanure are studied: 0.1, 0.033 and 0.002 M with a large excess of iodide ion in the catholyte (at least five times the amount of ferricyanide). The raw data intensity versus flow rate is presented (Fig. 5a) and then normalized to be compared with the simulation (Fig. 5b). The agreement between simulations and experiments is very good.

Fig. 5

a Experimental records of the intensity versus the flow rate for the charge reaction of ferrocyanide. Several initial concentrations $C_{0}$ and two channel thicknesses $X_{0}$ are investigated. The experiments are performed in large excess of iodide ion. b Curves after normalization of the intensity and comparison with simulation with $\Delta E=-0.3\,\hbox {V}$. The standard deviation between simulation and experiments is std = 0.1 (red circle), std = 0.016 (inverted blue triangle), std = 0.0004 (green triangle), std = 0.19 (square) (color figure online)

Previously, we demonstrate that the intensity and the yield given by the simulation give an excellent accordance both quantitatively and qualitatively with the experiments in discharge. The results also match for the intensity of the discharge reaction, but we have to change our voltage reference. Indeed, for the charge reaction in the previous part, the reaction at the catholyte was $3\hbox {I}^{-} \rightarrow \hbox {I}_{3}^{-} +2e^{-}$. This reaction is known as a rapid reaction. As we were in excess of iodine ions, the hypothesis than $E_\mathrm{ref}=E^{0}(\hbox {I}_{3}^{-}/\hbox {I}^{-})=0,54\,\hbox {V}$ is reasonable and we checked the good accordance between the experimental points and the simulation in Fig. 4. However, for the discharge of ferrocyanide, the cathode reaction is now $\hbox {I}_{3}^{-} +2e^{-} \rightarrow 3\hbox {I}^{-}$, which is known to have a very slow kinetics (El-Hallag 2010). Thus, the potential of the cathode is fixed because we have a large excess of triiodide, but its value is probably not equal to $E^{0}(\hbox {I}_{3}^{-}/\hbox {I}^{-})$. Experimentally, we find a perfect accordance between experimental points and the simulation taking $E_\mathrm{ref}=0.45$ V. The standard deviation is equal to 0.0009. The comparison is presented in Fig. 6 both on the normalized intensity and the yield of conversion with the Peclet number. As for the charge, we see the change of slope at low and high Peclet numbers. On the yield of conversion, we visualize a drop of conversion, exactly as for the simulated curves in Fig. 4 thanks to the measures of absorption at 420 nm.

Fig. 6

a Normalized intensity $\widetilde{I}$ versus Peclet number and comparison with the experiment. Experimental points are for the discharge reaction of ferrocyanide $\hbox {Fe}^{2+}(\hbox {CN})_{6}^{3-} {\mathop {\rightarrow }\limits ^{\text {discharge}}} \hbox {Fe}^{3+}(\hbox {CN})_{6}^{4-} + e^{-}$ with $[\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}]=0.002$ and $[\hbox {I}_{3}^{-}]=0.03M$. $\Delta E=-0.06\,\hbox {V}$. Fitting value: $D(\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-})=4 \times 10^{-10}$ $\hbox {m}^{2}/\hbox {s}$ and $E_\mathrm{ref}=0.45\,\hbox {V}$. std = 0.0009

4.2 Classical electrolytes: power curves

To go further in the analysis, power curves are also plotted for the discharge of the flow battery: $2\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-} + \hbox {I}_{3}^{-} {\mathop {\rightarrow }\limits ^{\rm discharge}} 2\hbox {Fe}^\mathrm{III}(\hbox {CN})_{6}^{3-} + 3\hbox {I}^{-}$. The fit of the power curves is realized using the same diffusion coefficient as before for the intensity curves, meaning $D(\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-})=4 \times 10^{-10}$ $\hbox {m}^{2}/\hbox {s}$ and $E_\mathrm{ref}=0.45$ V for the ferrocyanide limiting species.

The effect of the flow is well observed both with experiment and simulation Fig. 7: The higher the Peclet is, the more power is recovered in discharge with a peak power at 10 $\upmu$W for 20 $\upmu$L/min and 80 $\upmu$W at 5000 $\upmu$L/min. For a 3 $\text{cm}^{2}$ electrode, it corresponds to respectively 3.3 and 25 $\upmu \text{W/cm}^{2}$. This increase in the peak power comes from the continuous increase in current with the flow rate. The slope at the origin and the shape do not vary with the flow. In our model, we neglect the ohmic losses due to ionic conductivity. This approximation is reasonable considering the following rough calculations. The ohmic losses can be related to the approximate resistance between the anode and the cathode: $R=R_{\rm electrical\, connections}$ + $R_{\rm Nafion\, membrane}$ + $R_{\rm ionic\, conduction}$. $R=R_{\rm electrical\, connections}$ is the resistance of the wires and the connections. Carbon paper has a very good conductivity; this value does not exceed 2 $\Omega$. The contribution of the salt $\hbox {Na}_{2}\hbox {SO}_{4}$ can be calculated knowing the geometry of the channel and the conductivity (around 42 S/m for 1 M of salt). Thus, $R_{\rm ionic \,conduction}$ is less than 1 $\Omega$. Then, as the conductivity of the membrane Nafion is 10 S/cm for the proton in specifications and is known to be around five times less for $\hbox {Na}^{+}$ according to Okada et al. (1998), we can assume a conduction around 2 S/m for the Nafion membrane. With this value, the resistance $R_{\rm Nafion\, membrane}$ is also less than 1 $\Omega$. Eventually, the total resistance of the circuit is around 4 $\Omega$. We modified our MATLAB simulation to take into account the ohmic losses due to this internal resistance, and we found a decrease in the power peak of around 3% at 5 $\Omega$.This aspect appears as negligible.

After the study of power and intensity curves, a last parameter that can be studied for the classical electrolytes is the effect of kinetics and is detailed in the following part.

Fig. 7

Power curves for the discharge reaction of the battery $\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}/\hbox {I}_{3}^{-}$: Several flow rates are applied (20 $\upmu$L/min, 200 $\upmu$L/min, 800 $\upmu$L/min, 2000 $\upmu$L/min, 5000 $\upmu$L/min). The concentration of ferrocyanide is $[\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}]=0.007\,\hbox{M}$ and $[\hbox {I}_{3}^{-}]=0.035\,\hbox{M}$. Simulated curves are presented for the power curves taking $D=4 \times 10^{-10}$ $\hbox {m}^{2}/\hbox {s}$ and $E_\mathrm{ref}=0.45$ V. std = 0.01.

4.3 Kinetic effects

In the previous paragraph, intensity studies focused on the effect of the flow rate (Peclet number) and the voltage through the parameters $P_{1}=\frac{V_{m}X_{0}^{2}}{DZ_{0}}$ (Peclet number) and $P_{2}=\frac{nF\Delta E}{RT}$. Kinetics are actually captured the standard rate constant $k_{0}$ implied in the parameter $P_{3}=\frac{k_{1}X_{0}}{D}$ with $k_{1}=e^{\frac{\alpha nF(E_\mathrm{ref}-E^{0})}{RT}}$. The kinetic of the reaction was not a limiting parameter in the previous paragraph since the reaction studied was limited by the redox couple $\hbox {Fe}^\mathrm{III}(\hbox {CN})_6^{3-}/\hbox {Fe}^\mathrm{II}(\hbox {CN})_6^{4-}$ which has a well-known rapid kinetics. In this paragraph, we will focus on triiodide $\hbox {I}_{3}^{-}$.

For this purpose, we perform experiments using a low concentration of $[\hbox {I}_{3}^{-}]=0.03$ M in the catholyte and a large excess of $[\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}]=0.1$ M in the anolyte. Thus, the limiting reaction is now the discharge of triiodide: $\hbox {I}_{3}^{-} +2e^{-} \rightarrow 3\hbox {I}^{-}$. For this reaction, $n=2$ electrons and $D=8.5 \times 10^{-10}\hbox {m}^{2}/\hbox {s}$. The voltage $E_\mathrm{ref}$ is taken equal to the standard potential of ferricyanide $E^{0}(\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-}/\hbox {Fe}^\mathrm{II}(\hbox {CN})_{6}^{4-})=0.36$ V because the couple is rapid and in excess. The experimental normalized current is presented in Fig. 8 and compared with a group of simulated curves.

In Fig. 8, some of the simulated curves are plotted for several values of $k_{0}$ from 0.01 (rapid kinetic) to $10^{-9}$ m/s (slow kinetic). We observe a decrease in the slope from 1/3 to almost zero below $k_{0}=10^{-7}$ m/s. At this value of $k_{0}$, the intensity is no more limited by the diffusion but more by the slow charge transfer of the reaction. On the contrary, $k_{0}$ has no effect for values higher than $10^{-5}$ (rapid charge transfer): The slope is always 1/3. This remark justifies the fact that $k_{0}$ was not fitted accurately in the previous part, when the studied couple was $\hbox {Fe}^\mathrm{III}(\hbox {CN})_6^{3-}/\hbox {Fe}^\mathrm{II}(\hbox {CN})_6^{4-}$. We can also notice that for low Peclet number, the curves are not impacted by the kinetics except when the kinetics is very slow (for $k_{0}<10^{-8}$ m/s). In this case, the boundary between the diffusion regime and the kinetic regime tends to move toward Peclet numbers lower than 1.

On the experimental curve (red points in Fig. 8), we first notice that at high Peclet, the slope is no more equal to 1/3 but is close to 0.18. This remark is consistent with the fact that the reaction of triiodide is slow. We find a good overlay of the simulation and the experimental points for $k_{0}$ between $10^{-7}$ and $7 \times 10^{-8}$ m/s. We found $1.85 \times 10^{-5}$ m/s in El-Hallag (2010) but on a vitreous carbon electrode. As the value of $k_{0}$ depends on the nature of the electrode, quantitative comparison with the literature is difficult.

To the best of our knowledge, this observation of the decrease in the slope at high Peclet for a slow kinetics redox couple has never been investigated before. This is an original method, other than voltamperometry, to quantify the standard rate constant.

Fig. 8

Evolution of normalized intensity versus Peclet for the reaction $\hbox {I}_{3}^{-} {\mathop {\rightarrow }\limits ^{discharge}} 3\hbox {I}^{-} +2e^{-}$ (slow kinetics) and comparison with simulated curves at different values of $k_{0}$ i.e, several $P_{3}$. $[\hbox {I}_{3}^{-}]=0.03$ M in the catholyte and $[\hbox {Fe}^{2+}(\hbox {CN})_{6}]=0.1$ M in the anolyte. $\Delta E=-\,0.08\,\hbox {V}$. Fitting value: $D(\hbox {I}_{3}^{-})=8.5 \times 10^{-10}$ $\hbox {m}^{2}/\hbox {s}$. std = 0.04

5 Conclusion

In summary, we have studied the flow and the conversion process inside a redox flow cell. Experiments are carried out on an original millifluidic flow battery with ferrocyanide and iodide as electrolytes. We displayed both numerical and experimental data. The choice of these reactants is motivated by their ease of use, water solubility and price. Careful fundamental studies of the electrochemical conversion in flow are realized here. A numerical model successfully supports the experiments and is able to fit all the curves (power and current curves) with only two fitting values: the diffusion coefficient and the standard rate constants of the reaction. This non-dimensional model is adaptable to every channel geometry, concentration (Fig. 5) and kinetics (Fig. 8) thanks to four parameters. In particular, the Peclet number embeds the effect of the flow rate, which is the most important parameter in a flow battery. From a hydrodynamic point of view, two domains are visible for the intensity curves (Fig. 4): At low flow rates, the intensity recovery is due to the mass transfer by diffusion and the yield of conversion is total (if the overpotential applied is large enough). By comparison, at high flow rates, convection dominates over the diffusion and the current recovery is proportional to $Pe^{1/3}$. The conversion yield is lower than 100% and decreases dramatically with flow rate. If the process is limited by electrochemical reaction at the electrode, surprisingly, the current do not follow the scaling law $Pe^{1/3}$ but rather $Pe^{n}$ with $0<n<1/3$. For a very slow kinetics ($k_{0}<10^{-7}$ m/s), intensity does not depend of the Peclet number and the conversion yield decreases dramatically with flow rate. This original behavior is encountered in the case of slow reactions. It occurs when particles dispersions are used instead of solutes. Let us underline to conclude that the study of this situation is important for two reasons. From the academic point of view, this approach allows a fast and accurate determination of the kinetic constant. From the industrial point of view, the knowledge and the mastery of the electrochemical process at the electrode are fundamental when porous electrodes or turbulent flow at small scale is used. We recall that these last two roads are the most promising approaches to enhance the performances of a redox flow cell from the device point of view.