1 Introduction

Isolated microdroplets in another immiscible fluid have great potential in promoting the evolution of biological and chemical applications (Theberge et al. 2010). Picoliter droplets can serve as microreactors offering low reagent consumption and high system throughput. For example, their massive generations and extremely small volumes offer the possibility of manipulating single cells or molecules for high-throughput screening experiments. Two commonly used methods for droplet generation are based on channel-based microfluidics and inkjet printing technologies. Microfluidic devices have been developed to generate emulsion microdroplets using T-junction (Thorsen et al. 2001; Link et al. 2004) or flow-focusing structures (Anna et al. 2003). The inkjet printing technology has been recently employed in biological and chemical diagnostic assays as a promising method for efficient microarray fabrication. For example, Arrabito and Pignataro (2010) used the inkjet printing method to construct drug–target recognition assays in a simple microarray format. Chen et al. (2013) combined the inkjet technology with a multicapillary plate to develop a chemiluminescence immunoassay. Despite these achievements, inkjet printing-based array fabrication suffers from the evaporation of aqueous droplets, especially when the droplet volume reduces to picoliter scale. To address this issue, a few methods have been proposed, including the use of ultrasonic humidifiers (Kim et al. 2009; Zhang et al. 2011) and additive chemicals (Mugherli et al. 2009; Arrabito et al. 2013), to maintain a constant droplet volume. However, the risk of cross-contamination and incompatibility of the additive chemicals are additional problems. In our previous work (Sun et al. 2014), we demonstrated that picoliter compound droplets can form by directly depositing aqueous reagent onto sessile oil droplets. The formed water-in-oil droplet array was used for quantitative PCR analysis with minimal evaporation and cross-contamination. Droplet generation processes in microfluidic devices have been extensively studied in the last decade to understand the underlying physics (Garstecki et al. 2006; Lee et al. 2009; Chen et al. 2014a; Liu et al. 2015). However, little is known about the formation of compound droplets by the inkjet printing method.

The formation of compound droplets is a complex process involving interactions among three immiscible fluids. The structures of compound droplets are predictable (Aveyard and Clint 1997; Guzowski et al. 2012; Neeson et al. 2012) based on the Neumann’s relationship (Neumann 1894) at the triple-line among the interfaces. Three types of possible structures are non-engulfing, partial-engulfing, and complete-engulfing, corresponding to the spreading parameters, S i  = σ jk  − (σ ij  + σ ik ) (Torza and Mason 1969; Pannacci et al. 2008), where each σ represents the interfacial tension between phases i and j. However, if the triple-line is absent during the generation of compound droplets, small droplet can be fully encapsulated by the large droplet to form a core–shell structure regardless of the spreading parameters (Nie et al. 2005; Abate and Weitz 2009). These structures can be formed via traditional two-step mixing methods (Leal-Calderon et al. 2007; Shum and Weitz 2011) or microfluidic droplet generations (Abate and Weitz 2009; Shum et al. 2011; Chen et al. 2011; Josephides and Sajjadi 2014). Another method for forming compound droplets is the collision of two immiscible droplets in the air. Droplet collision of the same liquid has been studied for decades (Brazier-Smith et al. 1972; Ashgriz and Poo 1990; Qian and Law 1997). Only a few investigations considered binary (equal-size) droplet collision of immiscible droplets, with much attention paid to the fragmentation of the collided droplets (Chen and Chen 2006; Roisman et al. 2012). The formation process of compound droplets by depositing aqueous reagent onto sessile oil droplets is essentially an unequal-size droplet collision problem. The size difference allows the small droplet to penetrate into the big one, forming a compound droplet with a core–shell structure. It is of fundamental and practical interest to understand how the control parameters affect the formation of the desired structure.

Herein, we study the collision of a small water droplet with a large immiscible oil droplet resting on a substrate. We developed a three-phase volume-of-fluid method to simulate the collision dynamics complicated by the triple-line motion. Numerical methods and simulation settings are validated directly by experiments. We then carry out a systematic numerical study to explore the effects of inertia, viscous resistance, and spreading parameter on the final structures of the compound microdroplets. Regime maps of the structures are obtained to identify the transitions between the structures. In addition, a simplified model is established for the transition within the parameter space of practical applications.

2 Numerical methods

2.1 Numerical framework

The numerical simulations are based on the numerical framework of Gerris flow solver (http://gfs.sf.net). The accuracy of the code has been validated both numerically and experimentally for various two-phase flow problems (Popinet 2009; Chen et al. 2014b). The formulation accommodates the conservation equations for an incompressible flow with surface tension (Popinet 2009),

$$\rho (\partial_{t} {\mathbf{u}} + {\mathbf{u}}\cdot\nabla {\mathbf{u}}) = - \nabla p + \nabla \cdot \, \left( {2\mu {\mathbf{D}}} \right) + \sigma \kappa \delta_{\text{s}} {\mathbf{n}},$$
(1)
$$\nabla \cdot{\mathbf{u}} = \, 0,$$
(2)

where u is the velocity vector, ρ the fluid density, µ the dynamic viscosity, and D the deformation tensor defined as D ij  = (∂ i u j  + ∂ j u i )/2. The Dirac delta function δ s expresses the fact that the surface tension, σ, is concentrated on the interface. The curvature of the interface is denoted by κ, and n is the unit outward vector normal to the interface (Popinet 2009).

A volume-of-fluid (VOF) function c(x ,t) is introduced to trace the two-phase interface. c(x ,t) is defined as the volume fraction of a given fluid in each cell of the computational mesh. The density and viscosity can thus be written as

$$\rho \left( c \right) \, \equiv c\rho_{1} + \, \left( {1 \, - c} \right)\rho_{2} ,$$
(3)
$$\mu \left( c \right) \equiv c\mu_{1} + \, \left( {1 \, - c} \right)\mu_{2} ,$$

with ρ 1, ρ 2 and µ 1, µ 2 being the densities and viscosities of the first and second fluids, respectively. According to mass continuity, the advection equation for the density takes the following form regarding the volume fraction:

$$\partial_{t} c + \nabla \cdot \, \left( {c{\mathbf{u}}} \right) \, = \, 0.$$
(4)

A staggered temporal discretization of the volume fraction and pressure leads to a scheme that is second-order accurate in time (Popinet 2009). The discretized momentum equation is recast as a Helmholtz-type equation that can be solved by an improved, multilevel Poisson solver. The discretization of the viscous terms is a Crank–Nicolson type and second-order accurate. The spatial discretization is achieved using graded quadtree partitioning in two dimensions (Popinet 2009). A piecewise linear geometrical VOF scheme generalized for quadtree spatial discretization is used to solve the advection equation for the volume fraction (Brackbill et al. 1992). The combination of a balanced-force surface tension discretization and a height function curvature estimation (Popinet 2009) is used to circumvent the problem of parasitic currents (Brackbill et al. 1992; Popinet and Zaleski 1999).

The above numerical method allows a spatially and temporally varying resolution (Popinet 2009). The local mesh refinement or coarsening in the quadtree discretization is also extremely efficient and can be performed at every time step with minimal impact on overall performance. In the present paper, a gradient-based adaptive mesh refinement (Popinet 2009) is used to refine the interfaces according to the gradients of the volume fractions. The interiors of the oil and water droplets are also refined using phase-based criteria to reduce the viscous dissipation. The cell size of the gradient-based refinement is set to be 1/2 of that of the phase-based refinement.

2.2 Three-phase volume-of-fluid method

Figure 1a shows the schematic of the present problem. A small water droplet with a radius of R w moves with impact velocity U 0 toward a large oil droplet with a radius of R o and a height of H o resting on a substrate. The ambient fluid is air. These two droplets merge during a collision to form the water/oil interface and a triple-line among the three phases as shown in Fig. 1b. The motion of the triple-line is determined by the three interfacial tensions and the collision dynamics. To simulate such a three-phase problem, we extend the generic two-phase VOF method to handle three interfaces. Motivated by the decomposition of interfacial tension coefficients (Smith et al. 2002), we introduce three volume fractions, c w, c o, and c a, to the system for water, oil, and air, respectively. Each volume fraction is equal to one in the corresponding phase and equal to zero in the other two phases. There are two VOF interfaces between any two phases to describe the physical interfaces. The interface tensions on water/oil, water/air, and oil/air interfaces are \(\sigma_{\text{wo}} = \sigma_{\text{w}} + \sigma_{\text{o}} ,\)

$$\sigma_{\text{wa}} = \sigma_{\text{w}} + \sigma_{\text{a}} ,$$
(5)
$$\sigma_{\text{oa}} = \sigma_{\text{o}} + \sigma_{\text{a}} ,$$

respectively, where σ w, σ o, and σ a are the interfacial tensions of VOF interfaces of water, oil, and air, respectively. For given σ wo, σ wa, and σ oa, Eq. (5) is solved to determine σ w, σ o, and σ a.

Fig. 1
figure 1

a Schematic of a water droplet moving toward an oil droplet resting on a substrate (the density and viscosity of water are ρ w and µ w, respectively; the subscripts o and a stand for the properties for oil and air, respectively. The contact angle of the oil droplet is θ. The height of the oil droplet is H o); b balancing of the three interfacial tensions in the collided droplet (interfacial tensions at water/air, oil/air, and water/oil interfaces are σ wa, σ oa, and σ wo, respectively)

Full size image

2.3 Method validation

We validate the three-phase VOF method by the spreading of a water lens at the middle of a straight surface between air and oil, following Boyer et al. (2010). The droplet relaxes to a final structure (Fig. 2a) under the balancing of the interfacial tensions.

Fig. 2
figure 2

a Schematic of a water droplet spreading between the air and oil; b final structures of a water lens spreading between air and oil for different interfacial tensions (σ wa; σ oa; σ wo) = (1.0; 1.0; 1.0) and (0.8; 1.0; 1.4), where the interfacial tensions are scaled by σ oa

Full size image

Figure 2b shows the final structures of the liquid lens for two different combinations of (σ wa; σ oa; σ wo). The results are in close agreements with those in Boyer et al. (2010). We also propose a theoretical model to predict the radius r in Fig. 2a. The detailed model and additional validations are found in Supplemental Material. Nevertheless, we also validate the method by comparing simulations directly with experiments in Sect. 3.3.

3 Experimental validations

3.1 Experimental settings

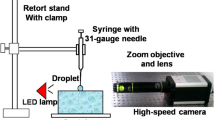
Experiments are carried out to validate the numerical simulations. The inkjet printing technology on a JetLab 4 inkjet platform (MicroFab Technologies Inc., USA) is used to deposit microdroplets perpendicularly to a silanized silicon dioxide substrate. Twenty droplets of mineral oil (M8410, Sigma-Aldrich, USA) are deposited continually using a 50-µm nozzle (MJ-AT-01-50, MicroFab Technologies Inc., USA) to form a large sessile droplet. A deionized water droplet is then deposited using a 30-µm nozzle (MJ-AT-01-30) onto the top of the oil droplet. The interfacial tensions are measured using the pendant droplet method (Theta tensiometer, Attension, Finland) and Wilhelmy plate method (K12 Mk5 processor tensiometer, KRUSS GmbH, Germany). Through a long-working-distance Nikon objective¨ (S Plan Fluor ELWD 20×/0.45) and a homemade tube lens with a cemented achromatic doublet, the collision dynamics of the microsize droplets is recorded by a high-speed camera (Phantom v7.3, Vision Research Inc., USA) at a resolution of 1.15 µm per pixel and a frame rate of 28,169 frames per second. See Figure S1 in Supplemental Material for photographs of the experimental installation.

By dissolving an oil-soluble surfactant, Span 80 (Sigma-Aldrich, USA), to the oil phase, we change σ wo while there are no notable changes of σ wa and σ oa. The spreading parameters of the oil phase, S o = σ wa − (σ wo + σ oa), are negative and positive for cases without and with the surfactant, respectively. The spreading parameters of water and air phase, S w = σ oa − (σ wo + σ wa) and S a = σ wo − (σ wa + σ oa), are less than zero for all the cases. Note that we can only measure the static σ wo when the chemical equilibration of the surfactant at the water/oil interfaces is reached. Since the adsorption kinetics of the surfactant on the interface is diffusion-controlled, the value of σ wo is not constant during the collision process. The deformation of the water/oil interface and flow around the interface also influences the concentration of the surfactant. Experimental measurement of the dynamic interfacial tension and theoretical analysis still remain a challenge (Tadros 2015). However, when the impact velocity is small, the final structure of the compound droplet is determined by the balancing of the static interface tensions. We selected Span 80 as a surfactant because the solubility of Span 80 in water is negligible in comparison to the oil phase (Peltonen and Yliruusi 2000). We can assume that, as long as the concentration used in the experiment and the measurement are the same, the measured interfacial tension is equal to the static interfacial tension in our experiment.

3.2 Experimental observations

Figure 3 shows the experimental snapshots for four different conditions. Similar to the binary droplet collision, the early dynamics involve approaching of the droplets, formation of the air film between the droplet, and rupture of the air film following by the merging of the droplets. Differently, for immiscible droplet collision, rupture of the air film results in formation of the triple-line. In addition, the capillary forces transmitted by the triple-line complicate the momentum balance of the two droplets. The Weber number and Reynolds number based on the physical properties of the water droplet are defined as \({\text{We}}_{\text{w}} = \rho_{\text{w}} U_{0}^{2} R_{\text{w}} /\sigma_{\text{wa}}\) and Rew = ρ w U 0 R w/µ w, respectively. The viscosity ratio of the oil and water phase is \(\lambda = \mu_{\text{o}} /\mu_{\text{w}}\). The Ohnesorge number relating the viscous forces to inertial and interfacial tension forces is defined as \({\text{Oh}} = \mu_{\text{w}} /\sqrt {\rho_{\text{w}} R_{\text{w}} \sigma_{\text{wa}} } = \sqrt {{\text{We}}_{\text{w}} } /\text{Re}_{\text{w}}\).

Fig. 3
figure 3

Experimental snapshots of a water droplet colliding with an oil droplet resting on a substrate. The interval of images is 35.5 µs. (ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ o = 2.6 × 10−2 Pa s, µ a = 1.8 × 10−5 Pa s, θ = 72.5°. a R o = 171.0 µm, R w = 22.5 µm, U 0 = 0.8 m/s, Wew = ρ w U 20 R w/σ wa = 0.2, Rew = ρ w U 0 R w/µ w = 18.0, Ohw = 0.025; b R o = 171.0 µm, R w = 22.0 µm, U 0 = 2.2 m/s, Wew = 1.5, Rew = 48.3, Ohw = 0.025; c R o = 171.0 µm, R w = 25.0 µm, U 0 = 3.3 m/s, Wew = 3.8, Rew = 82.4, Ohw = 0.024; d R o = 181.0 µm, R w = 26.0 µm, U 0 = 0.5 m/s, Wew = 0.1, Rew = 13.0, Ohw = 0.023. For a–c, σ wa = 72.60 mN/m, σ oa = 22.08 mN/m, and σ wo = 56.57 mN/m. For d, σ wa = 72.60 mN/m, σ oa = 22.08 mN/m, and σ wo = 6.68 mN/m)

Full size image

Figure 3a–c shows conditions under S o < 0 with varying impact velocities U 0. When U 0 is low (Fig. 3a), the motion of triple-line is faster than that of the water droplet. A rising of the triple-line is observed in the third image where the triple-line appears as a sharp black streak between the droplets (pointed with red arrow). The top profile of the water droplet is sharper than the original spherical shape due to the motion of the triple-line. After that, the water droplet is floating on the top of the oil droplet to form partial-engulfing structure due to the balancing of interfacial tensions. Note that the water droplet evaporates within about 1 s because of the small size. For a higher U 0 (Fig. 3b), the water droplet deforms to an oblate shape during the early collision as shown in the third image. Different from Fig. 3a, a concave profile at the bottom of the water droplet (pointed with red arrow) is observed, indicating the existence of a thin air film between the droplets. The formation of the triple-line is thus delayed. The concave profile disappears in the fifth images when the air film ruptures to form the triple-line, and the following dynamics are similar to the observations in Fig. 3a. For a much higher U 0 (Fig. 3c), the deformation of the water droplet is larger and a hat-like shape of the water droplet is observed in the third images. The final structure is the same as that in Fig. 3a, b. Figure 3d shows the collision dynamics for S o > 0 and U 0 = 0.5 m/s. After the formation of the triple-line in the third images, the water droplet is engulfed slowly by the oil droplet under the balance of the interface tensions until the water droplet is fully encapsulated by the oil droplet. In this complete-engulfing structure, the evaporation of the water droplet is thus prevented.

3.3 Comparative simulations

To determine the proper numerical setups that can match the experimental observations, simulations are carried out under the experimental conditions. An axisymmetric model (Popinet 2009) is used to reduce the computational cost. The water and oil droplets are initiated according to the setup in Fig. 1a. The impact velocity U 0 is applied uniformly to the water droplet. A constant contact angle θ is applied to the oil/air interface with free-slip boundary condition on the substrate. The outflow boundary condition is specified at the other domain boundaries. Since the Bond number based on the properties of the oil droplet \({\text{Bo}} = \rho_{\text{o}} gR_{\text{o}}^{2} /\sigma_{\text{oa}}\) is small (about 1.02 × 10−2), the effect of gravity is neglected here.

We first simulate the experimental situation in Fig. 3c with different grid sizes along the interfaces. Figure 4 illustrates the collision dynamics predicted by different grid sizes. Figure 4a, b shows that more details of the droplet deformations are resolved by finer grids. We find that the existing period of the air film increases with the grid resolution. The subsequent collision dynamics are influenced obviously by the rupture of the air film; see for example images in Fig. 4b, c at t = 0.05 ms. In practice, the rupture involves both macroscopic flow dynamics and microscopic intermolecular forces. Simulating detailed rupture dynamics is still a challenge. In the present macroscopic framework, the rupture is controlled by the grid size. Figure 5 shows that the simulation with 12 cells per R w (Fig. 4b) is consistent with the experiments in Fig. 3c. Good agreements are observed regarding the collision dynamics before and after the rupture of the air film. We also carry out simulations under the conditions in Fig. 3a, b and find that the grid resolution of R w/12 can reproduce the experimental observations well (see Figure S2 in Supplemental Material). Therefore, this grid size is used in the subsequent simulations.

Fig. 4
figure 4

Collision dynamics predicted by grid sizes of about R w/6 (a), R w/12 (b), and R w/24 (c) for the experimental condition in Fig. 3c. (ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ o = 2.6 × 10−2 Pa s, µ a = 1.8 × 10−5 Pa s, θ = 72.5°, R o = 171.0 µm, R w = 25.0 µm, U 0 = 3.3 m/s, σ wa = 72.60 mN/m, σ oa = 22.08 mN/m, and σ wo = 56.57 mN/m, Wew = 3.8, Rew = 82.4, Ohw = 0.024)

Full size image
Fig. 5
figure 5

Comparisons of experimental images (the first row) and numerical results (the second row) for the experimental condition in Fig. 3c. (ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ o = 2.6 × 10−2 Pa s, µ a = 1.8 × 10−5 Pa s, θ = 72.5°, R o = 171.0 µm, R w = 25.0 µm, U 0 = 3.3 m/s, σ wa = 72.60 mN/m, σ oa = 22.08 mN/m, and σ wo = 56.57 mN/m, Wew = 3.8, Rew = 82.4, Ohw = 0.024)

Full size image

4 Numerical results

The experiments provide basic understandings of the formation process of the compound droplet. A systematic numerical study is then carried out to explore the effect of control parameters on the final structures. The water/air and oil/air interfacial tensions are fixed as σ wa = 72 mN/m and σ oa = 28 mN/m, respectively, while the interfacial tension of water/oil interface σ wo varies from 56 to 44 mN/m. The corresponding S o is less than or equal to zero. Meanwhile, S w and S a are negative. The viscosity of water µ w is 1 × 10−3 Pa s, while µ o varies from 2 × 10−3 to 2 × 10−2 Pa s with an interval of 2 × 10−3 Pa s. We choose to non-dimensionalize the physical quantities using a capillary–inertial rescaling with length, mass, and time by R w, \(\rho_{\text{w}} R_{\text{w}}^{3}\), and (\(\rho_{\text{w}} R_{\text{w}}^{3} /\sigma_{\text{wa}}\))1/2, respectively. The non-dimensional impact velocity of the water droplet is thus We1/2. The three interfacial tensions are non-dimensionalized by two parameters, the dimensionless spreading parameter S o/σ wa, and the ratio of σ oa/σ wa, which is fixed to be 0.39 in this paper.

4.1 Tunable structures

Figure 6 illustrates the time sequences for three types of structures under different Weber number Wew and viscosity ratio λ (see also three-dimensional animations in Supplemental Material.) The dynamics at the early stage are similar for all cases. The water droplet approaches the oil droplet to rupture the thin air film between two droplets and forms a water/oil interface. The subsequent dynamics mainly consist of penetration and oscillation of the water droplet and the balancing of interfacial tensions at the triple-line.

Fig. 6
figure 6

Collision dynamics for three structures (see also three-dimensional animations in Supplemental Material). R o = 153.3 µm, R w = 28.3 µm, ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ a = 1.8 × 10−5 Pa s, θ = 72.5°. a Partial-engulfing (σ wa = 72 mN/m, σ oa = 28 mN/m, σ wo = 50 mN/m, S o/σ wa = −0.08, λ = 8, U 0 = 2.8 m/s, Wew = 3.1, Rew = 79.5, Ohw = 0.023); b complete-engulfing (σ wa = 72 mN/m, σ oa = 28 mN/m, σ wo = 44 mN/m, S o/σ wa = 0, λ = 20, U 0 = 5.6 m/s, Wew = 12.5, Rew = 159, Ohw = 0.023); c penetrative-engulfing (σ wa = 72 mN/m, σ oa = 28 mN/m, σ wo = 50 mN/m, S o/σ wa = −0.08, λ = 8, U 0 = 5.6 m/s, Wew = 12.5, Rew = 159, Ohw = 0.023)

Full size image

The penetration of the water droplet is quantified by the penetration length, L p, which is defined as the maximum distance between the bottom of the water droplet and the initial top of the oil droplet. When L p is small, the balancing of interfacial tensions at the triple-line determines the final structure. Two structures, partial-engulfing, and complete-engulfing are observed for S o < 0 and S o = 0 as shown in Fig. 6a, b, respectively. Note that, for complete-engulfing, the interfaces of the two droplets coincide at the top of the compound droplet. When L p is large, as shown in Fig. 6c, the penetration of the water droplet forces the triple-line to collapse and vanish at the top of the water droplet. Such a structure can be called penetrative-engulfing. Different from complete-engulfing, there is a considerable distance between the top of the compound droplet and the top of the encapsulated water droplet. The critical moment of penetrative-engulfing is that the triple-line is just about to collapse as shown in Fig. 6c at t = 0.11 ms. The cusp-shaped interface on the top of the water droplet is similar to the experimental observations in Li et al. (2014). Note that, in practice, the penetrative-engulfing structure is more stable than other two structures because the water droplets can fall along the interface of the compound droplet and reach the substrate eventually under gravity (Neeson et al. 2012; Sun et al. 2014).

4.2 Regime maps

We obtain regime maps for different spreading parameter S o/σ wa and height of the oil droplet H o while varying Wew and λ. Figure 7 shows regime maps for different S o/σ wa under H o/R w = 3.79. For each S o, there is a critical viscosity ratio λ c, beyond which the water droplet cannot penetrate into the oil droplet. For λ < λ c, the structure varies non-monotonically as Wew increases, taking Fig. 7a for example, with transitions from partial-engulfing to penetrative-engulfing and to partial-engulfing again. The lower transition for low-velocity collision shows that the critical Wew increases with λ. In contrary, the upper transition for high-velocity collision shows that the critical Wew decreases with λ.

Fig. 7
figure 7

Regime maps of the structures for S o/σ wa = −0.17 (a), −0.08 (b), and 0 (c) under H o/R w = 3.79. The solid lines representing the lower transitions are from the simple model discussed in Sect. 5.3. The dashed lines represent approximately the critical viscosity ratios for impenetrable oil droplet. (R o = 153.3 µm, R w = 28.3 µm, ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ a = 1.8 × 10−5 Pa s, θ = 72.5°, σ wa = 72 mN/m, σ oa = 28 mN/m, Ohw = 0.023. For a–c, σ wo = 56, 50 and 44 mN/m, respectively)

Full size image

We also determine regime maps for other two H o under S o/σ wa = 0. To maintain the size ratio of the droplets, we fix the radius of the oil droplet R o while changing both H o and contact angle θ correspondingly as shown in Fig. 8a. Comparing to the condition under H o/R w = 3.79 (Fig. 7c), penetrative-engulfing is promoted under H o/R w = 7.58 (Fig. 8b) and restricted under H o/R w = 2.81 (Fig. 8c). The critical viscosity ratio λ c thus decreases with the decrease in H o. This is because that the penetration is inhibited by the presence of the substrate through the modification of the flow field underneath the water droplet (Tang et al. 2016). The lower transition for H o/R w = 7.58 is nearly identical to that for H o/R w = 3.79, indicating that the effect of finite height on the final structure for low-velocity collision is limited for H o/R w = 3.79.

Fig. 8
figure 8

a Schematics for droplet collision with fixed size ratio and a varying height of the oil droplet. Regime maps for H o/R w = 7.58 (b) and 2.81 (c) under S o/σ wa = 0. The solid lines are from Fig. 7c for comparison. The dashed lines represent approximately the critical viscosity ratios for impenetrable oil droplet. (R o = 153.3 µm, R w = 28.3 µm, ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ a = 1.8 × 10−5 Pa s, σ wa = 72 mN/m, σ oa = 28 mN/m, σ wo = 44 mN/m, Ohw = 0.023)

Full size image

5 Discussions

5.1 Maximum deformation of water droplet

To gain insight regarding the deformation of the water droplet during the collision, we summarize the maximum lateral radius during the impact (as illustrated in the top inset of Fig. 9a), R max, for increasing Wew and λ under S o/σ wa = 0. Figure 9a shows that R max increases with Wew but is almost independent of λ. The weak dependence of droplet deformation on λ is also found for the other S o and is similar to the observation of droplet impact onto an immiscible bath (Lhuissier et al. 2013). Disparities for λ = 2 comparing to the other λ are caused by the large deformation of the low-viscosity oil droplet, which enlarges R max during the collision. For Wew < 2, the water droplet is stretched by the motion of the triple-line and R max is nearly independent of impact velocity. A correlation for data under Wew > 20 and λ > 2 gives

$$\frac{{R_{ \text{max} } - R_{\text{w}} }}{{R_{\text{w}} }} \approx 0.133\sqrt {{\text{We}}_{\text{w}} } .$$
(6)
Fig. 9
figure 9

a Evolution of the maximum lateral radius of the water droplet with Wew for different λ under S o/σ wa = 0. b Variation of the critical y c/R w with S o/σ wa for different viscosity ratio λ

Full size image

Equation (6) is similar to the experimental observation and theoretical prediction based on the momentum conservation of droplets impacting on a substrate (Villermaux and Bossa 2011), but with a smaller coefficient as the droplet deformation is altered by the downward motion.

5.2 Critical condition for penetrative-engulfing

Penetrative-engulfing happens when the triple-line can collapse at the top of the water droplet. If the water droplet is spherical and an instantaneous balance of the three interfacial tensions is achieved at a critical moment, the shape of the collided droplet should be a section of a nodoid when the triple-line is just about to collapse (Langbein 2002). However, unbalanced interfacial tensions at the triple-line and the deformations of the droplets make the critical shape difficult to predict. At low-velocity condition, the spreading of the oil droplet on the substrate is limited since the oil droplet is much larger than the water droplet. We can thus use the distance from the vanishing triple-line to the substrate, y c, to quantify the critical shape for penetration, as indicated in the inset of Fig. 9b. Figure 9b shows y c for conditions near the lower transition under different λ and S o/σ wa for H o/R w = 3.79. The critical y c increases with S o and is almost independent of λ and Wew. The critical condition for the penetrative-engulfing is thus dominantly determined by the geometrical requirement influenced by the three interfacial tensions.

5.3 Modeling the lower transition

Figure 10 shows the evolution of the velocity field during the early stage of a typical collision process. The droplets begin to interact with each other through a thin gas film (Fig. 10b). The air film ruptures rapidly after the droplets interact. The forming and vanishing of the air film thus have a negligible effect on the collision dynamics. After the water/oil interface forms, the water droplet spreads on the top of the oil droplet while moving downward. Figure 10c shows that the velocity vectors underneath the water droplet are approximately perpendicular to the water/oil interface. After the maximum deformation, the water droplet begins to recover its shape (Fig. 10d). Recovery motion couples with the downward motion to render the flow field more complex. Figure 10h shows that the droplet recovers to a nearly spherical shape when its velocity is approximately zero.

Fig. 10
figure 10

Time evolution of velocity contours and vectors during the early stage of a typical collision process. The physical parameters are the same as those in Fig. 6b. The time interval between the snapshots is 0.01 ms. (R o = 153.3 µm, R w = 28.3 µm, ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ a = 1.8 × 10−5 Pa s, θ = 72.5°, σ wa = 72 mN/m, σ oa = 28 mN/m, σ wo = 44 mN/m, λ = 20, U 0 = 5.6, S o/σ wa = 0, Wew = 12.5, Rew = 159, Ohw = 0.023)

Full size image

Based on above observations, we propose a simple model to understand the lower transition which is in the parameter space of practical applications. We consider the situation under H o/R w = 3.79, when the effect of finite height is negligible as indicated in Sect. 4.2. The penetration process is controlling by the competition of inertia of the water droplet, deformation of the droplets, viscous resistance of the oil phase, and the balancing of the three interfacial tensions. We show in Fig. 10c that velocity vectors underneath the water droplet are approximately perpendicular to the water/oil interface. The radial component of the viscous stress tensor underneath the water/oil interface is in the order of −4µ o U w/R(t) (Berberović et al. 2009), where U w is the velocity of the water droplet and R(t) the lateral radius of the deforming water droplet. Integration of the radial viscous stress over the area of the water/oil interface estimates the vertical force experienced by the water droplet. The integral can be reduced to the product of the radial viscous stress and the projected area of the water/oil interface onto the horizontal plane, πR(t)2. The vertical force due to the viscous resistance is thus in the order of

$$- 4\pi \mu_{\text{o}} U_{\text{w}} R\left( t \right).$$
(7)

Note that the form of the vertical force is comparable to that of the drag force exerting on a spherical particle given by the Stokes’ law.

The motion of the water droplet is then proportional to the viscous resistance,

$$m_{\text{w}} \dot{U}_{\text{w}} \propto - 4\pi \mu_{\text{o}} U_{\text{w}} R(t),$$
(8)

where \(m_{\text{w}} = 4/3\rho_{\text{w}} \pi R_{\text{w}}^{3}\) is the mass of the water droplet. Integration of Eq. (8) from the moment when the water droplet touches the oil droplet to the stop of the water droplet can give the relationship between the initial velocity U 0 and the penetration length L p of the water droplet. The time evolution of R(t) during the penetration is, however, difficult to predict. To obtain an explicit form, we replace R(t) by αR max to take the droplet deformation into account, where α is a constant of proportionality, which needs to be obtained from data correlations. The dimensionless form of the integral reduces to

$$\bar{L}_{\text{p}} \sim{\text{Re}}_{\text{w}} /3\alpha \lambda \bar{R}_{ \text{max} } ,$$
(9)

where \(\bar{L}_{\text{p}} = L_{\text{p}} /R_{\text{w}}\) and \(\bar{R}_{ \text{max} } = R_{ \text{max} } /R_{\text{w}}\).

Figure 7 shows that the regime of penetrative-engulfing expands with the increase in S o. This is because the released interfacial energy during penetration (approximately \(4\pi R_{\text{w}}^{2} \left( {\sigma_{\text{oa}} + S_{\text{o}} } \right)\)) (Li et al. 2014) transfers partially into kinetic energy of the water droplet. Penetrative-engulfing is thus promoted for larger S o . Figure 7(c) shows that penetrative-engulfing can happen at U 0 = 0 for λ ≤ 4. This means that the released interfacial energy is enough to overcome the viscous resistance. We can thus consider the effect of S o by the viscosity ratio λ 0 at Rew = 0. The above proportionality can be rewritten to be

$${\text{Re}}_{\text{w}} = 3\alpha (\lambda - \lambda_{0} )\bar{L}_{\text{p}} \bar{R}_{ \text{max} } .$$
(10)

Combining Eqs. (6), (10) can be further reduced to

$$\frac{{\sqrt {{\text{We}}_{\text{w}} } }}{{1 + \beta \sqrt {{\text{We}}_{\text{w}} } }} = 3\alpha {\text{Oh}}_{\text{w}} (\lambda - \lambda_{0} )\bar{L}_{\text{p}} ,$$
(11)

where β = 0.133 is the constant of proportionality in Eq. (6). By estimating the critical L p by H o − (y c − 2R w), we obtain the value of λ 0 for different S o and the constant factor α by correlations of the lower transitions using Eq. (11) for H o/R w = 3.79. The resulted boundaries show good agreements with the numerical results with α = 3/2. Figure 11a shows that the lower boundaries from numerical simulations collapse to each other in the \(\sqrt {{\text{We}}_{\text{w}} }\) versus \((\lambda - \lambda_{0} )\bar{L}_{\text{p}}\) plot.

Fig. 11
figure 11

a Comparison of the correlation of Eq. (11) and the simulation results near the lower boundaries under different S o (Filled symbols are for penetrative-engulfing, while hollow symbols are for partial-engulfing or complete-engulfing); b the variations of the ratio of loss of the kinetic energy to the initial energy when the water droplet is just about to penetrate into the oil droplet under H o/R w = 3.79 and S o/σ wa = 0

Full size image

We attempt to find the scaling of λ 0 based on the definition of Ohnesorge number \({\text{Oh}} = \mu /\sqrt {\rho R\sigma }\) since λ 0 is corresponding to U 0 = 0. When comparing viscous forces of the oil with inertial and interfacial tension forces by relating λ 0 µ w and \(\sqrt {\rho_{\text{w}} R_{\text{w}} \left| {S_{\text{o}} } \right|}\), or simply λ 0 and \(\sqrt {\left| {S_{\text{o}} /\sigma_{\text{wa}} } \right|}\), we find a linear dependence of λ 0 on \(\sqrt {\left| {S_{\text{o}} /\sigma_{\text{wa}} } \right|}\), as shown in the inset of Fig. 11a. This demonstrates that the effect of interfacial tensions on the regime boundary is properly considered by λ 0 in Eq. (11).

5.4 Critical viscosity ratio

The lower transition ends at the critical viscosity ratio λ c. The existence of λ c can be understood from the energy point of view. Figure 11b displays the ratio of the loss of kinetic energy and the initial kinetic energy of the water droplet when the droplet is just about to penetrate into the oil droplet for different We 1/2w and λ under H o/R w = 3.79 and S o/σ wa = 0. The ratio increases with the increase in λ for each We 1/2w , as a result of the increasing viscous resistance. The ratio also increases with We 1/2w for each λ since the deformation increases with We 1/2w to cause the increase in viscous dissipation. The critical condition for penetration happens when the ratio reaches to 1, suggesting that all the kinetic energy of the water droplet is lost. Figure 11b shows that the water droplet loses almost all the kinetic energy at λ = 12, regardless of how high We 1/2w is. Further increases in both λ and We 1/2w will increase the loss of kinetic energy during the collision. The penetration is thus not possible for λ > 12.

We have demonstrated that the regime of penetrative-engulfing expands with the increase in S o/σ wa since more interfacial energy is released to the system. For the same reason, the critical viscosity ratio λ c increases with S o/σ wa. The regime maps in Figs. 7 and 8 show that the critical viscosity ratio λ c also increases with H o due to the decrease in the resistance of the substrate.

5.5 Understanding the upper transition

The impact velocity near the upper transition is high enough to cause significant deformation and spreading of the oil droplet. Figure 11 demonstrates two conditions under same H o, S o/σ wa, and λ, but with different impact velocity U 0. The water droplet can penetrate into the oil droplet for Wew = 31.6, but cannot for Wew = 40.0. High-velocity collision generates a crater on the top of the oil droplet due to the large velocity gradient inside the oil droplet. The oil droplet deforms and spreads to reduce its instantaneous height. The critical shape for penetrative-engulfing is thus altered, and the critical y c decreases. Since L p ≈ H o − (y c − 2R w), the L p required for penetrative-engulfing increases due to the spreading of the oil droplet. Comparing images at t = 0.07 ms in Fig. 12a, b, the penetration lengths are similar for the two cases. However, the spreading of the oil droplet under Wew = 40.0 is greater than that under Wew = 31.6 to result in a larger required L p. The penetration is prevented since L p is smaller than the required one under Wew = 40.0. The upper transition is thus determined by the competition between the penetration of the water droplet and the spreading of the oil droplet.

Fig. 12
figure 12

Collision dynamics for two conditions near the upper transition under H o/R w = 3.79, S o/σ wa = −0.08, and λ = 8. a Penetrative-engulfing at Wew = 31.6; b partial-engulfing at Wew = 40.0. (R o = 153.3 µm, R w = 28.3 µm, ρ w = 998 kg/m3, ρ o = 840 kg/m3, ρ a = 1.2 kg/m3, µ w = 1.0 × 10−3 Pa s, µ a = 1.8 × 10−5 Pa s, θ = 72.5°, σ wa = 72 mN/m, σ oa = 28 mN/m, σ wo = 44 mN/m, Ohw = 0.023)

Full size image

Since the spreading of the oil droplet is influenced by the presence of the substrate, the upper transition varies with H o. The spreading becomes weaker for higher H o. For the same λ, the required L p for penetrative-engulfing decreases with the increase in H o to promote penetrative-engulfing. The critical Wew for the upper transition thus increases with H o as shown in Figs. 7c, 8b, c. For the same Wew, both the penetration and the spreading decrease with the increase in λ because of the increasing viscous resistance. Consequently, both L p and the required L p decrease with λ. Figures 7 and 8 show that the critical Wew at the upper transition reduces with λ, suggesting that the decrease in L p is quicker than that of the required L p.

6 Conclusions

We have investigated systematically the collision of a microsize water droplet with a sessile oil droplet, with focus on the structures of the formed compound droplet. A three-phase volume-of-fluid method is developed and validated experimentally to consider three phases and three types of interfaces, as well as the formation and vanishing of the triple-line among the three phases. Three final structures are identified by numerous simulations, namely partial-engulfing, complete-engulfing, and penetrative-engulfing. Regime maps of the structures regarding impact velocity and oil/water viscosity ratio are obtained for different spreading parameters of the oil phase and heights of the oil droplet. The oil droplet is found to be impenetrable when the viscosity ratio is higher than a critical one. For viscosity ratio lower than the critical one, the final structure varies non-monotonically with the increase in impact velocity, leading to two transitions. The lower transition boundary increases with the viscosity ratio under the competition between the inertia and viscosity. The maximum deformation of the water droplet and the critical shape for penetration at the lower transition are analyzed to establish a simple model for the lower transition. The upper transition is under the competition between the penetration of the water droplet and the spreading of the oil droplet. This study brings the basis of system design dedicated to the successful generation of water-in-oil droplets.