Flow-induced deformation of compliant microchannels and its effect on pressure–flow characteristics

Abstract

We report theoretical and experimental investigations of flow through compliant microchannels in which one of the walls is a thin PDMS membrane. A theoretical model is derived that provides an insight into the physics of the coupled fluid–structure interaction. For a fixed channel size, flow rate and fluid viscosity, a compliance parameter $f_{\text{p}}$ is identified, which controls the pressure–flow characteristics. The pressure and deflection profiles and pressure–flow characteristics of the compliant microchannels are predicted using the model and compared with experimental data, which show good agreement. The pressure–flow characteristics of the compliant microchannel are compared with that obtained for an identical conventional (rigid) microchannel. For a fixed channel size and flow rate, the effect of fluid viscosity and compliance parameter $f_{\text{p}}$ on the pressure drop is predicted using the theoretical model, which successfully confront experimental data. The pressure–flow characteristics of a non-Newtonian fluid (0.1 % polyethylene oxide solution) through the compliant and conventional (rigid) microchannels are experimentally measured and compared. The results reveal that for a given change in the flow rate, the corresponding modification in the viscosity due to the shear thinning effect determines the change in the pressure drop in such microchannels.

1 Introduction

Use of poly(dimethylsiloxane) (PDMS) microchannels has increased significantly in the last decades due to various reasons including low cost, transparency, durability, biocompatibility, compliance and ease of fabrication (Anoop and Sen 2015). But the development of theory describing the flow through these soft microchannels has not met the pace with which their application in various fields has increased. In case of pressure-driven flow through PDMS microchannels, finite deformation of the walls takes place depending on the pressure exerted by the fluid and the wall thickness. However, for simplicity, most of the research works in this area have neglected the presence of such deformation by using a considerably thicker wall (Hardy et al. 2009). The wall deformation plays an important role in the fluid flow characteristics in these channels, particularly when the wall thickness is small. A major difficulty in the development of this fluid flow theory is the complex fluid–structure interactions, which take place due to the compliance of the PDMS material. The governing equation for the fluid flow is nonlinear in nature, and the solution can be obtained by coupling with the elasticity equations of the walls (Gervais et al. 2006).

In spite of these difficulties, the development of fluid flow theory through these soft channels has practical significance in microscale pressure sensors (Hosokawa et al. 2002), cell sorting (Beech and Tegenfeldt 2008), peristaltic pumping (Jeong et al. 2005) and other applications. Thin PDMS layers have been used as diaphragms in microfluidic actuation devices including micropumps (Singh et al. 2015) and microflow stabilization devices (Iyer et al. 2015) and hold vital importance in biomedical applications. Recently, Pang et al. (2014) investigated the droplet formation in a compliant T-junction microchannel and found that deformation of the flexible wall enhances the monodispersity in the droplet size. Similarly, few other works report on the size control of the droplets via actuation of compliant microchannel wall using external pressure system (Hsiung et al. 2006; Lee et al. 2007; Lin et al. 2008). The pressure difference across a thin wall governs the wall deformation, which in turn changes the throat size of the droplet generator section and controls the generated droplet size. Thangawng et al. (2007) proposed a microdevice using ultrathin PDMS membrane, which can very well be used as mechanical and chemical sensor as well as to study the cellular mechanics. Compliant microchannels can have great significance in the study of the mechanics of single cells (Hou et al. 2009).

Fluid–structure interactions in channels are important in physiology to understand the flow phenomena in cardiovascular systems including diseased cardiovascular canals. Most of the blood vessel diseases including stenosis and atherosclerosis are very critical to human beings and animals, and are major causes of morbidity and mortality (Hardy et al. 2009) and curing them requires an understanding of the flow through blood vessels which are flexible in nature (varies from small capillaries of 10 µm diameter with 1 µm wall thickness to aorta of 25 mm diameter and 2 mm wall thickness (Mazumdar 2004). However, in situ testing of blood flow through such blood vessels becomes extremely challenging, and thus, it is important to develop suitable physical models to simulate fluid flow conditions. Investigations of the interaction between the fluid and capillary wall and its effect on the pressure drop are crucial for improved understanding of such diseases. Microchannels with thin compliant PDMS membrane as channel walls could be a suitable candidate for modeling fluid flow through arteries and blood vessels.

Understanding of the fluid–structure interplay in compliant microchannels is important for design of devices involving such channels. Earlier, there have been efforts to understand the fluid flow through collapsible tubes. Holt (1969) have studied flow through collapsible tubes and shown that with the changes in downstream pressure the collapsed tube automatically adjusts its resistance so that the flow rate remains constant. Shapiro (1977) have investigated one-dimensional theory of steady flow in a thin-walled tube, partially collapsed by a negative transmural pressure difference. Katz et al. (1969) have reported a lumped parameter system model for the flow through collapsible tubes based on their experimental studies, which was used to define the functional relationship between cross-section area and transmural pressure as well as relation between the energy loss coefficient and cross-sectional area. Also, Pedley and Luo (1998) have considered a 2D configuration representing collapsible tubes by taking a small segment of one wall replaced by a membrane under longitudinal tension and numerically calculated the membrane displacement. Gervais et al. (2006) investigated flow through flexible microchannels having wall thicknesses >6.0 mm, using confocal microscopy and provided an analytical model for pressure–flow characteristics. It was demonstrated that for the same pressure drop, it was possible to obtain higher flow rate as compared to rigid microchannel of identical size. Later, Hardy et al. (2009) studied the deformation of PDMS microchannels with walls having 1.5 mm and 3.0 mm thicknesses and has reported that the pressure drop through flexible walled microchannel is up to 35 % less than that through an identical rigid-walled channel. Cheung et al. (2012) reported a model for predicting the pressure–flow characteristics in a compliant microchannel from a known pressure–flow characteristics of an identical rigid channel using a deformability parameter α. The deformability parameter α was calculated from experimental results without realizing its dependence on the various physical parameters, which is illustrated in the present work.

Understanding of the fluid–structure interplay in compliant microchannels is important for the design of microdevices involving such compliant microchannels. Theoretical analysis of the fluid–structure interaction in deformable microchannels has been reported in recent literature (Gervais et al. 2006; Hardy et al. 2009; Cheung et al. 2012). However, the thickness of the walls considered in these works is much larger (>1 mm), whereas the thickness of the membrane wall considered in our work is <100 µm. Due to larger wall thickness used, the earlier investigations consider semi-infinite medium approximation in the analysis and such approximation does not hold true in our case since the entire wall membrane deflects. Hardy et al. (2009) clearly report that the semi-infinite medium approximation does not hold when the wall thickness <1.5 mm. Also, the proportionality constant $\alpha$ used in all the above theoretical models depends on the channel dimensions (Gervais et al. 2006), wall thicknesses (Hardy et al. 2009) and the liquid properties (Cheung et al. 2012). So, in their model, the value of $\alpha$ needs to be determined for each experimental conditions. Also, the above models require that the value of $\alpha$ be determined experimentally thus not self-sufficient. Our model is self-sufficient and overcomes the drawbacks of the above models reported in the literature. Very recently, Chakraborty et al. (2012) investigated experimentally and numerically the deformation of a thin flexible membrane (~100 µm) present only over a short length of the channel due to its interaction with the flow inside the channel.

In spite of such developments, pressure–flow characteristics of microchannels with a compliant wall of thickness ~100 µm (and with both Newtonian and non-Newtonian fluids) have not been investigated, which is reported in the present work. We report a compliance parameter which can be varied by varying a set of physical variables to represent channel compliance which in turn controls the pressure–flow characteristics as well as the deflection profile of the channel wall. First, a brief description of the device used in the proposed studies is reported. Next, an analytical model for predicting the pressure–flow characteristics of flow of a Newtonian fluid flow through a PDMS microchannel with a compliant wall is presented. Then, the device fabrication protocol and experimental setup is described. Further, the materials and methods are described. Finally, the results of the analytical model and experiments with both Newtonian and non-Newtonian fluids are presented and discussed.

2 Device description

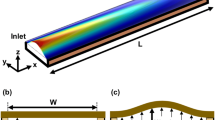
A schematic of the microchannel devices used in this work is depicted in Fig. 1. The device 1 (Fig. 1a) comprises a PDMS molded microchannel bonded with a glass slide which is referred as “conventional (rigid) microchannel.” The device 2 (Fig. 1b) comprises a PDMS molded microchannel bonded with a thin PDMS membrane which is referred as “compliant microchannel.” The top view of both the channels is presented in Fig. 1c. Both the conventional and compliant microchannels are of width $w$ and height $h_{0}$. In the flexible microchannel, the thickness of the membrane is $t_{\text{m}}$.When liquid flows through the compliant channel at a flow rate $Q$, the membrane wall deforms due to which the resulting pressure drop $\Delta p$ is less than that for a conventional microchannel of identical size at the same flow rate $Q$. The deformation profile of the membrane under nonzero flow conditions both across and along the flow directions is depicted in Fig. 1d, e, respectively. Due to fluid flow through the compliant microchannel, the deformation profile across a particular channel section is parabolic with a maximum deflection $\Delta h_{\hbox{max} } (z)$ at the center ($y$ = 0) and zero deflection at the side edges ($y$ = ${{ \pm w} \mathord{\left/ {\vphantom {{ \pm w} 2}} \right. \kern-0pt} 2}$), where the membrane is bonded with the PDMS substrate. Along the channel length, since the membrane is bonded at its left edge ($z$ = 0), there is a sharp increase in channel height because the fluid pressure is highest at the left edge ($z$ = 0) and the deflection becomes maximum at some distance downstream from this edge. This maximum deflection is denoted as the global maximum deflection $(\Delta h_{\hbox{max} } )_{\text{g}}$.

Fig. 1

Schematic of a device 1, conventional microchannel, thick PDMS molded microchannel bonded with glass slide; b device 2, compliant microchannel, thick PDMS molded microchannel bonded with a thin PDMS membrane; c top view of device 1 and device 2; d cross-sectional channel deformation; and e channel deformation along the flow direction

3 Theoretical model

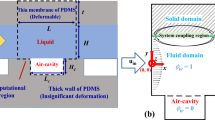
The analytical model for describing the flow through compliant microchannels is derived by coupling the theory of laminar flow to the structural deformation due to the hydrodynamic pressure exerted at the liquid–solid interface. The physical model of the problem is a rectangular microchannel having a thin membrane as one of its walls, as depicted in Fig. 2a. In pressure-driven flow, due to deflection of the membrane, the cross-sectional area increases and thus hydraulic resistance decreases. Under the assumption that flow inside the microchannel to be incompressible, steady, laminar and Newtonian, the Navier–Stokes equation which describes the flow behavior is given as follows,

$$- \rho \,\vec{v}\left( {\,\vec{\nabla } \cdot \vec{v}} \right) + \mu \,\nabla^{2} \vec{v} = \vec{\nabla }p$$

(1)

where $\rho$ is the fluid density, $\vec{v}$ is the fluid velocity, $p$ is the applied pressure and $\mu$ is the fluid dynamic viscosity. For a rigid rectangular microchannel, assuming the flow to be fully developed, the relationship between the flow rate $Q$ and pressure $p$ is of the form (Bruus 2009)

Fig. 2

a Parabolic shape of deformed thin wall at a positive discharge condition, b forces and c stresses acting on an infinitesimal strip of membrane wall

$$- \frac{\partial p(z)}{\partial z} = \frac{Q}{{h^{3} w}}\frac{12\mu }{{\left( {1 - 0.63\frac{h}{w}} \right)}}$$

(2)

It is to be noted that as compared to the complicated Fourier series form of the solution, the above simpler solution is accurate within 13 % for a limiting aspect ratio ${w \mathord{\left/ {\vphantom {w h}} \right. \kern-0pt} h}\sim1$ (Bruus 2009). Here, we couple the above differential equation with the constitutive relation for membrane deflection $h(z)$ in terms of the varying pressure along the flow direction $p(z)$ to derive the expression for the pressure–flow relationship. In this case, the two side walls and the lower wall of the channel are semi-infinite structures whose deformation is negligible, so that the channel cross-section could be assumed to be rectangular throughout. Under imposed flow condition, at a fixed cross-section along the microchannel, the local pressure $p(z)$ is responsible for the deflection of the compliant membrane wall. The expansion of the channel cross-section in turn would modify the fluid velocity and pressure distribution, which further controls the channel deformation and so on. The mathematical formulations would employ zero-displacement boundary condition along the PDMS membrane-bulk PDMS interface and fixed pressure boundary condition on the deformable channel wall. Due to the variation of the pressure inside the channel, the deformation is expected to vary along the flow direction (i.e., along z-direction). To formulate the constitutive relation for the variation in the channel height along z-direction $h(z)$, an accurate scale for the effective channel deflection $\Delta h$ can be estimated using the width-averaged displacement $\langle\Delta h\rangle$ as follows,

$$\frac{{\Delta A}}{{A_{0} }} = \frac{{w\langle\Delta h\rangle }}{{wh_{0} }} = \frac{{\langle\Delta h\rangle }}{{h_{0} }}$$

(3)

Thus, at any distance z downstream of the channel, the effective channel height is described by,

$$h(z) = h_{0} \left( {1 + \frac{\langle \Delta h\rangle (z)}{{h_{0} }}} \right)$$

(4)

At a fixed channel cross-section along the length of the microchannel, assuming deflection to be small, the deflection profile of the thin membrane wall is assumed to be parabolic in shape as follows,

$$\Delta h(y) = \Delta h_{\hbox{max} } \left( {1 - 4\frac{{y^{2} }}{{w^{2} }}} \right)$$

(5)

Thus, the relationship between the maximum and the average displacement can be obtained as $\langle \Delta h\rangle \sim\frac{2}{3}\Delta h_{\hbox{max} }$. So, we obtain the effective channel height as follows,

$$h(z) = h_{o} \left( {1 + \frac{2}{3}\frac{{\Delta h_{\hbox{max} } }}{{h_{o} }}} \right)$$

(6)

Generally, the use of Eq. (2) is valid for a rectangular channel of uniform cross section. In this case, due to the membrane deformation, the height of the channel varies in both y- and z directions. The parabolic variation in the channel height in the y-direction is accounted for by taking a rectangular cross section of an average height $h_{0} + \langle\Delta h\rangle$(see Eqs. 3–6). Also, as discussed later in Sect. 5, the variation in the average membrane deformation $\langle\Delta h\rangle$ in the z-direction (i.e., <30 µm) is quite small (as compared to the channel length (i.e., 30 mm). Thus, the use of Eq. (2) is a good approximation. Now, in order to find an expression for $\Delta h_{\hbox{max} }$ in terms of the local pressure $p(z)$, we perform force balance on an infinitesimally small strip of the membrane wall of length dz, as shown in Fig. 2b. The force acting on the membrane due to the pressure difference across the membrane $F_{\text{p}}$ is balanced by the restoring force $F_{\text{r}}$ that holds the membrane on the bulk PDMS. The lateral component of this restoring force $F_{r} \cos \alpha$ cancels out due to symmetry (as there is no lateral movement of the membrane). The vertical component of the force due to pressure difference $F_{\text{p}}$ and the restoring force $F_{r} \sin \alpha$ balance each other as follows,

$$p(z)\,\left( {w\,{\text{d}}z} \right) \approx - \sigma_{\text{m}} \,\left( {2\,{\text{d}}z\,t_{\text{m}} } \right)\sin \alpha = - \sigma_{\text{m}} \,\left( {2\,{\text{d}}z\,t_{\text{m}} } \right)\left. {\frac{{\partial (\Delta h)}}{\partial y}} \right|_{y = w/2}$$

(7)

Here, the pressure force $F_{\text{p}}$ is calculated as pressure $p(z)$ times the elemental membrane area $wdz$ and the restoring force $F_{r}$ is calculated as the membrane stress $\sigma_{\rm m}$ time the cross section of the membrane around both the rims $2dzt_{\rm m}$ (which is twice the membrane thickness $t_{\rm m}$ time the elemental length $dz$). For small angles $\alpha$, the sine is approximated as the tangent which is the slope of the membrane at its edges and can be found by calculating the derivative of the deflection curve at the rim of the membrane as $\left. {{{\partial (\Delta h)} \mathord{\left/ {\vphantom {{\partial (\Delta h)} {\partial y}}} \right. \kern-0pt} {\partial y}}} \right|_{{y = {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0pt} 2}}} = {{ - 4\,(\Delta h_{\hbox{max} } )} \mathord{\left/ {\vphantom {{ - 4\,(\Delta h_{\hbox{max} } )} w}} \right. \kern-0pt} w}$. Next, by solving for the pressure $p(z)$, we get

$$p(z) = \frac{{8\sigma_{\rm m} t_{\rm m} \Delta h_{\hbox{max} } }}{{w^{2} }}$$

(8)

The stress in the membrane wall (Fig. 2c) is a combination of residual stress $\sigma_{o}$ which may be already present when there is no deflection of the membrane and the stress $\sigma_{d}$ due to Hooke’s law generated by the deflection of the membrane (Schomburg 2011). Assuming zero residual stress in the membrane, we get

$$\sigma_{\rm m} = \sigma_{d}$$

(9)

The stresses due to membrane deflection $\sigma_{d}$ can be calculated from the strains $\varepsilon_{y}$ and $\varepsilon_{R}$ in the transverse and radial directions, respectively (since, $L \gg w$, the strain in the longitudinal direction is neglected). Now, according to Hooke’s law, the strains $\varepsilon_{y}$ and $\varepsilon_{R}$ can be expressed as

$$\varepsilon_{y} = \frac{1}{{E_{\rm m} }}\left( {\sigma_{y} + \nu_{\rm m} \sigma_{R} } \right)$$

(10)

$$\varepsilon_{R} = \frac{1}{{E_{\rm m} }}\left( {\sigma_{R} + \nu_{\rm m} \sigma_{y} } \right)$$

(11)

where $\nu_{\text{m}}$ and $E_{\text{m}}$ denote Poisson’s ratio and Young’s modulus of the membrane, respectively. For thin membranes, transverse strain is assumed to be constant over the entire membrane (Schomburg 2011) which can be estimated by the extension of the membrane along the neutral fiber of the membrane. The length of the resulting parabola in the deflected state of the membrane is given as (Bronstein and Semendjajew 1976)

$$L_{pa} \approx w\,\left[ {1 + \frac{8}{3}\left( {\frac{{\Delta h_{\hbox{max} } }}{w}} \right)^{2} - \frac{32}{5}\left( {\frac{{\Delta h_{\hbox{max} } }}{w}} \right)^{4} } \right]$$

(12)

From the above expression of the extended length of the parabola and undeformed width of the membrane $w$ and by using the assumption $\Delta h_{\hbox{max} } \ll y_{\text{o}}$, the transverse strain $\varepsilon_{y}$ can be obtained as

$$\varepsilon {}_{y}\, \approx \frac{{L_{pa} - w}}{w} = \frac{8}{3}\left( {\frac{{\Delta h_{\hbox{max} } }}{w}} \right)^{2}$$

(13)

The fact that the radial strain is still unknown is resolved using one of the two assumptions (Schomburg 2011): (a) transverse and radial strains are equal throughout the membrane, and (b) transverse strain is zero throughout the membrane. The second assumption is invalid in the present case as the membrane has a deflection profile along the y-direction and thus is subjected to nonzero transverse strain. Assuming that the tangential and radial strain are equal in magnitude throughout the membrane (transverse strain is tensile in nature but radial stress is compressive in nature, which results in $\varepsilon_{R} = - \varepsilon_{y}$), from Eqs. 10 and 11, we get,

$$\sigma_{y} = \varepsilon_{y} \left( {\frac{{E_{\rm m} }}{{1 - \nu_{\rm m} }}} \right) = \sigma_{\rm m}$$

(14)

Finally, using Eqs. 13, 14 and 8, we get

$$p(z) \approx \frac{64}{3}\,\frac{{t_{\rm m} \,E_{\rm m} }}{{w\,\left( {1 - \nu_{\rm m} } \right)}}\,\left( {\frac{{\Delta h_{\hbox{max} } }}{w}} \right)^{3}$$

(15)

If we substitute the expression for $\Delta h_{\hbox{max} }$ from the above equation in Eq. 6, we obtain

$$h(z) = h_{o} \left[ {1 + \frac{2}{{3h_{o} }}\left( {\frac{{3w^{4} \,(1 - \nu_{\rm m} )p(z)}}{{64t_{\rm m} E_{\rm m} }}} \right)^{{\frac{1}{3}}} } \right]$$

(16)

Equation 16 can be further expressed as

$$h(z) = h_{o} \left[ {1 + \left( {\frac{1}{72}\frac{{w^{4} \left( {1 - \nu_{\rm m} } \right)}}{{t_{\rm m} E_{\rm m} h_{0}^{3} }}p\left( z \right)} \right)^{{\frac{1}{3}}} } \right]$$

(17)

Now, we notice from Eq. 17 that for a fixed pressure drop $p(z)$, the deflection of the membrane wall is governed by a group of terms which are multiplied with the pressure drop. We combine these terms into a single parameter called the “Compliance Parameter $f_{\text{p}}$,” which is expressed as

$$f_{\text{p}} = \frac{1}{72}\left[ {\frac{{a^{3} w\left( {1 - \nu_{\rm m} } \right)}}{{t_{\rm m} E_{\rm m} }}} \right]$$

(18)

where $a = {w \mathord{\left/ {\vphantom {w {h_{o} }}} \right. \kern-0pt} {h_{o} }}$ is the aspect ratio of the channel. Further, if we rearrange the terms, the channel height can be expressed as

$$h\left( z \right) = h_{o} \left[ {1 + \left( {f_{\text{p}} p\left( z \right)} \right)^{{\frac{1}{3}}} } \right]$$

(19)

From Eq. 18, it is observed that the compliance parameter $f_{\text{p}}$ is inversely proportional to the membrane thickness and Young’s modulus of the membrane. This clearly shows that, with the channel dimensions $w$ and $h_{0}$ kept fixed, for a lower value of the product $t_{\rm m} E_{\rm m}$, the flexibility parameter $f_{\text{p}}$ is higher which provides higher membrane deflection $h(z)$. Now, if we substitute the expression for $h(z)$ in Eq. 2 and solve the resulting differential equation with the boundary condition $p\left( {z = L} \right) = 0$, we obtain an expression for flow rate $Q$ as follows,

$$\begin{aligned} Q & = \frac{{wh_{\text{o}}^{3} p}}{{12\mu \left( {L - z} \right)}}\left[ {1 + \frac{9}{4}\left( {f_{\text{p}} p} \right)^{{\frac{1}{3}}} + \frac{9}{5}\left( {f_{\text{p}} p} \right)^{{\frac{2}{3}}} + \frac{1}{2}\left( {f_{\text{p}} p} \right)} \right. \\ & \quad \left. { - 0.63\frac{{h_{\text{o}} }}{w}\left\{ {1 + 3\left( {f_{\text{p}} p} \right)^{{\frac{1}{3}}} + \frac{18}{5}\left( {f_{\text{p}} p} \right)^{{\frac{2}{3}}} + 2\left( {f_{\text{p}} p} \right) + \frac{3}{7}\left( {f_{\text{p}} p} \right)^{{\frac{4}{3}}} } \right\}} \right] \\ \end{aligned}$$

(20)

For a given flow rate $Q$, the above equation is solved using a simple MATLAB code to predict the pressure profile $p(z)$ along the microchannel. The pressure profile can be further used to compute the pressure drop $\Delta p$ across the channel and obtain the pressure drop $\Delta p$ versus flow rate $Q$ characteristics of Newtonian flows through a deformable rectangular microchannel (with a compliant wall). As observed, unlike flow through rigid microchannels, the pressure–flow relationship is nonlinear. However, the above nonlinear equation reduces to a simple expression describing the pressure–flow characteristics of Newtonian flows through rigid microchannel for a compliance parameter $f_{\text{p}} = 0$, as expected. If we rearrange the terms in Eq. 19, we get

$$p\left( z \right) = \frac{1}{{f_{\text{p}} }}\left[ {\frac{h\left( z \right)}{{h_{o} }} - 1} \right]^{3}$$

(21)

On substituting the above expression for $p(z)$ in Eq. 2 and solving the resulting differential equation with the boundary condition $h\left( {z = L} \right) = h_{o}$, we get the average (over cross section, ref. Eq. 3) deflection profile $h(z)$ as follows,

$$\left( {\frac{w}{{4h_{o} }}} \right)h^{4} - \left( {\frac{{2w + 0.63h_{o} }}{{5h_{o}^{2} }}} \right)h^{5} + \left( {\frac{{w + 1.26h_{o} }}{{6h_{o}^{3} }}} \right)h^{6} - \left( {\frac{0.09}{{h_{o}^{3} }}} \right)h^{7} = 4\mu f_{\text{p}} Q\left( {L - z} \right) + \frac{1}{60}wh_{o}^{3} - \left( {0.006} \right)h_{o}^{4}$$

(22)

Equation 22 is solved in MATLAB to predict the width-averaged height $h(z)$ of the microchannel of width $w$ and height $h_{0}$ along the flow (axial) direction in case of the flow of a given fluid of viscosity $\mu$ at any given flow rate $Q$.

4 Experiments

4.1 Device fabrication

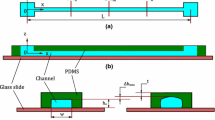
Standard soft lithography process was used to fabricate the PDMS microchannel devices. First, a flexi mask was designed in AutoCAD LT 2008 and printed at 40,000 dpi (Photozone Graphics, Mumbai, India). Then, 4″ silicon wafer (semiconductor Technology and Application, Milpitas, USA) was cleaned using RCA1, RCA2 and HF dip followed by DI water rinse and placed in oven for 2 min at 120 °C to remove moisture. Next, the wafer was spun-coated with photoresist SU8 2075 (Micro Chem Corp, Newton, USA) at 2750 rpm for 30 s with an acceleration of 300 rpm/s. Soft baking was done at 65 °C for 5 min followed by 95 °C for 10 min. Then, the photoresist was exposed to UV light (J500IR/VISIBLE, OAI Mask aligner, CA, USA) through the mask for 30 s. Next, post-exposure bake was done at 65 °C for 2 min followed by 95 °C for 8 min. Further, to obtain the SU8 pattern on top of silicon master, UV-exposed wafer was developed, and then, it was placed in oven at 100 °C for 30 min to further improve adhesion between photoresist and wafer. Once we obtained the silicon master, PDMS monomer and curing agent (Sylgard-184, Silicone Elastomer kit, Dow corning, USA) were mixed at mixing ratio 10:1 (except for the fabrication of conventional PDMS microchannels, where we used a mixing ratio of 5:1 in order to improve the rigidity of the channel (Wang et al. 2014)) and was degassed in a desiccator to remove air bubbles trapped during mixing. PDMS was then poured onto silicon master and was then cured inside a vacuum oven at 65 °C for 2.5 h. After curing, the hardened PDMS layer containing the channel structure was peeled off the silicon master and cut to size. A 1.5-mm biopsy punch (Shoney Scientific, Pondicherry, India) was used to punch fluidic access holes for the inlet/outlet and the pressure taps. For the fabrication of device 1 (conventional microchannel), PDMS layer containing channel was then bonded to a glass slide using oxygen plasma bonding. Finally to establish fluidic connection, PTFE tubings (Cheminert fittings-VICI, Germany) were glued to the access holes. To fabricate device 2 (compliant microchannel), poly(methyl methacrylate) (PMMA) sheets of size 9 × 9 × 0.15 cm were used to spin coat thin PDMS layers on its surface and then baked inside a vacuum oven at 65 °C for 3.5 h to obtain thin PDMS membranes. We have fabricated thin PDMS layers of two different thicknesses 100 and 55 µm. The PMMA sheets were spun-coated at speeds of 2200 and 1500 rpm for 40 s at an acceleration of 8 rpm/s for fabricating membrane of 100 and 55 µm thickness, respectively. The Young’s modulus of membranes of 55 and 100 µm is 1.362 and 1.184 MPa, respectively (Liu et al. 2009). The thin PDMS membranes (on PMMA sheets) were then bonded to the PDMS microchannel layer by using oxygen plasma bonding such that the thin PDMS membrane form one of the walls of the microchannel. After the bonding, the PMMA sheets were carefully peeled off from the bonded device. The SEM images of the membrane bonded channels (compliant channels) with two different membrane thicknesses are shown in Fig. 3c.

Fig. 3

a Detailed dimensions of microfluidic chip as well as channel; b schematic of experimental setup; c SEM images of the compliant microchannels, channel size 500 × 83 µm and different membrane wall thickness 100 and 55 µm; and d photograph of the setup used for the measurements

4.2 Materials and Methods

In most of our experiments, DI water (viscosity 0.000914 Pa.s at 24 °C) was used as the working fluid. In the studies involving the effect of viscosity on pressure–flow characteristics of Newtonian fluids, aqueous glycerol (20 and 40 % glycerol with viscosity 0.001564 and 0.003237 Pa s, respectively, at 24 °C) were used (Sajeesh et al. 2014). Further, with non-Newtonian fluids, 0.1 % polyethylene oxide (PEO) solution of nominal molecular weight 4 × 10⁶ (Sigma-Aldrich, USA) was used. The aqueous PEO solution was prepared by dissolving an appropriate amount of PEO in DI water at room temperature (24 °C). Solution was stirred continuously for sufficient time (≥12 h) using a magnetic stirrer to achieve complete homogenization. More details regarding the PEO solution preparation procedure are provided elsewhere (Ebagninin et al. 2009). For the fluorescence imaging experiments, we have used 2 % weight: weight solution of Rhodamine B dye.

4.3 Experimental setup

A schematic and photograph of the experimental setup are shown in Fig. 3b, d, respectively. The microchannel has five pressure tapping holes, which is shown in Fig. 3b. Detailed dimensions of the microfluidic chip and the channel are shown in Fig. 3a. A syringe pump (TSE systems, Germany) was used to infuse the working fluids through the microchannel device. The syringe pump was well calibrated before use in the experiments. The pressure drop measurements were taken using PX26–005DV differential pressure sensor with a DP25B S-230A display unit (Omega Stanford, USA), which is capable of measuring transient pressure drop across the pressure taps (with response time of approximately 1.0 ms). The pressure sensor was used as per the protocol reported by Cheung et al. (2012). In the pressure–flow characterization experiments, the pressure drops was measured for a length $L$ = 12 mm across the pressure tapping at $z = 12\;{\text{mm}}$ and $z = 24\;{\text{mm}}$ of the channel (as shown in Fig. 3b). Fluorescence imaging was used for measuring the deflection of the thin membrane walls at various conditions. In the fluorescence imaging experiments, we have used a straight microchannel (of length L = 36 mm) without any pressure tapping in it. Images of the channel at different flow rates and axial positions were captured using an inverted microscope (Carl Zeiss Axiovert A1) coupled with a high-speed camera (FASTCAM SA3 model, Photron USA, Inc.) interfaced with PC via Photron Fastcam Viewer 3 software. The fluorescence images were processed through Image J software to measure the intensity at different locations. The experiments were conducted inside an air-conditioned laboratory environment at a temperature of 24 °C to eliminate the effect of temperature on the viscosity of aqueous glycerol solution (sensitive to temperature change of even ±0.5 °C).

5 Results and discussion

5.1 Newtonian fluid

5.1.1 Pressure and deformation profile

The average pressure $p(z)$ at various axial locations along the microchannel predicted from theory (using Eq. 20) at various flow rates $Q$ is depicted in Fig. 4a. As expected, the pressure decreases downstream along the channel and at a fixed axial location, and the pressure is higher at higher flow rates $Q$. The pressure values are experimentally measured at five different locations along the channel for two different flow rates and compared with that predicted using the model, which shows good agreement. The error bars in the plot represent the standard deviation of the experimental data about the mean value. The variation of the pressure profile $p(z)$ for different values of the compliance parameters $f_{\text{p}}$ is depicted in Fig. 4b. The results show that, at any axial location, the pressure is lower for a higher compliance parameter $f_{\text{p}}$. A fluorescent dye (Rhodamine B) was infused into the channel at different flow rates, and the corresponding fluorescence images were captured. Figure 5 shows fluorescence image of the liquid dye in the channel at a flow rate of 100 µl/min. The captured fluorescence images were processed through ImageJ software, and gray scale intensity was plotted across a particular channel cross section (X − X′), as shown in Fig. 5. The gray scale intensity corresponds to the thickness of the liquid dye layer, i.e., at any location, a higher gray scale intensity indicates higher liquid dye thickness (due to higher membrane deflection). At a particular cross section, the gray scale intensity was calibrated by considering liquid dye thickness same as the undeformed channel height (i.e., zero deflection of the membrane) at the edges and then used for calculating the deflection profile. We used the fluorescence imaging technique mentioned above to capture the deflection profiles $h(y)$ of the membrane wall at the axial location $z$ = 18 mm at four different flow rates, as depicted in Fig. 6a.

Fig. 4

Pressure profile $p(z)$ along the microchannel: a effect of flow rate, w = 500 µm, h ₀ = 83 µm and, f _p  = 1.023446 × 10⁻⁵ Pa⁻¹ and b effect of compliance parameter f _p, w = 500 µm, h ₀ = 83 µm and Q = 500 µl/min

Fig. 5

Fluorescence micrograph of the Rhodamine dye flowing in the compliant microchannel and the corresponding channel cross section obtained after calibration ($Q = 100\;{\upmu \hbox{l}}/{ \hbox{min} }$, $z = 18\;{\text{mm}}$)

Fig. 6

a Deflection profile $h(y)$ of the membrane wall at various flow rates $Q$ obtained using fluorescence imaging and b maximum deflection of the membrane wall $h{}_{\hbox{max} }$ versus flow rate $Q$: comparison of model predictions with experimental data, $z$ = 18 mm, w = 500 µm, h ₀ = 83 µm and f _p = 1.023446 × 10⁻⁵ Pa⁻¹

As observed in Fig. 6a, there is significant increase in the deflection as we increase the flow rate $Q$ from 100 to 300 µl/min, but the increase in the deflection becomes less significant when the flow rate $Q$ is increased from 700 to 1000 µl/min. This is evident by the decreasing slope of the theoretical curve, as shown in Fig. 6b. The slope of the curve decreases with the increase in flow rate $Q$ indicating that the increase in deflection is less significant at higher flow rates. Also, in Fig. 6b, the theoretical predictions are compared with the experimental deflection data at various flow rates, which shows good agreement. The average deflection $\left\langle {\Delta h} \right\rangle$ at various axial locations predicted from theory (using Eq. 22) at various flow rates is depicted in Fig. 7a. It is observed that the deflection $\left\langle {\Delta h} \right\rangle$ is maximum near the channel entrance, where the pressure $p(z)$ is maximum and decreases downstream due to the decrease in pressure. Also, at higher flow rates, the average deflection is higher throughout the channel. At $Q$ = 1000 µl/min, $\left\langle {\Delta h} \right\rangle$ was experimentally measured at various axial locations $z$ and compared with the theoretically obtained deflection profile at the same flow rate, which show a good agreement. The effect of the compliance parameter $f_{\text{p}}$ predicted from theory (using Eq. 22) on the average membrane deflection $\left\langle {\Delta h} \right\rangle$ is shown in Fig. 7b. As observed, the average deflection $\left\langle {\Delta h} \right\rangle$ of the membrane increases throughout the channel with the increase in compliance parameter $f_{\text{p}}$. In Fig. 7a, the experimentally measured deflection $\left\langle {\Delta h} \right\rangle$ is highest at some distance away from the left edge of the channel, i.e., z = 0 at which the membrane is bonded with the PDMS substrate containing the microchannel (Fig. 1c). The $\left( {\Delta h_{\hbox{max} } } \right)_{\text{g}}$ is found to be 61 µm (using $\langle\Delta h\rangle \sim\frac{2}{3}\Delta h_{\hbox{max} }$) at $z$ = 6 mm.

Fig. 7

a Average axial deflection profile $\left\langle {\Delta h} \right\rangle$ of the membrane wall at various flow rates $Q$ with $f_{\text{p}}$ = 1.023446 × 10⁻⁵ Pa⁻¹ comparison with experimental data and b average axial deflection profile $\left\langle {\Delta h} \right\rangle$ of the membrane wall at various compliance parameters $f_{\text{p}}$, w = 500 µm, h ₀ = 83 µm, $Q$ = 1000 µl/min

5.1.2 Pressure–flow characteristics

Figure 8a shows a comparison between the experimentally measured pressure drop $\Delta p$ through conventional and flexible microchannels (of same size) with the theoretically predicted pressure drop $\Delta p$ in an identical rigid microchannel (with no wall deformation or deflection). The theoretically predicted pressure drop $\Delta p$-flow rate $Q$ characteristics for a rigid microchannel is linear, as expected. As observed, the pressure drop $\Delta p$-flow rate $Q$ characteristics of the conventional microchannel match well with that of the theoretically predicted characteristics within 5 %. The pressure drop $\Delta p$-flow rate $Q$ characteristics in the case of flow through the compliant microchannel deviate from that of the rigid (theory) and conventional microchannels at all flow rates due to the compliance of the microchannel wall. This deviation increases with increase in the flow rate $Q$ due to larger deflection of the membrane wall (up to flow rate $Q$ 1400 µl/min). Also, the deformation of the microchannel wall is the reason for the nonlinear nature of the pressure drop $\Delta p$-flow rate $Q$ characteristics of such microchannels. At a flow rate $Q$ above 1400 µl/min, the slope pressure drop $\Delta p$-flow rate $Q$ curve for the compliant microchannel tends to increase further. The pressure drop $\Delta p$ at 1000 µl/min for the compliant microchannel shows 70 % lower $\Delta p$ as compared to an identical conventional (rigid) microchannel under the same flow conditions. Figure 8b shows the comparison of pressure drop $\Delta p$-flow rate $Q$ characteristics obtained from experiments with that predicted using the theoretical model (Eq. 20), which show a close agreement with a maximum error of 18 %. This difference and the different slope of the pressure drop $\Delta p$-flow rate $Q$ characteristics curve predicted by the model could be attributed to the increase in the Young’s modulus $E_{\text{m}}$ of the thin membrane wall, which is expected with the decreasing wall thickness at higher flow rates, which is neglected in the theoretical model.

Fig. 8

a Comparison between measured pressure drop $\Delta p$ through conventional (rigid) and flexible microchannels with theoretically predicted pressure drop and b comparison of pressure drop $\Delta p$-flow rate $Q$ characteristics obtained from experiments with that predicted using the model, w = 500 µm, h ₀ = 83 µm, µ = 0.000914 Pa s, f _p = 1.023446 × 10⁻⁵ Pa⁻¹

5.1.3 Effect of fluid viscosity and compliance parameter

Figure 9a shows the effect of fluid viscosity $\mu$ on the pressure drop $\Delta p$ across a compliant microchannel predicted by the theoretical model and obtained from experiments, for various flow rates $Q$, with a fixed channel size ($w$ = 500 µm and $h_{0}$ = 83 µm) and compliance parameter $f_{\text{p}}$ = 1.023446 × 10⁻⁵ Pa⁻¹. As observed, the pressure drop $\Delta p$ increases linearly with the fluid viscosity $\mu$. The model predictions are in close agreement with the experimental data with a maximum error of 16 % at higher viscosity $\mu$ and flow rate $Q$. While the model and experiments have excellent agreement at lower viscosity $\mu$ and flow rate $Q$, the relatively large error at higher viscosity $\mu$ and flow rate $Q$ is possibly due to the neglect of the variation of Young’s modulus of the membrane $E_{\text{m}}$ in the model with membrane thickness $t_{\text{m}}$, which varies significantly at higher pressure drop $\Delta p$. The effect of compliance parameter $f_{\text{p}}$ on the pressure drop $\Delta p$ in a compliant microchannel, for different flow rates $Q$ and fixed channel size ($w$ = 500 µm and $h_{0}$ = 83 µm) and viscosity $\mu$ = 0.000914 Pa.s, predicted using the theoretical model and obtained from experiments is depicted in Fig. 9b. The results show that the pressure drop $\Delta p$ decreases nonlinearly with the flexibility parameter $f_{\text{p}}$ (ref. Eq. 20). It is also observed that the match between the theoretical predictions and experimental data is good at lower flow rates $Q$, but relatively large error is observed at higher flow rates $Q$, which is attributed to the neglect of the variation of the Young’s modulus of the membrane $E_{\text{m}}$ at higher flow rates $Q$, as discussed earlier. The importance of the compliance parameter can be inferred from Eqs. (21) and (22). From Eq. (22), we observe that for a fixed flow rate, a different value of the compliance parameter $f_{\text{p}}$ provides a modified profile for the channel height $h\left( z \right)$, which in turn offers a modified pressure profile $p\left( z \right)$. A higher value of $f_{\text{p}}$ leads to larger channel deformation and lower pressure drop $\Delta p$ across a microchannel. For a channel of fixed size, the $f_{\text{p}}$ can be controlled by varying the membrane thickness $t_{\text{m}}$ and material properties ($E_{\text{m}}$ and $\nu_{\text{m}}$). Additionally, the $f_{\text{p}}$ can be controlled by varying the aspect ratio $w/h_{0}$ and width $w$ of the undeformed channel. These parameters can be independently varied to obtain the required $f_{\text{p}}$. In order to achieve an increased flow rate $Q$ for a given driving pressure $\Delta p$ or to limit the pressure drop $\Delta p$ at a fixed flow rate $Q$, the value of $f_{\text{p}}$ required can be found out and accordingly the channel size, membrane thickness and properties can be fixed.

Fig. 9

a Effect of fluid viscosity $\mu$ on pressure drop $\Delta p$ for various flow rates $Q$, $w$ = 500 µm and $h_{0}$ = 83 µm,$f_{\text{p}}$ = 1.023446 × 10⁻⁵ Pa⁻¹, b effect of compliance parameter $f_{\text{p}}$ on the pressure drop $\Delta p$ for different flow rates $Q$, $w$ = 500 µm and $h_{0}$ = 83 µm, $\mu$ = 0.000914 Pa s

5.2 Pressure–flow characteristics with non-Newtonian fluid

We have performed experiments to obtain pressure drop $\Delta p$-flow rate $Q$ characteristics of 0.1 % polyethylene oxide (PEO) solution (molecular weight 4 × 10⁶ g mol⁻¹) through conventional (rigid) and compliant microchannels (of size 2000 × 83 µm, in compliant microchannel compliance parameter $f_{\text{p}}$ = 165.765 × 10⁻⁵ Pa⁻¹). It is reported that the 0.1 % PEO solution exhibits shear thinning behavior, whose viscosity $\mu_{\rm eff}$ variation with shear stress is reported elsewhere (Ebagninin et al. 2009). Figure 10 shows the pressure drop $\Delta p$-flow rate $Q$ characteristics of 0.1 % PEO solution in conventional (rigid) and compliant microchannels. We observe that in both cases the pressure drop $\Delta p$ first increases up to certain flow rate $Q$ and then starts decreasing with further increase in the flow rate. The pressure drop is a combined effect of the flow rate $Q$ as well as viscosity $\mu_{\rm eff}$ so it increases proportional to the flow rate as well as viscosity. However, since the solution is a shear thinning fluid, its viscosity $\mu_{\rm eff}$ would decrease at higher flow rates due to increase in the shear rate with flow rate $Q$. A higher flow rate $Q$ is expected to provide increased pressure drop $\Delta p$, but the resulting decrease in viscosity $\mu_{\rm eff}$ (due to increase in flow rate) would counteract to reduce the pressure drop. For the conventional (rigid) as well as compliant microchannel devices, the pressure drop $\Delta p$-flow rate $Q$ characteristics curves have two zones. In the first set of zone (zones $A^{\prime}$ and $A$ for the conventional and compliant microchannel devices, respectively), which are flow rate dominant zones, the effect of the increase in flow rate overcomes the decrease in viscosity $\mu_{\rm eff}$, and thus, the net effect is an increase in the pressure drop $\Delta p$ with increase in flow rate $Q$. In the second set of zones (zones $B^{\prime}$ and $B$ for the conventional and compliant microchannel devices, respectively), which are viscosity dominant zones, the effect of the decrease in viscosity $\mu_{\rm eff}$ overcomes the effect of increase in flow rate, and thus, the net effect is a decrease in the pressure drop $\Delta p$ with increase in flow rate $Q$.

Fig. 10

Pressure drop $\Delta p$-flow rate $Q$ characteristics of 0.1 % PEO solution (molecular weight = 4 × 10⁶ g mol⁻¹) with w = 2000 µm, h ₀ = 83 µm, $f_{\text{p}}$ = 165.765 × 10⁻⁵ Pa⁻¹

Now, let us compare the pressure drop $\Delta p$-flow rate $Q$ characteristics of the conventional (rigid) and compliant microchannels. We discussed in Sect. 5.1 that the compliant microchannels undergo large deflection of the compliant membrane walls, and thus, the effective flow cross-sectional area of the compliant microchannels is higher than that of the conventional (rigid) microchannels. So for the same flow rate $Q$, the shear rate in the compliant microchannels is smaller as compared to that in the conventional microchannels of identical channel size. This results in a higher effective viscosity $\mu_{\rm eff}$ of the same fluid while flowing through the compliant microchannel as compared to that through the conventional microchannel. The pressure drop $\Delta p$-flow rate $Q$ characteristics of the conventional and compliant microchannels can be compared over two distinct regions. In the region 1, the shear thinning effect (i.e., decrease in viscosity with increase in flow rate $Q$) is dominant, and thus, the pressure drop $\Delta p$ through the compliant microchannel is higher as compared to that through the conventional microchannel. On the other hand, in the region 2, the flow rate effect is dominant, and thus, the pressure drop $\Delta p$ through the conventional microchannel is higher as compared to that through the compliant microchannel.

6 Conclusions

In this work, we have reported the experimental and theoretical studies of pressure-driven flow through rectangular polymer microchannels, when one of the channel walls is a compliant polymer membrane of thickness $t_{\text{m}}$ below 100 µm. Considering Newtonian fluid, we have derived an analytical model for pressure as well as deformation profiles that provide an insight into the physics of coupled fluid–structure interaction in such channels. For a fixed channel size (width $w$ and height $h_{0}$), flow rate $Q$ and fluid viscosity $\mu$, we have identified a compliance parameter $f_{\text{p}} = f(t_{\text{m}} ,E_{\text{m}} ,\nu_{\text{m}} )$ that controls the pressure $\Delta p$-flow $Q$ characteristics. The average deflection $\left\langle {\Delta h} \right\rangle$ of the compliant wall shows that the rate of increase in deflection decreases with flow rate. The pressure $p(z)$ and deflection profiles $h(y),\left\langle {\Delta h} \right\rangle$ and pressure $\Delta p$-flow $Q$ characteristics of the compliant microchannel are predicted using the model and compared with experimental results, which show good agreement within 18 %. The pressure $\Delta p$-flow $Q$ characteristics of the compliant microchannel showed 63 % lower pressure drop as compared to an identical conventional microchannel under the same flow conditions. For a fixed channel size and flow rate $Q$, the effect of fluid viscosity $\mu$ and compliance parameter $f_{\text{p}}$ on the pressure drop $\Delta p$ is predicted using the theoretical model, which successfully confront the experimental data. Finally, the pressure $\Delta p$-flow $Q$ characteristics of a shear thinning non-Newtonian fluid (0.1 % PEO solution) in the compliant and conventional microchannels are experimentally measured and compared. It is observed that in both channels, the pressure drop initially increases due to flow rate but then decreases with flow rate due to the shear thinning effects. The effects of the increase in flow rate and decrease in viscosity due to shear thinning behavior determine the pressure drop in the compliant and conventional microchannels, in both the regions.