1 Introduction

Polyelectrolyte (PE) grafting renders incredible “smartness” to nanochannels. This “smartness” stems from the remarkable flexibility that is rendered to the nanochannels by this grafting. For example, depending on the nature of the grafted PE and alteration of its configuration as a response to system parameters (e.g. pH or electrolyte ion concentration), nanochannels may be used as nanofluidic diodes, as rectifier of current, as ion sensors (Ali et al. 2008, 2011; Siwy et al. 2005), and for gating and manipulation of ion transport (Xia et al. 2008; Yameen et al. 2009). While such widespread application of PE-grafted nanochannels involving ion transport is known, relatively less is known about the applications involving fluid transport. One well-known application involving fluid flow is the flow-valving action of the PE-grafted nanochannels caused by the particular drag response of the PE layer (Adiga and Brenner 2005, 2012). Another possible related application, as we have shown recently, can be the use of PE-grafted nanochannels as an excellent electrochemomechanical energy converter (Chanda et al. 2014; Chen and Das 2015d)—such conversion refers to the generation of electrical energy caused by the triggering of the streaming electric field (or streaming potential) in the presence of a background nanofluidic pressure-driven transport (Morrison and Osterle 1965; Yang et al. 2003). It is worthwhile to note that while there have been many studies on streaming potential calculations in PE-grafted channels (Duval et al. 2009, 2011a, b; Donath and Voigt 1986; Keh and Liu 1995; Keh and Ding 2003; Ohshima and Kondo 1990; Starov and Solomentsev 1993a, b; Ma and Keh 2007; Duval and Leeuwen 2004), we highlighted the manner in which such streaming potential generation will lead to highly efficient energy conversion in nanochannels with PE grafting. Our previous study considered a most simplified situation where the PE molecules were assumed to have constant charge density and the drag coefficient was assumed to be independent of the monomer distribution (Chanda et al. 2014; Chen and Das 2015d). In the proposed study, we provide a much more realistic treatment of this problem by assuming that the PE molecule exhibits pH-dependent charge density. Such a consideration leads to three distinct issues. Firstly, we need to account for the hydrogen and the hydroxyl ion distribution in the electric double layer (EDL) ionic distribution, with the EDLs forming on both sides of the PE layer–electrolyte interface. Secondly, such pH dependence necessitates consideration of a cubic monomeric distribution of the grafted PE molecule in order to address the unphysical discontinuities in the hydrogen ion concentration profile associated with the consideration of uniform monomer distribution (Chen and Das 2015a, b, c; Das et al. 2015). Finally, this cubic monomeric profile is considered while expressing the monomer distribution dependence of the drag coefficient for the fluid flow (Chen and Das 2015b; Das et al. 2015).

Our theoretical framework is based on first calculating the electrostatics of the PE–electrolyte interface, with the PE being grafted as “brushes” (Milner 1991; Netz and Andelman 2003; Zhulina et al. 1989) on the inner walls of the nanochannel. We assume that the PE electrostatic contribution is decoupled from the elastic and the excluded volume contributions of the PE molecule. This allows us to assume a constant thickness of the PE layer (i.e. the thickness is decided solely by the balance of the elastic and the excluded volume effects) while calculating the EDL electrostatics of the PE–electrolyte interface. In a couple of recent studies, we have quantitatively established the physical conditions (or parameter space) that allow such decoupling for the PE layers grafted on the inner walls of a nanochannel and forming “brushes” that have a height smaller than the nanochannel half height (Das et al. 2015; Chen and Das 2015c). Therefore, in the present study we work in this parameter space. This EDL electrostatics is subsequently used to calculate the velocity field, streaming potential, and the efficiency of the energy conversion. The salient issue here is that we obtain the velocity field by solving an integro-differential equation, which stems from the fact that the streaming electric field is not explicitly expressible in terms of the pressure-driven and electroosmotic (due to the streaming electric field) transport. We have used such integro-differential approach in one of our previous papers (Chen and Das 2015d); here, we provide a more rigorous analysis that accounts for the contribution of \(\hbox {H}^+\) and \(\hbox {OH}^-\) ions and at the same time accounts for the monomer distribution-dependent drag force (Adiga and Brenner 2007, 2012; Chen and Das 2015b; Das et al. 2015).

Our analyses express the hitherto unknown dependences of the streaming current and the efficiency in a PE-grafted nanochannel on factors such as the pH and the \(\hbox {pK}_{\mathrm{a}}\) (of the acid that dissociates to produce the negative charge of the PE layer). Our results further demonstrate a significantly high (4–5 %) efficiency of the electrochemomechanical energy conversion (Daiguji et al. 2004; Heyden et al. 2006) associated with the generation of the streaming electric field in PE-grafted nanochannels with pH-dependent charge density. This efficiency number is reasonable in the light of the experimental result on the streaming-electric-field-induced electrochemomechanical energy conversion (predicting an efficiency of approximately 3 %; Daiguji et al. 2004) and establishes the nanochannel with grafted PE layer with pH-dependent charge density as an important device for nanofluidic electrochemomechanical energy conversion.

2 Theory

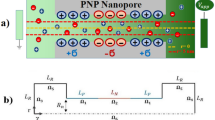
We consider a pressure-driven transport of an electrolyte solution in a soft charged nanochannel of height 2h (see Fig. 1) and study the streaming electric field and the efficiency of the resulting electrochemomechanical energy conversion. This “softness” of the nanochannel is attributed to a layer of wall-grafted ion-penetrable charged polyelectrolyte (PE) layer of thickness d (see Fig. 1). The grafting density is assumed to be large enough to ensure that the grafted PE molecules attain a brush-like configuration (Netz and Andelman 2003; Azzaroni 2012; Milner 1991). The charge on the PE layer is attributed to the pH-dependent ionization of the PE molecules; this ensures that the charge density of the PE layer is pH-dependent. This charging triggers an EDL ion distribution at either side of the PE layer–electrolyte interface. We shall first briefly discuss the EDL electrostatics of the system, which has already been discussed in detail in our previous papers (Chen and Das 2015a, b, c); this will be followed by the calculations of the velocity field, the streaming electric field, and the energy conversion efficiency.

Fig. 1
figure 1

Schematic of the pressure-driven transport in a nanochannel grafted with negatively charged pH-sensitive PE layer. In this schematic, we also show the direction of the streaming electric field or streaming potential \(E_{\mathrm{S}}\)

Full size image

2.1 Electrostatics

The total free energy change (\(\Delta F\)) associated with a grafted PE molecule system forming an EDL can be expressed as:

$$\begin{aligned} \Delta F=\Delta F_{\mathrm{PE}}+\Delta F_{\mathrm{EDL}}, \end{aligned}$$
(1)

where \(\Delta F_{\mathrm{PE}}\) is the free energy change associated with a single grafted PE molecule and \(\Delta F_{\mathrm{EDL}}\) is the free energy change associated with the EDL formation. One can express \(\Delta F_{\mathrm{PE}}\) as:

$$\begin{aligned} \Delta F_{\mathrm{PE}}=\Delta F_{\mathrm{PE},{\mathrm{ent}}}+\Delta F_{\mathrm{PE},{\mathrm{EV}}}+\Delta F_{\mathrm{PE},{\mathrm{elec}}}, \end{aligned}$$
(2)

where \(\Delta F_{\mathrm{PE},{\mathrm{ent}}}\), \(\Delta F_{\mathrm{PE},{\mathrm{EV}}}\), and \(\Delta F_{\mathrm{PE},{\mathrm{elec}}}\) are the free energy changes associated with the entropic (or elastic), excluded volume, and electrostatic contributions of the PE molecule. Calculations considering Eqs. (1) and (2) simultaneously have been provided before (Zhulina and Borisov 1997, 2011); however, these calculations may be inappropriate for cases where the PE charge density is a function of the pH (Chen and Das 2015a, b; Milne et al. 2014). This inappropriateness stems from enforcing the \(\hbox {H}^+\) ion concentration to obey the Boltzmann distribution both inside and outside the PE layer; such a consideration is incorrect and leads to unphysical discontinuities in the value and in the gradient of the \(\hbox {H}^+\) ion concentration at the PE layer–electrolyte interface, as established by our previous study (Chen and Das 2015a). The correct formulation that considers both Eqs. (1, 2) and at the same time provides a physically consistent description of the \(\hbox {H}^+\) ion concentration is still unknown. In several recent papers, we have proposed a simplified formulation where we have described the PE layer–EDL electrostatics in a framework that decouples the PE elastic and excluded volume effects from the PE electrostatic effects (Chanda et al. 2014; Chanda and Das 2014; Das 2014; Chen and Das 2015a, b, d; McDaniel et al. 2015; Andrews and Das 2015). Such an assumption ensures that the PE layer height is dictated entirely by the balance of the elastic and the excluded volume effects and is hence independent of the electrostatic and the EDL effects. Please note there have been a plethora of studies that have modelled the electrostatics and the electrokinetics of PE-grafted interfaces assuming a constant thickness of the PE layer (see the review papers (Ohshima 1995, 2012; Barbati and Kirby 2012; Ohshima 2009; Duval and Gaboriaud 2010; Duval et al. 2011c) and the articles cited in these review papers). All these calculations, therefore, have implicitly assumed such decoupling of the PE electrostatic effects from the PE elastic and excluded volume effects. Only very recently, we provided the physical conditions and the parameter space corresponding to which such decoupling is possible (Chen and Das 2015c; Das et al. 2015). We refrain from discussing this parameter space in detail here; however, we do assume that the present study is described in the same parameter space making the decoupling feasible.

Under these conditions, the free energy change associated with PE electrostatic effect and that associated with the resulting EDL formation must individually balance each other. Therefore, one may write:

$$\begin{aligned} \Delta F^\prime =\Delta F_{\mathrm{PE},{\mathrm{elec}}}+\Delta F_{\mathrm{EDL}}. \end{aligned}$$
(3)

Please note that \(\Delta F^\prime \approx \Delta F\) for \(\Delta F_{\mathrm{PE},{\mathrm{elec}}}\gg \left( \Delta F_{\mathrm{PE},{\mathrm{ent}}}+\Delta F_{\mathrm{PE},{\mathrm{EV}}}\right)\), whereas \(\Delta F^\prime \ll \Delta F\) for \(\Delta F_{\mathrm{PE},{\mathrm{elec}}}\ll \left( \Delta F_{\mathrm{PE},{\mathrm{ent}}}+\Delta F_{\mathrm{PE},{\mathrm{EV}}}\right)\). In our previous studies, we have derived the equilibrium EDL electrostatics starting from Eq. (3) (Chen and Das 2015a, c). Here, we briefly summarize these steps for the sake of completeness. Equation (3) can be rewritten as:

$$\begin{aligned} \Delta F^\prime =\int \Delta f\left( \psi ,\psi ^\prime ,n_\pm ,n_{\mathrm{H}^+},n_{\mathrm{OH}^-}\right) d^3{\mathbf {r}}, \end{aligned}$$
(4)

where \(\Delta f\) is the density of the free energy change, expressed as (considering the bottom half of the nanochannel):

$$\begin{aligned} \Delta f &= k_BT\sum _i\left[ n_i\left( \ln {\left( \frac{n_i}{n_{i,\infty }}\right) -1}\right) \right] -\frac{\epsilon _0\epsilon _r}{2}|\nabla \psi |^2 \\&\qquad+\,e\psi \left[ \sum _iz_in_i-\varphi n_{\mathrm{A}^-}\right] \quad \quad \left[ {\text{for}}-h\le y\le -h+d\right], \\ \Delta f &= k_BT\sum _i\left[ n_i\left( \ln {\left( \frac{n_i}{n_{i,\infty }}\right) -1}\right) \right] -\frac{\epsilon _0\epsilon _r}{2}|\nabla \psi |^2 \\&\qquad+\,e\psi \left[ \sum _iz_in_i\right] \quad \quad \quad\quad \quad \,\left[ {\text{for}}-h+d\le y\le 0\right]. \end{aligned}$$
(5)

In Eq. (5) in the right-hand side, the first term represents the entropic contribution due to the mixing of the ions, the second term represents the self-energy of the EDL electric field, and the third term represents the electrostatic energy of the PE ions (valid only within the PE layer) electrolyte, hydrogen, and hydroxyl ions. Further, \(\psi\) is the electrostatic potential, \(\epsilon _0\) is the permittivity of free space, \(\epsilon _r\) is the relative permittivity of the medium, \(k_BT\) is the thermal energy, e is the electronic charge, and \(z_i\), \(n_i\) and \(n_{i,\infty }\) are the valence, the number density and the bulk number density of ion of type i (\(i=\pm ,\hbox {H}^+,\hbox {OH}^-\)). Here, the electrolyte salt is assumed to be monovalent and symmetric (hence \(z_+=-z_-=1\)). Also in Eq. (5), \(n_{\mathrm{A}^-}\) is the number density of the negatively charged PE ions. Further, \(\varphi (y)\) is the dimensionless monomer distribution, which should obey a non-unique cubic distribution in y (detailed later) in order to avoid unphysical discontinuities associated with considering a constant \(\varphi\) for a PE layer with pH-dependent charge density (Chen and Das 2015a, b). The number densities of the negatively charged PE ions depend on local \(\hbox {H}^+\) ion concentration and can be expressed as:

$$\begin{aligned} n_{\mathrm{A}^-}=\frac{K_a^\prime \gamma _a}{K_a^\prime +n_{\mathrm{H}^+}}. \end{aligned}$$
(6)

Here, the anionic charge of the negatively charged PE layer is attributed to the ionization of the acid \(\hbox {HA}\) (\(\hbox {HA}\leftrightarrow \hbox {H}^++\hbox {A}^-\); ionization constant \(K_a\)). Also in Eq. (6), \(\gamma _a\) is the maximum site density of the chargeable groups of the PE layer and \(K_a^\prime =10^3N_{\mathrm{A}}K_a\) (\(N_{\mathrm{A}}\) is the Avogadro number). Please note that Eq. (5) is based on the assumption that the EDL is described by the mean-field electrostatics. Therefore, issues such as ion–ion correlations have not been considered. In fact, effects such as the consideration of finite ion sizes and finite solvent polarizability—these effects can be modelled within the mean-field framework—have also been neglected.

Governing equations are obtained by minimizing Eq. (4) with respect to the variables \(\psi\), \(n_\pm\), \(n_{\mathrm{H}^+}\) and \(n_{\mathrm{OH}^-}\). This eventually allows us to write (see Chen and Das 2015a, c as well as “Appendix” for detailed derivation) the equations governing the equilibrium as:

$$\begin{aligned} \bar{n}_{\pm }&= \exp \left( \mp \bar{\psi }\right) \quad \quad \quad \quad \quad \left[ {\text{for}} -1\le \bar{y} \le 0 \right] \end{aligned}$$
(7)
$$\begin{aligned} \bar{n}_{\mathrm{OH}^-} &= \left( \bar{n}_{\mathrm{OH}^-,\infty }\right) \exp \left( \bar{\psi }\right)\quad \left[ {\text{for}} -1\le \bar{y} \le 0 \right] \end{aligned}$$
(8)
$$\begin{aligned} \bar{\psi } &= -\frac{\ln \left( \frac{\bar{n}_{\mathrm{H}^+}}{\bar{n}_{\mathrm{H}^+,\infty }}\right) }{1+\frac{\bar{K}_a'\bar{\gamma }_a\varphi (\bar{y})}{\left( \bar{K}_a'+\bar{n}_{\mathrm{H}^+}\right) ^2}}\, \quad \left[ \text {for} -1 \le \bar{y} \le -1+\bar{d} \right] , \\ \bar{\psi } &= -\ln \left( \frac{\bar{n}_{\mathrm{H}^+}}{\bar{n}_{\mathrm{H}^+,\infty }}\right) \quad \quad \left[ {\text{for}} -1+\bar{d} \le \bar{y} \le 0 \right] . \end{aligned}$$
(9)
$$\begin{aligned} \frac{\hbox {d}^2\bar{\psi }}{\hbox {d}\bar{y}^2} &= \frac{1}{2\bar{\lambda }^2}\left[-\exp (-\bar{\psi })+(1+\bar{n}_{\mathrm{H}^+,\infty })\exp (\bar{\psi })+(\bar{n}_{\mathrm{OH}^-,\infty })\exp (\bar{\psi })\right. \\&\quad\left.-\,\bar{n}_{\mathrm{H}^+}+\frac{\bar{K}_a'\bar{\gamma }_a\varphi (\bar{y})}{\bar{K}_a'+\bar{n}_{\mathrm{H}^+}}\right] \quad ~ \left[ \text {for} -1 \le \bar{y} \le -1+\bar{d} \right] , \\ \frac{\hbox {d}^2\bar{\psi }}{\hbox {d}\bar{y}^2}&= \frac{1}{2\bar{\lambda }^2}[-\exp (-\bar{\psi })+(1+\bar{n}_{\mathrm{H}^+,\infty })\exp (\bar{\psi })+(\bar{n}_{\mathrm{OH}^-,\infty })\exp (\bar{\psi }) \\&\quad-\,\bar{n}_{\mathrm{H}^+,\infty }\exp \left( -\bar{\psi }\right) ] \quad \,\, \left[ {\text{for}} -1+\bar{d} \le \bar{y} \le 0 \right] . \end{aligned}$$
(10)

In the above equations, \(\bar{y} = \frac{y}{h,}\) \(\bar{d} = \frac{d}{h,}\) \(\bar{\psi } = \frac{e\psi }{k_BT,}\) \(\bar{n}_\pm =n_\pm /n_\infty\) (we assume \(n_{+,\infty }=n_{-,\infty }=n_\infty\)), \(\bar{n}_{\mathrm{H}^+} = \frac{n_{\mathrm{H}^+}}{n_{\infty }},\) \(\bar{n}_{\mathrm{OH}^-}=\frac{n_{\mathrm{OH}^-}}{n_\infty },\) \(\bar{n}_{\mathrm{H}^+,\infty }=\frac{n_{\mathrm{H}^+,\infty }}{n_\infty },\) \(\bar{n}_{\mathrm{OH}^-,\infty }=\frac{n_{\mathrm{OH}^-,\infty }}{n_\infty },\) \(\bar{K}_a' = \frac{K_a'}{n_\infty },\) \(\bar{\lambda }=\frac{\lambda }{h}\) (where \(\lambda = \sqrt{\frac{\epsilon _0 \epsilon _r k_BT}{2n_\infty e^2}}\) is the EDL thickness).

Equation (10) uses the Boltzmann distribution [see Eqs. (7–9)] to express the distribution of \(\bar{n}_\pm\), \(\bar{n}_{\mathrm{OH}^-}\), and \(\bar{n}_{\mathrm{H}^+}\) (outside the PE layer). On the other hand, Eq. (9) clearly shows that \(\hbox {H}^+\) ion distribution, on account of its reaction that causes the PE charging, does not obey the Boltzmann distribution within the PE layer—this has been the most important identification of our analysis of the EDL electrostatics of PE-grafted interfaces (see “Appendix” for the derivation and further related discussions Chen and Das 2015a, b, c). The other important issue of Eq. (10) is the manner in which \(n_{i,\infty }\)s are defined. We assume addition of an acid that furnishes the same anion as the anion of the electrolyte salt. As a result, we may write: \(n_{+,\infty }=n_\infty\) and \(n_{-,\infty }=n_\infty +n_{\mathrm{H}^+,\infty }\). From Eq. (10), it can be clearly noted that under the conditions that ensure weak concentration of \(\hbox {H}^+\) and \({\mathrm{OH}}^-\) ions relative to the electrolyte ions, i.e. \(\bar{n}_{\mathrm{H}^+} = \frac{n_{\mathrm{H}^+}}{n_{\infty }}\ll 1\), \(\bar{n}_{\mathrm{H}^+,\infty } = \frac{n_{\mathrm{H}^+,\infty }}{n_{\infty }}\ll 1\), and \(\bar{n}_{\mathrm{OH}^-,\infty }=\frac{n_{\mathrm{OH}^-,\infty }}{n_\infty }\ll 1\), the Poisson equation reduces to the classical Poisson–Boltzmann form (with additional contribution of the PE charge within the PE layer). In other words, the EDL structure is no longer influenced by the \(\hbox {H}^+\) and \(\hbox {OH}^-\) ions. Equations (9, 10) need to be solved simultaneously in the presence of the following dimensionless boundary conditions:

$$\begin{aligned}&\left( \frac{\hbox {d}\bar{\psi }}{\hbox {d}\bar{y}}\right) _{\bar{y}=-1} =0; \left( \frac{\hbox {d}\bar{\psi }}{\hbox {d}\bar{y}}\right) _{\bar{y}=0} =0 \\&\left( \bar{\psi }\right) _{\bar{y}=(-1+\bar{d})^+}=\left( \bar{\psi }\right) _{\bar{y}=(-1+\bar{d})^-}; \\&\left( \frac{\hbox {d}\bar{\psi }}{\hbox {d}\bar{y}}\right) _{\bar{y}=(-1+\bar{d})^+}=\left( \frac{\hbox {d}\bar{\psi }}{\hbox {d}\bar{y}}\right) _{\bar{y}=(-1+\bar{d})^-}. \end{aligned}$$
(11)

Finally, the monomer density distribution \(\varphi (\bar{y})\) is so selected that along with Eq. (9) it ensures that Eq. (11) leads to the following set of boundary conditions for \(\bar{n}_{\mathrm{H}^+}\):

$$\begin{aligned}&\left( \frac{\hbox {d}\bar{n}_{\mathrm{H}^+}}{\hbox {d}\bar{y}}\right) _{\bar{y}=-1} =0; \left( \frac{\hbox {d}\bar{n}_{\mathrm{H}^+}}{\hbox {d}\bar{y}}\right) _{\bar{y}=0} =0 \\&\left( \bar{n}_{\mathrm{H}^+}\right) _{\bar{y}=(-1+\bar{d})^+}=\left( \bar{n}_{\mathrm{H}^+}\right) _{\bar{y}=(-1+\bar{d})^-}; \\&\left( \frac{\hbox {d}\bar{n}_{\mathrm{H}^+}}{\hbox {d}\bar{y}}\right) _{\bar{y}=(-1+\bar{d})^+}=\left( \frac{\hbox {d}\bar{n}_{\mathrm{H}^+}}{\hbox {d}\bar{y}}\right) _{\bar{y}=(-1+\bar{d})^-}. \end{aligned}$$
(12)

Equation (9) is used in Eq. (10) to eliminate \(\bar{\psi }\) and express the differential equation entirely in terms of \(\bar{n}_{\mathrm{H}^+}\); this equation is subsequently solved in the presence of Eq. (12) to obtain the distribution of \(\bar{n}_{\mathrm{H}^+}\). This distribution is next used in Eq. (9) to obtain the corresponding distribution of \(\bar{\psi }\). Finally, the monomer distribution \(\varphi\), in addition to ensuring the attainment of Eq. (12) from Eq. (11), must also ensure (Zhulina and Borisov 1997; Zhulina et al. 1989)

$$\begin{aligned} \frac{1}{\sigma a^3}\int _{-h}^{-h+d} \varphi dy = N, \end{aligned}$$
(13)

where \(\sigma\) is the grafting density (having units of \(1/\hbox {m}^2\)), a is the Kuhn length (hence the volume of a monomer segment is \(\sim a^3\)), and N is the size (or the number of monomers) of a PE molecule. All these criteria are satisfied by a non-unique cubic distribution of \(\varphi\) expressed as (see Chen and Das 2015a for detailed derivation):

$$\begin{aligned} \varphi (\bar{y}) = \left( \frac{Na^3\sigma }{d}\right) \left( \frac{4}{\bar{d}^3}\right) \left( \bar{y}+1-\bar{d}\right) ^2 \left( \bar{y}+1+\frac{\bar{d}}{2} \right) . \end{aligned}$$
(14)

2.2 Calculation of the velocity field

We consider a pressure-driven background transport in this PE-grafted nanochannel. The flow is assumed to be steady, uni-directional, and hydrodynamically fully developed. Such nanochannel pressure-driven transport leads to a downstream migration of the mobile ions of the EDL, which in turn gives rise to the well-known streaming electric field or streaming potential \(E_{\mathrm{S}}\) (Chakraborty and Das 2008; Das and Chakraborty 2009; Das et al. 2009; Das and Chakraborty 2010). This electric field is in a direction opposite to the pressure-driven transport and gives rise to an induced electroosmotic transport that opposes the pressure-driven transport. Under these conditions, the velocity field u can be expressed as:

$$\begin{aligned}&\eta \frac{\hbox {d}^2u}{\hbox {d}y^2}-\frac{\hbox {d}p}{\hbox {d}x}+e(n_+-n_-+n_{\mathrm{H}^+}-n_{\mathrm{OH}^-})\;E_{\mathrm{S}}-\mu _cu=0 \\&\quad \quad \quad \quad \,\,~~~~~~~~~~~~~~~~~~~~~~~~~\left[{\text{for}} -h \le y \le -h+d \right] , \\&\eta \frac{\hbox {d}^2u}{\hbox {d}y^2}-\frac{\hbox {d}p}{\hbox {d}x}+e(n_+-n_-+n_{\mathrm{H}^+}-n_{\mathrm{OH}^-})\;E_{\mathrm{S}}=0 ~ \\&\quad \quad \quad \quad \,\,~~~~~~~~~~~~~~~~~~~~~~~~~\left[ {\text{for}}-h+d \le y \le 0\right] . \end{aligned}$$
(15)

In Eq. (15), \(\hbox {d}p/\hbox {d}x\) is the employed pressure gradient, \(\eta\) is the dynamic viscosity of the liquid, and \(\mu _c = (\frac{\varphi (y)}{b})^2\) (b is a parameter that has a unit of \(\hbox {length}/\sqrt{\hbox {viscosity}}\)) is the drag coefficient within the PE layer. Equation (15) is expressed under several simplifying assumptions. Firstly, we assume that the background flow field does not alter the shape of the grafted PE layer under steady state. Secondly, the timescale (\(\tau _{\mathrm{EDL}}\)) of distribution of the EDL ions (\(\tau _{\mathrm{EDL}}\sim \lambda ^2/D_{\mathrm{ion}}\sim ~10^{-10}-10^{-6}~\hbox {s}\), with EDL thickness \(\lambda \sim 1-100~\hbox {nm}\) and ion diffusivity \(D_{\mathrm{ion}}\sim 10^{-8}~\hbox {m}^2/({\hbox {Vs}})\)) is considered much smaller than the timescale associated with the pressure-driven liquid transport. This assumption allows us to consider the EDL ion distribution as quasi-steady with respect to the flow field, thereby sufficing to express the flow field through Eq. (15) without requiring the coupled Poisson–Nernst–Planck and Navier–Stokes equations to describe the flow field and ion transport (Milne et al. 2014). Thirdly, in Eq. (15) the drag coefficient (\(\mu _c\)) is expressed assuming that \(\mu _c\sim K^{2}\), where \(K^{-1}\) (which varies as \(\varphi ^{-1}\)) is the length that screens the background flow from the flow inside the grafted PE molecules. This analysis is borrowed from the idea of flow screening between the inside and the outside of a polymer coil where the background flow velocity is much larger than the velocity inside the polymer coil (Freed and Edwards 1974; Gennes 1976; Klein 1994); the justification of applying this analysis to the present case of grafted PE molecules is that the PE molecules (just like the polymer coil), being grafted, will have a velocity that is much smaller than the background velocity. Finally, we assume that the penetration depth (\(\ell _p\)) of the flow into the polymer brush is at least equal to the height of the PE layer (d). Considering a simplified situation where \(\ell _p\sim \ell _g\sim \sigma ^{-1/2}\) [where \(\ell _g\) is the spacing between grafted PE brushes and \(\sigma\) is the grafting density (Fredrickson and Pincus 1991; Harden and Cates 1996)], such a condition necessitates \(\sigma <1/d^2\).

Equation (15) can be expressed in dimensionless form as:

$$\begin{aligned} & \frac{\hbox {d}^2\bar{u}}{\hbox {d}\bar{y}^2}+\frac{u_r}{2\bar{\lambda }^2}\bar{E}_{\mathrm{S}}\left[\exp (-\bar{\psi })-(1+\bar{n}_{\mathrm{H}^+,\infty })\exp (\bar{\psi }) -\bar{n}_{\mathrm{OH}^-,\infty }\exp (\bar{\psi })\right.\\ &\quad\quad\quad\quad\left.+\,\bar{n}_{\mathrm{H}^+}\right]-\bar{\alpha }^2 \varphi ^2 \bar{u} =1\quad ~ \left[{\text{for}} -1 \le \bar{y} \le -1+\bar{d}\right] , \\ &\frac{\hbox {d}^2\bar{u}}{\hbox {d}\bar{y}^2}+\frac{u_r}{2\bar{\lambda }^2}\bar{E}_{\mathrm{S}}\left[\exp (-\bar{\psi })-(1+\bar{n}_{\mathrm{H}^+,\infty })\exp (\bar{\psi })-\bar{n}_{\mathrm{OH}^-,\infty }\exp (\bar{\psi })\right.\\ & \left.\quad\quad\quad\quad+\,\bar{n}_{\mathrm{H}^+,\infty }\exp (-\bar{\psi })\right] =1\quad ~\left[{\text{for}} -1+\bar{d} \le \bar{y} \le 0\right] . \end{aligned} $$
(16)

In Eq. (16), \(\bar{u}=\frac{u}{u_{p,0}}\) (where \(u_{p,0}=\frac{h^2}{\eta }\frac{\hbox {d}p}{\hbox {d}x}\) is pressure-driven velocity scale), \(u_r=\frac{u_{e,0}}{u_{p,0}}\) (where \(u_{e,0}=\frac{k_BT}{ez}\frac{\epsilon _0 \epsilon _r E_0}{\eta }\) is the electroosmotic velocity scale; \(E_0\) is the scale of the electric field), \(\bar{E}_{\mathrm{S}}=\frac{E_{\mathrm{S}}}{E_0}\), and \(\bar{\alpha }=\frac{h}{b\sqrt{\eta }}\). Please note that Eq. (16) uses Eqs. (7–9) to express the ion distributions. Solution of Eq. (16) is sought in the presence of the following dimensionless boundary conditions:

$$\begin{aligned} \begin{aligned} \left( \frac{\hbox {d}\bar{u}}{\hbox {d}\bar{y}}\right) _{\bar{y}=-1}=0; \left( \frac{\hbox {d}\bar{u}}{\hbox {d}\bar{y}}\right) _{\bar{y}=0}=0; \,~\\ \left( \bar{u}\right) _{\bar{y}=(-1+\bar{d})^+}=(\bar{u})_{\bar{y}=(-1+\bar{d})^-}; \,\,\\ \left( \frac{\hbox {d}\bar{u}}{\hbox {d}\bar{y}}\right) _{\bar{y}=(-1+\bar{d})^+}= \left( \frac{\hbox {d}\bar{u}}{\hbox {d}\bar{y}}\right) _{\bar{y}=(-1+\bar{d})^-}. \end{aligned} \end{aligned}$$
(17)

Of course, the solution of \(\bar{u}\) requires the value of the \(\bar{E}_{\mathrm{S}}\). Calculation of \(\bar{E}_{\mathrm{S}}\) is discussed in the following subsection.

2.3 Calculation of the streaming electric field \(E_{\mathrm{S}}\)

To obtain \(E_{\mathrm{S}}\), we consider that the net ionic current (per unit width) i is equal to zero, i.e.

$$\begin{aligned} i=2e\int _{-h}^{0} \left( u_+n_+ - u_-n_- + u_{\mathrm{H}^+}n_{\mathrm{H}^+}-u_{\mathrm{OH}^-}n_{\mathrm{OH}^-}\right) dy = 0, \end{aligned}$$
(18)

where \(u_i\) (\(i=\pm ,\hbox {H}^+,{\mathrm{OH}}^-\)) is the ion migration velocity, expressed as:

$$\begin{aligned} u_i=u+\frac{ez_iE_{\mathrm{S}}}{f_i}. \end{aligned}$$
(19)

Here, \(f_i\) is the ionic friction coefficient for ion i. In this formulation, we do not care about the nanochannel diffusion current (Chien et al. 2007). The main reason is that nanochannel diffusion current is typically an unsteady phenomenon, whereas the streaming potential and the conduction and the streaming (or advection) currents who balance to produce the streaming potential are necessarily a steady state phenomenon. In other words, at steady state, there will be no axial gradient of electrostatic potential or ion concentration; accordingly, diffusion current is not important for the scenario when a streaming potential has been established (which in turn indicates that a steady state has been attained in the nanochannel). Of course, one can always do an unsteady calculation and provide the diffusion current in such PE-grafted nanochannels; however, to do that, we shall have to first solve a problem of ion transport in the presence of an externally applied axial electric field (the presence of such an electric field will imply that there is an axial gradient of the electrostatic potential, generating the diffusion current) in such PE-grafted nanochannels; however, as already stated, this is strictly an unsteady problem that should be addressed in a separate study and has no connection with the present calculation of steady state streaming potential, conduction and advection currents.

Using Eqs. (7, 8, 9, 19) in Eq. (18), we finally obtain the dimensionless streaming electric field as:

$$\begin{aligned}&\bar{E}_{\mathrm{S}}=\frac{\int _{-1}^{0}\bar{u}\left[ -\exp (-\bar{\psi })+(1+\bar{n}_{\mathrm{H}^+,\infty })\exp (\bar{\psi })-\bar{n}_{\mathrm{H}^+}+(\bar{n}_{\mathrm{OH}^-,\infty })\exp (\bar{\psi })\right] d\bar{y}}{u_r\int _{-1}^{0}[R_+ \exp (-\bar{\psi })+R_- (1+\bar{n}_{\mathrm{H}^+,\infty })\exp (\bar{\psi }) + R_{\mathrm{H}^+}\bar{n}_{\mathrm{H}^+}+R_{\mathrm{OH}^-}(\bar{n}_{\mathrm{OH}^-,\infty })\exp (\bar{\psi })]d\bar{y}}, \end{aligned}$$
(20)

where \(R_i=\frac{e^2z_i^2\eta }{\epsilon _0 \epsilon _r k_B T f_i}\) is a dimensionless parameter, often interpreted as the inverse of the ionic Peclet number (Chakraborty and Das 2008). Please note that for the case where the electrolyte ion number density (\(n_\infty\)) is much larger than the number density of \(\hbox {H}^+\) and \({\mathrm{OH}}^-\) ions (i.e. \(\bar{n}_{\mathrm{H}^+} = \frac{n_{\mathrm{H}^+}}{n_{\infty }}\ll 1\), \(\bar{n}_{\mathrm{H}^+,\infty } = \frac{n_{\mathrm{H}^+,\infty }}{n_{\infty }}\ll 1\), and \(\bar{n}_{\mathrm{OH}^-,\infty }=\frac{n_{\mathrm{OH}^-,\infty }}{n_\infty }\ll 1\)), Eq. (20) reduces to:

$$\begin{aligned}&\bar{E}_{\mathrm{S}}=\frac{2}{u_r}\frac{\int _{-1}^0\bar{u}\sinh {(\bar{\psi })}d\bar{y}}{R_+\int _{-1}^0\exp {(-\bar{\psi })}d\bar{y}+R_-\int _{-1}^0\exp {(\bar{\psi })}d\bar{y}}. \end{aligned}$$
(21)

We have obtained this exact same form of the streaming potential in our previous paper (Chen and Das 2015d), where we did not consider the effect of the \(\hbox {H}^+\) and \({\mathrm{OH}}^-\) ions.

Since we do not have an explicit expression for \(\bar{u}\), Eq. (20) will imply that in order to obtain the velocity field \(\bar{u}\) by using Eq. (16), one needs to solve an integro-differential equation in \(\bar{u}\). In other words, since \(\bar{E}_{\mathrm{S}}\) appearing in Eq. (16) is expressed by using Eq. (20), the result is an integro-differential equation in \(\bar{u}\). We solved this integro-differential equation to obtain the streaming potential in one of our recent studies (Chen and Das 2015d); in that study (Chen and Das 2015d), we computed the streaming electric field in a PE-grafted nanochannel with large constant charge densities (large enough to invalidate the use of Debye–Hückel linearization). In the present study, we address a much more complete problem, where this charge density is assumed to be pH dependent, which in turn necessitates consideration of \(\hbox {H}^+\) and \({\mathrm{OH}}^-\) ions in the EDL ion distribution and enforces a particular distribution of the chargeable monomers of the PE molecule. It is worthwhile to note here that solution of such integro-differential equation is necessitated by the fact that it is not possible to express \(\bar{u}\) as an explicit combination of the pressure gradient and the electrostatic potential distribution \(\bar{\psi }\), while such explicit formulation is standard for nanochannels without the PE grafting (Chakraborty and Das 2008; Das and Chakraborty 2009, 2010; Das et al. 2009); for nanochannels with PE grafting, it is possible only for the special case of PE with constant pH-independent small charge densities (which allows the use of Debye–Hückel linearization Chanda et al. 2014).

This integro-differential equation is solved numerically in the presence of the boundary conditions expressed in Eq. (17). This numerical treatment requires application of a suitable iteration procedure; the starting guess profile of the iteration is typically the \(\bar{u}\) profile obtained for the analytical case in our previous study (Chanda et al. 2014). Once \(\bar{u}\) has been obtained by solving this integro-differential equation, we can use Eq. (20) to obtain \(\bar{E}_{\mathrm{S}}\), given the fact that we already know the distribution of \(\bar{\psi }\) and \(\bar{n}_{\mathrm{H}^+}\).

Fig. 2
figure 2

Transverse variation of a dimensionless electrostatic potential \(\bar{\psi }\) and b dimensionless velocity field \(\bar{u}\) for different values of \(\hbox {pK}_{\mathrm{a}}\) and \(\hbox {pH}_\infty\). Variation of c dimensionless streaming electric field \(\bar{E}_{\mathrm{S}}\) and d electrochemomechanical energy conversion efficiency \(\xi\) with \(\hbox {pH}_\infty\) for different values of \(\hbox {pK}_{\mathrm{a}}\). For all plots, we use \(h=100\,\hbox {nm}\), \(c_\infty = 10^{-4}\,\hbox {M}\) (note \(n_\infty =10^3N_{\mathrm{A}}c_\infty\), where \(N_{\mathrm{A}}\) is the Avogadro number), \(\bar{d}=0.3\), \(\gamma _a=10^{-4}\,\hbox {M}\), \(u_r=1\), \(\alpha =1\), \(R_i=1\), and \(Na^3\sigma /d=1\)

Full size image
Fig. 3
figure 3

Transverse variation of a dimensionless electrostatic potential \(\bar{\psi }\) and b dimensionless velocity field \(\bar{u}\) for different values of \(c_\infty\) and \(\hbox {pH}_\infty\). Variation of c dimensionless streaming electric field \(\bar{E}_{\mathrm{S}}\) and d electrochemomechanical energy conversion efficiency \(\xi\) with \(\hbox {pH}_\infty\) for different values of \(c_\infty\). For all plots, we use \(h=100\,\hbox {nm}\), \(\bar{d}=0.3\), \(\gamma _a=10^{-4}\,\hbox {M}\), \(u_r=1\), \(\alpha =1\), \(\hbox {pK}_{\mathrm{a}}=4\), \(R_i=1\), and \(Na^3\sigma /d=1\)

Full size image

2.4 Calculation of efficiency of the electrochemomechanical energy conversion

Generation of the nanofluidic streaming current (\(i_{\mathrm{S}}\)) and the streaming electric field (\(E_{\mathrm{S}}\)) is a process of nanoscale electrochemomechanical energy conversion (Daiguji et al. 2004; Heyden et al. 2006), since the mechanical energy of the pressure-driven flow and the chemical energy of the EDL are converted to the electrical energy associated with the generation of \(i_{\mathrm{S}}\) and \(E_{\mathrm{S}}\). This efficiency \(\xi\) of this energy conversion can be expressed as:

$$\begin{aligned} \xi =\frac{P_{\mathrm{out}}}{P_{\mathrm{in}}}. \end{aligned}$$
(22)

Here, \(P_{\mathrm{in}}\) and \(P_{\mathrm{out}}\) are the input and the output powers (per unit area), expressed as:

$$\begin{aligned}&P_{\mathrm{out}}=\frac{1}{4}i_{\mathrm{S}} E_{\mathrm{S}}, \\&P_{\mathrm{in}}=\left| -\frac{\hbox {d}p}{\hbox {d}x}\right| Q_{\mathrm{in}}. \end{aligned}$$
(23)

Here,

$$\begin{aligned} i_{\mathrm{S}}= 2e \int _{-h}^0 u \left( n_+ - n_- +n_{\mathrm{H}^+ } -n_{\mathrm{OH}^-}\right) dy, \end{aligned}$$
(24)

and \(Q_{in}\) is the input volume flow rate per unit width, expressed as:

$$\begin{aligned} Q_{\mathrm{in}}=2\int _{-h}^0 u_p dy, \end{aligned}$$
(25)

Here, \(u_p\) is the pure pressure-driven velocity field expressed as \(u_p=-\frac{\hbox {d}p}{\hbox {d}x}\frac{h^2}{2\eta }\left( 1-\frac{y^2}{h^2}\right)\). Using Eqs. (7, 8, 9, 23, 24, 25) in Eq. (22), we can finally express \(\xi\) as:

$$\begin{aligned} \xi =\frac{u_r\int _{-1}^0 \bar{u} \left[ \exp (-\bar{\psi }) - (1+\bar{n}_{\mathrm{H}^+,\infty })\exp (\bar{\psi }) +\bar{n}_{\mathrm{H}^+} -(\bar{n}_{\mathrm{OH}^-,\infty }) \exp (\bar{\psi })\right] d\bar{y}}{8 \bar{\lambda }^2 \int _{-1}^0 \bar{u}_p d \bar{y}} \end{aligned}$$
(26)

where \(\bar{u}_p=u_p/u_{p,0}\). It is worthwhile to note here that this efficiency is calculated based on the actual input flow rate. There are examples, where the efficiency has been calculated based on the reduced flow rate, caused by the generation of the streaming-electric-field-induced electroosmotic transport that opposes the pressure-driven transport (Bandopadhyay et al. 2013; Bandopadhyay and Chakraborty 2012). Such a consideration leads to an artificial increase in the efficiency, which is incorrect. Rather, this efficiency should always be calculated based on the input power and the input velocity as has been done by Daiguji et al. (2004) as well as our previous study (Chanda et al. 2014).

Fig. 4
figure 4

Transverse variation of a dimensionless electrostatic potential \(\bar{\psi }\) and b dimensionless velocity field \(\bar{u}\) for different values of \(\bar{d}=d/h\) and \(\hbox {pH}_\infty\). Variation of c dimensionless streaming electric field \(\bar{E}_{\mathrm{S}}\) and d electrochemomechanical energy conversion efficiency \(\xi\) with \(\hbox {pH}_\infty\) for different values of \(\bar{d}=d/h\). For all plots, we use \(h=100\,\hbox {nm}\), \(c_\infty =10^{-4}~\hbox {M}\), \(\gamma _a=10^{-4}\,\hbox {M}\), \(u_r=1\), \(\alpha =1\), \(\hbox {pK}_{\mathrm{a}}=4\), \(R_i=1\), and \(Na^3\sigma /d=1\)

Full size image

3 Results

Figure 2 demonstrates the pH and the \(\hbox {pK}_{\mathrm{a}}\) dependences of the dimensionless streaming electric field (\(\bar{E}_{\mathrm{S}}\)) and the energy conversion efficiency \(\xi\). Prior to discussing these dependences, we first discuss the corresponding dependence of the transverse variation of the dimensionless electrostatic potential (\(\bar{\psi }\)) on these parameters. We have provided this result on electrostatic potential in our previous studies (Chen and Das 2015a, c); we repeat it here in order to better explain the nature of variation of \(\bar{E}_{\mathrm{S}}\) and \(\xi\). Enhancement of the bulk pH (or \(\hbox {pH}_\infty\)), which implies a decrease in the concentration of the \(\hbox {H}^+\) ions in the bulk, will favour the forward reaction of the reaction \(\hbox {HA}\leftrightarrow \hbox {H}^++\hbox {A}^-\); consequently, there will be an enhanced ionization and hence enhanced charging of a grafted PE molecule. This enhanced charging ensures an enhanced magnitude of the EDL electrostatic potential; consequently, for larger \(\hbox {pH}_\infty\), \(\bar{\psi }\) demonstrates a more enhanced magnitude at a given transverse location and for a given \(\hbox {pK}_{\mathrm{a}}\) (see Fig. 2a). On the contrary, an enhanced \(\hbox {pK}_{\mathrm{a}}\) will imply a smaller value of the ionization constant \(K_a\) (of the acid \(\hbox {HA}\)), which in turn will lower the concentration of \(\hbox {A}^-\) and hence lower the charging of the PE layer. As a result, for larger \(\hbox {pK}_{\mathrm{a}}\), \(\bar{\psi }\) shows a reduced value for a given \(\hbox {pH}_\infty\) and for a given transverse location (see Fig. 2a). It is worthwhile to note that there is a finite electrostatic potential at the channel centreline for all values of \(\hbox {pH}_\infty\) and d/h. This stems from the fact that the corresponding EDL thickness (\(\lambda\)) is \(\sim 30~nm\) (since \(c_\infty =10^{-4}\)); hence \(\lambda /h\approx 1/3\), ensuring significant (though weak) value of the electrostatic potential at the channel centreline. For weak values of electrostatic potentials (\(|\bar{\psi }|<1\) or \(|\bar{\psi }|\sim 1\)), an increase in the electrostatic potential enhances the streaming current. This stems from the fact that for such ranges of the electrostatic potential, an increase in the counterion concentration caused by an increase in the magnitude of the electrostatic potential invariably increases the streaming electric field (Chakraborty and Das 2008; Das and Chakraborty 2009). For larger values of the electrostatic potentials (\(|\bar{\psi }|\gg 1\)), the enhancement of counterion concentration (on account of the increase in the electrostatic potential) may lead to a more pronounced enhancement of the conduction current, which in turn may decrease the streaming electric field (Chakraborty and Das 2008; Das and Chakraborty 2009). In the present case, \(|\bar{\psi }|\) is substantially small; as a consequence, an increase in \(|\bar{\psi }|\) increases \(\bar{E}_{\mathrm{S}}\). Hence, we witness an increase in \(\bar{E}_{\mathrm{S}}\) with an increase in \(\hbox {pH}_\infty\) and a decrease in \(\hbox {pK}_{\mathrm{a}}\) (see Fig. 2c). Therefore, enhancement of \(\bar{E}_{\mathrm{S}}\) with \(\hbox {pH}_\infty\) is caused by an enhanced charging (for reasons already discussed) of the PE layer and an equivalent enhanced magnitude of the electrostatic potential. Of course, such \(\hbox {pH}_\infty\)-dependent enhancement in \(\bar{E}_{\mathrm{S}}\) is witnessed only when the corresponding \(\hbox {H}^+\) ion concentration is comparable to the corresponding electrolyte ion concentration; therefore, we find (see Fig. 2c) at larger \(\hbox {pH}_\infty\) (=6) \(\bar{E}_{\mathrm{S}}\) starts to saturate and shows relatively weak increase with \(\hbox {pH}_\infty\). Enhanced magnitude of the streaming electric field will lead to a larger magnitude of the electroosmotic transport opposing the pressure-driven flow field; consequently, the magnitude of \(\bar{u}\) is smaller at a given transverse location for a larger \(\hbox {pH}_\infty\) and smaller \(\hbox {pK}_{\mathrm{a}}\) (see Fig.  2b). Please note that here \(\bar{u}=u/u_{p,0}<0\) implies a positive value of u, since \(u_{p,0}\) is negative [see below Eq. (16) for the definition of \(u_{p,0}\)]. This is commensurate with \(\bar{E}_{\mathrm{S}}=E_{\mathrm{S}}/E_0>0\), which implies \(E_{\mathrm{S}}<0\), since \(E_0<0\) [see below Eq. (16) for the definition of \(E_0\)]. Finally, in Fig. 2d, we show the variation of the electrochemomechanical energy conversion efficiency \(\xi\); the enhancement of \(\xi\) with an increase in \(\hbox {pH}_\infty\) and a decrease in \(\hbox {pK}_{\mathrm{a}}\) follows directly from the corresponding variation of the streaming current and the streaming electric field.

Figure 3 provides the pH and the electrolyte concentration (\(c_\infty\)) dependence of the \(\bar{E}_{\mathrm{S}}\) and \(\xi\). The pH dependence has already been discussed in detail. Weaker concentration of the electrolyte salt leads to a more enhanced value of the EDL thickness \(\lambda\), since \(\lambda \propto 1/\sqrt{c_\infty }\). Enhanced \(\lambda\) will imply a weaker screening of the EDL electrostatic potential (on either side of the PE layer–EDL interface), thereby ensuring an enhanced magnitude of \(\bar{\psi }\) for a smaller \(c_\infty\) value (see Fig.  3a). This also implies a much larger magnitude of the channel centreline electrostatic potential for smaller \(c_\infty\). Consequently, following the discussions provided for Fig. 2, we may infer that an enhanced \(c_\infty\) leads to an enhanced \(\bar{E}_{\mathrm{S}}\) (for a given \(\hbox {pH}_\infty\), see Fig. 3c), a weakened magnitude of \(\bar{u}\) (for a given transverse location and for a given \(\hbox {pH}_\infty\), see Fig. 3b), and an enhanced electrochemomechanical energy conversion efficiency (for a given \(\hbox {pH}_\infty\), see Fig.  3d).

Finally, Fig. 4 shows the effect of the pH and the PE layer thickness on \(\bar{E}_{\mathrm{S}}\) and \(\xi\). Enhanced \(\bar{d}=d/h\) (or PE layer thickness) will imply larger number of the PE charges, which in turn will lead to a larger value of \(\bar{\psi }\) (see Fig. 4a). Such dependence of \(\bar{\psi }\) on \(\bar{d}\) has previously been reported by us (Chanda et al. 2014). Such enhanced \(\bar{\psi }\) ensures that an increase in \(\bar{d}\) enhances \(\bar{E}_{\mathrm{S}}\) (for a given \(\hbox {pH}_\infty\), see Fig. 4c), lowers the magnitude of \(\bar{u}\) (for a given transverse location and for a given \(\hbox {pH}_\infty\), see Fig.  4b), and increases the electrochemomechanical energy conversion efficiency (for a given \(\hbox {pH}_\infty\), see Fig. 4d).

Comparison of Figs. 2, 3 and 4 will allow selection of the appropriate parameter space that will enable electrochemomechanical energy conversion of maximum efficiency. We find that we obtain an efficiency value of around 4–5 % for optimal choices of system parameters (e.g. please see Fig. 4d). This is a significantly high number given the 3 % efficiency value reported in pioneering experiments of Daiguji et al. (2004). We shall like to mention here that our results should not be compared with the several theoretical results that report an efficiency of nearly 100 % (Bandopadhyay et al. 2013; Bandopadhyay and Chakraborty 2012). The reason is that these high efficiency values result from erroneous definition of the input power, where the input velocity is considered as the velocity reduced due to the impact of the streaming electric field.

Our theoretical calculations proposed here can be used to show that by pumping a weak acid electrolyte solution (\(c_\infty =10^{-5} \hbox {M}\) and pH = 6) with 5 bar pressure continuously into PE-grafted nanochannels (with the channel height of \(h=100\,\hbox {nm}\)) that constitute a 1 cm \(\times\) 1 cm porous material (with the thickness of 1mm and a high porosity ratio of 60 %), a 5 watt electrical power (sufficient to light up an LED lamp) can be generated, provided the supposed technical issues related to, for example, electrode polarization and pressure resistance can be overcome.

4 Discussion

4.1 Comparison with experimental results

We compare our theoretical predictions with the experimental results of Duval et al. (2009), Zimmermann et al. (2014), and Zimmermann et al. (2013). These comparisons also provide a validity of our proposed theoretical model. Comparisons are made for the variation of the streaming current (\(i_{\mathrm{S}}\)) as a function of the pH and the salt concentration. While we do not attempt a direct quantitative comparison, we do find the exact same trend in the theoretical prediction of \(i_{\mathrm{S}}\) as compared to the experimental findings. For example, our theory predicts first an increase and then a saturation in \(i_{\mathrm{S}}\) with an increase in salt concentration for a given pH and given a \(\hbox {pK}_{\mathrm{a}}\) (see Fig. 5a). Exactly similar findings are obtained from the experiments on streaming currents conducted at the interfaces grafted with poly(ethylene oxide) or PEO brushes (see Fig. 2a in Ref. Zimmermann et al. 2014) and a hydrogel layer (see Fig. 6a in Ref. Duval et al. 2009). Our theory also predicts a monotonic increase in the magnitude of the negative value of \(i_{\mathrm{S}}\) with pH (pH always in the acidic range and not too small) (see Fig. 5b). Qualitatively exactly similar results are obtained from experiments on interfaces grafted with PEO brushes (see Fig. 2b in Ref. Zimmermann et al. 2014).

Fig. 5
figure 5

Variation of the dimensionless streaming current with a \(c_\infty\) for different values of \(c_\infty\) and b \(c_\infty\) for different values of \(\hbox {pH}_\infty\). Other parameters are same as that of Fig. 3. These results, obtained using our theoretical model, allow to compare our theoretical predictions with the existing experiments

Full size image

4.2 Comparison with findings of existing theoretical studies

It is worthwhile to compare the findings of this study in the light of the results from the existing theoretical studies (Duval et al. 2009, 2011a, b; Zimmermann et al. 2010, 2013, 2014). There are several aspects in which this study and its results are distinct in comparison with that of the existing similar theoretical calculations. First and foremost, the analysis in this study is unique in the sense that it solves an integro-differential equation to obtain the nanochannel streaming potential. Such an approach has only been used once ever before in one of our previous studies (Chen and Das 2015d). Secondly, the calculations are provided for nanochannels; therefore, PE brushes are nanoconfined PE brushes, which are unlike the PE brushes grafted to single interfaces (Zimmermann et al. 2014) or surfaces of microchannels (Duval et al. 2009, 2011a; Zimmermann et al. 2010). Thirdly, we provide results that depict the competitive interplay between pH, \(\hbox {pK}_{\mathrm{a}}\), ion concentration, and PE brush thickness relative to the nanoconfinement in the overall variation of the streaming potential. Such explicit roles of \(\hbox {pK}_{\mathrm{a}}\) and relative thickness of the PE brushes have rarely been identified in the context of nanoscale streaming potential in soft nanochannels. Finally, we provide the energy conversion efficiency in such pH-responsive soft nanochannels; such a thing has also never been reported previously.

4.3 Selection of the thickness of the PE brush layer: choice of cubic monomer profile

One of the key issues associated with the PE or polymer brushes is the selection of the appropriate monomer distribution. This distribution depends on the nature of the polymer or PE chain, the nature of the solvent, the concentration of the polymer in the solvent, etc. Nature of the polymer chain dictates whether or not one can neglect the chain correlations. For cases where such correlations cannot be neglected, a self-consistent field theory (SCFT) has been proposed for uncharged polymer chains yielding quadratic profile for the monomer distribution for monodisperse chains (Milner et al. 1988a, b) and a deviation from this quadratic profile for poly-disperse chains (with the poly-dispersity being triggered by the presence of heterogeneities in the chain lengths Milner et al. 1989; Zimmermann et al. 2014). While this self-consistent field theory is the most appropriate representation of the brush monomer profile, it suffers from a key limitation. This limitation is that either of these two profiles (quadratic or the profile that is slightly deviated from it) is based on the assumption that the correlations between the polymer chain segments are represented as binary collisions. Therefore, this simplistic profile is not an appropriate representation of the case where the polymer contains backbone charges (i.e. it is a PE), triggering an EDL-mediated interaction between the segments. In fact, it is rather recently that there have been attempts to study the profiles of PE brushes using this SCFT framework with appropriate consideration of the PE charges and the resulting EDL ion distribution (Witte et al. 2009; Wang et al. 2004; Quan et al. 2014; Wang and Tong 2014). However, barring only one study by Witte et al. (2009) virtually none of these studies account for pH-dependent charge density of the PE brushes. Also this study by Witte et al. does not provide the explicit variation of the monomer density profile as a function of pH, neither does it account for the pH-dependent charging explicitly in expressing the electrostatic contribution of the PE charge in the overall Hamiltonian. These limitations of the SCFT can be typically associated with the extreme complexities of the governing equations that necessitate employing an extremely tedious numerical approach, often forbidding the incorporation of novel physical issues associated with the nature of charging of the PE.

A much more tractable and simplified approach involves cases where one disregards the correlation effects between the segments of the PE brush. Such a situation is possible if one considers the PE brushes as Gaussian chain (where there are no chain–chain correlations) or operates in a specified phase space where these correlations can be neglected even for real chains (Milner et al. 1988a; Dolan and Edwards 1974, 1975). For such cases, an analytically tractable mean-field approach, often known as the strong stretching theory or SST, is proposed by the works of Zhulina et al. (1989), Zhulina and Borisov (1997), Zhulina and Borisov (2011). This approach proposes a monomer density profile of the form \(\sqrt{A+By^2}+C\) for uncharged polymer brushes (Zhulina et al. 1989). Of course, this approach allows for a much easy incorporation of the PE charge, effect of pH dependence of this charge, and the resulting distribution of the electrolyte ions forming the EDL. Typical monomer density profiles are combinations of quadratic and exponential profiles (Zhulina and Borisov 2011). A simplified version of this model by Zhulina and co-workers is the well-known Scheutjens–Fleer model (Israels et al. 1994; Lyatskaya et al. 1995) that substantially simplifies the description of the EDL electrostatics by resorting to replace the Poisson–Boltzmann description by a description based on the net electroneutrality of the system. Therefore, the expected state of the art in modelling the monomer distribution of grafted PE brushes is either the more rigorous (and only tractable numerically) SCFT for PE chains (that may not be suitable to unravel the impact of pH-dependent PE charge density on the monomer profile), or the more tractable SST that seems more apt to incorporate the specifics of pH dependence of PE charge density.

Given that we are interested to analyse the case of PE brushes with pH-dependent charge density, it is more logical to focus on the SST of Zhulina and co-workers, since this is the only existing mean-field theory that has so far been able to quantify the effect of pH-dependent charge density on the overall monomer distribution (Zhulina and Borisov 2011). In our recent study (Chen and Das 2015a), we discovered a major issue with the SST in the context of modelling the electrostatics for the case of PE brushes with pH-dependent charge density. It stemmed from the fact that the hydrogen ion distribution was always assumed to obey Boltzmann distribution both inside and outside the PE layer. As we demonstrated in theory section as well as in the detailed derivation in “Appendix” section, such a consideration is incorrect and provides an energetically inconsistent picture, since the free energy is not minimized with respect to \(\hbox {H}^+\) ion concentration. We did this minimization with respect to \(\hbox {H}^+\) ion concentration; these new equations are the appropriate free energy representation of the problem, since the free energy has been minimized with respect to all the governing variables. Now the resulting equations are such that they need to be coupled with a particular kind of monomer distribution \(\varphi (\bar{y})\) that simultaneously ensures the four conditions illustrated in Eqs. (12, 13); this is possible with the non-unique cubic monomer profile.

There is a major assumption in our analysis (which yields this cubic monomeric distribution). This assumption is that the PE thickness is independent of the electrostatic effects. This is possible when \(\Delta F_{\mathrm{PE},{\mathrm{elec}}}\gg \left( \Delta F_{\mathrm{PE},{\mathrm{ent}}}+\Delta F_{\mathrm{PE},{\mathrm{EV}}}\right)\), or \(\Delta F_{\mathrm{PE},{\mathrm{elec}}}\ll \left( \Delta F_{\mathrm{PE},{\mathrm{ent}}}+\Delta F_{\mathrm{PE},{\mathrm{EV}}}\right)\). Under such conditions (satisfied by \(\sigma \ll 1/(at)\) or \(\sigma \gg 1/(at)\), where \(\sigma\) is the grafting density, a is the PE Kuhn length, t is the PE thickness Chen and Das 2015c), the electrostatic energy of the PE brush and the resulting EDL balances each other, and this in turn dictates the electrostatics of the problem. Therefore, this cubic monomer distribution is the distribution of the chargeable sites of the PE brushes. This implies that if we have a situation where \(\Delta F_{\mathrm{PE},{\mathrm{elec}}}\gg \left( \Delta F_{\mathrm{PE},{\mathrm{ent}}}+\Delta F_{\mathrm{PE},{\mathrm{EV}}}\right)\) or \(\Delta F_{\mathrm{PE},{\mathrm{elec}}}\ll \left( \Delta F_{\mathrm{PE},{\mathrm{ent}}}+\Delta F_{\mathrm{PE},{\mathrm{EV}}}\right)\) and the PE exhibits a pH-dependent charge density, the PE chargeable sites must demonstrate a non-unique cubic distribution. It is evident that this is a simplified approach. A more rigorous approach should necessitate solution of the SST considering the elastic, excluded volume, and electrostatic energy of the PE brush molecule as well as the EDL energy with the consideration of explicit \(\hbox {H}^+\) ions (or in other words, the free energy should be minimized with respect to the \(\hbox {H}^+\) ion number density distribution). Such a formulation is missing in the existing literature, and we plan to take it up in a future problem. Of course, the ultimate calculation should be the SCFT modelling (with finite correlation effects) of the PE brush molecule with explicit consideration of the \(\hbox {H}^+\) ions. Such a step will provide the final answer in the context of the configuration and the monomer distribution of a PE brush with pH-dependent charge density.

5 Conclusion

In this paper, we provide a theory to calculate the streaming electric field and the efficiency of the resulting electrochemomechanical energy conversion in a nanochannel grafted with a PE molecule with pH-dependent charge density. Our analyses, based on appropriate free energy description of the problem as well as solution of a rigorous integro-differential equation, provide new insights into the role of the bulk pH and the \(\hbox {pK}_{\mathrm{a}}\) of the dissociating acid (which charges the PE layer) in the streaming electric field and the energy conversion. We establish that the energy conversion efficiency can be substantially high (~4 to 5 %) for optimum parameter choices; this finding emboldens our previous studies (Chanda et al. 2014; Chen and Das 2015d) and establishes PE-grafted nanochannels as an efficient nanofluidic electrochemomechanical energy converter under most practical conditions.