1 Introduction

Ultrasonic manipulation of particles exploits the acoustic radiation force to provide a contactless handling method for particles suspended in a fluid. It is also referred to as acoustophoresis and allows the handling of a wide range of particle types. The important attribute is the difference in the material properties (density and compressibility) between the particle and the surrounding fluid, creating a scatterer in the fluid. For bulk acoustic wave devices the typical frequency is in the 1 MHz range and μm sized particles are manipulated. Different manipulation strategies and techniques have been published such as particle separation, focusing, concentration, removal, trapping, mixing and moving (Lenshof et al. 2012; Augustsson and Laurell 2012; Evander and Nilsson 2012; Dual et al. 2012). These manipulation techniques are required for particle handling in lab-on-a-chip devices or micrototal analysis systems to realize various kinds of analysis steps.

In combination with the translation of particles due to the acoustic radiation force, the rotational manipulation offers a new controllable degree of freedom for the movement of particles. Therefore the application field can be extended. There is a high demand for controlled alignment and deposition of non-spherical objects such as microwires and nanowires (Bentley et al. 2004). Moreover, the alignment of biological fibers such as collagen is of interest (Lee et al. 2006; Guo and Kaufman 2007). In lab-on-a-chip applications micromotors, stirrers or valves can be realized. Also, there is a growing interest for microassembly techniques (Bogue 2011; Vandaele et al. 2005), where controllable positioning and orientation of objects is needed for the manufacturing of complex 3D microsystems. Herein, a major challenge is the unwanted bonding of objects to neighboring surfaces. Ultrasonic manipulation is well suited as it allows the positioning of objects and provides levitation at the same time. Ultrasonic microassembly is an important application of acoustically actuated microrobotics. Moreover, the long term study of biological cells is an interesting application (Wiklund et al. 2012a) because ultrasonic particle manipulation is well known to be biocompatible (Wiklund 2012). The ability to control the orientation of a cell or cell cluster will help in the investigation of biological processes. For other particle manipulation techniques such as dielectrophoresis (Sun and Morgan 2011; Fan et al. 2005), magnetic (Barbic et al. 2001) or optical (Friese et al. 2001) manipulation the rotation and alignment of objects has been intensively investigated.

There are only a few publications concerning experimental work with the acoustic radiation torque which arises from the acoustic radiation pressure distribution on the surface of a non-spherical particle. The focus of these publications is on the development of composite materials with non-spherical particles, using ultrasonic standing waves for the arrangement and alignment. Brodeur (1991) studied the acoustic layering and reorientation as a function of fiber dimensions for fibers shorter than one fourth of the acoustic wavelength. For the experimental part, paper-making fibers (length 0.2–3 mm) suspended in water and an excitation frequency of 72 kHz were used. Brodeur verified experimentally that acoustic reorientation is a faster process than acoustic displacement and explained the results with a simplified theoretical investigation of the fiber motion. Saito et al. (1998) studied the fabrication of polymer composites by solidification of a particle suspension in ultrasonic standing waves. Experiments were carried out with glass rods (diameter 10 μm) at an excitation frequency of 3 MHz. Yamahira et al. (2000) studied the behavior of polystyrene fibers in a one-dimensional standing wave. The equations of motion for a fiber have been derived by evaluation of the force and torque generated by the radiation pressure, the buoyancy force and the drag force. In a simplified model, the fiber was represented as a chain of small spheres. Experiments were carried out with polystyrene fibers with a diameter of 0.5 mm and lengths between 5 and 20 mm at frequencies of 25 and 46 kHz. The motion of the fiber as well as the influence of the length and position was compared with the simplified model.

Beside the rotation of particles with the acoustic radiation torque, which is the topic of this paper, there exist other acoustic methods for the rotation of particles. The viscous torque is generated by two orthogonal standing waves shifted in phase and the resulting near boundary streaming inside the viscous boundary layer spins an axisymmetric object. This phenomenon has first been observed experimentally by Wang et al. (1977). An analytical solution of the viscous torque on a sphere is given by Lee and Wang (1989) which was extended by Lamprecht et al. (2013) for the case of a rotating sphere including experimental validation. Another example is an acoustic vortex beam (Bessel vortex beam), carrying orbital angular momentum along the propagation direction which can be transferred to a particle depending on the object scattering and absorbing properties (Silva et al. 2012; Anhäuser et al. 2012). Surface acoustic waves (SAW) have been used for the actuation of motors for Lab-on-a-chip and micro–electro–mechanical systems (MEMS) applications (Zhang and Cheng 2010; Tjeung et al. 2011). Also, an acoustic needle was used to rotate trapped particles around its tip (Hu et al. 2005; Zhang et al. 2008).

This paper discusses in Sect. 2 the acoustic radiation torque acting on a non-spherical particle and a finite element model for the simulation of the torque is presented. The simulation results for a microfiber and the influence of different parameters such as frequency, fiber size and position are evaluated in Sect. 2.2. The rotational motion of a fiber and the parameters which define the maximal angular velocity are presented in Sect. 2.3. Beside the alignment, the acoustic radiation torque can be used for a continuous rotation of objects. Different approaches to experimentally realize a rotation of non-spherical particles are developed and discussed in Sect. 3. The first rotation technique is based on successively changing the orientation of the standing wave. Three additional methods for a continuous rotation are presented. They rely on the modulation of one single parameter such as amplitude, phase or frequency.The experimental investigation of the different rotation methods can be found in Sect. 4.

2 Acoustic radiation torque

A spherical particle experiences an acoustic radiation force in an ultrasonic standing wave. A non-spherical particle is additionally subjected to an acoustic radiation torque. Over time, this leads to a change of the angular orientation of the particle. The acoustic radiation torque is a nonlinear acoustic effect caused by the angular momentum transfer from an acoustic field to a scatterer (Fan et al. 2008). Maidanik (1958) published a theory about the torque due to acoustic radiation pressure. This theory was used to derive the torque on a plane disk of arbitrary shape excited by a plane progressive wave. Fan et al. (2008) derived the acoustic radiation torque on an irregularly shaped scatterer for an arbitrary sound field. However, surface integrals involved can only be evaluated analytically for a limited number of situations, e.g., a spheroid in a plane standing-wave field. Additionally, the scatterer has to be small compared to the wavelength of the sound field. An analytical solution for a fiber (long cylinder) is not feasible. The above theories are restricted to the case of objects immersed in an inviscid fluid. Nevertheless, in practice they are useful approximations, when the streaming is weak and the viscous boundary layer is small compared to the object size (Zhang and Marston 2011).

Hasheminejad and Sanaei (2007) derived an exact expression for the acoustic radiation torque and force on infinite elastic cylinder with elliptic cross section in 2D. An analytical expression with an infinite series of Mathieu functions was developed. The influence of the ellipticity and the angle of wave incidence has been investigated on a stainless steel cylinder immersed in water. Wang and Dual (2010) also derived an analytical solution for rigid cylinders with elliptical cross section based on Mathieu functions. This analytical model has been used to validate the finite element simulation for the acoustic radiation torque in Sect. 2.1.

Brodeur (1991) derived for his study of paper fibers a rough estimation for the torque on a cylinder in a 1D standing wave. Based on Putterman et al. (1989) the torque for a non-spherical object in a standing wave should be proportional to its volume and the mean acoustic energy density. Another rough estimation for the torque on a fiber is given by Yamahira et al. (2000), who represented the fiber as a chain of small spheres and uses the expression of the acoustic radiation pressure on a small sphere from Yosioka and Kawasima (1955). The interaction between neighboring spheres was not considered.

2.1 Numerical Simulation of acoustic radiation torque

The analytical solutions are restricted to cases with a simple scatterer geometry and a simple acoustic field. This is the motivation for a numerical simulation of the acoustic radiation torque on a non-spherical object such as a fiber. In general, any kind of particle with no restrictions concerning the size, shape and material can be modeled at any position and orientation in an arbitrary acoustic field. The viscosity of the fluid is neglected here, which is valid when the viscous boundary layer is small compared to the object size. Also, the influence of a nearby wall (Dual et al. 2012) or another particle can be considered when the viscous boundary layer is small compared to the distance.

For the calculation of the torque, the scattered acoustic field has to be determined based on a given background field (incident field). The acoustic radiation torque \(\mathbf{T}^{\mathrm{rad}}\) on an object can be calculated as the surface integral of time averaged second-order pressure and the momentum flux tensor at the object surface \(S_0\) (Dual et al. 2012):

$$\begin{aligned} \mathbf{T}^{\mathrm{rad}} = - \int \limits _{S_0} {\mathrm{d}}S \bigg \{ {\mathbf{r}} \times \Big [ \Big ( \frac{1}{2} \frac{1}{\rho _0 c_0^2} \left\langle p_1^2\right\rangle - \frac{1}{2} \rho _0 \left\langle \mathbf{v}_1^2 \right\rangle \Big ) \mathbf{n} + \rho _0 \left\langle ( \mathbf{n}\cdot \mathbf{v}_1 ) \mathbf{v}_1 \right\rangle \Big ] \bigg \} \end{aligned}$$
(1)

where \(\rho _0, c_0\) are the fluid density and speed of sound, respectively. The position vector r points from the center of mass to a point on the surface of the scatterer and n is the outward normal vector of the scatterer surface. The time averaged squared first order pressure and velocity field are denoted by \(\left\langle p_1^2 \right\rangle\) and \(\left\langle \mathbf{v}_{1}^{2} \right\rangle\), respectively. The calculation was done numerically with the finite element software COMSOL Multiphysics 4.2.

The scattering object (the fiber) is placed in the middle of the model with its centroid at the origin of the coordinate system. The fiber is modeled as a linear elastic solid using the solid mechanics module. In the solid domain, the dependent variable is the displacement field u and the time harmonic wave equation for a linear elastic continuum is solved for the given material parameters and boundary conditions. The boundary condition on the surface of the fiber is a load from the fluid, implemented as \(-p \mathbf{n}\), where p is the pressure from the acoustic domain.

The surrounding of the fiber (the fluid) is modeled with the pressure acoustics module. The dependent variable in the acoustic domain is the pressure p and the Helmholtz equation is solved for the given material parameters and boundary conditions. The fluid is affected by the solid motion, modeled as acceleration continuity in surface normal direction. The outer boundary of the fluid is a perfectly matched layer (PML) which absorbs the wave, avoiding any reflections of the scattered field back into the acoustic domain. An important part is the definition of the acoustic background field (incident pressure field). The use of a background pressure field \(p_{\mathrm{b}}\) is very convenient as it allows the creation of arbitrary acoustic fields and also defines the position of the fiber inside the acoustic field.

Parameter studies have been performed with numerical simulations. Depending on the aspect ratio of the fiber or the size of the parameter set, 3D or 2D simulations have been chosen in order to keep the computational time within reasonable limits. For the 3D model, about \(5 \times 10^{5}\) tetrahedral elements of quadratic order have been used to resolve the field quantities. A time harmonic analysis for a certain frequency f was performed. For the calculation of the torque, the values of the pressure p and velocity v are needed to perform the integration along the fiber surface. The equations for the acoustic radiation torque (Eq. 1) can be implemented in COMSOL whereas a line integration or a surface integration is evaluated for the 2D or 3D case, respectively. Additionally, the acoustic radiation force can be calculated by deleting the position vector r in Eq. 1.

The validation of the model was done with an analytical solution for the torque on a rigid ellipse in a one-dimensional standing wave (Wang and Dual 2010). The agreement between the analytical solution and the simulation was remarkable with a relative error below 0.01 % for the tested frequency range between 10 kHz and 20 MHz.

2.2 Results of the numerical simulation for a glass fiber

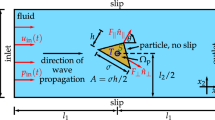
The FEM simulation has been used to evaluate the behavior of a non-spherical particle, in particular a glass fiber as it was used in the experimental parts of this study. The standard model parameters of the elastic glass fiber used later are: fiber length \(l_{\mathrm{f}} = 200\,\upmu \hbox {m}\), diameter \(d_{\mathrm{f}} = 15\,\upmu \hbox {m}\), Young’s modulus \(E_{\mathrm{f}} = 73\,\hbox {GPa}\), Poisson’s ratio \(\nu _{\mathrm{f}} = 0.18\) and density \(\rho _{\mathrm{f}} = 2,600\,\hbox {kg/m}^{3}\). The fiber was assumed to have spherical ends (radius \(d_{\mathrm{f}}/2\)) in order to avoid sharp edges where a very fine discretization would be necessary otherwise. The fiber is surrounded by water (\(\rho _0 =998\,\hbox {kg/m}^{3}, c_0 = 1,481\,\hbox {m/s}\)) and positioned at an angle \(\alpha = 45^{\circ }\) in the pressure node of a standing wave in x-direction with an amplitude \(P_{\mathrm{a}}\) of \(1 \times 10^5\,\hbox {Pa}\) (Fig. 1). The orientation of the nodal pressure line is given by the angle \(\beta = 90^{\circ }\) which spans between the nodal pressure line and the x-axis. The frequency is \(f = 1 \hbox {MHz}\) and the corresponding wavelength in the fluid is \(\lambda = 1,481\,\upmu \hbox {m}\). Different parameters have been varied and the torque was analyzed.

2.2.1 Frequency

The influence of the frequency on the torque will be discussed first. The frequency was varied between 10 kHz and 10 MHz. The results can be seen in Fig. 1. The red dashed line is representing a glass fiber. The other lines are for various densities which is discussed below.

For the glass fiber in the frequency range below 500 kHz, where the wavelength is at least ten times larger than the fiber length, the torque stays nearly constant at \(1 \times 10^{-14}\,\hbox {Nm}\). This characteristic is unexpected as the acoustic radiation force on a compressible circular cylinder is proportional to the frequency for the long wavelength approximation (Wei et al. 2004). The investigation of particle trajectories at various frequency ranges might be a relevant topic. Brodeur (1991) showed that the reorientation is faster than the displacement of a fiber at a frequency of 72 kHz. As the acoustic radiation force decreases with decreasing frequency, the dynamic behavior of a fiber in the kHz range might differ from the MHz range concerning the timescale of the translation and reorientation.

For frequencies above 1 MHz the ratio of wavelength \(\lambda\) to the length \(l_{\mathrm{f}}^{*}\) becomes relevant, where \(l_{\mathrm{f}}^{*}\) is the projected length of the glass fiber on the wave vector (x-direction). There is a local maximum of the torque at \(l_{\mathrm{f}}^*/\lambda = 0.42\) or 4.35 MHz. The torque vanishes at a ratio of 0.71 or 7.4 MHz. This can be explained, if the fiber is modeled as a chain of spheres as shown by Yamahira et al. (2000). The multiplication of the forces with the distance of the sphere from the rotation axis and subsequent summation gives the overall torque. The maximum torque does not appear at a chain length of a quarter wavelength because a decrease of the wavelength means an increase of the frequency which leads to higher forces at the spheres and a higher torque. For a ratio \(l_{\mathrm{f}}^*/\lambda\) higher than 0.5, the forces on the spheres at the end of the chain are changing sign.

The acoustic field also excites resonances of an elastic particle which affects the scattering field. This leads to an increase or decrease of the torque depending on the phase shift between particle vibration and the acoustic background field. For an elongated object like a glass fiber, bending resonance modes occur at lower frequencies than the longitudinal modes. The first, second and third bending modes appear at 1,606, 4,343 and 8,275 kHz, respectively, including the additional mass loading of the surrounding fluid. The corresponding peak in the torque graph can be seen for the first and third bending mode. The second bending mode which is antisymmetric is not excited by the acoustic field at the fiber position in the nodal pressure plane. To ensure that there is no correlation between the frequency at maximum torque and the second bending mode frequency various glass fiber aspect ratios have been modeled.

Fig. 1
figure 1

Results of a FEM simulation for the acoustic radiation torque \(T^{\mathrm{rad}}\) on an elastic fiber as a function of the frequency in logarithmic scales. In the top row the definitions of the 1D standing pressure wave (background field \(p_{\mathrm{b}}\)) and the fiber variables are shown. The red dashed line represents the result for a glass fiber with a density of \(\rho _{\mathrm{f}}=2,600\,\hbox {kg/m}^{3}\). The first and third bending modes of the glass fiber at 1,606 and 8,275 kHz are depicted. Additionally the fiber density (\(\rho _{\mathrm{f}} = 998\,\hbox {kg/m}^{3}\)) is set to the density of water (black line) and this fiber density was increased by 1 and 10 % (gray lines). The Young’s modulus and Poisson’s ratio of the fiber remain constant at \(E_{\mathrm{f}} = 73\,\hbox {GPa}\) and \(\nu _{\mathrm{f}} = 0.18\), respectively (color figure online)

Full size image

2.2.2 Density

The acoustic radiation torque \(T^{\mathrm{rad}}\) as function of the frequency was simulated for various fiber densities \(\rho _{\mathrm{f}}\). The result is plotted also in Fig. 1. A fiber with an equal density as the surrounding water shows a different characteristic in the low frequency range. The torque is increasing quadratically with the frequency. This is in contrast to the glass fiber or a fixed fiber (infinite density). The effect of an increase of the fiber density of 1 and 10 % relative to the water density is plotted in Fig. 1. The torque is constant at low frequencies and successively approaches the response of the fiber with equal density as water. The reason for this effect is unknown and needs to be investigated further.

2.2.3 Angular position

The influence of the angular position \(\alpha\) on the torque is very relevant for rotation and alignment. The torque \(T^{\mathrm{rad}}\) on a glass fiber (standard model parameters) was simulated for various angular positions \(\alpha\) and fiber lengths \(l_{\mathrm{f}}\). The length of the fiber is varied between 50 and 1,200 μm. The results can be seen in Fig. 2.

A fiber which is much shorter than the wavelength shows a perfect sinusoidal characteristic. This is the case for the 50 μm fiber which is more than ten times shorter than the wavelength. The torque has maxima at the positions of 45° and 135°, acting in positive or negative direction. At the positions of 0°, 90° and 180° the torque is zero. Only the position of 90° will be a stable position for a particle which is free to rotate as the torque is always directed toward the 90° position. On the other hand, in the vicinity of the 0° position, the fiber will rotate in clockwise direction for \(\alpha < 0^{\circ }\) and rotate counterclockwise for \(\alpha > 0^{\circ }\). With increasing fiber length to wavelength ratio \((l_{\mathrm{f}}/\lambda )\), the maximum of the torque is shifted toward 90°. There are two aspects which are important for the position of the maximum torque. The effective lever arm which is increasing when approaching 90° and the force magnitude with its maximum in between the pressure node and anti-node. For a fiber length of about \(l_{\mathrm{f}} > 1,000\,\upmu \hbox {m}\) and therefore a ratio \((l_{\mathrm{f}}/\lambda ) > 0.68\) the characteristic changes significantly. The angular positions of 0° and 180° become stable positions and two additional unstable positions where the torque is zero appear. The angle α of the additional unstable zero-crossing depends on the length of the fiber.

Fig. 2
figure 2

The normalized torque \(T^{\mathrm{rad}} / T^{\mathrm{rad}}_{\mathrm{max}}\) as a function of the angular position \(\alpha\) for an elastic glass fiber. The fiber with a diameter \(d_{\mathrm{f}}\) of 15 μm is placed in the pressure node of a 1D standing wave in x-direction. Various fiber length \(l_{\mathrm{f}}\) between 50 and 1,200 μm are depicted. The corresponding fiber length to wavelength ratio \((l_{\mathrm{f}}/\lambda )\) is given in brackets

Full size image

2.2.4 Length and diameter

The influence of the fiber length and diameter on the resulting torque is examined next to analyze the importance of the aspect ratio. In the simulations, the parameters from the standard model are used and only the length \(l_{\mathrm{f}}\) or diameter \(d_{\mathrm{f}}\) are varied. A 2D simulation is chosen in order to allow a large variation of the length and diameter.

The fiber length \(l_{\mathrm{f}}\) was varied from 15 to 1,500 μm. The results can be seen in Fig. 3a. At a fiber length of 15 μm the resulting torque is zero as the object is circular since diameter and length are equal in size. For a range of the fiber length from 50 to 800 μm the curve can be fitted with a power-law function and the proportionality is \(T^{\mathrm{rad}} \propto l_{\mathrm{f}}^{3/2}\). The maximum torque is at a length of 1,020 μm which belongs to a ratio \(l_{\mathrm{f}}^{*} / \lambda\) of about 0.49. A further increase of the fiber length strongly decreases the torque. The peaks in the graph belong to bending modes of the fiber which are excited by the acoustic field.

Fig. 3
figure 3

a Torque per unit depth \({}^{\text {2D}}T^{\mathrm{rad}}\) as a function of the fiber length \(l_{\mathrm{f}}\) for a frequency of 1 MHz plotted in logarithmic scale. The diameter \(d_{\mathrm{f}}\) of the 2D elastic glass fiber is 15 μm. The standard fiber length of 200 μm and the wavelength \(\lambda\) and half a wavelength are depicted with a gray dashed line. b Torque per unit depth \({}^{\text {2D}} T^{\mathrm{rad}}\) as a function of the fiber diameter \(d_{\mathrm{f}}\) plotted in logarithmic scale. The length \(l_{\mathrm{f}}\) of the 2D elastic glass fiber is 200 μm. The standard fiber diameter of 15  μm is depicted with a gray dashed line

Full size image

The influence of the diameter on the torque can be seen in Fig. 3b. The diameter was varied from 0.1 to 200 μm. For thin fibers in the range of 0.1–20 μm the torque per unit depth shows a linear behavior in the logarithmic plot and can be fitted with a power-law function. The torque per unit depth is approximately proportional to the diameter. For a real 3D fiber, the depth of the fiber correlates with the fiber diameter. Therefore the torque dependence on the diameter will be quadratic (\(T^{\mathrm{rad}} \propto d_{\mathrm{f}}^{2}\)). For a diameter of 80 μm the torque reaches a maximum at a ratio \(d_{\mathrm{f}}/l_{\mathrm{f}}\) of 0.4. For larger diameters the torque is decreasing as the fiber becomes more circular than elongated. For a diameter of 200 μm the fiber is circular and the resulting torque is zero.

2.2.5 Position

The acoustic radiation force and torque depend on the position and orientation of the fiber in the acoustic field. For the development of rotation techniques it is of interest to know the equilibrium position and positions of maximum torque. The FEM simulation was used to evaluate the force and torque for a range of positions and fiber orientations. For a glass fiber with \(l_{\mathrm{f}} < \frac{1}{4} \lambda\) in a 1D standing wave, the equilibrium position is at the nodal pressure plane with an orientation perpendicular to the wave propagation. As shown above, a fiber with \(\frac{1}{4} \lambda <l_{\mathrm{f}} < \frac{1}{2} \lambda\) has an additional equilibrium position at the pressure anti-nodes with an orientation of the fiber in wave propagation direction which was shown theoretically and experimentally by Yamahira et al. (2000). For fibers larger than half a wavelength, the force and torque characteristic is complicated and depends strongly on the fiber length.

The behavior of a fiber in a 2D pressure field was simulated as well. The 2D pressure field is a superposition of two orthogonal standing waves with equal amplitude and phase. The conclusion of this simulation is that for all orientations, the center of the fiber is forced to the position where a nodal pressure line is and the velocity term \(\left\langle v^2\right\rangle\) has a maximum. The torque for a fiber in the equilibrium position is always directed toward \(\alpha = 135^{\circ }\) or 315°, which is congruent with the nodal pressure lines. This agrees with the experimental results. Here, only fibers shorter than a quarter wavelength were considered. For longer fibers, the behavior gets even more complex as in a 1D standing wave. Beside the length, also the material properties of the fiber are affecting the behavior where the \(\left\langle p^2\right\rangle\) or \(\left\langle v^2\right\rangle\) field can be dominating. For a fiber with equal density as the surrounding fluid, the velocity field can be neglected and the behavior is only affected by the \(\left\langle p^2\right\rangle\) term.

2.3 Rotational motion of non-spherical particles

In order to describe the rotational motion of a particle, Newton’s second law for rotational motion about a fixed axis can be used. For simplicity, a plane rotation is assumed here. Applying this to the rotation of a fiber with acoustic radiation torque leads to:

$$\begin{aligned} I \frac{\partial \varOmega }{\partial t} + T^{\mathrm{drag}}(\varOmega ) + T^{\mathrm{misc}} = T^{\mathrm{rad}} \end{aligned}$$
(2)

where I is the moment of inertia of the fiber and the fluid portion that is attached to it. The hydrodynamic drag torque \(T^{\mathrm{drag}}(\varOmega )\) is a function of the angular velocity \(\varOmega\), and \(T^{\mathrm{rad}}\) is the driving torque of the rotation. The variable \(T^{\mathrm{misc}}\) represents all unknown effects which are influencing the rotation. These effects might be buoyancy, gravity, friction due to contact with a wall or acoustic streaming. For the further calculations and discussions these effects are neglected. It is assumed that buoyancy and gravity have no influence due to the setup and the symmetric fiber. The influence of the acoustic streaming is difficult to estimate. This phenomenon is presented theoretically in Sadhal (2012), and the typical streaming patterns in acoustic cavities can be found in Wiklund et al. (2012b). It is believed that the resulting torque is zero for a symmetric streaming pattern and the symmetric rotating fiber.

There is no analytical solution available for the drag torque on a rotating fiber. Therefore, a FEM simulation was performed to evaluate the torque and the influence of parameters such as fiber length, diameter and distance to a wall and to provide a model to handle different object shapes and aspect ratios such as the model for the acoustic radiation torque. For the simulation, COMSOL Multiphysics 4.2 has been used. The creeping flow module solves the Stokes equation for the stationary situation. The standard parameters of the simulation are a fiber length \(l_{\mathrm{f}}\) of 200 μm, a diameter \(d_{\mathrm{f}}\) of 15 μm, spherical fiber ends, an angular velocity \(\varOmega\) of \({2\pi }\) rad/s and the fluid properties of water with density \(\rho = 998\,\hbox {kg/m}^{3}\) and dynamic viscosity \(\eta = 1 \times 10^{-3}\,\hbox {Pa\,s}\). A drag torque \(T^{\mathrm{drag}}\) of \(2.464 \times 10^{-14}\, \hbox {Nm}\) has been found. An accurate model was presented by Tirado and Garcia de la Torre (1980) to calculate the rotational friction coefficient of cylinders over a wide range of length to diameter ratios. The model derived by Tirado and Garcia de la Torre (1980) gives a drag torque of \(2.6362 \times 10^{-14}\,\hbox {Nm}\). The difference to the performed simulation is only 6.7 %.

The acoustic radiation torque and the drag torque can be set equal under the following assumptions: The fiber is performing a steady state rotation (angular velocity \(\varOmega\) is constant) where the drag torque is the only resistive torque and the acoustic radiation torque is the only driving torque. Here, only the rotation around the z-axis at the center of the fiber is considered.

As \(T^{\mathrm{drag}} \propto \varOmega\), the maximal angular velocity can be increased by reducing \(T^{\mathrm{drag}}\) or increasing \(T^{\mathrm{rad}}\). The acoustic radiation torque can be strongly increased when the pressure amplitude is increased since \(T^{\mathrm{rad}} \propto P^2_{\mathrm{a}}\). The pressure amplitude can be increased by increasing the applied peak-to-peak voltage of the exciting piezoelectric element: \(P_{\mathrm{a}} \propto U_{\mathrm{pp}}\) as shown in Bruus (2012), if linearity is assumed. The frequency has also an influence on the acoustic radiation torque. When the wavelength is much larger than the fiber length, the influence can be neglected for a glass fiber in water (Fig. 1) as the acoustic radiation torque is nearly constant.

The drag torque can be decreased by increasing the distance to a cavity wall. For a distance to diameter ratio \(h_{\mathrm{f}}/d_{\mathrm{f}} = 4\), the influence of the wall is weak and for a ratio of \(10\) it becomes negligible.

The fiber length \(l_{\mathrm{f}}\) is influencing the acoustic radiation torque as well as the drag torque. The following influence has been found for fibers of a ratio \(l_{\mathrm{f}}/d_{\mathrm{f}} > 3\) and \(l_{\mathrm{f}}^* / \lambda\,<\,0.4: T^{\mathrm{rad}} \propto l_{\mathrm{f}}^{1.5}\) and \(T^{\mathrm{drag}} \propto l_{\mathrm{f}}^{2.6}\). Therefore, a longer fiber has a slower maximal angular velocity.

The fiber diameter is also affecting both torques. For a diameter of 0.1 to 20 μm or a ratio of \(l_{\mathrm{f}}/d_{\mathrm{f}} > 10\) the influence on the acoustic radiation torque is \(T^{\mathrm{rad}} \propto d_{\mathrm{f}}^{2}\). For the drag torque the proportionality is more complicated but it can be assumed that it is less than linear. Therefore, a larger diameter leads to a higher maximal angular velocity.

3 Methods for rotation of non-spherical particles

It is possible to use the acoustic radiation torque not only for alignment but also for the continuous and controlled rotation of objects. Therefore, a varying pressure field with a controllable orientation of the nodal pressure line is necessary. The first rotation technique changes the orientation of a one-dimensional standing wave in a stepwise manner. The other rotation methods are for continuous rotation and alignment at arbitrary orientations using two-dimensional standing waves. Here, a single parameter (amplitude, phase or frequency) is modulated, whereas modulation is understood as the slow variation of a parameter over time, i.e. with a variation in the range of seconds compared to the actuation frequency in the MHz range.

3.1 Changing of propagation direction of one-dimensional standing waves

A non-spherical particle aligns in a one-dimensional standing wave perpendicular to the wave propagation direction due to the acoustic radiation torque. After alignment at the equilibrium position, a further rotation of the object can only be induced by rotating the nodal pressure plane of the 1D standing wave to a new direction and therefore changing the propagation direction of the one-dimensional standing wave. The most intuitive setup for the change of the propagation direction is a movable transducer unit such as presented by  Haake and Dual (2005) for rectilinear motion. Here we focus on a realization with a closed chamber and fixed excitations. For the variation of the propagation direction of a one-dimensional standing wave in a fluidic cavity, the hexagonal configuration is the simplest implementation concerning the excitation and the design. A square chamber is not possible as the change of the propagation direction has to be smaller than 90°. For exactly 90° the torque on the object is zero. This is an unstable equilibrium orientation and the direction of rotation is uncertain. The hexagonal chamber provides parallel walls and a change of the propagation direction of 60°. Chamber designs with a higher number of parallel walls such as an octagonal chamber lead to a change of the propagation direction of 45°. The four necessary actuators require a more complex system, and the interference between different propagation directions increases.

The hexagonal configuration of the chamber allows to setup standing waves with a wave vector oriented along three different directions in the xy plane. An alternating excitation of three actuators allows the complete rotation of an object in 60° steps. Figure 4 shows schematically the three standing waves created by one of the active piezoelectric actuators (marked red). A nodal pressure line is assumed to be in the middle of the parallel chamber walls. A free fiber (black arrow) is moving to the pressure node and aligns perpendicular to the wave propagation direction. The orientation of the object \(\alpha\) equals the orientation of the nodal pressure line. By switching from excitation 1 to excitation 2 or 3 the fiber rotates 60° clockwise or counterclockwise, respectively. For a complete rotation of 360° in clockwise direction the sequence 1–2–3 has to be excited two times. For a counterclockwise rotation the sequence is 1–3–2. The rotation speed for a complete rotation of 360° is defined by the switching frequency between the actuators. The fiber rotation can be stopped only at discrete angular positions defined by the chamber. However, it might be possible to apply a mode switching technique presented by Glynne-Jones et al. (2010) for the arbitrary orientation of particles.

Fig. 4
figure 4

Schematic depiction of the alternating excitation of three actuators in combination with a hexagonal chamber for rotation of non-spherical objects. a The active piezoelectric actuator 1 excites a 1D standing wave in x-direction with a pressure node in the middle of the chamber. A fiber (black arrow) will align with an angular position \(\alpha = 90^{\circ }\). b By switching to actuator 2 the wave propagation direction changes by 60° and the fiber aligns perpendicular to the new direction. c The actuator 3 aligns the fiber at an orientation of \(\alpha = -30^{\circ }\) and the fiber has done a rotation of 120° compared to the orientation when actuator 1 is active

Full size image

The maximal length of an object is limited by the wavelength and the angle for the change of the propagation direction and can be determined with the finite element simulation of the acoustic radiation torque. A maximal fiber length to wavelength ratio (\(l_{\mathrm{f}} / \lambda\)) of 0.79 was determined. Figure 2 illustrates also the length limit for this rotation technique. The fiber with a length of 1,200 μm (\(l_{\mathrm{f}} / \lambda = 0.81\)) has a negative torque at \(\alpha = 30^{\circ }\) and is therefore not rotating to the orientation of the nodal pressure line at 90°. If the aspect ratio of the fiber changes strongly, the length limit is changing as well.

3.2 Amplitude modulation

The basis of this method is the superposition of two orthogonal ultrasonic modes excited by two sources. With the slow variation of the amplitude over time, the nodal pressure line and therefore the angular position of an object can be changed. The basic system consists of a square chamber with one excitation for a standing wave in x-direction and another excitation for a standing wave in y-direction. The details of this method are presented by the same authors in Schwarz et al. (2013). The resulting pressure field has been used to compare different ways to achieve rotation and to evaluate the characteristics of different excitations.

3.3 Phase modulation

In a cavity, a 2D mode can be expressed as \((m,n)\), where the first variable stands for the number of nodes of the pressure wave in x-direction and the second variable for the y-direction. In a perfect square chamber with rigid walls, the modes \((m,n)\) and \((n,m)\) exist at the exact same frequency. All degenerated modes, meaning the superposition of both modes for various amplitudes, are also at the same frequency. Due to the slightly compliant walls and therefore interaction of the structure and the fluid, the modes can be slightly separated by a small frequency difference. Due to the damping in the system, both the resonance peaks corresponding to both modes are overlapping. The phase modulation of two degenerated ultrasonic standing modes leads to a local rotation of the pressure field. Two degenerated modes which are slightly separated in frequency are needed to induce the rotation.

For a better understanding of this rotation method and to confirm that the degenerated and separated modes are responsible for this rotation, a simple 2D finite element model is developed. The model consists of a square acoustic domain with a length of 1 mm, surrounded by a square solid domain with edge length 1.5 mm. Figure 5a shows the model. The material of the acoustic domain is water with the following properties: density of \(998\,\hbox {kg/m}^{3}\) and speed of sound of \(1,481\,[1+ i/(1,000)]\,\hbox {ms}^{-1}\) including damping. The material of the solid frame is steel with a Young’s modulus of 190 GPa, a Poisson’s ratio of 0.25 and a density of 7,850 \(\hbox {kg/m}^{3}\). The fluid structure interaction between the steel frame and the fluidic cavity is implemented. The actuation of the model is done with a prescribed displacement \(\pm u_0\) in x-direction and \(\pm v_0 \hbox {e}^{{\mathrm{i}}\varDelta \varphi }\) in y-direction including a phase shift \(\varDelta \varphi\), as shown in Fig. 5a.

Fig. 5
figure 5

a Simulation of the rotation due to phase modulation with a 2D model of a cavity, filled with water and surrounded by a steel frame. The excitation is done by a prescribed displacement in the x- and y-direction at the outer side walls of the steel frame. b Modal analysis of the model showing the two slightly separated modes. c Absolute pressure \(\left| p\right|\) for a time harmonic analysis at a constant excitation frequency of 1,470.35 kHz and for different phase values \(\varDelta \varphi\). The white arrow represents the equilibrium orientation of a fiber in the pressure field

Full size image

The amplitude for the prescribed displacement is 1 nm and equal for the x- and y-direction. A modal analysis of the model is shown in Fig. 5b. There are two slightly separated modes at 1,468.8 and 1,471.9 kHz. Even though the system is a perfect square, there are two separated modes due to the compliance of the steel frame. The corner regions of the steel frame are stiffer than the sides. The mode with pressure anti-nodes at the side walls is therefore at a lower frequency. The absolute pressure \(\left| p\right|\) for a time harmonic analysis with different phase values \(\varDelta \varphi\) is shown in Fig. 5c. The excitation frequency is 1,470.35 kHz which is exactly half way between the two modes. The nodal pressure line performs a local rotation if the phase is varied. There exist four rotation spots in a domain \(\lambda _x \times \lambda _y\) whereas two spots rotate clockwise and the other two counterclockwise. This is identical to the amplitude modulation

For a uniform rotation of the nodal pressure line, the phase shift \(\varDelta \varphi (t)\) has to be varied linearly over time. The variation of the phase shift is much slower (in the order of seconds) compared to the periodic time of the excitation (in the order of μs).

3.4 Frequency modulation

Frequency modulation leads to the local rotation of the pressure field if two slightly separated modes exist. This method is related to the rotation with phase modulation as two modes are needed. For the rotation with frequency modulation, the modes can be one-dimensional compared to the phase modulation were degenerated modes are necessary. This method relies strongly on the bandwidth of the resonance modes and the frequency difference \(\varDelta f\) between them which is typically in the kHz range. One method to enforce a separation of two modes is a small asymmetry. A nearly square chamber where one edge length differs slightly from the other length leads to such an asymmetry.

A simple finite element model is presented here to describe this rotation technique. The model consists of only a 3D fluidic cavity, modeled with the acoustics module of COMSOL 4.2 and is depicted in Fig. 6a. The edge lengths are \(L_x = 1\,{\hbox {mm}}, L_y = 1.005\,{\hbox {mm}}\) and \(L_z = 0.2\,{\hbox {mm}}\). The cavity is surrounded by sound-hard walls and the excitation is implemented with a normal acceleration at the bottom of the cavity, shown as a red triangle in Fig. 6a. The place and shape of the excitation is arbitrary. Important, however, is that all modes shown in Fig. 6c can be excited, therefore the excitation should be asymmetric. The material of the acoustic domain is water with the following properties: density of \(998\,\hbox {kg/m}^{3}\) and speed of sound of \(1,481\,[1+ i/(2Q)]\,\hbox {m/s}\), where Q is the Q-factor (Gröschl 1998).

Fig. 6
figure 6

a Simulation of the rotation due to frequency modulation with a 3D model of a fluidic cavity. The cavity is surrounded by hard walls and the excitation is implemented with a normal acceleration at the bottom of the cavity shown as a red triangle. b Result of a modal analysis showing the modes with one wavelength in the y-direction and one wavelength in the x-direction at different frequencies. c The absolute pressure field \(\left| p\right|\) inside the cavity is plotted for five characteristic frequencies for a Q-factor of 500. The white arrow represents the equilibrium orientation of a non-spherical object in the pressure field (color figure online)

Full size image

The result of a modal analysis is shown in Fig. 6b. The two one-dimensional modes occur at slightly different frequencies. The mode in y-direction is at a lower frequency as the edge length is chosen to be slightly larger. The larger the length difference of \(L_x\) and \(L_y\), the larger is the frequency difference.

For a Q-factor of 500 the modes are overlapping. The pressure field for characteristic frequencies is shown in Fig. 6c. The transition of the different patterns can be explained with the phase difference between both modes. At a frequency of 1,470 kHz, both modes are weakly excited and in phase, leading to a diamond shaped pattern. At 1,473.6 kHz the mode in y-direction has a high amplitude and is dominating. In between both modes at 1,477.3 kHz, both modes are weakly excited and the first mode has a phase shift of nearly 180° compared to the second mode, leading to the cross shaped pattern. For a frequency of 1,481 kHz the mode in x-direction has a high amplitude and is dominating. At a frequency of 1,485 kHz both modes are weakly excited and are in phase, again leading to the diamond shaped pattern. With a continuous frequency sweep from 1,470 to 1,485 kHz, the nodal pressure line is locally rotating. There exist four rotation spots in a domain \(\lambda _x \times \lambda _y\) where two spots are performing a clockwise rotation and the other two a counterclockwise rotation. This is identical to the amplitude and phase modulation techniques presented above. One frequency modulation (sweep from start frequency to stop frequency) would lead to a rotation of 180°. The direction of rotation depends on the direction of the frequency sweep and the rotational velocity is defined by the time, necessary for two sweeps.

Important for the rotation is the interplay between the frequency difference \(\varDelta f\) and the Q-factor. For a high Q-factor of 5,000 both modes will be completely separated with virtually no overlap. For a sweep in the frequency range of 1,470–1,485 kHz, only the two pure modes are visible with very weak pressure amplitudes for frequencies in between them. If the Q-factor is too low (Q = 200), the overlap of the peaks increases and the resulting pressure pattern is not suitable for particle rotation. The phase difference \(\theta\) at the frequency in between both modes (1,477.3 kHz) has to be >90° to ensure a rotation and θ has to be <180° to ensure the overlapping of the two separated modes and a sufficient pressure amplitude in between the two modes. The optimum has been found for a phase difference \(\theta\) of 135°.

This rotation technique leads to a varying rotation speed as the amplitude is changing during the sweep. Nevertheless, the excitation is simple compared to the other methods because only one excitation is needed and a frequency sweep is very simple to implement. On the other hand, it is difficult to precisely control the Q-factor which is very important for this rotation technique as it defines the overlap of the two resonances.

4 Experimental results

Three different methods, the stepwise change of the propagation direction, the amplitude modulation and the phase modulation have been tested experimentally with microdevices, operating at frequencies in the MHz range. Particle clumps with elliptical shape and microglass fibers have been used as rotation objects. For the frequency modulation it was not possible to obtain experimental data as none of the designed devices supplied a sufficient interplay between the frequency difference \(\varDelta f\) and the Q-factor.

4.1 Changing of the propagation direction

The rotation was realized with a hexagonal chamber and the device is depicted in Fig. 7a. It is based on the microdevices presented in Neild et al. (2007), Oberti et al. (2007). The main changes concern the fluidic chamber and the actuation. The fluidic chamber is a hexagon with a width of 3 mm. The actuation consists of three individual piezoelectric elements with an electrode area of 2.8 mm \(\times\) 0.7 mm and a thickness of 0.5 mm. The transducers are aligned with the fluidic chamber walls and fixed on the back side of the silicon plate.

Fig. 7
figure 7

a Exploded view of the device with the hexagonal chamber etched into silicon and three separated piezoelectric elements on the back side for actuation. b Rotation of a glass fiber (\(l_{\mathrm{f}}=205 \, \upmu \hbox {m}, d_{\mathrm{f}}=15\, \upmu \hbox {m}\)) in a hexagonal chamber at a frequency of 1,730 kHz. The excitation is switched from transducer 1 to transducer 2 and to transducer 3. The red line depicts the actuated piezoelectric element (color figure online)

Full size image

The width between parallel walls in the fluidic chamber is identical, therefore the resonance frequencies for the standing waves are very similar for all three directions. An actuation of a standing wave in only one direction is possible by selectively actuating one of the piezoelectric transducers. The three piezoelectric transducers are connected to one signal generator (DS345, Stanford Research Systems) and one amplifier (2100 RF power amplifier, ENI) by a switch with a predefined actuation sequence and a tunable switching frequency. The disadvantage of this simple actuation setup is that all transducers are actuated with the same frequency. Due to manufacturing inaccuracy, the perfect actuation frequency deviates for each transducer within 30 kHz. Therefore, a compromise frequency has to be used, where all directions work acceptably. However, this can lead to deviations in the angular alignment of the object because the lines of zero pressure are slightly bent.

The rotation of a glass fiber with a length \(l_{\mathrm{f}}\) of 205  μm and a diameter \(d_{\mathrm{f}}\) of 15 μm suspended in DI-water was setup. The mode with seven nodal pressure lines at a frequency of 1,730 kHz and an excitation voltage \(V_{\mathrm{rms}}\) of 18 V was used. A sequence of the clockwise rotation is shown in Fig. 7b. Each frame represents the excitation of one of the three transducers.

A plot of the angular position \(\alpha\) of the fiber versus time is shown in Fig. 8. Each frame of the video is represented by a black dot. The connecting gray line is for better illustration. The discrete steps of the curve belong to the correspondent actuator noted on the right side of the graph. The plot is for two complete rotations of the glass fiber. The time for one rotation is 6.35 s and the average rotation speed is therefore 9.45 rpm. This corresponds to a switching frequency between the actuators of 0.945 Hz. The instantaneous rotation speed at the 60° steps is much larger than the average rotation speed. The rotation was too fast to be captured properly by the video with a frame rate of 18 frames/s. The 60° rotation is completed in between two frames. Therefore, the instantaneous rotational speed is at least 180 rpm.

Fig. 8
figure 8

Angular orientation \(\alpha\) of a glass fiber in a hexagonal chamber rotating in clockwise direction. Each Frame of the video (18 frames/s) is represented by a black dot. The connecting gray line is for better illustration. The discrete steps of the curve belong to the actuator noted on the right side of the graph. The gray dashed lines mark the theoretical angular position for each actuator

Full size image

The maximal average rotational speed of the fiber for this setup was determined to be approximately 34 rpm. The rotational speed is limited by the drag torque which balances with the acoustic radiation torque. In addition to the drag torque, adhesion and friction influences the maximal rotation speed. The fiber density is higher than the density of the surrounding fluid, so the fiber is very likely partially in contact with the cavity bottom. The friction could be avoided by acoustic levitation of the fiber or adjustment of the density difference between fluid and fiber.

The time \(t_{\mathrm{step}}\) the fiber needs to rotate by one 60° step can be used to evaluate the pressure amplitude or the maximal instantaneous rotational speed. The influence of friction, gravitation, etc. are neglected to simplify matters. The drag torque \(T^{\mathrm{drag}}(\varOmega ) = \tilde{D} \varOmega\) depends linearly on the angular velocity \(\varOmega\) with \(\varOmega = {\mathrm{d}} \alpha / {\mathrm{d}}t\) and \(\tilde{D} = 4.121 \times 10^{-15}\,{\hbox {Nm/(rad/s)}}\) being the drag torque coefficient. The pressure amplitude \(P_{\mathrm{a}}\) gives the maximum acoustic radiation torque \(\hat{T}^{\mathrm{rad}} = P_{\mathrm{a}}^2 \cdot 2.052 \times 10^{-24}\,{\hbox {Nm/Pa}{^2}}\). Assuming a standing wave in x-direction, the acoustic radiation torque is \(T^{\mathrm{rad}}(\alpha ) = \hat{T}^{\mathrm{rad}} \sin (2 \alpha )\) which can be seen in Fig. 2. In a first step the moment of inertia is neglected and the resulting differential equation

$$\begin{aligned} \tilde{D} \frac{{\mathrm{d}}\alpha }{{\mathrm{d}}t} = \hat{T}^{\mathrm{rad}} \sin (2 \alpha ) \end{aligned}$$
(3)

can be solved by separation of the variables. The solution is:

$$\begin{aligned} \alpha (t) = \arctan \left( \tan \left( \alpha (0) \right) {\mathrm exp} \left[ \frac{2 {\hat{T}}^{\mathrm{rad}} t}{\tilde{D}} \right] \right) \end{aligned}$$
(4)

where \(\alpha (0)\) is the start angular position of the fiber at \(t=0\) which is 30° in this case.

The step time can be calculated as a function of \(\hat{T}^{\mathrm{rad}}\) or the pressure \(P_{\mathrm{a}}\) by replacing \(\alpha (t)\) by the final orientation of the fiber at \(t = t_{\mathrm{step}}\). The results for various \(\alpha\) close to 90° are evaluated. The angular position of the fiber after \(t = t_{\mathrm{step}}\) can only be estimated because the exact angular orientation of the nodal pressure line is unknown. Therefore an \(\alpha\) between 80° and 89° has been used for the estimation of the pressure. It is expected that for \(t_{\mathrm{step}} = 0.056\,{\hbox {s}}\) (18 frames/s) the pressure \(P_{\mathrm{a}}\) is in the range of 0.2–0.3 MPa. This is in the same range as the pressure estimated in square chambers, used for amplitude modulation experiments. A more accurate prediction would be possible with a high-speed camera where the angular position of the rotating fiber can be resolved during the switching process. This would allow the fitting of the curve \(\alpha (t)\) to the experimental data.

The angular velocity is not constant during the switching process. A peak instantaneous angular velocity of 31.1 rad/s or 297 rpm was determined using Eq. 4. The maximum acoustic radiation torque was \(\hat{T}^{\mathrm{rad}} = 1.28 \times 10^{-13}\,{\hbox {Nm}}\) for an assumed pressure \(P_{\mathrm{a}}\) of 0.25 MPa.

Due to the high accelerations, the full differential equation with inertial terms was solved numerically to ensure that the inertial terms can be neglected for the above situation.

4.2 Amplitude modulation

Experiments have been performed in microdevices with square chambers using copolymer particles or a microglass fiber. A continuous rotation was successfully demonstrated and the method allowed to stop the rotation at arbitrary angular positions. The details of the device and the experiment are presented by the same authors in Schwarz et al. (2013).

Moreover, the simulation results for the acoustic radiation torque will be applied to the experimental data. In Fig. 9 the rotation of a microglass fiber (diameter of 15 μm and length of 210 μm) is depicted. The angular position of the glass fiber is plotted over time for two rotation cycles (720°). The black dots represent the angle α of the fiber for each frame in the video. The gray line represents the expected average angular position for the rotation time \(T_{\mathrm{M}} = 1.67\,{\hbox {s}}\) and a corresponding rotational speed of 36 rpm. The gray line accentuates the variation in the rotational speed. The reasons for the deviation are unbalanced amplitudes, a not perfectly excited mode and the variation of the total pressure due to the linear amplitude modulation.

Fig. 9
figure 9

Rotation of a glass fiber with a length of 210 μm and a diameter of 15 μm using amplitude modulation of two ultrasonic modes. The actuation frequency was 1,085 kHz and the maximum applied voltage \(V_{\mathrm{rms}}\) was 20 V. Angular position \(\alpha\) of the fiber plotted over time for two complete rotations (720°). The black dots represent the angle of the fiber for each frame in the video. The gray line is the average expected angular position at a rotation speed of 36 rpm (rotation time \(T_{\mathrm{M}} = 1.67\,{\hbox {s}}\))

Full size image

The rotational motion of the fiber can be analyzed with the considerations of Sect. 2.3. When the angular orientation of the fiber \(\alpha\) is equal to the nodal pressure line \(\beta\) the acoustic radiation torque on the fiber will be zero. The orientation of the nodal pressure line is changing due to the amplitude modulation. The drag torque, due to the movement in the viscous fluid, arises because of the rotation of the fiber which follows the nodal pressure line. The drag torque is proportional to the angular velocity of the fiber. The acoustic radiation torque is balanced with the drag torque. For a fiber rotation with the maximum angular velocity, the maximal acoustic radiation torque arises on the fiber at an angle difference between \(\beta\) and \(\alpha\) of 45°. For a very slow rotation the angle difference is nearly zero. For rotations in between the maximum angular velocity and no rotation the angle difference is in between 45° and 0°.

The simulation of the acoustic radiation torque allows the additional estimation of the pressure amplitude during the experiment. The increase of the average rotational velocity was possible until about 40 rpm. In the experiment instantaneous velocities of 150–200 rpm were reached during parts of one rotation due to unbalanced amplitudes.

The pressure amplitude in the cavity can be roughly estimated with the experimentally determined angular velocity. The drag torque of a rotating fiber with the same size as in the experiment and for an angular velocity \(\varOmega\) of \(4.19\,{\hbox {rad/s}}\) (40 rpm) has been modeled. The drag torque \(T^{\mathrm{drag}}\) is \(1.836 \times 10^{-14}\,\)Nm. The acoustic radiation torque has been determined for the frequency of 1085 kHz and the mode with \(m = 4\) and \(n = 2\). The position of the fiber was the same as in the experiment, and an orientation of 45° was implemented to reach the maximal torque. The acoustic radiation torque as function of the pressure amplitude is \(T^{\mathrm{rad}}(P_{\mathrm{a}}) = P_{\mathrm{a}}^{2} \cdot {5.844 \times 10^{-25}} \, {\hbox {Nm}}\). Therefore, the pressure amplitude \(P_{\mathrm{a}}\) is 0.18 MPa. The influence of the cavity bottom was neglected. Assuming a wall to fiber distance of 5 μm, the drag torque increases to \(T^{\mathrm{drag}} = 3.977 \times 10^{-14}\,{\hbox {Nm}}\) giving a pressure of 0.26 MPa. The determination of an exact value is not possible as the distance to the cavity bottom, and the influence of possible contact are unknown. The higher instantaneous velocities of 150–200 rpm during parts of the rotation allow to assume that the pressure amplitude is higher than calculated above. For these instantaneous velocities, a pressure amplitude of 0.34–0.4 MPa was determined.

Of interest is the theoretical maximal rotational velocity for a glass fiber as used in the experiments. The following assumptions are used. A pressure amplitude of 0.5 MPa is reasonable for a microodevice d(Barnkob et al. 2010). The frequency is 1 MHz, and a one-dimensional mode is excited. The fiber is assumed to float in the middle of the cavity without any influence of the walls or other particles. The simulated radiation torque \(T^{\mathrm{rad}}\) is \(3.57 \times 10^{-13}\) Nm. The drag torque as function of the angular velocity is \(T^{\mathrm{drag}}(\varOmega ) = \varOmega \cdot {4.382 \times 10^{-15}} \, \hbox {Nm}\). This results in a theoretical maximal angular velocity \(\varOmega\) of 82 rad/s and therefore a rotational speed of 780 rpm. An improvement of the device toward the excitation of a higher pressure amplitude and free floating fiber can result in a very high rotational speed as the influence of the pressure amplitude is quadratic.

4.3 Phase modulation

The experiments have been performed using the microdevice presented in Schwarz et al. (2013). For the characterization of the device behavior, first copolymer particles have been used. This allows the observation of the whole cavity by using a high amount of particles. For the excitation, two possibilities exist. One is the method described in the theory section (Sect. 3.3), where two electrodes are excited with the exact same frequency and the phase of one signal \(\varDelta \varphi (t)\) is varied slowly over time. The direction of the rotation is defined by the sign of the phase shift and the rotational velocity by the time \(T_{\mathrm{M}}\) for two modulations of the phase \(\varDelta \varphi\) from 0 to \(2\pi\).

Another method is the excitation with two slightly different frequencies \(f_1\) and \(f_2\). A slight frequency difference between both signals (\(\varDelta f \approx 1 {Hz}\)) will lead to a slow linearly varying phase shift over time between both signals. The difference \(f_2 - f_1 = \varDelta f\) between both frequencies determines the rotational speed. The modulation time \(T_{\mathrm{M}}\) for an object rotation of 360° is defined as \(T_{\mathrm{M}} = 2 / \left| \varDelta f \right|\). The direction of rotation is depending on which of the two frequencies is larger.

The rotation of particle clumps is shown in Fig. 10, a rotation of 180° is depicted.

Fig. 10
figure 10

A 180° rotation of 36 particle clumps formed out of 17 μm copolymer particles with phase modulation. The excitation frequency for electrode 1 was \(f_1 = 1,434\,{\hbox {kHz}}\) and for electrode 2 \(f_2 = 1,434\,{\hbox {kHz}} + 1.12\,{\hbox {Hz}}\). The excitation voltage \(V_{\mathrm{rms}}\) was 18 V. A domain of \(\lambda _x \times \lambda _y\) is highlighted with a white square for better observation of the changing pattern shapes

Full size image

The square fluidic cavity of the microdevice was filled with copolymer particles with a diameter of 17 μm. The excitation frequency for electrode 1 was \(f_1 = 1,434\,{\hbox {kHz}}\) and \(f_2 = 1,434\,{\hbox {kHz}} + \varDelta f\) for electrode 2. The frequency matches to 3 wavelengths in the x- and y-direction of the cavity. This leads to a formation of 36 clumps. A domain of \(\lambda _x \times \lambda _y\) is highlighted with a white square to show the change of the pattern from (a) to (e). The different patterns are as follows: (a) diamond shape, (b) lines perpendicular to x-direction, (c) cross pattern, (d) lines perpendicular to y-direction and (e) diamond shape. The rotation of the clumps is a continuous rotation but not fully uniform as can be seen from the times given for every image of Fig. 10. The \(\varDelta f\) was approximately 1.12 Hz which leads to a rotation time \(T_{\mathrm{M}}\) of 1.79 s and therefore an average rotational speed of 33 rpm. In contrast to the amplitude modulation, the particle clumps are separated and not merging during the rotation.

The rotational manipulation with phase modulation was also performed with glass fibers and is shown in Fig. 11. In the fluidic cavity filled with DI-water, there is fiber A and fiber B rotating in different locations. Fiber A consists of two glass fibers sticking together with a total length of 315 μm. The fiber B is a single glass fiber with a length of 215 μm. The actuation frequencies were \(f_1= 1,158\,{\hbox {kHz}}\) and \(f_2 = 1,158\,{\hbox {kHz}} + 0.55\,{\hbox {Hz}}\) leading to a rotation time of \(T_{\mathrm {M}} = 3.64\,{\hbox {s}}\) per 360° rotation and a rotational speed of 16.5 rpm. The excitation frequency corresponds to 2.5 wavelengths in the x- and y-direction. In Fig. 11, the orientation \(\alpha\) of both fibers is plotted. The fibers both rotate in clockwise direction. Beside the average rotational velocity of 16 rpm, instantaneous angular velocities of 82 rpm can be found. The rotation is not uniform due to unbalanced amplitudes of the modes and possible contact with the cavity floor.

Fig. 11
figure 11

Rotational manipulation of two glass fibers with phase modulation. Fiber A (black cross) consists of two glass fibers sticking together and has a total length of 315 μm. The fiber B (gray circle) is a single glass fiber with a length of 215 μm. The actuation frequencies are \(f_1= 1,158\, {\hbox {kHz}}\) at electrode 1 and \(f_2 = 1158\,{\hbox {kHz}} + 0.55\,{\hbox {Hz}}\) at electrode 2. The excitation voltage \(V_{\mathrm{rms}}\) was 20 V. The rotation time \(T_{\mathrm{M}}\) is 3.64 s for a 360° rotation. The plot is showing the orientation \(\alpha\) of the glass fibers plotted as function of time

Full size image

The maximum observed average rotational speed of a fiber was 30 rpm. The maximum average angular velocity depends on the applied acoustic radiation torque and is limited by the drag torque and friction force of the fiber at the cavity bottom. A detailed discussion can be found in Sect. 2.3. The maximum rotational speed is comparable with the amplitude modulation where an average rotational speed of 40 rpm was observed. It is assumed that the pressure is in the same range as for the amplitude modulation. The cavity and excitation are identical, and the rotation techniques are comparable as well.

5 Conclusion

The rotation of particles by means of the acoustic radiation torque arising from ultrasonic standing waves was investigated. A finite element simulation of the acoustic radiation torque was used to evaluate the behavior of a microglass fiber. The acoustic radiation torque on a glass fiber stays nearly constant at low frequencies (kHz range) for wavelengths 10 times larger than the fiber. This is in contrast to the acoustic radiation force which is proportional to the frequency. The equilibrium position and orientation of a fiber, shorter than a quarter wavelength is at the pressure nodes, aligned perpendicular to the wave propagation direction. For larger fibers, additional equilibrium positions occur. For fibers that are short compared to the acoustic wavelength, the torque varies approximately sinusoidally as function of the orientation difference between the fiber and the nodal pressure line.

The first presented rotation method using the acoustic radiation torque is based on changing the propagation direction of one-dimensional standing waves in a stepwise manner. A hexagonal cavity design was used in combination with three piezoelectric transducers to change the orientation of the standing wave in 60° steps. The rotating object stops only at discrete angular positions, defined by the cavity. This rotation method is less complicated due to 1D standing waves but restricted to discrete rotation steps.

The rotation with amplitude, phase and frequency modulation is similar in the characteristic of the resulting pressure field. The amplitude modulation offers the best control for a uniform rotation, but besides a signal generator, additional equipment is necessary. The mechanism behind the phase modulation is more complicated due to the separated degenerated modes. The excitation is simple but achieving a uniform rotation is difficult. As an advantage, the merging of close by particle clumps can be avoided during the rotation. This can be useful for the separated mixing of particle clusters in one chamber. The frequency modulation convinced with only one excitation and a simple frequency sweep but the Q-factor needs to be precisely controlled. All methods were appropriate for the arbitrary alignment of elongated objects.

The acoustic radiation torque and the pressure amplitude were estimated by comparison with the drag torque. The calculation of both variables from the amplitude modulation experiments led to 0.18 MPa and \(1.84 \times 10^{-14}\) Nm, respectively. For the instantaneous velocities of up to 200 rpm, a maximal pressure amplitude of 0.4 MPa was determined with a corresponding maximal acoustic radiation torque of \(9.4 \times 10^{-14}\) Nm. For a reasonable pressure amplitude of 0.5 MPa, a perfect mode and a levitated fiber, a radiation torque of \(3.6 \times 10^{-13}\) Nm and a rotational speed of 780 rpm should be possible. The quadratic influence of the pressure leads to this strong increase.